Toroidal Vortices of Energy in Tightly Focused Second-Order Cylindrical Vector Beams
Abstract
:1. Introduction
2. Methods
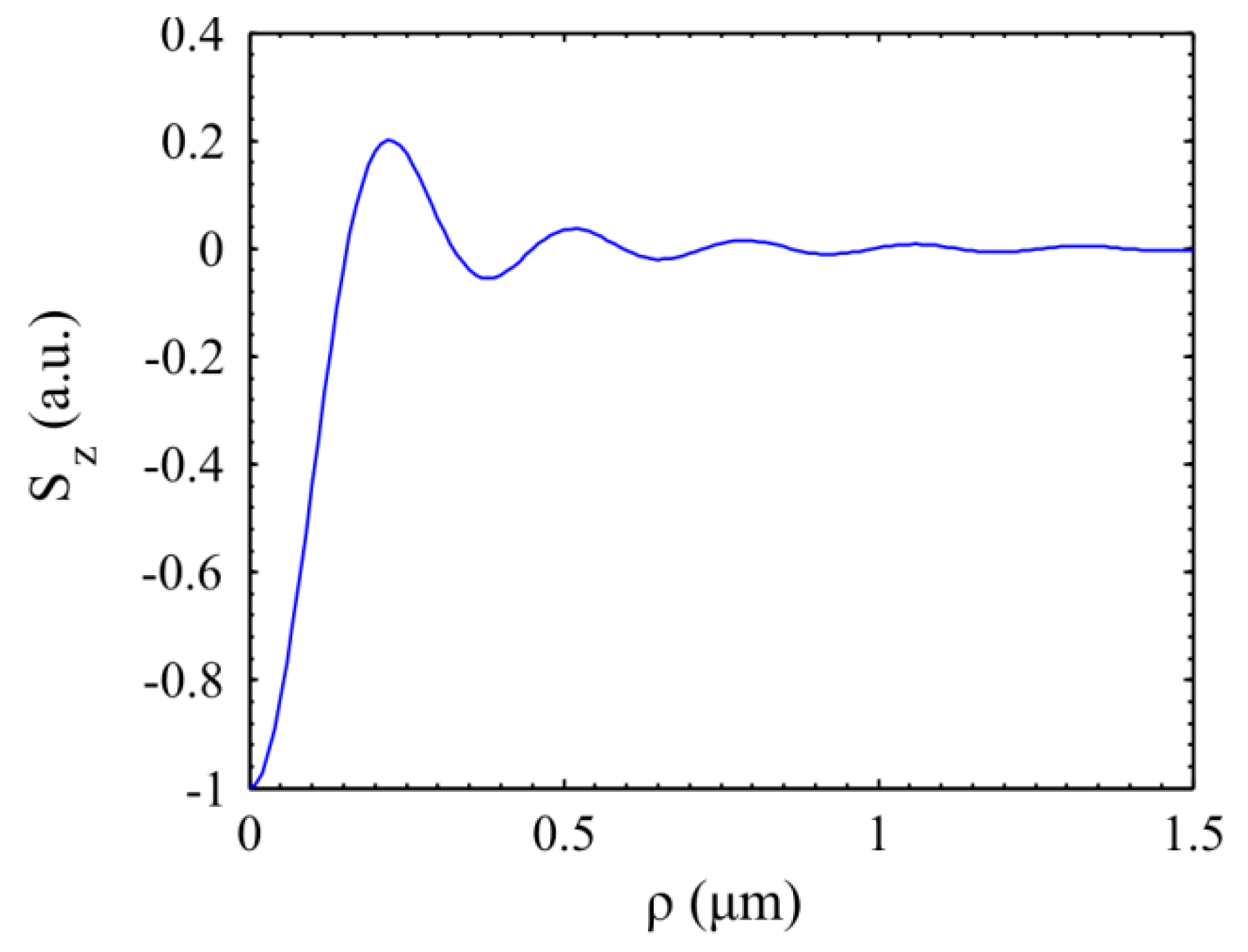
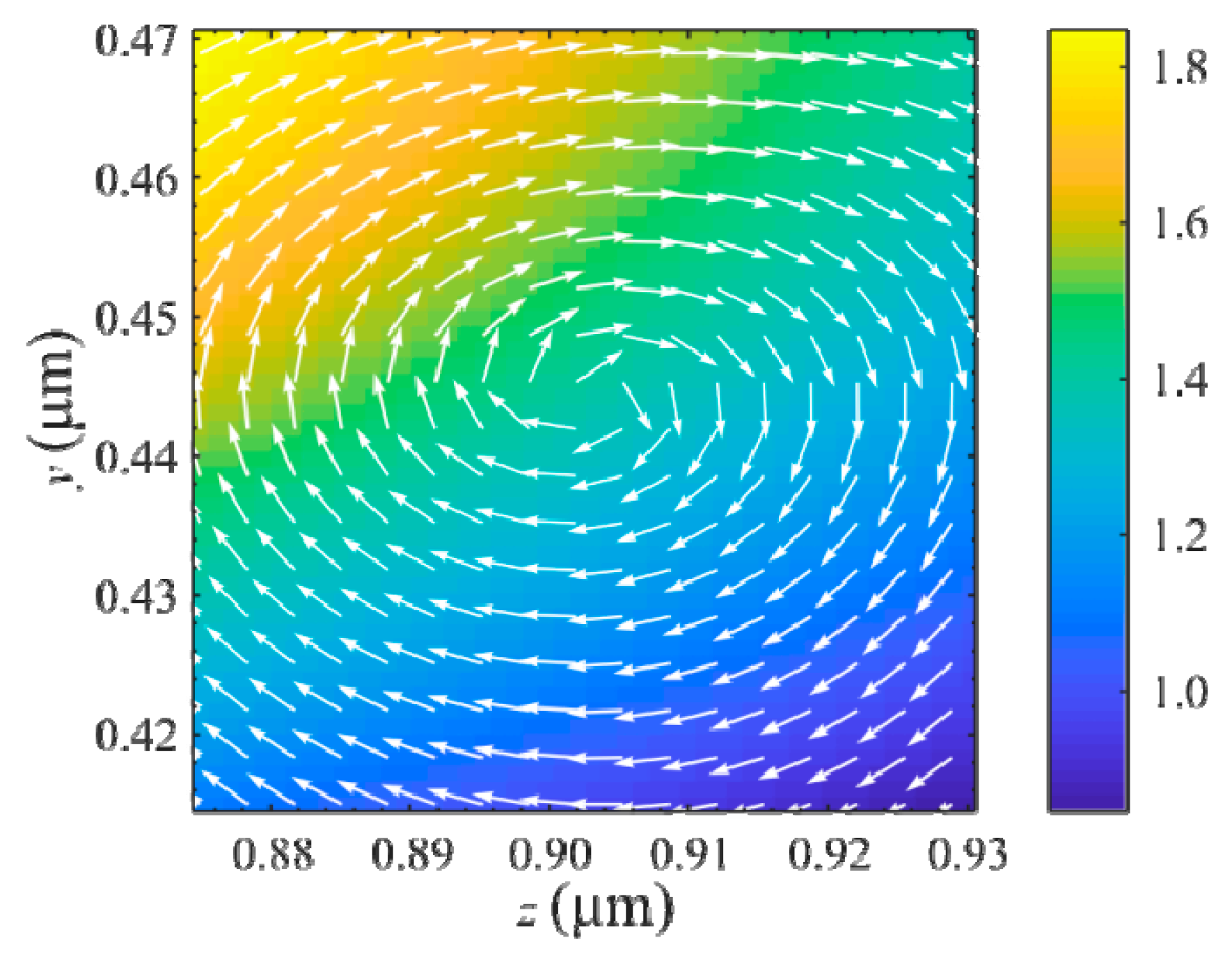
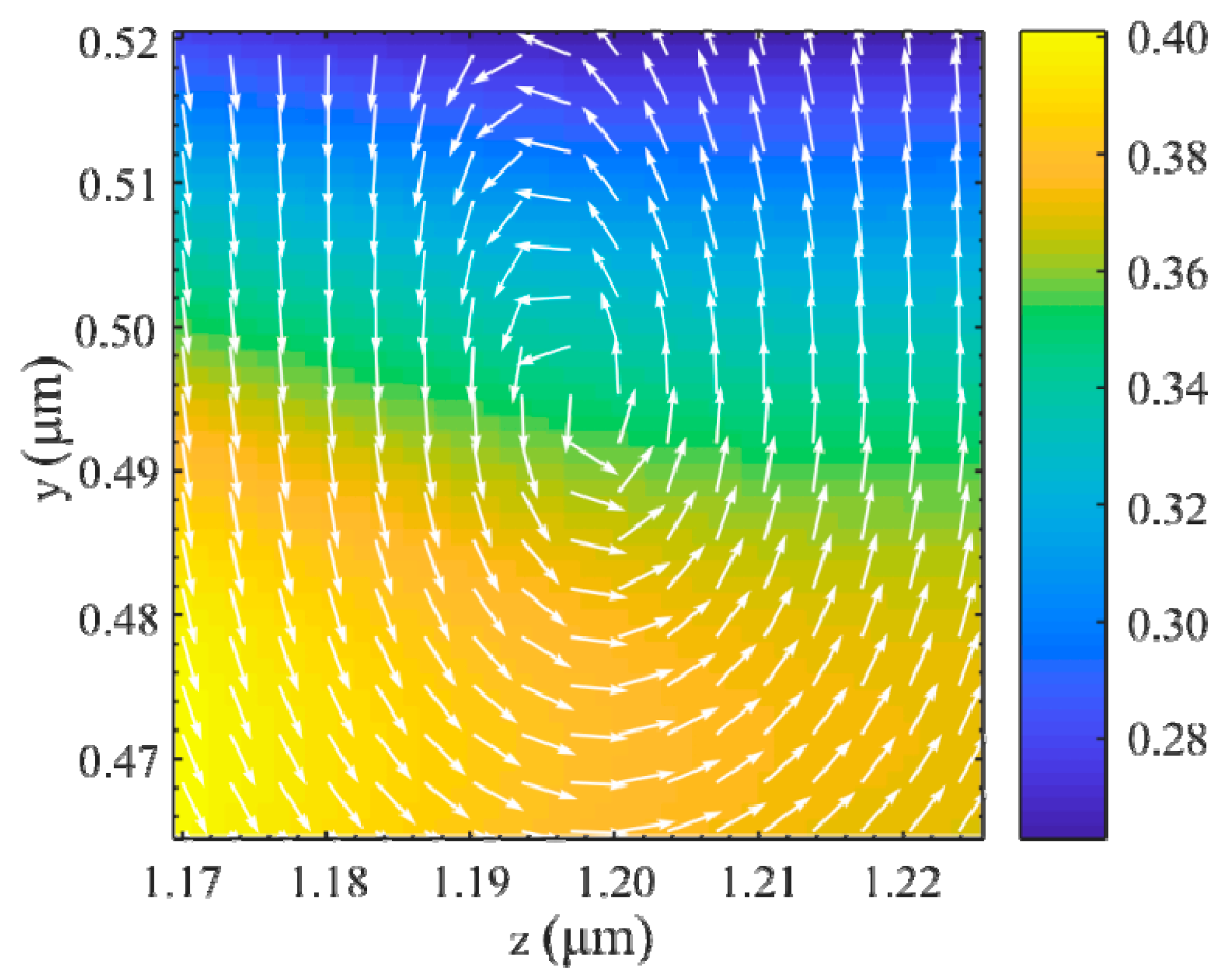
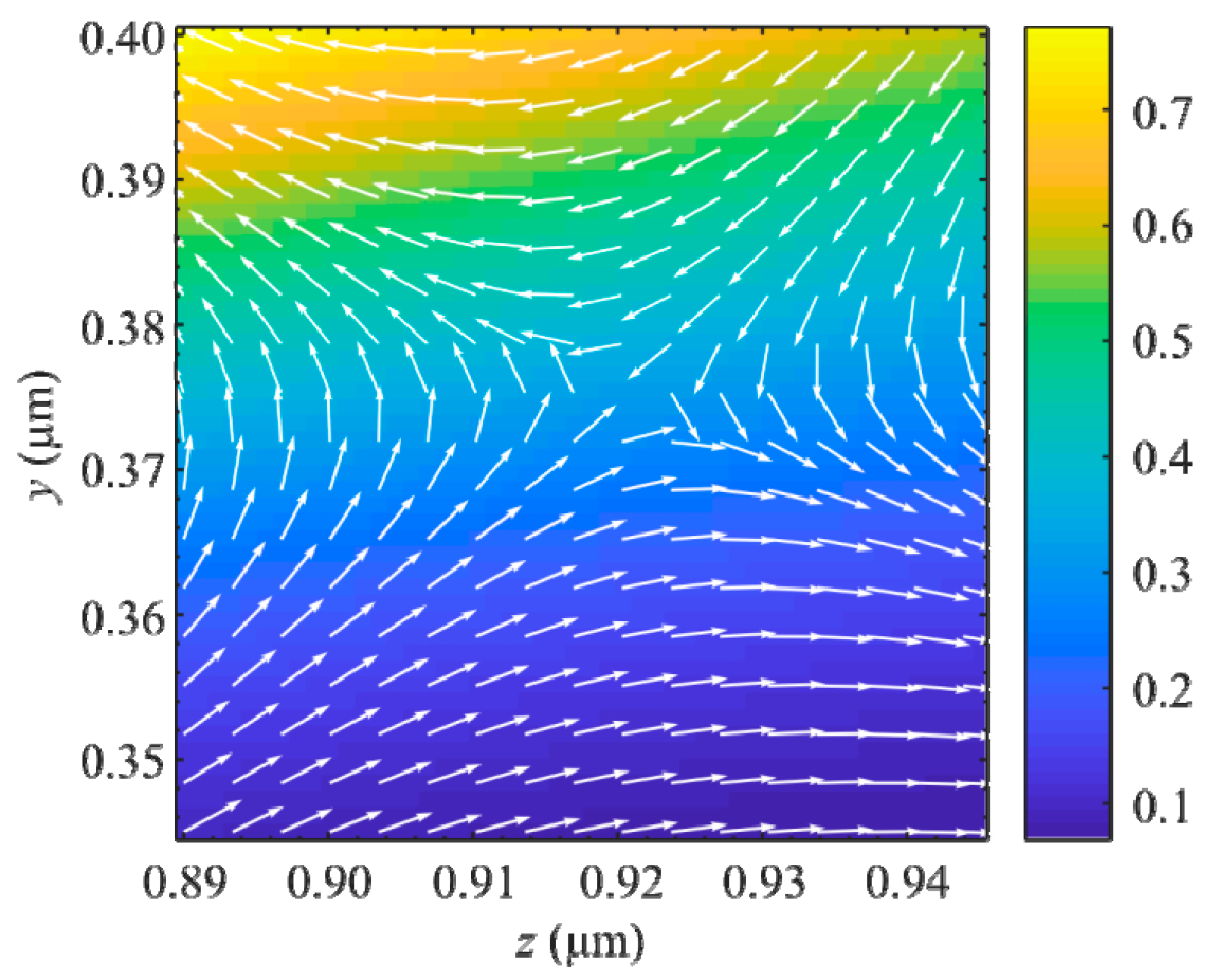
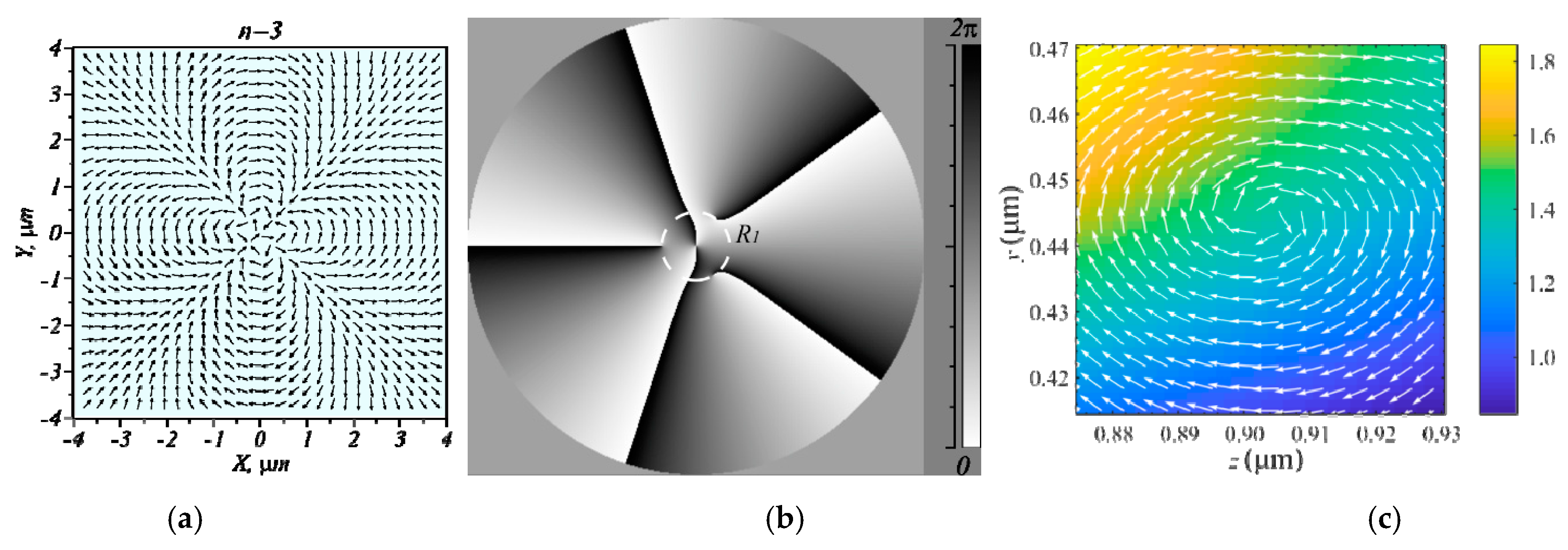
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dorn, R.; Quabis, S.; Leuchs, G. Sharper focus for a radially polarized light beam. Phys. Rev. Lett. 2003, 91, 233901. [Google Scholar] [CrossRef]
- Chong, C.T.; Sheppard, C.; Wang, H.; Shi, L.; Lukyanchuk, B. Creation of a needle of longitudinally polarized light in vacuum using binary optics. Nat. Photonics 2008, 2, 501–505. [Google Scholar]
- Yu, Y.; Huang, H.; Zhou, M.; Zhan, Q. Engineering of multi-segmented light tunnel and flattop focus with designed axial lengths and gaps. Opt. Commun. 2018, 407, 398–401. [Google Scholar] [CrossRef]
- Zheng, C.; Su, S.; Zang, H.; Ji, Z.; Tian, Y.; Chen, S.; Mu, K.; Wei, L.; Fan, Q.; Wang, C.; et al. Characterization of the focusing performance of axial line-focused spiral zone plates. Appl. Opt. 2018, 57, 3802–3807. [Google Scholar] [CrossRef] [PubMed]
- Lin, J.; Chen, R.; Jin, P.; Cada, M.; Ma, Y. Generation of longitudinally polarized optical chain by 4 π focusing system. Opt. Commun. 2015, 340, 69–73. [Google Scholar] [CrossRef]
- Yu, Y.; Zhan, Q. Generation of uniform three-dimensional optical chain with controllable characteristics. J. Opt. 2015, 17, 105606. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, B.; Dong, Y.; Wang, S.; Zhu, Z.; Bo, F.; Li, X. Generation of equilateral-polygon-like flat-top focus by tightly focusing radially polarized beams superposed with off-axis vortex arrays. Opt. Express 2017, 25, 26844. [Google Scholar] [CrossRef]
- Chen, H.; Tripathi, S.; Toussaint, K.C. Demonstration of flat-top focusing under radial polarization illumination. Opt. Lett. 2014, 39, 834. [Google Scholar] [CrossRef]
- Gao, X.-Z.; Pan, Y.; Zhang, G.-L.; Zhao, M.-D.; Ren, Z.-C.; Tu, C.-G.; Li, Y.-N.; Wang, H.-T. Redistributing the energy flow of tightly focused ellipticity-variant vector optical fields. Photonics Res. 2017, 5, 640. [Google Scholar] [CrossRef]
- Man, Z.; Bai, Z.; Zhang, S.; Li, X.; Li, J.; Ge, X.; Zhang, Y.; Fu, S. Redistributing the energy flow of a tightly focused radially polarized optical field by designing phase masks. Opt. Express 2018, 26, 23935. [Google Scholar] [CrossRef]
- Man, Z.; Li, X.; Zhang, S.; Bai, Z.; Lyu, Y.; Li, J.; Ge, X.; Sun, Y.; Fu, S. Manipulation of the transverse energy flow of azimuthally polarized beam in tight focusing system. Opt. Commun. 2019, 431, 174–180. [Google Scholar] [CrossRef]
- Jiao, X.; Liu, S.; Wang, Q.; Gan, X.; Li, P.; Zhao, J. Redistributing energy flow and polarization of a focused azimuthally polarized beam with rotationally symmetric sector-shaped obstacles. Opt. Lett. 2012, 37, 1041. [Google Scholar] [CrossRef] [PubMed]
- Pan, Y.; Gao, X.-Z.; Zhang, G.-L.; Li, Y.; Tu, C.; Wang, H.-T. Spin angular momentum density and transverse energy flow of tightly focused kaleidoscope-structured vector optical fields. APL Photonics 2019, 4, 096102. [Google Scholar] [CrossRef] [Green Version]
- Wu, G.; Wang, F.; Cai, Y. Generation and self-healing of a radially polarized Bessel-Gauss beam. Phys. Rev. A. 2014, 89, 043807. [Google Scholar] [CrossRef]
- Stafeev, S.S.; Kotlyar, V.V.; Nalimov, A.G.; Kozlova, E.S. The non-vortex inverse propagation of energy in a tightly focused high-order cylindrical vector beam. IEEE Photonics J. 2019, 11, 4500810. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Kovalev, A.A.; Nalimov, A.G. Energy density and energy flux in the focus of an optical vortex: Reverse flux of light energy. Opt. Lett. 2018, 43, 2921–2924. [Google Scholar] [CrossRef]
- Rondón-Ojeda, I.; Soto-Eguibar, F. Properties of the Poynting vector for invariant beams: Negative propagation in Weber beams. Wave Motion 2018, 78, 176–184. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Stafeev, S.S.; Kovalev, A.A. Reverse and toroidal flux of light fields with both phase and polarization higher-order singularities in the sharp focus area. Opt. Express 2019, 27, 16689–16702. [Google Scholar] [CrossRef]
- Li, H.; Wang, C.; Tang, M.; Li, X. Controlled negative energy flow in the focus of a radial polarized optical beam. Opt. Express 2020, 28, 18607–18615. [Google Scholar] [CrossRef]
- Richards, B.; Wolf, E. Electromagnetic diffraction in optical systems, II. Structure of the image field in an aplanatic system. Proc. R. Soc. A 1959, 253, 358–379. [Google Scholar]
- Ignatowsky, V.S. Diffraction by a lens having arbitrary opening. Trans. Opt. Inst. Petrograd 1920, 1, 4. [Google Scholar]
- Braunbek, W.; Laukien, G. Features of refraction by a semi-plane. Optik 1952, 9, 174–179. [Google Scholar]
- Wolter, H. Concerning the path of light upon total reflection. J. Opt. A Pure Appl. Opt. 2009, 11, 090401. [Google Scholar] [CrossRef]
- Dennis, M.R.; Götte, J.N. Beam shifts for pairs of plane waves. J. Opt. 2013, 15, 014015. [Google Scholar] [CrossRef]
- Bekshaev, A.Y. Subwavelength particles in an inhomogeneous light field: Optical forces associated with the spin and orbital energy flows. J. Opt. 2013, 15, 044004. [Google Scholar] [CrossRef] [Green Version]
- Neugebauer, M. Linear and angular momenta in tightly focused vortex segmented beams of light (Invited Paper). Chin. Opt. Lett. 2017, 15, 030003. [Google Scholar] [CrossRef] [Green Version]
- Stafeev, S.S.; Kotlyar, V.V. Toroidal polarization vortices in tightly focused beam with singularity. Comput. Opt. 2020, 44, 685–690. [Google Scholar] [CrossRef]
- Sukhov, S.; Dogariu, A. On the concept of “tractor beams”. Opt. Lett. 2010, 35, 3847–3849. [Google Scholar] [CrossRef]
- Stafeev, S.S.; Kotlyar, V.V. Elongation of the area of energy backflow through the use of ring apertures. Opt. Commun. 2019, 450, 67–71. [Google Scholar] [CrossRef]
- Freund, I. Polarization singularity indices in Gaussian laser beams. Opt. Commun. 2002, 201, 251–270. [Google Scholar] [CrossRef]
- Zhan, Q. Cylindrical vector beams: From mathematical concepts to applications. Adv. Opt. Photon. 2009, 1, 1–57. [Google Scholar] [CrossRef]
- Wang, X.; Ding, J.; Ni, W.; Guo, C.; Wang, H. Generation of arbitrary vector beams with a spatial light modulator and a common path interferometric arrangement. Opt. Lett. 2007, 32, 3549–3551. [Google Scholar] [CrossRef] [PubMed]
- Berry, M.V. Optical vortices evolving from helicoidal integer and fractional phase steps. J. Opt. A Pure Appl. Opt. 2004, 6, 259–268. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stafeev, S.S.; Kozlova, E.S.; Kotlyar, V.V. Toroidal Vortices of Energy in Tightly Focused Second-Order Cylindrical Vector Beams. Photonics 2021, 8, 301. https://doi.org/10.3390/photonics8080301
Stafeev SS, Kozlova ES, Kotlyar VV. Toroidal Vortices of Energy in Tightly Focused Second-Order Cylindrical Vector Beams. Photonics. 2021; 8(8):301. https://doi.org/10.3390/photonics8080301
Chicago/Turabian StyleStafeev, Sergey S., Elena S. Kozlova, and Victor V. Kotlyar. 2021. "Toroidal Vortices of Energy in Tightly Focused Second-Order Cylindrical Vector Beams" Photonics 8, no. 8: 301. https://doi.org/10.3390/photonics8080301
APA StyleStafeev, S. S., Kozlova, E. S., & Kotlyar, V. V. (2021). Toroidal Vortices of Energy in Tightly Focused Second-Order Cylindrical Vector Beams. Photonics, 8(8), 301. https://doi.org/10.3390/photonics8080301





