Photo-Switching of Protein Dynamical Collectivity
Abstract
:1. Introduction
2. Materials and Methods
2.1. Sample Preparation
2.2. THz Measurements
2.3. CD Measurements
2.4. MD Calculations
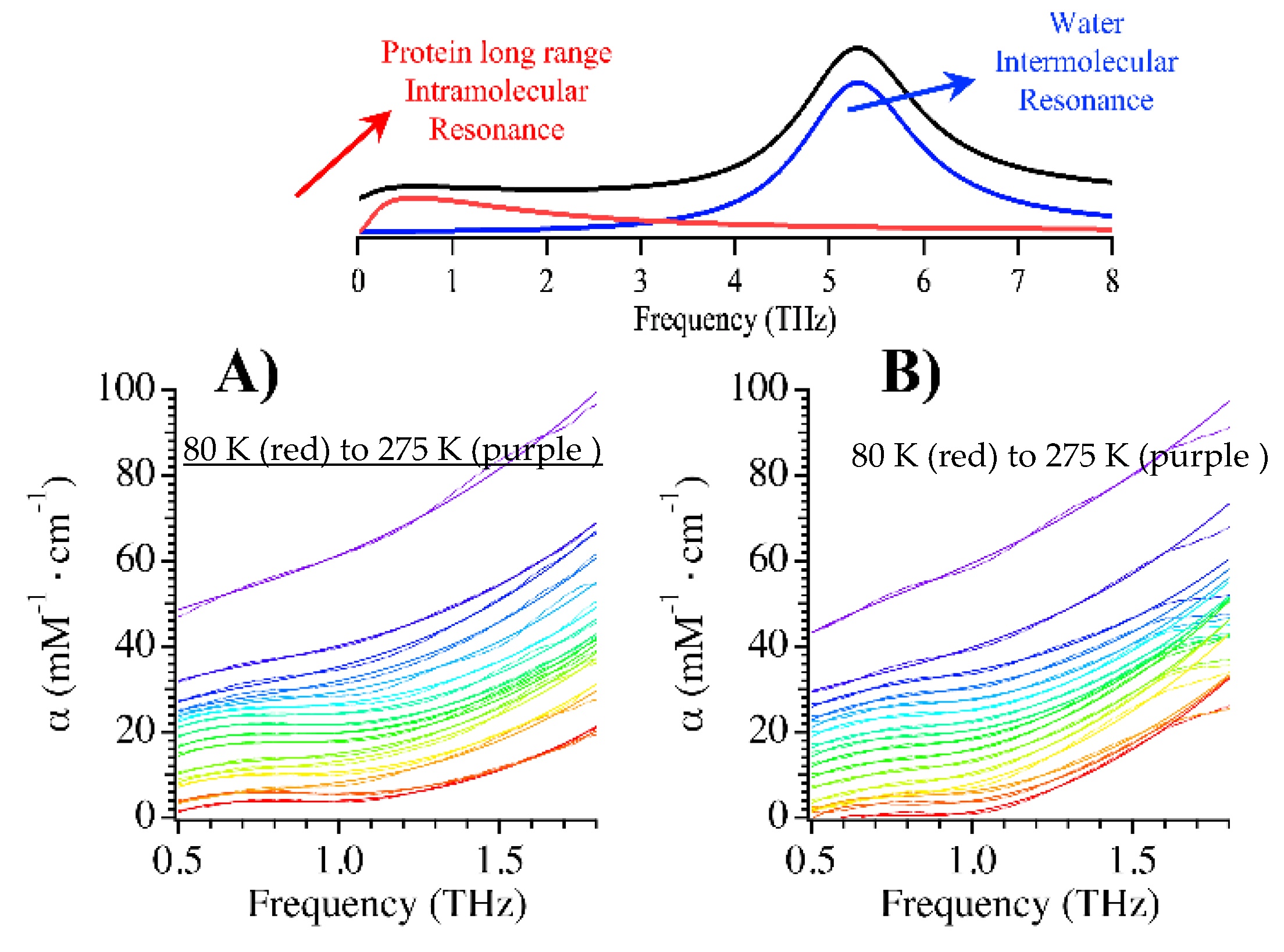
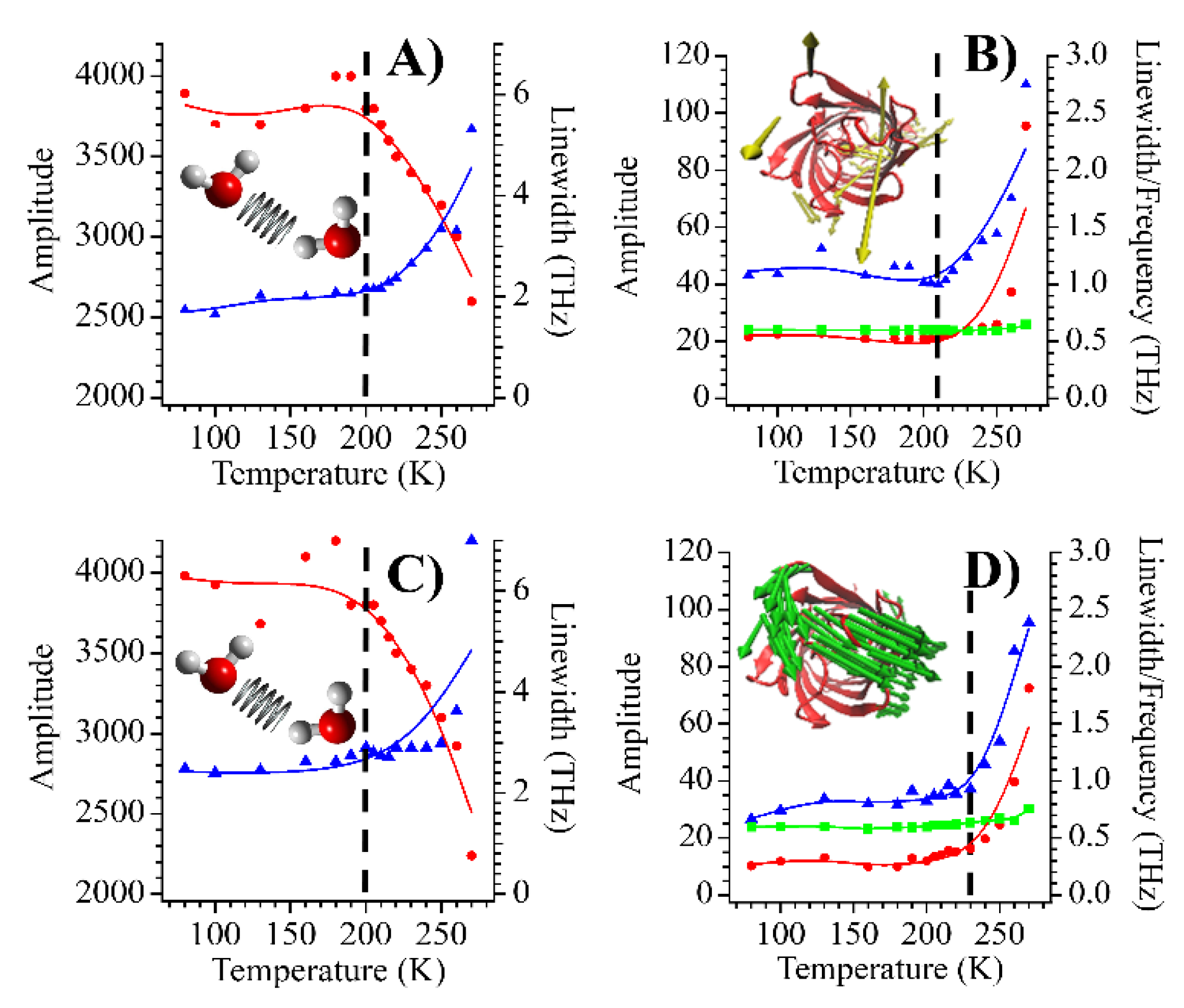
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tolbert, L.M.; Baldridge, A.; Kowalik, J.; Solntsev, K.M. Collapse and Recovery of Green Fluorescent Protein Chromophore Emission through Topological Effects. Accounts Chem. Res. 2012, 45, 171–181. [Google Scholar] [CrossRef] [PubMed]
- Zimmer, M. Green fluorescent protein (GFP): Applications, structure, and related photophysical behavior. Chem. Rev. 2002, 102, 759–781. [Google Scholar] [CrossRef] [PubMed]
- Tsien, R.Y. The Green Fluorescent Protein. Annu. Rev. Biochem. 1998, 67, 509–544. [Google Scholar] [CrossRef] [PubMed]
- Stavrov, S.S.; Solntsev, K.M.; Tolbert, L.M.; Huppert, D. Probing the decay coordinate of the green fluorescent protein: Arrest of cis-trans isomerization by the protein significantly narrows the fluorescence spectra. J. Am. Chem. Soc. 2006, 128, 1540–1546. [Google Scholar] [CrossRef]
- Shaner, N.C.; Lin, M.Z.; McKeown, M.R.; Steinbach, P.A.; Hazelwood, K.L.; Davidson, M.W.; Tsien, R.Y. Improving the photostability of bright monomeric orange and red fluorescent proteins. Nat. Methods 2008, 5, 545–551. [Google Scholar] [CrossRef] [Green Version]
- Carpentier, P.; Violot, S.; Blanchoin, L.; Bourgeois, D. Structural basis for the phototoxicity of the fluorescent protein KillerRed. FEBS Lett. 2009, 583, 2839–2842. [Google Scholar] [CrossRef] [PubMed]
- Kao, Y.-T.; Zhu, X.; Min, W. Protein-flexibility mediated coupling between photoswitching kinetics and surrounding viscosity of a photochromic fluorescent protein. Proc. Natl. Acad. Sci. USA 2012, 109, 3220–3225. [Google Scholar] [CrossRef] [Green Version]
- Mizuno, H.; Mal, T.K.; Wälchli, M.; Kikuchi, A.; Fukano, T.; Ando, R.; Jeyakanthan, J.; Taka, J.; Shiro, Y.; Ikura, M.; et al. Light-dependent regulation of structural flexibility in a photochromic fluorescent protein. Proc. Natl. Acad. Sci. USA 2008, 105, 9227–9232. [Google Scholar] [CrossRef] [Green Version]
- Shaner, N.C.; Campbell, R.E.; Steinbach, P.A.; Giepmans, B.N.G.; Palmer, A.E.; Tsien, R.Y. Improved monomeric red, orange and yellow fluorescent proteins derived from Discosoma sp. red fluorescent protein. Nat. Biotechnol. 2004, 22, 1567–1572. [Google Scholar] [CrossRef]
- Shu, X.K.; Shaner, N.C.; Yarbrough, C.A.; Tsien, R.Y.; Remington, S.J. Novel chromophores and buried charges control color in mFruits. Biochemistry 2006, 45, 9639–9647. [Google Scholar] [CrossRef]
- Liu, R.; Liang, Q.N.; Du, S.Q.; Hu, X.J.; Ding, Y. The crystal structure of red fluorescent protein TagRFP-T reveals the mechanism of its superior photostability. Biochem. Biophys. Res. Commun. 2016, 477, 229–234. [Google Scholar] [CrossRef]
- Dean, K.M.; Lubbeck, J.L.; Binder, J.K.; Schwall, L.R.; Jimenez, R.; Palmer, A.E. Analysis of red-fluorescent proteins provides insight into dark-state conversion and photodegradation. Biophys. J. 2011, 101, 961–969. [Google Scholar] [CrossRef] [Green Version]
- Niessen, K.A.; Xu, M.; Markelz, A.G. Terahertz optical measurements of correlated motions with possible allosteric function. Biophys. Rev. 2015, 7, 201–216. [Google Scholar] [CrossRef] [Green Version]
- George, D.K.; Knab, J.R.; He, Y.; Kumauchi, M.; Birge, R.R.; Hoff, W.D.; Markelz, A.G. Photoactive Yellow Protein Terahertz Response: Hydration, Heating and Intermediate States. IEEE Trans. Terahertz Sci. Technol. 2013, 3, 288–294. [Google Scholar] [CrossRef]
- Yamamoto, N.; Ohta, K.; Tamura, A.; Tominaga, K. Broadband Dielectric Spectroscopy on Lysozyme in the Sub-Gigahertz to Terahertz Frequency Regions: Effects of Hydration and Thermal Excitation. J. Phys. Chem. B 2016, 120, 4743–4755. [Google Scholar] [CrossRef] [PubMed]
- Karplus, M.; Kuriyan, J. Molecular dynamics and protein function. Proc. Natl. Acad. Sci. USA 2005, 102, 6679–6685. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yada, H.; Nagai, M.; Tanaka, K. Origin of the fast relaxation component of water and heavy water revealed by terahertz time-domain attenuated total reflection spectroscopy. Chem. Phys. Lett. 2008, 464, 166–170. [Google Scholar] [CrossRef]
- van Exter, M.; Fattinger, C.; Grischkowsky, D. Terahertz time-domain spectroscopy of water vapor. Opt. Lett. 1989, 14, 1128–1130. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, X.C. Pulsed terahertz tomography. J. Phys. D Appl. Phys. 2004, 37, R1. [Google Scholar] [CrossRef] [Green Version]
- He, Y.; Ku, P.I.; Knab, J.R.; Chen, J.Y.; Markelz, A.G. Protein Dynamical Transition Does Not Require Protein Structure. Phys. Rev. Lett. 2008, 101, 178103. [Google Scholar] [CrossRef] [PubMed]
- Brooks, B.R.; Bruccoleri, R.E.; Olafson, B.D.; States, D.J.; Swaminathan, S.; Karplus, M. CHARMM: A program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem. 1983, 4, 187–217. [Google Scholar] [CrossRef]
- Brooks, B.R.; Brooks, C.L.; MacKerell, A.D.; Nilsson, L.; Petrella, R.J.; Roux, B.; Won, Y.; Archontis, G.; Bartels, C.; Boresch, S.; et al. CHARMM: The Biomolecular Simulation Program. J. Comput. Chem. 2009, 30, 1545–1614. [Google Scholar] [CrossRef] [PubMed]
- Chapagain, P.P.; Regmi, C.K.; Castillo, W. Fluorescent protein barrel fluctuations and oxygen diffusion pathways in mCherry. J. Chem. Phys. 2011, 135, 235101. [Google Scholar] [CrossRef] [Green Version]
- Jo, S.; Kim, T.; Iyer, V.G.; Im, W. CHARMM-GUI: A web-based graphical user interface for CHARMM. J. Comput. Chem. 2008, 29, 1859–1865. [Google Scholar] [CrossRef]
- He, Y.; Chen, J.; Knab, J.; Zheng, W.; Markelz, A. Evidence of Protein Collective Motions on the Picosecond Timescale. Biophys. J. 2011, 100, 1058–1065. [Google Scholar] [CrossRef] [Green Version]
- Ding, T.; Middelberg, A.P.J.; Huber, T.; Falconer, R.J. Far-infrared spectroscopy analysis of linear and cyclic peptides, and lysozyme. Vib. Spectrosc. 2012, 61, 144–150. [Google Scholar] [CrossRef]
- Heyden, M.; Tobias, D.J.; Matyushov, D.V. Terahertz absorption of dilute aqueous solutions. J. Chem. Phys. 2012, 137, 235103. [Google Scholar] [CrossRef]
- Nakagawa, H.; Joti, Y.; Kitao, A.; Kataoka, M. Hydration Affects Both Harmonic and Anharmonic Nature of Protein Dynamics. Biophys. J. 2008, 95, 2916–2923. [Google Scholar] [CrossRef] [Green Version]
- Doster, W.; Cusack, S.; Petry, W. Dynamical transition of myoglobin revealed by inelastic neutron scattering. Nature 1989, 337, 754–756. [Google Scholar] [CrossRef]
- Zaccai, G. How soft is a protein? A protein dynamics force constant measured by neutron scattering. Science 2000, 288, 1604–1607. [Google Scholar] [CrossRef] [Green Version]
- Heyden, M.; Tobias, D.J. Spatial Dependence of Protein-Water Collective Hydrogen-Bond Dynamics. Phys. Rev. Lett. 2013, 111, 218101. [Google Scholar] [CrossRef]
- Stadler, A.M.; Garvey, C.J.; Bocahut, A.; Sacquin-Mora, S.; Digel, I.; Schneider, G.J.; Natali, F.; Artmann, G.M.; Zaccai, G. Thermal fluctuations of haemoglobin from different species: Adaptation to temperature via conformational dynamics. J. R. Soc. Interface 2012, 9, 2845–2855. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Doster, W. The dynamical transition of proteins, concepts and misconceptions. Eur. Biophys. J. 2008, 37, 591–602. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.; Fenimore, P.W.; Frauenfelder, H.; Mezei, F.; Swenson, J.; Young, R.D. Protein fluctuations explored by inelastic neutron scattering and dielectric relaxation spectroscopy. Philos. Mag. 2008, 88, 3877–3883. [Google Scholar] [CrossRef]
- Kawaguchi, S.; Kambara, O.; Shibata, M.; Kandori, H.; Tominaga, K. Low-frequency dynamics of bacteriorhodopsin studied by terahertz time-domain spectroscopy. Phys. Chem. Chem. Phys. 2010, 12, 10255–10262. [Google Scholar] [CrossRef]
- Yamamoto, K.; Tominaga, K.; Sasakawa, H.; Tamura, A.; Murakami, H.; Ohtake, H.; Sarukura, N. Terahertz Time-Domain Spectroscopy of Amino Acids and Polypeptides. Biophys. J. 2005, 89, L22–L24. [Google Scholar] [CrossRef] [Green Version]
- Perticaroli, S.; Nickels, J.D.; Ehlers, G.; Sokolov, A.P. Rigidity, Secondary Structure, and the Universality of the Boson Peak in Proteins. Biophys. J. 2014, 106, 2667–2674. [Google Scholar] [CrossRef] [Green Version]
- Mori, T.; Jiang, Y.; Fujii, Y.; Kitani, S.; Mizuno, H.; Koreeda, A.; Motoji, L.; Tokoro, H.; Shiraki, K.; Yamamoto, Y.; et al. Detection of boson peak and fractal dynamics of disordered systems using terahertz spectroscopy. Phys. Rev. E 2020, 102, 022502. [Google Scholar] [CrossRef]
- Schirò, G.; Fichou, Y.; Gallat, F.-X.; Wood, K.; Gabel, F.; Moulin, M.; Härtlein, M.; Heyden, M.; Colletier, J.-P.; Orecchini, A.; et al. Translational diffusion of hydration water correlates with functional motions in folded and intrinsically disordered proteins. Nat. Commun. 2015, 6, 6490. [Google Scholar] [CrossRef]
- Wood, K.; Frölich, A.; Paciaroni, A.; Moulin, M.; Härtlein, M.; Zaccai, G.; Tobias, D.J.; Weik, M. Coincidence of Dynamical Transitions in a Soluble Protein and Its Hydration Water: Direct Measurements by Neutron Scattering and MD Simulations. J. Am. Chem. Soc. 2008, 130, 4586–4587. [Google Scholar] [CrossRef]
- Møller, U.; Cooke, D.G.; Tanaka, K.; Jepsen, P.U. Terahertz reflection spectroscopy of Debye relaxation in polar liquids [Invited]. J. Opt. Soc. Am. B 2009, 26, A113–A125. [Google Scholar] [CrossRef]
- Penkov, N.; Shvirst, N.; Yashin, V.; Fesenko, E.; Fesenko, E. Terahertz Spectroscopy Applied for Investigation of Water Structure. J. Phys. Chem. B 2015, 119, 12664–12670. [Google Scholar] [CrossRef]
- Vinh, N.Q.; Sherwin, M.S.; Allen, S.J.; George, D.K.; Rahmani, A.J.; Plaxco, K.W. High-precision gigahertz-to-terahertz spectroscopy of aqueous salt solutions as a probe of the femtosecond-to-picosecond dynamics of liquid water. J. Chem. Phys. 2015, 142, 164502. [Google Scholar] [CrossRef]
- Twardowski, J.; Anzenbacher, P.; Masson, M.R. Raman and IR Spectroscopy in Biology and Biochemistry; Ellis Horwood: Chichester, UK, 1994. [Google Scholar]
- Genzel, L.; Kremer, F.; Poglitsch, A.; Bechtold, G. Relaxation processes on a picosecond time scale in hemoglobin and poly(L-alanine) observed by millimeter-wave spectroscopy. Biopolymers 1983, 22, 1715–1729. [Google Scholar] [CrossRef]
- Genzel, L.; Santo, L.; Shen, S.C. Far-Infrared Spectroscopy of Biomolecules. In Spectroscopy of Biological Molecules: Theory and Applications—Chemistry, Physics, Biology, and Medicine; Sandorfy, C., Theophanides, T., Eds.; Springer: Dordrecht, The Netherlands, 1984; pp. 609–619. [Google Scholar]
- Poglitsch, A.; Kremer, F.; Genzel, L. Picosecond relaxations in hydrated lysozyme observed by mm-wave spectroscopy. J. Mol. Biol. 1984, 173, 137–142. [Google Scholar] [CrossRef]
- Powell, J.W.; Edwards, G.S.; Genzel, L.; Kremer, F.; Wittlin, A.; Kubasek, W.; Peticolas, W. Investigation of far-infrared vibrational modes in polynucleotides. Phys. Rev. A 1987, 35, 3929–3939. [Google Scholar] [CrossRef]
- Powell, J.W.; Peticolas, W.L.; Genzel, L. Observation of the far-infrared spectrum of five oligonucleotides. J. Mol. Struct. 1991, 247, 107–118. [Google Scholar] [CrossRef]
- Wittlin, A.; Genzel, L.; Kremer, F.; Häseler, S.; Poglitsch, A.; Rupprecht, A. Far-infrared spectroscopy on oriented films of dry and hydrated DNA. Phys. Rev. A 1986, 34, 493–500. [Google Scholar] [CrossRef] [PubMed]
- Zakaria, H.A.; Fischer, B.M.; Bradley, A.P.; Jones, I.; Abbott, D.; Middelberg, A.P.; Falconer, R.J. Low-frequency spectroscopic analysis of monomeric and fibrillar lysozyme. Appl. Spectrosc. 2011, 65, 260–264. [Google Scholar] [CrossRef]
- Kaatze, U. Complex permittivity of water as a function of frequency and temperature. J. Chem. Eng. Data 1989, 34, 371–374. [Google Scholar] [CrossRef]
- Stadler, A.M.; Digel, I.; Embs, J.P.; Unruh, T.; Tehei, M.; Zaccai, G.; Buldt, G.; Artmann, G.M. From powder to solution: Hydration dependence of human hemoglobin dynamics correlated to body temperature. Biophys. J. 2009, 96, 5073–5081. [Google Scholar] [CrossRef] [Green Version]
- Frolov, E.N.; Gvosdev, R.; Goldanskii, V.I.; Parak, F.G. Differences in the dynamics of oxidized and reduced cytochrome c measured by Mössbauer spectroscopy. JBIC J. Biol. Inorg. Chem. 1997, 2, 710–713. [Google Scholar] [CrossRef]
- Paciaroni, A.; Orecchini, A.; Cornicchi, E.; Marconi, M.; Petrillo, C.; Haertlein, M.; Moulin, M.; Sacchetti, F. Coupled thermal fluctuations of proteins and protein hydration water on the picosecond timescale. Philos. Mag. 2008, 88, 4071–4077. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.-H.; Liu, L.; Fratini, E.; Baglioni, P.; Faraone, A.; Mamontov, E. Observation of fragile-to-strong dynamic crossover in protein hydration water. Proc. Natl. Acad. Sci. USA 2006, 103, 9012–9016. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Duan, C.; Adam, V.; Byrdin, M.; Ridard, J.; Kieffer-Jaquinod, S.; Morlot, C.; Arcizet, D.; Demachy, I.; Bourgeois, D. Structural Evidence for a Two-Regime Photobleaching Mechanism in a Reversibly Switchable Fluorescent Protein. J. Am. Chem. Soc. 2013, 135, 15841–15850. [Google Scholar] [CrossRef] [PubMed]
- Doster, W. The protein-solvent glass transition. Biochim. Biophys. Acta Proteins Proteom. 2010, 1804, 3–14. [Google Scholar] [CrossRef]
- Bragger, J.M.; Dunn, R.V.; Daniel, R.M. Enzyme activity down to-100 degrees C. Biochim. Biophys. Acta Protein Struct. Molec. Enzym. 2000, 1480, 278–282. [Google Scholar] [CrossRef]
- Malardier-Jugroot, C.; Head-Gordon, T. Separable cooperative and localized translational motions of water confined by a chemically heterogeneous environment. Phys. Chem. Chem. Phys. 2007, 9, 1962–1971. [Google Scholar] [CrossRef] [PubMed]
- Shinyashiki, N.; Yamamoto, W.; Yokoyama, A.; Yoshinari, T.; Yagihara, S.; Kita, R.; Ngai, K.L.; Capaccioli, S. Glass Transitions in Aqueous Solutions of Protein (Bovine Serum Albumin). J. Phys. Chem. B 2009, 113, 14448–14456. [Google Scholar] [CrossRef]
- Schiro, G.; Caronna, C.; Natali, F.; Cupane, A. Direct Evidence of the Amino Acid Side Chain and Backbone Contributions to Protein Anharmonicity. J. Am. Chem. Soc. 2010, 132, 1371–1376. [Google Scholar] [CrossRef] [PubMed]
- Fenimore, P.W.; Frauenfelder, H.; McMahon, B.H.; Young, R.D. Proteins are paradigms of stochastic complexity. Phys. A 2005, 351, 1–13. [Google Scholar] [CrossRef]
- Fenimore, P.W.; Frauenfelder, H.; McMahon, B.H.; Young, R.D. Bulk-solvent and hydration-shell fluctuations, similar to alpha- and beta-fluctuations in glasses, control protein motions and functions. Proc. Natl. Acad. Sci. USA 2004, 101, 14408–14413. [Google Scholar] [CrossRef] [Green Version]
- Schenk, A.; Ivanchenko, S.; Röcker, C.; Wiedenmann, J.; Nienhaus, G.U. Photodynamics of Red Fluorescent Proteins Studied by Fluorescence Correlation Spectroscopy. Biophys. J. 2004, 86, 384–394. [Google Scholar] [CrossRef] [Green Version]
- Bell, A.F.; Stoner-Ma, D.; Wachter, R.M.; Tonge, P.J. Light-driven decarboxylation of wild-type green fluorescent protein. J. Am. Chem. Soc. 2003, 125, 6919–6926. [Google Scholar] [CrossRef]
- Liu, Y.; Kim, H.R.; Heikal, A.A. Structural basis of fluorescence fluctuation dynamics of green fluorescent proteins in acidic environments. J. Phys. Chem. B 2006, 110, 24138–24146. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Habuchi, S.; Cotlet, M.; Gensch, T.; Bednarz, T.; Haber-Pohlmeier, S.; Rozenski, J.; Dirix, G.; Michiels, J.; Vanderleyden, J.; Heberle, J.; et al. Evidence for the isomerization and decarboxylation in the photoconversion of the red fluorescent protein DsRed. J. Am. Chem. Soc. 2005, 127, 8977–8984. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiménez-Banzo, A.; Nonell, S.; Hofkens, J.; Flors, C. Singlet Oxygen Photosensitization by EGFP and its Chromophore HBDI. Biophys. J. 2008, 94, 168–172. [Google Scholar] [CrossRef] [Green Version]
- Jimenez-Banzo, A.; Ragas, X.; Abbruzzetti, S.; Viappiani, C.; Campanini, B.; Flors, C.; Nonell, S. Singlet oxygen photosensitisation by GFP mutants: Oxygen accessibility to the chromophore. Photochem. Photobiol. Sci. 2010, 9, 1336–1341. [Google Scholar] [CrossRef]
- Vegh, R.B.; Bravaya, K.B.; Bloch, D.A.; Bommarius, A.S.; Tolbert, L.M.; Verkhovsky, M.; Krylov, A.I.; Solntsev, K.M. Chromophore Photoreduction in Red Fluorescent Proteins Is Responsible for Bleaching and Phototoxicity. J. Phys. Chem. B 2014, 118, 4527–4534. [Google Scholar] [CrossRef]
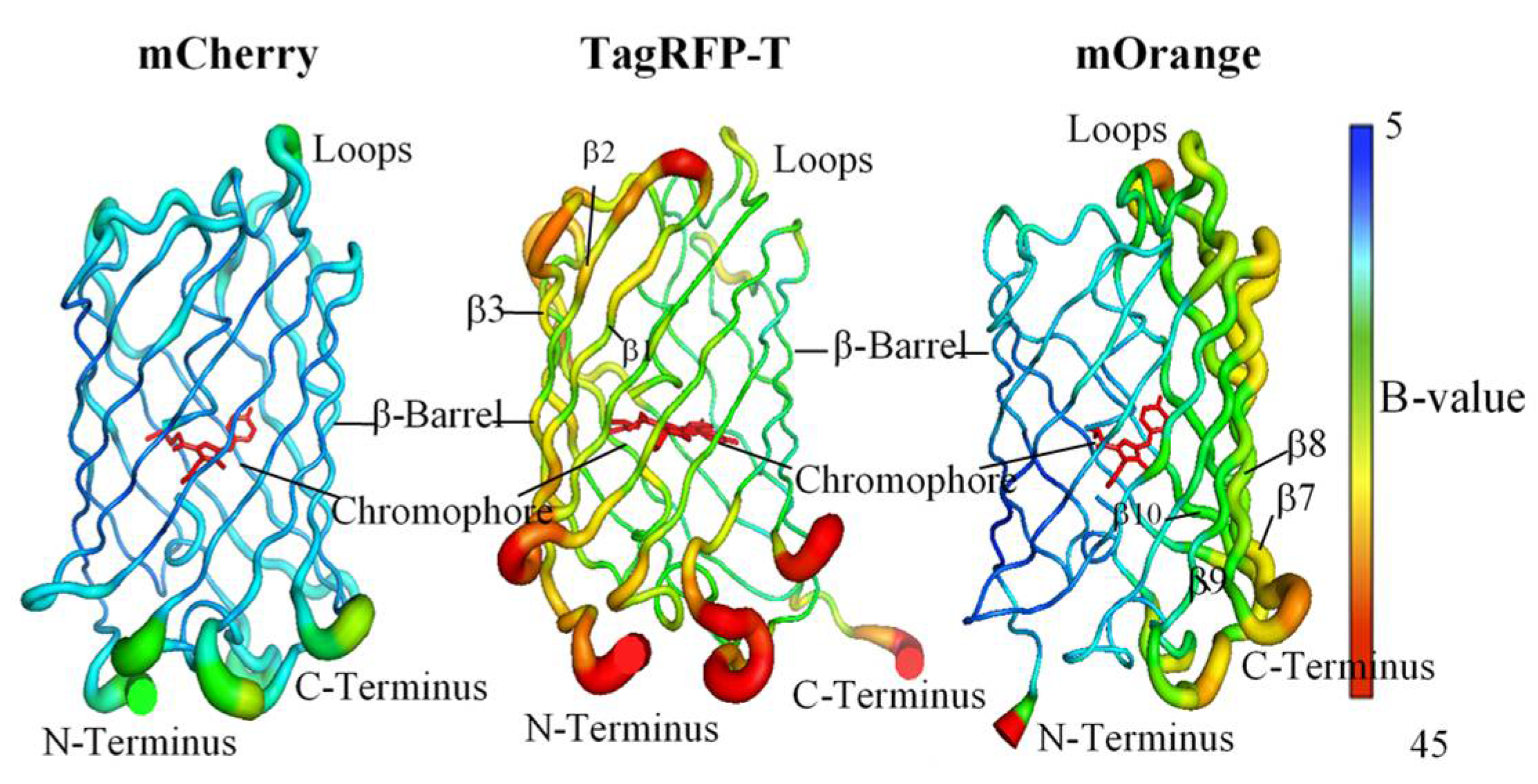
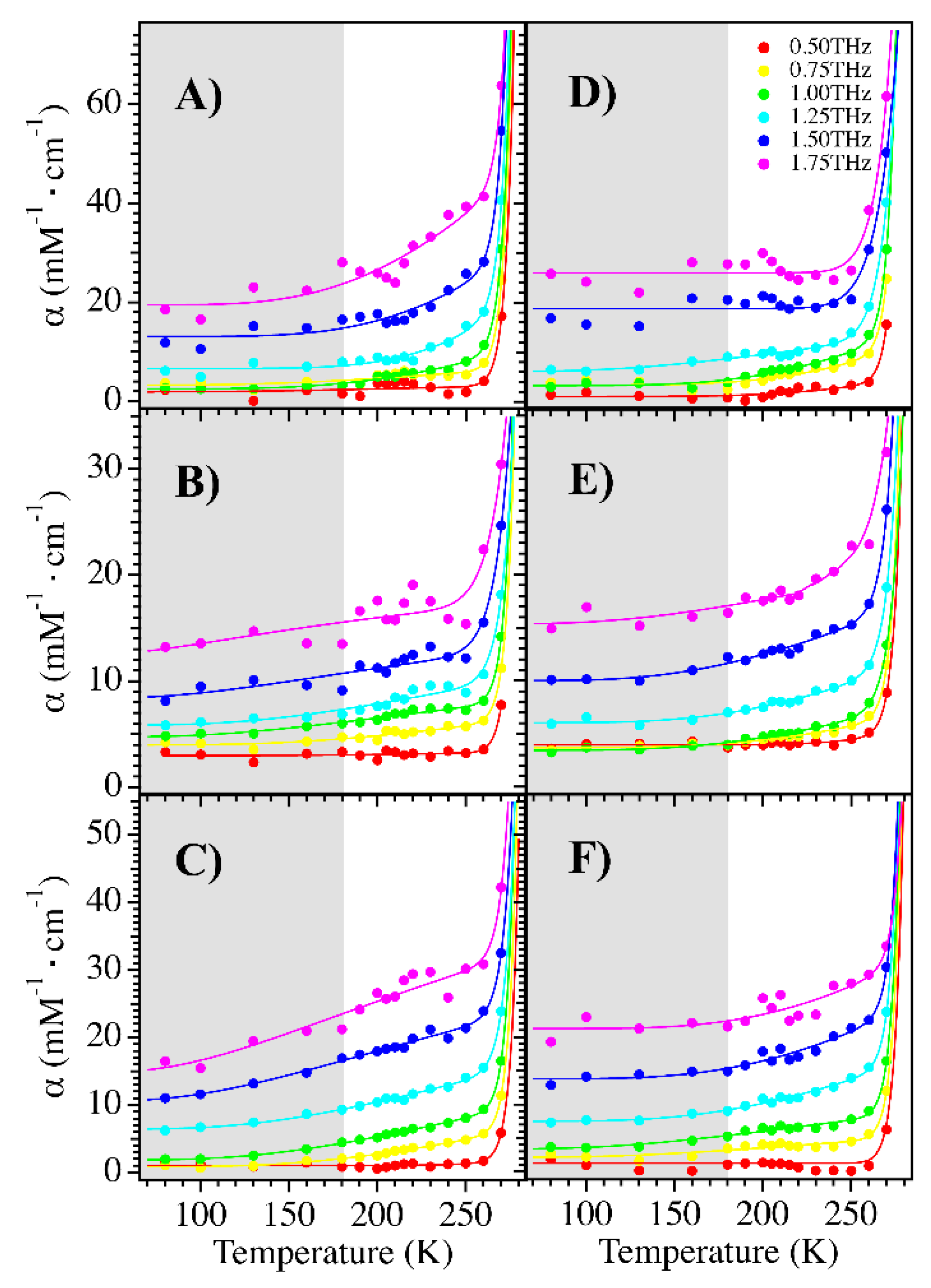
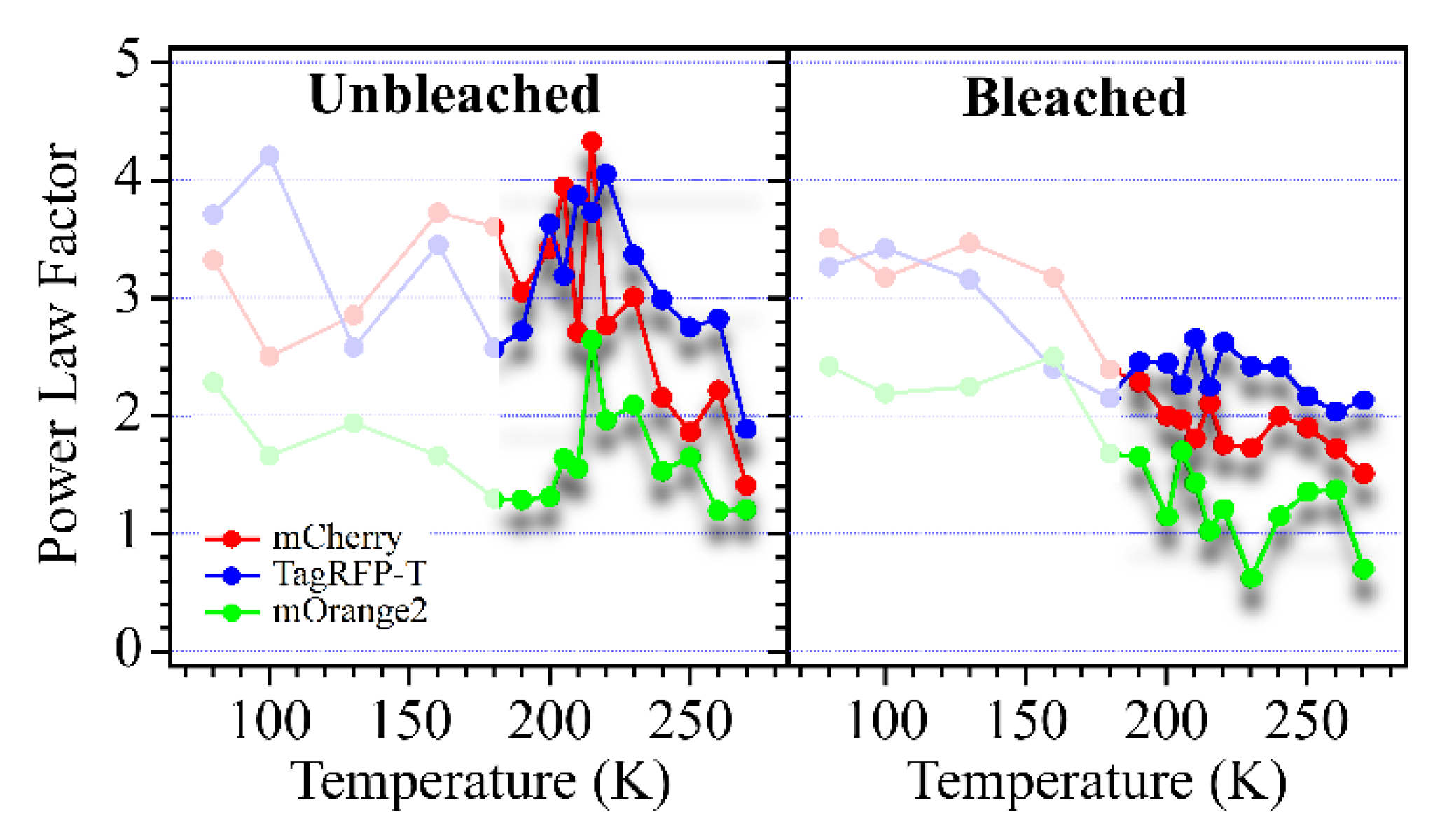
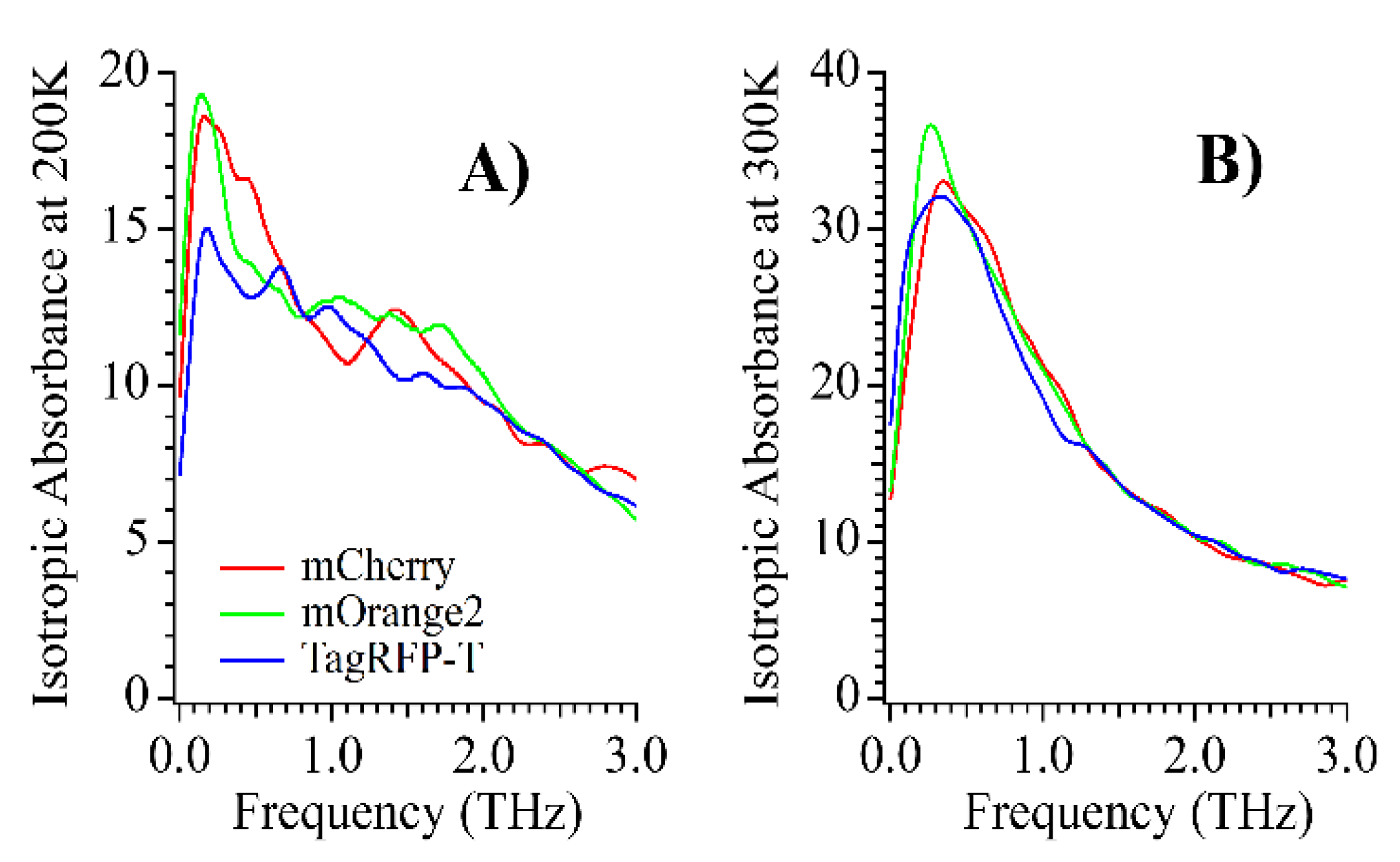
| mCherry | TagRFP-T | mOrange2 | |
|---|---|---|---|
| TM, Unbleached (K) | 359 ± 2 | 345 ± 1 | 353 ± 4 |
| TM, Bleached (K) | 373 ± 2 | 350 ± 1 | 367 ± 4 |
| k*Unbleached | 43 ± 14 | 18 ± 1 | 21 ± 3 |
| k*Bleached | 45 ± 4 | 22 ± 3 | 31 ± 9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, M.; George, D.; Jimenez, R.; Markelz, A. Photo-Switching of Protein Dynamical Collectivity. Photonics 2021, 8, 302. https://doi.org/10.3390/photonics8080302
Xu M, George D, Jimenez R, Markelz A. Photo-Switching of Protein Dynamical Collectivity. Photonics. 2021; 8(8):302. https://doi.org/10.3390/photonics8080302
Chicago/Turabian StyleXu, Mengyang, Deepu George, Ralph Jimenez, and Andrea Markelz. 2021. "Photo-Switching of Protein Dynamical Collectivity" Photonics 8, no. 8: 302. https://doi.org/10.3390/photonics8080302
APA StyleXu, M., George, D., Jimenez, R., & Markelz, A. (2021). Photo-Switching of Protein Dynamical Collectivity. Photonics, 8(8), 302. https://doi.org/10.3390/photonics8080302





