Singular Warped Beams Controlled by Tangent Phase Modulation
Abstract
:1. Introduction
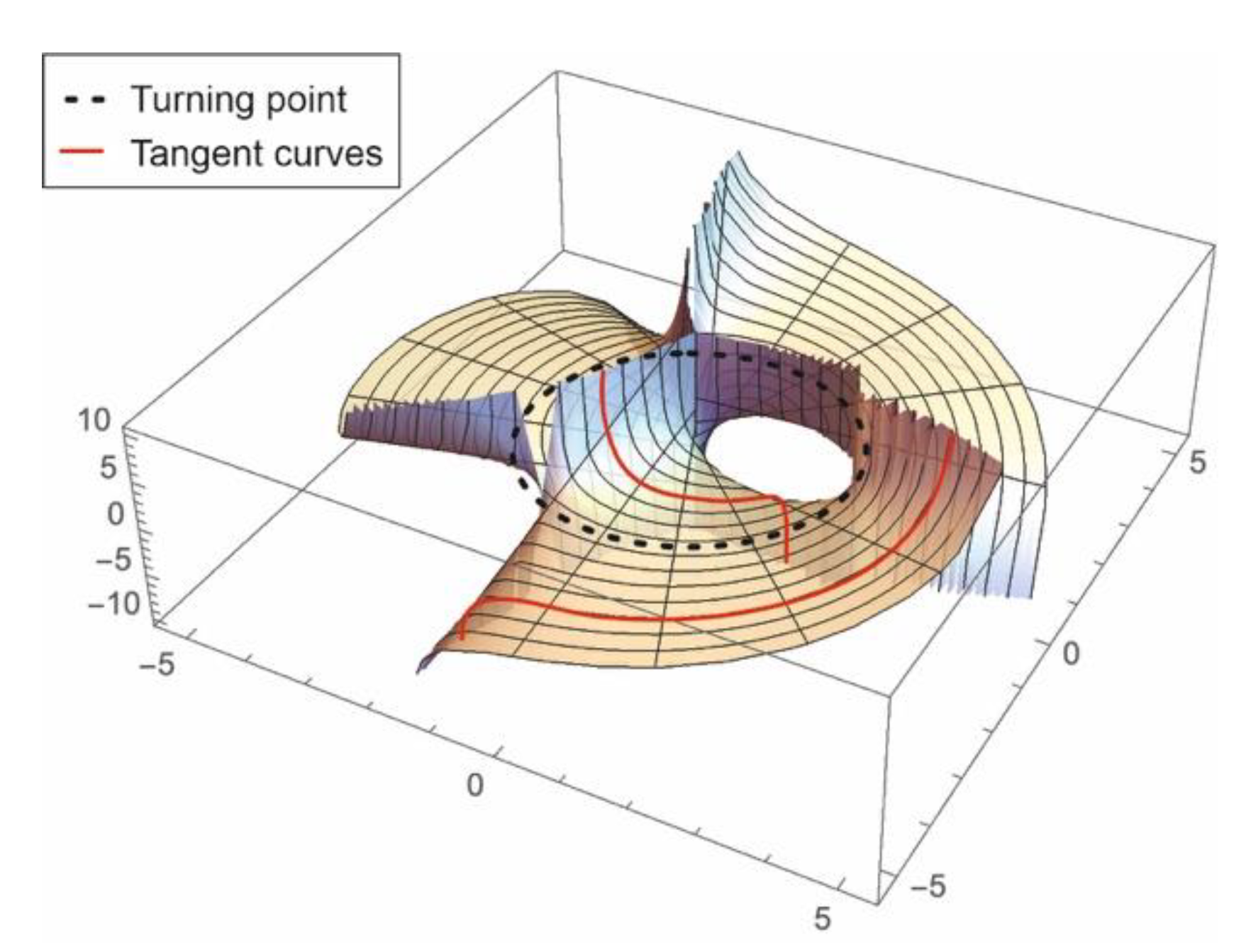
2. Phase Modulation
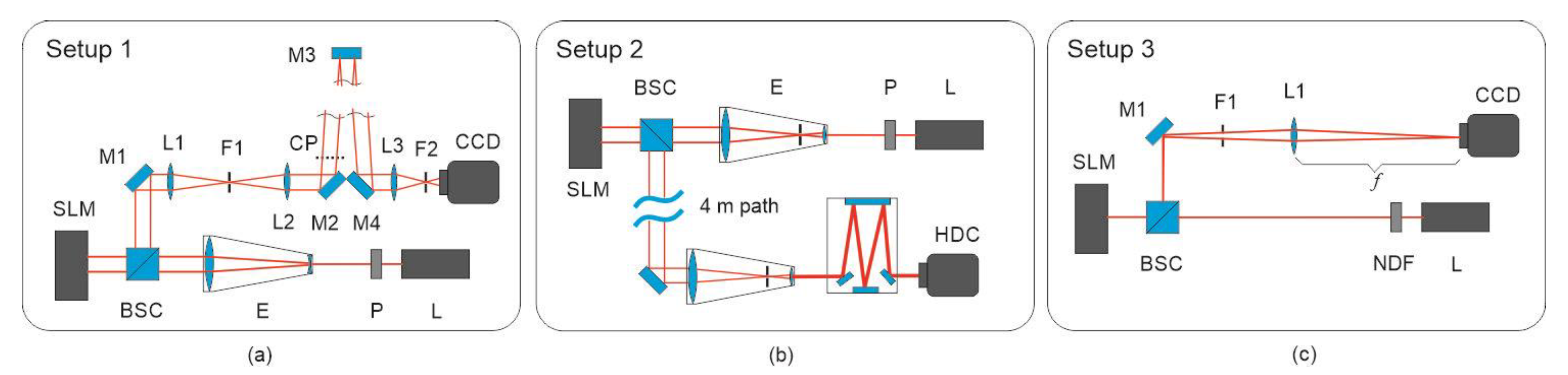
3. Experiment
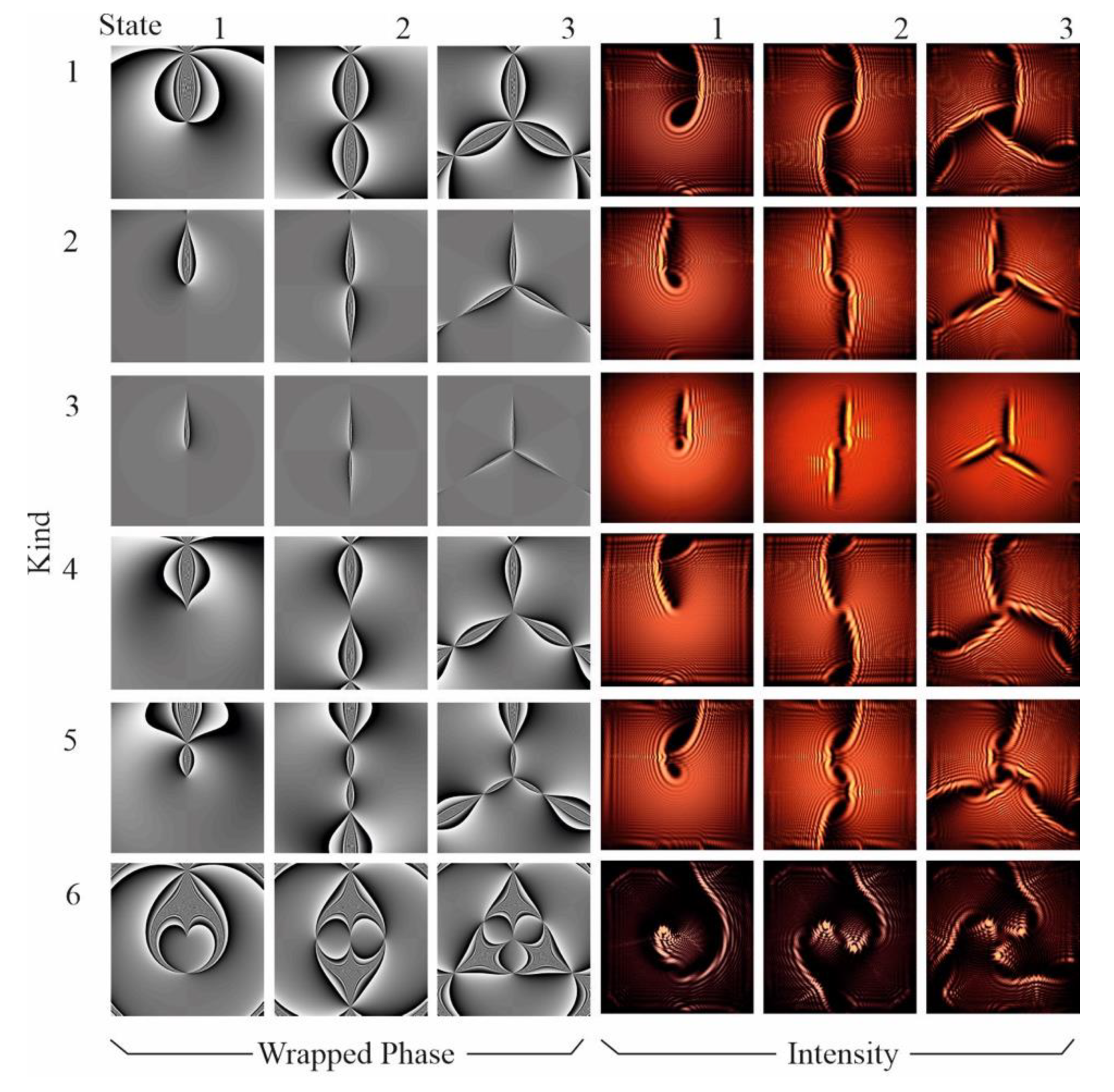
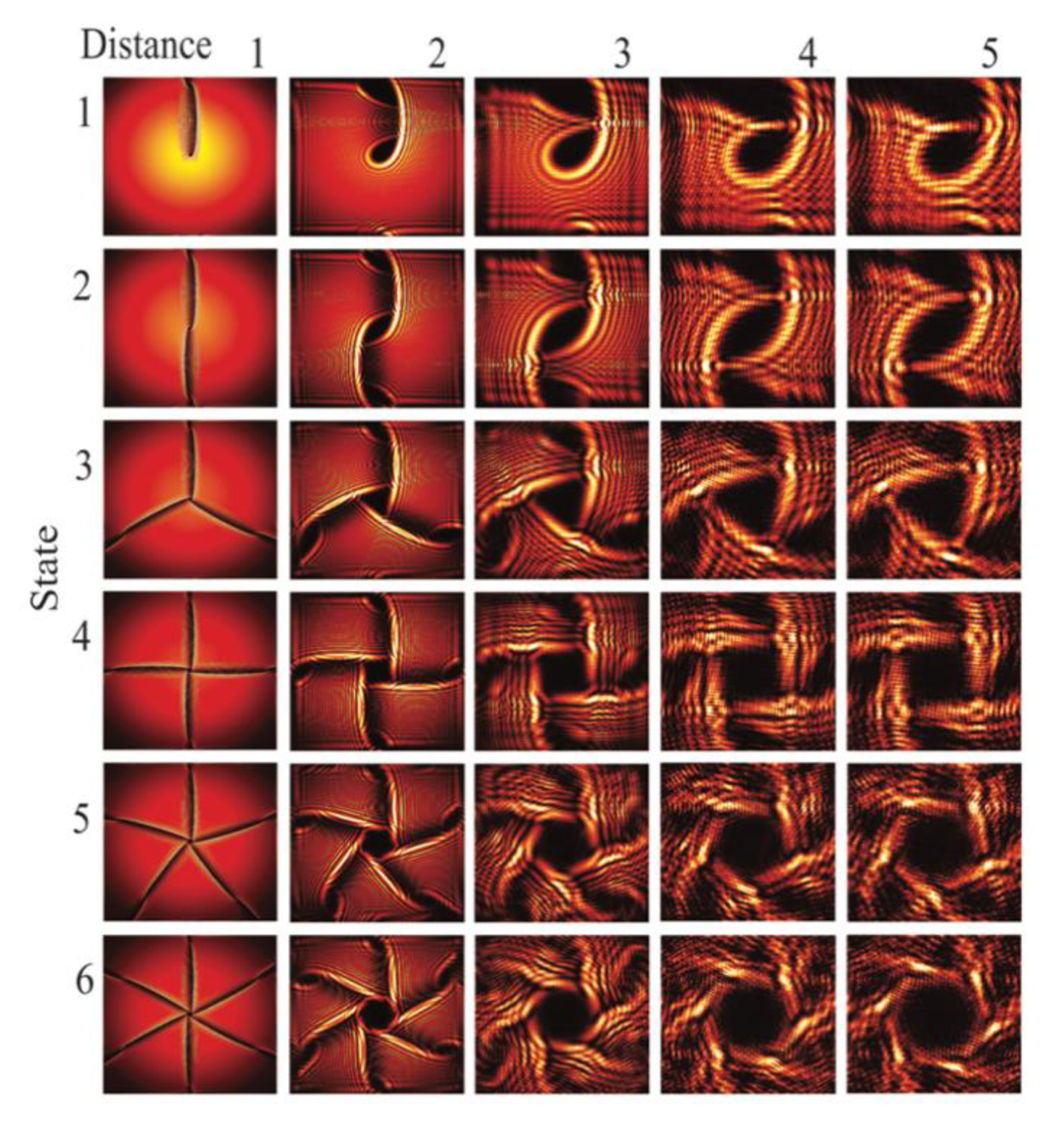
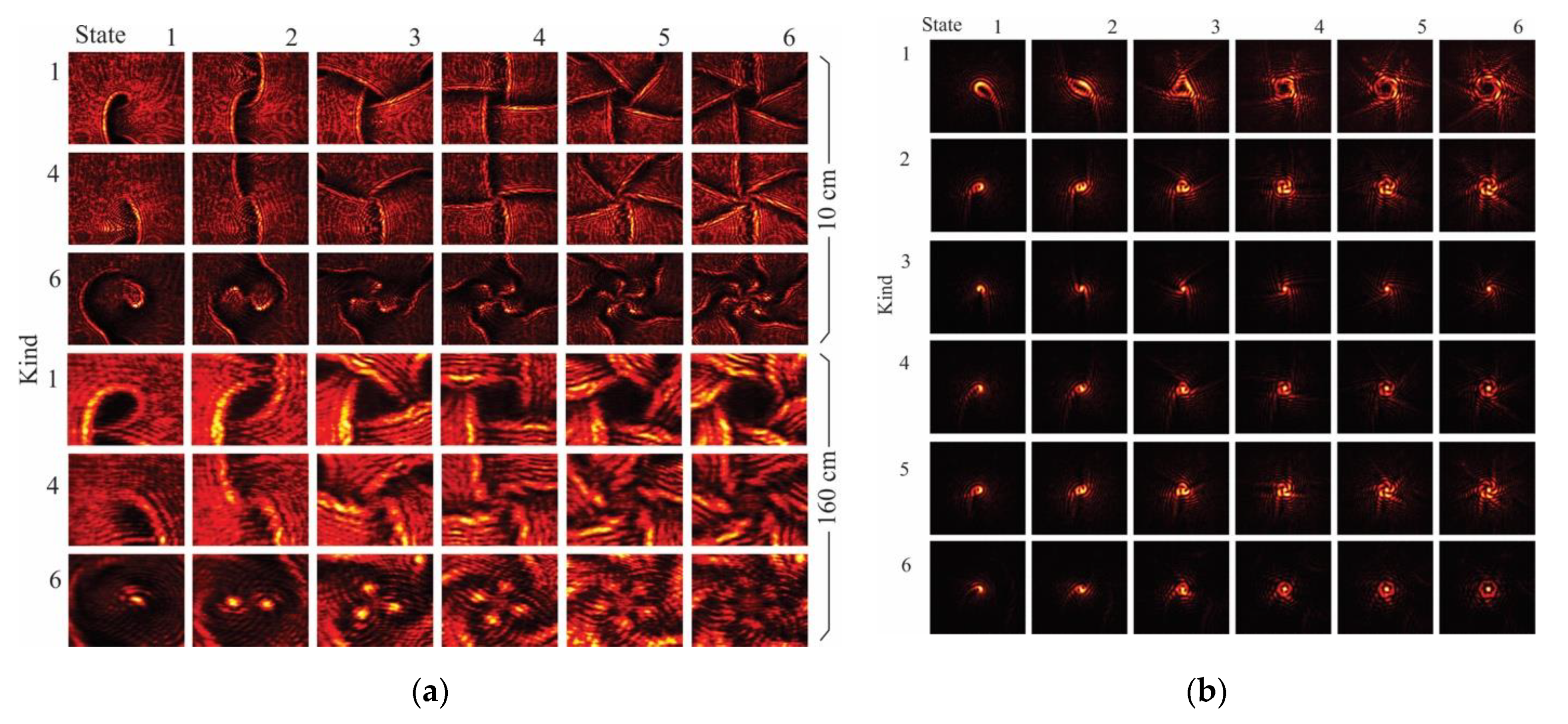
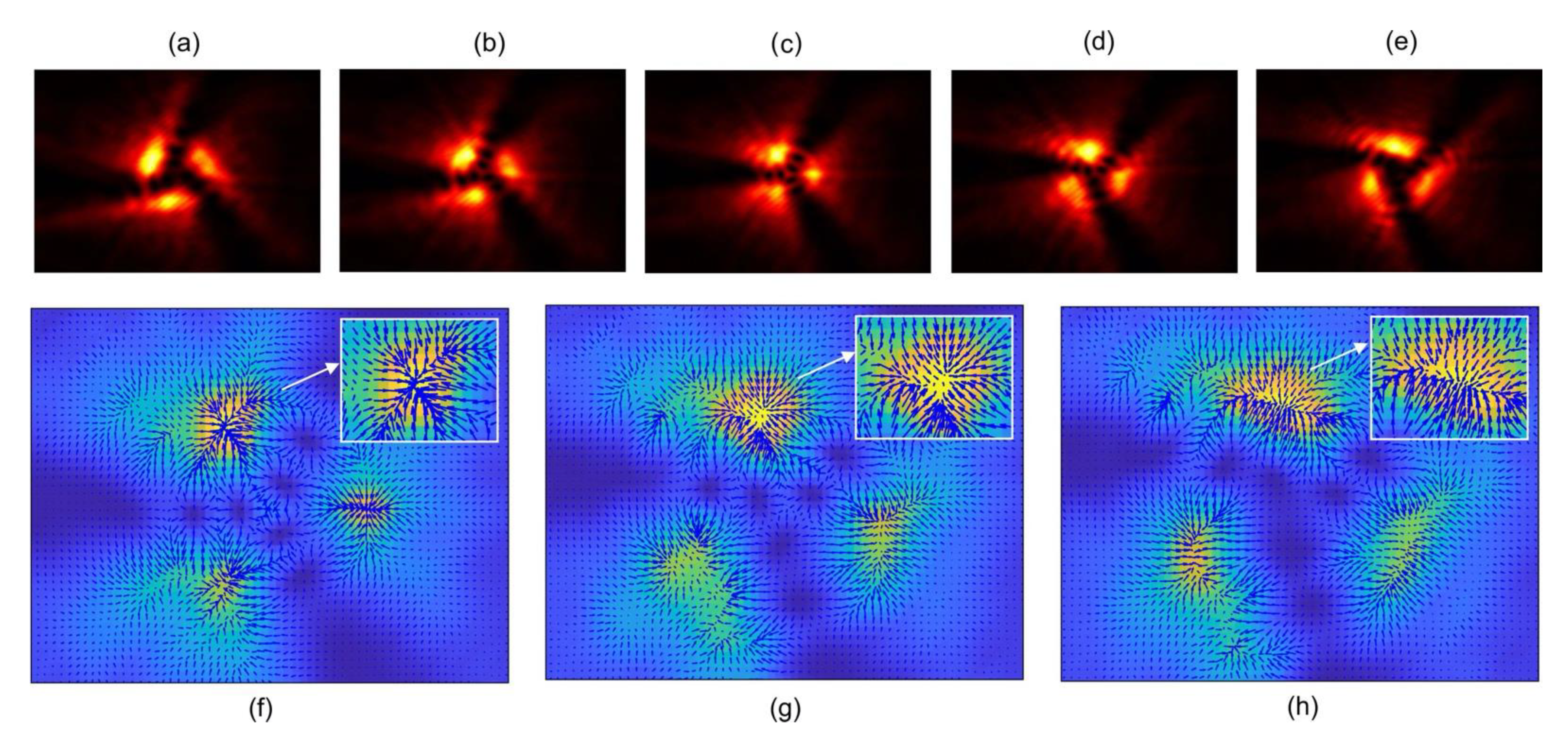
4. Results and Discussion
4.1. Analysis
4.2. Application
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rubinsztein-Dunlop, H.; Forbes, A.; Berry, M.V.; Dennis, M.R.; Andrews, D.L.; Mansuripur, M.; Denz, C.; Alpmann, C.; Banzer, P.; Bauer, T.; et al. A Roadmap to structured light. J. Opt. 2016, 19, 013001. [Google Scholar] [CrossRef]
- Lamperska, W.; Masajada, J.; Drobczyński, S.; Wasylczyk, P. Optical vortex torque measured with optically trapped microbarbells. Appl. Opt. 2020, 59, 4703–4707. [Google Scholar] [CrossRef] [PubMed]
- Gahagan, K.T.; Swartzlander, G. Optical vortex trapping of particles. Opt. Lett. 1996, 21, 827–829. [Google Scholar] [CrossRef] [PubMed]
- Tian, Y.; Wang, L.; Duan, G.; Yu, L. Multi-trap optical tweezers based on composite vortex beams. Opt. Commun. 2021, 485, 126712. [Google Scholar] [CrossRef]
- Palacios, D.; Rozas, D.; Swartzlander, J.G.A. Observed Scattering into a Dark Optical Vortex Core. Phys. Rev. Lett. 2002, 88, 103902. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Song, H.; Zhang, R.; Zhao, Z.; Liu, C.; Pang, K.; Song, H.; Du, J.; Willner, A.N.; Almaiman, A.; et al. Increasing system tolerance to turbulence in a 100-Gbit/s QPSK free-space optical link using both mode and space diversity. Opt. Commun. 2021, 480, 126488. [Google Scholar] [CrossRef]
- Davis, J.A.; Cottrell, D.M.; Campos, J.; Yzuel, M.; Moreno, I. Encoding amplitude information onto phase-only filters. Appl. Opt. 1999, 38, 5004–5013. [Google Scholar] [CrossRef]
- Meltaus, J.; Salo, J.; Noponen, E.; Salomaa, M.; Viikari, V.; Lonnqvist, A.; Koskinen, T.; Saily, J.; Hakli, J.; Ala-Laurinaho, J.; et al. Millimeter-wave beam shaping using holograms. IEEE Trans. Microw. Theory Tech. 2003, 51, 1274–1280. [Google Scholar] [CrossRef]
- Bekshaev, A.; Karamoch, A. Spatial characteristics of vortex light beams produced by diffraction gratings with embedded phase singularity. Opt. Commun. 2008, 281, 1366–1374. [Google Scholar] [CrossRef]
- Lóxpez-Mariscal, C.; Gutiérrez-Vega, J.C.; Milne, G.; Dholakia, K. Orbital angular momentum transfer in helical Mathieu beams. Opt. Express 2006, 14, 4182–4187. [Google Scholar] [CrossRef]
- Hernández-Hernández, R.J.; Terborg, R.A.; Ricardez-Vargas, I.; Volke-Sepúlveda, K. Experimental generation of Mathieu-Gauss beams with a phase-only spatial light modulator. Appl. Opt. 2010, 49, 6903–6909. [Google Scholar] [CrossRef]
- Alonzo, C.A.; Rodrigo, P.J.; Glückstad, J. Helico-conical optical beams: A product of helical and conical phase fronts. Opt. Express 2005, 13, 1749–1760. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.-H.; Roichman, Y.; Grier, D. Optical solenoid beams. Opt. Express 2010, 18, 6988–6993. [Google Scholar] [CrossRef] [Green Version]
- Daria, V.R.; Palima, D.Z.; Glückstad, J. Optical twists in phase and amplitude. Opt. Express 2011, 19, 476–481. [Google Scholar] [CrossRef] [Green Version]
- MacDonald, M.; Volke-Sepulveda, K.; Paterson, L.; Arlt, J.; Sibbett, W.; Dholakia, K. Revolving interference patterns for the rotation of optically trapped particles. Opt. Commun. 2002, 201, 21–28. [Google Scholar] [CrossRef]
- Zhang, P.; Huang, S.; Hu, Y.; Hernandez, D.; Chen, Z. Generation and nonlinear self-trapping of optical propelling beams. Opt. Lett. 2010, 35, 3129–3131. [Google Scholar] [CrossRef]
- Sui, X.; Zhao, J.; Liu, B.; Yan, Z.; Cao, C.; Zhou, S. Self-acceerating fan-shaped beams along arbitrary trajectories: A new tool for optical manipulation. J. Opt. 2016, 19, 015611. [Google Scholar] [CrossRef]
- Lu, Z.; Yan, B.; Chang, K.; Qiao, Y.; Li, C.; Hu, J.; Xu, T.; Zhang, H.; Lin, W.; Yue, Y.; et al. Space division multiplexing technology based on transverse wavenumber of Lommel–Gaussian beam. Opt. Commun. 2021, 488, 126835. [Google Scholar] [CrossRef]
- Ashkin, A. Acceleration and Trapping of Particles by Radiation Pressure. Phys. Rev. Lett. 1970, 24, 156–159. [Google Scholar] [CrossRef] [Green Version]
- Ashkin, A.; Dziedzic, J.M.; Bjorkholm, J.E.; Chu, S. Observation of a single-beam gradient force optical trap for dielectric particles. Opt. Lett. 1986, 11, 288–290. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ashkin, A. Optical trapping and manipulation of neutral particles using lasers. Proc. Natl. Acad. Sci. USA 1997, 94, 4853–4860. [Google Scholar] [CrossRef] [Green Version]
- Neuman, K.; Block, S.M. Optical trapping. Rev. Sci. Instrum. 2004, 75, 2787–2809. [Google Scholar] [CrossRef]
- Moffitt, J.R.; Chemla, Y.R.; Smith, S.B.; Bustamante, C. Recent advances in optical tweezers. Annu. Rev. Biochem. 2008, 77, 205–228. [Google Scholar] [CrossRef] [Green Version]
- Friese, M.E.J.; Enger, J.; Rubinsztein-Dunlop, H.; Heckenberg, N.R. Optical angular-momentum transfer to trapped absorbing particles. Phys. Rev. A 1996, 54, 1593–1596. [Google Scholar] [CrossRef] [Green Version]
- Bustamante, C. Of torques, forces, and protein machines. Protein Sci. 2009, 13, 3061–3065. [Google Scholar] [CrossRef]
- Parkin, S.J.; Vogel, R.; Persson, M.; Funk, M.; Loke, V.L.Y.; Nieminen, T.A.; Heckenberg, N.R.; Rubinsztein-Dunlop, H. Highly birefringent vaterite microspheres: Production, characterization and applications for optical micromanipulation. Opt. Express 2009, 17, 21944–21955. [Google Scholar] [CrossRef]
- Peters, E.; Funes, G.; Anguita, J.A. Singular beams based on tangential phase warp. Opt. Lett. 2019, 44, 3769–3772. [Google Scholar] [CrossRef] [PubMed]
- He, H.; Heckenberg, N.; Rubinsztein-Dunlop, H. Optical Particle Trapping with Higher-order Doughnut Beams Produced Using High Efficiency Computer Generated Holograms. J. Mod. Opt. 1995, 42, 217–223. [Google Scholar] [CrossRef]
- Anguita, J.A.; Herreros, J.; Djordjevic, I.B. Coherent multimode OAM superpositions for multidimensional modulation. IEEE Photon. J. 2014, 6, 1–11. [Google Scholar] [CrossRef]
- Cojoc, D.; Garbin, V.; Ferrari, E.; Businaro, L.; Romanato, F.; Di Fabrizio, E. Laser trapping and micro-manipulation using optical vortices. Microelectron. Eng. 2005, 78, 125–131. [Google Scholar] [CrossRef]
- Melo, B.; Brandão, I.; Da, B.S.P.; Rodrigues, R.; Khoury, A.; Guerreiro, T. Optical trapping in a dark focus. Phys. Rev. Appl. 2020, 14, 034069. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Funes, G.; Peters, E.; Anguita, J. Singular Warped Beams Controlled by Tangent Phase Modulation. Photonics 2021, 8, 343. https://doi.org/10.3390/photonics8080343
Funes G, Peters E, Anguita J. Singular Warped Beams Controlled by Tangent Phase Modulation. Photonics. 2021; 8(8):343. https://doi.org/10.3390/photonics8080343
Chicago/Turabian StyleFunes, Gustavo, Eduardo Peters, and Jaime Anguita. 2021. "Singular Warped Beams Controlled by Tangent Phase Modulation" Photonics 8, no. 8: 343. https://doi.org/10.3390/photonics8080343





