Light Confinement with Structured Beams in Gold Nanoparticle Suspensions
Abstract
1. Introduction
2. Material and Methods
2.1. Nanoparticle Synthesis
2.2. Nonlinearity: z-Scan Analysis
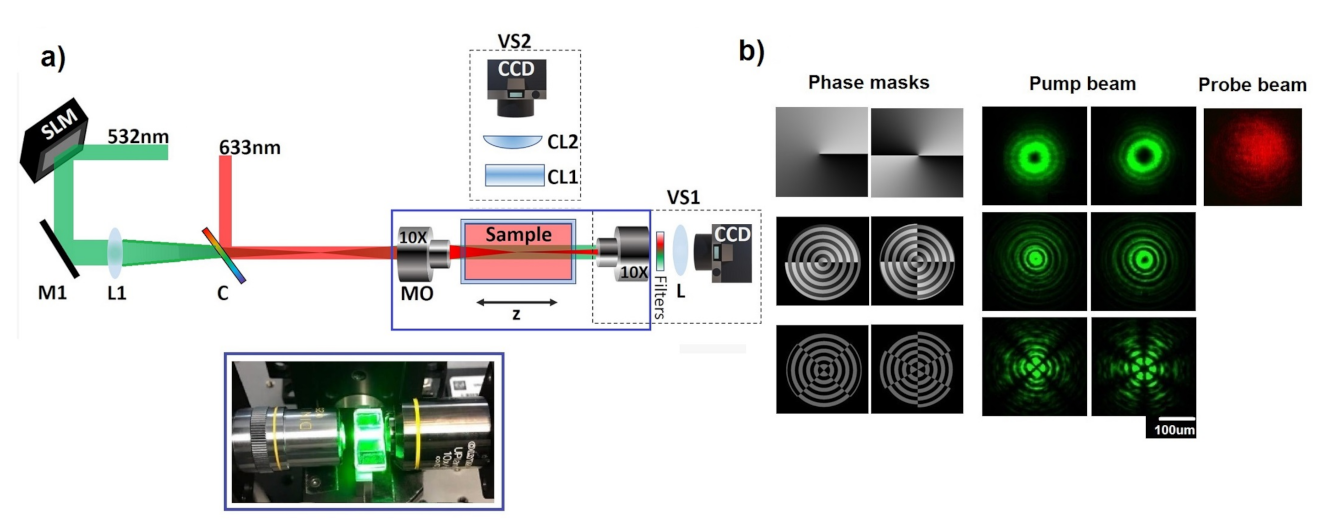
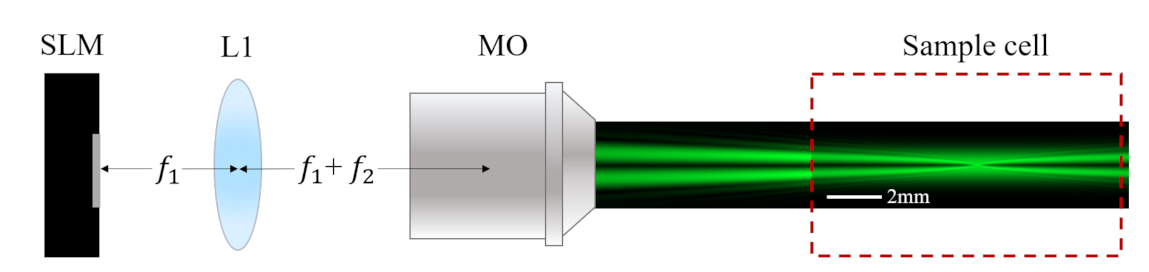
2.3. Experimental Set-Up and Characterization
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| NP | Metal Nanoparticles |
| CW | Continuous Wavelength |
| BGN | Bio-synthesized Gold Nanoparticles |
| TEM | Transmission Electron Microscope |
| SLM | Spatial Light Modulator |
| OAM | Optical Angular Momentum |
| MO | Microscope Objective |
| C | (Beam) Combiner |
| CCD | Charge Coupled Device |
| SV | Simple Vortex |
| BV | Bessel Vortex |
| BC | Bessel-Cosine |
| VS1 | Visualisation System 1 |
| VS2 | Visualisation System 2 |
References
- Wilson, M.; Kannangara, K.; Smith, G.; Simmons, M.; Raguse, B. Nanotechnology: Basic Science and Emerging Technologies; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Roco, M.C.; Mirkin, C.A.; Hersam, M.C. Nanotechnology Research Directions for Societal Needs in 2020: Summary of International Study. J. Nanopart. Res. 2011, 13, 897–919. [Google Scholar] [CrossRef]
- Boisseau, P.; Loubaton, B. Nanomedicine, nanotechnology in medicine. C. R. Phys. 2011, 12, 620–636. [Google Scholar] [CrossRef]
- Rogers, B.; Adams, J.; Pennathur, S. Nanotechnology: Understanding Small Systems; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Fardad, S.; Salandrino, A.; Heinrich, M.; Zhang, P.; Chen, Z.; Christodoulides, D.N. Plasmonic resonant solitons in metallic nanosuspensions. Nano Lett. 2014, 14, 2498–2504. [Google Scholar] [CrossRef]
- Sathyavathi, R.; Krishna, M.B.; Rao, S.V.; Saritha, R.; Rao, D.N. Biosynthesis of silver nanoparticles using Coriandrum sativum leaf extract and their application in nonlinear optics. Adv. Sci. Lett. 2010, 3, 138–143. [Google Scholar] [CrossRef]
- Begum, N.A.; Mondal, S.; Basu, S.; Laskar, R.A.; Mandal, D. Biogenic synthesis of Au and Ag nanoparticles using aqueous solutions of Black Tea leaf extracts. Coll. Surf. B Biointerfaces 2009, 71, 113–118. [Google Scholar] [CrossRef] [PubMed]
- Marchiol, L. Synthesis of metal nanoparticles in living plants. It. J. Agron. 2012, 7, 274–282. [Google Scholar] [CrossRef]
- Gardea-Torresdey, J.L.; Gomez, E.; Peralta-Videa, J.R.; Parsons, J.G.; Troiani, H.; Jose-Yacaman, M. Alfalfa sprouts: A natural source for the synthesis of silver nanoparticles. Langmuir 2003, 19, 1357–1361. [Google Scholar] [CrossRef]
- Park, Y.; Hong, Y.; Weyers, A.; Kim, Y.; Linhardt, R. Polysaccharides and phytochemicals: A natural reservoir for the green synthesis of gold and silver nanoparticles. IET Nanobiotechnol. 2011, 5, 69–78. [Google Scholar] [CrossRef] [PubMed]
- Souza, R.F.; Alencar, M.A.; da Silva, E.C.; Meneghetti, M.R.; Hickmann, J.M. Nonlinear optical properties of Au nanoparticles colloidal system: Local and nonlocal responses. Appl. Phys. Lett. 2008, 92, 201902. [Google Scholar] [CrossRef]
- Reyna, A.S.; De Araujo, C.B. Guiding and confinement of light induced by optical vortex solitons in a cubic–quintic medium. Opt. Lett. 2016, 41, 191–194. [Google Scholar] [CrossRef] [PubMed]
- Kelly, T.S.; Ren, Y.X.; Samadi, A.; Bezryadina, A.; Christodoulides, D.; Chen, Z. Guiding and nonlinear coupling of light in plasmonic nanosuspensions. Opt. Lett. 2016, 41, 3817–3820. [Google Scholar] [CrossRef]
- Shvedov, V.; Cyprych, K.; Salazar-Romero, M.Y.; Izdebskaya, Y.; Krolikowski, W. Nonlinear propagation and quasi self-confinement of light in plasmonic resonant media. Opt. Express 2018, 26, 23196–23206. [Google Scholar] [CrossRef]
- Balbuena Ortega, A.; Brambila, E.; López Gayou, V.; Delgado Macuil, R.; Orduña Diaz, A.; Zamilpa Alvarez, A.; Arzola, A.; Volke-Sepúlveda, K. Light control through a nonlinear lensing effect in a colloid of biosynthesized gold nanoparticles. J. Mod. Opt. 2019, 66, 502–511. [Google Scholar] [CrossRef]
- Balbuena Ortega, A.; Torres-González, F.; López Gayou, V.; Delgado Macuil, R.; Cardoso Sakamoto, J.; Arzola, A.; Assanto, G.; Volke-Sepulveda, K. Guiding light with singular beams in nanoplasmonic colloids. Appl. Phys. Lett. 2021, 118, 061102. [Google Scholar] [CrossRef]
- Snyder, A.W.; Ladouceur, F. Light Guiding Light: Letting Light Be the Master of Its Own Destiny. Opt. Photon. News 1999, 10, 35. [Google Scholar] [CrossRef]
- Stegeman, G.I.; Segev, M. Optical spatial solitons and their interactions: Universality and diversity. Science 1999, 286, 1518–1523. [Google Scholar] [CrossRef] [PubMed]
- Assanto, G.; Fratalocchi, A.; Peccianti, M. Spatial solitons in nematic liquid crystals: From bulk to discrete. Opt. Express 2007, 15, 5248–5259. [Google Scholar] [CrossRef]
- Chen, Z.; Segev, M.; Christodoulides, D.N. Optical spatial solitons: Historical overview and recent advances. Rep. Progress Phys. 2012, 75, 086401. [Google Scholar] [CrossRef]
- Snyder, A.W.; Sheppard, A. Collisions, steering, and guidance with spatial solitons. Opt. Lett. 1993, 18, 482–484. [Google Scholar] [CrossRef]
- Fratalocchi, A.; Piccardi, A.; Peccianti, M.; Assanto, G. Nonlinearly controlled angular momentum of soliton clusters. Opt. Lett. 2007, 32, 1447–1449. [Google Scholar] [CrossRef]
- Piccardi, A.; Alberucci, A.; Bortolozzo, U.; Residori, S.; Assanto, G. Soliton gating and switching in liquid crystal light valve. Appl. Phys. Lett. 2010, 96, 071104. [Google Scholar] [CrossRef]
- Izdebskaya, Y.V.; Rebling, J.; Desyatnikov, A.; Assanto, G.; Kivshar, Y.S. All-optical switching of a signal by a pair of interacting nematicons. Opt. Express 2012, 20, 24701–24707. [Google Scholar] [CrossRef] [PubMed]
- Salazar-Romero, M.Y.; Ayala, Y.A.; Brambila, E.; Lopez-Peña, L.A.; Sciberras, L.; Minzoni, A.A.; Terborg, R.A.; Torres, J.P.; Volke-Sepúlveda, K. Steering and switching of soliton-like beams via interaction in a nanocolloid with positive polarizability. Opt. Lett. 2017, 42, 2487–2490. [Google Scholar] [CrossRef] [PubMed]
- Perumbilavil, S.; Piccardi, A.; Barboza, R.; Buchnev, O.; Kauranen, M.; Strangi, G.; Assanto, G. Beaming random lasers with soliton control. Nat. Commun. 2018, 9, 3863. [Google Scholar] [CrossRef] [PubMed]
- Assanto, G. Nematicons: Reorientational solitons from optics to photonics. Liq. Cryst. Rev. 2018, 6, 170–194. [Google Scholar] [CrossRef]
- Kivshar, Y.S.; Luther-Davies, B. Dark optical solitons: Physics and applications. Phys. Rep. 1998, 298, 81–197. [Google Scholar] [CrossRef]
- Desyatnikov, A.; Torner, L.; Kivshar, Y. Optical vortices and vortex solitons. Prog. Opt. 2005, 47, 1–60. [Google Scholar]
- Andersen, D.R.; Hooton, D.E.; Swartzlander, G.A.; Kaplan, A.E. Direct measurement of the transverse velocity of dark spatial solitons. Opt. Lett. 1990, 15, 783–785. [Google Scholar] [CrossRef] [PubMed]
- Allan, G.; Skinner, S.; Andersen, D.; Smirl, A.L. Observation of fundamental dark spatial solitons in semiconductors using picosecond pulses. Opt. Lett. 1991, 16, 156–158. [Google Scholar] [CrossRef]
- Luther-Davies, B.; Xiaoping, Y. Waveguides and Y junctions formed in bulk media by using dark spatial solitons. Opt. Lett. 1992, 17, 496–498. [Google Scholar] [CrossRef]
- Luther-Davies, B.; Yang, X. Steerable optical waveguides formed in self-defocusing media by using dark spatial solitons. Opt. Lett. 1992, 17, 1755–1757. [Google Scholar] [CrossRef]
- Nye, J.F.; Berry, M.V. Dislocations in wave trains. Proc. R. Soc. Lond. A Math. Phys. Sci. 1974, 336, 165–190. [Google Scholar]
- Snyder, A.; Poladian, L.; Mitchell, D. Stable black self-guided beams of circular symmetry in a bulk Kerr medium. Opt. Lett. 1992, 17, 789–791. [Google Scholar] [CrossRef] [PubMed]
- Swartzlander, G., Jr.; Law, C. Optical vortex solitons observed in Kerr nonlinear media. Phys. Rev. Lett. 1992, 69, 2503. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Segev, M.; Christodoulides, D.N.; Feigelson, R.S. Waveguides formed by incoherent dark solitons. Opt. Lett. 1999, 24, 1160–1162. [Google Scholar] [CrossRef]
- Passier, R.; Chauvet, M.; Wacogne, B.; Devaux, F. Light-induced waveguide by a finite self-trapped vortex beam in a photorefractive medium. J. Opt. 2011, 13, 085502. [Google Scholar] [CrossRef]
- Gadonas, R.; Jarutis, V.; Paškauskas, R.; Smilgevičius, V.; Stabinis, A.; Vaičaitis, V. Self-action of Bessel beam in nonlinear medium. Opt. Commun. 2001, 196, 309–316. [Google Scholar] [CrossRef]
- Johannisson, P.; Anderson, D.; Lisak, M.; Marklund, M. Nonlinear Bessel beams. Opt. Commun. 2003, 222, 107–115. [Google Scholar] [CrossRef]
- Rotschild, C.; Cohen, O.; Manela, O.; Segev, M.; Carmon, T. Solitons in nonlinear media with an infinite range of nonlocality: First observation of coherent elliptic solitons and of vortex-ring solitons. Phys. Rev. Lett. 2005, 95, 213904. [Google Scholar] [CrossRef]
- Porras, M.A.; Parola, A.; Faccio, D.; Dubietis, A.; Di Trapani, P. Nonlinear unbalanced Bessel beams: Stationary conical waves supported by nonlinear losses. Phys. Rev. Lett. 2004, 93, 153902. [Google Scholar] [CrossRef]
- Maleshkov, G.; Neshev, D.N.; Dreischuh, A. Nonlinear beam steering by fractional vortex dipoles. Phys. Rev. A 2009, 80, 053828. [Google Scholar] [CrossRef]
- Jukna, V.; Milián, C.; Xie, C.; Itina, T.; Dudley, J.; Courvoisier, F.; Couairon, A. Filamentation with nonlinear Bessel vortices. Opt. Express 2014, 22, 25410–25425. [Google Scholar] [CrossRef] [PubMed]
- Porras, M.A.; Ramos, F. Quasi-ideal dynamics of vortex solitons embedded in flattop nonlinear Bessel beams. Opt. Lett. 2017, 42, 3275–3278. [Google Scholar] [CrossRef] [PubMed]
- García-Riquelme, J.L.; Ramos, F.; Porras, M.A. Optical vortex trapping and annihilation by means of nonlinear Bessel beams in nonlinear absorbing media. J. Opt. Soc. Am. B 2018, 35, 3030–3038. [Google Scholar] [CrossRef]
- Stoyanov, L.; Dimitrov, N.; Stefanov, I.; Neshev, D.; Dreischuh, A. Optical waveguiding by necklace and azimuthon beams in nonlinear media. J. Opt. Soc. Am. B 2017, 34, 801–807. [Google Scholar] [CrossRef]
- Rose, P.; Boguslawski, M.; Denz, C. Nonlinear lattice structures based on families of complex nondiffracting beams. New J. Phys. 2012, 14, 033018. [Google Scholar] [CrossRef]
- Izdebskaya, Y.; Assanto, G.; Krolikowski, W. Observation of stable-vector vortex solitons. Opt. Lett. 2015, 40, 4182–4185. [Google Scholar] [CrossRef] [PubMed]
- Izdebskaya, Y.V.; Shvedov, V.G.; Jung, P.S.; Krolikowski, W. Stable vortex soliton in nonlocal media with orientational nonlinearity. Opt. Lett. 2018, 43, 66–69. [Google Scholar] [CrossRef]
- Laudyn, U.A.; Kwaśny, M.; Karpierz, M.A.; Assanto, G. Vortex nematicons in planar cells. Opt. Express 2020, 28, 8282–8290. [Google Scholar] [CrossRef] [PubMed]
- Kwaśny, M.; Karpierz, M.A.; Assanto, G.; Laudyn, U.A. Optothermal vortex-solitons in liquid crystals. Opt. Lett. 2020, 45, 2451–2453. [Google Scholar] [CrossRef]
- Brzobohatỳ, O.; Chvátal, L.; Šiler, M.; Zemánek, P. Complex colloidal structures with non-linear optical properties formed in an optical trap. Opt. Express 2020, 28, 37700–37707. [Google Scholar] [CrossRef]
- Sheik-Bahae, M.; Said, A.A.; Wei, T.H.; Hagan, D.J.; Van Stryland, E.W. Sensitive measurement of optical nonlinearities using a single beam. IEEE J. Quantum Electron. 1990, 26, 760–769. [Google Scholar] [CrossRef]
- Ashkin, A.; Dziedzic, J.M.; Bjorkholm, J.E.; Chu, S. Observation of a single-beam gradient force optical trap for dielectric particles. Opt. Lett. 1986, 11, 288–290. [Google Scholar] [CrossRef] [PubMed]
- Franke-Arnold, S.; Allen, L.; Padgett, M. Advances in optical angular momentum. Laser Photon. Rev. 2008, 2, 299–313. [Google Scholar] [CrossRef]
- Karimi, E.; Zito, G.; Piccirillo, B.; Marrucci, L.; Santamato, E. Hypergeometric-Gaussian modes. Opt. Lett. 2007, 32, 3053–3055. [Google Scholar] [CrossRef] [PubMed]
- Jorge, K.C.; Riva, R.; Rodrigues, N.A.; Sakamoto, J.M.; Destro, M.G. Scattered light imaging method (SLIM) for characterization of arbitrary laser beam intensity profiles. Appl. Opt. 2014, 53, 4555–4564. [Google Scholar] [CrossRef]
- Smyth, N.; Piccardi, A.; Alberucci, A.; Assanto, G. Highly nonlocal optical response: Benefit or drawback? J. Nonl. Opt. Phys. Mat. 2016, 25, 1650043. [Google Scholar] [CrossRef]
- Laudyn, U.; Piccardi, A.; Kwasny, M.; Karpierz, M.; Assanto, G. Thermo-optic soliton routing in nematic liquid crystals. Opt. Lett. 2018, 43, 2296–2299. [Google Scholar] [CrossRef] [PubMed]
- Assanto, G.; Khan, C.; Piccardi, A.; Smyth, N.F. Temperature control of nematicon trajectories. Phys. Rev. E 2019, 100, 062702. [Google Scholar] [CrossRef]
- Jung, P.S.; Krolikowski, W.; Laudyn, U.A.; Trippenbach, M.; Karpierz, M.A. Supermode spatial optical solitons in liquid crystals with competing nonlinearities. Phys. Rev. A 2017, 95, 023820. [Google Scholar] [CrossRef]
- Ramaniuk, A.; Trippenbach, M.; Jung, P.S.; Christodoulides, D.N.; Krolikowski, W.; Assanto, G. Scalar and vector supermode solitons owing to competing nonlocal nonlinearities. Opt. Express 2021, 29, 8015–8023. [Google Scholar] [CrossRef] [PubMed]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balbuena Ortega, A.; Torres-González, F.E.; López Gayou, V.; Delgado Macuil, R.; Assanto, G.; Volke-Sepulveda, K. Light Confinement with Structured Beams in Gold Nanoparticle Suspensions. Photonics 2021, 8, 221. https://doi.org/10.3390/photonics8060221
Balbuena Ortega A, Torres-González FE, López Gayou V, Delgado Macuil R, Assanto G, Volke-Sepulveda K. Light Confinement with Structured Beams in Gold Nanoparticle Suspensions. Photonics. 2021; 8(6):221. https://doi.org/10.3390/photonics8060221
Chicago/Turabian StyleBalbuena Ortega, Argelia, Felix E. Torres-González, Valentin López Gayou, Raul Delgado Macuil, Gaetano Assanto, and Karen Volke-Sepulveda. 2021. "Light Confinement with Structured Beams in Gold Nanoparticle Suspensions" Photonics 8, no. 6: 221. https://doi.org/10.3390/photonics8060221
APA StyleBalbuena Ortega, A., Torres-González, F. E., López Gayou, V., Delgado Macuil, R., Assanto, G., & Volke-Sepulveda, K. (2021). Light Confinement with Structured Beams in Gold Nanoparticle Suspensions. Photonics, 8(6), 221. https://doi.org/10.3390/photonics8060221





