Sensitivity-Tunable Oscillator-Accelerometer Based on Optical Fiber Bragg Grating
Abstract
1. Introduction
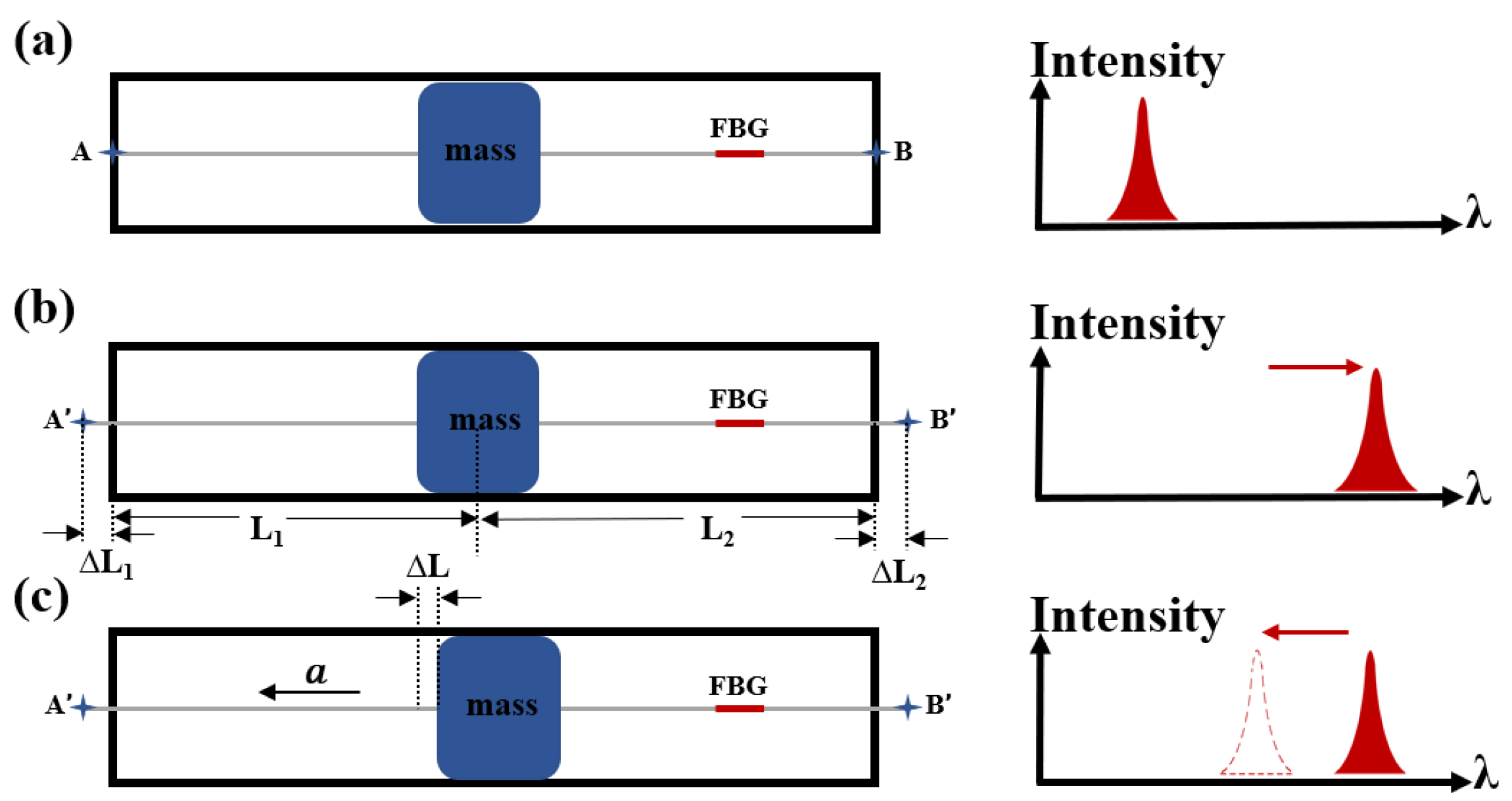
2. Sensing Principle and Design of FBG-Based Accelerometer
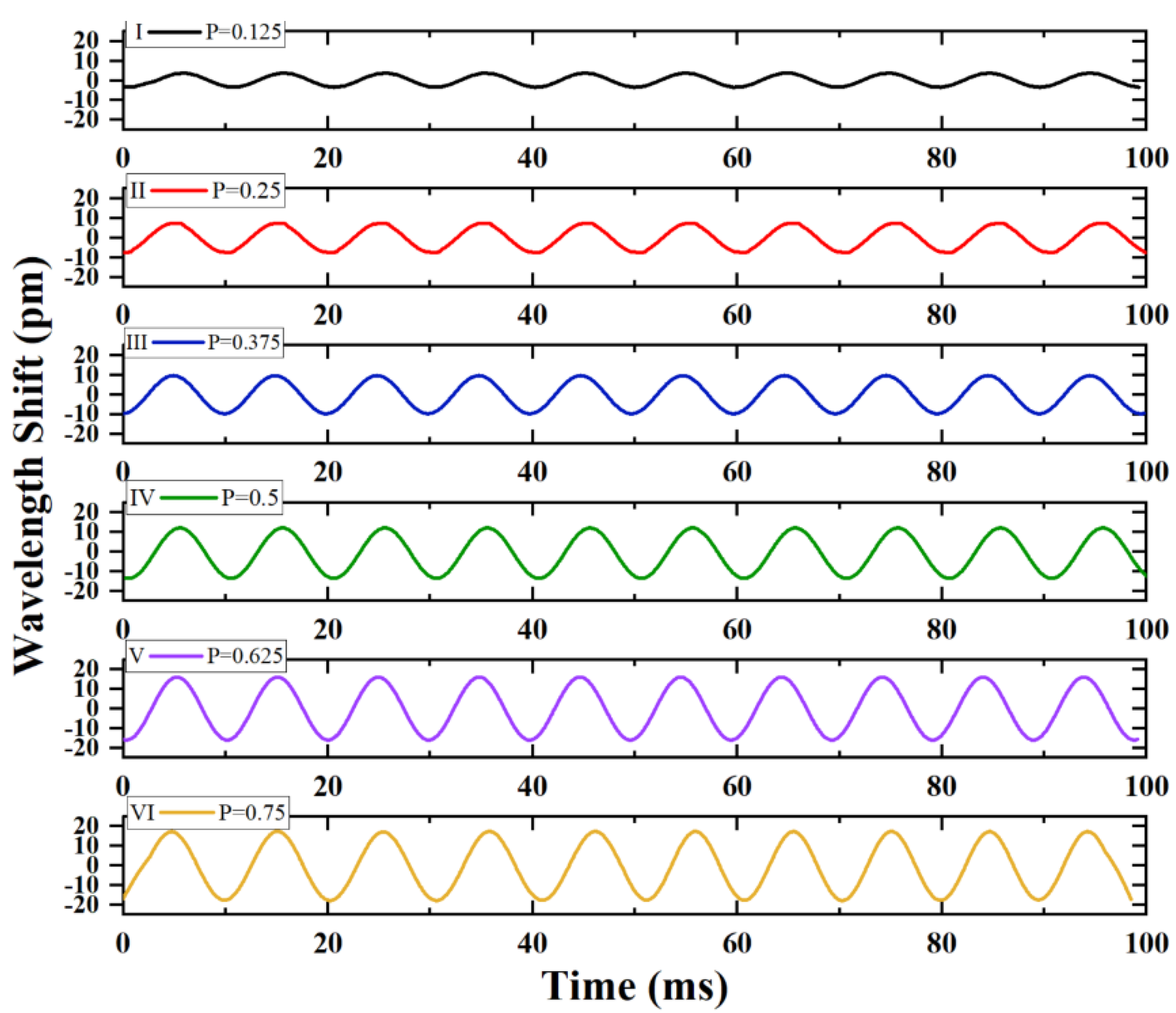
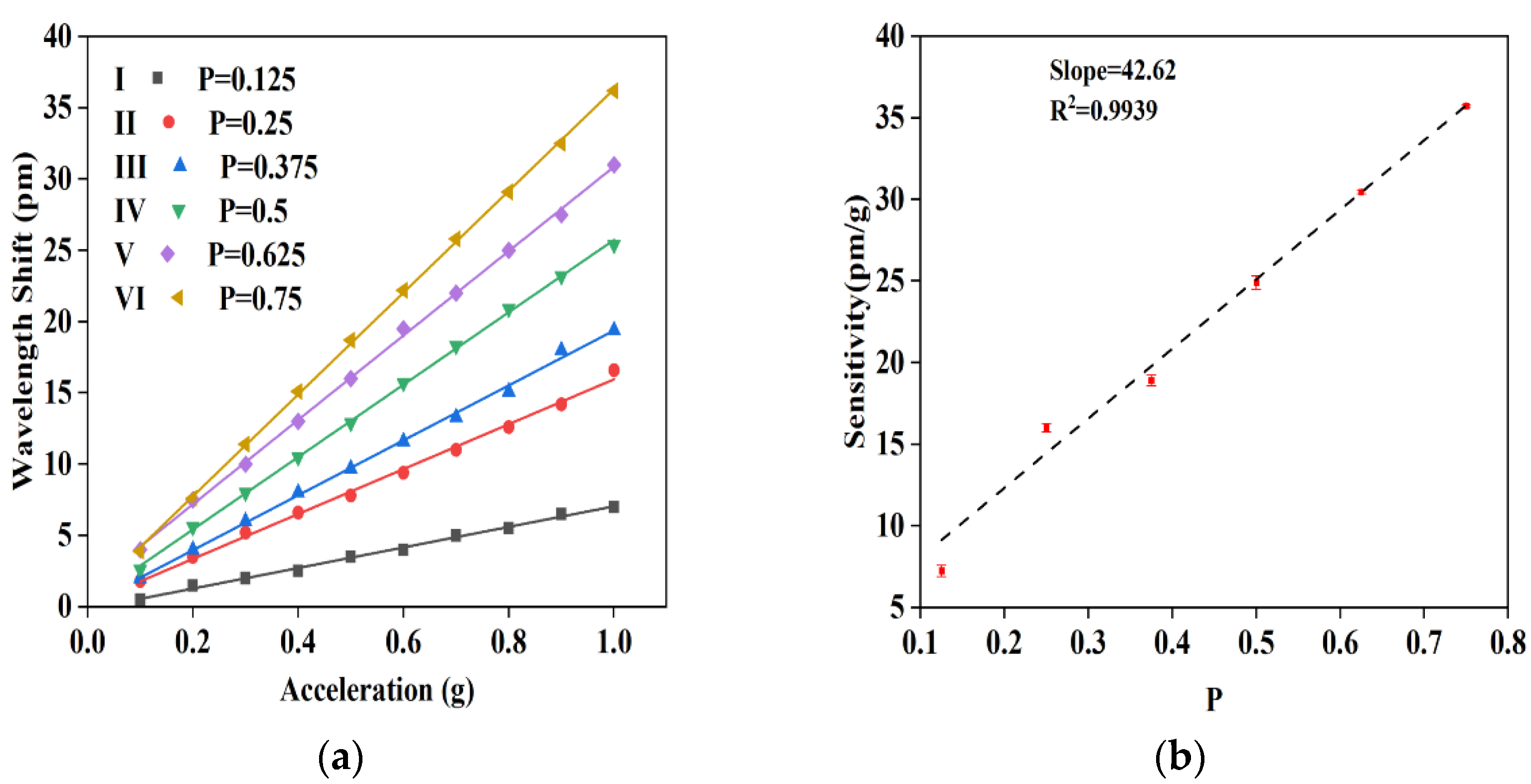
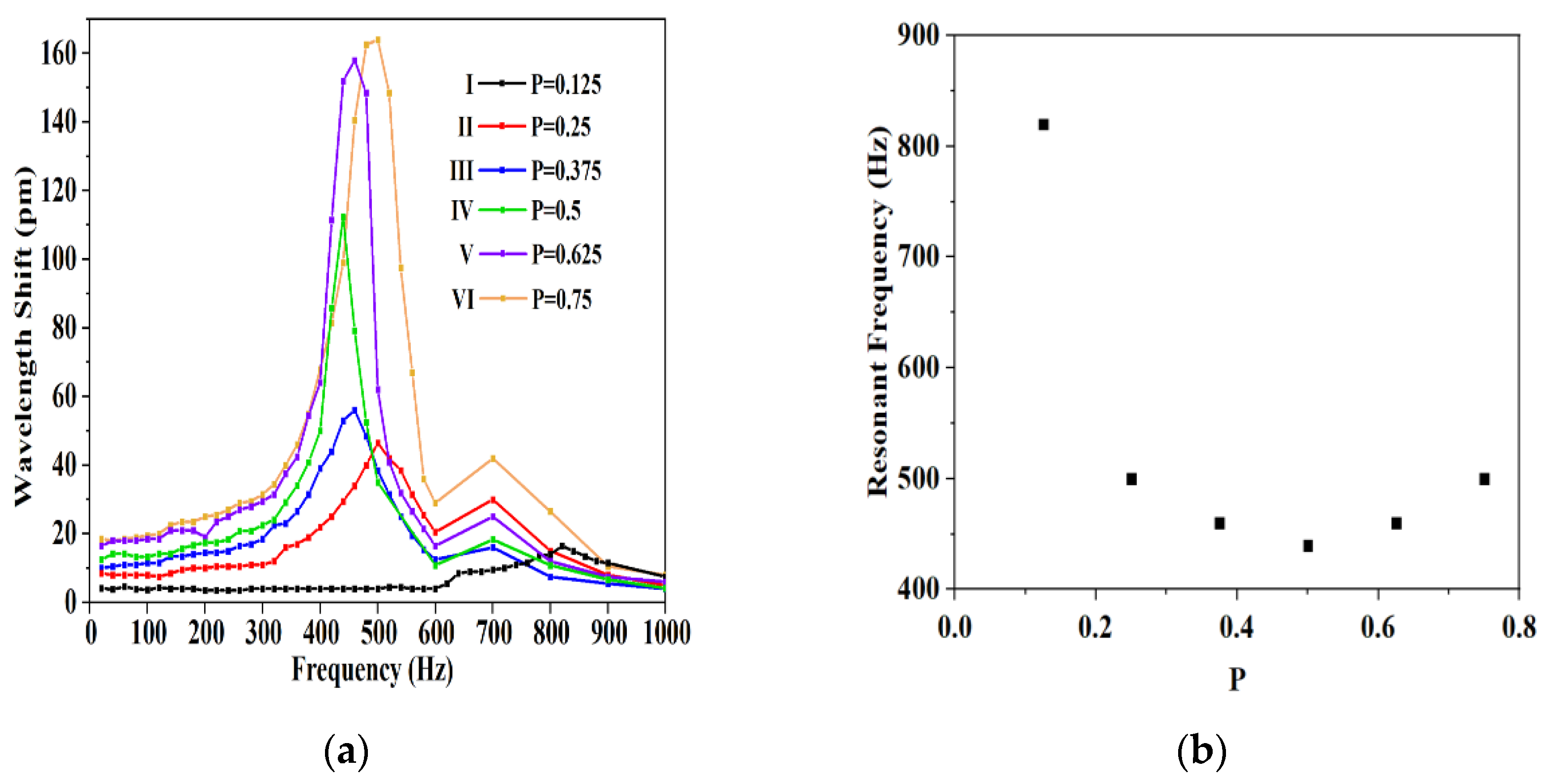
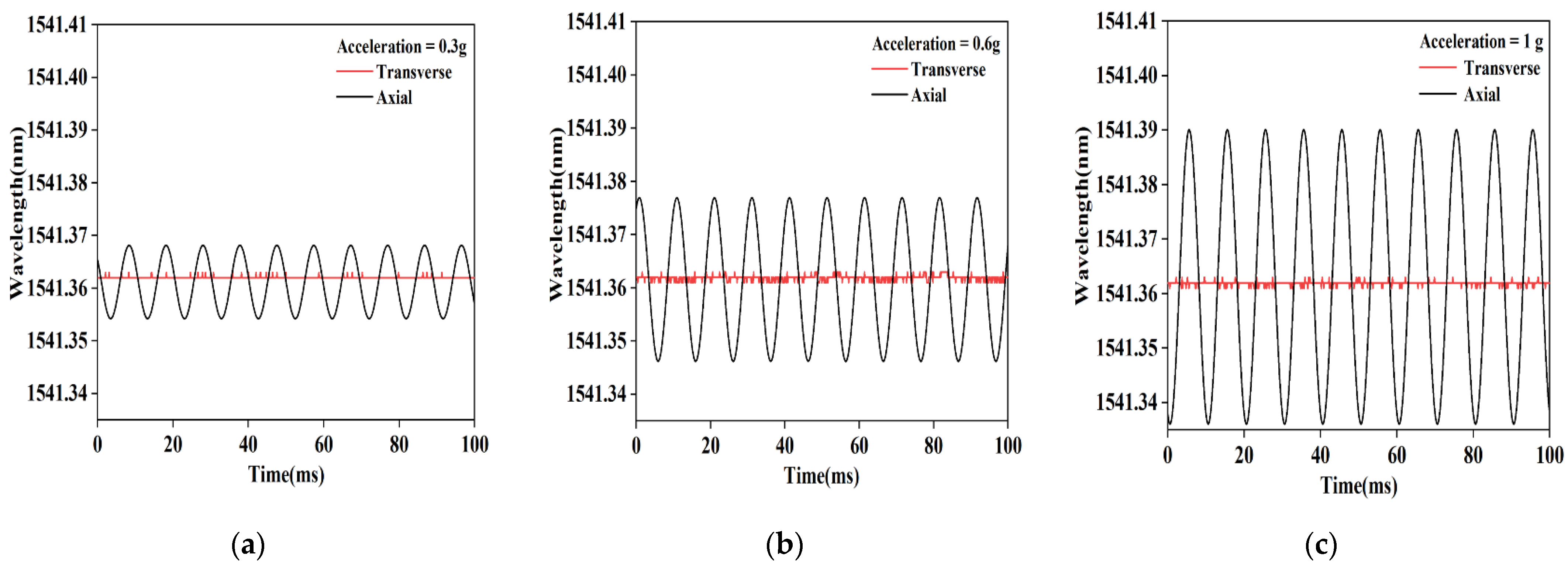
3. Characterization of the Accelerometer
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stolarik, M.; Nedoma, J.; Martinek, R.; Kepak, S.; Hrubesova, E.; Pinka, M.; Kolarik, J. New Methods to Seismic Monitoring: Laboratory Comparative Study of Michelson Fiber-Optic Interferometer and Pneumatic Measurement Systems. Photonics 2021, 8, 147. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, Z.; Huang, W.; Liu, W.; Li, L.; Li, F. Fiber laser sensors for micro seismic monitoring. Measurement 2016, 79, 203–210. [Google Scholar] [CrossRef]
- Yuan, L.; Liu, Z.; Yang, J.; Guo, C. Fiber Optic Brownian Motion Force Sensor. In Proceedings of the 12th International Conference on Optical Fiber Sensors, Cancun, Mexico, 23–27 October 2006. [Google Scholar] [CrossRef]
- Wu, X.; Zhang, F.; Zhang, X.; Li, S. Performance comparison of fiber laser geophones and moving-coil geophones. In Proceedings of the International Symposium on Optoelectronic Technology and Application 2014, Beijing, China, 13–15 May 2014; Volume 9297. [Google Scholar]
- Lu, Y.; Li, Z.; Liao, W.I. Damage monitoring of reinforced concrete frames under seismic loading using cement-based piezoelectric sensor. Mater. Struct. 2011, 44, 1273–1285. [Google Scholar] [CrossRef]
- Jackson, D.A.; Ribeiro, A.L.; Reekie, L.; Archambault, J.L. Simple multiplexing scheme for a fiber-optic grating sensor network. Opt. Lett. 1993, 18, 1192–1194. [Google Scholar] [CrossRef] [PubMed]
- Berkoff, T.; Kersey, A. Experimental demonstration of a fiber Bragg grating accelerometer. IEEE Photonics Technol. Lett. 1996, 8, 1677–1679. [Google Scholar] [CrossRef]
- Spero, R.E.; Whitcomb, S.E. The Laser Interferometer Gravitational-wave Observatory (LIGO). Opt. Photonics News 1995, 6, 35–39. [Google Scholar] [CrossRef]
- Gutiérrez, N.; Galvin, P.; Lasagni, F. Low weight additive manufacturing FBG accelerometer: Design, characterization and testing. Measurement 2018, 117, 295–303. [Google Scholar] [CrossRef]
- Peng, P.; Yang, J.; Gao, F. High-sensitivity fiber optic accelerometer based on multilayer fiber coils. In Proceedings of the 23rd International Conference on Optical Fibre Sensors, Santander, Spain, 2–6 June 2014. [Google Scholar]
- Yu, H.; Luo, Z.; Zheng, Y.; Ma, J.; Li, Z.; Jiang, X.; Li, Z. Temperature-Insensitive Vibration Sensor with Kagomé Hollow-Core Fiber Based Fabry–Perot Interferometer. J. Light. Technol. 2019, 37, 2261–2269. [Google Scholar] [CrossRef]
- Liu, T.; Cheng, J.; Lv, D.; Luo, Y.; Yan, Z.; Wang, K.; Liu, C.; Liu, D.; Sun, Q. DBR Fiber Laser Based High-Resolution Accelerometer Network. J. Light. Technol. 2019, 37, 2946–2953. [Google Scholar] [CrossRef]
- Guo, Y.; Zhang, D.; Fu, J.; Liu, S.; Zhu, F. Development and operation of a fiber Bragg grating based online monitoring strategy for slope deformation. Sens. Rev. 2015, 35, 348–356. [Google Scholar] [CrossRef]
- Todd, M.D.; Johnson, G.A.; Althouse, B.A.; Vohra, S.T. Flexural beam-based fiber Bragg grating accelerometers. IEEE Photonics Technol. Lett. 1998, 10, 1605–1607. [Google Scholar] [CrossRef]
- Du, J.; Li, L.; Fan, X.; Liu, Q.; He, Z. Sensitivity Enhancement for Fiber Bragg Grating Sensors by Four Wave Mixing. Photonics 2015, 2, 426–439. [Google Scholar] [CrossRef]
- Chen, X.; Wang, E.; Jiang, Y.; Zhan, H.; Li, H.; Lyu, G.; Sun, S. Generalized Resonance Sensor Based on Fiber Bragg Grating. Photonics 2021, 8, 156. [Google Scholar] [CrossRef]
- Feng, D.; Qiao, X.; Yang, H.; Rong, Q.; Wang, R.; Du, Y.; Hu, M.; Feng, Z. A Fiber Bragg Grating Accelerometer Based on a Hybridization of Cantilever Beam. IEEE Sens. J. 2014, 15, 1532–1537. [Google Scholar] [CrossRef]
- Mita, A.; Yokoi, I. Fiber bragg grating accelerometer for structural health monitoring. In Proceedings of the Fifth International Conference on Motion and Vibration Control (MOVIC 2000), Sydney, Australia, 4–8 December 2000. [Google Scholar]
- Wang, J.; Wei, L.; Li, R.; Liu, Q.; Yu, L.; Li, T.; Tan, Y. An FBG-Based 2-D Vibration Sensor with Adjustable Sensitivity. IEEE Sens. J. 2017, 17, 4716–4724. [Google Scholar] [CrossRef]
- Li, T.; Tan, Y.; Han, X.; Zheng, K.; Zhou, Z. Diaphragm Based Fiber Bragg Grating Acceleration Sensor with Temperature Compensation. Sensors 2017, 17, 218. [Google Scholar] [CrossRef] [PubMed]
- Guo, T.; Zhang, T.; Li, Y.; Qiao, X. Highly Sensitive FBG Seismometer With a 3D-Printed Hexagonal Configuration. J. Light. Technol. 2020, 38, 4588–4595. [Google Scholar] [CrossRef]
- Zhang, Y.; Qiao, X.; Liu, Q.; Yu, D.; Gao, H.; Shao, M.; Wang, X. Study on a fiber Bragg grating accelerometer based on com-pliant cylinder. Opt. Fiber Technol. 2015, 26, 229–233. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, J.; Gan, P.; Hu, Z.; Hu, Y. Design and Analysis of a Novel Dual FBG Accelerometer Based on Lantern Shape Metallic Shells. IEEE Sens. J. 2017, 17, 5130–5135. [Google Scholar] [CrossRef]
- Wang, X.; Guo, Y.; Xiong, L.; Wu, H. High-Frequency Optical Fiber Bragg Grating Accelerometer. IEEE Sens. J. 2018, 18, 4954–4960. [Google Scholar] [CrossRef]


| Parameter | I | II | III | IV | V | VI |
|---|---|---|---|---|---|---|
| P | 0.125 | 0.25 | 0.375 | 0.5 | 0.625 | 0.75 |
| Sensitivity (pm/g) | 7.6 | 15.8 | 19.3 | 25.4 | 30.6 | 35.7 |
| Frequency (Hz) | 820 | 500 | 460 | 440 | 460 | 500 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, X.; Tao, J.; Song, Q.; Sun, Y.; Yang, J.; Yan, Z. Sensitivity-Tunable Oscillator-Accelerometer Based on Optical Fiber Bragg Grating. Photonics 2021, 8, 223. https://doi.org/10.3390/photonics8060223
Xiao X, Tao J, Song Q, Sun Y, Yang J, Yan Z. Sensitivity-Tunable Oscillator-Accelerometer Based on Optical Fiber Bragg Grating. Photonics. 2021; 8(6):223. https://doi.org/10.3390/photonics8060223
Chicago/Turabian StyleXiao, Xiangpeng, Jinpeng Tao, Qingguo Song, Yuezhen Sun, Jiang Yang, and Zhijun Yan. 2021. "Sensitivity-Tunable Oscillator-Accelerometer Based on Optical Fiber Bragg Grating" Photonics 8, no. 6: 223. https://doi.org/10.3390/photonics8060223
APA StyleXiao, X., Tao, J., Song, Q., Sun, Y., Yang, J., & Yan, Z. (2021). Sensitivity-Tunable Oscillator-Accelerometer Based on Optical Fiber Bragg Grating. Photonics, 8(6), 223. https://doi.org/10.3390/photonics8060223




