Featured Application
This article is an extensive overview of the different types of in-fiber interferometric-based sensors and their technology.
Abstract
In-fiber interferometric-based sensors are a rapidly growing field, as these sensors exhibit many desirable characteristics compared to their regular fiber-optic counterparts and are being implemented in many promising devices. These sensors have the capability to make extremely accurate measurements on a variety of physical or chemical quantities such as refractive index, temperature, pressure, curvature, concentration, etc. This article is a comprehensive overview of the different types of in-fiber interferometric sensors that presents and discusses recent developments in the field. Basic configurations, a brief approach of the operating principle and recent applications are introduced for each interferometric architecture, making it easy to compare them and select the most appropriate one for the application at hand.
1. Introduction
In-fiber-optic sensors are one of the fastest developing research areas due to their advantages of light weight, small size, immunity to electromagnetic interference, multiplexing capability, simultaneous sensing ability of two or more measurands, compatibility with fiber-based systems, and usage in various environments, which can be challenging for traditional sensors. In a typical fiber optic interferometric sensor, the light is divided in at least two arms of the interferometer and at least one part of the light interacts with the measurand (a quantity or physical effect that is intended to be measured). However, the current trend in fiber optic interferometers is to miniaturize the sensors for micro-scale applications. Thus, traditional bulk optic components such as beam splitting, beam combining, etc., have been replaced by small-sized fiber devices that enable the sensors to operate on fiber scales. These interferometers have two optical paths in one physical line and one of the optical paths should be arranged to be easily affected by external perturbations. Thus, the in-line structure offers several advantages such as compactness, simplicity, easy alignment, high coupling efficiency, and high stability [1]. Since the interferometers provide a lot of temporal and spectral information, the measurand can be quantitatively determined by various means for detecting the changes in the wavelength, phase, intensity, frequency, bandwidth, and so on. With these sensing indicators, they can give remarkable performance with large dynamic range, high accuracy, and high sensitivity.
In the sensing process, it is vital to use an appropriate interference technology that will allow accurate measurement of the sensing parameter, whereas at the same time the performance of a fiber sensor (sensitivity, resolution, etc.) also depends on the sensing elements, i.e., the optical fiber used. Many specialty fibers have been employed, providing attractive features and increased performance, while assembly-free sensor schemes supported by femtosecond laser micromachining and etching technology are directly fabricated on an optical fiber, achieving more compact structures with high robustness. However, regardless of which fabrication approach is used, it is necessary to develop in-fiber interferometric sensors with not only high performance but also low fabrication cost and complexity. Several articles have presented a thorough theoretical background on fiber optic interferometric sensors and their principles of operation [1,2,3]
In this article, a thorough survey of recent research on in-fiber interferometric-based sensors is presented, in which different architectures are discussed, such as Fabry-Perot, Mach-Zehnder, Michelson, Sagnac, and multiple in-fiber structures comprise multiple interferometers and attain enhanced sensitivity measurements. Thus, Section 2 will present a classification of the most commonly used in-fiber interferometers as sensors, their architectures, operating principles, application areas in comprehensive tables and signal processing methods for optical path difference demodulation. In Section 3, concluding remarks and a discussion are presented, and finally Section 4 offers a conclusion.
2. In-Fiber Interferometric-Based Sensors
Optical fibers have been investigated at various sensor areas owing to many unique features that greatly improve the performance of interferometric systems, such as small size, light weight, multiplexing, remote sensing, high flexibility, low propagating loss, high sensitivity, low fabrication cost, small form factor, high accuracy, immunity to electromagnetic interference, and robustness to high temperature and irradiation, which make them attractive for many applications [4,5]. Optical interferometric technology is based on the interference of two or more light beams launched from the same light source propagating through air or different mediums with different optical paths and arriving simultaneously at a point in space or on the surface of an object. The optical path difference (OPD) due to the perturbation introduced in the sensor influences the phase difference which is directly encoded into the interference fringe patterns in the acquired spectrum. Therefore, by measuring the changes in the interference spectrum, one can obtain information about the changes in optical paths in an optical measurement system. Based on this mechanism, optical interferometers are widely used for accurate measurements of many physical quantities, such as refractive index, temperature, pressure, curvature, and displacement, etc.
Fiber optic and in-fiber interferometric sensors have been intensively developed for the past few decades. As a result, many special data acquisition methods, digital signal processing algorithms, and demodulation techniques have been developed to recover the measured phase signals. Amongst the well-known examples are the phase generated carrier (PGC) demodulation technique [6,7,8], phase-shifting interferometry (PSI) [9] and white light interferometry (WLI) [10,11,12]. However, WLI based on broadband light sources or tunable lasers can directly measure the interference in spectrum domain Equation (1), and is widely accepted as the most advanced method due to its absolute cavity length measurement with sub-nanometer resolution and independence from signal intensity fluctuation, while it provides the capability to easily realize sensor multiplexing [13].
Multiparameter interferometric sensors have only recently attracted attention due to increasing demand in industrial processes which often require sensing of more than one physical or chemical parameter simultaneously [14]. In order to avoid cross sensitivity among the measurands, for example temperature dependency in RI measurements, the right solution is the design of an appropriate transducing mechanism that is selective in nature towards the measurement of a desired perturbation [15,16,17,18,19,20,21,22,23]. Some designs include the use of PCF to reduce temperature dependency [24] in combination with short taper segments for excitation of multiple modes [25], peanut structures [26] etc. The majority of current research is focused on dual-parameter sensors, while three or more is quite rare due to the very complex design and the need for advanced algorithms for signal processing, also posing the question of cost compared to multiplexed individual sensors.
Moreover, as mentioned earlier, with optical fiber sensor technology it is very easy to realize sensor multiplexing, which can reduce the cost of a single point sensor, greatly improve the cost performance of the sensing system, and give the optical fiber sensor more advantages than the traditional sensor [27]. The multiplexed system is comprised of an array of sensor elements connected by fiber. There are several categorizations depending on the location of the sensors and/or the number of measurands that each sensor can measure, and the multiplexed sensors can come in various network topologies [28,29]. The multiplexing technologies used are mainly time division multiplexing (TDM), frequency division multiplexing (FDM), wavelength division multiplexing (WDM), code division multiplexing (CDM), and space division multiplexing (SDM) [30]. While multiplexed sensors are facing challenges such as power requirements and losses that greatly determine the maximum number of sensors in the network, there is a great demand for such structures and the research interest in the area continues to grow.
In the following sections, fiber interferometric Fabry-Perot, Mach-Zehnder, Michelson and Sagnac schemes are discussed in detail, presenting their basic configurations, a brief approach to the principle of operation and recent applications. Moreover, multiple in-fiber structures comprise multiple interferometers, and the attainment of enhanced sensitivity measurements are also considered.
2.1. Fabry-Perot-Based Sensors
In-fiber Fabry–Perot interferometry (FOFPI) is an accurate and well-established sensing technology that is used to monitor a wide range of physical and chemical parameters, such as strain, temperature, vibration, pressure, concentration, and refractive index. FOFPI sensors have several attractive characteristics, such as high sensitivity, high resolution, low cost, small size, and linear response, and can tolerate high pressure and strain, while they are less affected by corrosion, and the phase of the interference signal (Equation (2)) is linearly proportional to the optical length [31].
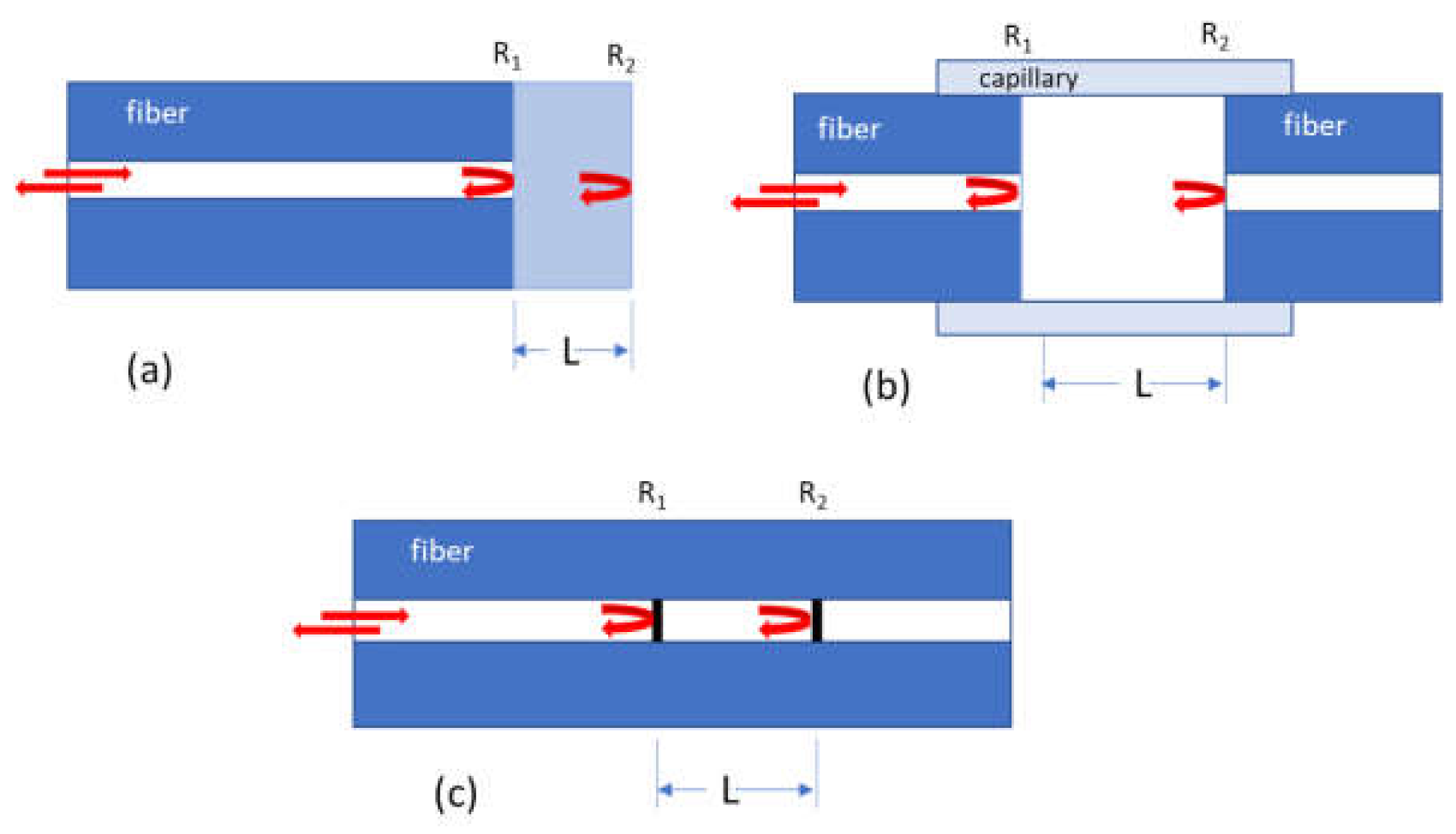
FOFPIs are devices with simple configurations, and they can be classified into two basic categories, extrinsic and intrinsic, depending on the way reflectors are formed. In the former case, the reflectors, forming a cavity, are separated by an air gap or any other material, and a cleaved single-mode (SMF) or multimode (MMF) fiber is used as a means to guide the light (Figure 1a) [32,33]. Alternatively, two cleaved pieces of fiber at a distance, supported by an external structure (capillary), create a cavity filled with air or any other material (Figure 1b) [34,35]. The extrinsic FOFPI sensor, although based on the Fabry-Perot concept, uses the reflections from an external cavity formed outside the fiber of interest, thus the optical fiber is simply a transmission medium that guides the light to (and/or back from) the interaction region. The extrinsic structure has the merit of sensing displacement since the phase value of the FOFPI signal can be directly affected by the displacement of the external reflecting surface. In the intrinsic case, the reflectors are formed within the fiber, creating a more compact structure, as illustrated in Figure 1c, and the cavity material in this case is glass [36]. In general, the fabrication of extrinsic FOFPI sensors is easier, although there are several challenging issues, such as the alignment of the fiber pieces and high coupling losses, while intrinsic FOFPI sensors require high-cost equipment, such as femtosecond laser micromachining or acid etching technology [36,37].
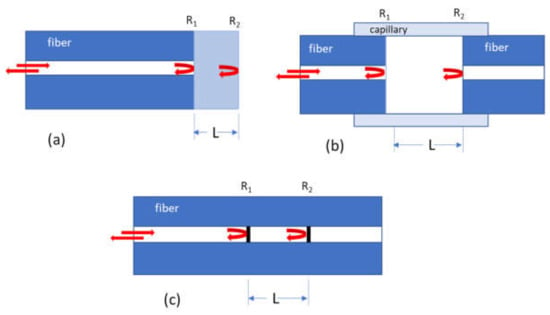
Figure 1.
The different FOFPI types: (a) extrinsic type where the cavity is formed outside the fiber (b) extrinsic type where the cavity is formed between two fibers and (c) intrinsic type where the cavity is formed by two reflecting components along the fiber.
The FOFPI sensor has a microcavity with parallel reflectors (Figure 1), achieving multiple interference of the reflected beams. When the cavity is subjected to a change due to external parameters (temperature, strain, refractive index, etc.) a phase change will be induced between the reflected beams, resulting in a shift in the reflection spectrum. By measuring the spectrum shift, one can gage the effect of the parameter under investigation. The reflective optical intensity can be expressed as [38]
where I1 and I2 are the intensities of the two reflected beams and φ is the phase difference of the two beams given by
where n is the reflective index of the medium in the cavity, L is the length of the Fabry-Perot cavity defined as the separation of the reflectors, and λ is the light wavelength used. The period of the FOFPI spectrum at λ (fringe separation) is given by the free spectral range (FSR)
while the finesse F, characterizing the sharpness of the fringes, is defined as
where R is the reflectance of the reflectors. In most FOFPI sensor applications, F is low to allow the interferometer to work in the linear regime over a large detection area of the measurand.
FOFPI sensors can be used in a variety of applications, primarily for temperature (Table 1), pressure (Table 2) and refractive index (Table 3), providing stable and compact solutions. In [39], the proposed sensor was based on a Myral polymer (commercially available), and MMF presented an easy way to fabricate micro-displacement sensors exhibiting a sensitivity of 24.1 nm/μm, while [40] proposed a compact reflection-based modal interferometer consisting of an SMF and a small piece of PCF (photonic crystal fiber) for nano-displacement with a sensitivity of 32 pm/nm.

Table 1.
Temperature sensitivity of FOFPI.

Table 2.
Pressure sensitivity of FOFPI.

Table 3.
Refractive index sensitivity of FOFPI.
A curvature measuring sensor was proposed [41] forming an extrinsic cavity using two pieces of SMF and a capillary silica tube filled with air, showing a maximum sensitivity of 68.52 pm/m−1 in the linear curvature response, which is a very good candidate for medical applications.
Acoustic sensors play a very important role in acoustic pressure detection, underwater acoustic detection, and acoustic monitoring applications. In [42], compact infrasound was proposed with a sensitivity of 4.32 μm/Pa for a range of frequencies from 1–20 Hz. A cantilever device was presented in [17] with ultrahigh acoustic pressure sensitivity equal to 198.3 nm/Pa@1 kHz and a linear response to temperature attaining an 83 nm/°C temperature responsivity. Ni et al. [43] implemented an ultrawide band acoustic sensor based on a graphene film with a frequency response from 5 Hz-0.8 MHz and a minimum detectable pressure of 0.77 Pa/Hz1/2@5 Hz and 33.97 μPa/Hz1/2@10 kHz. Finally, a very good review article [44] summarized the state of the art in fiber-optic technologies applicable for hypersonic wind tunnels on popular FOFPI sensors.
Fiber-optic gas pressure sensors are very attractive for many biomedical, civil engineering and aerospace applications, and they can be used to measure pressure under high temperature due to schemes that display resistance to harsh environments. The authors in [45] presented a dual capillary fiber-tip gas sensor exhibiting a high sensitivity of 4147 pm/MPa within a range of 0–1.52 MPa. A hollow-core photonic bandgap fiber (HC-PBF) with a side-opened channel was demonstrated in [46], indicating a gas pressure sensitivity of 4.24 nm/MPa, two orders of magnitude higher than that of a fiber-optic sensor with a closed cavity. A 3-D printed FPI sensor on a fiber tip was presented in [47], where a device with a 90 μm cavity length exhibited a sensitivity of 4.097 nm/MPa, while the same device can be used to measure a temperature sensitivity of 156.8 pm/°C within a range from 20 to 70°C. Moreover, an ultracompact fiber-optic differential gas sensor that employs a metal–organic framework (MOF) based on dual Fabry-Perot (FP) nanocavities was presented in [48], and although measured thus far only for CO2, exhibiting an enhanced sensitivity of 48.5 mV/CO2 Vol%, it can be used with various gases when different MOFs are utilized.
A compact hydrogen sensor [34] with a sensitivity of 1.4 nm/H2 Vol% as well as two sensors measuring relative humidity (RH) [33,49] with a maximum sensitivity of 81.05 pm/(%RH) and a range of 90–95% RH respectively, have been reported. Furthermore, an FOFPI sensor has been fabricated with the capability of measuring molecular transport diffusivity [50], allowing us to investigate concentration-dependent diffusivity in zeolitic materials under harsh conditions.
Magnetic field sensors [35,51] exhibit a magnetic field sensitivity of 1510 nm/MT within a range from 0.368–3.086 mT for the former and 44 pm/mT for the latter, achieving a better sensitivity than using fiber Bragg grating (FBG).
A low-cost sensor based on a polyethylene diaphragm was developed for vibration measurements [32], obtaining a sensitivity of 135 mV/g in a range of 20 Hz–1.5 kHz.
FOFPI sensors targeting biomedical applications have recently attracted much research [52,53]. In [52], a proposed immunosensor could differentiate antibody-containing sera, while the authors in [53] verified that TiO2 reflective films deposited on the tip of an SMF are very promising candidates for tuning FOFPI reflectivity, specifically in a range close to that of silica fiber.
Furthermore, multiparameter monitoring FOFPI has been presented for the evaluation of mechanical vibrations and magnetic fields [19], thicknesses of liquid layers and refractive indexes (RI) [18], strains and magnetic fields [35], temperature and RI [58,59], pressure and temperature [16,17,47,69], and strain and temperature [15].
2.2. Mach-Zehnder-Based Sensors
Fiber-optic Mach-Zehnder interferometers (FOMZIs) are the majority of sensors utilized; however, they exhibit inherent complexity due to their structure. In an MZI sensor, a laser beam is injected into the fiber, which splits equally into the upper arm (called the sensing arm) and the lower arm (called the reference arm). At the exit of the MZI, the two beams recombine to create an interference pattern. Changes in the length of the sensing arm, and perhaps changes in the surrounding material, disturb the output (interference pattern) and hence generate a phase difference, which can be further analyzed to determine the effect on the parameter under investigation. To achieve high sensitivity, the sensing segment, and therefore the whole device, must be long [70].
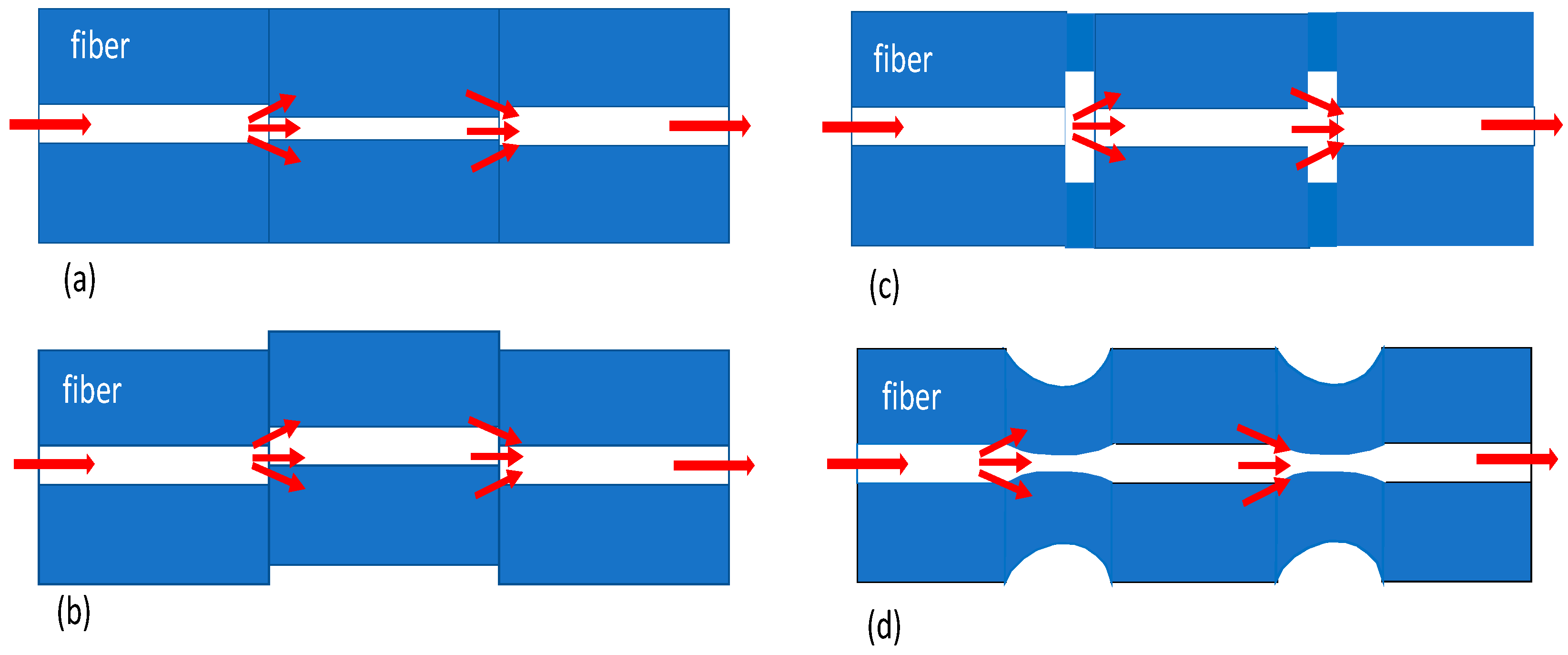
Figure 2 shows various structures for FOMZI sensors. As shown in Figure 2a, part of the core mode in the second segment, due to a thinner fiber, is guided in the core of the SMF fiber, and part is guided in the cladding of a thin core fiber (TCF), while at the third segment, they couple back at the core modes of the SMF [71,72]. Another way of splitting the beam into core and cladding modes is by creating a core misalignment, as shown in Figure 2b [73,74]. Due to fiber misalignment, part of the core mode is coupled to several cladding modes, where the number of cladding modes can be adjusted depending on the misalignment of the fibers. The same effect as before shows the insertion of MMF segments between pieces of SMF, as in Figure 2c [75,76], where the beam is guided not only in the core but also in the cladding. One more FOMZI scheme is shown in Figure 2d [22,77,78], where the insertion of two tapered pieces of fiber will force the core mode, due to the change in diameter, to couple into cladding modes and again back to core modes.
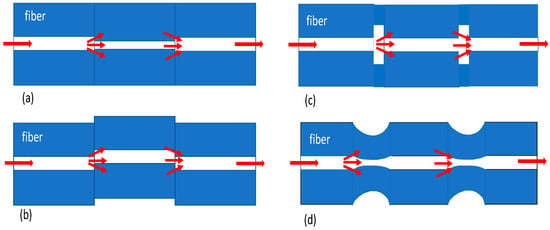
Figure 2.
Various types of FOMZI sensor: (a) core diameter mismatch with smaller core fiber, (b) core diameter offset, (c) core diameter mismatch with larger core fiber, and (d) core diameter mismatch using tapering segments of fiber.
In all of the above cases, the creation of the cladding modes and their coupling with the core mode produces interference, which under predefined conditions provides a compact yet very effective FOMZI. The interferometric sensor has the same physical lengths in both the reference and sensing arms; however, they have different optical path lengths due to the modal dispersion, i.e., the cladding mode has a lower effective index than the core mode, and the smaller the fiber diameter, the stronger the evanescent field. In general, FOMZIs are usually more tolerant and versatile structures that can be used in different designs, thus providing high sensitivity values.
The optical intensity at the output of the FOMZI can be expressed by Equation (1) where I1 and I2 are the intensities of light propagating in the core and in the cladding, respectively, while φ is the phase difference of the core and the cladding propagating modes and is given by
where Δneff is the difference between the effective indices of the core mode and cladding modes, L is the fiber length between the splitter and the combiner part of the structure and λ is the light wavelength used [79]. The intensity of the interference signal is minimal (i.e., a dip) when the phase difference is an odd multiple of π and the wavelength of the minimum light intensity is
Thus, the free spectral range (FSR) of the optical interference spectrum can be expressed as
FOMZI sensor technologies are routinely used to measure physical parameters such as temperature (Table 4), curvature (Table 5) and refractive index (Table 6), providing stable and compact solutions.

Table 4.
Temperature sensitivity of FOMZI.

Table 5.
Curvature sensitivity of FOMZI.

Table 6.
Refractive index sensitivity of FOMZI.
Furthermore, a FOMZI can be used as a relative humidity (RH) sensor, which is very useful in the medical storage and biochemical fields [75,80,81,82]. In [75], a simple structure alternating SMF with two segments of MMF achieved a sensitivity of 0.48346 dB/%RH for a humidity range from 15% to 80%. A dumbbell-shaped FOMZI was proposed in [80], where the sensitivity was improved from 0.0002 to 0.020 nm/% RH with a ZnO coating. In [81], a FOMZI is made by splicing a segment of a few-mode fiber (FMF) between two segments of a no-core fiber (NCF) and two segments of SMFs located outside the two NCFs, attaining a sensitivity of 0.191 and 0.061 nm/% RH in the corresponding 30–55% and 55–95% ranges. Finally, the authors in [82] used a tapering section of polarization maintaining and elliptic core fiber fixed as a U-shape with a sensitivity of 114.7 pm/RHU in a range from 30% to 90% RH.
A number of FOMZI-based sensors for strain sensing have been proposed and demonstrated using different types of configurations, such as segments of four-core fiber spliced between two SMFs exhibiting a sensitivity of 1.78 pm/με [21], a fiber-optic sensor using fiber ring cavity laser [83] with a sensitivity of 2.21 pm/με, a five-core fiber sandwiched between two SMFs [84] with a corresponding sensitivity of 0.8 pm/με, and finally a grapefruit micro-structured fiber with 1.97 pm/με strain sensitivity [85].
A sensor head using an SMF–MMF–PCF–SMF structure with a fusion splicing method [86] was used for liquid level monitoring, reporting sensitivities of −1.032 μw/cm, −1.197 μw/cm, and −1.489 μw/cm for three different mediums. A simpler structure with two fibers with different diameters in an axial offset was reported in [87] with a value of 6 pm/mm for the liquid level sensitivity.
Many biochemical and biomedical processes require real-time monitoring of the pH level. In [71], a sensor based on a biocompatible pH-sensitive material was proposed using a structure composed of a thin core fiber covered with a polymer material inserted between two segments of SMFs. The sensor emerged in different materials, providing promising results for pH in a broad measurement range. Furthermore, a microfiber taper interferometer coated by highly ordered pore array-conjugated polymer membranes exhibited a DNA concentration sensitivity of 2.393 nm/log M (M is the molar concentration) [88]. The proposed interferometer is suitable for medical, environmental, and biochemical process monitoring.
A FOMZI was constructed using a small stub of hollow-core PCF between SMFs with air gaps at both interfaces [89]. The sensor exhibited a sensitivity of 4.3 pm/% CO2, providing a simple and compact method for the environmental monitoring of CO2. A Fe2O3-coated tapered microfiber structure was presented in [90], which can be used for the detection of harmful gas ammonia in an environment with a sensitivity of 1.30 pm/ppm in the range from 0 ppm to 11.640 ppm ammonia gas at room temperature.
Different FOMZI designs have also been proposed for the measurement of physical parameters such as torsion [91], lateral stress [92] and gas pressure [93]. All devices used a segment of specialty fiber, i.e., a two-core nonzero dispersion shifted fiber (NZ–DSF), erbium-doped fiber (EDF) and a twin-core fiber, respectively, in an offset between two pieces of SMFs with corresponding sensitivities of 0.070 nm/o of fiber twist for torsion, 0.00455/μm for lateral stress and 9.6 nm/MPa for the gas pressure sensor.
Magnetic fluid (MF) has attracted much attention recently as a sensing material due to a variety of magneto-optical properties. A compact and low-cost magnetic field sensor was developed by [94] using a microfiber mode interferometer coated with MF with a high sensitivity up to −293 pm/Oe, detecting the transmission spectrum.
Many of the above presented sensors are multiparameter sensors, i.e., temperature and displacement [104], bending and temperature [20], strain, refractive index (RI) and curvature [21], RI and liquid level [86], strain, temperature and curvature [22,25], strain, temperature, RI and curvature [83], temperature and curvature [99,100], strain and bending [84], RI, and temperature and liquid level [87], having the advantage of monitoring multiple parameters with the same device.
2.3. Michelson-Based Sensor
The fiber-optic Michelson interferometer (FOMI) is quite similar to a FOMZI since the FOMI uses reflection modes instead of transmission and analogous fabrication methods and operation principles.
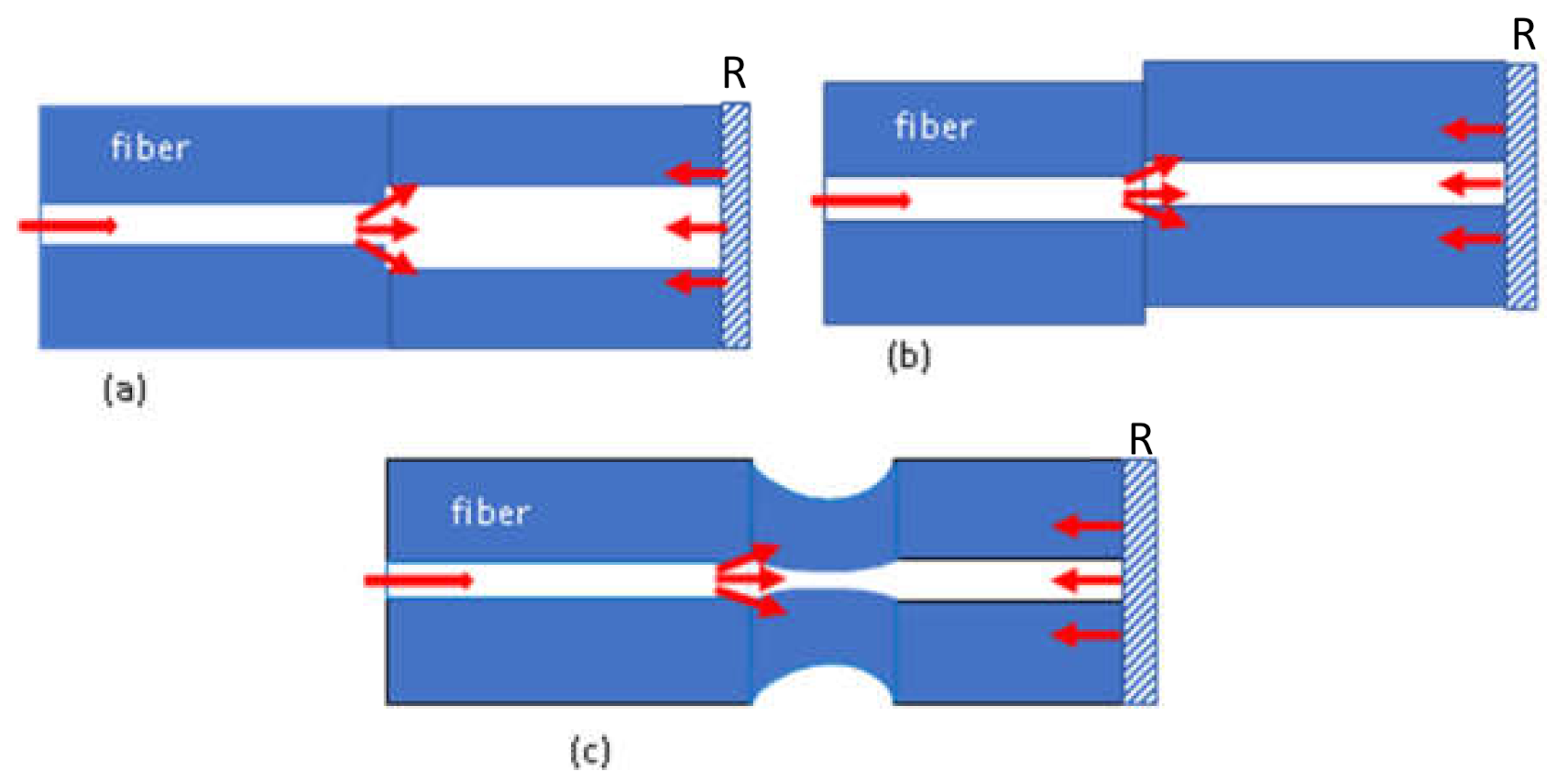
Figure 3 presents typical configurations of a FOMI. Figure 3a presents a FOMI comprised of two segments of fibers with different core diameters [120,121], while in Figure 3b, the pieces of the same fiber are offset [122,123]. Finally, in Figure 3c, a taper segment is sandwiched between two pieces of single-mode fibers (SMFs) [124,125]. The second piece of fiber, in all cases, has a reflector at its end. The effective refractive index difference between the core mode and dominant high-order cladding modes gives rise to the phase difference.
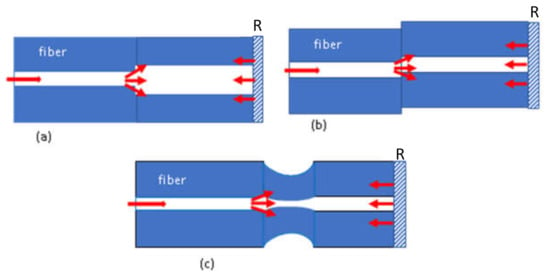
Figure 3.
Various types of FOMI sensors: (a) core diameter mismatch with larger core fiber, (b) core diameter offset, (c) core diameter mismatch using a tapering segments of fiber.
The optical intensity at the output of the FOMI can be expressed by Equation (1) where I1 and I2 are the intensities of the core and higher-order dominant cladding modes, respectively, R is the reflectivity of the end face of the last piece of fiber, and φ is the accumulated phase difference of the core and the cladding modes [126], which is given by
where Δneff is the effective difference between the refractive index of the core and the dominant cladding modes and L is the length between the contact of the two fibers and the reflector. The intensity of the interference signal is minimal (i.e., a dip) when the phase difference φ = π(2m + 1) and m = 0, 1, 2 …; thus, the free spectral range (FSR) of the optical interference spectrum can be expressed as
FOMI sensors are mainly used to measure physical parameters such as temperature (Table 7) and refractive index (Table 8), providing compact solutions.

Table 7.
Temperature sensitivity of FOMI.

Table 8.
Refractive index sensitivity of FOMI.
Additionally, a FOMI can be used as a relative humidity sensor [122,127] presenting a sensitivity of −0.166 dB/% RH and −0.083 dB/% RH, while the second structure is relatively more cost effective than the first one.
Furthermore, an adiabatic biconical fused fiber taper spliced to an SMF [125] can be used as a displacement and curvature sensor for high-resolution optical instrumentation processes where mechanical bending is an important physical parameter to determine deformations, displacements, and curvature radiuses.
Moreover, multiparameter monitoring FOMIs have been implemented for simultaneous measurement, such as temperature and refractive index [23,124].
2.4. Sagnac-Based Sensors
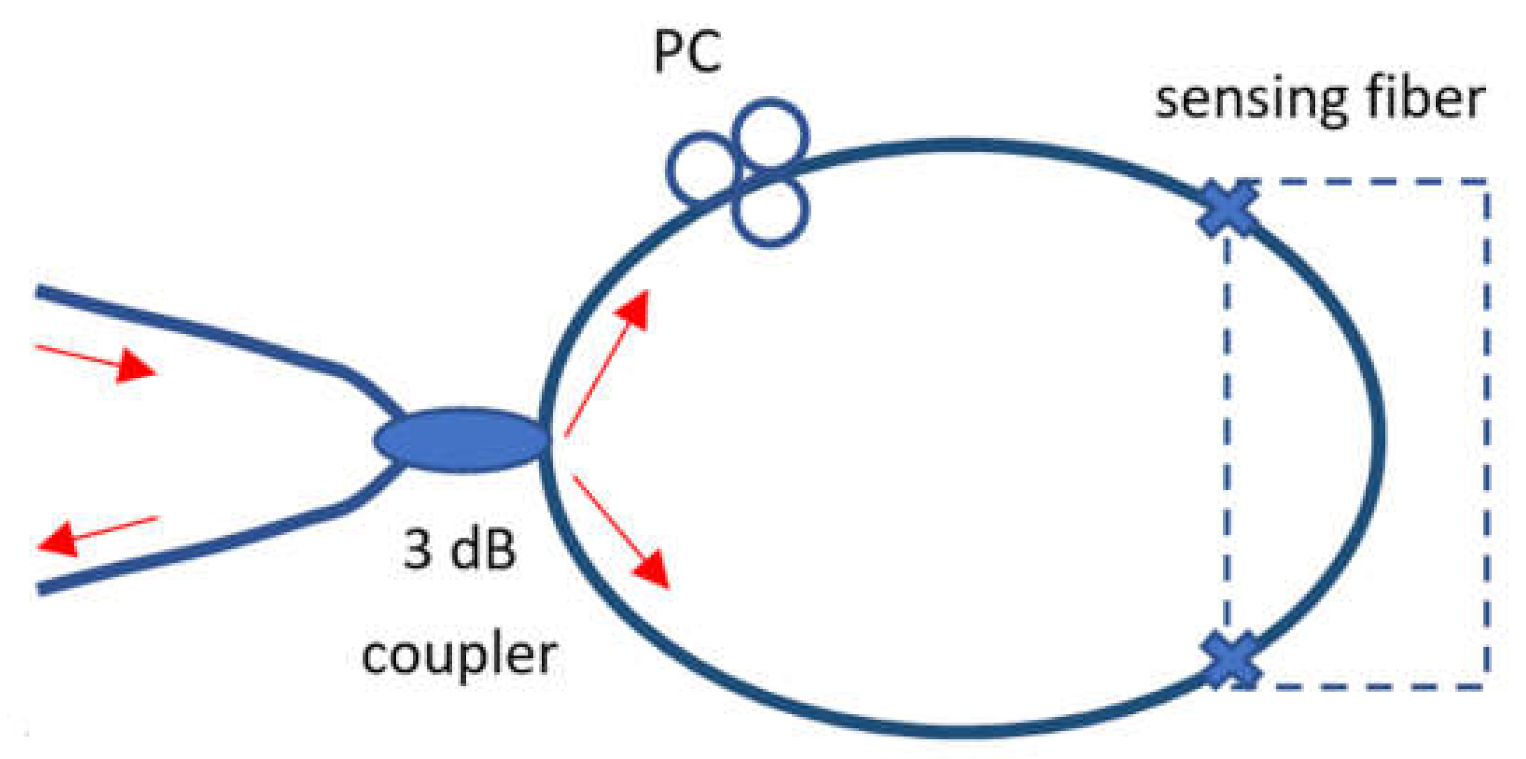
The fiber-optic Sagnac interferometer (FOSI) is a very simple structure consisting of a loop of fibers along which two beams travel in opposite directions with different polarization states. A FOSI is very attractive due to its insensitivity to the environment. A schematic in Figure 4 presents the incoming beam, which is split by a 3 dB coupler, and the two beams propagate in the fiber loop in counter-directions (clockwise and counterclockwise) recombined on the same coupler after a complete loop in the fiber. The optical path difference is defined by the polarization-dependent propagating speed of the mode guided along the loop. The state of polarization is controlled by a polarization controller (PC), and to maximize the polarization dependency of the interferometer, the sensing part of the FOSI is usually a specialty fabricated fiber, i.e., a highly birefringent fiber, polarization maintaining fiber, [131,132,133], etc.
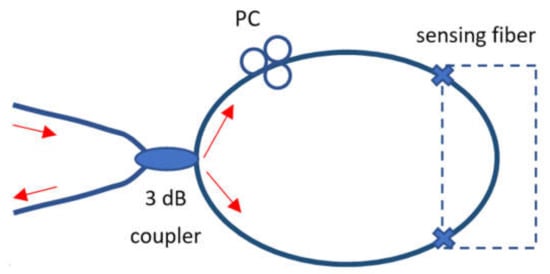
Figure 4.
Schematic of FOSI based on Sagnac interferometer indicating the sensing part which is usually a specialty fabricated fiber.
At the output of the FOSI, an interference pattern is created between the two beams polarized along the fast and slow axes, and the phase difference is expressed by
where L is the length of the fiber loop and B is the birefringence of the fiber, defined as (nf-ns), and nf and ns are the effective refractive indices of the fast and slow modes, respectively.
A Sagnac interferometer has the advantages of a compact structure, i.e., high stability, ease of fabrication, and self-balancing characteristics, so it is widely used in the design of optical fiber sensors, such as temperature (Table 9), strain [132,134] and pressure sensors [135,136].

Table 9.
Temperature sensitivity of FOSI.
Li et al. [132] presented a FOSI structure, with a polarization maintaining only few mode fibers as a sensing element, where interference occurs between both the polarization and spatial modes, known as polarimetric and intermodal interference. The results reveal that the temperature coefficient is 0.123 nm/°C for the LP01x-LP11x mode and 0.091 nm/°C for the LP01y-LP11y mode, while the strain coefficient is 1.97 pm/με for intermodal interference between the LP01x and LP11x modes and 0.98 pm/με for the intermodal interference between the LP01y and LP11y modes. A two semicircular-hole fiber with a germanium (Ge)-doped elliptical core in the center and two large semicircular holes in the cladding was reported in [134], introducing a highest twist sensitivity of 5.01 nm/° for twist angles ranging from 370°–400°, and the sensor can also be used to discriminate the torsion direction, providing a sensitivity of 1.15 nm/° over a twist angle range from 270°–350°.
A pressure vector sensor based on a short section of polarization maintaining fiber was introduced in [135] demonstrating a sensitivity of 2330 pm/(Nm) in its free form and 780 pm/(Nm) after being in aluminum in a range of 0-100 N. Moreover, a pore water pressure FOSI with a six-hole suspended-core polarization-maintaining photonic crystal fiber (SC-PM-PCF) and a commercial polarization-maintaining photonic crystal fiber (PM-PCF) was presented in [136] exhibiting a sensitivity of 304.41 kPa/nm of PM-PCF and 254.75 kPa/nm for the SC-PM-PCF, respectively.
Magnetic field sensing is very important in military and industrial applications and electric power transmission. A ferrofluid-filled high birefringence photonic crystal fiber (HB-PCF) was introduced in [137], while in [138], a single-mode microfiber was used in a Sagnac loop, and the twist area of the FOSI was a fiber with ferrofluid cladding. The corresponding sensitivities were 0.073 nm/mT for the former and ~5 pm/mT for the latter.
A FOSI can also be used to measure humidity, and in [133], a high-birefringence elliptical microfiber was spliced in a Sagnac loop without any humidity-sensitive coating. The achieved sensitivity was 201.25 pm/% RH, while if a segment of Panda fiber was inserted in the loop as a reference, the sensitivity could reach 422.2 pm/% RH in a range from 30% RH to 90% RH.
Multiparameter monitoring FOSIs have been implemented with the ability to measure, for example, temperature and strain [132], torsion, strain and temperature [134], and temperature and torsion [140].
2.5. Multiple In-Fiber Interferometric Sensors
Improving the sensor sensitivity is an efficient method to attain high-resolution sensors. Many recent research articles are in pursuit of new mechanisms to increase the sensitivity of the developed structures, and one effective way is by implementing two or more interferometric schemes to produce a superimposed interference spectrum. In multiple in-fiber interferometric sensors, even the smallest disturbance in the sensing spectrum will cause a more pronounced overall change in the superimposed spectrum due to the second interferometer.
Multiple interferometric structures can be classified into two categories [134,135]: (a) compact and (b) separate architectures, both with their pros and cons.
The compact architectures can be divided further into two types: (i) cascaded, where the sensor consists of cascaded interferometers [141,142,143,144,145,146,147,148,149] and (ii) parallel, with the interferometers in a parallel architecture [141,150,151].
The separate architectures can be further classified as (i) common, where the sensor consists of two interferometers of the same type, either (ia) in a cascaded manner, such as two Sagnac [152], two Fabry-Perot [153] or two MZIs [154], or (ib) in parallel, such as two MZIs [155,156], and (ii) different, where the sensor consists of two different types of interferometer, such as [157,158].
Table 10 and Table 11 present selected in-fiber interferometric sensors of the compact (cascaded and parallel) and separate (common and different) types, the sensitivity of the measured parameter and the amplification factor of the sensitivity compared to the simple structure.

Table 10.
Compact type of multiple in-fiber interferometric sensors.

Table 11.
Separate type of multiple in-fiber interferometric sensors.
The separate types of in-fiber interferometric sensors are the easiest to fabricate with relatively low cost, where usually one of the interferometers is the sensing interferometer and the other is the reference interferometer, and it is easy to isolate the sensing from the reference; however, they limit the overall length of the sensor, especially the cascaded type. In the compact type of in-fiber interferometric sensors, the fabrication procedure is more elaborate using the fusion splicing, acid-etching, and the femtosecond laser micromachining technique, providing very precise and compact structures, while in many cases the proposed architectures use segments of specialty fiber, i.e., colorless, hollow core, photonic crystal, or dual-core fibers.
Recently, Vernier-effect has been employed to fiber-optic sensing for the magnification of spectrum shift. The sensors consist of two cascaded two-beam interferometers or multi-beam interferometers with small FSR differences. The total output spectrum is a superposition of the spectrums of individual interferometers. The peak appears at the wavelength where the interference peaks of individual interferometers overlap, and the intensity of each peak is determined by the amount of the overlap. The envelope of the interference spectrum is usually obtained by the curve fitting method [148,150,151,152,156,157,159,160] in the implementation based on the Vernier effect while in the case of modified Vernier effect coverings interferometers with larger FSRs the Inverse Fast Fourier Transform (IFFT) is used [154]. Moreover, in [143] an enhancement of 6.6 times in ultrasound sensitivity has been achieved using single mode fiber with core-offset fused unequal-length fiber segments.
2.6. Signal Processing Methods for Optical Path Difference Demodulation
Optical path difference (OPD) demodulation is a subject of fundamental importance in spectral interferometry applications. In interferometric sensing applications, the change of the optical path difference, defined as the difference between the sensing and the reference paths, is related to the physical parameters being measured (measurand); as a result, the key to signal processing is to make an accurate measurement of the OPD [161].
There are several methods proposed in the literature, mainly falling into two categories: intensity demodulation in which the intensity of a guided beam is modulated in response to the measurand at the sensing path [162,163] and usually uses a laser as a light source; and wavelength tracking that involves a broadband source and a spectrometer [162,164]. Although intensity demodulation provides fast response, the outcome is influenced by power source stability and optical losses, while on the other hand the wavelength tracking provides higher resolution and accuracy. However, both methods suffer from fringe direction ambiguity which limits the dynamic range to only one free spectrum range (FSR) thus preventing the sensor being used over a large dynamic range [10,162,163].
To overcome the aforementioned drawback there are many methods proposed such as the two-point interrogation [10], and the fast Fourier transformed (FFT) interrogation [9,10,161,164]. Nevertheless, the former is very sensitive to noise and furthermore often leads to unreliable determination of the peak order due to the measurement error of the peak wavelengths and drift of the system, resulting in abrupt discontinuities (jumps) in phase in the demodulation process [13,161] while the resolution of the FFT method is usually limited by the spectral width of the broadband light source and sampling resolution of the OSA (Optical Signal Analyzer). Additionally, more complex signal processing methods have been demonstrated providing more accurate phase estimations, better accuracy, and resolution such as cross correlation (CC) algorithm [165], minimum mean square error algorithm (MMSE) [166], maximum likelihood estimation (MLE) [162,167,168], and the least square fitting algorithm (LSFA) [169]; however, the computational complexity of these types of algorithms make real-time measurement difficult. A number of summarizing contributions in the literature report on the advantages and drawbacks of each one depending on the specific practical application [8,10,161,164,170].
In the case of multiple in-fiber interferometric sensors and for the compact multiparameter interferometric sensors there are several approaches that can be applied to extract individual interferometers’ path length variations from the acquired spectrum. Amongst these are the matrix method [14,171,172], the most commonly used, although it assumes linear relationships among sensed optical and measured output parameters, and a highly efficient method that can yield very low crosstalk among measured parameters and high-measurement resolution which is based on inverse discrete Fourier transform (IDFT) [14,173].
3. Concluding Remarks and Discussion
In this article, a comprehensive survey of recent research on in-fiber interferometric-based sensors is presented, where different architectures are discussed, such as Fabry-Perot, Mach-Zehnder, Michelson, Sagnac and combinations in multiple in-fiber structures. In the sensing process, it is vital to use the appropriate interference technology that will allow accurate measurement of the sensing parameter. Furthermore, the performance of the fiber sensor (sensitivity, resolution, etc.) depends not only on the sensing technology but also on the sensing elements, i.e., the optical fiber used. Thus, in many cases, specialty fibers such as photonic crystal fibers (PCFs) and hollow core PCFs (HC-PCFs) [25,56,86,89,109,110,127,139] have several advantages, such as an increase in the sensing capability of the devices, controllable birefringence and dispersion [174] and temperature insensitivity, by taking advantage of the presence of air holes [68,114,118,127], while in the Sagnac case they are adjusted to display high birefringence [136,137]. Material-filled PCFs are also very attractive since air holes can be filled with functional materials [68,110,139], providing excellent properties. Another type of fiber that is used specifically for the MZI and Michelson [21,74,83,84,97,99,128] interferometric sensors is multicore fiber (MCF), which acts as a multipath MZI (m-MZI), and it has been demonstrated that higher sensitivity to phase change along with a more elaborate interference pattern output can be obtained compared to single interferometers [175]. Recently, optical microfibers and thin core fibers have attracted the attention of researchers [54,71,79,93,104,108,123,129] as suitable platforms for in-fiber interferometric sensors, providing very good values regarding the sensitivity of the measured parameters, large evanescent fields, strong optical confinement, flexibility, configurability, and robustness [176]. Moreover, there are other types of fiber used, such as nonzero dispersion shifted fiber (NZ-DSF) for the arms of the FOMZI [121], a novel hetero-structured cladding solid-core photonic bandgap fiber (HCSC-PBGF) [95], an erbium-doped fiber (EDF) chosen because of the higher refractive index contrast between the core and cladding [92], an eccentric core fiber suitable for directional bending measurement [105], a noncore fiber acting as splitting and recombining light due to a mismatch of mode field diameters [81,101], and polarization maintaining fibers [131,135].
Another fabrication approach is an assembly-free sensor scheme supported by femtosecond laser micromachining and etching technology, where interferometric sensors are directly fabricated on an optical fiber, achieving more compact structures with high robustness. Several examples can demonstrate the effectiveness of this approach, such as the rapid fabrication of embedded 3D channels with flexible orientations inside an optical fiber [37], a microchannel inscription to vertically cross the cavity to allow liquid to flow in [38], an intrinsic FOFPI force sensor fabrication [36], a three-dimensional (3D)-printed FOFPI pressure sensor based on direct laser writing [47], a side-opened channel drilled through the hollow core of an HC-PBF in a FOFPI [46], cutting off part of the MMF and drilling openings on one air hole of the dual side-hole fiber (DSHF) in a FOMZI [150], a FOMZI formation [98], a microchannel inscription in the form of an interferometer arm in a FOMZI [93], and microchannel drilling through one core of a twin core fiber (TCF) [177]. The drawback of this approach is the high cost of the necessary equipment and the elaborate fabrication methods, which makes batches difficult to manufacture. Thus, it is necessary to develop in-fiber interferometric sensors not only with high performance but also keeping the fabrication cost at a low level, such as in [121], where the proposed interferometer was an assembly free-based structure with excellent robustness and was fabricated by using a fiber lensing machine rather than an expensive femtosecond laser.
In general, regarding the stability and robustness of the structure, the core-offset schemes are more robust than tapering or peanut structures and, compared to other interferometers, the MZI structure, which works in the transmission direction, is the only one that is unsuitable for probe sensors.
Finally, optical fibers offer many unique characteristics, and interferometric sensor performance can be greatly improved; however, optical fiber properties, such as birefringence, dispersion, temperature dependence and nonlinear effects, can influence the ultimate performance of a system and must be considered in the design of new sensor applications.
4. Conclusions
In conclusion, in-fiber interferometric based sensors are rapidly growing in use, since they exhibit many desirable characteristics that can benefit the fabrication of many interesting devices. The resulting sensors hold numerous advantages over regular optical fiber-based counterparts, including small size, light weight, robustness, fast response, high sensitivity, and immunity to electromagnetic interference. With sensing areas spanning refractive index, biochemical, temperature, current, displacement, bend, surface, acceleration, force, rotation, acoustic, electric field and magnetic field, in-fiber interferometric-based sensors are very promising devices.
Funding
This research received no external funding.
Conflicts of Interest
The author declares no conflict of interest.
References
- Lee, B.H.; Kim, Y.H.; Park, K.S.; Eom, J.B.; Kim, M.J.; Rho, B.S.; Choi, H.Y. Interferometric fiber optic sensors. Sensors 2012, 12, 2467–2486. [Google Scholar] [CrossRef] [Green Version]
- Kang, J.U. Fiber Optic Sensing and Imaging; Springer: New York, NY, USA, 2013; ISBN 9781461474821. [Google Scholar]
- Zhu, T.; Wu, D.; Liu, M.; Duan, D.W. In-line fiber optic interferometric sensors in single-mode fibers. Sensors 2012, 12, 10430–10449. [Google Scholar] [CrossRef] [Green Version]
- Sweeney, D.C.; Schrell, A.M.; Liu, Y.; Petrie, C.M. Metal-embedded fiber optic sensor packaging and signal demodulation scheme towards high-frequency dynamic measurements in harsh environments. Sensors Actuators A Phys. 2020, 312, 112075. [Google Scholar] [CrossRef]
- Lyu, D.; Peng, J.; Huang, Q.; Zheng, W.; Xiong, L.; Yang, M. Radiation-resistant optical fiber Fabry-Perot interferometer used for high-temperature sensing. IEEE Sens. J. 2020, 1748, 57–61. [Google Scholar] [CrossRef]
- Suematsu, M.; Takeda, M. Wavelength-shift interferometry for distance measurements using the Fourier transform technique for fringe analysis. Appl. Opt. 1991, 30, 4046. [Google Scholar] [CrossRef] [PubMed]
- Fischer, E.; Dalhoff, E.; Heim, S.; Hofbauer, U.; Tiziani, H.J. Absolute interferometric distance measurement using a FM-demodulation technique. Appl. Opt. 1995, 34, 5589. [Google Scholar] [CrossRef] [PubMed]
- Martinek, R.; Nedoma, J.; Fajkus, M.; Kahankova, R.; Konecny, J.; Janku, P.; Kepak, S.; Bilik, P.; Nazeran, H. A phonocardiographic-based fiber-optic sensor and adaptive filtering system for noninvasive continuous fetal heart rate monitoring. Sensors 2017, 17, 890. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, G.; Hou, W.; Han, M. Unambiguous Peak Recognition for a Silicon Fabry-Pérot Interferometric Temperature Sensor. J. Light. Technol. 2018, 36, 1970–1978. [Google Scholar] [CrossRef]
- Han, M. Theoretical and Experimental Study of Low-Finesse Extrinsic Fabry-Perot Interferometric Fiber Optic Sensors. Ph.D. Thesis, Virginia Tech, Blacksburg, VA, USA, 2006. [Google Scholar]
- Liu, G.; Sheng, Q.; Hou, W.; Han, M. High-resolution, large dynamic range fiber-optic thermometer with cascaded Fabry–Perot cavities. Opt. Lett. 2016, 41, 5134. [Google Scholar] [CrossRef]
- Yi, J. High-resolution interrogation technique for fiber optic extrinsic Fabry-Perot interferometric sensors by the peak-to-peak method. Appl. Opt. 2008, 47, 925–932. [Google Scholar] [CrossRef]
- Han, M.; Zhang, Y.; Shen, F.; Pickrell, G.R.; Wang, A. Signal-processing algorithm for white-light optical fiber extrinsic Fabry–Perot interferometric sensors. Opt. Lett. 2004, 29, 1736. [Google Scholar] [CrossRef] [PubMed]
- Pevec, S.; Donlagić, D. Multiparameter fiber-optic sensors: A review. Opt. Eng. 2019, 58, 072009. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Yang, H.Z.; Qiao, X.G.; Hu, M.L.; Feng, Z.Y.; Wang, R.; Rong, Q.; Gunawardena, D.S.; Lim, K.S.; Ahmad, H. Strain measurement at high temperature environment based on Fabry-Perot interferometer cascaded fiber regeneration grating. Sensors Actuators A Phys. 2016, 248, 199–205. [Google Scholar] [CrossRef]
- Sun, B.; Wang, Y.; Qu, J.; Liao, C.; Yin, G.; He, J.; Zhou, J.; Tang, J.; Liu, S.; Li, Z.; et al. Simultaneous measurement of pressure and temperature by employing Fabry-Perot interferometer based on pendant polymer droplet. Opt. Express 2015, 23, 1906. [Google Scholar] [CrossRef] [Green Version]
- Chen, K.; Yang, B.; Deng, H.; Guo, M.; Zhang, B.; Yang, Y.; Liu, S.; Zhao, Y.; Peng, W.; Yu, Q. Simultaneous measurement of acoustic pressure and temperature using a Fabry-Perot interferometric fiber-optic cantilever sensor. Opt. Express 2020, 28, 15050. [Google Scholar] [CrossRef] [PubMed]
- Marzejon, M.; Karpienko, K.; Mazikowski, A.; Jȩdrzejewska-Szczerska, M. Fibre-optic sensor for simultaneous measurement of thickness and refractive index of liquid layers. Metrol. Meas. Syst. 2019, 26, 561–568. [Google Scholar] [CrossRef]
- Sheng, Q.; Liu, G.; Uddin, N.; Reinke, M.L.; Han, M. Fiber-Optic Silicon Fabry-Perot Interferometric Bolometer: The Influence of Mechanical Vibration and Magnetic Field. J. Light. Technol. 2020, 38, 2547–2554. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, W.; Chen, L.; Yan, T.; Wang, L.; Wang, B.; Zhou, Q. A fiber bending vector sensor based on M-Z interferometer exploiting two hump-shaped tapers. IEEE Photon. Technol. Lett. 2015, 27, 1240–1243. [Google Scholar] [CrossRef]
- Li, C.; Ning, T.; Zhang, C.; Li, J.; Zhang, C.; Wen, X.; Lin, H.; Pei, L. All-fiber multipath Mach–Zehnder interferometer based on a four-core fiber for sensing applications. Sensors Actuators A Phys. 2016, 248, 148–154. [Google Scholar] [CrossRef]
- Sun, B.; Huang, Y.; Liu, S.; Wang, C.; He, J.; Liao, C.; Yin, G.; Zhao, J.; Liu, Y.; Tang, J.; et al. Asymmetrical in-fiber Mach-Zehnder interferometer for curvature measurement. Opt. Express 2015, 23, 14596. [Google Scholar] [CrossRef] [Green Version]
- Musa, S.M.A.; Baharin, N.F.; Azmi, A.I.; Ibrahim, R.K.R.; Abdullah, A.S.; Mohd Noor, M.Y.; Qi, H. Double-clad fiber Michelson interferometer for measurement of temperature and refractive index. Microw. Opt. Technol. Lett. 2018, 60, 822–827. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, X.G.; Cai, L.; Zhang, Y.N. Measurement of RI and Temperature Using Composite Interferometer with Hollow-Core Fiber and Photonic Crystal Fiber. IEEE Trans. Instrum. Meas. 2016, 65, 2631–2636. [Google Scholar] [CrossRef]
- Dash, J.N.; Jha, R. Mach-Zehnder interferometer based on tapered PCF with an up-tapered joint for curvature, strain and temperature interrogation. J. Opt. 2016, 18. [Google Scholar] [CrossRef]
- Bian, J.; Lang, T.; Kong, W.; Chen, J. A polarization maintaining fiber sensor for simultaneous measurement of temperature and strain. Optik 2016, 127, 10090–10095. [Google Scholar] [CrossRef]
- Liu, D.; Sun, Q.; Lu, P.; Xia, L.; Sima, C. Research progress in the key device and technology for fiber optic sensor network. Photonic Sens. 2016, 6, 1–25. [Google Scholar] [CrossRef] [Green Version]
- Jones, J.D.C.; McBride, R. Multiplexing optical fiber sensors. Opt. Fiber Sens. Technol. 1998, 2, 117–166. [Google Scholar] [CrossRef]
- Li, W.; Yuan, Y.; Yang, J.; Yuan, L. Review of Optical Fiber Sensor Network Technology Based on White Light Interferometry. Photonic Sens. 2021, 11, 31–44. [Google Scholar] [CrossRef]
- Liu, T.G.; Yu, Z.; Jiang, J.F.; Liu, K.; Zhang, X.Z.; Ding, Z.Y.; Wang, S.; Hu, H.F.; Han, Q.; Zhang, H.X.; et al. Advances of some critical technologies in discrete and distributed optical fiber sensing research. Wuli Xuebao Acta Phys. Sin. 2017, 66. [Google Scholar] [CrossRef]
- Rajibul Islam, M.; Mahmood Ali, M.; Lai, M.H.; Lim, K.S.; Ahmad, H. Chronology of fabry-perot interferometer fiber-optic sensors and their applications: A review. Sensors 2014, 14, 7451–7488. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Yu, B.; Wu, X.; Shi, J.; Ge, Q.; Zhang, G.; Guo, M.; Zhang, Y.; Fang, S.S.; Zuo, C. Low-cost fiber optic extrinsic Fabry–Perot interferometer based on a polyethylene diaphragm for vibration detection. Opt. Commun. 2020, 457, 124332. [Google Scholar] [CrossRef]
- Maciak, E. Low-coherence interferometric fiber optic sensor for humidity monitoring based on nafion® thin film. Sensors 2019, 19, 629. [Google Scholar] [CrossRef] [Green Version]
- Zhou, X.; Ma, F.; Ling, H.; Yu, B.; Peng, W.; Yu, Q. A compact hydrogen sensor based on the fiber-optic Fabry-Perot interferometer. Opt. Laser Technol. 2020, 124, 105995. [Google Scholar] [CrossRef]
- Costa, G.K.B.; Gouvêa, P.M.P.; Soares, L.M.B.; Pereira, J.M.B.; Favero, F.; Braga, A.M.B.; Palffy-Muhoray, P.; Bruno, A.C.; Carvalho, I.C.S. In-fiber Fabry-Perot interferometer for strain and magnetic field sensing. Opt. Express 2016, 24, 14690. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, X.; Bai, H.; Shao, H.; Pan, H.; Pang, F.; Wang, T. Force sensors based on intrinsic fiber Fabry-Perot interferometer fabricated by the femtosecond laser. Opt. InfoBase Conf. Pap. 2014, 3–6. [Google Scholar] [CrossRef]
- Yuan, L.; Huang, J.; Lan, X.; Wang, H.; Jiang, L.; Xiao, H. All-in-fiber optofluidic sensor fabricated by femtosecond laser assisted chemical etching. Opt. Lett. 2014, 39, 2358. [Google Scholar] [CrossRef]
- Liao, C.R.; Hu, T.Y.; Wang, D.N. Optical fiber Fabry-Perot interferometer cavity fabricated by femtosecond laser micromachining and fusion splicing for refractive index sensing. Opt. Express 2012, 20, 22813. [Google Scholar] [CrossRef] [PubMed]
- Gutierrez-Rivera, M.; Jauregui-Vazquez, D.; Garcia-Mina, D.F.; Sierra-Hernandez, J.M.; Estudillo-Ayala, J.M.; Almanee, M.; Rojas-Laguna, R. Fiber Optic Fabry-Perot Micro-Displacement Sensor Based on Low-Cost Polymer Film. IEEE Sens. J. 2020, 20, 4719–4725. [Google Scholar] [CrossRef]
- Dash, J.N.; Jha, R.; Dass, S. Ultrasensitive displacement sensor based on photonic crystal fiber modal interferometer. Opt. Sensors, 2014 2014, 40, 467–470. [Google Scholar] [CrossRef]
- Monteiro, C.S.; Ferreira, M.S.; Silva, S.O.; Kobelke, J.; Schuster, K.; Bierlich, J.; Frazão, O. Fiber Fabry-Perot interferometer for curvature sensing. Photonic Sens. 2016, 6, 339–344. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Lu, P.; Liu, L.; Liao, H.; Sun, Y.; Ni, W.; Fu, X.; Jiang, X.; Liu, D.; Zhang, J.; et al. An Infrasound Sensor Based on Extrinsic Fiber-Optic Fabry-Perot Interferometer Structure. IEEE Photon. Technol. Lett. 2016, 28, 1264–1267. [Google Scholar] [CrossRef]
- Ni, W.; Lu, P.; Fu, X.; Zhang, W.; Shum, P.P.; Sun, H.; Yang, C.; Liu, D.; Zhang, J. Ultrathin graphene diaphragm-based extrinsic Fabry-Perot interferometer for ultra-wideband fiber optic acoustic sensing. Opt. Express 2018, 26, 20758. [Google Scholar] [CrossRef] [PubMed]
- Qiu, H.; Min, F.; Yang, Y. Fiber optic sensing technologies potentially applicable for hypersonic wind tunnel harsh environments. Adv. Aerodyn. 2020, 2. [Google Scholar] [CrossRef]
- Xu, B.; Wang, C.; Wang, D.N.; Liu, Y.; Li, Y. Fiber-tip gas pressure sensor based on dual capillaries. Opt. Express 2015, 23, 23484. [Google Scholar] [CrossRef] [PubMed]
- Tang, J.; Yin, G.; Liao, C.; Liu, S.; Li, Z.; Zhong, X.; Wang, Q.; Zhao, J.; Yang, K.; Wang, Y. High-Sensitivity Gas Pressure Sensor Based on Fabry-Pérot Interferometer with a Side-Opened Channel in Hollow-Core Photonic Bandgap Fiber. IEEE Photon. J. 2015, 7, 1–7. [Google Scholar]
- Wei, H.; Chen, M.; Krishnaswamy, S. Three-dimensional-printed Fabry–Perot interferometer on an optical fiber tip for a gas pressure sensor. Appl. Opt. 2020, 59, 2173. [Google Scholar] [CrossRef]
- Kim, H.-T.; Hwang, W.; Liu, Y.; Yu, M. Ultracompact gas sensor with metal-organic-framework-based differential fiber-optic Fabry-Perot nanocavities. Opt. Express 2020, 28, 29937. [Google Scholar] [CrossRef] [PubMed]
- Shrivastav, A.M.; Gunawardena, D.S.; Liu, Z.; Tam, H.Y. Microstructured optical fiber based Fabry–Pérot interferometer as a humidity sensor utilizing chitosan polymeric matrix for breath monitoring. Sci. Rep. 2020, 10, 1–10. [Google Scholar] [CrossRef]
- Yang, R.; Xu, Z.; Zeng, S.; Jing, W.; Trontz, A.; Dong, J. A fiber optic interferometric sensor platform for determining gas diffusivity in zeolite films. Sensors 2018, 18, 90. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, F.; Jiang, Y.; Gao, H.; Jiang, L. A high-finesse fiber optic Fabry-Perot interferometer based magnetic-field sensor. Opt. Lasers Eng. 2015, 71, 62–65. [Google Scholar] [CrossRef]
- Cano-Velázquez, M.S.; López-Marín, L.M.; Hernández-Cordero, J. Fiber optic interferometric immunosensor based on polydimethilsiloxane (PDMS) and bioactive lipids. Biomed. Opt. Express 2020, 11, 1316. [Google Scholar] [CrossRef]
- Hirsch, M.; Majchrowicz, D.; Wierzba, P.; Weber, M.; Bechelany, M.; Jędrzejewska-Szczerska, M. Low-coherence interferometric fiber-optic sensors with potential applications as biosensors. Sensors 2017, 17, 261. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Zhang, Y.; Ren, C.; Sui, Z.; Li, J. A high sensitivity temperature sensing probe based on microfiber fabry-perot interference. Sensors 2019, 19, 1819. [Google Scholar] [CrossRef] [Green Version]
- Zhuang, Y. Embedded Fiber Optic Sensors for Temperature Monitoring of Continuous Casting Mold. Master’s Thesis, Missouri University of Science and Technology, Rolla, MO, USA, 2018. [Google Scholar]
- Ding, W.; Jiang, Y.; Gao, R.; Liu, Y. High-temperature fiber-optic Fabry-Perot interferometric sensors. Rev. Sci. Instrum. 2015, 86, 1–5. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, S.; Yan, G.; Zhou, B.; Lee, E.H.; He, S. Open-Cavity Fabry-Perot Interferometer Based on Etched Side-Hole Fiber for Microfluidic Sensing. IEEE Photon. Technol. Lett. 2015, 27, 1813–1816. [Google Scholar] [CrossRef]
- Huang, Y.W.; Tao, J.; Huang, X.G. Research progress on F-P interference-based fiber-optic sensors. Sensors 2016, 16, 1424. [Google Scholar] [CrossRef] [Green Version]
- Dash, J.N.; Jha, R. Inline microcavity-based PCF interferometer for refractive index and temperature sensing. IEEE Photon. Technol. Lett. 2015, 27, 1325–1328. [Google Scholar] [CrossRef]
- Wang, M.; Yang, Y.; Huang, S.; Wu, J.; Zhao, K.; Li, Y.; Peng, Z.; Zou, R.; Lan, H.; Ohodnicki, P.R.; et al. Multiplexable high-temperature stable and low-loss intrinsic Fabry-Perot in-fiber sensors through nanograting engineering. Opt. Express 2020, 28, 20225. [Google Scholar] [CrossRef]
- Ma, W.; Jiang, Y.; Hu, J.; Jiang, L.; Zhang, T. Microelectromechanical system-based, high-finesse, optical fiber Fabry–Perot interferometric pressure sensors. Sens. Actuators A Phys. 2020, 302, 111795. [Google Scholar] [CrossRef]
- Ma, W.; Jiang, Y.; Gao, H. Miniature all-fiber extrinsic Fabry-Pérot interferometric sensor for high-pressure sensing under high-temperature conditions. Meas. Sci. Technol. 2019, 30, 025104. [Google Scholar] [CrossRef]
- Guo, X.; Zhou, J.; Du, C.; Wang, X. Highly sensitive miniature all-silica fiber tip fabry-perot pressure sensor. IEEE Photon. Technol. Lett. 2019, 31, 689–692. [Google Scholar] [CrossRef]
- Zhu, C.; Chen, Y.; Zhuang, Y.; Fang, G.; Liu, X.; Huang, J. Optical Interferometric Pressure Sensor Based on a Buckled Beam with Low-Temperature Cross-Sensitivity. IEEE Trans. Instrum. Meas. 2018, 67, 950–955. [Google Scholar] [CrossRef]
- Tan, X.; Li, X.; Geng, Y.; Yin, Z.; Wang, L.; Wang, W.; Deng, Y. Polymer Microbubble-Based Fabry-Perot Fiber Interferometer and Sensing Applications. IEEE Photon. Technol. Lett. 2015, 27, 2035–2038. [Google Scholar] [CrossRef]
- Li, X.; Shao, Y.; Yu, Y.; Zhang, Y.; Wei, S. A highly sensitive fiber-optic fabry–perot interferometer based on internal reflection mirrors for refractive index measurement. Sensors 2016, 16, 794. [Google Scholar] [CrossRef] [Green Version]
- Yang, B.; Yang, B.; Zhang, J.; Yin, Y.; Niu, Y.; Ding, M. A sensing peak identification method for fiber extrinsic fabry–perot interferometric refractive index sensing. Sensors 2019, 19, 96. [Google Scholar] [CrossRef] [Green Version]
- Tian, J.; Lu, Z.; Quan, M.; Jiao, Y.; Yao, Y. Fast response Fabry–Perot interferometer microfluidic refractive index fiber sensor based on concave-core photonic crystal fiber. Opt. Express 2016, 24, 20132. [Google Scholar] [CrossRef]
- Liu, F.; He, X.; Yu, L.; Pan, Y.; Xie, B.; Yi, D.; Gu, L.; Zhang, M. The Applications of Interferometric Fiber-Optic Sensors in Oilfield. In Proceedings of the 2018 Progress in Electromagnetics Research Symposium (PIERS-Toyama), Toyama, Japan, 1–4 August 2018; pp. 1664–1671. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhao, H.; Lv, R.Q.; Zhao, J. Review of optical fiber Mach–Zehnder interferometers with micro-cavity fabricated by femtosecond laser and sensing applications. Opt. Lasers Eng. 2019, 117, 7–20. [Google Scholar] [CrossRef]
- Engholm, M.; Hammarling, K.; Andersson, H.; Sandberg, M.; Nilsson, H.E. A bio-compatible fiber optic pH sensor based on a thin core interferometric technique. Photonics 2019, 6, 11. [Google Scholar] [CrossRef] [Green Version]
- Ahsani, V.; Ahmed, F.; Jun, M.B.G.; Bradley, C. Tapered fiber-optic mach-zehnder interferometer for ultra-high sensitivity measurement of refractive index. Sensors 2019, 19, 1652. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Li, X.G.; Cai, L. A highly sensitive Mach-Zehnder interferometric refractive index sensor based on core-offset single mode fiber. Sens. Actuators A Phys. 2015, 223, 119–124. [Google Scholar] [CrossRef]
- Yu, F.; Xue, P.; Zheng, J. Enhancement of Refractive Index Sensitivity by Bending a Core-Offset In-Line Fiber Mach-Zehnder Interferometer. IEEE Sens. J. 2019, 19, 3328–3334. [Google Scholar] [CrossRef]
- Bian, C.; Cheng, Y.; Zhu, W.; Tong, R.; Hu, M.; Gang, T. A Novel Optical Fiber Mach-Zehnder Interferometer Based on the Calcium Alginate Hydrogel Film for Humidity Sensing. IEEE Sens. J. 2020, 20, 5759–5765. [Google Scholar] [CrossRef]
- Marrujo-Garcia, S.; Hernandez-Romano, I.; Torres-Cisneros, M.; May-Arrioja, D.A.; Minkovich, V.P.; Monzon-Hernandez, D. Temperature-independent curvature sensor based on in-fiber mach-zehnder interferometer using hollow-core fiber. J. Light. Technol. 2020, 38, 4166–4173. [Google Scholar] [CrossRef]
- Bhardwaj, V.; Singh, V.K. Fabrication and characterization of cascaded tapered Mach-Zehnder interferometer for refractive index sensing. Sens. Actuators A Phys. 2016, 244, 30–34. [Google Scholar] [CrossRef]
- Harris, J.; Lu, P.; Larocque, H.; Chen, L.; Bao, X. In-fiber Mach-Zehnder interferometric refractive index sensors with guided and leaky modes. Sens. Actuators B Chem. 2015, 206, 246–251. [Google Scholar] [CrossRef]
- Li, L.; Xia, L.; Xie, Z.; Liu, D. All-fiber Mach-Zehnder interferometers for sensing applications. Opt. Express 2012, 20, 11109. [Google Scholar] [CrossRef] [PubMed]
- Lokman, A.; Arof, H.; Harun, S.W.; Harith, Z.; Rafaie, H.A.; Nor, R.M. Optical Fiber Relative Humidity Sensor Based on Inline Mach-Zehnder Interferometer With ZnO Nanowires Coating. IEEE Sens. J. 2016, 16, 312–316. [Google Scholar] [CrossRef]
- Fan, X.; Wang, Q.; Zhou, M.; Liu, F.; Shen, H.; Wei, Z.; Wang, F.; Tan, C.; Meng, H. Humidity sensor based on a graphene oxide-coated few-mode fiber Mach-Zehnder interferometer. Opt. Express 2020, 28, 24682. [Google Scholar] [CrossRef] [PubMed]
- Fu, H.; Jiang, Y.; Ding, J.; Zhang, J. Low Temperature Cross-Sensitivity Humidity Sensor Based on a U-Shaped Microfiber Interferometer. IEEE Sens. J. 2017, 17, 644–649. [Google Scholar] [CrossRef]
- Li, C.; Ning, T.; Li, J.; Zhang, C.; Zhang, C.; Lin, H.; Pei, L. Fiber-Optic Laser Sensor Based on All-Fiber Multipath Mach—Zehnder Interferometer. IEEE Photon. Technol. Lett. 2016, 28, 1908–1911. [Google Scholar] [CrossRef]
- Guan, C.; Zhong, X.; Mao, G.; Yuan, T.; Yang, J.; Yuan, L. In-line Mach-Zehnder interferometric sensor based on a linear five-core fiber. IEEE Photon. Technol. Lett. 2015, 27, 635–638. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, Y.; Liu, Z.; Chen, D.; Lu, C.; Tam, H.-Y. Sensitive Mach–Zehnder interferometric sensor based on a grapefruit microstructured fiber by lateral offset splicing. Opt. Express 2020, 28, 26564. [Google Scholar] [CrossRef]
- Dhara, P.; Singh, V.K. Effect of MMF stub on the sensitivity of a photonic crystal fiber interferometer sensor at 1550 nm. Opt. Fiber Technol. 2015, 21, 154–159. [Google Scholar] [CrossRef]
- Castellani, C.E.S.; Ximenes, H.C.B.; Silva, R.L.; Frizera-Neto, A.; Ribeiro, M.R.N.; Pontes, M.J. Multi-Parameter Interferometric Sensor Based on a Reduced Diameter Core Axial Offseted Fiber. IEEE Photon. Technol. Lett. 2017, 29, 239–242. [Google Scholar] [CrossRef]
- Huang, Y.; Tian, Z.; Sun, L.-P.; Sun, D.; Li, J.; Ran, Y.; Guan, B.-O. High-sensitivity DNA biosensor based on optical fiber taper interferometer coated with conjugated polymer tentacle. Opt. Express 2015, 23, 26962. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, F.; Ahsani, V.; Nazeri, K.; Marzband, E.; Bradley, C.; Toyserkani, E.; Jun, M.B.G. Monitoring of carbon dioxide using hollow-core photonic crystal fiber mach–zehnder interferometer. Sensors 2019, 19, 3357. [Google Scholar] [CrossRef] [Green Version]
- Fu, H.; Wang, Q.; Ding, J.; Zhu, Y.; Zhang, M.; Yang, C.; Wang, S. Fe2O3 nanotube coating micro-fiber interferometer for ammonia detection. Sens. Actuators B Chem. 2020, 303, 127186. [Google Scholar] [CrossRef]
- Huerta-Mascotte, E.; Sierra-Hernandez, J.M.; Mata-Chavez, R.I.; Jauregui-Vazquez, D.; Castillo-Guzman, A.; Estudillo-Ayala, J.M.; Guzman-Chavez, A.D.; Rojas-Laguna, R. A core-offset mach zehnder interferometer based on a non-zero dispersion-shifted fiber and its torsion sensing application. Sensors 2016, 16, 856. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yu, X.; Bu, D.; Chen, X.; Zhang, J.; Liu, S. Lateral Stress Sensor Based on an In-Fiber Mach-Zehnder Interferometer and Fourier Analysis. IEEE Photon. J. 2016, 8, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Liao, C.; Wang, Y.; Xu, L.; Wang, D.; Dong, X.; Liu, S.; Wang, Q.; Yang, K.; Zhou, J. Highly-sensitive gas pressure sensor using twin-core fiber based in-line Mach-Zehnder interferometer. Opt. Express 2015, 23, 6673. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.; Dong, X.; Chan, C.C.; Shum, P.P.; Su, H. Optical fiber magnetic field sensor based on magnetic fluid and microfiber mode interferometer. Opt. Commun. 2015, 336, 5–8. [Google Scholar] [CrossRef]
- Hu, X.; Shen, X.; Wu, J.; Peng, J.; Yang, L.; Li, J.; Li, H.; Dai, N. All fiber M-Z interferometer for high temperature sensing based on a hetero-structured cladding solid-core photonic bandgap fiber. Opt. Express 2016, 24, 21693. [Google Scholar] [CrossRef] [PubMed]
- Gao, S.; Ji, C.; Ning, Q.; Chen, W.; Li, J. High-sensitive Mach-Zehnder interferometric temperature fiber-optic sensor based on core-offset splicing technique. Opt. Fiber Technol. 2020, 56, 102202. [Google Scholar] [CrossRef]
- Naeem, K.; Kim, B.H.; Kim, B.; Chung, Y. High-Sensitivity Temperature Sensor Based on a. IEEE Sens. J. 2015, 15, 3998–4003. [Google Scholar] [CrossRef]
- Pallarés-Aldeiturriaga, D.; Rodriguez-Cobo, L.; Quintela, A.; Lopez-Higuera, J.M. In-fiber Mach-Zehnder interferometer inscribed with femtosecond laser for high temperature sensing. In Proceedings of the 2017 25th Optical Fiber Sensors Conference (OFS), Jeju, Korea, 24–28 April 2017. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Chen, D.; Li, H.; Feng, G.; Yang, J. In-Line Mach-Zehnder Interferometric Sensor Based on a Seven-Core Optical Fiber. IEEE Sens. J. 2017, 17, 100–104. [Google Scholar] [CrossRef]
- Raji, Y.M.; Lin, H.S.; Ibrahim, S.A.; Mokhtar, M.R.; Yusoff, Z. Intensity-modulated abrupt tapered Fiber Mach-Zehnder Interferometer for the simultaneous sensing of temperature and curvature. Opt. Laser Technol. 2016, 86, 8–13. [Google Scholar] [CrossRef] [Green Version]
- Hu, P.; Chen, Z.; Yang, M.; Yang, J.; Zhong, C. Highly sensitive liquid-sealed multimode fiber interferometric temperature sensor. Sens. Actuators A Phys. 2015, 223, 114–118. [Google Scholar] [CrossRef]
- Hernandez-Romano, I.; Monzon-Hernandez, D.; Moreno-Hernandez, C.; Moreno-Hernandez, D.; Villatoro, J. Highly Sensitive Temperature Sensor Based on a Polymer-Coated Microfiber Interferometer. IEEE Photon. Technol. Lett. 2015, 27, 2591–2594. [Google Scholar] [CrossRef]
- Yi, D.; Huo, Z.; Geng, Y.; Li, X.; Hong, X. PDMS-coated no-core fiber interferometer with enhanced sensitivity for temperature monitoring applications. Opt. Fiber Technol. 2020, 57, 102185. [Google Scholar] [CrossRef]
- Wu, J.; Miao, Y.; Song, B.; Lin, W.; Zhang, K.; Zhang, H.; Liu, B.; Yao, J. Simultaneous measurement of displacement and temperature based on thin-core fiber modal interferometer. Opt. Commun. 2015, 340, 136–140. [Google Scholar] [CrossRef]
- Kong, J.; Ouyang, X.; Zhou, A.; Yuan, L. Highly Sensitive Directional Bending Sensor Based on Eccentric Core Fiber Mach-Zehnder Modal Interferometer. IEEE Sens. J. 2016, 16, 6899–6902. [Google Scholar] [CrossRef]
- Wang, R.; Zhao, J.; Sun, Y.; Yu, H.; Zhou, N.; Zhang, H.; Jia, D. Wearable respiration monitoring using an in-line few-mode fiber Mach-Zehnder interferometric sensor. Biomed. Opt. Express 2020, 11, 316. [Google Scholar] [CrossRef]
- Dass, S.; Jha, R. Micrometer wire assisted inline Mach-Zehnder interferometric curvature sensor. IEEE Photon. Technol. Lett. 2015, 28, 31–34. [Google Scholar] [CrossRef]
- Luo, H.; Sun, Q.; Li, X.; Yan, Z.; Li, Y.; Liu, D.; Zhang, L. Refractive index sensitivity characteristics near the dispersion turning point of the multimode microfiber-based Mach–Zehnder interferometer. Opt. Lett. 2015, 40, 5042. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Q.; Kong, L.; Dang, Y.; Xia, F.; Zhang, Y.; Zhao, Y.; Hu, H.; Li, J. High sensitivity refractive index sensor based on splicing points tapered SMF-PCF-SMF structure Mach-Zehnder mode interferometer. Sens. Actuators B Chem. 2016, 225, 213–220. [Google Scholar] [CrossRef] [Green Version]
- Nazeri, K.; Ahmed, F.; Ahsani, V.; Joe, H.; Bradley, C.; Toyserkani, E.; Jun, M.B.G. Interferometer for Gas Sensing. Sensors 2020, 20, 2807. [Google Scholar] [CrossRef] [PubMed]
- Yu, F.; Liu, B.; Zou, Q.; Xue, P.; Zheng, J. Influence of temperature on the refractive index sensor based on a core-offset in-line fiber Mach-Zehnder interferometer. Opt. Fiber Technol. 2020, 58, 102293. [Google Scholar] [CrossRef]
- Yu, F.; Xue, P.; Zhao, X.; Zheng, J. Investigation of an in-line fiber Mach–Zehnder interferometer based on peanut-shape structure for refractive index sensing. Opt. Commun. 2019, 435, 173–177. [Google Scholar] [CrossRef]
- Wang, Q.; Wei, W.; Guo, M.; Zhao, Y. Optimization of cascaded fiber tapered Mach-Zehnder interferometer and refractive index sensing technology. Sens. Actuators B Chem. 2016, 222, 159–165. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, X.G.; Cai, L.; Yang, Y. Refractive index sensing based on photonic crystal fiber interferometer structure with up-tapered joints. Sens. Actuators B Chem. 2015, 221, 406–410. [Google Scholar] [CrossRef] [Green Version]
- Yu, F.; Xue, P.; Zheng, J. Study of an in-line fiber Mach-Zehnder interferometer with peanut-shape structure for refractive index sensing. In Proceedings of the Asia Communications and Photonics Conference, Hangzhou, China, 26–29 October 2018. [Google Scholar] [CrossRef]
- Gong, T.; Liu, X.; Wang, Z.; Liu, Y. Ultrasensitivity steel surface corrosion noncontacted monitoring based on a mismatching fused Mach-Zehnder interferometric fiber sensor. IEEE Sens. J. 2020, 2018, 12732–12738. [Google Scholar] [CrossRef]
- Guo, D.; Wu, L.; Yu, H.; Zhou, A.; Li, Q.; Mumtaz, F.; Du, C.; Hu, W. Tapered multicore fiber interferometer for refractive index sensing with graphene enhancement. Appl. Opt. 2020, 59, 3927. [Google Scholar] [CrossRef] [PubMed]
- Dash, J.N.; Jha, R. PCF Modal Interferometer Based on Macrobending for Refractive Index Sensing. IEEE Sens. J. 2015, 15, 5291–5295. [Google Scholar] [CrossRef]
- Fu, H.; Li, H.; Shao, M.; Zhao, N.; Liu, Y.; Li, Y.; Yan, X.; Liu, Q. TCF-MMF-TCF fiber structure based interferometer for refractive index sensing. Opt. Lasers Eng. 2015, 69, 58–61. [Google Scholar] [CrossRef]
- Nguyen, L.V.; Warren-Smith, S.C.; Ebendorff-Heidepriem, H.; Monro, T.M. Interferometric high temperature sensor using suspended-core optical fibers. Opt. Express 2016, 24, 8967. [Google Scholar] [CrossRef]
- Yin, J.; Liu, T.; Jiang, J.; Liu, K.; Wang, S.; Zou, S.; Wu, F. Assembly-Free-Based Fiber-Optic Micro-Michelson Interferometer for High Temperature Sensing. IEEE Photon. Technol. Lett. 2016, 28, 625–628. [Google Scholar] [CrossRef]
- Sun, H.; Shao, M.; Han, L.; Liang, J.; Zhang, R.; Fu, H. Large core-offset based in-fiber Michelson interferometer for humidity sensing. Opt. Fiber Technol. 2020, 55, 102153. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, Y.; Liao, C.; Sun, B.; He, J.; Yin, G.; Liu, S.; Li, Z.; Wang, G.; Zhong, X.; et al. Intensity modulated refractive index sensor based on optical fiber Michelson interferometer. Sens. Actuators B Chem. 2015, 208, 315–319. [Google Scholar] [CrossRef]
- Sun, Q.; Luo, H.; Luo, H.; Lai, M.; Liu, D.; Zhang, L. Multimode microfiber interferometer for dual-parameters sensing assisted by Fresnel reflection. Opt. Express 2015, 23, 12777. [Google Scholar] [CrossRef]
- Salceda-Delgado, G.; Martinez-Rios, A.; Selvas-Aguilar, R.; Álvarez-Tamayo, R.I.; Castillo-Guzman, A.; Ibarra-Escamilla, B.; Durán-Ramírez, V.M.; Enriquez-Gomez, L.F. Adaptable optical fiber displacement-curvature sensor based on a modal michelson interferometer with a tapered single mode fiber. Sensors 2017, 17, 1259. [Google Scholar] [CrossRef] [Green Version]
- Hu, P.; Dong, X.; Ni, K.; Chen, L.H.; Wong, W.C.; Chan, C.C. Sensitivity-enhanced Michelson interferometric humidity sensor with waist-enlarged fiber bitaper. Sens. Actuators B Chem. 2014, 194, 180–184. [Google Scholar] [CrossRef]
- Shao, M.; Sun, H.; Liang, J.; Han, L.; Feng, D. In-Fiber Michelson Interferometer in Photonic Crystal Fiber for Humidity Measurement. IEEE Sens. J. 2021, 21, 1561–1567. [Google Scholar] [CrossRef]
- Duan, L.; Zhang, P.; Tang, M.; Wang, R.; Zhao, Z.; Fu, S.; Gan, L.; Zhu, B.; Tong, W.; Liu, D.; et al. Heterogeneous all-solid multicore fiber based multipath Michelson interferometer for high temperature sensing. Opt. Express 2016, 24, 20210. [Google Scholar] [CrossRef] [PubMed]
- Zhao, N.; Fu, H.; Shao, M.; Yan, X.; Li, H.; Liu, Q.; Gao, H.; Liu, Y.; Qiao, X. High temperature probe sensor with high sensitivity based on Michelson interferometer. Opt. Commun. 2015, 343, 131–134. [Google Scholar] [CrossRef]
- Cardona-Maya, Y.; Botero-Cadavid, J.F. Refractive index desensitized optical fiber temperature sensor. Rev. Fac. Ing. 2017, 86–90. [Google Scholar] [CrossRef]
- Song, B.; Zhang, H.; Miao, Y.; Lin, W.; Wu, J.; Liu, H.; Yan, D.; Liu, B. Highly sensitive twist sensor employing Sagnac interferometer based on PM-elliptical core fibers. Opt. Express 2015, 23, 15372. [Google Scholar] [CrossRef]
- Li, A.; Wang, Y.; Hu, Q.; Shieh, W. Few-mode fiber based optical sensors. Opt. Express 2015, 23, 1139. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.P.; Li, J.; Jin, L.; Ran, Y.; Guan, B.O. High-birefringence microfiber Sagnac interferometer based humidity sensor. Sens. Actuators B Chem. 2016, 231, 696–700. [Google Scholar] [CrossRef] [Green Version]
- Htein, L.; Gunawardena, D.S.; Liu, Z.; Tam, H.-Y. Two semicircular-hole fiber in a Sagnac loop for simultaneous discrimination of torsion, strain and temperature. Opt. Express 2020, 28, 33841. [Google Scholar] [CrossRef]
- He, X.; Ma, C.; Wang, X.; Wang, Z.; Yuan, L. Pressure vector sensor based on an orthogonal optical path Sagnac interferometer. Opt. Express 2020, 28, 7969. [Google Scholar] [CrossRef]
- Feng, W.Q.; Liu, Z.Y.; Tam, H.Y.; Yin, J.H. The pore water pressure sensor based on Sagnac interferometer with polarization-maintaining photonic crystal fiber for the geotechnical engineering. Meas. J. Int. Meas. Confed. 2016, 90, 208–214. [Google Scholar] [CrossRef]
- Zhao, Y.; Wu, D.; Lv, R.Q.; Li, J. Magnetic Field Measurement Based on the Sagnac Interferometer With a Ferrofluid-Filled High-Birefringence Photonic Crystal Fiber. IEEE Trans. Instrum. Meas. 2016, 65, 1503–1507. [Google Scholar] [CrossRef]
- Lv, F.; Han, C.; Ding, H.; Wu, Z.; Li, X. Magnetic Field Sensor Based on Microfiber Sagnac Loop Interferometer and Ferrofluid. IEEE Photon. Technol. Lett. 2015, 27, 2327–2330. [Google Scholar] [CrossRef]
- Liu, Q.; Li, S.G.; Shi, M. Fiber Sagnac interferometer based on a liquid-filled photonic crystal fiber for temperature sensing. Opt. Commun. 2016, 381, 1–6. [Google Scholar] [CrossRef]
- Shao, L.Y.; Zhang, X.; He, H.; Zhang, Z.; Zou, X.; Luo, B.; Pan, W.; Yan, L. Optical fiber temperature and torsion sensor based on Lyot-Sagnac interferometer. Sensors 2016, 16, 1774. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, Y.; Li, X.; Zhang, Y.N.; Zhao, Y. Fiber-optic sensors based on Vernier effect. Meas. J. Int. Meas. Confed. 2021, 167, 108451. [Google Scholar] [CrossRef]
- Cui, Y.; Jiang, Y.; Liu, T.; Hu, J.; Jiang, L. A Dual-Cavity Fabry-Perot Interferometric Fiber-Optic Sensor for the Simultaneous Measurement of High-Temperature and High-Gas-Pressure. IEEE Access 2020, 8, 80582–80587. [Google Scholar] [CrossRef]
- Fan, H.; Chen, L.; Bao, X. Fiber-Optic Sensor Based on Core-Offset Fused Unequal-Length Fiber Segments to Improve Ultrasound Detection Sensitivity. IEEE Sens. J. 2020, 20, 9148–9154. [Google Scholar] [CrossRef]
- Zheng, Y.; Chen, L.H.; Dong, X.; Yang, J.; Long, H.Y.; So, P.L.; Chan, C.C. Miniature pH Optical Fiber Sensor Based on Fabry-Perot Interferometer. IEEE J. Sel. Top. Quantum Electron. 2016, 22, 331–335. [Google Scholar] [CrossRef]
- Zhang, P.; Tang, M.; Gao, F.; Zhu, B.; Zhao, Z.; Duan, L.; Fu, S.; Ouyang, J.; Wei, H.; Shum, P.P.; et al. Simplified hollow-core fiber-based fabry-perot interferometer with modified vernier effect for highly sensitive high-temperature measurement. IEEE Photon. J. 2015, 7, 1–10. [Google Scholar] [CrossRef]
- Li, X.G.; Zhao, Y.; Cai, L.; Wang, Q. Simultaneous Measurement of RI and Temperature Based on a Composite Interferometer. IEEE Photon. Technol. Lett. 2016, 28, 1839–1842. [Google Scholar] [CrossRef]
- Dominguez-Flores, C.E.; Rodriguez-Quiroz, O.; Monzon-Hernandez, D.; Ascorbe, J.; Corres, J.M.; Arregui, F.J. Dual-Cavity Fiber Fabry-Perot Interferometer Coated with SnO2for Relative Humidity and Temperature Sensing. IEEE Sens. J. 2020, 20, 14195–14201. [Google Scholar] [CrossRef]
- Zhao, Y.; Tong, R.J.; Chen, M.Q.; Peng, Y. Relative humidity sensor based on Vernier effect with GQDs-PVA un-fully filled in hollow core fiber. Sensors Actuators A Phys. 2019, 285, 329–337. [Google Scholar] [CrossRef]
- Hu, J.; Smietana, M.; Wang, T.; Lang, T.; Shao, L.; Gu, G.; Zhang, X.; Liu, Y.; Song, X.; Song, Z.; et al. Dual Mach-Zehnder Interferometer Based on Side-Hole Fiber for High-Sensitivity Refractive Index Sensing. IEEE Photon. J. 2019, 11. [Google Scholar] [CrossRef]
- Lin, H.; Liu, F.; Guo, H.; Zhou, A.; Dai, Y. Ultra-highly sensitive gas pressure sensor based on dual side-hole fiber interferometers with Vernier effect. Opt. Express 2018, 26, 28763. [Google Scholar] [CrossRef]
- Zhang, S.; Yin, L.; Zhao, Y.; Zhou, A.; Yuan, L. Bending sensor with parallel fiber Michelson interferometers based on Vernier-like effect. Opt. Laser Technol. 2019, 120, 105679. [Google Scholar] [CrossRef]
- Shao, L.Y.; Luo, Y.; Zhang, Z.; Zou, X.; Luo, B.; Pan, W.; Yan, L. Sensitivity-enhanced temperature sensor with cascaded fiber optic Sagnac interferometers based on Vernier-effect. Opt. Commun. 2015, 336, 73–76. [Google Scholar] [CrossRef]
- Ushakov, N.A.; Markvart, A.A.; Liokumovich, L.B. Pulse Wave Velocity Measurement with Multiplexed Fiber Optic Fabry-Perot Interferometric Sensors. IEEE Sens. J. 2020, 20, 11302–11312. [Google Scholar] [CrossRef]
- Liao, H.; Lu, P.; Fu, X.; Jiang, X.; Ni, W.; Liu, D.; Zhang, J. Sensitivity amplification of fiber-optic in-line Mach–Zehnder Interferometer sensors with modified Vernier-effect. Opt. Express 2017, 25, 26898. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Huang, L.; Liu, C.; Wang, H.; Sun, S.; Yang, D. Sensitivity-Enhanced Fiber Temperature Sensor Based on Vernier Effect and Dual In-Line Mach-Zehnder Interferometers. IEEE Sens. J. 2019, 19, 7983–7987. [Google Scholar] [CrossRef]
- Xie, L.; Sun, B.; Chen, M.; Zhang, Z. Sensitivity enhanced temperature sensor with serial tapered two-mode fibers based on the Vernier effect. Opt. Express 2020, 28, 32447. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Wang, S.; Jin, R.B.; Feng, M.; Wu, S.; Zhang, L.; Lu, P. All-Optical demodulation fiber acoustic sensor with real-Time controllable sensitivity based on optical vernier effect. IEEE Photon. J. 2019, 11. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, Y.; Zhao, Y.; Jiang, J.; He, X.; Yang, W.; Zhu, Z.; Gao, W.; Li, L. Sensitivity-enhanced temperature sensor by hybrid cascaded configuration of a Sagnac loop and a F-P cavity. Opt. Express 2017, 25, 33290. [Google Scholar] [CrossRef]
- Claes, T.; Bogaerts, W.; Bienstman, P. Experimental characterization of a silicon photonic biosensor consisting of two cascaded ring resonators based on the Vernier-effect and introduction of a curve fitting method for an improved detection limit. Opt. Express 2010, 18, 22747. [Google Scholar] [CrossRef] [Green Version]
- Zhang, P.; Tang, M.; Gao, F.; Zhu, B.; Fu, S.; Ouyang, J.; Shum, P.P.; Liu, D. Cascaded fiber-optic Fabry-Perot interferometers with Vernier effect for highly sensitive measurement of axial strain and magnetic field. Opt. Express 2014, 22, 19581. [Google Scholar] [CrossRef] [PubMed]
- Ma, C.; Wang, A. Signal processing of white-light interferometric low-finesse fiber-optic Fabry—Perot sensors. Appl. Opt. 2013, 52, 127–138. [Google Scholar] [CrossRef]
- Yu, Z.; Wang, A. Fast White Light Interferometry Demodulation Algorithm for Low-Finesse Fabry-Pérot Sensors. IEEE Photon. Technol. Lett. 2015, 27, 817–820. [Google Scholar] [CrossRef]
- Bhatia, V.; Murphy, K.A.; Claus, R.O.; Tran, T.A.; Greene, J.A. Recent developments in optical-fiber-based extrinsic Fabry-Perot interferometric strain sensing technology. Smart Mater. Struct. 1995, 4, 246–251. [Google Scholar] [CrossRef]
- Yu, Q.; Zhou, X. Pressure sensor based on the fiber-optic extrinsic fabry-perot interferometer. Photonic Sens. 2011, 1, 72–83. [Google Scholar] [CrossRef] [Green Version]
- Xie, J.; Wang, F.; Pan, Y.; Wang, J.; Hu, Z.; Hu, Y. High resolution signal-processing method for extrinsic Fabry-Perot interferometric sensors. Opt. Fiber Technol. 2015, 22, 1–6. [Google Scholar] [CrossRef]
- Zhou, X.; Yu, Q. Wide-Range Displacement Sensor Based on Fiber-Optic Fabry–Perot Interferometer for Subnanometer Measurement. IEEE Sens. J. 2011, 11, 1602–1606. [Google Scholar] [CrossRef]
- Li, C.; Chen, S.; Zhu, Y. Maximum Likelihood Estimation of Optical Path Length in Spectral Interferometry. J. Light. Technol. 2017, 35, 4880–4887. [Google Scholar] [CrossRef]
- Qi, Y.; Chen, W.; Xie, J.; Lei, X. A fast Maximum Likelihood Estimation algorithm for demodulating Fiber White-Light Interferometry. J. Phys. Conf. Ser. 2018, 1065. [Google Scholar] [CrossRef]
- Wu, Y.; Xia, L.; Cai, N.; Zhu, L. A Highly Precise Demodulation Method for Fiber Fabry-Perot Cavity through Spectrum Reconstruction. IEEE Photon. Technol. Lett. 2018, 30, 435–438. [Google Scholar] [CrossRef]
- Chen, H.; Liu, J.; Zhang, X.; Wang, W.; Ma, Z.; Lv, W.; Guo, Z. High-Order Harmonic-Frequency Cross-Correlation Algorithm for Absolute Cavity Length Interrogation of White-Light Fiber-Optic Fabry-Perot Sensors. J. Light. Technol. 2020, 38, 953–960. [Google Scholar] [CrossRef]
- Wang, H.; Meng, H.; Xiong, R.; Wang, Q.; Huang, B.; Zhang, X.; Yu, W.; Tan, C.; Huang, X. Simultaneous measurement of refractive index and temperature based on asymmetric structures modal interference. Opt. Commun. 2016, 364, 191–194. [Google Scholar] [CrossRef]
- Ni, X.; Wang, M.; Guo, D.; Hao, H.; Zhu, J. A Hybrid Mach-Zehnder Interferometer for Refractive Index and Temperature Measurement. IEEE Photon. Technol. Lett. 2016, 28, 1850–1853. [Google Scholar] [CrossRef]
- Mayrargue, S.; Blu, T. Relationship between high-resolution methods and discrete Fourier transform. Proc. ICASSP, IEEE Int. Conf. Acoust. Speech Signal Process. 1991, 5, 3321–3324. [Google Scholar] [CrossRef] [Green Version]
- Russell, P. Applied physics: Photonic crystal fibers. Science 2003, 299, 358–362. [Google Scholar] [CrossRef] [PubMed]
- Weihs, G.; Reck, M.; Weinfurter, H.; Zeilinger, A. All-fiber three-path Mach–Zehnder interferometer. Opt. Lett. 1996, 21, 302. [Google Scholar] [CrossRef] [Green Version]
- Chen, G.Y. A Review of Microfiber and Nanofiber Based Optical Sensors. Open Opt. J. 2014, 7, 32–57. [Google Scholar] [CrossRef]
- Li, Z.; Liao, C.; Song, J.; Wang, Y.; Wang, Y. Ultrasensitive magnetic field sensor based on in-fiber Mach-Zehnder interferometer and magnetic fluid. Opt. InfoBase Conf. Pap. 2014, 4, 197–201. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).