Akinetic Swept-Source Master–Slave-Enhanced Optical Coherence Tomography
Abstract
1. Introduction
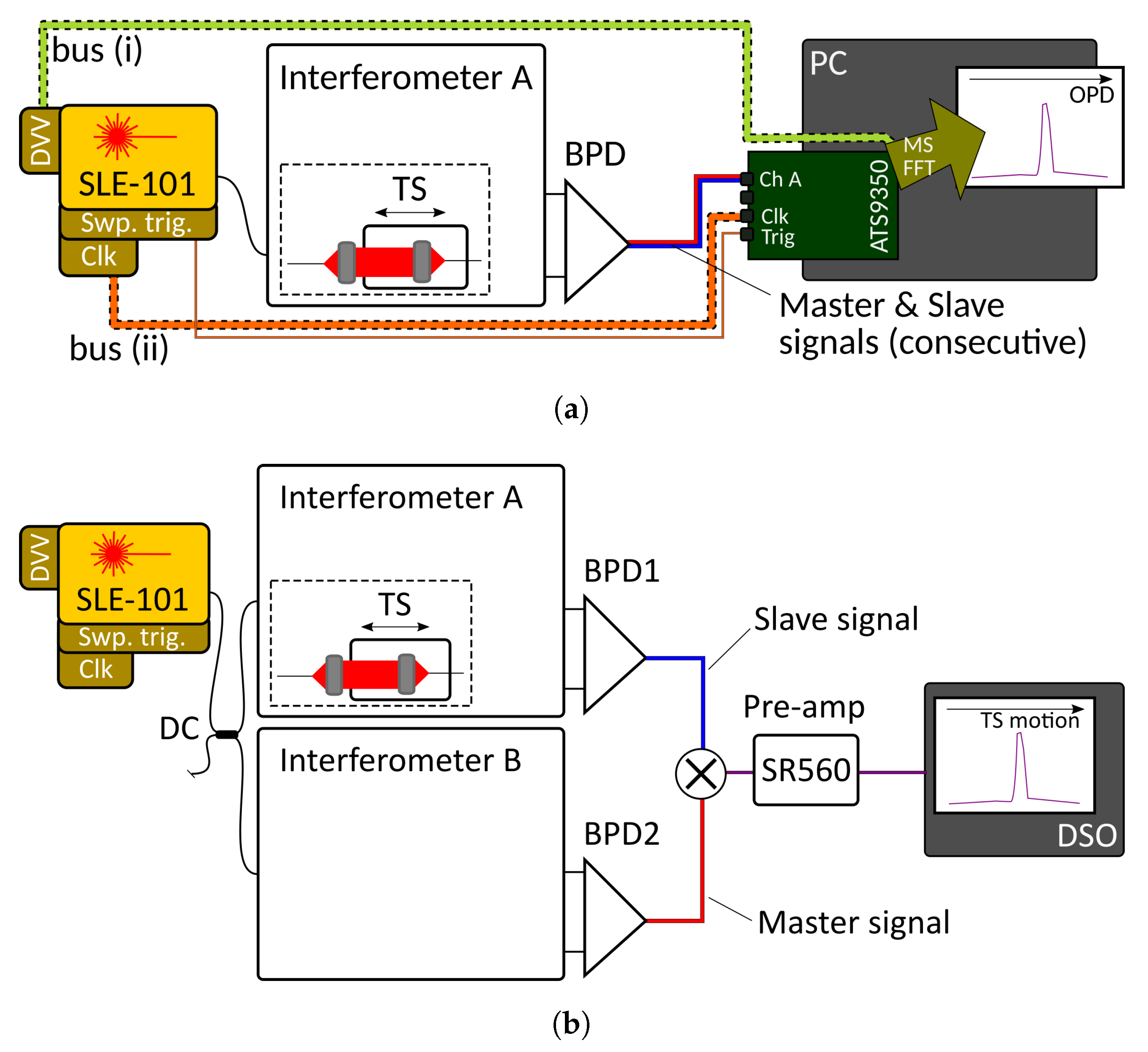
2. Materials and Methods
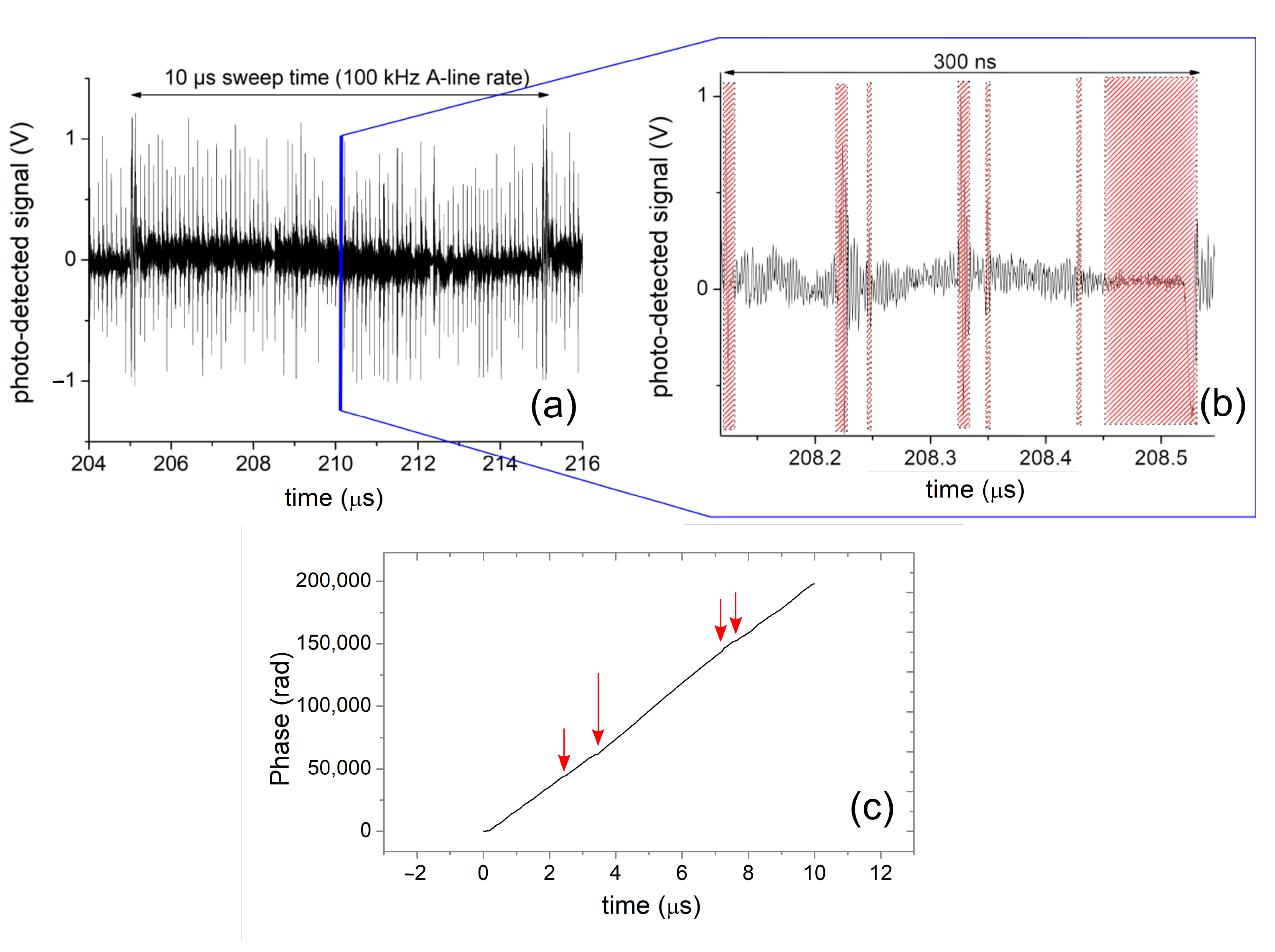
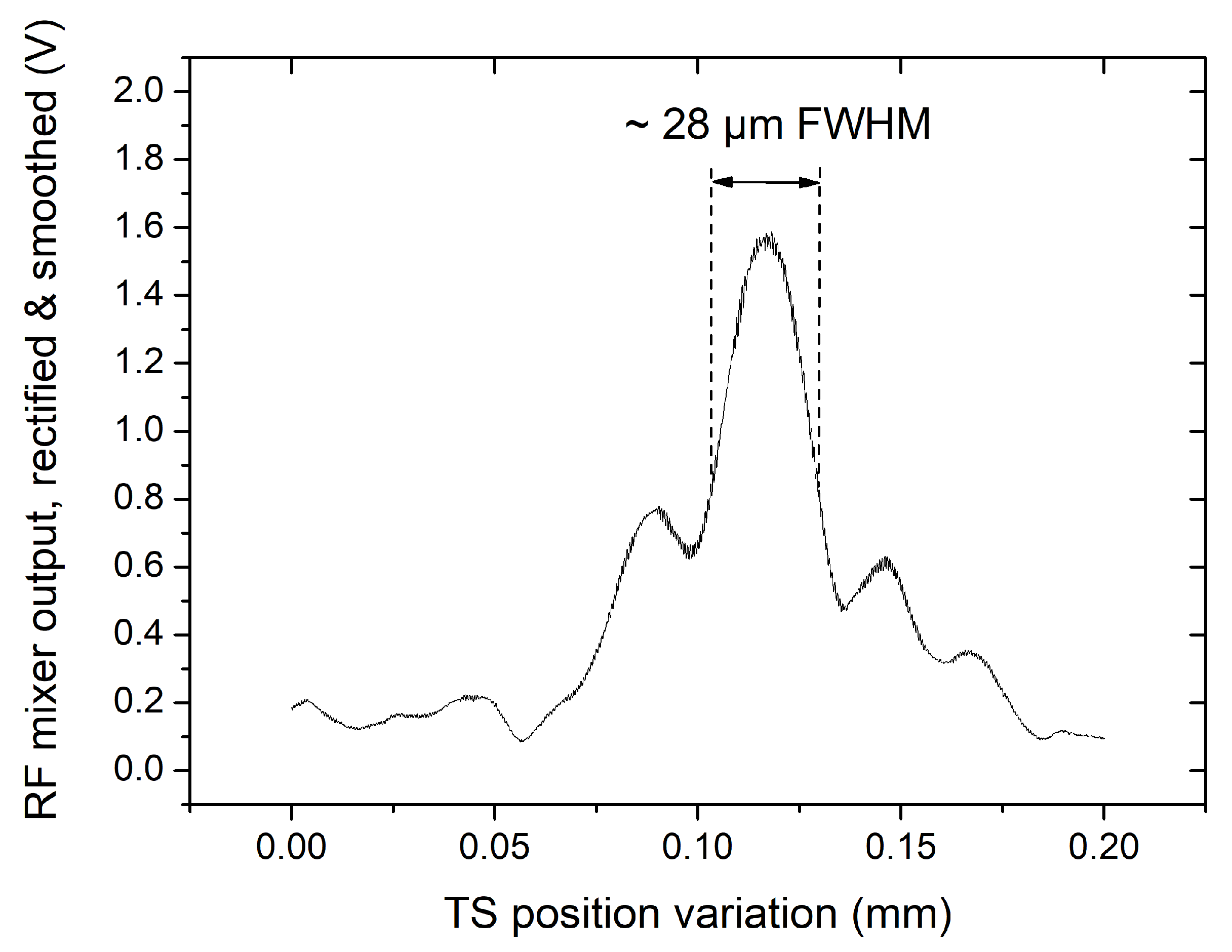
2.1. Channelled Spectrum Processing for MS–OCT
3. Results
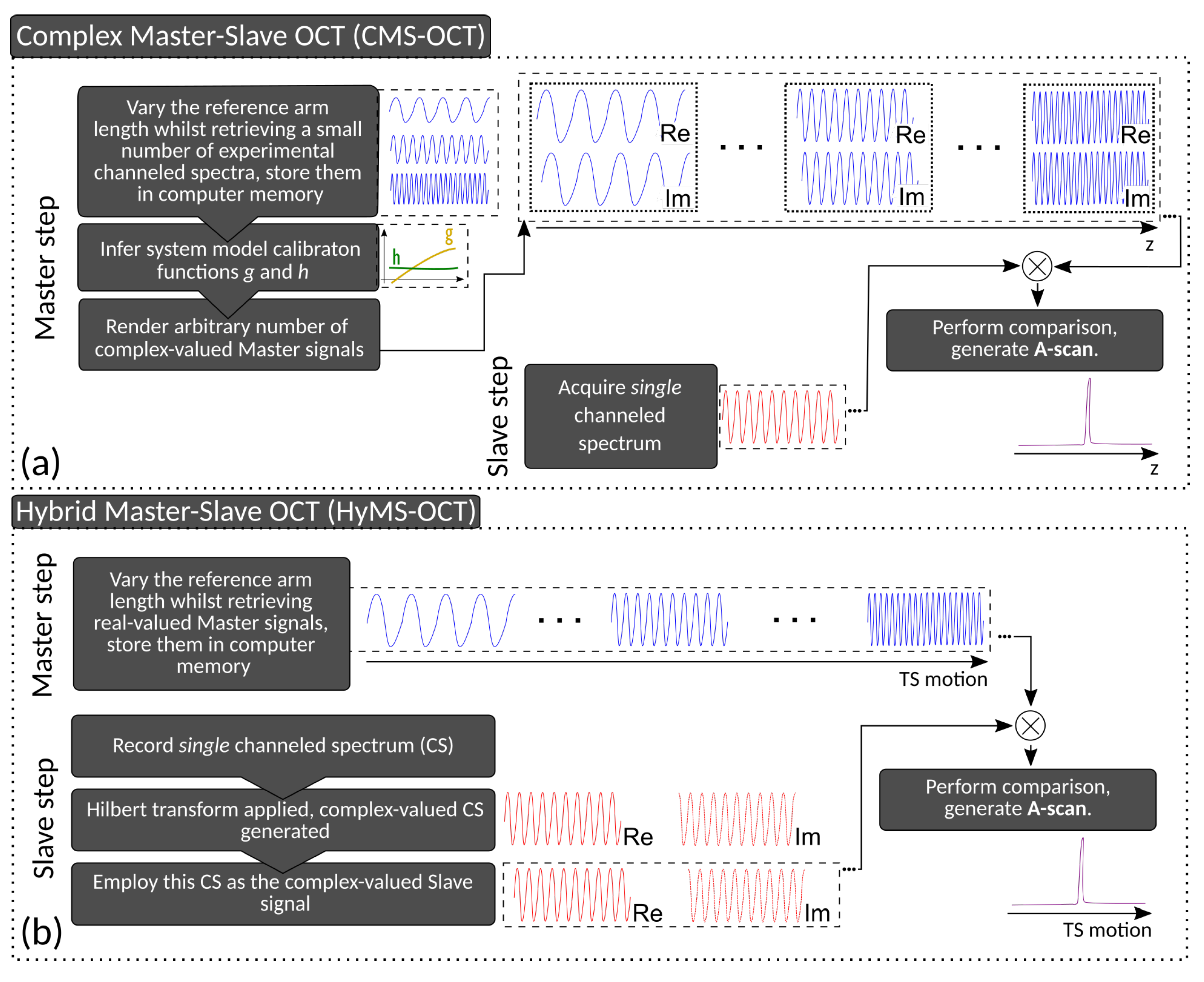
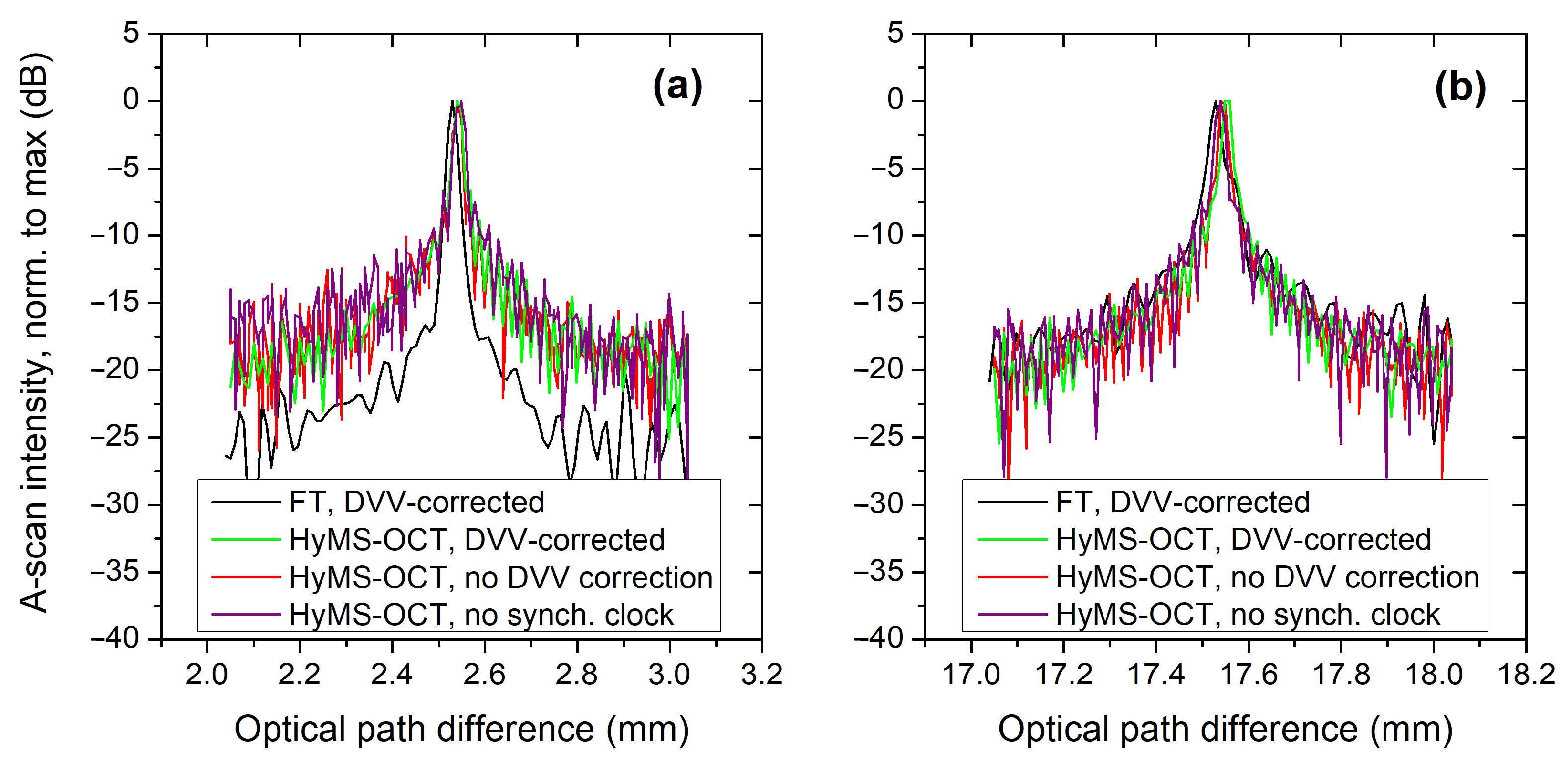
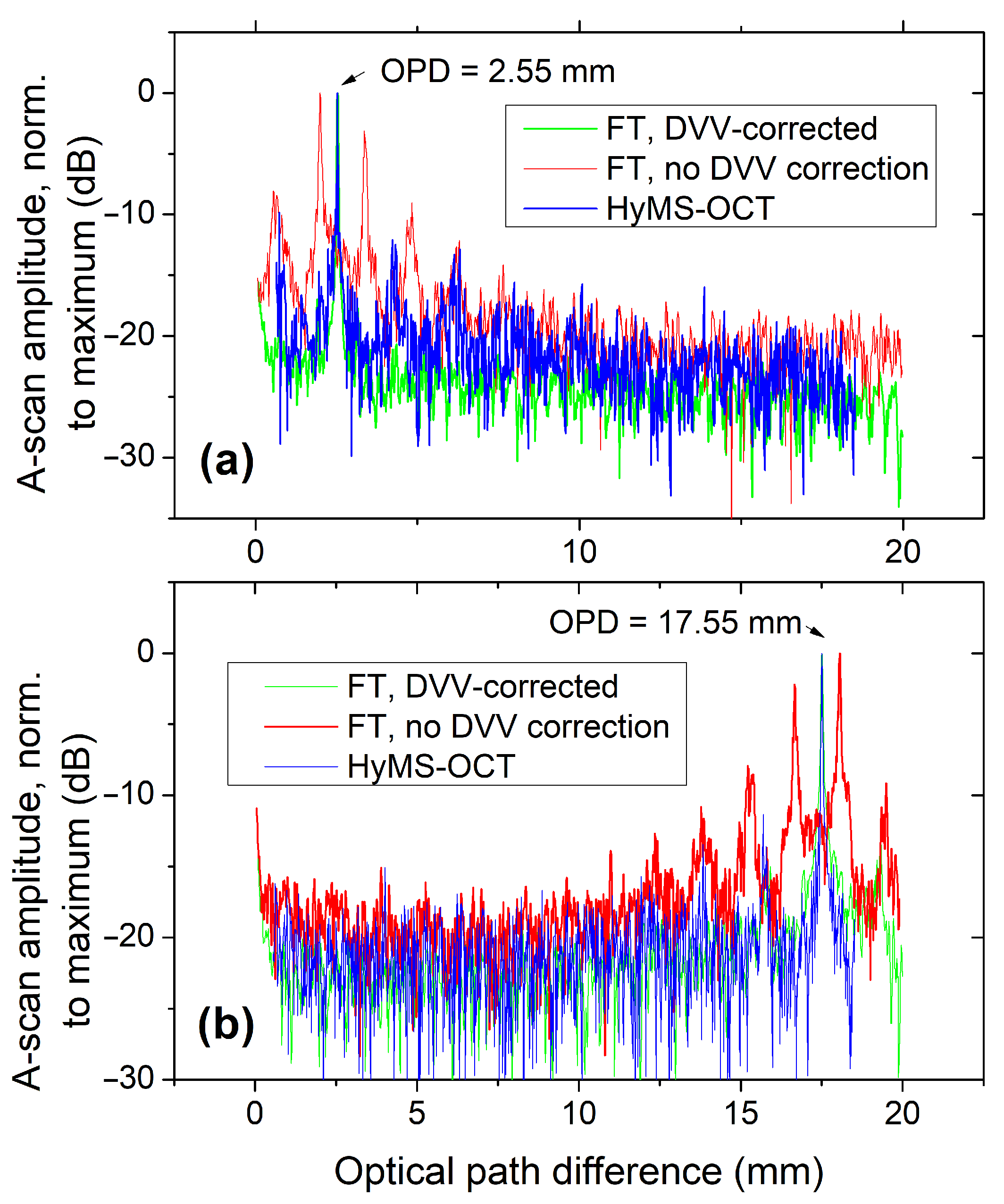
3.1. Complex Master–Slave/Hybrid Master–Slave Operation with Pre-Stored Masks
- Interferogram corrected with the DVV data, having been sampled with the source’s clock signal (both (i) and (ii) buses connected to the digitiser in Figure 2a);
- Interferogram not corrected with the DVV data, but still sampled with the source’s clock signal (bus (ii) only in Figure 2a connected);
- Interferogram sampled with the digitiser card’s built-in clock signal (). Due to the asynchronous operation, the DVV correction is not possible (both (i) and (ii) buses in Figure 2a disconnected).
3.2. Down-Conversion (DC) OCT Implementation with Two Physical Interferometers
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Swanson, E.A. OCT Technology Transfer and the OCT Market. In Optical Coherence Tomography: Technology and Applications; Drexler, W., Fujimoto, J.G., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 2529–2571. [Google Scholar] [CrossRef]
- Leitgeb, R.; Hitzenberger, C.; Fercher, A. Performance of fourier domain vs. time domain optical coherence tomography. Opt. Express 2003, 11, 889. [Google Scholar] [CrossRef] [PubMed]
- Minneman, M.P.; Ensher, J.; Crawford, M.; Derickson, D. All-Semiconductor High-Speed Akinetic Swept-Source for OCT. In Optical Sensors and Biophotonics; Paper 831116; Optical Society of America: Shanghai, China, 2011; p. 831116. [Google Scholar] [CrossRef]
- Wang, Z.; Potsaid, B.; Chen, L.; Doerr, C.; Lee, H.C.; Nielson, T.; Jayaraman, V.; Cable, A.E.; Swanson, E.; Fujimoto, J.G. Cubic meter volume optical coherence tomography. Optica 2016, 3, 1496. [Google Scholar] [CrossRef] [PubMed]
- Park, J.; Carbajal, E.F.; Chen, X.; Oghalai, J.S.; Applegate, B.E. Phase-sensitive optical coherence tomography using an Vernier-tuned distributed Bragg reflector swept laser in the mouse middle ear. Opt. Lett. 2014, 39, 6233–6236. [Google Scholar] [CrossRef] [PubMed]
- MacDougall, D.; Farrell, J.; Brown, J.; Bance, M.; Adamson, R. Long-range, wide-field swept-source optical coherence tomography with GPU accelerated digital lock-in Doppler vibrography for real-time, middle ear diagnostics. Biomed. Opt. Express 2016, 7, 4621–4635. [Google Scholar] [CrossRef] [PubMed]
- Song, S.; Xu, J.; Wang, R.K. Long-range and wide field of view optical coherence tomography for in vivo 3D imaging of large volume object based on akinetic programmable swept source. Biomed. Opt. Express 2016, 7, 4734–4748. [Google Scholar] [CrossRef] [PubMed]
- Salas, M.; Augustin, M.; Felberer, F.; Wartak, A.; Laslandes, M.; Ginner, L.; Niederleithner, M.; Ensher, J.; Minneman, M.P.; Leitgeb, R.A.; et al. Compact akinetic swept source optical coherence tomography angiography at 1060 nm supporting a wide field of view and adaptive optics imaging modes of the posterior eye. Biomed. Opt. Express 2018, 9, 1871–1892. [Google Scholar] [CrossRef] [PubMed]
- Podoleanu, A.G.; Bradu, A. Master–slave interferometry for parallel spectral domain interferometry sensing and versatile 3D optical coherence tomography. Opt. Express 2013, 21, 19324. [Google Scholar] [CrossRef] [PubMed]
- Rivet, S.; Maria, M.; Bradu, A.; Feuchter, T.; Leick, L.; Podoleanu, A. Complex master slave interferometry. Opt. Express 2016, 24, 2885. [Google Scholar] [CrossRef] [PubMed]
- Podoleanu, A.; Cernat, R.; Bradu, A. Down-conversion en-face optical coherence tomography. Biomed. Opt. Express 2019, 10, 772. [Google Scholar] [CrossRef] [PubMed]
- Bradu, A.; Maria, M.; Podoleanu, A.G. Demonstration of tolerance to dispersion of master/slave interferometry. Opt. Express 2015, 23, 14148. [Google Scholar] [CrossRef] [PubMed]
- Marques, M.J.; Rivet, S.; Bradu, A.; Podoleanu, A. Complex master-slave for long axial range swept-source optical coherence tomography. OSA Contin. 2018, 1, 1251. [Google Scholar] [CrossRef]
- Siddiqui, M.; Nam, A.S.; Tozburun, S.; Lippok, N.; Blatter, C.; Vakoc, B.J. High-speed optical coherence tomography by circular interferometric ranging. Nat. Photonics 2018, 12, 111–116. [Google Scholar] [CrossRef] [PubMed]
- Lippok, N.; Lippok, N.; Vakoc, B.J.; Vakoc, B.J.; Vakoc, B.J. Resolving absolute depth in circular-ranging optical coherence tomography by using a degenerate frequency comb. Opt. Lett. 2020, 45, 371–374. [Google Scholar] [CrossRef] [PubMed]
- Chun, S.K.; Jang, H.; Cho, S.W.; Park, N.S.; Kim, C.S. Unfolding displacement measurement method for the aliasing interferometer signal of a wavelength-comb-swept laser. Opt. Express 2018, 26, 5789–5799. [Google Scholar] [CrossRef] [PubMed]
- Marques, M.J.; Cernat, R.; Ensher, J.; Bradu, A.; Podoleanu, A. Master-slave principle applied to an electrically tunable swept source-OCT system. In Optical Coherence Tomography and Coherence Domain Optical Methods in Biomedicine XXIV; International Society for Optics and Photonics: San Francisco, CA, USA, 2020; Volume 11228, p. 112280D. [Google Scholar] [CrossRef]
- Insight Akinetic Swept Lasers Enabling OCT and SS-OCT Angiography|Insight. Available online: https://www.sweptlaser.com/content/insight-akinetic-swept-lasers-enabling-oct-and-ss-oct-angiography (accessed on 27 May 2020).
- Bradu, A.; Rivet, S.; Podoleanu, A. Master/slave interferometry – ideal tool for coherence revival swept source optical coherence tomography. Biomed. Opt. Express 2016, 7, 2453. [Google Scholar] [CrossRef] [PubMed]

| Method | Transform-Limited | FFT (No Dispersion Compensation) | CMS–OCT | HyMS–OCT | |
|---|---|---|---|---|---|
| Sampling Protocol | |||||
| DVV-corrected, 400 MHz source clock | 11.6 | ||||
| Sampling Protocol | Peak Width (m) | SNR (dB) |
|---|---|---|
| no DVV correction, 400 MHz source clock | 12.57 | 19.6 |
| 12.47 | 22.4 | |
| asynchronous operation, 500 MHz clock from digitiser | 14.82 | 18.3 |
| 14.64 | 20.8 |
| Method | Transform-Limited | FFT (No Dispersion Compensation) | CMS–OCT | HyMS–OCT | |
|---|---|---|---|---|---|
| Sampling Protocol | |||||
| DVV-corrected, 400 MHz source clock | n/a | ||||
| Advantages | Disadvantages |
|---|---|
|
|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marques, M.J.; Cernat, R.; Ensher, J.; Bradu, A.; Podoleanu, A. Akinetic Swept-Source Master–Slave-Enhanced Optical Coherence Tomography. Photonics 2021, 8, 141. https://doi.org/10.3390/photonics8050141
Marques MJ, Cernat R, Ensher J, Bradu A, Podoleanu A. Akinetic Swept-Source Master–Slave-Enhanced Optical Coherence Tomography. Photonics. 2021; 8(5):141. https://doi.org/10.3390/photonics8050141
Chicago/Turabian StyleMarques, Manuel J., Ramona Cernat, Jason Ensher, Adrian Bradu, and Adrian Podoleanu. 2021. "Akinetic Swept-Source Master–Slave-Enhanced Optical Coherence Tomography" Photonics 8, no. 5: 141. https://doi.org/10.3390/photonics8050141
APA StyleMarques, M. J., Cernat, R., Ensher, J., Bradu, A., & Podoleanu, A. (2021). Akinetic Swept-Source Master–Slave-Enhanced Optical Coherence Tomography. Photonics, 8(5), 141. https://doi.org/10.3390/photonics8050141








