1. Introduction
With the evolution of technology, the impact of sensors on human life has increased. The significant impact of optical systems is due to the emergence of fiber optics in 1960 [
1]. The features such as low attenuation and insensitivity to electromagnetic fields have allowed optical systems to replace electronic communications. In addition, they have enabled the design of ultra-sensitive optical sensors with applicability in nanotechnology [
2].
The cleaved-tip optical sensors are the simplest [
3]. When used alone, they are only intensity sensors. However, when they are coupled to reflective surfaces [
4] or when coatings are deposited on the tip [
5], in addition to the intensity operation, they can also operate at wavelength because they allow the implementation of Fabry–Perot interferometers (FPI) [
6]. The operation of an FPI is unidirectional where, initially, part of the beam is reflected, and another part is transmitted forming two beams. The transmitted beam is then reflected travelling a distance that is twice the length of the interferometer. Finally, the two beams overlap resulting in the interference pattern. Although in certain areas there are sensory architectures with higher sensitivity and the possibility of multiple measurements [
7,
8,
9], the cleaved-tip sensors are the easiest to control and manufacture in addition to covering a higher number of research areas.
Despite the vast advances in the development of optical sensors, it was only in 2011 that the Vernier effect was applied in interferometry [
10]. This phenomenon is based on the optical waves beat where two waves appear, the envelope and the carrier [
11]. Normally, measurements are based on the envelope wave because it shows the highest sensitivity. In the case of interferometry, the effect is in the wavelength dimension, so spectral optical waves are used.
Currently there are several interferometric displacement sensors. From these, the Mach–Zehnder with a sensitivity of 1.53 nm/μm [
12] stands out for a wide range. For a narrow range, the application of surface plasmon resonance (SPR) with a sensitivity of 10.32 nm/μm for a micrometric range [
13] and a sensitivity of 31.45 nm/nm for a nanometric range [
14] stand out. Recently a new strain sensor architecture based on a push-pull deformation method was reported [
15].
In this work, the enhanced Vernier effect combined with the push-pull method is presented. This sensor consists of two FPIs formed by two cleaved tips and a mirror. The signal from the two interferometers are overlapped by means of a 3 dB fiber coupler, resulting the Vernier effect. In this research, the sensitivity of the single interferometer is compared with the sensitivity of the enhanced Vernier effect envelope, both with the same free spectral range (FSR). In addition, it also presents the results regarding the maximization of displacement sensors with enhanced Vernier effect.
2. Materials and Methods
The Vernier effect consists on the overlapping of two optical waves, a concept similar to the beat of two sound waves [
16]. This optical phenomenon results in the formation of two new waves: the envelope and the carrier. Usually, optical sensors are based on the traditional Vernier effect, where one of the interferometers is referenced and another is the sensing probe. However, in this paper, the enhanced Vernier effect is presented, and it uses two sensing interferometers which move in opposite directions [
17]. One of the major problems with this type of Vernier effect is the lack of sensors with symmetrical sensitivities. Thus arises the application of the push-pull method in interferometry, allowing symmetrical variations of two equal interferometers. This results in two sensors with symmetric sensitivities allowing the maximization of the enhanced Vernier effect [
15].
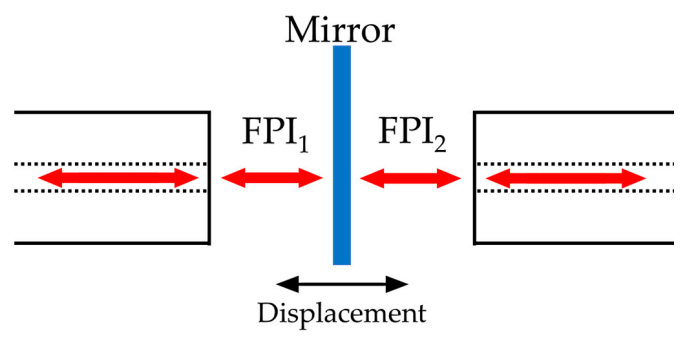
The architecture of the two interferometers is presented in
Figure 1 and it is composed by two cleaved fibers and a double-sided reflecting surface. The two interferometers are linked together with a 3 dB coupler. The operating method consists in dividing the light beam into two beams that through the cleaved fibers and the reflecting surface form two Fabry–Perot interferometers (FPIs).
The optical signal of the two interferometers is overlapped by means of the coupler forming the output signal of the sensor. The intensity of a FPI can be written as:
where Δ
ϕ = πnL/λ,
n is the refractive index,
L is the interferometer length,
λ is the wavelength and
I0 is the difference in intensity of the optical paths. If the optical signal is coupled between fibers, a π/2 phase must be added to Δ
ϕ. Thus, the sensor output signal is described by:
where the indices 1 and 2 allow identify the two interferometers, the components Δ
ϕ1 − Δ
ϕ2 and Δ
ϕ1 + Δ
ϕ2 correspond to the envelope and the carrier, respectively.
Figure 2 presents the simulation of Equation (2) with two cavities-one with 500 μm and the other with 600 μm-and a refraction index of 1.00027316. The length of the interferometers can be written as
L =
L0 + Δ
L, where
L0 is the initial length and
ΔL is the mirror displacement. Therefore, taking into account that the interferometers are submitted to a symmetric displacement, Equation (2) can be rewritten as follows:
where
γ = πn/2λ. As can be seen, the envelope of the enhanced Vernier effect has a sensitivity two-fold that of the one achieved for a single FPI. Furthermore, the envelope does not depend on the length of the interferometers allowing the result of ultra-sensitive displacement sensors with macroscopic FPIs to be replicated.
To evaluate the efficiency of the implementation of the Vernier effect, the
M-factor is considered and is given by [
16]:
where Δ
λenv is the free spectral range (FSR) of the envelope and Δ
λ1 is the FSR of a single interferometer. With the appearance of the enhanced Vernier effect, new factors have emerged to evaluate the performance of the Vernier effect [
18]:
where
sensenv and
senscarr are the envelope and the carrier sensitivities, respectively,
where Δ
λcarr is the
FSR of the carrier and,
where
MVernier is = 1 for the traditional Vernier effect, < 1 for reduced case and > 1 for the enhanced case.
3. Results
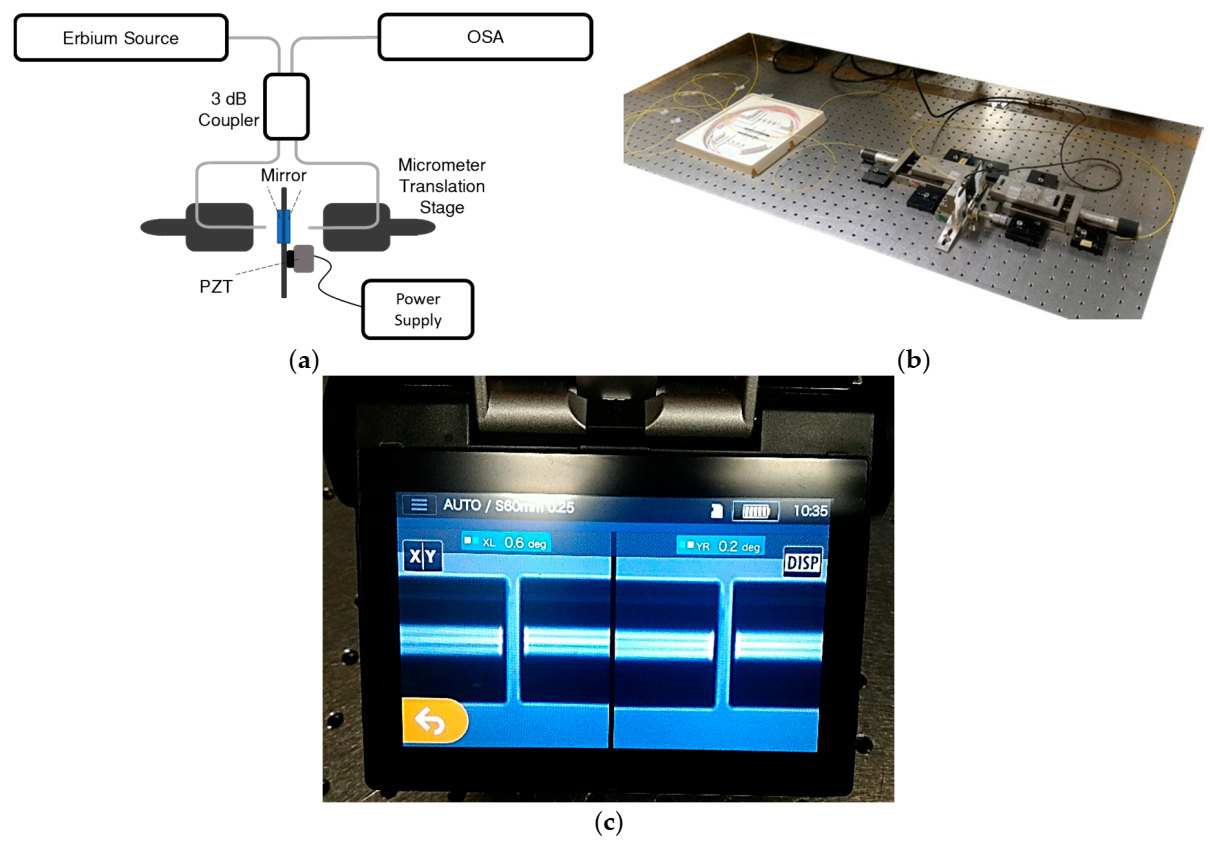
The setup used to characterize the sensor is shown in
Figure 3. The mechanical part consists of a double-sided reflective silver surface coupled to a piezoelectric with a displacement of 180.0 ± 0.2 nm/V. Also, a standard optical fiber (SMF28), an erbium broadband source, centered at 1550 nm and a bandwidth of 90 nm, and an optical spectral analyzer (OSA, “YOKOGAWA AQ5370C”) with a resolution of 0.02 nm, were used. All the splices in the system were made with a conventional splice machine (“Sumitomo Electric—Type-72C”, Osaka, Japan). The overlap of the interferometers signals is obtained with a 3 dB fiber coupler. The fiber cleavage was performed by “Fiber Cleaver FC-6RS” which provides a cleavage angle of less than 1° (
Figure 3c).
The sensor characterization involved nano-step measurement provided by the piezoelectric device. To determine the efficiency of the displacement sensor, a single interferometer with a length of 73 ± 2 μm was initially developed, which allowed only three fringes in the bandwidth supplied by the erbium source (
Figure 4a) to be obtained. Varying the distance between the fiber and the reflecting surface resulted in
Figure 4b where a sensitivity of 29.2 ± 0.3 nm/μm with a
r2 of 0.9995 was obtained.
Following, the Vernier effect was investigated. Since the accuracy of the envelope measurement increases with the increase of the carrier frequency, the sensitivity of a single interferometer with a length of 15.4 ± 0.5 mm was first studied (
Figure 5), where a sensitivity of 0.95 ± 0.05 nm/μm with a
r2 of 0.995 was achieved. Thus, the interferometers used to generate the Vernier effect have a lower sensitivity than the reference single interferometer. In this case, the FSR is 0.07 nm.
Now, a second fiber has been added allowing to obtain the Vernier effect. Although both interferometers have the same length (15.4 ± 0.5 mm), they differ by a value close to 70 μm. Hence an envelope with only three fringes appears (
Figure 6). This last feature is important because it allows us to compare the envelope of this sensor with the first singular interferometer that is present in this paper.
In this case, the envelope sensitivity was 60 ± 1 nm/μm with a r2 of 0.998 (which is shown in Figure 8) and the carrier had a negligible sensitivity. The envelope sensitivity was two-fold that obtained by the reference single interferometer. the FSR for the envelope and carrier was 18 nm and 0.07 nm, respectively. Therefore, the M-factor is 257, Msens = 360, MFSR = 257, MVernier = 1.4.
The last characterization was to optimize the proposed setup in order to obtain the maximum sensitivity of this configuration. In this case, we used two interferometers with a length of 6.1 ± 0.2 mm each and by reducing the difference between the two interferometers, an envelope with only one fringe was achieved, as depicted in
Figure 7. The sensitivity obtained was 254 ± 6 nm/μm with an
r2 of 0.9990 (which is shown in
Figure 8) for the envelope, and 0.160 ± 0.005 nm/μm with a
r2 of 0.992 for the carrier. Also, the
FSR for the envelope and the carrier was 75 nm 0.09 nm respectively. Therefore, the
M-factor was 1071,
Msens = 1587,
MFSR = 833,
MVernier = 1.9.
Table 1 summarizes all the values.
4. Discussion
Figure 8 presents the comparison of the different sensitivities obtained in each case. As can be seen, the displacement sensitivity of the two interferometers with the Vernier effect (60 ± 1 nm/μm) is two-fold the one obtained with the single interferometer (29.2 ± 0.3 nm/ μm), with the same FSR. In addition, when the two interferometers are optimized, the maximum sensitivity obtained is 254 ± 6 nm/μm corresponding to an
M-factor of 1071 and a
MVernier of 1.9. Therefore, the sensor using the enhanced Vernier effect was more efficient than the traditional Vernier effect besides the fact that the maximum sensitivity obtained was 24 times higher than the SPR-based sensor for a micrometric range [
13]. Furthermore, the Vernier effect allows a sensor whose implementation is easier to be obtained because the performance depends on the relation between the interferometers and not on the specific length of each FPI. Thus, it is possible to develop giant sensitivities in ranges where the sensitivity of a single interferometer is low.
5. Conclusions
This research compares the sensitivity of a single FPI and the Vernier effect performed with two FPIs for the same number of fringes. The results reveal that the Vernier effect envelope, where 60 ± 1 nm/μm is achieved, has twice the sensitivity of the single FPI, 29.2 ± 0.3 nm/ μm. Moreover, with the optimization of the system, an envelope sensitivity of 254 ± 6 nm/μm with M-factor of 1071 and a MVernier of 1.9 was obtained and corresponded to a resolution of 79 pm (considering the spectral resolution of 0.02 nm). In addition, the sensitivity of the Vernier effect envelope depends only on the relationship between interferometers, which allows problems in the production of ultra-sensitive sensors to be overcome as well as the same sensitivity for any distance of the fibers to the reflecting surface to be observed. This new displacement sensor architecture allows the implementation of giant-sensitive non evasive measurements with high relevance in areas such as micro and nano manufacturing and biology.