Neural Network DPD for Aggrandizing SM-VCSEL-SSMF-Based Radio over Fiber Link Performance
Abstract
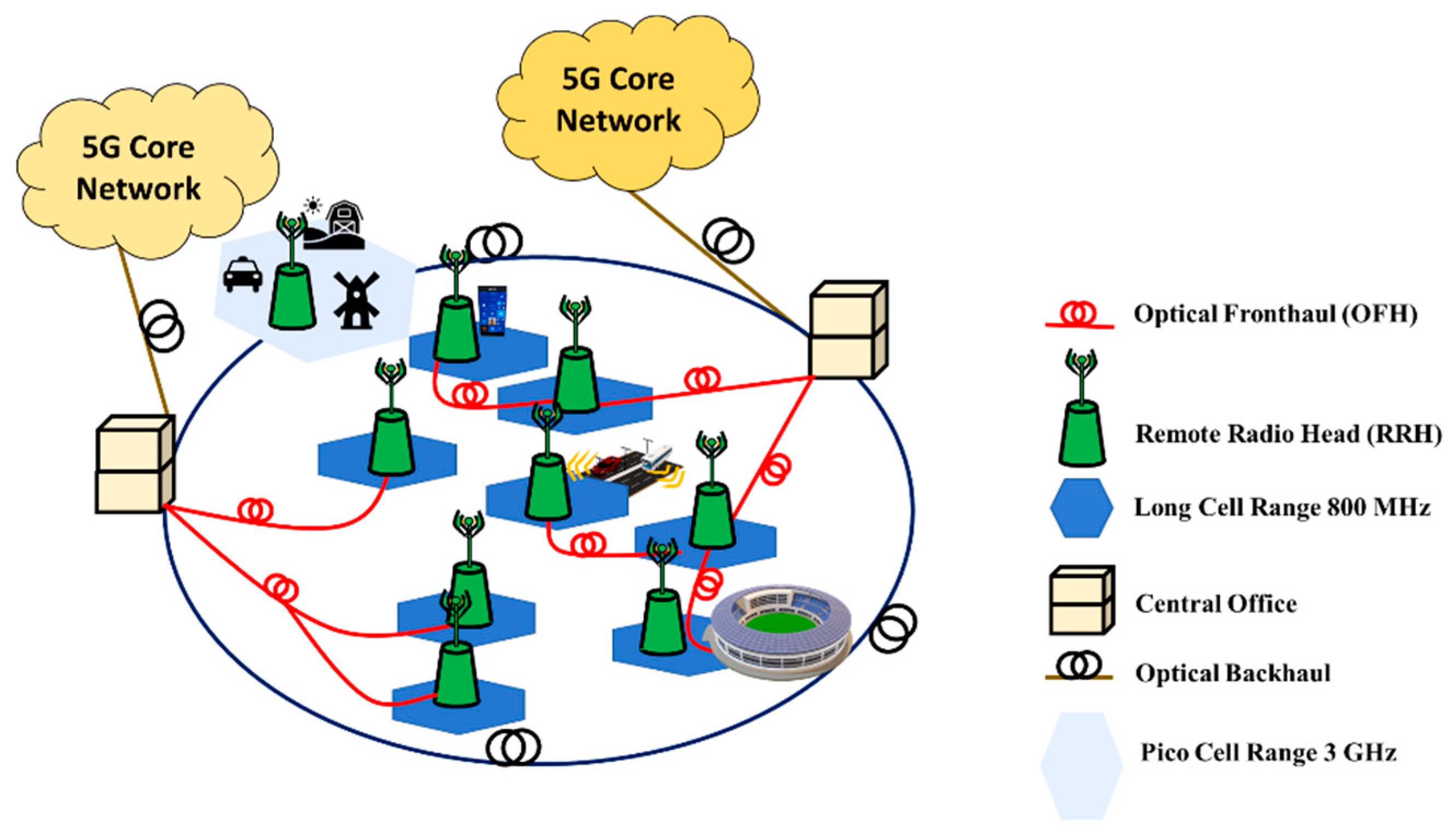
1. Introduction
- A novel NN-based DPD algorithm is proposed for the linearization of RoF links.
- This NN-DPD method has been implemented with a new training method without the utilization of indirect learning architecture where a separate RoF-NN is used to first model the RoF link. Once modelled, by back propagating the error through RoF-NN, the DPD-NN is trained.
- The complexity of the proposed algorithms is estimated.
- For the first time, an experimental comparative study has been conducted where DPD-NN, DPD-MP and DPD-GMP are compared in terms of Adjacent Channel Power Ration (ACPR) and Error Vector Magnitude (EVM).
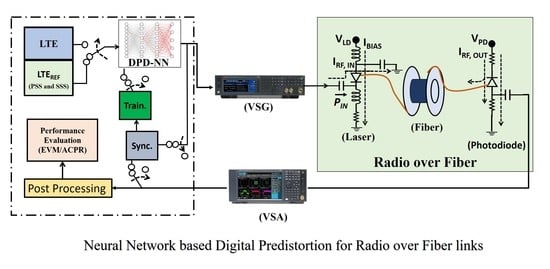
2. Neural Network-Based DPD Architecture
2.1. NN Model Characteristics and Design
- A DPD NN is utilized to predistort the “real” RoF link.
- An RoF NN model is required to train the DPD NN.
2.2. C. NN Training
| Algorithm 1. Training Performed |
| ← for i Z do ← : // RoF Transmission ← Train on , // Update RoF NN Model // Freeze NN weights of ← Train on . // Use () ← : // Predistort end for |
3. Comparison with Volterra Method
3.1. Modelling Approach
3.1.1. Memory Polynomial Model
3.1.2. Generalized Memory Polynomial Model
3.2. Estimation Algorithm
4. Complexity Considerations
5. Experimental Setup
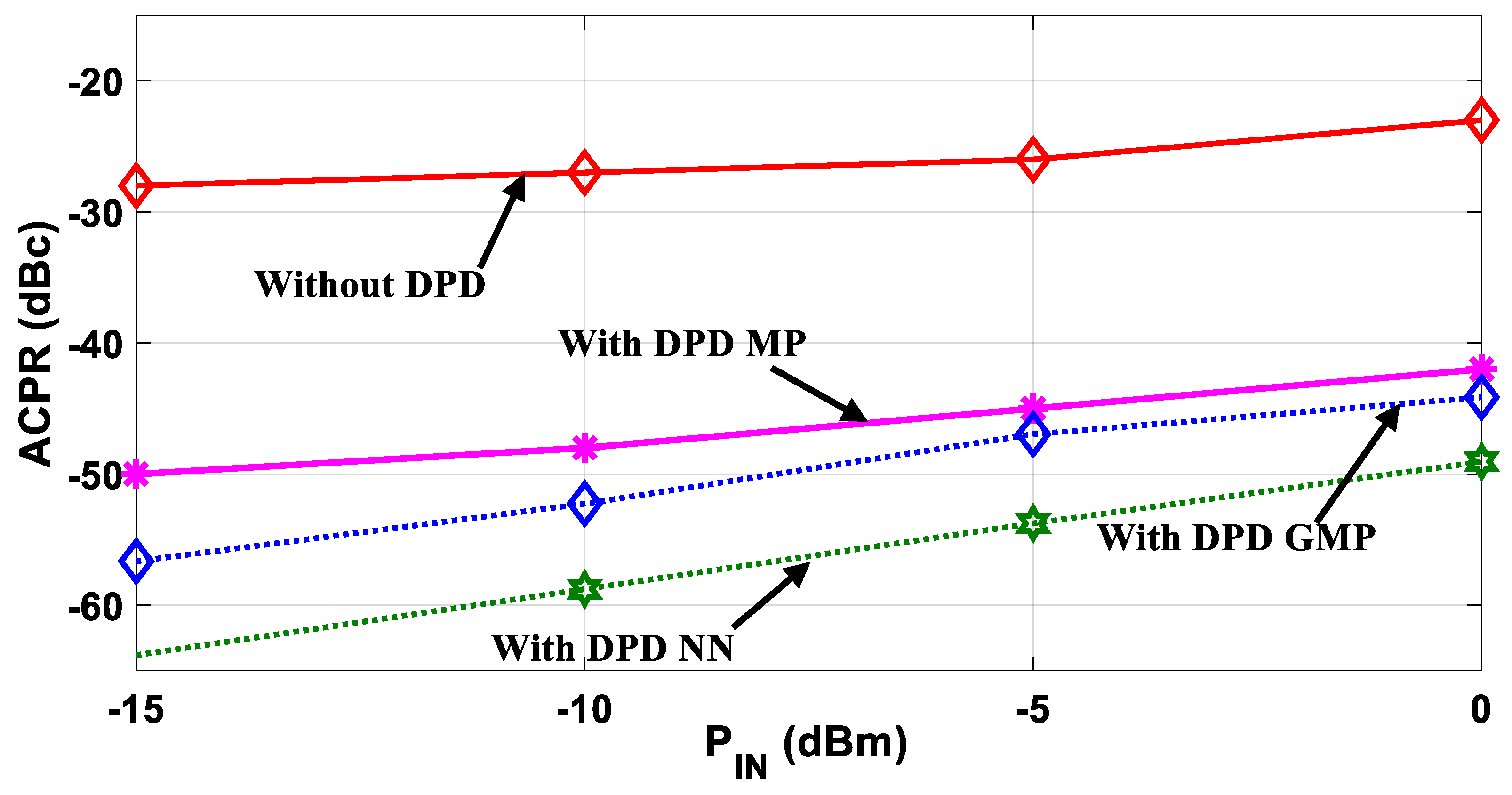
6. Experimental Results and Discussion
7. Real Time Realization of the NN DPD Method
8. Hardware Limitations
9. Possible Future Directions
10. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hadi, M.U.; Awais, M.; Raza, M. Multiband 5G NR-over-Fiber System Using Analog Front Haul. In Proceedings of the 2020 International Topical Meeting on Microwave Photonics (MWP), Matsue, Japan, 23–26 November 2020; pp. 136–139. [Google Scholar]
- 3GPP, User Equipment (UE) Radio Transmission and Reception; Part 3: Range 1 and Range 2 Interworking Operation with Other Radios, 2019, TS 38.101-3 Version 16.0.0 Release 16. Available online: https://ieeexplore.ieee.org/document/9314547 (accessed on 5 January 2021).
- Hadi, M.U. Digital Signal Processing Techniques Applied to Radio over Fiber Systems. Ph.D. Thesis, Engineering Alma Mater Studiorum University of Bologna, Bologna, Italy, 2020. [Google Scholar] [CrossRef]
- Khurshid, K.; Khan, A.A.; Siddiqui, H.; Rashid, I.; Hadi, M.U. Big Data Assisted CRAN Enabled 5G SON Architecture. J. ICT Res. Appl. 2019, 13, 93–106. [Google Scholar] [CrossRef]
- Hadi, M.U.; Nanni, J.; Polleux, J.L.; Traverso, P.A.; Tartarini, G. Direct digital predistortion technique for the compensation of laser chirp and fiber dispersion in long haul radio over fiber links. Opt. Quantum Electron. 2019, 51, 205. [Google Scholar] [CrossRef]
- Hadi, M.U.; Kantana, C.; Traverso, P.A.; Tartarini, G.; Venard, O.; Baudoin, G.; Polleux, J.L. Assessment of digital predistortion methods for DFB-SSMF radio-over-fiber links linearization. Microw. Opt. Technol. Lett. 2020, 62, 540–546. [Google Scholar] [CrossRef]
- Zhang, X.; Zhu, R.; Shen, D.; Liu, T. Linearization Technologies for Broadband Radio-Over-Fiber Transmission Systems. Photonics 2014, 1, 455–472. [Google Scholar] [CrossRef]
- Li, H.; Verplaetse, M.; Verbist, J.; van Kerrebrouck, J.; Breyne, L.; Wu, C.H.; Bogaert, L.; Moeneclaey, B.; Yin, X.; Bauwelinck, J.; et al. Real-Time 100-GS/s Sigma-Delta Modulator for All-Digital Radio-Over-Fiber Transmission. J. Lightwave Technol. 2020, 38, 386–393. [Google Scholar] [CrossRef]
- Hadi, M.U.; Jung, H.; Ghaffar, S.; Traverso, P.A.; Tartarini, G. Optimized digital radio over fiber system for medium range communication. Opt. Commun. 2019, 443, 177–185. [Google Scholar] [CrossRef]
- Wang, J.; Jia, Z.; Campos, L.A.; Knittle, C. Delta-Sigma Modulation for Next Generation Fronthaul Interface. J. Lightwave Technol. 2019, 37, 2838–2850. [Google Scholar] [CrossRef]
- Hadi, M.U.; Traverso, P.A.; Tartarini, G.; Jung, H. Experimental characterization of Sigma Delta Radio over fiber system for 5G C-RAN downlink. ICT Express 2020, 6, 23–27. [Google Scholar] [CrossRef]
- Hadi, M.U.; Jung, H.; Traverso, P.; Tartarini, G. Experimental evaluation of real-time sigma-delta radio over fiber system for fronthaul applications. Int. J. Microw. Wirel. Technol. 2020, 1–10. [Google Scholar] [CrossRef]
- Hadi, M.U.; Murtaza, G. Enhancing distributed feedback-standard single mode fiber-radio over fiber links performance by neural network digital predistortion. Microw. Opt. Technol. Lett. 2021, 1–8. [Google Scholar] [CrossRef]
- Fuochi, F.; Hadi, M.U.; Nanni, J.; Traverso, P.A.; Tartarini, G. Digital predistortion technique for the compensation of nonlinear effects in radio over fiber links. In 2016 IEEE 2nd International Forum on Research and Technologies for Society and Industry Leveraging a Better Tomorrow (RTSI); IEEE: Bologna, Italy, 2016; pp. 1–6. [Google Scholar]
- Hadi, M.U.; Traverso, P.A.; Tartarini, G.; Venard, O.; Baudoin, G.; Polleux, J.L. Digital Predistortion for Linearity Improvement of VCSEL-SSMF-Based Radio-Over-Fiber Links. IEEE Microw. Wireless Comp. Lett. 2019, 29, 155–157. [Google Scholar] [CrossRef]
- Vieira, L.C.; Gomes, N.J. Experimental demonstration of digital predistortion for orthogonal frequency-division multiplexing-radio over fibre links near laser resonance. IET Optoelectron. 2015, 9, 310–316. [Google Scholar] [CrossRef]
- Hadi, M.U.; Nanni, J.; Traverso, P.A.; Tartarini, G.; Venard, O.; Baudoin, G.; Polleux, J.L. Linearity Improvement of VCSELs based Radio over Fiber Systems utilizing Digital Predistortion. Adv. Sci. Technol. Eng. Syst. J. 2019, 4, 156–163. [Google Scholar] [CrossRef]
- Hadi, M.U.; Nanni, J.; Venard, O.; Baudoin, G.; Polleux, J.L.; Tartarini, G. Practically Feasible Closed-Loop Digital Predistortion for VCSEL-MMF-Based Radio-over-Fiber links. Radioengineering 2020, 29, 37–43. [Google Scholar] [CrossRef]
- Liu, S.; Xu, M.; Wang, J.; Lu, F.; Zhang, W.; Tian, H.; Chang, G. A Multilevel Artificial Neural Network Nonlinear Equalizer for Millimeter-Wave Mobile Fronthaul Systems. J. Lightwave Technol. 2017, 35, 4406–4417. [Google Scholar] [CrossRef]
- Liu, S.; Mididoddi, C.K.; Zhou, H.; Li, B.; Xu, W.; Wang, C. Single-Shot Sub-Nyquist RF Signal Reconstruction Based on Deep Learning Network. In Proceedings of the 2018 International Topical Meeting on Microwave Photonics (MWP), Toulouse, France, 22–25 October 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Yang, H.; Zeng, J.; Zheng, Y.; Jung, H.D.; Huiszoon, B.; Zantvoort, J.H.C.; Tangdiongga, E.; Koonen, A.M.J. Evaluation of effects of MZM nonlinearity on QAM and OFDM signals in RoF transmitter. In Proceedings of the 2008 International Topical Meeting on Microwave Photonics jointly held with the 2008 Asia-Pacific Microwave Photonics Conference, Gold Coast, Australia, 9 September–3 October 2008; pp. 90–93. [Google Scholar]
- Marcuse, D.; Chraplyvy, A.R.; Tkach, R.W. Effect of fiber nonlinearity on long-distance transmission. J. Lightwave Technol. 1991, 9, 121–128. [Google Scholar] [CrossRef]
- Inoue, K.; Toba, H. Wavelength conversion experiment using fiber four-wave mixing. IEEE Photonics Technol. Lett. 1992, 4, 69–72. [Google Scholar] [CrossRef]
- Vagionas, C.; Ruggeri, E.; Tsakyridis, A.; Kalfas, G.; Leiba, Y.; Miliou, A.; Pleros, N. Linearity Measurements on a 5G mmWave Fiber Wireless IFoF Fronthaul Link with analog RF beamforming and 120° degrees steering. IEEE Commun. Lett. 2020, 24, 2839–2843. [Google Scholar] [CrossRef]
- Morgan, D.R.; Ma, Z.; Ding, L. Reducing measurement noise effects in digital predistortion of RF power amplifiers. In Proceedings of the IEEE International Conference on Communications, Anchorage, AK, USA, 11–15 May 2003; Volume 4, pp. 2436–2439. [Google Scholar]
- Psaltis, D.; Sideris, A.; Yamamura, A.A. A multilayered neural network controller. IEEE Control Syst. Mag. 1988, 8, 17–21. [Google Scholar] [CrossRef]
- Eun, C.; Powers, E.J. A new volterra predistorter based on the indirect learning architecture. IEEE Trans. Signal Process. 1997, 45, 223–227. [Google Scholar]
- Paaso, H.; Mammela, A. Comparison of Direct Learning and Indirect Learning Predistortion Architectures. In Proceedings of the 2008 IEEE International Symposium on Wireless Communication Systems, Reykjavik, Iceland, 21–24 October 2008; pp. 309–313. [Google Scholar]
- Musumeci, F.; Rottondi, C.; Nag, A.; Macaluso, I.; Zibar, D.; Ruffini, M.; Tornatore, M. An overview on 934 application of machine learning techniques in optical networks. IEEE Commun. Surv. Tutor. 2019, 21, 1383–1408. [Google Scholar] [CrossRef]
- He, J.; Lee, J.; Kandeepan, S.; Wang, K. Machine Learning Techniques in Radio-over-Fiber Systems and Networks. Photonics 2020, 7, 105. [Google Scholar] [CrossRef]
- Hadi, M.U. Mitigation of nonlinearities in analog radio over fiber links using machine learning approach. ICT Express 2020, in press. [Google Scholar] [CrossRef]
- Hadi, M.U.; Basit, A.; Khurshid, K. Nonlinearities Mitigation in Radio over Fiber Links for Beyond 5G C-RAN Applications using Support Vector Machine Approach. In Proceedings of the 2020 IEEE 23rd International Multitopic Conference (INMIC), Bahawalpur, Pakistan, 5–7 November 2020; pp. 1–4. [Google Scholar]
- Anttila, L.; Handel, P.; Valkama, M. Joint mitigation of power amplifier and I/Q modulator impairments in broadband direct-conversion transmitters. IEEE Trans. Microw. Theory Tech. 2010, 58, 730–739. [Google Scholar] [CrossRef]
- Yu, Y.; Zhu, Q. A novel time synchronization for 3GPP LTE cell search. In Proceedings of the 2013 8th International Conference on Communications and Networking in China (CHINACOM), Guilin, China, 14–16 August 2013; pp. 328–331. [Google Scholar] [CrossRef]
- Zhang, J.; Xia, L.; Zhu, M.; Hu, S.; Xu, B.; Qiu, K. Fast remodelling for nonlinear distortion mitigation based on transfer learning. Opt. Lett. 2019, 44, 4243–4246. [Google Scholar] [CrossRef]
- Pan, S.J.; Yang, Q. A survey on transfer learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar] [CrossRef]









| Specifications | Values |
|---|---|
| Optimizer | ADAM |
| Loss Function | Mean Square Error |
| Hidden Layers | 6 |
| Neurons per layer | 25 |
| Hidden Layer Type | ReLu |
| Regularization | L1 |
| Link Components | Values |
|---|---|
| SM-VCSEL | |
| Wavelength | 850 nm |
| 5 mA | |
| 2 mA | |
| RIN | −130 dB/Hz |
| SSMF | |
| Length | 1 km |
| Attenuation | 3 dB/km |
| PD | |
| Responsivity | 0.71 A/W |
| Bandwidth | 2.5 GHz |
| Model | ACPR (dBc) | EVM (%) |
|---|---|---|
| No DPD | −25 | 8 |
| MP | −35 | 2.2 |
| GMP | −40 | 2 |
| NN | −50 | 1.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hadi, M.U.; Awais, M.; Raza, M.; Khurshid, K.; Jung, H. Neural Network DPD for Aggrandizing SM-VCSEL-SSMF-Based Radio over Fiber Link Performance. Photonics 2021, 8, 19. https://doi.org/10.3390/photonics8010019
Hadi MU, Awais M, Raza M, Khurshid K, Jung H. Neural Network DPD for Aggrandizing SM-VCSEL-SSMF-Based Radio over Fiber Link Performance. Photonics. 2021; 8(1):19. https://doi.org/10.3390/photonics8010019
Chicago/Turabian StyleHadi, Muhammad Usman, Muhammad Awais, Mohsin Raza, Kiran Khurshid, and Hyun Jung. 2021. "Neural Network DPD for Aggrandizing SM-VCSEL-SSMF-Based Radio over Fiber Link Performance" Photonics 8, no. 1: 19. https://doi.org/10.3390/photonics8010019
APA StyleHadi, M. U., Awais, M., Raza, M., Khurshid, K., & Jung, H. (2021). Neural Network DPD for Aggrandizing SM-VCSEL-SSMF-Based Radio over Fiber Link Performance. Photonics, 8(1), 19. https://doi.org/10.3390/photonics8010019