Proposal of Highly Efficient Quantum Well Microring Resonator-Loaded Optical Phase Modulator Integrated with Antenna-Coupled Electrodes for Radio-over-Fiber
Abstract
1. Introduction
2. Device Design and Operation Principle
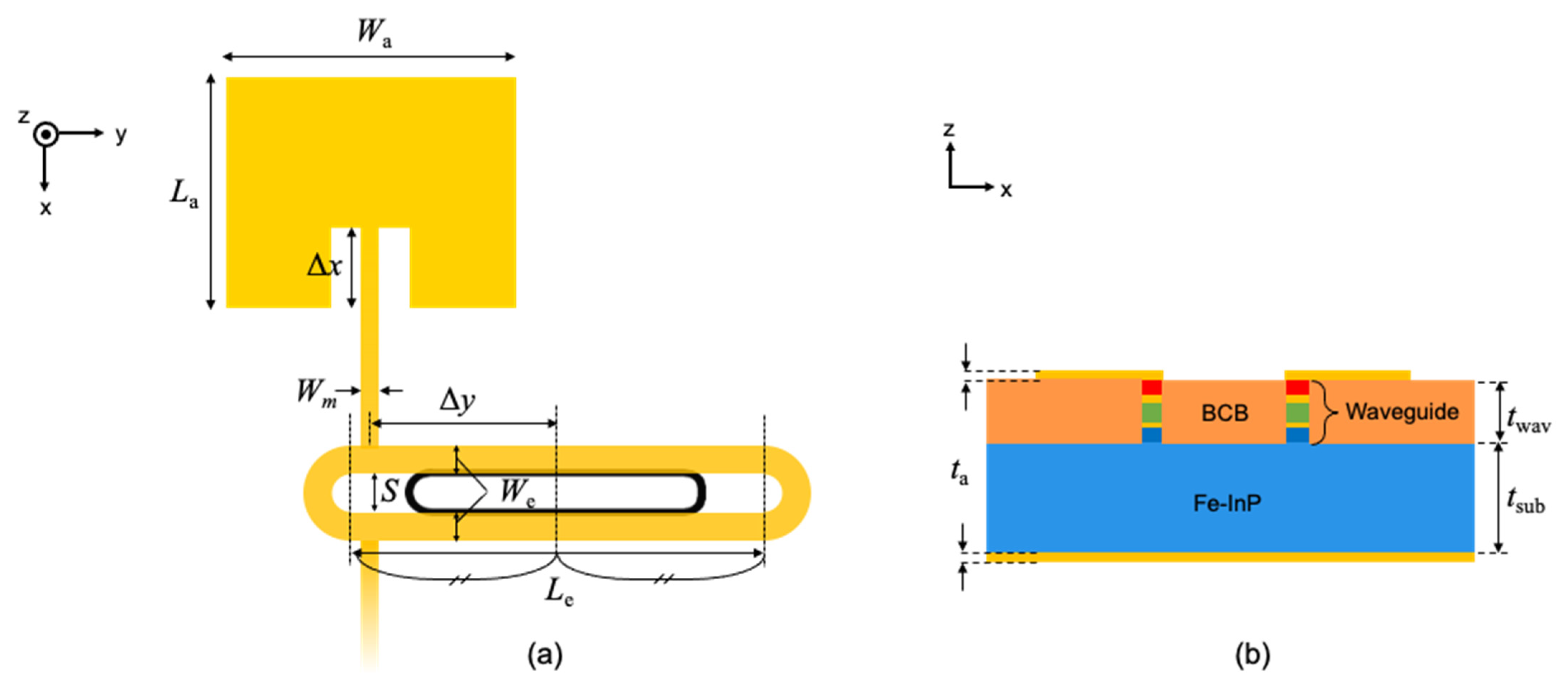
2.1. Device Design
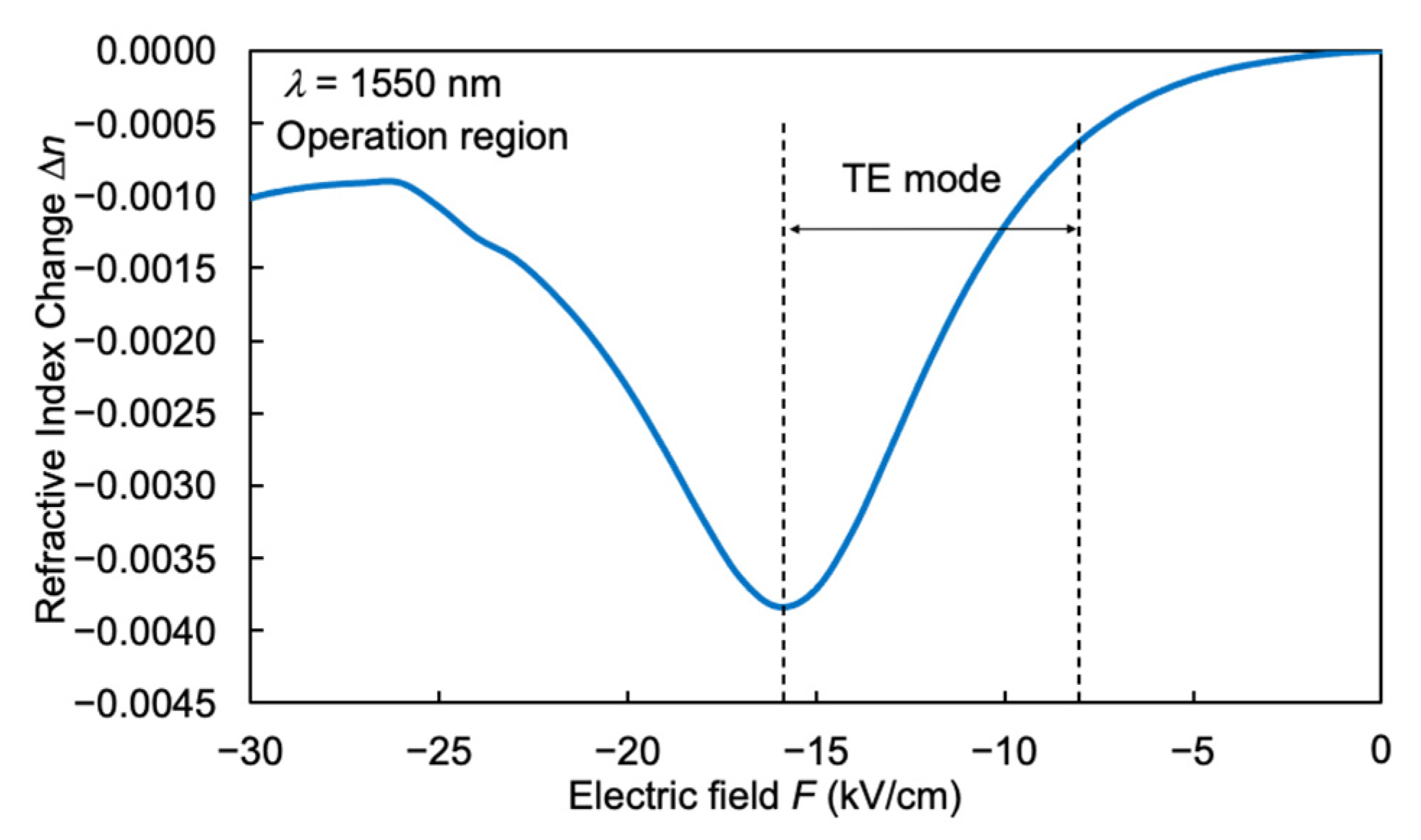
2.1.1. Large Electrorefractive Index Change in InGaAs/InAlAs FACQW
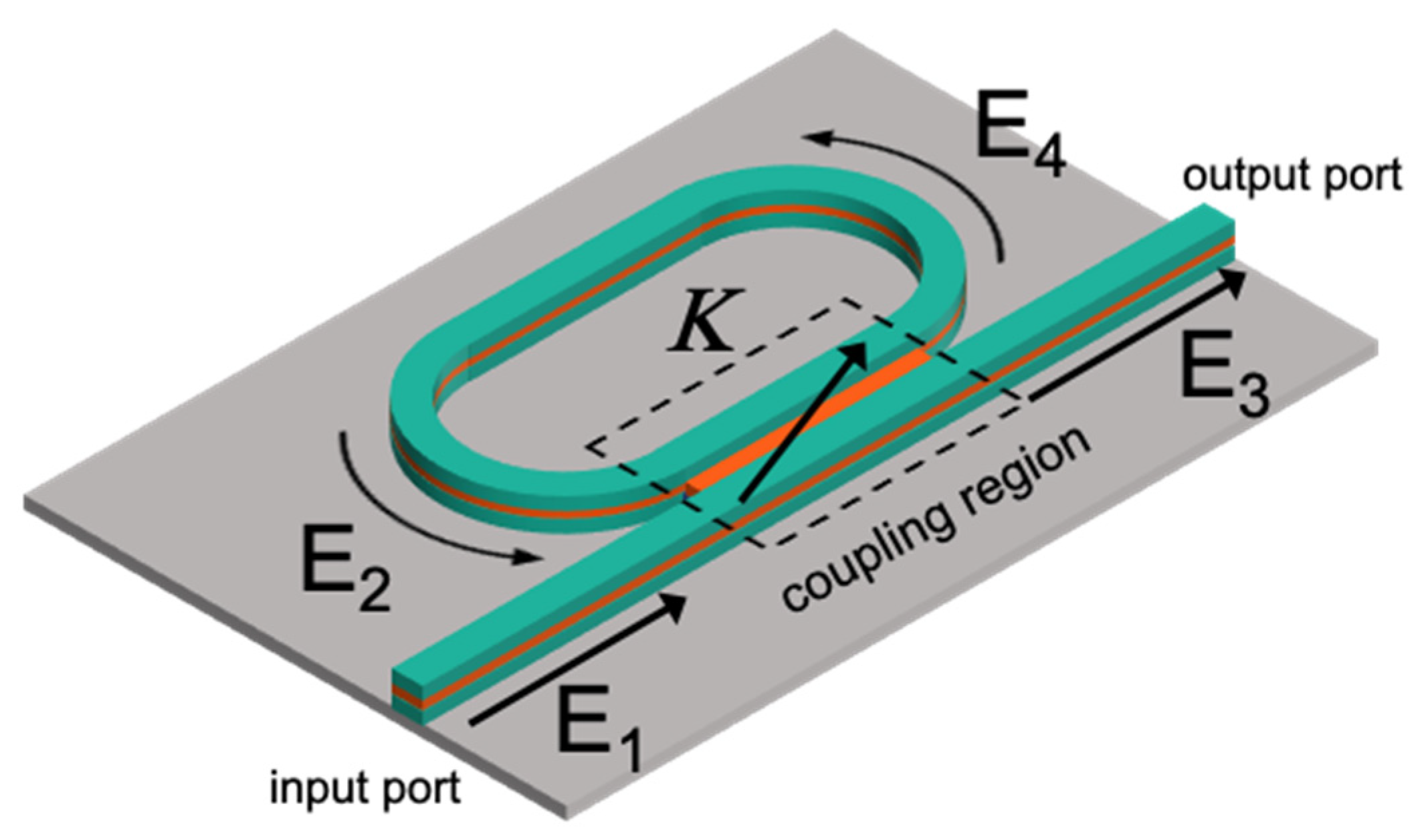
2.1.2. Microring Resonator
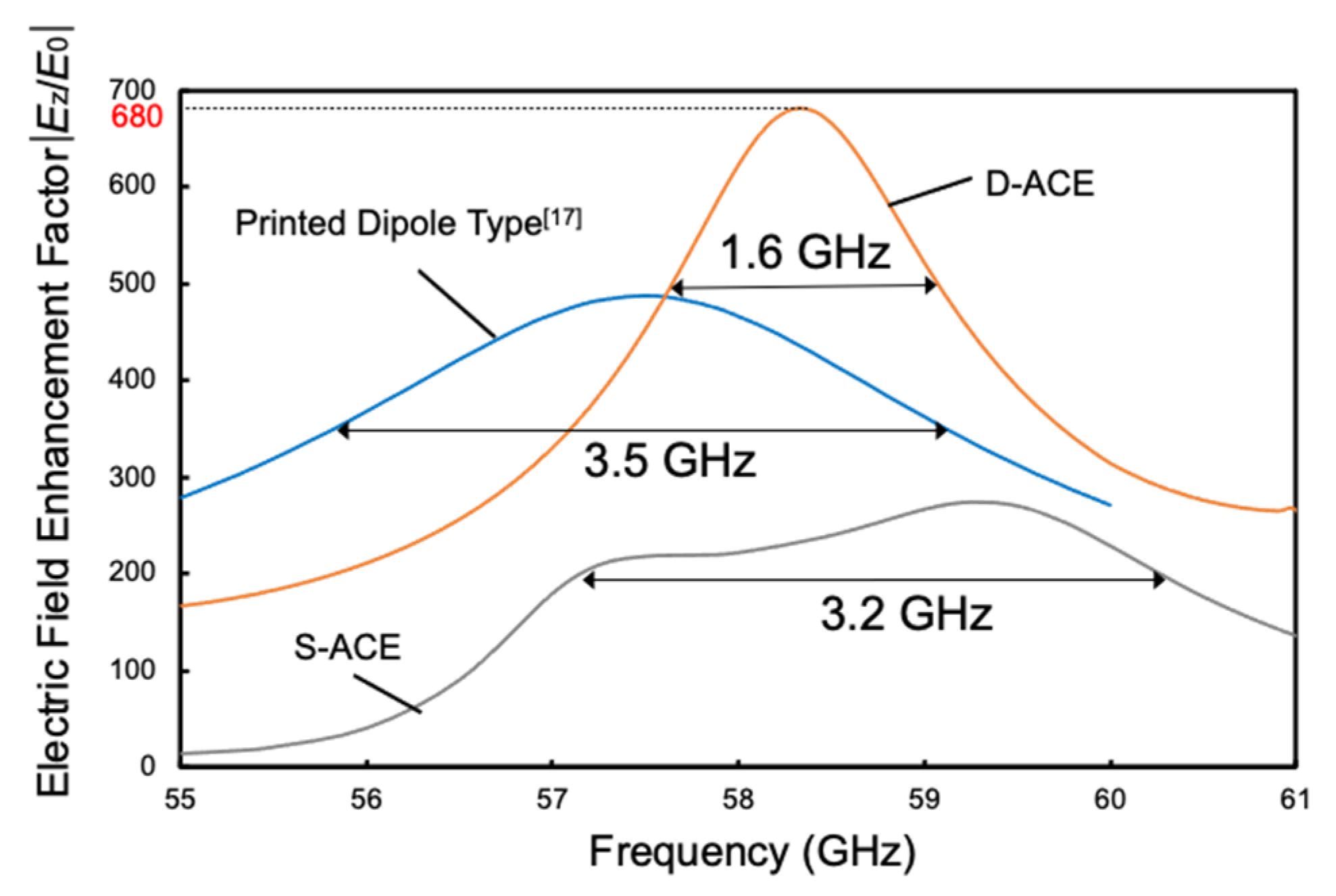
2.1.3. Antenna Coupled Electrode
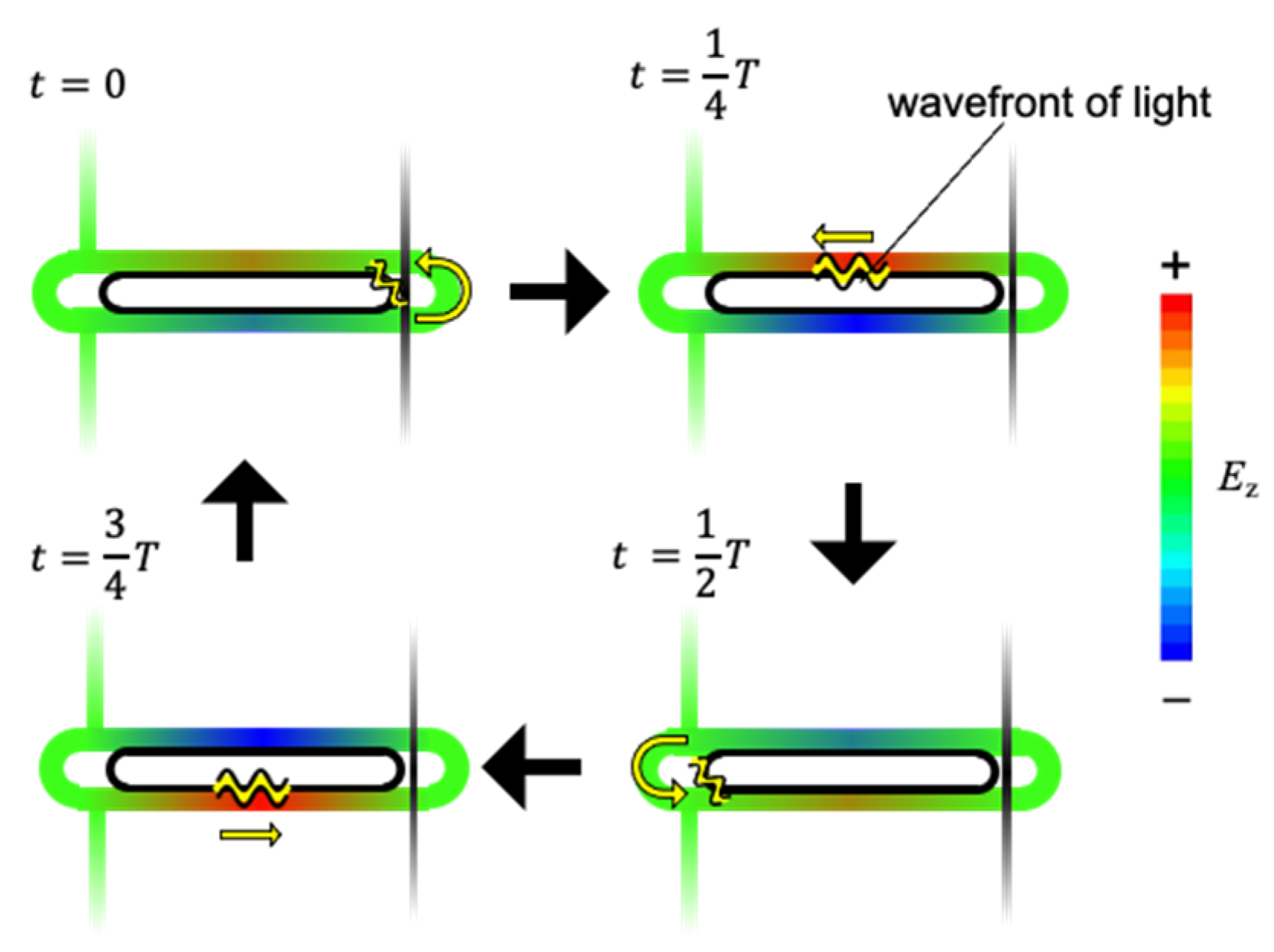
2.2. Operation Principle
3. Result and Discussion
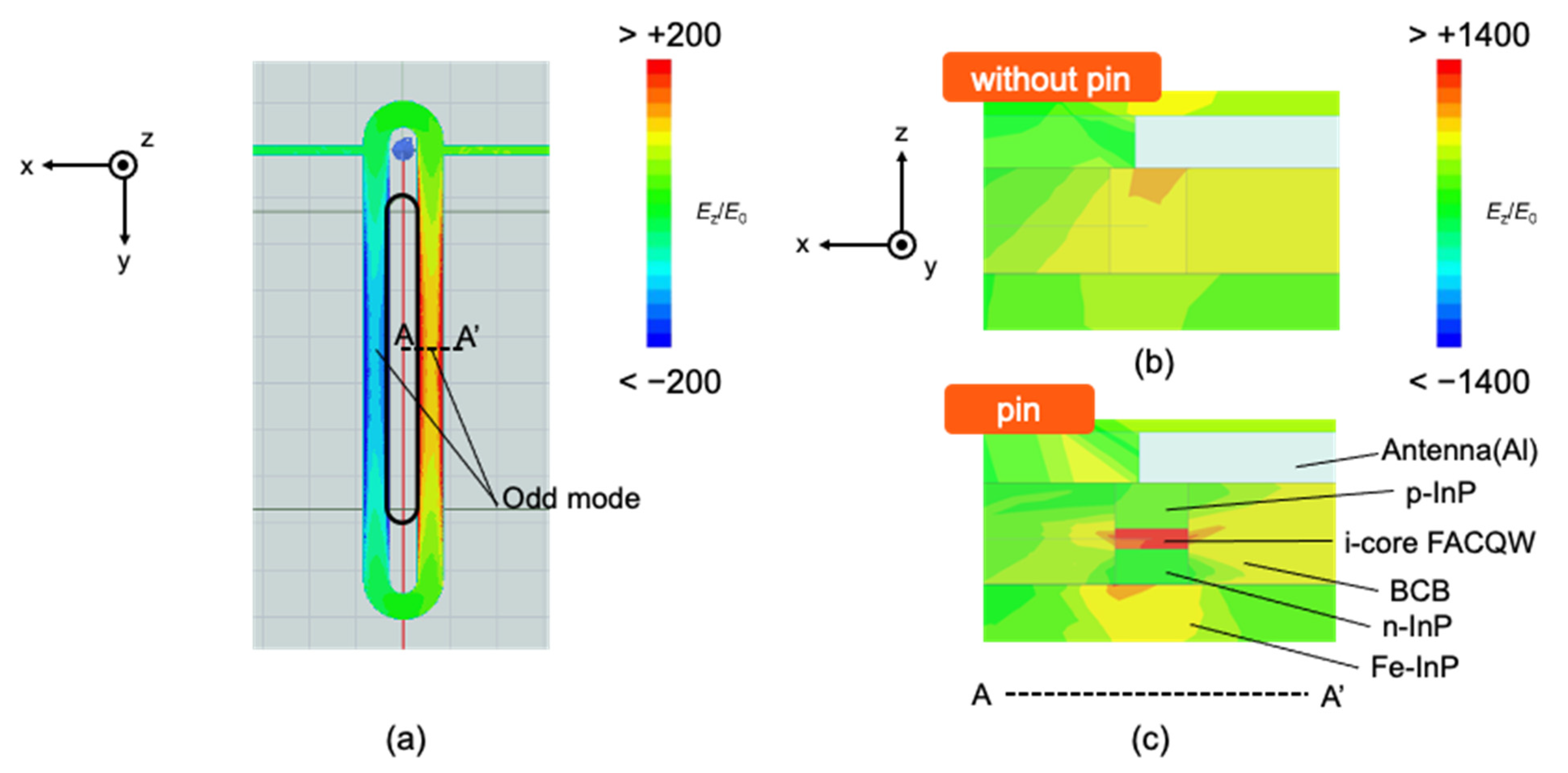
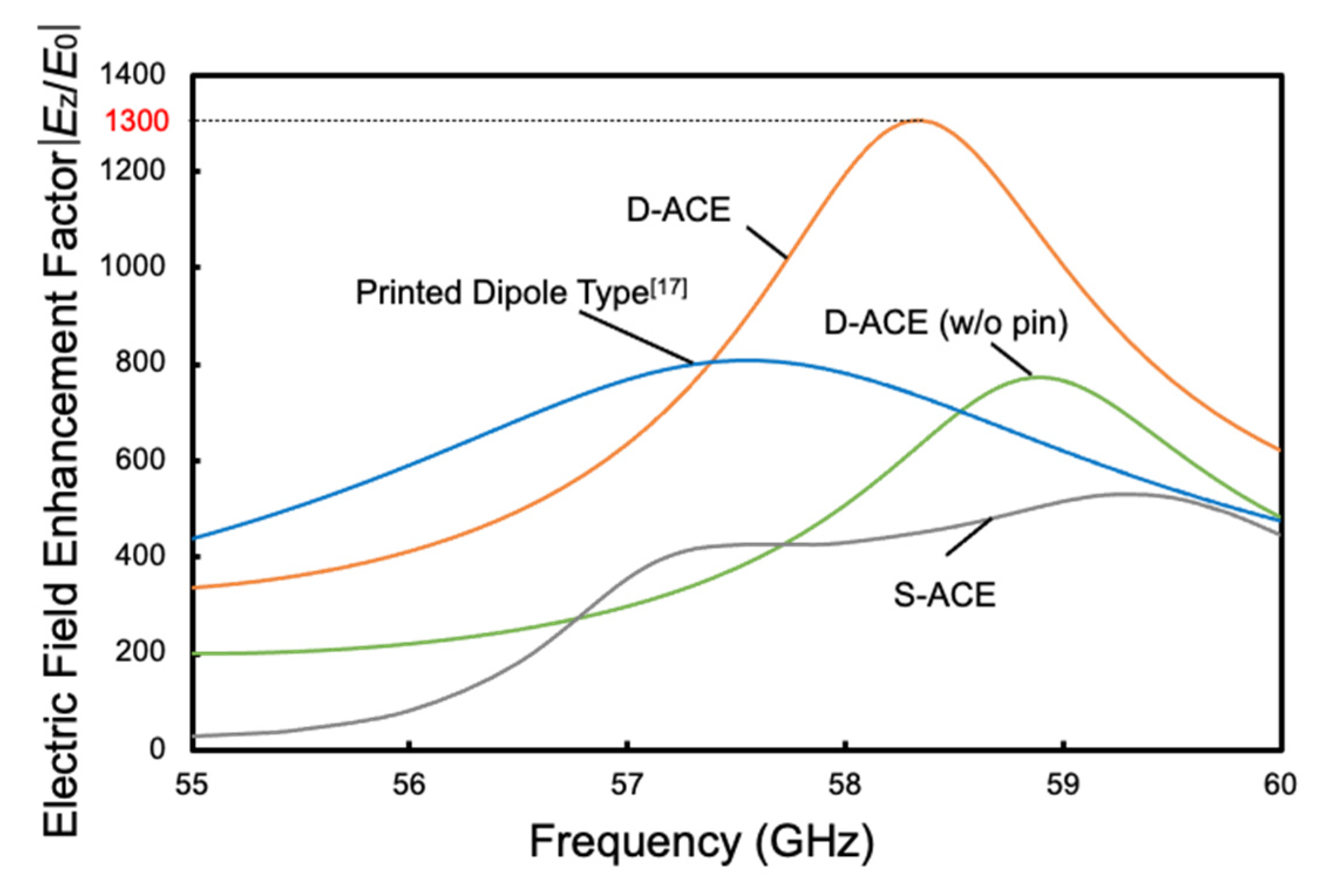
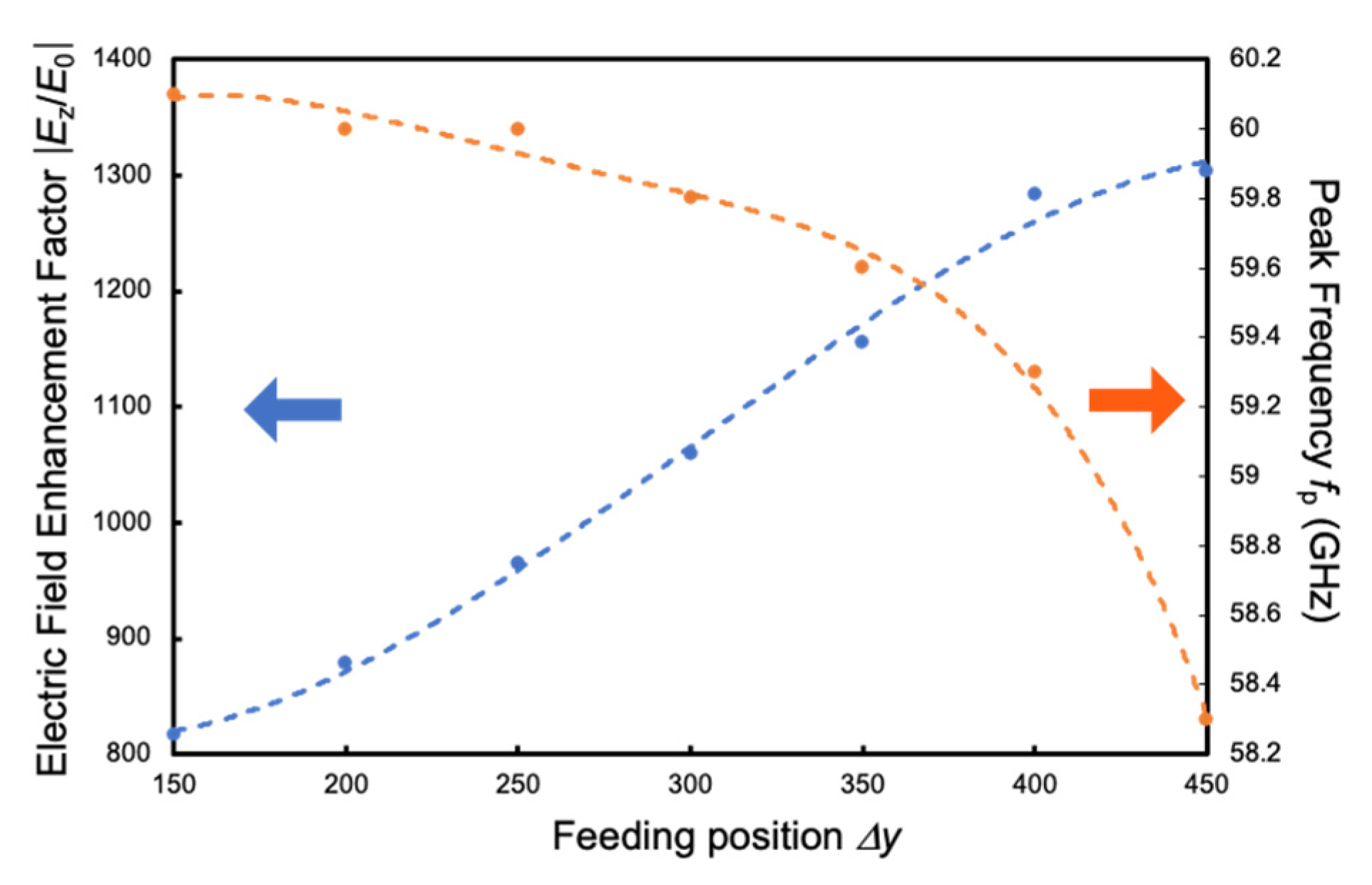
3.1. MMW Characteristics
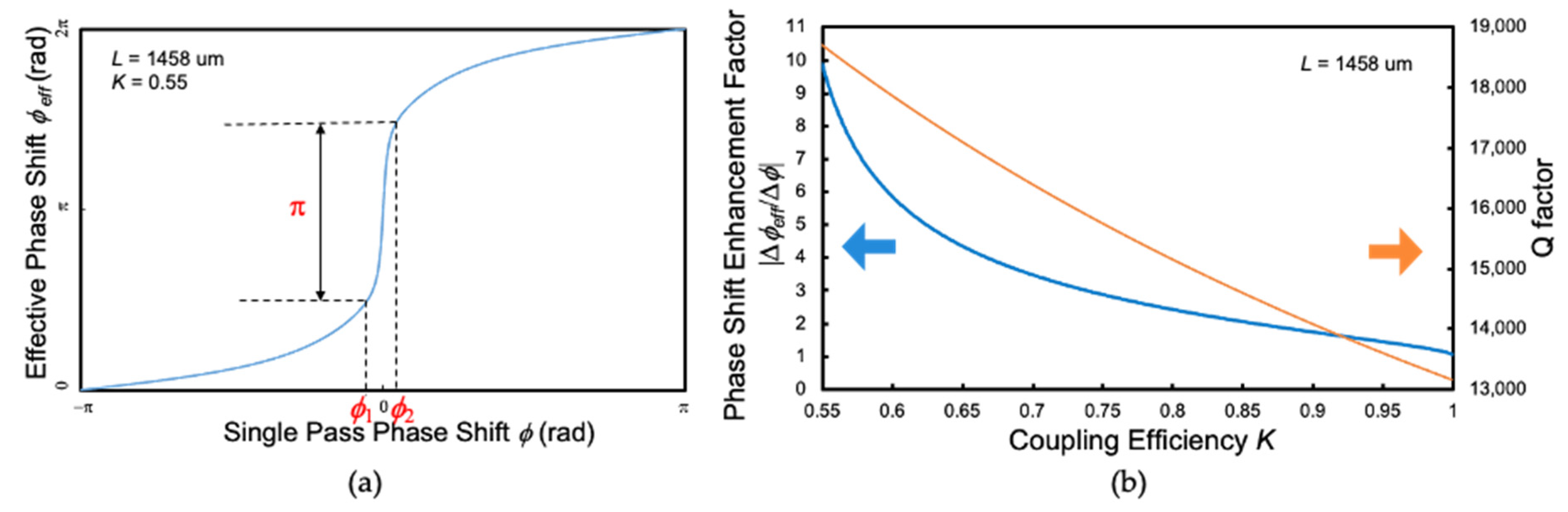
3.2. Phase Modulation Characteristics
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Koji, T.; Naganori, S.; Kazuaki, T. 60 GHz band wireless access technology based on IEEE 802.11ad/WiGig and its future perspectives. IEICE Tech. Rep. 2017, 116, 207–212. [Google Scholar]
- Singh, H.; Prasad, R.; Bonev, B. The Studies of Millimeter Waves at 60 GHz in Outdoor Environments for IMT Applications: A State of Art. Wirel. Pers. Commun. 2018, 100, 463–474. [Google Scholar] [CrossRef]
- Ghasempour, Y.; da Silva, C.R.C.M.; Cordeiro, C.; Knightly, E.W. IEEE 802.11ay: Next-Generation 60 GHz Communication for 100 Gb/s Wi-Fi. IEEE Commun. Mag. 2017, 55, 186–192. [Google Scholar] [CrossRef]
- Beas, J.; Castanon, G.; Aldaya, I.; Aragon-Zavala, A.; Campuzano, G. Millimeter-Wave Frequency Radio over Fiber Systems: A Survey. IEEE Commun. Surv. Tutor. 2013, 15, 1593–1619. [Google Scholar] [CrossRef]
- Capmany, J.; Novak, D. Microwave Photonics Combines Two Worlds. Nat. Photonics 2007, 1, 319–330. [Google Scholar] [CrossRef]
- Marti, J.; Capmany, J. Microwave Photonics and Radio-over-Fiber Research. IEEE Microw. Mag. 2009, 10, 96–105. [Google Scholar] [CrossRef]
- Seeds, A.J.; Williams, K.J. Microwave Photonics. J. Lightwave Technol. 2006, 24, 4628–4641. [Google Scholar] [CrossRef]
- Ng’oma, A.; Lin, C.; He, L.Y.W.; Jiang, W.; Annunziata, F.; Chen, J.; Shih, P.; George, J.; Chi, S. 31 Gbps RoF System Employing Adaptive Bit-Loading OFDM Modulation at 60 GHz. In Proceedings of the 2011 Optical Fiber Communication Conference and Exposition and the National Fiber Optic Engineers Conference, Los Angeles, CA, USA, 6–10 March 2011; pp. 1–3. [Google Scholar]
- Cao, Z.; Ma, Q.; Smolders, A.B.; Jiao, Y.; Wale, M.J.; Oh, C.W.; Wu, H.; Koonen, A.M.J. Advanced Integration Techniques on Broadband Millimeter-Wave Beam Steering for 5G Wireless Networks and Beyond. IEEE J. Quantum Electron. 2016, 52, 1–20. [Google Scholar] [CrossRef]
- Murata, H. Millimeter-Wave-Band Electro-Optic Modulators Using Antenna-Coupled Electrodes for Microwave Photonic Applications. J. Lightwave Technol. 2020, 38, 5485–5491. [Google Scholar] [CrossRef]
- Sheehy, F.T.; Bridges, W.B.; Schaffner, J.H. 60 GHz and 94 GHz Antenna-Coupled LiNbO3 Electrooptic Modulators. IEEE Photonics Technol. Lett. 1993, 5, 307–310. [Google Scholar] [CrossRef]
- Wijayanto, Y.N.; Murata, H.; Okamura, Y. Electrooptic Millimeter-Wave–Lightwave Signal Converters Suspended to Gap-Embedded Patch Antennas on Low-k Dielectric Materials. IEEE J. Sel. Top. Quantum Electron. 2013, 19, 33–41. [Google Scholar] [CrossRef]
- Salamin, Y.; Baeuerle, B.; Heni, W.; Abrecht, F.C.; Josten, A.; Fedoryshyn, Y.; Haffner, C.; Bonjour, R.; Watanabe, T.; Burla, M.; et al. Microwave Plasmonic Mixer in a Transparent Fibre–Wireless Link. Nat. Photonics 2018, 12, 749–753. [Google Scholar] [CrossRef] [PubMed]
- Herrera, O.D.; Kim, K.; Voorakaranam, R.; Himmelhuber, R.; Wang, S.; Demir, V.; Zhan, Q.; Li, L.; Norwood, R.A.; Nelson, R.L.; et al. Silica/Electro-Optic Polymer Optical Modulator with Integrated Antenna for Microwave Receiving. J. Lightwave Technol. 2014, 32, 3861–3867. [Google Scholar] [CrossRef]
- Zhang, X.; Hosseini, A.; Subbaraman, H.; Wang, S.; Zhan, Q.; Luo, J.; Jen, A.K.-; Chen, R.T. Integrated Photonic Electromagnetic Field Sensor Based on Broadband Bowtie Antenna Coupled Silicon Organic Hybrid Modulator. J. Lightwave Technol. 2014, 32, 3774–3784. [Google Scholar] [CrossRef]
- Park, D.H.; Pagán, V.R.; Murphy, T.E.; Luo, J.; Jen, A.K.-Y.; Herman, W.N. Free Space Millimeter Wave-Coupled Electro-Optic High Speed Nonlinear Polymer Phase Modulator with in-Plane Slotted Patch Antennas. Opt. Express 2015, 23, 9464–9476. [Google Scholar] [CrossRef]
- Miyazeki, Y.; Arakawa, T. Proposal of InGaAs/InAlAs Multiple Quantum Well Mach–Zehnder Modulator Integrated with Array of Planar Antennas. Jpn. J. Appl. Phys. 2019, 58, SJJE05. [Google Scholar] [CrossRef]
- Miyazeki, Y.; Yokohashi, H.; Kodama, S.; Murata, H.; Arakawa, T. InGaAs/InAlAs Multiple-Quantum-Well Optical Modulator Integrated with a Planar Antenna for a Millimeter-Wave Radio-over-Fiber System. Opt. Express 2020, 28, 11583–11596. [Google Scholar] [CrossRef]
- Arakawa, T.; Toya, T.; Ushigome, M.; Yamaguchi, K.; Ide, T.; Tada, K. InGaAs/InAlAs Five-Layer Asymmetric Coupled Quantum Well Exhibiting Giant Electrorefractive Index Change. Jpn. J. Appl. Phys. 2011, 50, 032204. [Google Scholar] [CrossRef]
- Kaneshige, H.; Ueyama, Y.; Yamada, H.; Yajima, H.; Arakawa, T.; Kokubun, Y. InGaAs/InAlAs Multiple Quantum Well Mach–Zehnder Modulator with Single Microring Resonator. Jpn. J. Appl. Phys. 2012, 51, 02BG01. [Google Scholar] [CrossRef]
- Kaneshige, H.; Gautam, R.; Ueyama, Y.; Katouf, R.; Arakawa, T.; Kokubun, Y. Low-Voltage Quantum Well Microring-Enhanced Mach-Zehnder Modulator. Opt. Express 2013, 21, 16888–16900. [Google Scholar] [CrossRef]
- Murata, H.; Miyanaka, R.; Okamura, Y. Wireless Space-Division-Multiplexed Signal Discrimination Device Using Electro-Optic Modulator with Antenna-Coupled Electrodes and Polarization-Reversed Structures. Int. J. Microw. Wirel. Technol. 2012, 4, 399–405. [Google Scholar] [CrossRef]
- Bogaerts, W.; De Heyn, P.; Van Vaerenbergh, T.; De Vos, K.; Kumar Selvaraja, S.; Claes, T.; Dumon, P.; Bienstman, P.; Van Thourhout, D.; Baets, R. Silicon Microring Resonators. Laser Photonics Rev. 2012, 6, 47–73. [Google Scholar] [CrossRef]
- Gupta, K.C.; Garg, R.; Bahl, I.J. Microstrip Lines and Slotlines; Artech House: Norwood, MA, USA, 1979. [Google Scholar]
- Enokihara, A.; Yajima, H.; Murata, H.; Okamura, Y. Electro-Optic Intensity Modulator Using Higher-Order Resonant Electrode with Polarization-Reversed Structure. In Proceedings of the 2005 European Microwave Conference, Paris, France, 4–6 October 2005. [Google Scholar] [CrossRef]
- Kirschning, M.; Jansen, R.H. Accurate Wide-Range Design Equations for the Frequency-Dependent Characteristic of Parallel Coupled Microstrip Lines. IEEE Trans. Microw. Theory Tech. 1984, 32, 83–90. [Google Scholar] [CrossRef]
- Enokihara, A.; Yajima, H.; Murata, H.; Okamura, Y. Guided-Wave EO Intensity Modulator Using Coupled Microstrip Line Electrode of Higher-Order Harmonic Resonance Combined with Polarization-Reversed Structure. IEICE Trans. Electron. 2007, E90-C, 1096–1104. [Google Scholar] [CrossRef]
- Tada, K.; Arakawa, T.; Kazuma, K.; Kurosawa, N.; Noh, J.H. Influence of One Monolayer Thickness Variation in GaAs/AlGaAs Five-Layer Asymmetric Coupled Quantum Well upon Electrorefractive Index Change. Jpn. J. Appl. Phys. 2001, 40, 656–661. [Google Scholar] [CrossRef]






| Parameters | Value |
|---|---|
| Microstrip antenna | |
| Peak operational frequency, fp | 58.3 GHz |
| Length, La | 633 mm |
| Width, Wa | 954 mm |
| Feeding position, Δx | 265 mm |
| Micro-strip line width, Wm | 20 mm |
| Thickness, ta | 1 mm |
| Coupled microstrip resonant electrode | |
| Length, Le (D-ACE) | 930 mm |
| (S-ACE) | 940 mm |
| Width, We | 55 mm |
| Electrode separation, S | 450 mm |
| Feeding position, Δy | 60 mm |
| Microring resonator | |
| Free spectral range, Δl | 0.48 nm |
| Group index, ng | 3.43 |
| Thickness, twav | 2 mm |
| MRR round-trip length, L | 1458 mm |
| Coupling efficient, K | 0.55~0.95 |
| Quality factor, Q | 4729~12,954 |
| Operating frequency, fQ | 10~17 GHz |
| Substrate | |
| Thickness, tsub | 200 mm |
| Dielectric constant, eFe-InP | 12.49 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kamada, H.; Arakawa, T. Proposal of Highly Efficient Quantum Well Microring Resonator-Loaded Optical Phase Modulator Integrated with Antenna-Coupled Electrodes for Radio-over-Fiber. Photonics 2021, 8, 37. https://doi.org/10.3390/photonics8020037
Kamada H, Arakawa T. Proposal of Highly Efficient Quantum Well Microring Resonator-Loaded Optical Phase Modulator Integrated with Antenna-Coupled Electrodes for Radio-over-Fiber. Photonics. 2021; 8(2):37. https://doi.org/10.3390/photonics8020037
Chicago/Turabian StyleKamada, Hiro, and Taro Arakawa. 2021. "Proposal of Highly Efficient Quantum Well Microring Resonator-Loaded Optical Phase Modulator Integrated with Antenna-Coupled Electrodes for Radio-over-Fiber" Photonics 8, no. 2: 37. https://doi.org/10.3390/photonics8020037
APA StyleKamada, H., & Arakawa, T. (2021). Proposal of Highly Efficient Quantum Well Microring Resonator-Loaded Optical Phase Modulator Integrated with Antenna-Coupled Electrodes for Radio-over-Fiber. Photonics, 8(2), 37. https://doi.org/10.3390/photonics8020037





