Application of 150 kHz Laser for High-Order Harmonic Generation in Different Plasmas

Abstract

Application of high pulse repetition rate lasers opens the way for increasing the average flux of the high-order harmonics generating in the ions- and nanoparticles-containing plasmas ablated on the surfaces of various metal targets. We demonstrate the harmonic generation of 37 fs, 150 kHz, 1030 nm, 0.5 mJ pulses in different plasmas. The formation of plasma plumes on the surfaces of carbon, titanium, boron, zinc, and manganese targets was performed during laser ablation, using 250 fs pulses from the same laser. The ablation of the mixed powder of boron nanoparticles and silver microparticles was used for generation of harmonics with high yield. Harmonics up to the fortieth orders from the carbon plasma were obtained. The estimated conversion efficiencies in laser-produced plasmas were ≤10⁻⁵. The photon flux for a single harmonic generating in carbon plasma was estimated to be 8 × 10¹³ photons/s.

1. Introduction

High pulse repetition coherent extreme ultraviolet (XUV) sources are required in different areas, such as the recovery of molecular frame photoelectron distribution from the time-of-flight imaging [1], coincidence measurements where more than one detected particle needs to be linked to the same ionization event, such as in cold target recoil ion momentum spectroscopy and reaction microscopy [2,3,4,5], experiments on correlated two-electron emission from solids [6], etc. The most frequently used technique for the formation of the sources of coherent XUV radiation is the high-order harmonic generation (HHG) in gases. HHG at different pulse repetition rates was reported in the case of gas media [7,8,9,10,11]. However, the main drawback of HHG is the low conversion efficiency. Usually, when using gas jets, the conversion efficiency does not exceed 10⁻⁶.

Another option is the HHG in plasma. Most of the harmonic generation studies in laser-produced plasmas (LPPs) have been carried out on static targets. Meanwhile, the application of ablated plasma using 1 kHz class lasers causes a considerable change in the surface properties of a static target, resulting in the deterioration of the plasma conditions and harmonic generation. Even at a relatively low pulse repetition rate the stability of harmonics decreases after a few hundred shots on the same place of the surface. One can assume that movement of the plasma along the target surface or application of the rotating target can improve the stability of the harmonic yield.

Using a motorized rotating target notably improves the stability of HHG from LPPs, particularly in the case of high pulse repetition rate lasers, and significantly minimize the modification of the target surface that could cause degradation of harmonic yield [12]. The periodic change of the ablation zone allows the cooling down of the heated area, and maintains stable plasma formation. Correspondingly, the application of fiber chirped pulse amplification systems, delivering higher pulse repetition rates (100 kHz and higher) compared with commonly used Ti: sapphire class lasers, may open new opportunities for HHG from LPPs. Different processes, such as the local field enhancement in quantum dots [13], resonance enhancement of single harmonics in metal plasmas [14], the realization of the quasi-phase matching conditions in periodically modulated plasma plumes [15,16], and nonlinear spectroscopy of ablated materials [17], could be more easily analyzed using the high pulse repetition coherent XUV sources.

The generation of high harmonics from gas jets allowed achieving μW harmonics between 45 nm and 61 nm (H23–H17), at a repetition rate of 50 kHz [18]. Here, we report the application of the fiber laser system with a high repetition rate (150 kHz) for the studies of HHG in LPPs. We demonstrate that the application of this laser allows achieving the harmonic flux up to 8 × 10¹³ photons/s.

2. Experimental Arrangements

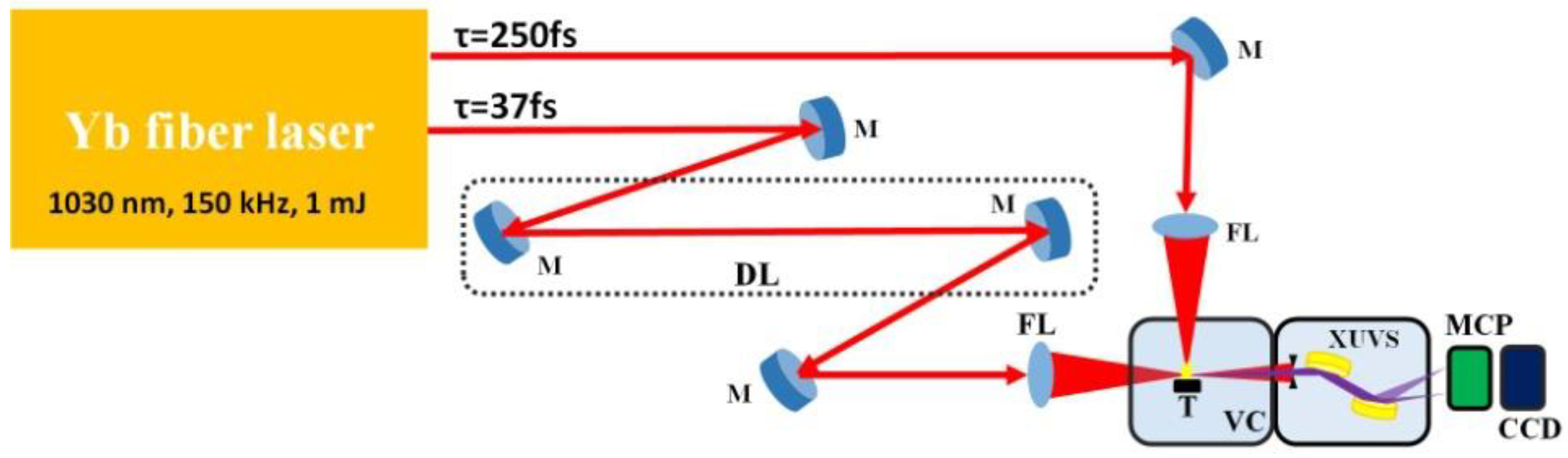
We used the Yb-doped fiber laser (Active Fiber System). The radiation from the first port of this laser (250 fs, 1030 nm, 50–150 kHz, 0.3 mJ) was used as heating pulses, and directed towards the vacuum chamber to ignite the plasma (fluence F = 0.5 J cm⁻², intensity I_hp = 2 × 10¹² W cm⁻²) on the target (Figure 1). Previous studies of HHG in plasmas using heating pulses of different duration (i.e., nanosecond, picosecond and femtosecond pulses) have revealed that the optimal values of fluencies for these three groups of pulse durations are centered in the region of a few J cm⁻². Meanwhile, the corresponding intensities at these conditions are distinguished from each other by a few orders. Thus, the most reliable parameter here is the fluence, rather than the intensity of heating pulses. The vacuum in the target chamber was maintained at 5 × 10⁻⁴ mbar. There was no pressure effect on the harmonics generation in laser-produced plasmas. After producing plasma plumes, the harmonics started generating from the neutral atoms or low-ionized atoms. The harmonic output depended on the excitation state of laser-produced plasma. Highly excited plasma can destroy the phase-matching conditions due to the dispersion induced by the large concentration of free electrons in LPPs. The density of plasma at the focal point of driving femtosecond pulse was estimated to be ~2 × 10¹⁷ cm⁻³, which corresponded to the pressure of ~10 mbar.

The focused driving pulses from second port (37 fs, 1030 nm, 50–150 kHz, 1 mJ) propagated through LPP (I_dp = 2 × 10¹⁴ W cm⁻²), at a distance of 0.3 mm above the target surface. The delay between heating and driving pulses was installed by using the optical delay line. The studies of HHG in different metal plasmas were carried out at different delays between the heating and driving pulses. At the used delays (25, 50, and 100 ns), the maximum density of ejected particles from three groups of studied materials possessing different atomic weight reaches the axis of propagation of the driving femtosecond beam, thus allowing highest nonlinear optical response from the plasma plume. The optimal values of the delays were determined by the anticipated velocities of plasma clouds (~1.2 × 10⁴, 6 × 10³, and 3 × 10³ m/s), for the particles with different atomic weight (B and C of similar weight (11 and 12), Mn and Zn of approximately similar weight (54 and 65), and Ti (204)), and the distance between the target surface and driving beam (0.3 mm). The harmonics and plasma emission were detected using a flat field grazing-incidence XUV spectrometer (H+P Spectroscopy). The radiation was reflected by a gold-coated cylindrical mirror towards the grating. We used a flat field grating (Hitachi) with 1200 lines/mm. The grating diffracts and focuses the harmonics in the dispersive plane, and reflects them in the perpendicular direction onto a 90 mm long rectangular microchannel plate (Hamamatsu). The spectral content of the emission was imaged and detected by a CCD camera.

Carbon (C), titanium (Ti), boron (B), zinc (Zn) and manganese (Mn) rods were used as the targets for ablation. The cylindrical rods with a diameter of 15 mm and a length of 30 mm were installed on the rotating motor, with the driving pulse propagating at a distance of 200–300 μm above the target surface. The application of rotating targets allows for the improvement of harmonic stability in the case of 150 kHz ablation. Boron was also represented in the shape of the nanometer-sized powder (mean size of 100 nm), which was pressed together with silver microparticles (MPs, mean size of 70 µm) to form the tablets for better connectivity. The silver MPs were added to the boron nanoparticles (NPs) powder at the 1:3 weight ratio, to strengthen the tablets and to prevent them from fast disintegration during laser ablation. This powdered target was chosen for comparative studies with the ablated boron bulk target and the nanoparticles formed “in-situ” during the ablation of carbon, titanium, and manganese. The shape of this pressed target allowed for rotating during HHG experiments, to avoid the fast destruction of the optimal conditions of plasma formation. Our studies showed that, independently to the method of rotating target formation, the principle of rotation during ablation becomes crucial for maintaining the proper conditions of harmonics generation in the plasma plumes formed at a high pulse repetition rate.

The irradiation of the fresh surface of target by each next pulse is not a necessary requirement for achieving harmonic stability. The heating shots can overlap on the target surface during its rotation, until the overheating notably changes the conditions of plasma formation on the corrupted surface. Earlier, in the case of 1 kHz repetition rate lasers, the commonly used rotating speed was varied between 20 and 30 rotations per minute (rpm) for different targets [12,19]. This rotation speed allowed achieving the stable harmonic output. However, even at 5 rpm, the stability of harmonic yield was significantly better compared with unmovable target. In the case of 20 rpm speed of the targets ablated by 1 kHz pulses, approximately 30 pulses overlapped on the same spot.

In the case of ablation using 150 kHz pulses, we used the rotating speeds up to 1000 rpm to analyze optimal conditions for the generation of stable harmonics. Most of our experiments were carried out at 150 rpm. However, the harmonic yield started to gradually decrease after some time from the beginning of ablation. In that case, approximately 400 laser shots were overlapped on the same spot. The increase of rotation speed up to 600 rpm did not allow the improvement of harmonic stability. Thus, in the case of 150 kHz ablation, the main factor of instability was the insufficient flow of heat out from the surface of heated spot. However, the harmonic stability improved once we dragged the rotating target up and down. The optimization of this vertical movement of the target allows ensuring the reliable continuous generation of harmonics from LPP.

We did not carry out the comparative studies of HHG in gases and plasmas using a 150 kHz laser. Meanwhile, such studies were reported earlier in different laboratories using lower pulse repetition rate lasers [19,20,21,22], and showed the prevalence of the latter medium over gases from the point of view of conversion efficiency towards the coherent short-wavelength radiation.

3. Results

The excitation of plasma plumes was controlled by changing the fluence of heating femtosecond pulses. In these studies, we moved a focusing lens to change the heating beam spot size on the target surface, to control the fluence of the heating pulses. This method allowed the fine tuning of the heating conditions on the target surface.

In the case of strong ablation, the plasma emission was too intense compared with harmonic emission. However, the most important obstacle was the appearance of large concentration of the free electrons destroying the optimal phase matching conditions between the driving and harmonic waves. We chose the optimal fluence for plasma formation (F = 0.5 J cm⁻²) by determining the strongest harmonic yield at different conditions of ablation. The optimal intensity of heating pulses at these conditions was equal to I_hp = 2 × 10¹² W cm⁻². The corresponding intensities of heating pulses for two other used fluencies (F = 1.0 J cm⁻² and F = 2.0 J cm⁻²) were equal to I_hp = 4 × 10¹² W cm⁻² and I_hp = 8 × 10¹² W cm⁻², respectively.

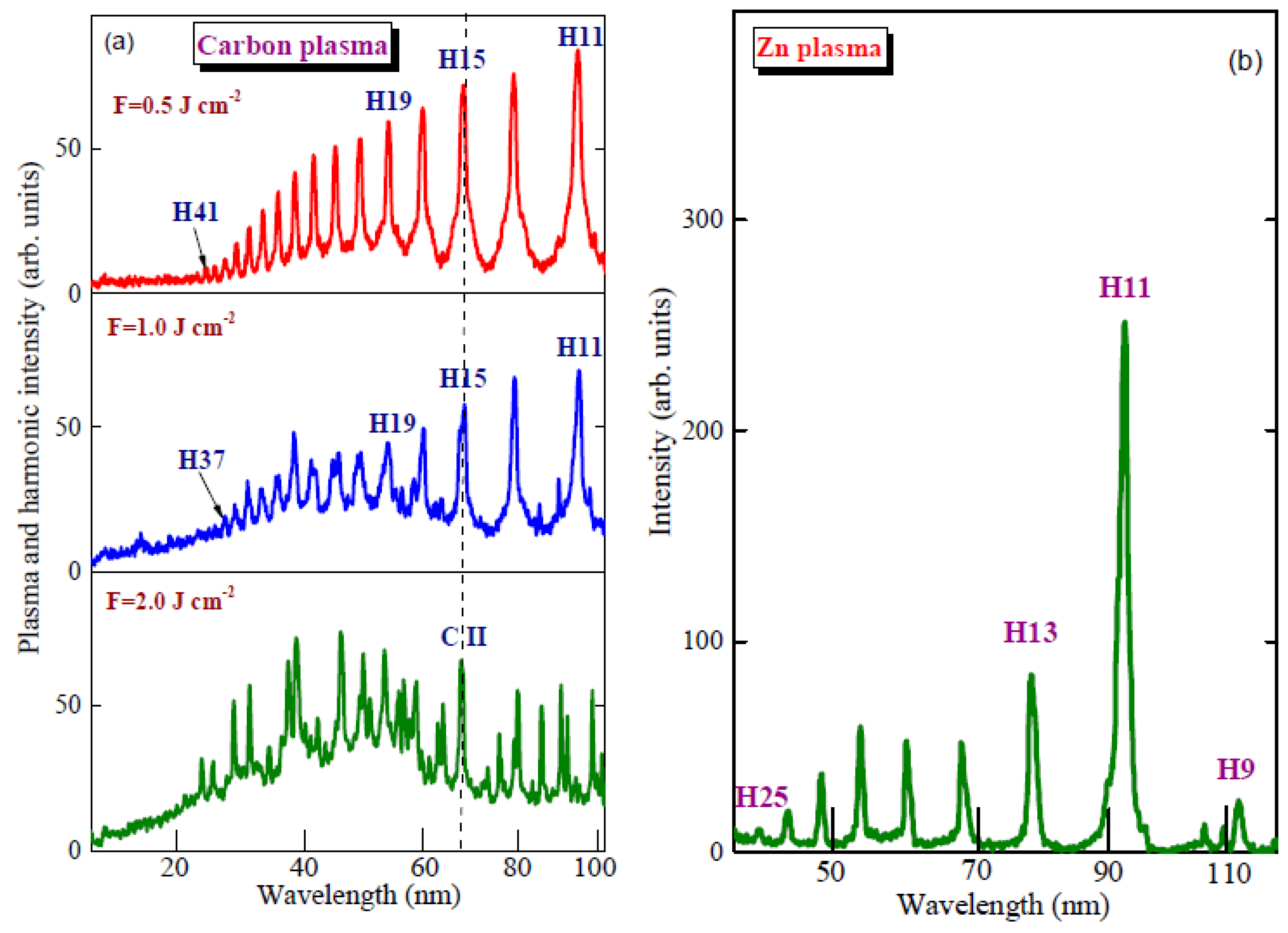
Figure 2a shows the harmonic and plasma emission spectra during the ablation of the carbon target at three different conditions of experiments. Upper panel demonstrates the pure and narrow harmonics extended up to the 41st order (λ = 25.1 nm, cutoff energy E_c = 49.3 eV) at 0.5 J cm⁻² fluence of 250 fs heating pulses.

Middle panel spectrum was obtained at F = 1 J cm⁻² fluence of heating pulses on the carbon target. This stronger ablation did not enhance the harmonic yield due to the deterioration of the phase matching conditions, despite the growth of the concentration of carbon plasma. One can see the appearance of some strong plasma emission lines. The emission from plasma still did not exceed the harmonic emission, since we avoided the formation of highly excited plasmas. While the harmonic cutoff expectably was not significantly changed, the larger amount of free electrons appearing during plasma formation, as well as the excitation of carbon atoms and ions, caused some deterioration of the phase matching conditions between interacting waves achieved in previous case (upper panel), which resulted in a decrease of harmonic yield.

The spectral resolution of XUV spectrometer was equal to 0.5 nm. The natural width of harmonics in the 60 nm range was 0.7 nm, while the observed bandwidth was 2 nm and higher. Thus, the spectral resolution of our spectrometer allowed distinguishing the detuning of harmonic out from the resonance conditions. The appearance of the broadened harmonics (middle panel) was attributed to the propagation of the driving pulses through the denser plasma, containing a larger amount of free electrons.

The bottom panel of Figure 2a shows the plasma emission spectrum in the case of twice higher fluence of 250 fs pulses (2 J cm⁻²), without the propagation of 37 fs pulses through such plasma. At these conditions of plasma formation, only a few lowest order harmonics appeared alongside the strong emission lines once the driving pulses propagated through such plasma. Note that, at these conditions of excitation, plasma emission is characterized by a broadband background.

One can see the coincidence of the strong emission lines with some of the harmonics. These conditions did not affect the envelope of harmonic distribution. Particularly, the presence of the strong ionic emission of CII in XUV range at 68.7 nm (dashed line in Figure 2a) did not affect the yield of nearby harmonic (H15), which points out the absence of the influence of ionic transitions on the harmonic efficiency. Notice that here we are talking about the single-particle response related with the microprocess of the resonance-induced enhancement of single harmonic, rather than multi-particle response, related with the macroprocess of the phase mismatch, leading to a decrease of a whole set of harmonics.

In the case shown in the upper panel of Figure 2a, the low fluence of heating pulses (0.5 J cm⁻²) was used. At these conditions of ablation, no 68.7 nm plasma emission was observed, which has been proved by stopping the propagation of 37 fs driving pulses. Thus, here, we detected only harmonic emission. The confirmation of the overlap of harmonic and emission line and optimization of heating conditions was as follows. We blocked the driving pulses in front of the interaction zone of these pulses with LPP and collected the emission spectrum from plasma at different fluencies of heating pulses. Then, we removed the blocker and reduced the fluence of heating pulses for optimization of the output of HHG emission from this plasma.

Actually, there is a very small difference between this emission (68.7 nm) and the wavelength of 15th harmonic (68.66 nm), which cannot be distinguished by our spectrometer. Probably, first signs of plasma emission could be seen in the second panel of this figure when we used twice stronger fluence of heating pulses (1 J cm⁻²). However, the appearance of incoherent emission, which confirms the presence of such excited ions in the plasmas, did not resulted in the enhancement of neither 15th harmonic (compare this harmonic with the neighboring ones) nor other harmonic orders.

There are a few previous studies of plasma HHG where the resonance enhancement of single harmonic was attributed to the strong oscillator strength of the nearby transition (for example [23,24]). The resonance enhancement of single harmonic relies on the closeness or overlapping of the wavelength of this harmonic with the wavelength of strong transition of electron from the excited state to the ground state. The strength of transition, which is defined by its oscillator strength (gf), plays an important role in the enhancement of the nonlinear response of neutral or ionized atoms. The enhancement of single harmonic can be observed in the vicinity of some ionic transition possessing high values of gf. The 68.7 nm C II line is actually made of three transitions with relatively large gfs (1.3, 0.71 and 0.14 [25]). However, the experiment using 1030 nm radiation showed neither the enhancement nor suppression of H15. We would like to point out that similar absence of the influence of these transitions was observed in the case of 800 nm class lasers when 11th harmonic in the vicinity of this C II line also did not enhance [19,21,26,27].

The resonance enhancement of the single harmonic of 800 nm femtosecond driving pulses has initially been demonstrated at low pulse repetition rate conditions (10 Hz [28,29]). This mechanism shows the advantage in the enhancement of a single harmonic or a group of harmonics in the vicinity of some transitions possessing high gfs. To demonstrate this effect in the case of 150 kHz class laser sources, one has to resolve the problem of stable plasma formation. Otherwise, the impeding processes restricting HHG conversion efficiency using such lasers can strongly diminish the advantages in using the plasma media demonstrating resonance effect. We were able to stabilize LPP and to analyze the conditions of the coincidence of the strong emission lines of CII and some harmonic orders (particularly, H15) of the 1030 nm laser. As it is seen in the middle panel of Figure 2a, our studies showed the absence of resonance enhancement of harmonics, in spite of the closeness of some harmonic orders and emission lines.

Meanwhile, our studies confirmed that resonance-induced processes do not depend on the pulse repetition rate of driving radiation, and can be analyzed using 150 kHz class lasers. To prove this assumption, we present the enhancement of single (11th) harmonic (λ = 93.6 nm) of 1030 nm radiation generating in zinc plasma (Figure 2b). Initially, the role of ionic resonances of Zn near the 9th and 10th harmonics of Ti: sapphire laser (800 nm) in amplifying these harmonics was discussed in [30]. Ablation of the zinc target allows generating harmonics in the presence of plasma emission lines. The observed HHG spectra under these conditions have shown the resonance-induced amplification at different wavelengths, corresponding to different transitions. In particular, the use of a near-infrared laser and its second harmonic (1300 nm + 650 nm [8]) for pumping Zn plasma led to the generation of amplified H15 (86.7 nm), which was due to the influence of some strong Zn II transitions, particularly the 3d¹⁰4s–3d⁹4s4p transition [31]. Our studies suggest that this ionic transition can be responsible for the enhancement of H11 while using the 1030 nm laser.

There are a number of theoretical approaches that describe the effect of resonance on the microscopic response (for instance [32,33,34,35,36,37,38,39,40]). However, the mechanism of this resonant amplification is still debatable. From previous observations, it can be deduced that the strong oscillator strength of neighboring ion transitions does not necessarily cause harmonic amplification, since other processes, such as phase mismatch, can reduce the role of the resonant process. In other words, the influence of a single-particle-induced micro-process can be suppressed by the influence of a collective (i.e., multi-particle-induced) macro-process associated with the phase relations between the driving and harmonic waves.

Some experimental observations point out the collective nature of HHG from laser plumes. Previous studies showed the enhanced single harmonic during HHG from the laser plasmas [8,41]. In resonance conditions, when the frequency of the harmonic is close to the frequency of an atomic or ion transition, the change in the wavenumber of a single harmonic can be significant, and the effect of free electron-induced phase mismatch can be compensated for by atomic dispersion for a certain harmonic order. To the best of our knowledge, there is no information in literature about the wavenumber shift for a single harmonic in the resonance conditions. One can assume that the part of harmonic in resonance with the discussed ionic transition of zinc can be enhanced due to a resonance-induced increase of the nonlinear optical response of the laser plasma. This means that propagation effects may play a decisive role in the formation of the suitable phase matching conditions between the driving and harmonic fields in the vicinity of the above-mentioned ionic transition [8]. In that case, an improvement in the phase conditions for generating a single harmonic can be achieved.

The amplification of a particular harmonic can be associated with a modification of the refractive index of the plasma in the region of anomalous dispersion near the blue side of ionic transitions, which can create conditions for phase matching between the waves of the particular harmonic and the driving pulse. The influence of the single particle induced mechanism can be compensated for by the influence of the collective (i.e., multiparticle) processes related with the phase relations between the driving and harmonic waves. Notice that the absence of resonance-induced enhancement of 15th harmonic during our studies using carbon LPP could be due to the insignificant excitation of the refereed C II transition, as well as the low concentration of carbon ions at the conditions corresponding to the maximal HHG conversion efficiency. Notice that we did not observe the emission of the 68.7 nm line alongside the emission of H15, as well as other plasma emission lines (see two upper panels of Figure 2).

The process of HHG does not depend on the repetition rate of driving pulses. The reasons to carry out these studies are related to the demonstration of HHG in the plasmas produced at high pulse repetition rate, which allowed one to achieve the highest flux of coherent XUV photons. The main restriction of plasma HHG during ablation of targets by high pulse repetition rate pulses is a difficulty in the formation of the stable laser-produced plasma plumes as the nonlinear media for generation of stable harmonics. Two upper panels of Figure 2 correspond to optimized HHG as a result of suitable excitation conditions of ablating target. At the high fluence of heating pulses, the concentration of free electrons is high enough to change the optimal phase conditions between of the driving femtosecond pulses and generating high-order harmonics. Thus, the optimization of targets ablation at a high pulse repetition rate is important for the further application of such LPPs as the suitable media for HHG.

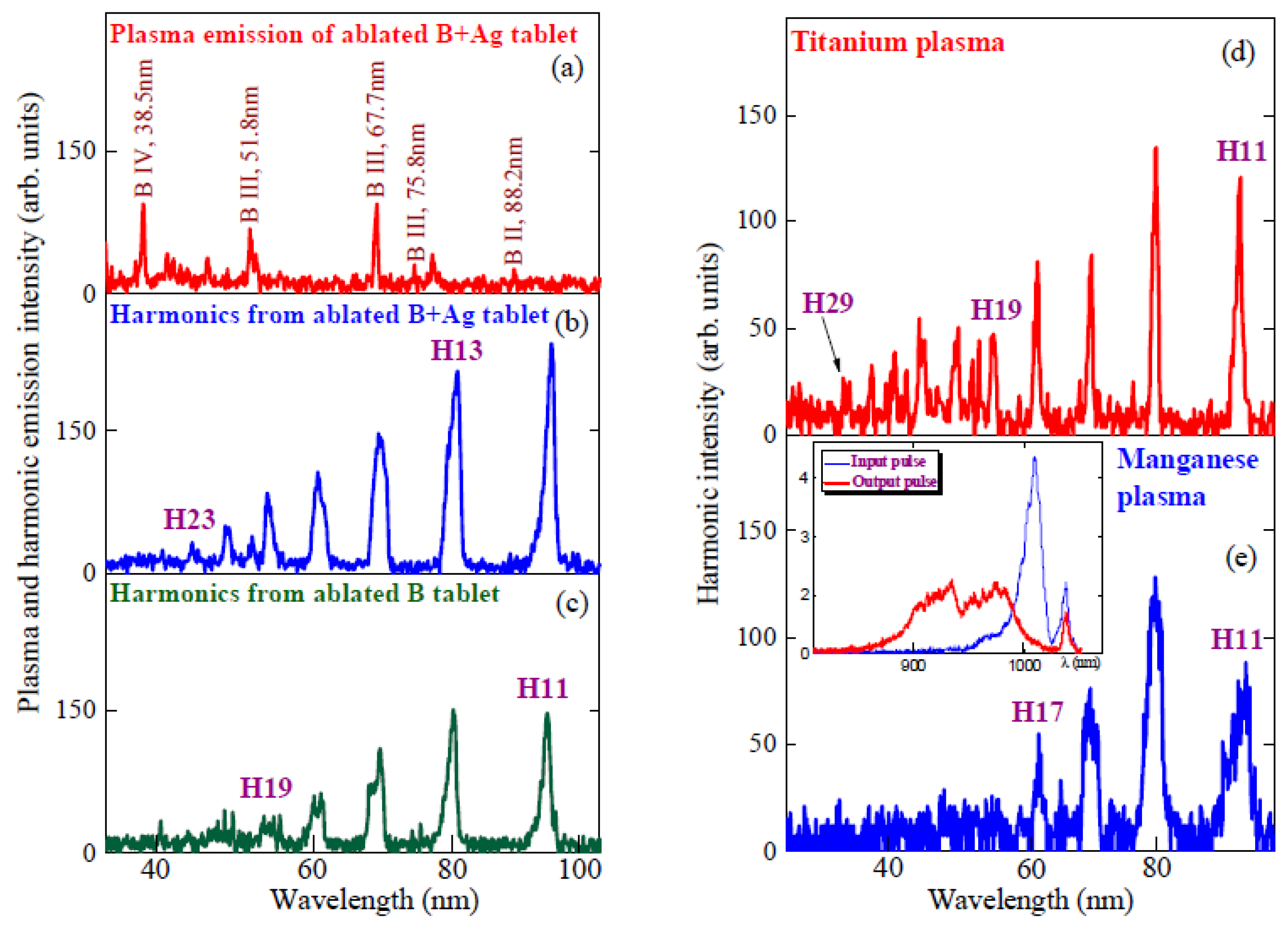
The other three LPPs containing B, Ti, and Mn species showed less efficient HHG compared to the carbon plasma, while maintaining the same properties and dependences of the coherent XUV emission. Plasma emission from the ablated tablet containing the mixture of B NPs and Ag MPs, even at three-fold increase of the fluence of heating pulse with regard to the optimal value of this parameter, was attributed to the transitions of the singly to triply ionized B, while no ionic lines from the heated Ag MPs was observed (Figure 3a). As mentioned earlier, the weight ratio of these two components (B and Ag) was 3:1, so one would expect that the latter species should also emit in the XUV region. The absence of emission from Ag MPs can be attributed to insufficient excitation for evaporation compared with B NPs. One can assume that LPP at these conditions consisted of only B NPs and, correspondingly, those particles alongside the boron atoms and ions were responsible for HHG. We observed only low-order harmonics from this plasma (H23, λ = 44.7 nm; Figure 3b). One can note that silver being properly ablated serves as a medium for efficient harmonic generation, with the cutoffs in the range of 12 to 18 nm [42,43]. The absence of higher-order harmonics points out the absence or insignificant amount of Ag particles in the plasma during the propagation of 37 fs pulses. We analyzed the harmonic emission at similar experimental conditions while ablating the bulk boron, which did not contain silver MPs (Figure 3c). One can see the approximately similar spectral distribution of lower-order harmonics, like in the case of ablated B NP + Ag MPs target. We compared the harmonic emission from the ablated B NPs + Ag MPs and bulk boron target. Though the harmonic efficiency in the former case was larger, the cutoffs in both cases were approximately similar to each other (Figure 3b,c).

These studies showed the peculiarities of harmonics generation in the complex plasmas produced on the mixed powdered targets. Similar to the cases of carbon and zinc plasmas, the repetition rate of driving pulses at proper conditions of plasma formation allows observing the harmonic emission from the powdered NPs, while at the same time, increasing the average power of generated high-order harmonics from the nanostructured LPPs.

Harmonic spectra from titanium and manganese plasmas are shown in Figure 3d,e. The broadening of the harmonic spectra was observed in the case of Mn and nanoparticle plasma plumes. The appearance of the broadened harmonics was attributed to the propagation of the driving pulses through the denser plasma, containing a larger amount of free electrons. The main reason for this process is the phase modulation of driving radiation, which led to the rearrangement of the spectrum and intensity of generated harmonics. The self-phase modulation (SPM) of laser pulses is widely used for the explanation of frequently reported generation of additional frequencies in the spectrum of the harmonics of laser radiation [44,45]. We analyzed the conditions of harmonic spectra broadening at a comparatively “weak” influence of the SPM on the spectral properties of harmonics. This term refers to the conditions under which the spectral and spatial parameters of radiation to be converted change insignificantly upon passage through the nonlinear medium. The SPM of a laser pulse increases with the increase of laser intensity or particle density in the plasma plume.

In the case of Ti plasma, no impeding processes prevented the phase-matched HHG during propagation through the LPP, in spite of the appearance of the ionic lines alongside the shorter wavelength harmonics (Figure 3d; see the spectral range between H19 and H29). Contrary to that, the used Mn LPP caused a strong broadening of the harmonic spectra (Figure 3e). SPM leading to the broadening of the harmonic spectra from Mn plasma can also be attributed to the strong excitation of LPP on the surface of Mn target at high fluence of heating pulses. In that case, the broadened spectra of harmonics compared with those generated in Ti plasma were observed. SPM depends on the condition and parameters of LPP. The excitation of plasma on the surface of Mn target requires less fluence compared with other metal targets, which was shown during the comparative studies of HHG in different LPPs [46]. In this case, the intensity of heating pulses was high enough for excitation of the double charged ions of Mn. The presence of additional free electrons in LPP led to the SPM of driving pulses, which caused the broadening of the harmonic spectra.

The broadening and blue-shifting of the HHG spectra were also observed at the high intensity of driving pulses. It can be explained by appearance of the blue-shifted components in the spectrum of driving pulse (see inset in Figure 3e). One can see the appearance of the blue components in the spectra of the driving pulses propagated through LPP during HHG in plasma. This figure shows a modulation of the spectrum of driving pulses during propagation through the plasma plumes excited on the surface of metal targets. We examined the spectrum of driving pulses before (input pulses; blue thin curve) and after (output pulses; red thick curve) propagation through the plasmas produced by strong heating pulses. One can see the spectral broadening and shift of femtosecond driving pulses after propagation of plasma plumes, due to the group velocity dispersion of different spectral components of the 37 fs pulses. Notice that, at optimal conditions of laser ablation and plasma formation, the spectral shape of driving pulse after propagation through the plasma plume remains unchanged. The term “optimal conditions” refers to the case when we were able to achieve the maximal yield of harmonics.

There is no accumulation effect on the broadening of femtosecond driving pulses at the high repetition rate. The interval between pulses at 150 kHz ablation is ~6 µs. During this period, the plasma entirely disappears, and a new ablation will be produced on the fresh surface. Thus, from the context of pulse repetition rate, the broadening of high-order harmonics does not depend on this parameter, provided that the interval between pulses becomes larger than the lifetime of plasma (~100–300 ns). Notice that this time interval corresponds to the MHz class lasers.

The availability in the formation of the stable B, Ti, and Mn plasmas at the used pulse repetition rate allowed making the conclusion that the latter parameter does not play important role in the relative intensities of harmonics from different plasmas. Particularly, carbon plasma has demonstrated to be the efficient medium using other wavelengths (1300 nm, 800 nm, 400 nm) and different pulse repetition rates of laser sources. The stabilization of plasma formation at 150 kHz ablation allowed concluding about the smaller HHG conversion efficiency in above metal plasmas with regard to the carbon plasma. Thus, the high repetition rate of driving pulses at proper conditions of plasma formation leads to increasing the average power and flux of generating high-order harmonics, while also allowing the analysis of different processes demonstrated using the low pulse repetition rate lasers.

Notice that the application of the 1030 nm wavelength in these studies did not allow the observation of the resonance enhancement of harmonics in Mn plasma, which has been demonstrated using other laser sources (800 nm [47] and 1820 nm [48]). This difference in harmonic spectra using various laser sources points out the role of proper matching of the wavelengths of some harmonics and ionic transitions possessing high oscillator strengths.

4. Discussion

The demonstration of the high flux of harmonics from different plasmas opens doors for further developments in the nonlinear spectroscopy of ablated materials. With the demonstration of highest average flux of harmonics reported so far, one can define the plasma as a very effective medium for coherent XUV sources formation [49,50,51].

The main goal of this work was to demonstrate the harmonic generation from the plasmas produced by 150 kHz class laser. However, independently of which pulse repetition rate was used, the principles of optimal plasma formation are similar for the single shot, 10 Hz, 1 kHz, 100 kHz, etc., cases. The term “optimal” refers to the conditions when the driving beam propagates through the maximally dense plasma arriving on the pass of driving pulse, with minimal impeding factors decreasing the harmonic conversion efficiency. The requirements to minimize the impeding factors, such as phase mismatch, strong incoherent plasma emission and additional thermal loading on the target surface, remain the same for each of abovementioned regimes of pulse repetition rate. In this context, the formation of the stable plasma plume using 150 kHz class lasers needs additional efforts for maintaining stable harmonic yield from such laser-produced plasma. One of options is the programmable movement of rotating target up and down, which can further diminish the instability issue.

The physics of plasmas could be developed further only in the case of notable steps in handling the extremes of this state of matter, particularly, by determining stable plasma conditions at the high pulse repetition rate of its formation. The 150 kHz repetition rate XUV harmonics pave the way for the time-resolved experiments, which need high statistics. Additionally, the developed system can capture the photo-induced rare events in matter and supply sophisticated time resolved measurements with high temporal accuracy and high signal. The maintenance of relatively stable harmonics generation requires significant improvements in target operations under such high repetition rates, which were achieved in present studies. Another important novelty of our study is a high flux of harmonics. Even at the present state of plasma formation using high pulse repetition lasers, we achieved sufficient stability of harmonics, allowing their use for temporal characterization, as well as other applications.

The measurements of pulse energy in the XUV range are difficult to carry out in each HHG study. Previous studies of harmonics from different plasmas included the quantitative measurements of coherent XUV yield. Taking into account the similarity of relative intensities of harmonics from different plasmas, one can estimate the flux of harmonic emission using previous measurements of HHG conversion efficiency (~10⁻⁵, Ganeev, R.A., et al. [21,52]). The flux of single (H25, E = 30 eV) harmonics in present studies using carbon LPP was estimated to be 8 × 10¹³ photons/s. The corresponding fluxes obtained from other LPPs were 4 × 10¹³ (B NP + Ag MP), 2 × 10¹³ (Mn, B, and Ti) and 1.5 × 10¹³ (Zn) photons/s.

The average flux of harmonics achieved in this study is high enough to compare with the maximal harmonic fluxes reported in the case of gas HHG. Recently, high flux from argon gas was reported using similar high pulse repetition source [53]. They produced ~7 × 10¹⁴ photons/s of high-order harmonic in argon, which corresponds to ~2 mW average power in the case of their 166 kHz laser source. However, this flux was obtained using the third harmonic (344 nm) of the 1030 laser, and can be compared with our case taking into account the λ⁻⁵ rule, which gives ~ 250×-fold growth of harmonic yield in the case of 344 nm pump compared with 1030 nm pump. Meanwhile, the maximal flux reported in the case of 1030 nm pump was less than 10¹¹ photons/s, which is significantly smaller than the flux achieved during our studies. It is not surprising, since the HHG conversion efficiency of 1030 nm pulses in plateau range in their case was measured to be about 1 × 10⁻⁸ (500 nW from 45 W) in the 30–40 eV spectral range. Notice that, at 1030 nm pump, we achieved higher cutoff than that in refereed paper at the same wavelength (>62 eV and <50 eV, respectively). Furthermore, notice that the concentration of argon gas in those studies was 15 times larger than the concentration of particles in our plasmas. This comparison also points out the higher conversion efficiency in the case of HHG, in plasmas compared with gas media.

5. Conclusions

In conclusion, the reported study of HHG using 150 kHz laser is a first demonstration of the high pulse repetition rate ablation for this process. Previous studies were limited by 1 kHz class lasers [12,21,22]. The details of application of the rotating target for improvement of stability of the low and harmonics from plasma in the case of low and high pulse repetition rates of laser-matter interactions have been described earlier in [54,55]. In present studies, the harmonics were generated in carbon, boron, manganese, zinc, and titanium plasmas using 150 kHz laser. The flux of single (H25, E = 30 eV) harmonics in present studies using carbon LPP was estimated to be 8 × 10¹³ photons/s. The corresponding fluxes obtained from other LPPs were 4 × 10¹³ (B NP + Ag MP), 2 × 10¹³ (Mn, B, and Ti) and 1.5 × 10¹³ (Zn) photons/s. We were able to demonstrate the resonance enhancement of single harmonic, HHG in nanoparticles, and other harmonic generation effects, using 1030 nm, 150 kHz, 37 fs laser source.