Insights of Hysteresis Behaviors in Perovskite Solar Cells from a Mixed Drift-Diffusion Model Coupled with Recombination
Abstract
1. Introduction
2. Methods
3. Results and Discussion
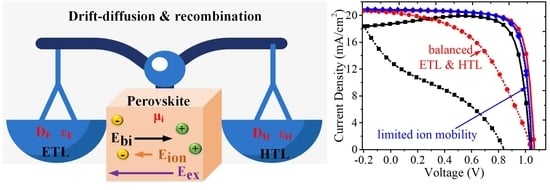
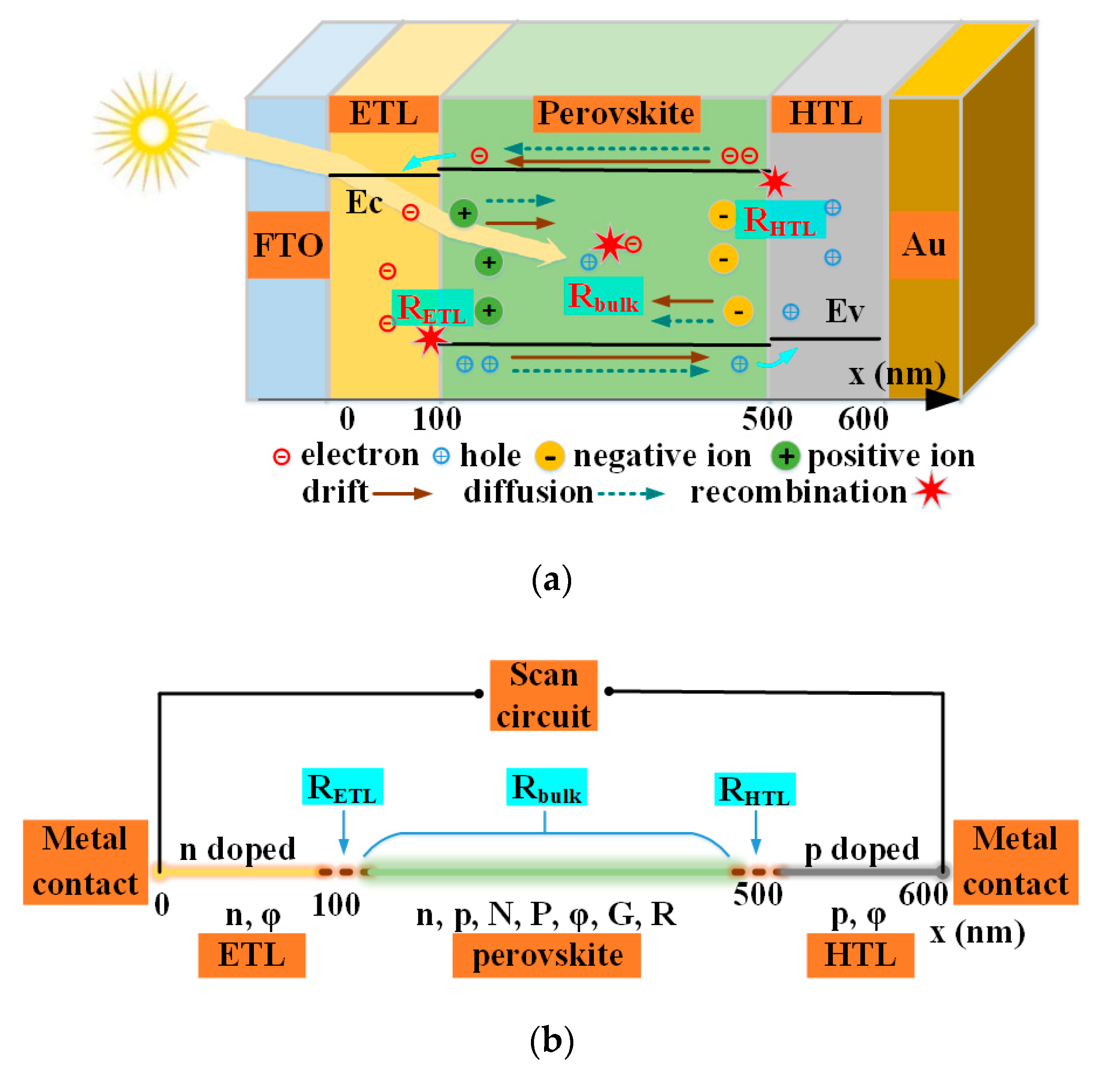
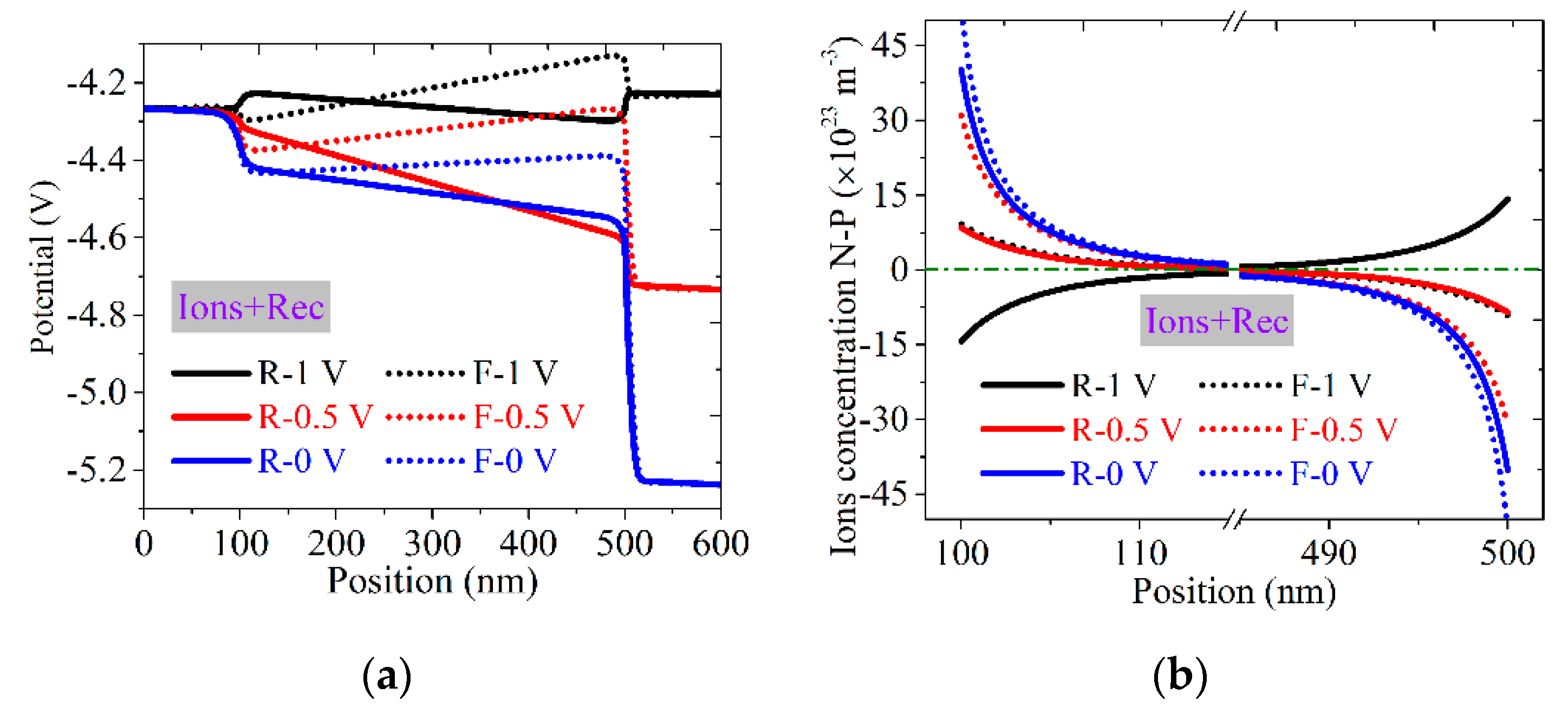
3.1. Hysteresis Origin and Generating Principles
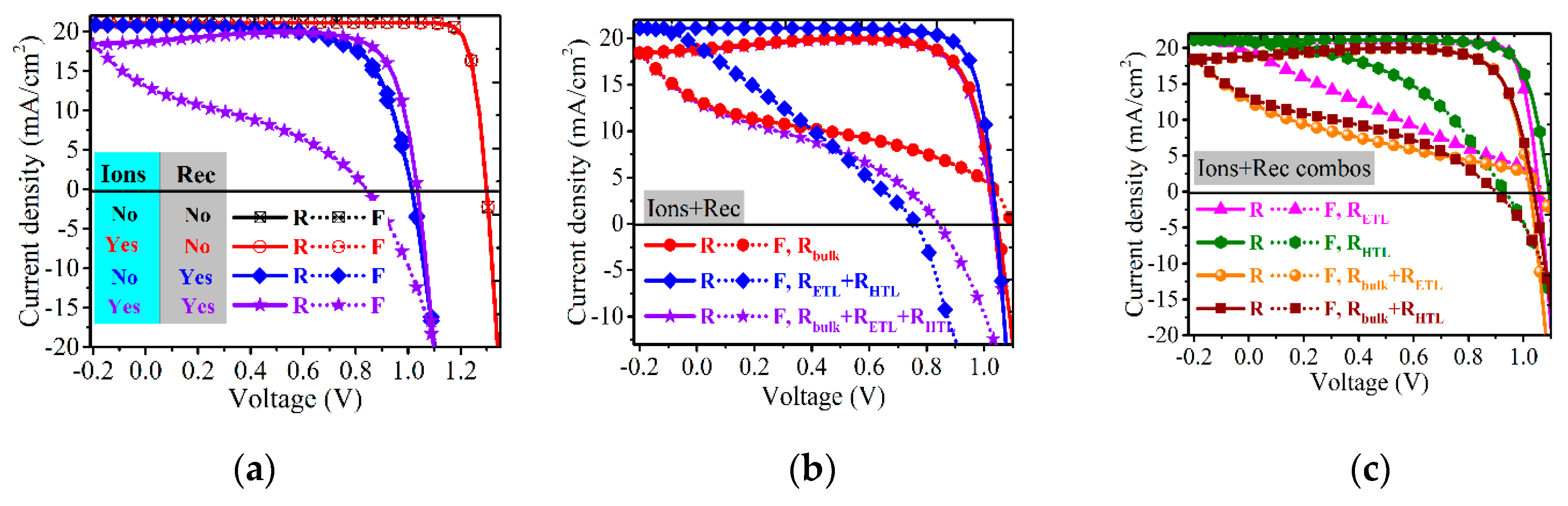
3.1.1. Essential Conditions for Hysteresis Reproduction Numerically
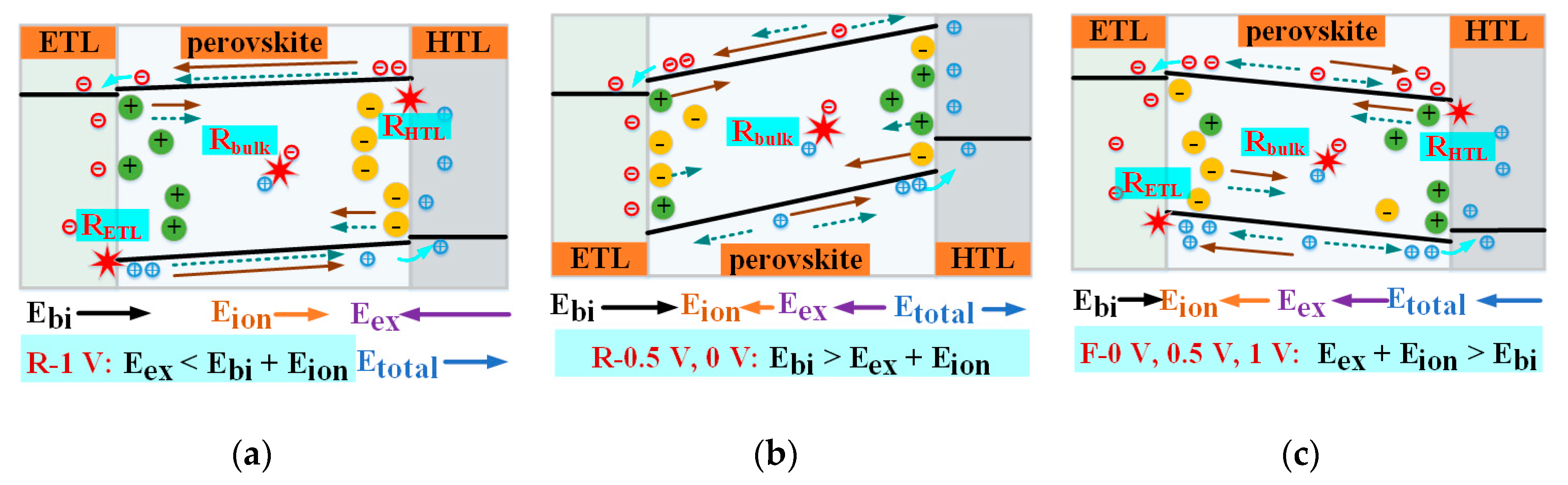
3.1.2. Hysteresis Generating Principles
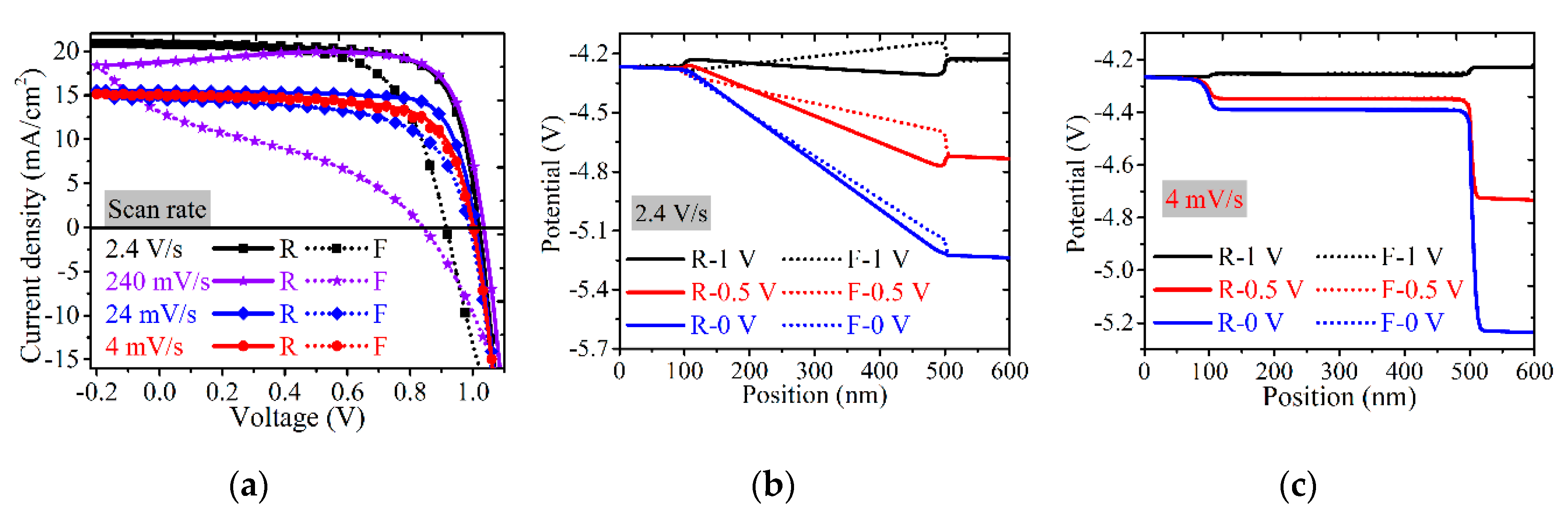
3.2. Measurement Protocols Improvement to Suppress Hysteresis
3.2.1. Scan Rates
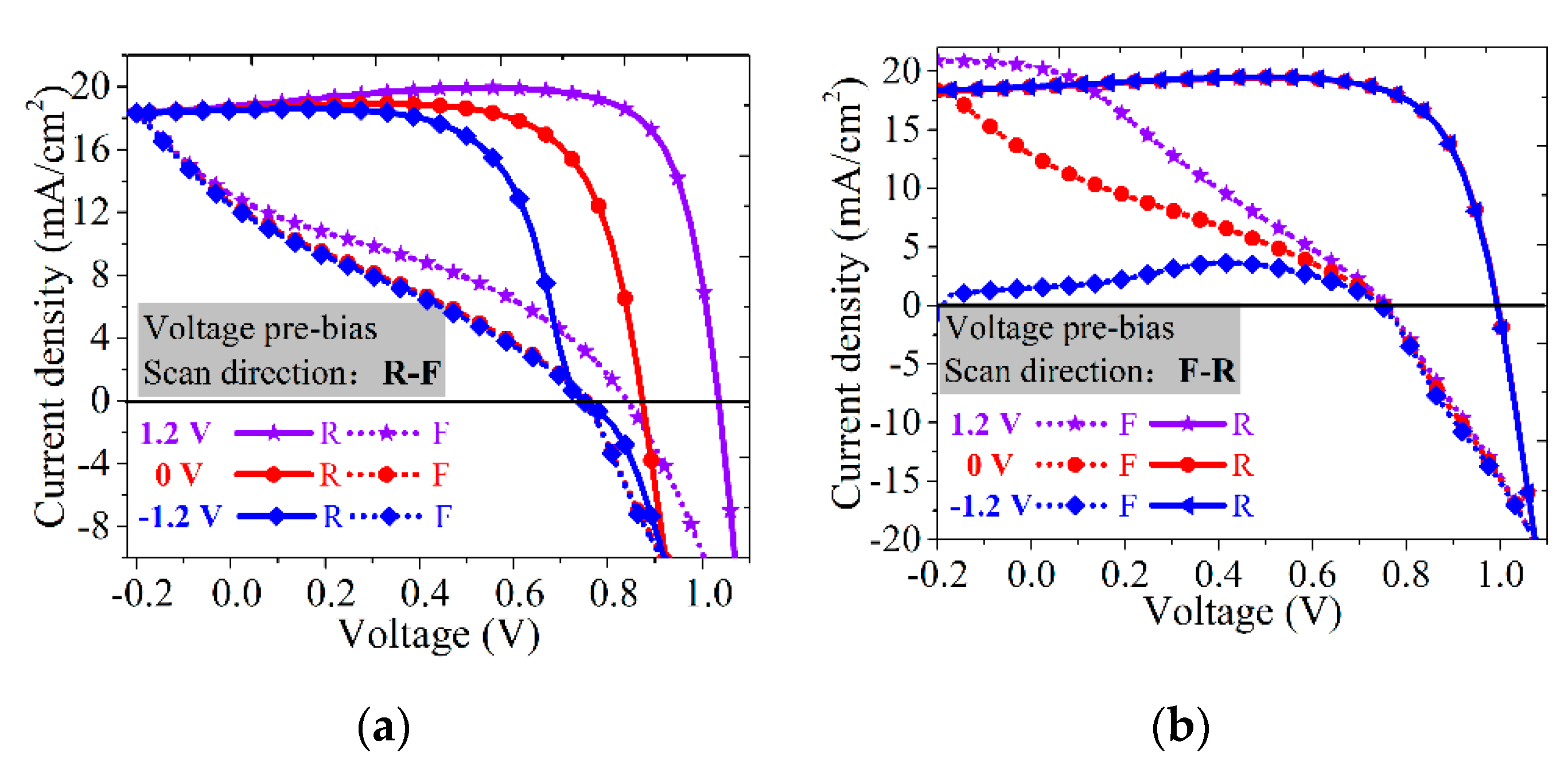
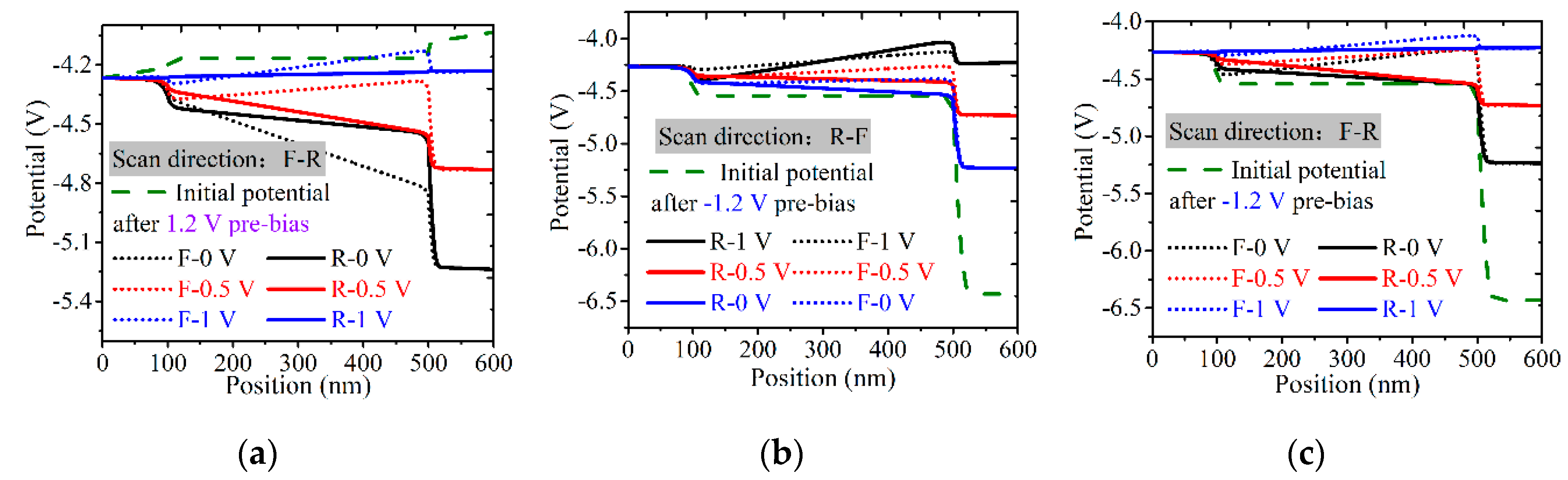
3.2.2. Scan Direction and Pre-Bias Treatment
3.3. Materials Improvement to Suppress Hysteresis
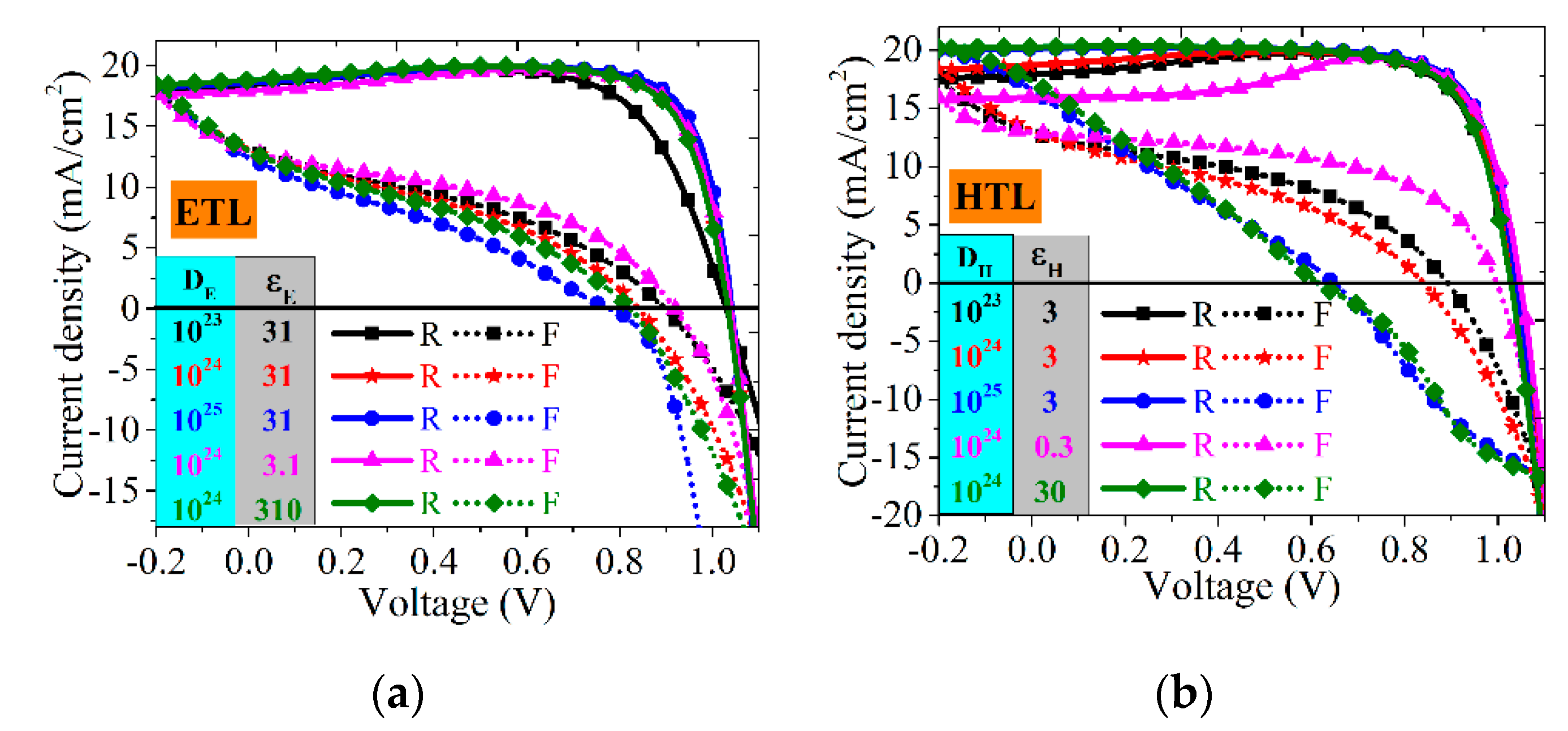
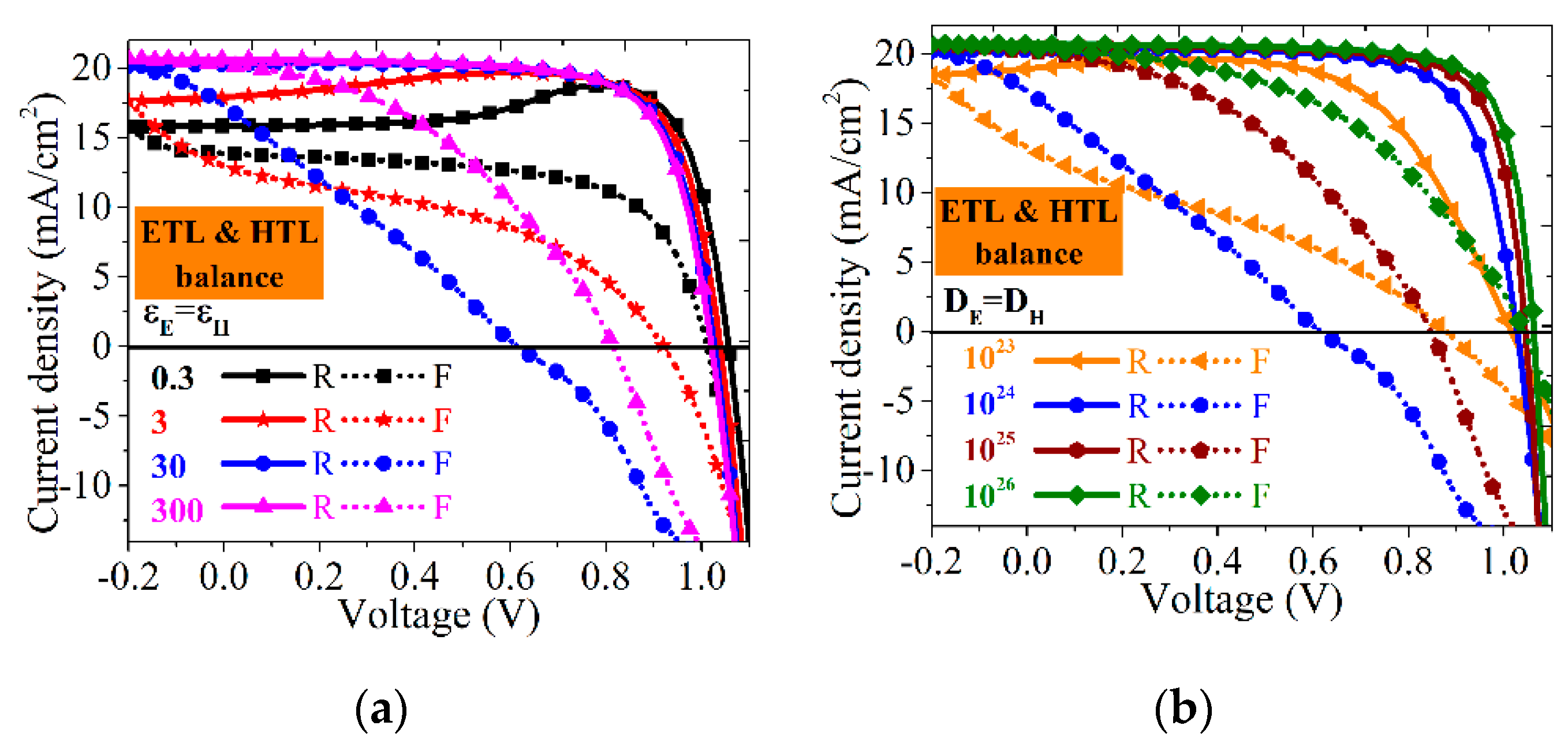
3.3.1. Transport Layers Properties
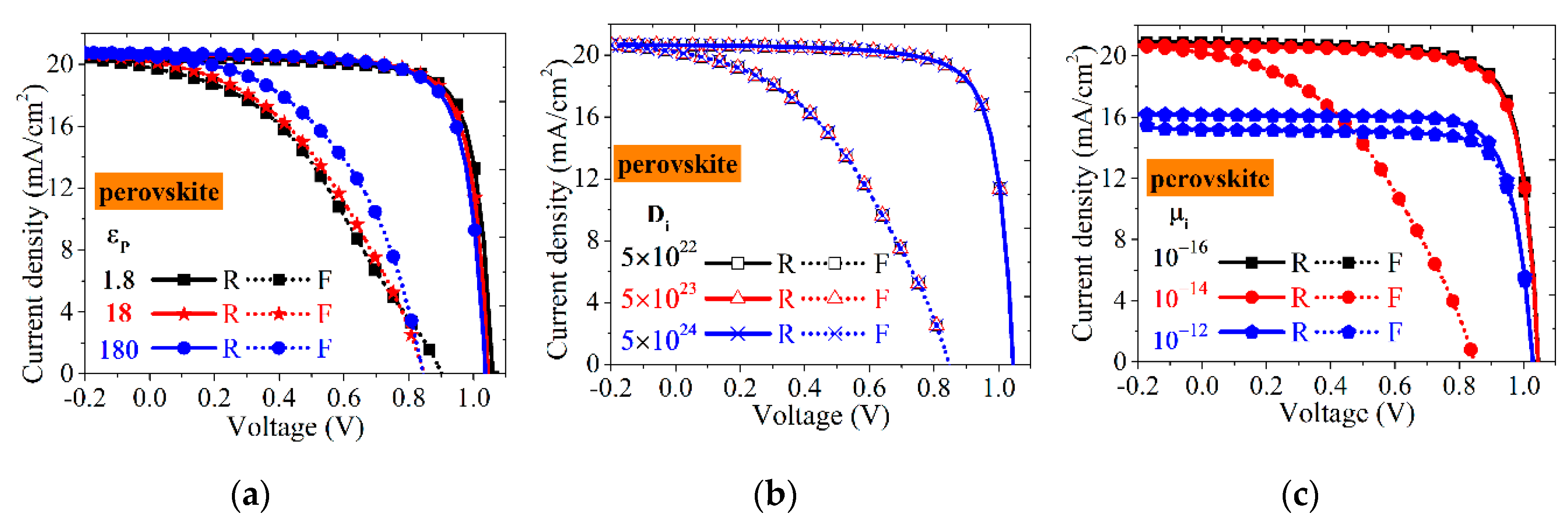
3.3.2. Perovskite Layer Properties
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Liu, X.; Cheng, Y.; Liu, C.; Zhang, T.; Zhang, N.; Zhang, S.; Chen, J.; Xu, Q.; Ouyang, J.; Gong, H. 20.7% highly reproducible inverted planar perovskite solar cells with enhanced fill factor and eliminated hysteresis. Energy Environ. Sci. 2019, 12, 1622–1633. [Google Scholar] [CrossRef]
- Min, H.; Kim, M.; Lee, S.U.; Kim, H.; Kim, G.; Choi, K.; Lee, J.H.; Seok, S.I. Efficient, Stable Solar Cells by Using Inherent Bandgap of Alpha-Phase Formamidinium Lead Iodide. Science 2019, 366, 749–753. [Google Scholar] [CrossRef]
- NREL. Best Research-Cell Efficiency Chart. Available online: https://www.nrel.gov/pv/cell-efficiency.html (accessed on 6 June 2020).
- Kim, D.; Jung, H.J.; Park, I.J.; Larson, B.W.; Dunfield, S.P.; Xiao, C.; Kim, J.; Tong, J.; Boonmongkolras, P.; Ji, S.G.; et al. Efficient, Stable Silicon Tandem Cells Enabled by Anion-Engineered Wide-Bandgap Perovskites. Science 2020, 368, 155–160. [Google Scholar] [CrossRef] [PubMed]
- Liu, P.; Wang, W.; Liu, S.; Yang, H.; Shao, Z. Fundamental Understanding of Photocurrent Hysteresis in Perovskite Solar Cells. Adv. Energy Mater. 2019, 9, 1803017. [Google Scholar] [CrossRef]
- Jacobs, D.A.; Wu, Y.; Shen, H.; Barugkin, C.; Beck, F.J.; White, T.P.; Weber, K.; Catchpole, K.R. Hysteresis Phenomena in Perovskite Solar Cells: The Many and Varied Effects of Ionic Accumulation. Phys. Chem. Chem. Phys. 2017, 19, 3094–3103. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Wen, X.; Sheng, R.; Huang, S.; Deng, X.; Green, M.A.; Ho-Baillie, A. Mobile Ion Induced Slow Carrier Dynamics in Organic–Inorganic Perovskite CH3NH3PbBr3. ACS Appl. Mater. Interfaces 2016, 8, 5351–5357. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Yang, M.; Priya, S.; Zhu, K. Origin of J–V Hysteresis in Perovskite Solar Cells. J. Phys. Chem. Lett. 2016, 7, 905–917. [Google Scholar] [CrossRef]
- Van Reenen, S.; Kemerink, M.; Snaith, H.J. Modeling Anomalous Hysteresis in Perovskite Solar Cells. J. Phys. Chem. Lett. 2015, 6, 3808–3814. [Google Scholar] [CrossRef]
- Diao, X.-F.; Tang, Y.-L.; Xie, Q.; Chen, D.-L.; Li, S.-X.; Liu, G.-F. Study on the Property of Electron-Transport Layer in the Doped Formamidinium Lead Iodide Perovskite Based on DFT. ACS Omega 2019, 4, 20024–20035. [Google Scholar] [CrossRef]
- Eames, C.; Frost, J.M.; Barnes, P.R.; O’regan, B.C.; Walsh, A.; Islam, M.S. Ionic Transport in Hybrid Lead Iodide Perovskite Solar Cells. Nat. Commun. 2015, 6, 7497. [Google Scholar] [CrossRef]
- Richardson, G.; O’Kane, S.E.J.; Niemann, R.G.; Peltola, T.A.; Foster, J.M.; Cameron, P.J.; Walker, A.B. Can Slow-Moving Ions Explain Hysteresis in the Current–Voltage Curves of Perovskite Solar Cells? Energy Environ. Sci. 2016, 9, 1476–1485. [Google Scholar] [CrossRef]
- Calado, P.; Telford, A.M.; Bryant, D.; Li, X.; Nelson, J.; O’Regan, B.C.; Barnes, P.R.F. Evidence for Ion Migration in Hybrid Perovskite Solar Cells with Minimal Hysteresis. Nat. Commun. 2016, 7, 13831. [Google Scholar] [CrossRef] [PubMed]
- Courtier, N.E.; Cave, J.M.; Walker, A.B.; Richardson, G.; Foster, J.M. Ionmonger: A Free and Fast Planar Perovskite Solar Cell Simulator with Coupled Ion Vacancy and Charge Carrier Dynamics. J. Comput. Electron. 2019, 18, 1435–1449. [Google Scholar] [CrossRef]
- Courtier, N.E.; Richardson, G.; Foster, J.M. A fast and robust numerical scheme for solving models of charge carrier transport and ion vacancy motion in perovskite solar cells. Appl. Math. Model. 2018, 63, 329–348. [Google Scholar] [CrossRef]
- Courtier, N.E.; Cave, J.M.; Foster, J.M.; Walker, A.B.; Richardson, G. How Transport Layer Properties Affect Perovskite Solar Cell Performance: Insights from a Coupled Charge Transport/Ion Migration Model. Energy Environ. Sci. 2019, 12, 396–409. [Google Scholar] [CrossRef]
- Shen, H.; Jacobs, D.A.; Wu, Y.; Duong, T.; Peng, J.; Wen, X.; Fu, X.; Karuturi, S.K.; White, T.P.; Weber, K.; et al. Inverted Hysteresis in CH3NH3PbI3 Solar Cells: Role of Stoichiometry and Band Alignment. J. Phys. Chem. Lett. 2017, 8, 2672–2680. [Google Scholar] [CrossRef]
- Xiang, J.; Li, Y.; Huang, F.; Zhong, D. Effect of Interfacial Recombination, Bulk Recombination and Carrier Mobility on The J–V Hysteresis Behaviors of Perovskite Solar Cells: A Drift-Diffusion Simulation Study. Phys. Chem. Chem. Phys. 2019, 21, 17836–17845. [Google Scholar] [CrossRef] [PubMed]
- Nemnes, G.A.; Besleaga, C.; Tomulescu, A.G.; Palici, A.; Pintilie, L.; Manolescu, A.; Pintilie, I. How Measurement Protocols Influence the Dynamic J-V Characteristics of Perovskite Solar Cells: Theory and Experiment. Sol. Energy 2018, 173, 976–983. [Google Scholar] [CrossRef]
- Walter, D.; Fell, A.; Wu, Y.; Duong, T.; Barugkin, C.; Wu, N.; White, T.; Weber, K. Transient Photovoltage in Perovskite Solar Cells: Interaction of Trap-Mediated Recombination and Migration of Multiple Ionic Species. J. Phys. Chem. C 2018, 122, 11270–11281. [Google Scholar] [CrossRef]
- Bi, D.; Tress, W.; Dar, M.I.; Gao, P.; Luo, J.; Renevier, C.; Schenk, K.; Abate, A.; Giordano, F.; Baena, J.-P.C. Efficient Luminescent Solar Cells Based on Tailored Mixed-Cation Perovskites. Sci. Adv. 2016, 2, e1501170. [Google Scholar] [CrossRef]
- Wang, Z.; Lin, Q.; Wenger, B.; Christoforo, M.G.; Lin, Y.-H.; Klug, M.T.; Johnston, M.B.; Herz, L.M.; Snaith, H.J. High Irradiance Performance of Metal Halide Perovskites for Concentrator Photovoltaics. Nat. Energy 2018, 3, 855. [Google Scholar] [CrossRef]
- Foster, J.M.; Snaith, H.J.; Leijtens, T.; Richardson, G. A model for the operation of perovskite based hybrid solar cells: Formulation, analysis, and comparison to experiment. SIAM J. Appl. Math. 2014, 74, 1935–1966. [Google Scholar] [CrossRef]
- Yin, W.-J.; Yang, J.-H.; Kang, J.; Yan, Y.; Wei, S.-H. Halide perovskite materials for solar cells: A theoretical review. J. Mater. Chem. A 2015, 3, 8926–8942. [Google Scholar] [CrossRef]
- Rong, Y.; Hu, Y.; Ravishankar, S.; Liu, H.; Hou, X.; Sheng, Y.; Mei, A.; Wang, Q.; Li, D.; Xu, M. Tunable Hysteresis Effect for Perovskite Solar Cells. Energy Environ. Sci. 2017, 10, 2383–2391. [Google Scholar] [CrossRef]
- Peng, J.; Wu, Y.; Ye, W.; Jacobs, D.A.; Shen, H.; Fu, X.; Wan, Y.; Duong, T.; Wu, N.; Barugkin, C.; et al. Interface Passivation Using Ultrathin Polymer-Fullerene Films for High-Efficiency Perovskite Solar Cells with Negligible Hysteresis. Energy Environ. Sci. 2017, 10, 1792–1800. [Google Scholar] [CrossRef]
- Shao, Y.; Xiao, Z.; Bi, C.; Yuan, Y.; Huang, J. Origin and Elimination of Photocurrent Hysteresis by Fullerene Passivation in CH3NH3PbI3 Planar Heterojunction Solar Cells. Nat. Commun. 2014, 5, 5784. [Google Scholar] [CrossRef]
- Snaith, H.J.; Abate, A.; Ball, J.M.; Eperon, G.E.; Leijtens, T.; Noel, N.K.; Stranks, S.D.; Wang, J.T.-W.; Wojciechowski, K.; Zhang, W. Anomalous Hysteresis in Perovskite Solar Cells. J. Phys. Chem. Lett. 2014, 5, 1511–1515. [Google Scholar] [CrossRef]
- Tress, W.; Marinova, N.; Moehl, T.; Zakeeruddin, S.; Nazeeruddin, M.K.; Grätzel, M. Understanding the Rate-Dependent J–V Hysteresis, Slow Time Component, and Aging in CH3NH3PbI3 Perovskite Solar Cells: The Role of a Compensated Electric Field. Energy Environ. Sci. 2015, 8, 995–1004. [Google Scholar] [CrossRef]
- Bruno, A.; Cortecchia, D.; Chin, X.Y.; Fu, K.; Boix, P.P.; Mhaisalkar, S.; Soci, C. Temperature and Electrical Poling Effects on Ionic Motion in MAPbI3 Photovoltaic Cells. Adv. Energy Mater. 2017, 7, 1700265. [Google Scholar] [CrossRef]
- Anghel, D.V.; Nemnes, G.A.; Pintilie, I.; Manolescu, A. Modelling J–V Hysteresis in Perovskite Solar Cells Induced by Voltage Poling. Phys. Scr. 2019, 94, 125809. [Google Scholar] [CrossRef]
- Cai, F.; Yang, L.; Yan, Y.; Zhang, J.; Qin, F.; Liu, D.; Cheng, Y.-B.; Zhou, Y.; Wang, T. Eliminated Hysteresis and Stabilized Power Output over 20% in Planar Heterojunction Perovskite Solar Cells by Compositional and Surface Modifications to the Low-Temperature-Processed TiO2 Layer. J. Mater. Chem. A 2017, 5, 9402–9411. [Google Scholar] [CrossRef]
- Correa-Baena, J.-P.; Saliba, M.; Buonassisi, T.; Grätzel, M.; Abate, A.; Tress, W.; Hagfeldt, A. Promises and challenges of perovskite solar cells. Science 2017, 358, 739–744. [Google Scholar] [CrossRef] [PubMed]
- Park, N.-G.; Grätzel, M.; Miyasaka, T.; Zhu, K.; Emery, K. Towards stable and commercially available perovskite solar cells. Nat. Energy 2016, 1, 16152. [Google Scholar] [CrossRef]
| Parameters | ETL(E) | Perovskite(P) | HTL(H) | Reference |
|---|---|---|---|---|
| Permittivity εE,P,H | 31 | 18 | 3 | [13,18,20,23] |
| Bandgap Eg (eV) | 3 | 1.6 | 3.2 | [13,16,18] |
| Doping concentration DE,H (m−3) | 1024 | —— | 1024 | [13,16,25] |
| Effective density of state in conduction band NC (m−3) | 1026 | 5 × 1024 | 1026 | [18] |
| Effective density of state in valence band NV (m−3) | 1026 | 5 × 1024 | 1026 | [18] |
| Electron affinity (eV) | 4.15 | 3.95 | 2.15 | [13,20] |
| Electron mobility μn (m2/(V∙s)) | 10−8 | 2 × 10−4 | 10−8 | [13,20] |
| Hole mobility μp (m2/(V∙s)) | 10−8 | 2 × 10−4 | 10−8 | [13,20] |
| Ion concentration Di (m−3) | —— | 5 × 1023 | —— | [13,16] |
| Ion mobility μi (m2/(V∙s)) | —— | 10−14 | —— | [13,16] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, C.; Shan, X.; Xie, T. Insights of Hysteresis Behaviors in Perovskite Solar Cells from a Mixed Drift-Diffusion Model Coupled with Recombination. Photonics 2020, 7, 47. https://doi.org/10.3390/photonics7030047
Yang C, Shan X, Xie T. Insights of Hysteresis Behaviors in Perovskite Solar Cells from a Mixed Drift-Diffusion Model Coupled with Recombination. Photonics. 2020; 7(3):47. https://doi.org/10.3390/photonics7030047
Chicago/Turabian StyleYang, Chongqiu, Xiaobiao Shan, and Tao Xie. 2020. "Insights of Hysteresis Behaviors in Perovskite Solar Cells from a Mixed Drift-Diffusion Model Coupled with Recombination" Photonics 7, no. 3: 47. https://doi.org/10.3390/photonics7030047
APA StyleYang, C., Shan, X., & Xie, T. (2020). Insights of Hysteresis Behaviors in Perovskite Solar Cells from a Mixed Drift-Diffusion Model Coupled with Recombination. Photonics, 7(3), 47. https://doi.org/10.3390/photonics7030047