Free Electron Laser Measurement of Liquid Carbon Reflectivity in the Extreme Ultraviolet
Abstract
1. Introduction
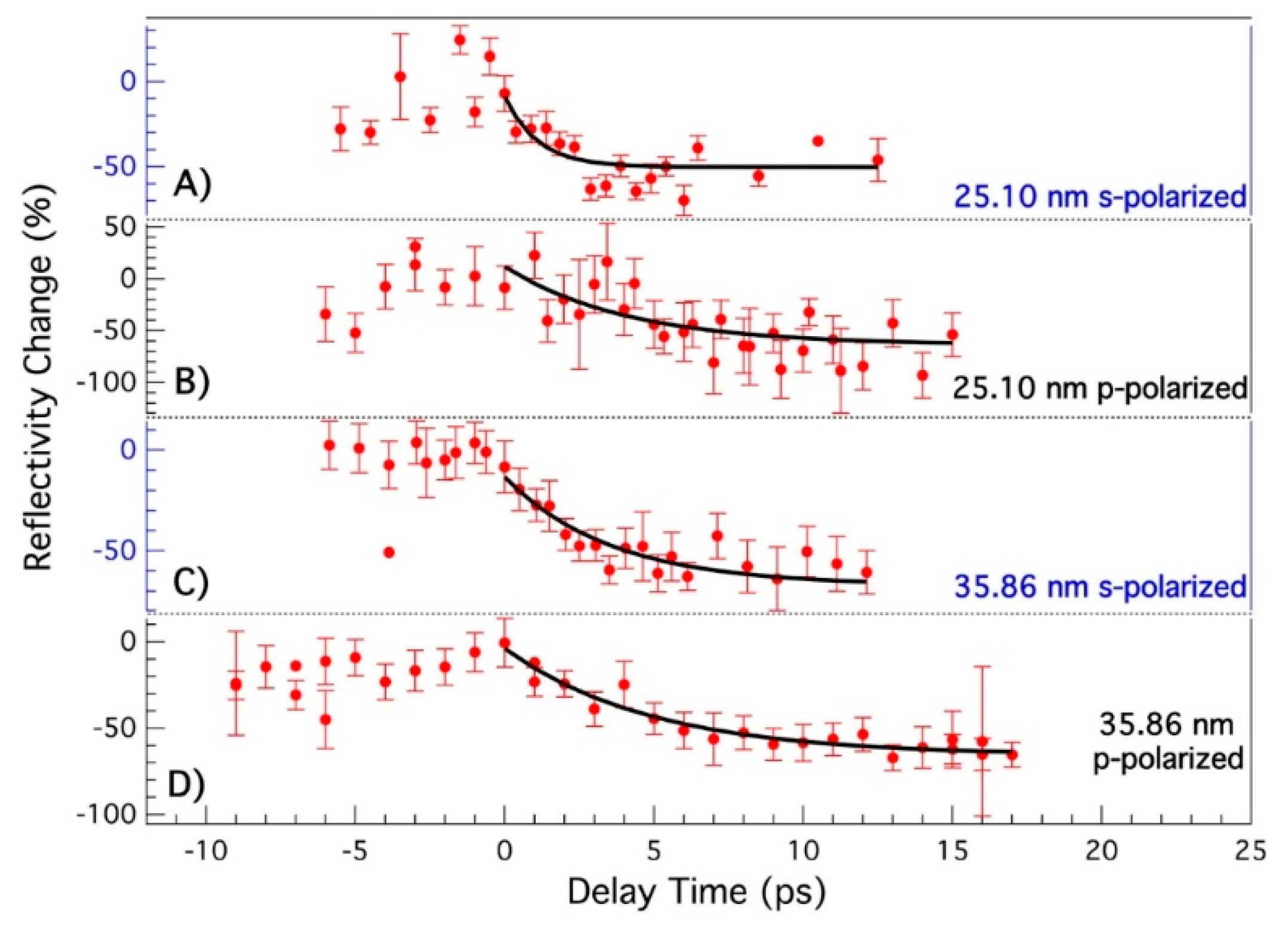
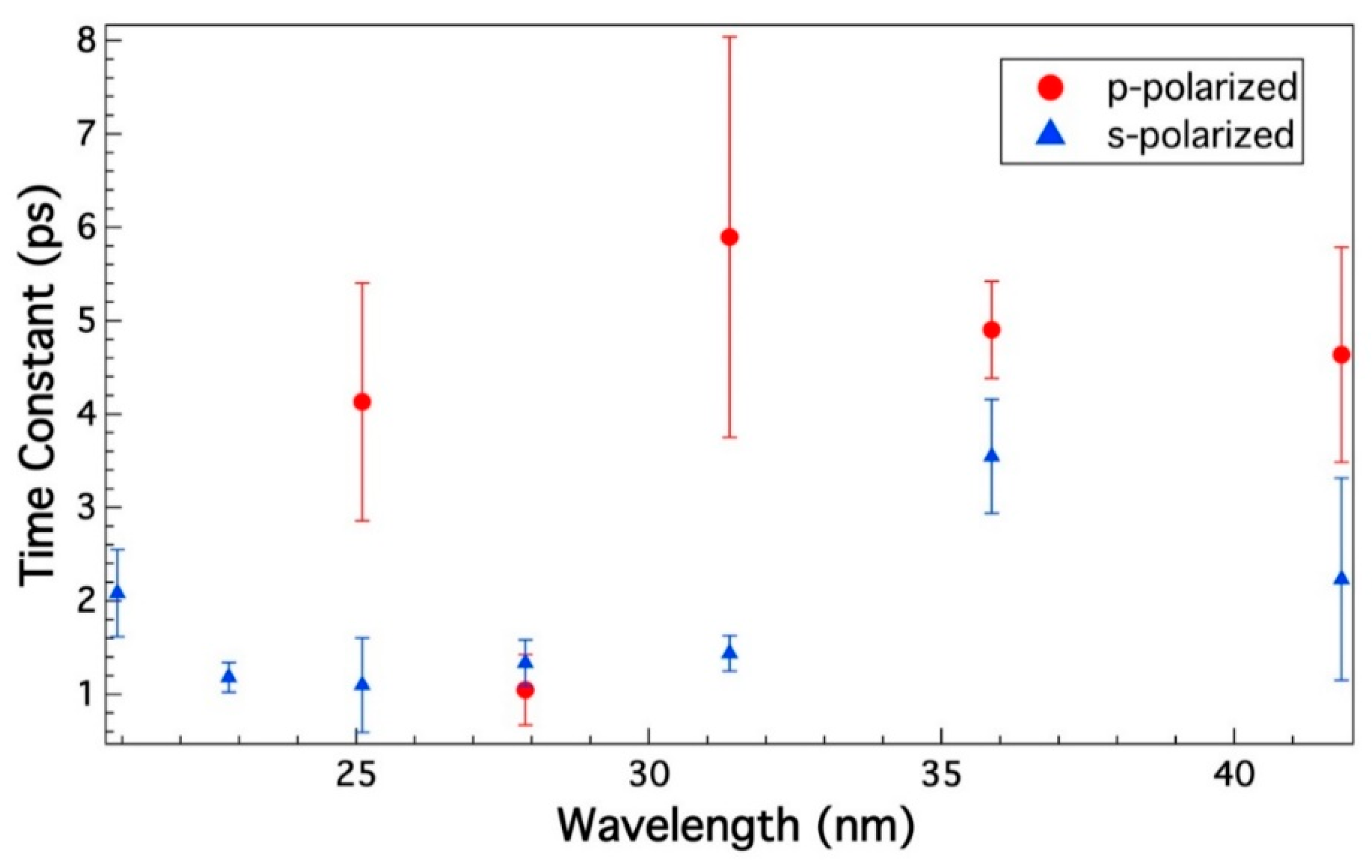
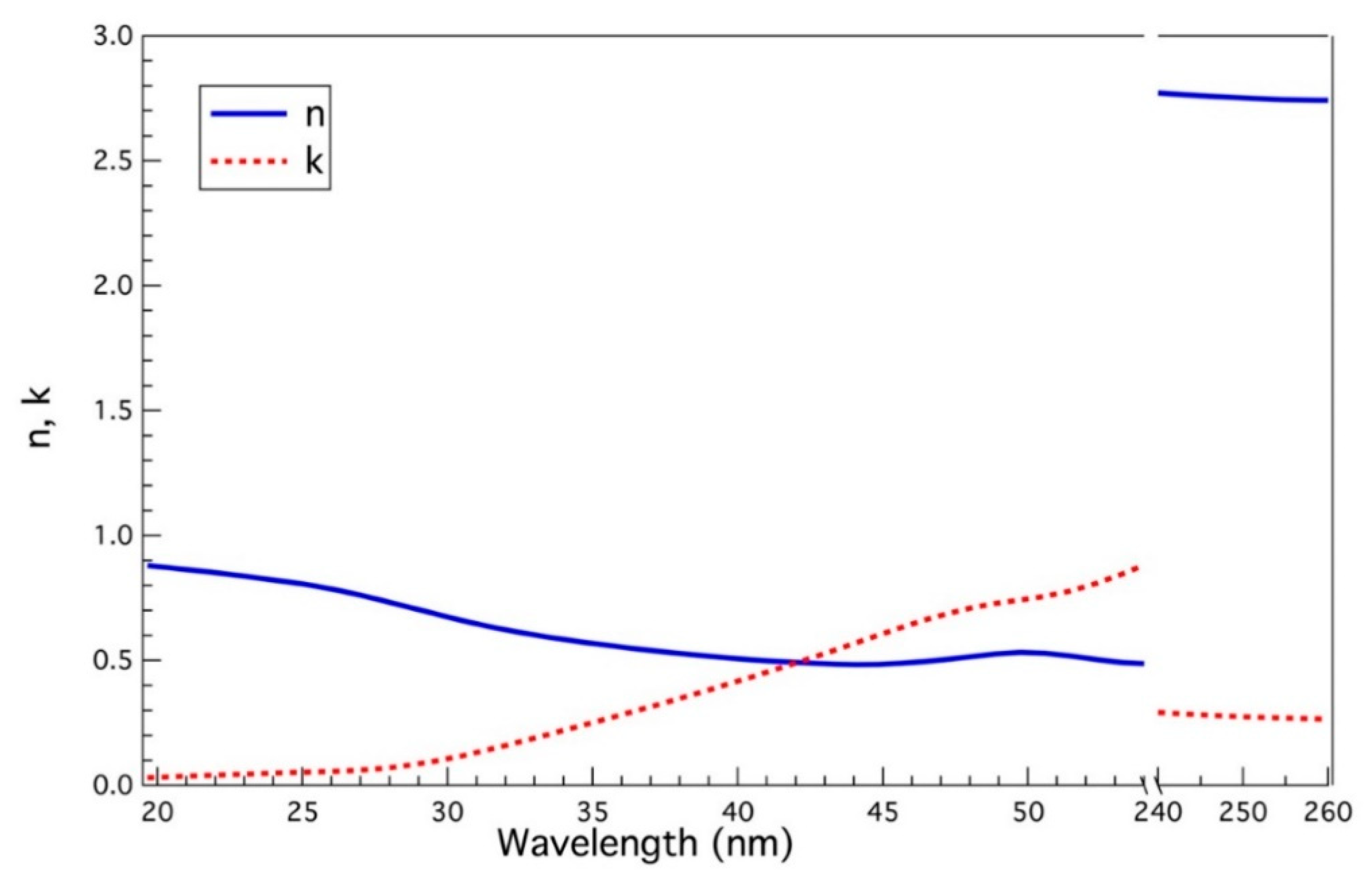
2. Results
3. Discussion
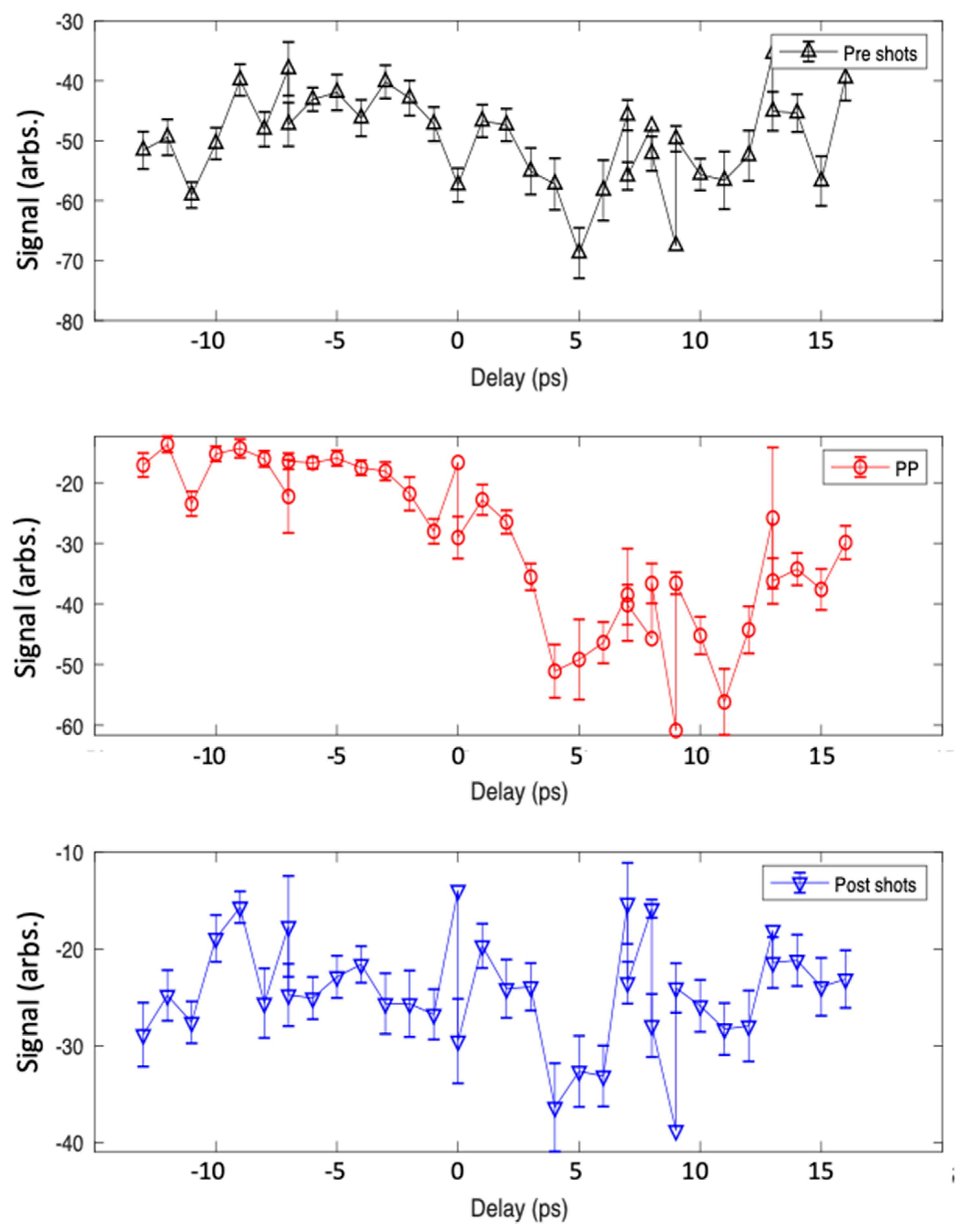
4. Materials and Methods
- (i)
- Three FEL pulses well before the arrival (unpumped reflectivity);
- (ii)
- One value followed very shortly after the pump pulse (pump-probe);
- (iii)
- One value 100 ms after the pump pulse (post damage reflectivity).
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| FEL | Free electron laser |
| FWHM | Full-width-half-maximum |
| EUV | Extreme ultraviolet |
| a-C | Amorphous carbon |
References
- Bonse, J.; Wiggins, S.M.; Solis, J. Ultrafast phase transitions after femtosecond laser irradiation of indium phosphide. J. Appl. Phys. 2004, 96, 2628–2631. [Google Scholar] [CrossRef]
- Suess, R.J.; Bingham, N.S.; Charipar, K.M.; Kim, H.; Mathews, S.A.; Piqué, A.; Charipar, N.A. Ultrafast Phase Transition Dynamics in Strained Vanadium Dioxide Films. Adv. Mater. Interfaces 2017, 4, 1700810. [Google Scholar] [CrossRef]
- Mo, M.; Murphy, S.; Chen, Z.; Fossati, P.; Li, R.; Wang, Y.; Wang, X.; Glenzer, S. Visualization of ultrafast melting initiated from radiation-driven defects in solids. Sci. Adv. 2019, 5, eaaw0392. [Google Scholar] [CrossRef] [PubMed]
- Koenig, M.; Benuzzi-Mounaix, A.; Ravasio, A.; Vinci, T.; Ozaki, N.; Lepape, S.; Batani, D.; Huser, G.; Hall, T.; Hicks, D.; et al. Progress in the study of warm dense matter. Plasma Phys. Control. Fusion 2005, 47, B441–B449. [Google Scholar] [CrossRef]
- Vinko, S.M.; Ciricosta, O.; Cho, B.I.; Engelhorn, K.; Chung, H.-K.; Brown, C.R.D.; Burian, T.; Chalupský, J.; Falcone, R.W.; Graves, C.; et al. Creation and diagnosis of a solid-density plasma with an X-ray free-electron laser. Nature 2012, 482, 59–62. [Google Scholar] [CrossRef] [PubMed]
- Hull, C.J.; Raj, S.L.; Saykally, R.J. The Liquid State of Carbon. Chem. Phys. Lett. 2020, 749, 137341. [Google Scholar] [CrossRef]
- Hau-Riege, S.P.; Boutet, S.; Barty, A.; Bajt, S.; Bogan, M.J.; Frank, M.; Andreasson, J.; Iwan, B.; Seibert, M.M.; Hajdu, J.; et al. Sacrificial Tamper Slows Down Sample Explosion in FLASH Diffraction Experiments. Phys. Rev. Lett. 2010, 104, 064801. [Google Scholar] [CrossRef]
- Savvatimskiy, A.I. Measurements of the melting point of graphite and the properties of liquid carbon (a review for 1963–2003). Carbon 2005, 43, 1115–1142. [Google Scholar] [CrossRef]
- Whitley, H.D.; Sanchez, D.M.; Hamel, S.; Correa, A.A.; Benedict, L.X. Molecular Dynamics Simulations of Warm Dense Carbon. Contrib. Plasma Phys. 2015, 55, 390–398. [Google Scholar] [CrossRef]
- Johnson, S.L.; Heimann, P.A.; MacPhee, A.G.; Lindenberg, A.M.; Monteiro, O.R.; Chang, Z.; Lee, R.W.; Falcone, R.W. Bonding in Liquid Carbon Studied by Time-Resolved X-Ray Absorption Spectroscopy. Phys. Rev. Lett. 2005, 94, 057407. [Google Scholar] [CrossRef]
- Lomba, E.; López-Martín, J.L.; Anta, J.A.; Hoye, J.S.; Kahl, G. A theoretical approach to the tight-binding band structure of liquid carbon and silicon beyond linear approximations. J. Chem. Phys. 1997, 106, 10238–10247. [Google Scholar] [CrossRef]
- Brown, C.R.D.; Gericke, D.O.; Cammarata, M.; Cho, B.I.; Döppner, T.; Engelhorn, K.; Förster, E.; Fortmann, C.; Fritz, D.; Galtier, E.; et al. Evidence for a glassy state in strongly driven carbon. Sci. Rep. 2014, 4, 5214. [Google Scholar] [CrossRef] [PubMed]
- Bundy, F.P. Pressure-temperature phase diagram of elemental carbon. Phys. A Stat. Mech. Its Appl. 1989, 156, 169–178. [Google Scholar] [CrossRef]
- Reitze, D.H.; Ahn, H.; Downer, M.C. Optical properties of liquid carbon measured by femtosecond spectroscopy. Phys. Rev. B 1992, 45, 2677–2693. [Google Scholar] [CrossRef]
- Shin, T.; Teitelbaum, S.W.; Wolfson, J.; Kandyla, M.; Nelson, K.A. Extended two-temperature model for ultrafast thermal response of band gap materials upon impulsive optical excitation. J. Chem. Phys. 2015, 143, 194705. [Google Scholar] [CrossRef]
- Rämer, A.; Osmani, O.; Rethfeld, B. Laser damage in silicon: Energy absorption, relaxation, and transport. J. Appl. Phys. 2014, 116, 053508. [Google Scholar] [CrossRef]
- Fedosejevs, R.; Ottmann, R.; Sigel, R.; Kühnle, G.; Szatmari, S.; Schäfer, F.P. Absorption of femtosecond laser pulses in high-density plasma. Phys. Rev. Lett. 1990, 64, 1250–1253. [Google Scholar] [CrossRef]
- Milchberg, H.M.; Freeman, R.R. Light absorption in ultrashort scale length plasmas. J. Opt. Soc. Am. BJosab 1989, 6, 1351–1355. [Google Scholar] [CrossRef]
- Masciovecchio, C.; Battistoni, A.; Giangrisostomi, E.; Bencivenga, F.; Principi, E.; Mincigrucci, R.; Cucini, R.; Gessini, A.; D’Amico, F.; Borghes, R.; et al. EIS: The scattering beamline at FERMI. J. Synchrotron Radiat. 2015, 22, 553–564. [Google Scholar] [CrossRef]
- Danailov, M.B.; Bencivenga, F.; Capotondi, F.; Casolari, F.; Cinquegrana, P.; Demidovich, A.; Giangrisostomi, E.; Kiskinova, M.P.; Kurdi, G.; Manfredda, M.; et al. Towards jitter-free pump-probe measurements at seeded free electron laser facilities. Opt. Express 2014, 22, 12869–12879. [Google Scholar] [CrossRef]
- Allaria, E.; Diviacco, B.; Callegari, C.; Finetti, P.; Mahieu, B.; Viefhaus, J.; Zangrando, M.; De Ninno, G.; Lambert, G.; Ferrari, E.; et al. Control of the Polarization of a Vacuum-Ultraviolet, High-Gain, Free-Electron Laser. Phys. Rev. X 2014, 4, 041040. [Google Scholar] [CrossRef]
- Mincigrucci, R.; Principi, E.; Bencivenga, F.; Foglia, L.; Gessini, A.; Kurdi, G.; Simoncig, A.; Masciovecchio, C. Transient EUV Reflectivity Measurements of Carbon upon Ultrafast Laser Heating. Photonics 2017, 4, 23. [Google Scholar] [CrossRef]
- Tobey, R.I.; Siemens, M.E.; Cohen, O.; Li, Q.; Murnane, M.M.; Kapteyn, H.C.; Nelson, K.A. Ultrafast Extreme Ultraviolet Holography: Dynamic Monitoring of Surface Deformation. In Proceedings of the Ultrafast Phenomena XV; Corkum, P., Jonas, D.M., Miller, R.J.D., Weiner, A.M., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 42–44. [Google Scholar]
- Meitzner, J.; Moore, F.G.; Tillotson, B.M.; Kevan, S.D.; Richmond, G.L. Time-resolved measurement of free carrier absorption, diffusivity, and internal quantum efficiency in silicon. Appl. Phys. Lett. 2013, 103, 092101. [Google Scholar] [CrossRef]
- Zel’dovič, J.B.; Rajzer, J.P.; Hayes, W.D. Physics of Shock Waves and High-Temperature Hydrodynamic Phenomena; Unabridged, unaltered republ. in 1 vol. of the 2-vol. work orig. publ. in Engl. in 1966 and 1967 by Acad. Press, New York. With new pref.; Dover Publ.: Mineola, NY, USA, 2002; ISBN 978-0-486-42002-8. [Google Scholar]
- Silva, S.R.P. Properties of Amorphous Carbon; The Institution of Engineering and Technology: London, UK, 2008; ISBN 978-0-86341-777-1. [Google Scholar]
- Larruquert, J.I.; Marcos, L.V.R.; Méndez, J.A.; Martin, P.J.; Bendavid, A. High reflectance ta-C coatings in the extreme ultraviolet. Opt. Express 2013, 21, 27537–27549. [Google Scholar] [CrossRef]
- Kuzmenko, A.B. Kramers–Kronig constrained variational analysis of optical spectra. Rev. Sci. Instrum. 2005, 76, 083108. [Google Scholar] [CrossRef]
- Mincigrucci, R.; Giangrisostomi, E.; Principi, E.; Battistoni, A.; Bencivenga, F.; Cucini, R.; Gessini, A.; Izzo, M.; Masciovecchio, C. Liquid Carbon Reflectivity at 19 nm. Photonics 2015, 2, 50–56. [Google Scholar] [CrossRef]
- Roussel, E.; Allaria, E.; Callegari, C.; Coreno, M.; Cucini, R.; Mitri, S.D.; Diviacco, B.; Ferrari, E.; Finetti, P.; Gauthier, D.; et al. Polarization Characterization of Soft X-Ray Radiation at FERMI FEL-2. Photonics 2017, 4, 29. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raj, S.L.; Devlin, S.W.; Mincigrucci, R.; Schwartz, C.P.; Principi, E.; Bencivenga, F.; Foglia, L.; Gessini, A.; Simoncig, A.; Kurdi, G.; et al. Free Electron Laser Measurement of Liquid Carbon Reflectivity in the Extreme Ultraviolet. Photonics 2020, 7, 35. https://doi.org/10.3390/photonics7020035
Raj SL, Devlin SW, Mincigrucci R, Schwartz CP, Principi E, Bencivenga F, Foglia L, Gessini A, Simoncig A, Kurdi G, et al. Free Electron Laser Measurement of Liquid Carbon Reflectivity in the Extreme Ultraviolet. Photonics. 2020; 7(2):35. https://doi.org/10.3390/photonics7020035
Chicago/Turabian StyleRaj, Sumana L., Shane W. Devlin, Riccardo Mincigrucci, Craig P. Schwartz, Emiliano Principi, Filippo Bencivenga, Laura Foglia, Alessandro Gessini, Alberto Simoncig, Gabor Kurdi, and et al. 2020. "Free Electron Laser Measurement of Liquid Carbon Reflectivity in the Extreme Ultraviolet" Photonics 7, no. 2: 35. https://doi.org/10.3390/photonics7020035
APA StyleRaj, S. L., Devlin, S. W., Mincigrucci, R., Schwartz, C. P., Principi, E., Bencivenga, F., Foglia, L., Gessini, A., Simoncig, A., Kurdi, G., Masciovecchio, C., & Saykally, R. J. (2020). Free Electron Laser Measurement of Liquid Carbon Reflectivity in the Extreme Ultraviolet. Photonics, 7(2), 35. https://doi.org/10.3390/photonics7020035






