Wave Front Tuning of Coupled Hyperbolic Surface Waves on Anisotropic Interfaces
Abstract
1. Introduction
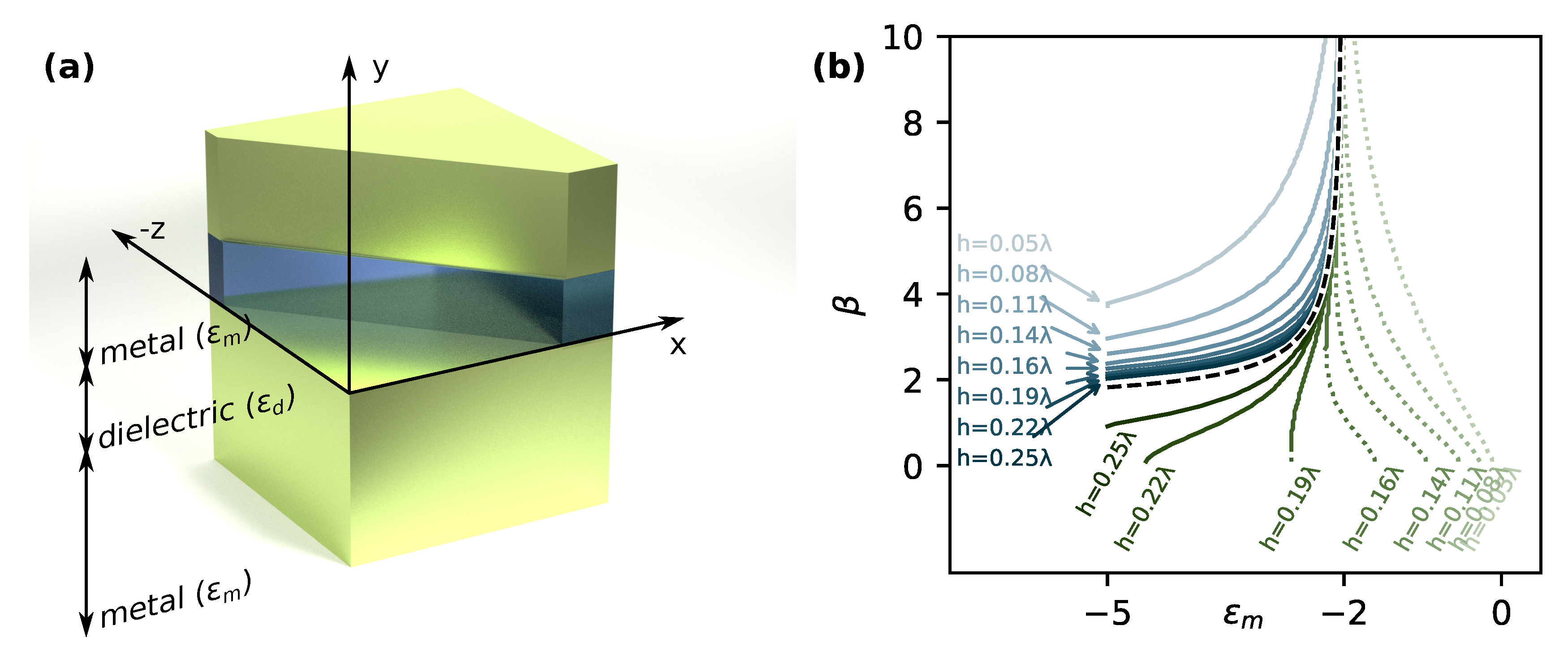
2. Symmetric Isotropic System (Metal-Dielectric-Metal)
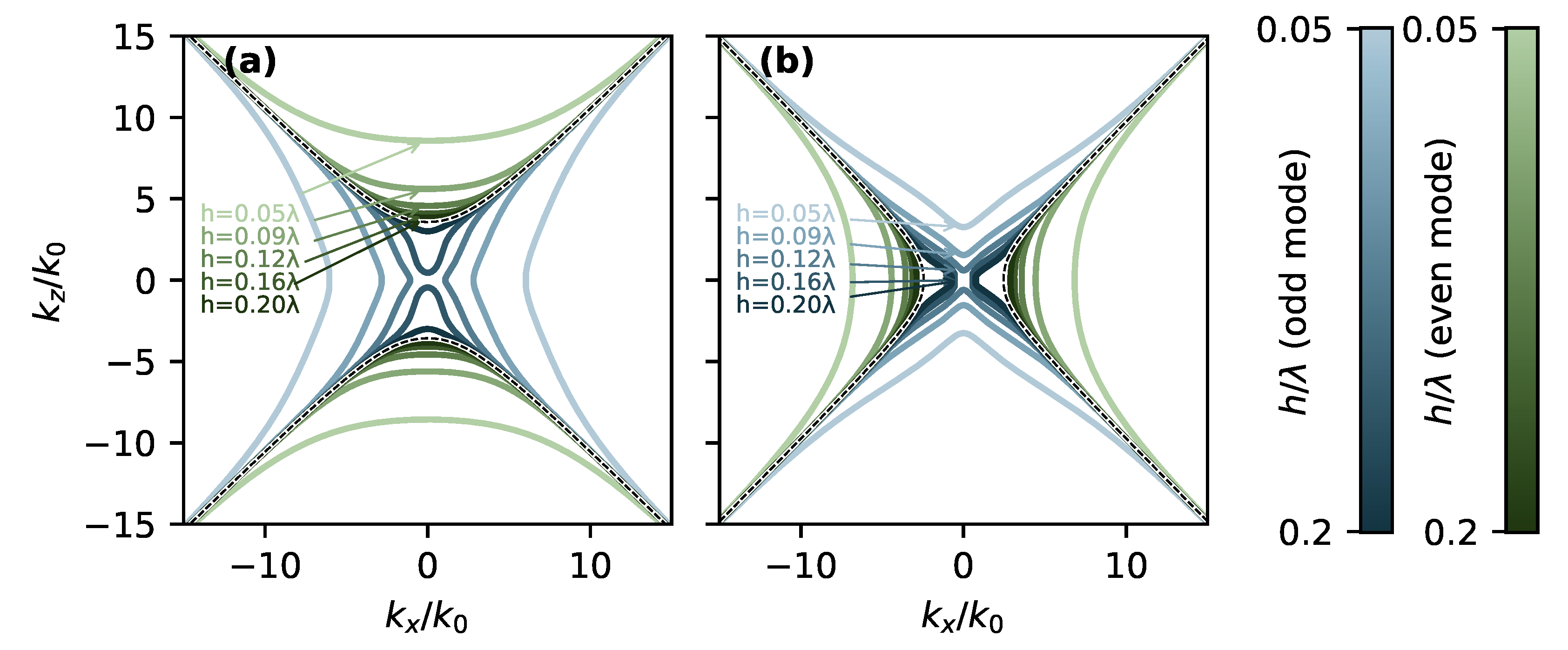
3. Symmetric Anisotropic System (Uniaxial Metal-Isotropic Dielectric-Uniaxial Metal)
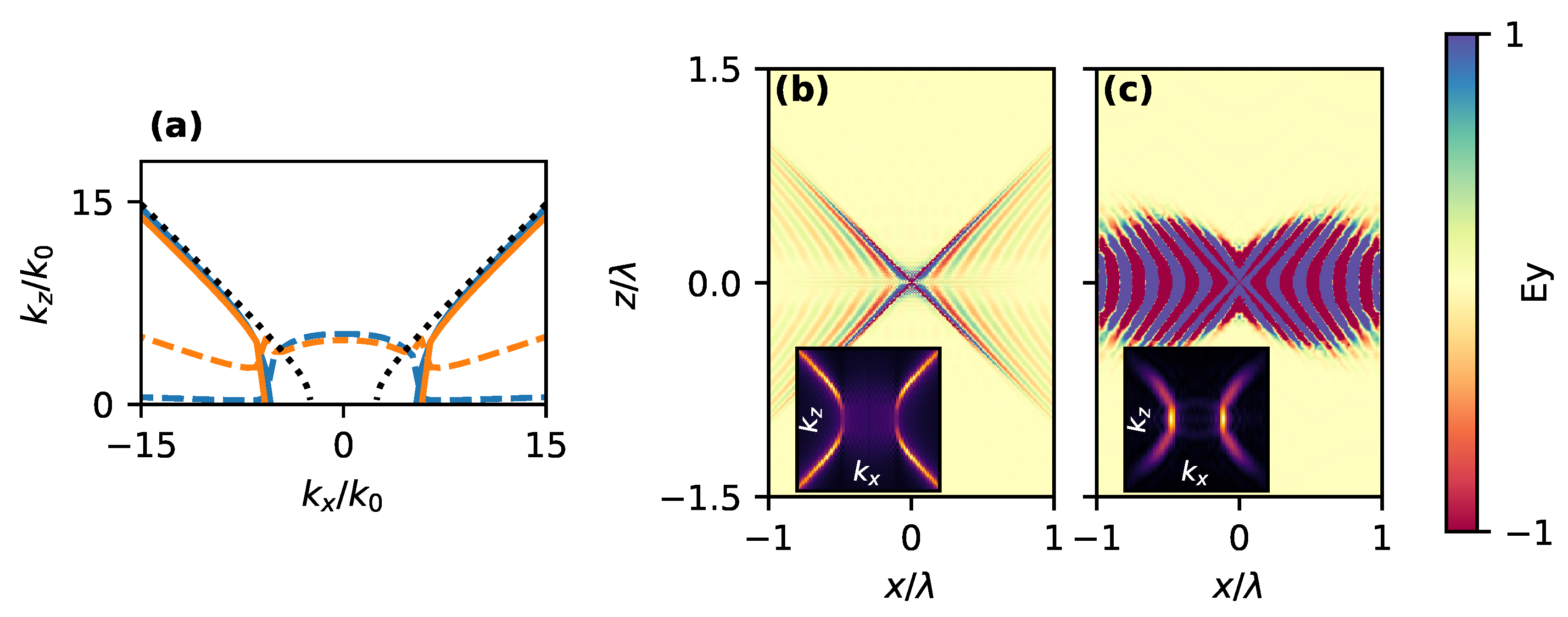
4. Asymmetric Anisotropic System (Uniaxial Metal-Isotropic Dielectric-Isotropic Metal)
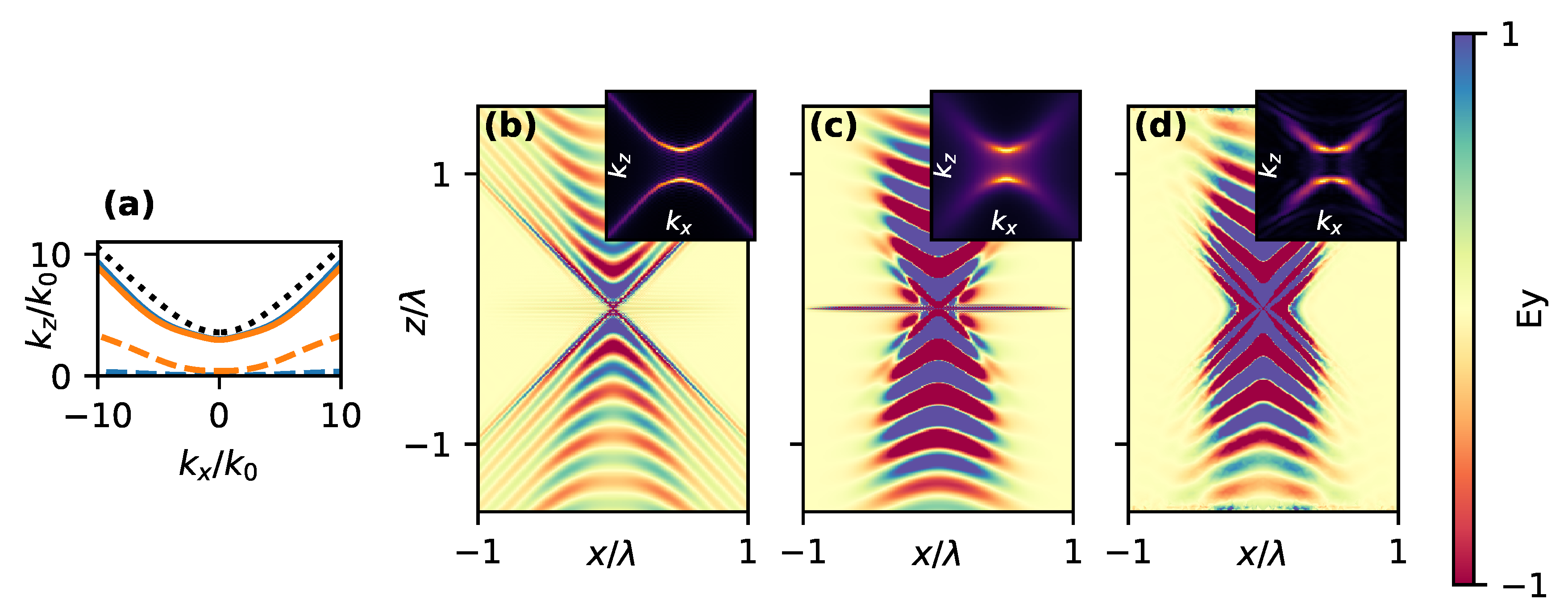
5. Wave Front Tuning of Hyperbolic Surface Waves on Anisotropic Interfaces
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| HSW | Hyperbolic Surface Wave |
| HMM | Hyperbolic Metamaterial |
| TE | Transverse Electric |
| TM | Transverse Magnetic |
References
- Polo, J.; Lakhtakia, A. Surface electromagnetic waves: A review. Laser Photonics Rev. 2011, 5, 234–246. [Google Scholar] [CrossRef]
- Takayama, O.; Bogdanov, A.A.; Lavrinenko, A.V. Photonic surface waves on metamaterial interfaces. J. Phys. Condens. Matter 2017, 29, 463001. [Google Scholar] [CrossRef]
- Barnes, W.L.; Dereux, A.; Ebbesen, T.W. Surface plasmon subwavelength optics. Nature 2003, 424, 824–830. [Google Scholar] [CrossRef] [PubMed]
- Maier, S. Plasmonics: Fundamentals and Applications; Springer: New York, NY, USA, 2007. [Google Scholar]
- Han, Z.; Bozhevolnyi, S.I. Radiation guiding with surface plasmon polaritons. Rep. Prog. Phys. 2012, 76, 016402. [Google Scholar] [CrossRef] [PubMed]
- Yeh, P.; Yariv, A.; Cho, A.Y. Optical surface waves in periodic layered media. Appl. Phys. Lett. 1978, 1978 32, 104–105. [Google Scholar] [CrossRef]
- Liscidini, M.; Sipe, J.E. Analysis of Bloch-surface-wave assisted diffraction-based biosensors. J. Opt. Soc. Am. B 2009, 26, 279–289. [Google Scholar] [CrossRef]
- Descrovi, E.; Sfez, T.; Quaglio, M.; Brunazzo, B.; Dominici, L.; Michelotti, F.; Herzig, H.P.; Martin, O.J.F.; Giorgis, F. Bloch surface waves on ultrathin polymeric ridges. Nano Lett. 2010, 10, 2087–2091. [Google Scholar] [CrossRef]
- Sinibaldi, A.; Danz, N.; Descrovi, E.; Munzert, P.; Schulz, U.; Sonntag, F.; Dominici, L.; Michelotti, F. Direct comparison of the performance of Bloch surface wave and surface plasmon polariton sensors. Sens. Actuators B Chem. 2012, 174, 292–298. [Google Scholar] [CrossRef]
- Yu, L.; Barakat, E.; Sfez, T.; Hvozdara, L.; Francesco, J.D.; Herzig, H.P. Manipulating Bloch surface waves in 2D: A platform concept-based flat lens. Light. Sci. Appl. 2014, 3, e124. [Google Scholar] [CrossRef]
- Dyakonov, M. New type of electromagnetic wave propagating at an interface. Sov. Phys. JETP 1988, 67, 714–716. [Google Scholar]
- Takayama, O.; Crasovan, L.-C.; Johansen, S.K.; Mihalache, D.; Artigas, D.; Torner, L. Dyakonov surface waves: A review. Electromagnetics 2008, 28, 126–145. [Google Scholar] [CrossRef]
- Takayama, O.; Crasovan, L.; Artigas, D.; Torner, L. Observation of Dyakonov surface waves. Phys. Rev. Lett. 2009, 102, 043903. [Google Scholar] [CrossRef] [PubMed]
- Takayama, O.; Nikitin, A.Y.; Martin-Moreno, L.; Torner, L.; Artigas, D. Dyakonov surface wave resonant transmission. Opt. Express 2011, 19, 6339–6347. [Google Scholar] [CrossRef] [PubMed]
- Takayama, O.; Artigas, D.; Torner, L. Coupling plasmons and dyakonons. Opt. Lett. 2012, 37, 1983–1985. [Google Scholar] [CrossRef] [PubMed]
- Takayama, O.; Artigas, D.; Torner, L. Practical dyakonons. Opt. Lett. 2012, 37, 4311–4313. [Google Scholar] [CrossRef] [PubMed]
- Takayama, O.; Artigas, D.; Torner, L. Lossless directional guiding of light in dielectric nanosheets using Dyakonov surface waves. Nat. Nanotechnol. 2014, 9, 419–424. [Google Scholar] [CrossRef]
- Crasovan, L.-C.; Takayama, O.; Artigas, D.; Johansen, S.K.; Mihalache, D.; Torner, L. Enhanced localization of Dyakonov-like surface waves in left-handed materials. Phys. Rev. B 2006, 74, 155120. [Google Scholar] [CrossRef]
- Gao, J.; Lakhtakia, A.; Lei, M. On Dyakonov-Tamm waves localized to a central twist defect in a structurally chiral material. J. Opt. Soc. Am. B 2009, 26, 1615–1621. [Google Scholar] [CrossRef]
- Pulsifer, D.P.; Faryad, M.; Lakhtakia, A. Observation of the Dyakonov-Tamm wave. Phys. Rev. Lett. 2013, 111, 243902. [Google Scholar] [CrossRef]
- Pulsifer, D.P.; Faryad, M.; Lakhtakia, A.; Hall, A.S.; Liu, L. Experimental excitation of the Dyakonov–Tamm wave in the grating-coupled configuration. Opt. Lett. 2014, 39, 2125–2128. [Google Scholar] [CrossRef]
- Abbas, F.; Lakhtakia, A.; Naqvi, Q.A.; Faryad, M. An optical-sensing modality that exploits Dyakonov–Tamm waves. Photon. Res. 2015, 3, 5–8. [Google Scholar] [CrossRef]
- Mackay, T.G.; Zhou, C.; Lakhtakia, A. Dyakonov–Voigt surface waves. Proc. R. Soc. A 2019, 475, 20190317. [Google Scholar] [CrossRef] [PubMed]
- Jacob, Z.; Narimanov, E.E. Optical hyperspace for plasmons: Dyakonov states in metamaterials. Appl. Phys. Lett. 2008, 93, 221109. [Google Scholar] [CrossRef]
- Repän, T.; Takayama, O.; Lavrinenko, L.V. Hyperbolic surface waves on anisotropic materials without hyperbolic dispersion. Opt. Express 2020. submitted. [Google Scholar]
- Smith, D.R.; Schurig, D. Electromagnetic Wave Propagation in Media with Indefinite Permittivity and Permeability Tensors. Phys. Rev. Lett. 2003, 90, 077405. [Google Scholar] [CrossRef]
- Krishnamoorthy, H.N.S.; Jacob, Z.; Narimanov, E.; Kretzschmar, I.; Menon, V.M. Topological transitions in metamaterials. Science 2012, 336, 205–209. [Google Scholar] [CrossRef]
- Cortes, C.L.; Newman, W.; Molesky, S.; Jacob, Z. Quantum nanophotonics using hyperbolic metamaterials. J. Opt. 2012, 14, 063001. [Google Scholar] [CrossRef]
- Drachev, V.P.; Podolskiy, V.A.; Kildishev, A.V. Hyperbolic metamaterials: New physics behind a classical problem. Opt. Express 2013, 21, 15048–15064. [Google Scholar] [CrossRef]
- Poddubny, A.; Iorsh, I.; Belov, P.; Kivshar, Y. Hyperbolic metamaterials. Nat. Photonics 2013, 7, 948–957. [Google Scholar] [CrossRef]
- Shekhar, P.; Atkinson, J.; Jacob, Z. Hyperbolic metamaterials: Fundamentals and applications. Nano Converg. 2014, 1, 14. [Google Scholar] [CrossRef]
- Ferrari, L.; Wu, C.; Lepage, D.; Zhang, X.; Liu, Z. Hyperbolic metamaterials and their applications. Prog. Quantum Electron. 2015, 40, 1–40. [Google Scholar] [CrossRef]
- Takayama, O.; Lavrinenko, A.V. Optics with hyperbolic materials [Invited]. J. Opt. Soc. Am. B 2019, 36, F38–F48. [Google Scholar] [CrossRef]
- Kildishev, A.V.; Boltasseva, A.; Shalaev, V.M. Planar photonics with metasurfaces. Science 2013, 339, 1232009. [Google Scholar] [CrossRef] [PubMed]
- Kapitanova, P.V.; Ginzburg, P.; Rodríguez-Fortuño, F.J.; Filonov, D.S.; Voroshilov, P.M.; Belov, P.A.; Poddubny, A.N.; Kivshar, Y.S.; Wurtz, G.A.; Zayats, A.V. Photonic spin Hall effect in hyperbolic metamaterials for polarization-controlled routing of subwavelength modes. Nat. Commun. 2014, 5, 3226. [Google Scholar] [CrossRef] [PubMed]
- High, A.A.; Devlin, R.C.; Dibos, A.; Polking, M.; Wild, D.S.; Perczel, J.; de Leon, N.P.; Lukin, M.D.; Park, H. Visible-frequency hyperbolic metasurface. Nature 2015, 522, 192–196. [Google Scholar] [CrossRef] [PubMed]
- Takayama, O.; Shkondin, E.; Bodganov, A.; Panah, M.E.A.; Golenitskii, K.; Dmitriev, P.; Repän, T.; Malureanu, R.; Belov, P.; Jensen, F.; et al. Mid-infrared surface waves on a high aspect ratio nanotrench platform. ACS Photon. 2017, 4, 2899–2907. [Google Scholar] [CrossRef]
- Takayama, O.; Dmitriev, P.; Shkondin, E.; Yermakov, O.; Panah, M.; Golenitskii, K.; Jensen, F.; Bogdanov, A.; Lavrinenko, A. Experimental observation of Dyakonov plasmons in the mid-infrared. Semiconductors 2018, 52, 442–446. [Google Scholar] [CrossRef]
- Li, P.; Dolado, I.; Alfaro-Mozaz, F.J.; Casanova, F.; Hueso, L.E.; Liu, S.; Edgar, J.H.; Nikitin, A.Y.; Vélez, S.; Hillenbrand, R. Infrared hyperbolic metasurface based on nanostructured van der Waals materials. Science 2018, 359, 892–896. [Google Scholar] [CrossRef]
- Ma, W.; Alonso-González, P.; Li, S.; Nikitin, A.Y.; Yuan, J.; Martín-Sánchez, J.; Taboada-Gutiérrez, J.; Amenabar, I.; Li, P.; Vélez, S.; et al. In-plane anisotropic and ultra-low-loss polaritons in a natural van der Waals crystal. Nature 2018, 562, 557–562. [Google Scholar] [CrossRef]
- Shin, H.; Fan, S. All-angle negative refraction for surface plasmon waves using a metal-dielectric-metal structure. Phys. Rev. Lett. 2006, 96, 073907. [Google Scholar] [CrossRef]
- Sarid, D. Modern Introduction to Surface Plasmons: Theory, Mathematica Modeling, and Applications; Cambridge University Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Chen, C.-L. Foundations for Guided-Wave Optics; Wiley-Interscience: Hoboken, NJ, USA, 2007. [Google Scholar]
- Malitson, I.H. A redetermination of some optical properties of calcium fluoride. Appl. Opt. 1963, 2, 1103–1107. [Google Scholar] [CrossRef]
- Rodríguez-de Marcos, L.V.; Larruquert, J.I.; Méndez, J.A.; Aznárez, J.A. Self-consistent optical constants of MgF2, LaF3, and CeF3 films. Opt. Mater. Express 2017, 7, 989–1006. [Google Scholar] [CrossRef]
- Repän, T.; Novitsky, A.; Willatzen, M.; Lavrinenko, A.V. Pseudocanalization regime for magnetic dark-field hyperlenses. Phys. Rev. B 2017, 96, 195166. [Google Scholar] [CrossRef]
- Gomez-Diaz, J.S.; Tymchenko, M.; Alu, A. Hyperbolic plasmons and topological transitions over uniaxial metasurfaces. Phys. Rev. Lett. 2015, 114, 233901. [Google Scholar] [CrossRef]
- Yermakov, O.Y.; Ovcharenko, A.I.; Song, M.; Bogdanov, A.A.; Iorsh, I.V.; Kivshar, Y.S. Hybrid waves localized at hyperbolic metasurfaces. Phys. Rev. B 2015, 91, 235423. [Google Scholar] [CrossRef]
- Samusev, A.; Mukhin, I.; Malureanu, R.; Takayama, O.; Permyakov, D.V.; Sinev, I.V.; Baranov, D.; Yermakov, O.; Iorsh, I.V.; Bogdanov, A.A.; et al. Polarization-resolved characterization of plasmon waves supported by an anisotropic metasurface. Opt. Express 2017, 26, 32631–32639. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Repän, T.; Takayama, O.; Lavrinenko, A.V. Wave Front Tuning of Coupled Hyperbolic Surface Waves on Anisotropic Interfaces. Photonics 2020, 7, 34. https://doi.org/10.3390/photonics7020034
Repän T, Takayama O, Lavrinenko AV. Wave Front Tuning of Coupled Hyperbolic Surface Waves on Anisotropic Interfaces. Photonics. 2020; 7(2):34. https://doi.org/10.3390/photonics7020034
Chicago/Turabian StyleRepän, Taavi, Osamu Takayama, and Andrei V. Lavrinenko. 2020. "Wave Front Tuning of Coupled Hyperbolic Surface Waves on Anisotropic Interfaces" Photonics 7, no. 2: 34. https://doi.org/10.3390/photonics7020034
APA StyleRepän, T., Takayama, O., & Lavrinenko, A. V. (2020). Wave Front Tuning of Coupled Hyperbolic Surface Waves on Anisotropic Interfaces. Photonics, 7(2), 34. https://doi.org/10.3390/photonics7020034





