Abstract
A photonic surface wave, a propagating optical mode localized at the interface of two media, can play a significant role in controlling the flow of light at nanoscale. Among various types of such waves, surface waves with hyperbolic dispersion or simply hyperbolic surface waves supported on anisotropic metal interfaces can be exploited to effectively control the propagation of lightwaves. We used semi-analytical and numerical methods to study the nature of surface waves on several configurations of three-layers metal–dielectric–metal systems including isotropic and anisotropic cases where the metal cladding layers were assumed to have infinite thickness. We used semi-analytical and numerical approaches to study the phenomena. We showed that the propagation of surface wave can be tuned from diverging to converging in the plane of the interface by the combination of metals with different anisotropic properties.
1. Introduction
A photonic surface wave or surface electromagnetic wave is a propagating electromagnetic mode localized at the interface of two dissimilar media. Its electromagnetic fields decay exponentially away from the boundary [1,2]. Surface waves supported on various interfaces have been investigated having among others traditional surface plasmon polaritons [3,4,5], Bloch surface waves on periodic boundaries and Tamm states on terminated dielectric photonic crystals faces [6,7,8,9,10]. One peculiar property of surface waves supported on interfaces of anisotropic media enabling us to control the flow of light is directionality of their propagation [2]. In the case of dielectric anisotropic media whose permittivity tensor components are all positive, Dyakonov surface waves are supported [11,12,13,14,15,16,17], as well as other variations including the ones on left-handed materials [18], Dyakonov-Tamm surface waves [19,20,21,22], and Dyakonov-Voigt surface waves [23]. When one or all of permittivity tensor components are negative, surface wave with hyperbolic dispersion, so-called Dyakonov plasmons [24] or hyperbolic surface waves (HSWs) [25], can be supported. Hyperbolic metamaterials (HMMs) with negative and positive permittivity tensor components [26,27,28,29,30,31,32,33] support directional surface waves [34,35,36,37,38,39,40]. In the case of anisotropic metal, when all permittivity tensor components are negative, there exist hyperbolic surface waves, as well [25]. Controlling the propagation of light on the surface is the hallmark of surface wave, opening up new ways for manipulating light at nanoscale, such as, enabling directional quantum emitters [24,34], or steering of optical signals [17,36].
Here, we show that propagation direction of surface waves can be tuned by three layers system composed of different anisotropic layers. Motivation for use of a three-layer system comes from Shin and Fan [41], where they discussed negative refraction of surface waves using a three-layer system. First, we start with a structure composed of isotropic metal and dielectric layers. Then, we study a symmetric metal–isotropic dielectric– metal structure with identical uniaxial metal layers. To the best of our knowledge, such metal-dielectric-metal system with uniaxial metal layers is considered for the first time. Tuning of dispersion of surface waves by two cladding uniaxial metal layers is a novel way of controlling light propagation. Note that through out the article, the uniaxial media have their optical axes in the plane of interface. Furthermore, we study asymmetric metal–isotropic dielectric– metal structures where uniaxial metal layers differ from each other in order to tune the hyperbolic dispersion of surface waves. Finally, we combine two different three layer systems in series in order to impose possible tuning of the wave front of surface waves.
2. Symmetric Isotropic System (Metal-Dielectric-Metal)
We first look onto symmetric three layer system Figure 1a, consisting of two semi-infinite metallic layers (), separated by a dielectric layer () with thickness h. For the analysis, we assume purely real (lossless) material parameters, but in numerical simulations we consider lossy media. There is no analytic explicit formula for modes dispersion in this three-layer system [4,42,43]. However, at least for this case we can derive an implicit equation for the guided modes.
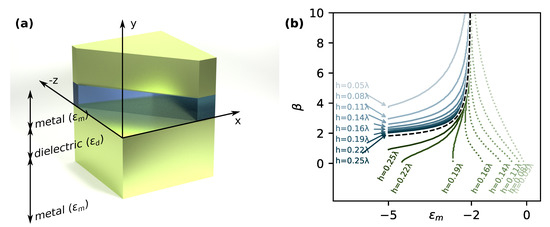
Figure 1.
(a) Geometry for isotropic three-layer system under consideration, metal-dielectric-metal layers. A dielectric (spacer) layer with thickness, h, is sandwiched between two metal layers. (b) Propagation constant of modes, in three-layer system for various spacer layer thicknesses, h. Blue lines indicate even modes, while green solid (dotted) lines indicate odd modes with normal (reversed) phase propagation direction.
As this is an isotropic system, we can limit the analysis to TM modes only, as TE modes do not support surface modes [4]. We assume a plane wave solution
where . We then use the interface conditions to reach the implicit dispersion relation
where are corresponding y-components of the wave vectors in media 1 and 2 assuming propagation constant
The system can support two modes, depending on the sign chosen in Equation (2). We shall refer to these modes as odd (−) and even (+) modes, indicating parity of the fields. Note that in case of we recover solution for the single interface: [4]
We solve numerically Equation (2) and plot the solutions for various spacer (isotropic dielectric layer) thicknesses h in Figure 1b. First we note that as h is increased both even and odd solutions converge towards the solution of a single interface (Equation (3)), as expected. Second thing to consider is that the even mode is always above the single interface solution, whereas the odd mode is below. As larger for the same frequency implies larger , this means that the fields on the two interfaces are stronger coupled for the odd mode. Therefore, for small h the odd solution is significantly altered by coupling of the fields on the two interfaces.
Now, we need to calculate total energy flux in z-direction in order to check whether a mode given by is forward- or backward-propagation. Integrating power flux and plugging in Equation(1) reads
from which we get a straightforward expression in the bottom layer
In the dielectric spacer we have now two modes, one propagating towards , the other towards . From symmetry of the system we can fix the the amplitudes of the modes and then we get the following result of the integration
where the signs indicate even and odd modes. Adding the two contributions gives the total energy flux in z-direction. We have calculated this numerically for the modes in Figure 1b. Here the permittivity of the dielectric layer is = 2 close to that of calcium fluoride [44] and magnesium fluoride [45]. Note that odd mode is also referred to as symmetric mode and short-range surface plasmon polariton (SPP), and even mode as antisymmetric mode and long-range SPP, respectively [5].
3. Symmetric Anisotropic System (Uniaxial Metal-Isotropic Dielectric-Uniaxial Metal)
We consider a symmetric system consisting of a dielectric layer () with thickness h, which is sandwiched between two semi-infinite anisotropic layers [], instead of isotropic metallic layer as in Figure 1a. Note that the optical axes of both uniaxial anisotropic layers are parallel and lie in the plane of the interfaces along z-axis through out the article. Following results for the isotropic case we expect existence of even and odd modes in the system. Due to the amount of plane wave terms in the three layers (in total we have six terms: forward- and backwards propagating TE and TM waves in the dielectric along with ordinary and extraordinary waves in each of the anisotropic layers) we do not expect to reach an analytic expression for dispersion relation in the general case of anisotropic three-layer system. Therefore we will resort to numerical solutions to the equations.
However, there are some useful asymptotic cases that can be noted. Most importantly, we note that coupling between the two interfaces scales with . In a limit where we let , to infinity this coupling term goes to zero (as implies also ). It follows that the asymptotic behavior is identical to the HSW solution on a single interface [25]. However, in the opposite case of small , we instead are looking at the “strong coupling” limit, when dispersion deviates significantly from the one of a single interface case. This is especially true for the odd mode, which due its field profile experiences stronger coupling than the even mode.
As in the case of HSWs on a single interface [25], we can, in the same way, classify HSWs in a three layer system into type-1 and type-2 HSWs, as shown in Figure 2. For a large spacer thickness the three-layer system behaves similarly to a single interface, but for small thicknesses the behavior diverges. We show this in Figure 2, where we plot HSW dispersions for a type-1 and a type-2 system for various thicknesses. Similar to the isotropic case, the even mode is less affected by coupling of fields on the two interfaces, and therefore the even mode better resembles the corresponding single interface solution [25].
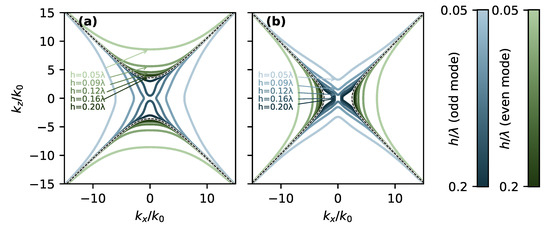
Figure 2.
Even (green) and odd modes (blue lines) in symmetric three layer system (uniaxial metal-isotropic dielectric-uniaxial metal), for various spacer (isotropic dielectric layer) thicknesses. Both (a) type-1 , and (b) type-2 , systems are shown. The black dotted line shows solution from corresponding two-layer system of uniaxial metal and isotropic dielectric interface. The black dashed line shows single-interface solution.
On the contrary, the odd mode is significantly affected by coupling, especially with decreasing spacer thickness h. Importantly, we note that in the strong coupling regime we can effectively force the type-1 HSW to look like a type-2 mode (and vice versa). A type-2 HSW on a single interface (the black dashed line in Figure 2b) is characterized by low-k cutoff: for there is no propagation allowed in z-direction. Figure 2a shows that by decreasing the spacer layer we can evolve the odd mode of type-1 such that it also exhibits the low-k cutoff, in principle behaving close to a type-2 HSW.
As we showed for the isotropic three-layer system, the even mode was identified by larger propagation constant , and thus weaker coupling between the two interfaces. Due to the weaker coupling we assume that the even mode always follows behavior of the single interface solution. This means that waves on the type-1 interface it will exhibit coinciding energy and phase propagation along the z-direction and on the type-2 interface it phase and energy propagation directions will be anti-parallel.
The odd mode, on the other hand, exhibits stronger coupling between the two interfaces. Indeed, this is the reason why phase propagation can be reversed in the isotropic case. Thus we can expect that the phase propagation direction might not follow from the single interface solution. Hence, for the cases considered here we used numerical calculations to verify that the propagation direction matches the expectation from the single interface solution.
To study wave propagation on the interfaces we use full-wave FEM simulations (using COMSOL Multiphysics) and simple semi-analytical approach based on angular spectrum representation [46]. For this calculations we Fourier transform fields into plane wave components and then propagate them using numerically calculated propagation constant . In doing this we neglect reflections and scattering from the interfaces. The full-wave simulations give complete picture of field propagation but have high computational requirements due to needing 3D geometry along with very fine mesh in the thin dielectric layer. In Figure 3 and Figure 4 we now look on the field profiles of the odd and even modes of the type-2 structure (Figure 2b, with spacer thickness ). We show both full-wave FEM simulations and semi-analytical calculations. To ensure convergence in numerical simulations we allow for weak losses materials in the calculations:
Figure 3 and Figure 4b,c show the influence of loss of the uniaxial layers on surface waves in both wavevector space and real space. With increased losses (from to ), high-k components degrade and disappear, resulting in the complete change of the surface wave propagation pattern.
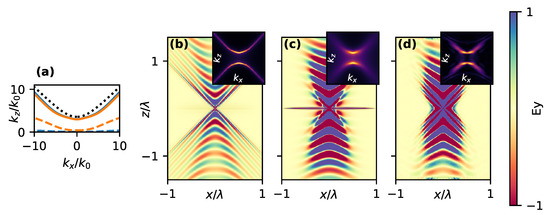
Figure 3.
(a) Real and imaginary parts of the propagation constant for the odd mode in the three layer system (details in the text) for losses (blue) and (orange). Dotted black line indicates corresponding dispersion of single interface. (b,c) Semi-analytically calculated field profiles for losses (b) and (c). (d) Full-wave simulations of the field profile for losses . Insets show Fourier transformed fields, showing dispersion of the propagating waves.
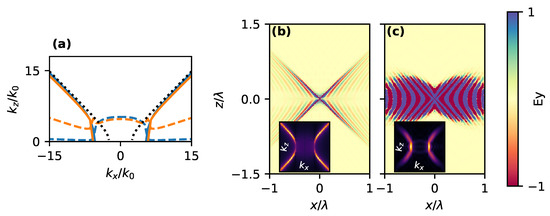
Figure 4.
(a) Real and imaginary parts of the propagation constant for the even mode in the three layer system (details in the text) for losses (blue) and (orange). The black line shows corresponding HMM dispersion. (b) Semi-analytically calculated field profiles for losses . (c) Full-wave simulations of the field profile for losses . Insets show Fourier transformed fields, showing dispersion of the propagating waves.
4. Asymmetric Anisotropic System (Uniaxial Metal-Isotropic Dielectric-Isotropic Metal)
In the previous section we showed that a symmetric anisotropic three layers system supports two HSW modes. We presented a system that produced a negative phase velocity (in comparison to a “reference” two layers system) for the odd mode. However, the system also supports an even mode, which does not produce the desired dispersion for the surface wave. In order to suppress the unwanted even mode we now consider an asymmetric three layers system. The dielectric spacer layer (with thickness ) is now sandwiched between an anisotropic medium (given by Equations (7) and (8)) and an isotropic metal with . In order to avoid any new modes we constrain to . This means that the interface between the isotropic metal and dielectric, –, does not support a surface mode on its own since the propagation constant (Equation (3)) is imaginary.
In Figure 5a, we explore effect of on dispersion of the HSW mode. We see that the asymmetric system has significantly altered dispersion in the low-k regime by flattening out the HSW dispersion. Looking at propagation of waves (Figure 5b,c) this manifests as an additional beam: we see the usual narrow high-k beams, but also a wider beam propagating straight ahead (corresponding to the flat low-k regime). This suggests that by combining anisotropic and isotropic metals in the asymmetric system, we can modify the dispersion of surface waves from conventional “hyperbolic” to other shapes. This provides another way to tune the dispersion alternative to the metasurface approaches with structured nanofilms [47,48,49]. However, this behavior is not suitable for phase compensation purposes as this structure can not achieve perfect pseudocanalization for the single anisotropic interface: phase of these low-k waves will not be properly compensated.
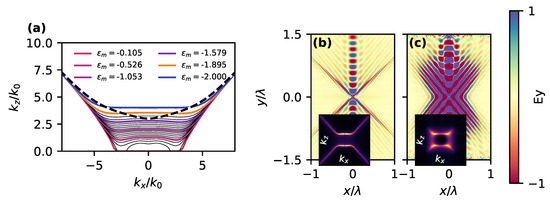
Figure 5.
(a) Propagation constant for the symmetric three layer system (dashed black line, uniaxial metal-isotropic dielectric-uniaxial metal) and for asymmetric (uniaxial metal-isotropic dielectric-isotropic metal) system, plotted for various different . Orange line indicates chosen for the simulations. (b) Semi-analytically calculated fields for low-loss () system. (c) Simulated fields as per FEM simulations with .
5. Wave Front Tuning of Hyperbolic Surface Waves on Anisotropic Interfaces
In the previous sections we covered engineering of phase propagation properties of surface waves in a three-layer system. The idea now is to combine HSWs on a single interface with a two-layer system, which is engineered to have opposite phase propagation properties. In such combined system where there is effectively no phase accumulated during propagation (so-called pseudo-canalizing operation [46]), allowing beams to propagate with minimal distortion. To achieve that we combine two media with “complementary” dispersion (see Figure 6). One part of the system is an anisotropic interface supporting HSWs, with and (indicated with (2) in Figure 6). The thickness of the dielectric layer is h = 0.1 . The phase-compensating part, with opposite phase propagation, is either realized by a symmetric three layer system (Figure 3) or an asymmetric system (Figure 5).
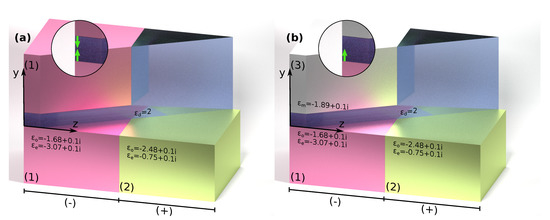
Figure 6.
Geometry for the two pseudocanalizing systems, with symmetric (a) and nonsymmetric (b) three layer system, with anisotropic media indicated by (1) and (2) and the metal for asymmetric system shown with (3). Insets indicate placement of dipole sources to excite the waves. In (a) the sources are aligned such to only excite the odd mode. (+) and (-) indicate regions with normal and reversed phase propagation, respectively.
The symmetric system offers better phase compensation, as there the surface waves resemble closely the HSWs on a single anisotropic interface. However, this approach is less practical, because we artificially suppress the unwanted even mode for better illustration of the effect. As shown in Figure 6a we excite the waves using two anti-parallel dipoles to ensure that mainly the odd mode is excited.
Another approach is to employ the asymmetric three-layer design, where only the odd-like mode exists. This comes at the cost of distorted HSW dispersion, leading to worse pseudocanalization. However, for this structure we can use a more realistic single point source without worrying about exciting any unwanted modes.
We show results of full-wave simulations of the structures in Figure 7. For comparison we included fields calculated semi-analytically as well. This approach neglects reflections from the interfaces and thus, these calculations are only included for a qualitative proof-of-concept reference. However, these calculations enable fast calculations for a low loss case, allowing showing pseudocanalizing behavior. On the other hand, for the 3D finite-element simulations finer mesh (with quickly growing computational costs) is required to resolve fine spatial features, which become present with decreasing losses. From full-wave simulations we see that reflection from the interfaces is an important aspect. For example, in ref. [41], which discusses negative phase propagation for isotropic surface waves, the authors introduced an optimized system to improve mode overlap to reduce reflections from the three-layer system.
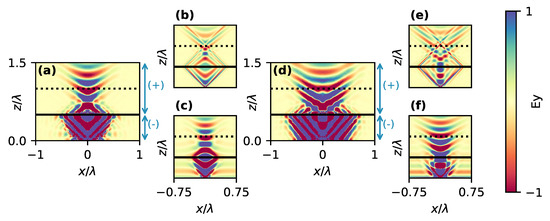
Figure 7.
Comparison of surface wave implementations of a pseudocanalizing system. Full-wave simulation results of a symmetric system are shown in (a), with corresponding semi-analytical calculations with reduced losses () in (b) and full losses () in (c). Similarly (d) shows FEM results of an asymmetric system, with corresponding semi-analytically calculated fields for in (e) and in (f). (+) and (-) indicate regions with normal and reversed phase propagation [with geometry and material parameters specified Figure 6a for (a)–(c) and Figure 6b for (d)–(f)]. The dashed line shows the distance for which waves travelled equal distance through the two regions with opposite phase propagation properties. With ideal pseudocanalization the original source fields would be restored here.
We see that the symmetric system can offer relatively good performance in the low-loss case (Figure 7b) and in case of higher losses () the performance is expectedly reduced, but nevertheless, full-wave simulations (Figure 7a) match relatively well with the simplified calculations (Figure 7c). However, for more practical case of asymmetrical design the pseudocanalization performance is degraded even for the simplified calculations (Figure 7e), while the full-wave simulations (Figure 7d) show differences with the semi-analytical calculations (Figure 7f). This is likely due to reflections from the boundary between the parts of the system, which could be reduced by optimizing overlap between the modes in the two uniaxial metal layers similar to ref. [41].
6. Conclusions
We study hyperbolic surface waves supported on three layer structures with two layers being uniaxial anisotropic metal layers. We show that such structures support modes with hyperbolic dispersion similar to hyperbolic metamaterials. By engineering the three layer structure, material anisotropy and dielectric spacer thickness, it is possible to tune the dispersion from a simple hyperbolic to more diversified ones. By combining two different three- layer systems, wave front shapes can also be controlled varying from diverging to converging, resembling the so-called pseudocanalization regime. We also carried out proof-of-concept simulations with close-to-real parameters showing that the pseudocanalization regime with hyperbolic surface waves is feasible.
Author Contributions
Conceptualization, T.R. and A.V.L.; formal analysis, T.R.; software, T.R.; investigation, T.R.; writing—original draft preparation, T.R.; writing—review and editing, O.T.; supervision, A.V.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Sihtasutus Archimedes (Kristjan Jaak scholarship), Villum Fonden DarkSILD project (11116), and Independent Research Fund Denmark, DFF Research Project 2 “PhotoHub” (8022-00387B).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| HSW | Hyperbolic Surface Wave |
| HMM | Hyperbolic Metamaterial |
| TE | Transverse Electric |
| TM | Transverse Magnetic |
References
- Polo, J.; Lakhtakia, A. Surface electromagnetic waves: A review. Laser Photonics Rev. 2011, 5, 234–246. [Google Scholar] [CrossRef]
- Takayama, O.; Bogdanov, A.A.; Lavrinenko, A.V. Photonic surface waves on metamaterial interfaces. J. Phys. Condens. Matter 2017, 29, 463001. [Google Scholar] [CrossRef]
- Barnes, W.L.; Dereux, A.; Ebbesen, T.W. Surface plasmon subwavelength optics. Nature 2003, 424, 824–830. [Google Scholar] [CrossRef] [PubMed]
- Maier, S. Plasmonics: Fundamentals and Applications; Springer: New York, NY, USA, 2007. [Google Scholar]
- Han, Z.; Bozhevolnyi, S.I. Radiation guiding with surface plasmon polaritons. Rep. Prog. Phys. 2012, 76, 016402. [Google Scholar] [CrossRef] [PubMed]
- Yeh, P.; Yariv, A.; Cho, A.Y. Optical surface waves in periodic layered media. Appl. Phys. Lett. 1978, 1978 32, 104–105. [Google Scholar] [CrossRef]
- Liscidini, M.; Sipe, J.E. Analysis of Bloch-surface-wave assisted diffraction-based biosensors. J. Opt. Soc. Am. B 2009, 26, 279–289. [Google Scholar] [CrossRef]
- Descrovi, E.; Sfez, T.; Quaglio, M.; Brunazzo, B.; Dominici, L.; Michelotti, F.; Herzig, H.P.; Martin, O.J.F.; Giorgis, F. Bloch surface waves on ultrathin polymeric ridges. Nano Lett. 2010, 10, 2087–2091. [Google Scholar] [CrossRef]
- Sinibaldi, A.; Danz, N.; Descrovi, E.; Munzert, P.; Schulz, U.; Sonntag, F.; Dominici, L.; Michelotti, F. Direct comparison of the performance of Bloch surface wave and surface plasmon polariton sensors. Sens. Actuators B Chem. 2012, 174, 292–298. [Google Scholar] [CrossRef]
- Yu, L.; Barakat, E.; Sfez, T.; Hvozdara, L.; Francesco, J.D.; Herzig, H.P. Manipulating Bloch surface waves in 2D: A platform concept-based flat lens. Light. Sci. Appl. 2014, 3, e124. [Google Scholar] [CrossRef]
- Dyakonov, M. New type of electromagnetic wave propagating at an interface. Sov. Phys. JETP 1988, 67, 714–716. [Google Scholar]
- Takayama, O.; Crasovan, L.-C.; Johansen, S.K.; Mihalache, D.; Artigas, D.; Torner, L. Dyakonov surface waves: A review. Electromagnetics 2008, 28, 126–145. [Google Scholar] [CrossRef]
- Takayama, O.; Crasovan, L.; Artigas, D.; Torner, L. Observation of Dyakonov surface waves. Phys. Rev. Lett. 2009, 102, 043903. [Google Scholar] [CrossRef] [PubMed]
- Takayama, O.; Nikitin, A.Y.; Martin-Moreno, L.; Torner, L.; Artigas, D. Dyakonov surface wave resonant transmission. Opt. Express 2011, 19, 6339–6347. [Google Scholar] [CrossRef] [PubMed]
- Takayama, O.; Artigas, D.; Torner, L. Coupling plasmons and dyakonons. Opt. Lett. 2012, 37, 1983–1985. [Google Scholar] [CrossRef] [PubMed]
- Takayama, O.; Artigas, D.; Torner, L. Practical dyakonons. Opt. Lett. 2012, 37, 4311–4313. [Google Scholar] [CrossRef] [PubMed]
- Takayama, O.; Artigas, D.; Torner, L. Lossless directional guiding of light in dielectric nanosheets using Dyakonov surface waves. Nat. Nanotechnol. 2014, 9, 419–424. [Google Scholar] [CrossRef]
- Crasovan, L.-C.; Takayama, O.; Artigas, D.; Johansen, S.K.; Mihalache, D.; Torner, L. Enhanced localization of Dyakonov-like surface waves in left-handed materials. Phys. Rev. B 2006, 74, 155120. [Google Scholar] [CrossRef]
- Gao, J.; Lakhtakia, A.; Lei, M. On Dyakonov-Tamm waves localized to a central twist defect in a structurally chiral material. J. Opt. Soc. Am. B 2009, 26, 1615–1621. [Google Scholar] [CrossRef]
- Pulsifer, D.P.; Faryad, M.; Lakhtakia, A. Observation of the Dyakonov-Tamm wave. Phys. Rev. Lett. 2013, 111, 243902. [Google Scholar] [CrossRef]
- Pulsifer, D.P.; Faryad, M.; Lakhtakia, A.; Hall, A.S.; Liu, L. Experimental excitation of the Dyakonov–Tamm wave in the grating-coupled configuration. Opt. Lett. 2014, 39, 2125–2128. [Google Scholar] [CrossRef]
- Abbas, F.; Lakhtakia, A.; Naqvi, Q.A.; Faryad, M. An optical-sensing modality that exploits Dyakonov–Tamm waves. Photon. Res. 2015, 3, 5–8. [Google Scholar] [CrossRef]
- Mackay, T.G.; Zhou, C.; Lakhtakia, A. Dyakonov–Voigt surface waves. Proc. R. Soc. A 2019, 475, 20190317. [Google Scholar] [CrossRef] [PubMed]
- Jacob, Z.; Narimanov, E.E. Optical hyperspace for plasmons: Dyakonov states in metamaterials. Appl. Phys. Lett. 2008, 93, 221109. [Google Scholar] [CrossRef]
- Repän, T.; Takayama, O.; Lavrinenko, L.V. Hyperbolic surface waves on anisotropic materials without hyperbolic dispersion. Opt. Express 2020. submitted. [Google Scholar]
- Smith, D.R.; Schurig, D. Electromagnetic Wave Propagation in Media with Indefinite Permittivity and Permeability Tensors. Phys. Rev. Lett. 2003, 90, 077405. [Google Scholar] [CrossRef]
- Krishnamoorthy, H.N.S.; Jacob, Z.; Narimanov, E.; Kretzschmar, I.; Menon, V.M. Topological transitions in metamaterials. Science 2012, 336, 205–209. [Google Scholar] [CrossRef]
- Cortes, C.L.; Newman, W.; Molesky, S.; Jacob, Z. Quantum nanophotonics using hyperbolic metamaterials. J. Opt. 2012, 14, 063001. [Google Scholar] [CrossRef]
- Drachev, V.P.; Podolskiy, V.A.; Kildishev, A.V. Hyperbolic metamaterials: New physics behind a classical problem. Opt. Express 2013, 21, 15048–15064. [Google Scholar] [CrossRef]
- Poddubny, A.; Iorsh, I.; Belov, P.; Kivshar, Y. Hyperbolic metamaterials. Nat. Photonics 2013, 7, 948–957. [Google Scholar] [CrossRef]
- Shekhar, P.; Atkinson, J.; Jacob, Z. Hyperbolic metamaterials: Fundamentals and applications. Nano Converg. 2014, 1, 14. [Google Scholar] [CrossRef]
- Ferrari, L.; Wu, C.; Lepage, D.; Zhang, X.; Liu, Z. Hyperbolic metamaterials and their applications. Prog. Quantum Electron. 2015, 40, 1–40. [Google Scholar] [CrossRef]
- Takayama, O.; Lavrinenko, A.V. Optics with hyperbolic materials [Invited]. J. Opt. Soc. Am. B 2019, 36, F38–F48. [Google Scholar] [CrossRef]
- Kildishev, A.V.; Boltasseva, A.; Shalaev, V.M. Planar photonics with metasurfaces. Science 2013, 339, 1232009. [Google Scholar] [CrossRef] [PubMed]
- Kapitanova, P.V.; Ginzburg, P.; Rodríguez-Fortuño, F.J.; Filonov, D.S.; Voroshilov, P.M.; Belov, P.A.; Poddubny, A.N.; Kivshar, Y.S.; Wurtz, G.A.; Zayats, A.V. Photonic spin Hall effect in hyperbolic metamaterials for polarization-controlled routing of subwavelength modes. Nat. Commun. 2014, 5, 3226. [Google Scholar] [CrossRef] [PubMed]
- High, A.A.; Devlin, R.C.; Dibos, A.; Polking, M.; Wild, D.S.; Perczel, J.; de Leon, N.P.; Lukin, M.D.; Park, H. Visible-frequency hyperbolic metasurface. Nature 2015, 522, 192–196. [Google Scholar] [CrossRef] [PubMed]
- Takayama, O.; Shkondin, E.; Bodganov, A.; Panah, M.E.A.; Golenitskii, K.; Dmitriev, P.; Repän, T.; Malureanu, R.; Belov, P.; Jensen, F.; et al. Mid-infrared surface waves on a high aspect ratio nanotrench platform. ACS Photon. 2017, 4, 2899–2907. [Google Scholar] [CrossRef]
- Takayama, O.; Dmitriev, P.; Shkondin, E.; Yermakov, O.; Panah, M.; Golenitskii, K.; Jensen, F.; Bogdanov, A.; Lavrinenko, A. Experimental observation of Dyakonov plasmons in the mid-infrared. Semiconductors 2018, 52, 442–446. [Google Scholar] [CrossRef]
- Li, P.; Dolado, I.; Alfaro-Mozaz, F.J.; Casanova, F.; Hueso, L.E.; Liu, S.; Edgar, J.H.; Nikitin, A.Y.; Vélez, S.; Hillenbrand, R. Infrared hyperbolic metasurface based on nanostructured van der Waals materials. Science 2018, 359, 892–896. [Google Scholar] [CrossRef]
- Ma, W.; Alonso-González, P.; Li, S.; Nikitin, A.Y.; Yuan, J.; Martín-Sánchez, J.; Taboada-Gutiérrez, J.; Amenabar, I.; Li, P.; Vélez, S.; et al. In-plane anisotropic and ultra-low-loss polaritons in a natural van der Waals crystal. Nature 2018, 562, 557–562. [Google Scholar] [CrossRef]
- Shin, H.; Fan, S. All-angle negative refraction for surface plasmon waves using a metal-dielectric-metal structure. Phys. Rev. Lett. 2006, 96, 073907. [Google Scholar] [CrossRef]
- Sarid, D. Modern Introduction to Surface Plasmons: Theory, Mathematica Modeling, and Applications; Cambridge University Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Chen, C.-L. Foundations for Guided-Wave Optics; Wiley-Interscience: Hoboken, NJ, USA, 2007. [Google Scholar]
- Malitson, I.H. A redetermination of some optical properties of calcium fluoride. Appl. Opt. 1963, 2, 1103–1107. [Google Scholar] [CrossRef]
- Rodríguez-de Marcos, L.V.; Larruquert, J.I.; Méndez, J.A.; Aznárez, J.A. Self-consistent optical constants of MgF2, LaF3, and CeF3 films. Opt. Mater. Express 2017, 7, 989–1006. [Google Scholar] [CrossRef]
- Repän, T.; Novitsky, A.; Willatzen, M.; Lavrinenko, A.V. Pseudocanalization regime for magnetic dark-field hyperlenses. Phys. Rev. B 2017, 96, 195166. [Google Scholar] [CrossRef]
- Gomez-Diaz, J.S.; Tymchenko, M.; Alu, A. Hyperbolic plasmons and topological transitions over uniaxial metasurfaces. Phys. Rev. Lett. 2015, 114, 233901. [Google Scholar] [CrossRef]
- Yermakov, O.Y.; Ovcharenko, A.I.; Song, M.; Bogdanov, A.A.; Iorsh, I.V.; Kivshar, Y.S. Hybrid waves localized at hyperbolic metasurfaces. Phys. Rev. B 2015, 91, 235423. [Google Scholar] [CrossRef]
- Samusev, A.; Mukhin, I.; Malureanu, R.; Takayama, O.; Permyakov, D.V.; Sinev, I.V.; Baranov, D.; Yermakov, O.; Iorsh, I.V.; Bogdanov, A.A.; et al. Polarization-resolved characterization of plasmon waves supported by an anisotropic metasurface. Opt. Express 2017, 26, 32631–32639. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).