Pupil Function in Pseudophakia: Proximal Miosis Behavior and Optical Influence
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants
2.2. Pupil Size Measurement
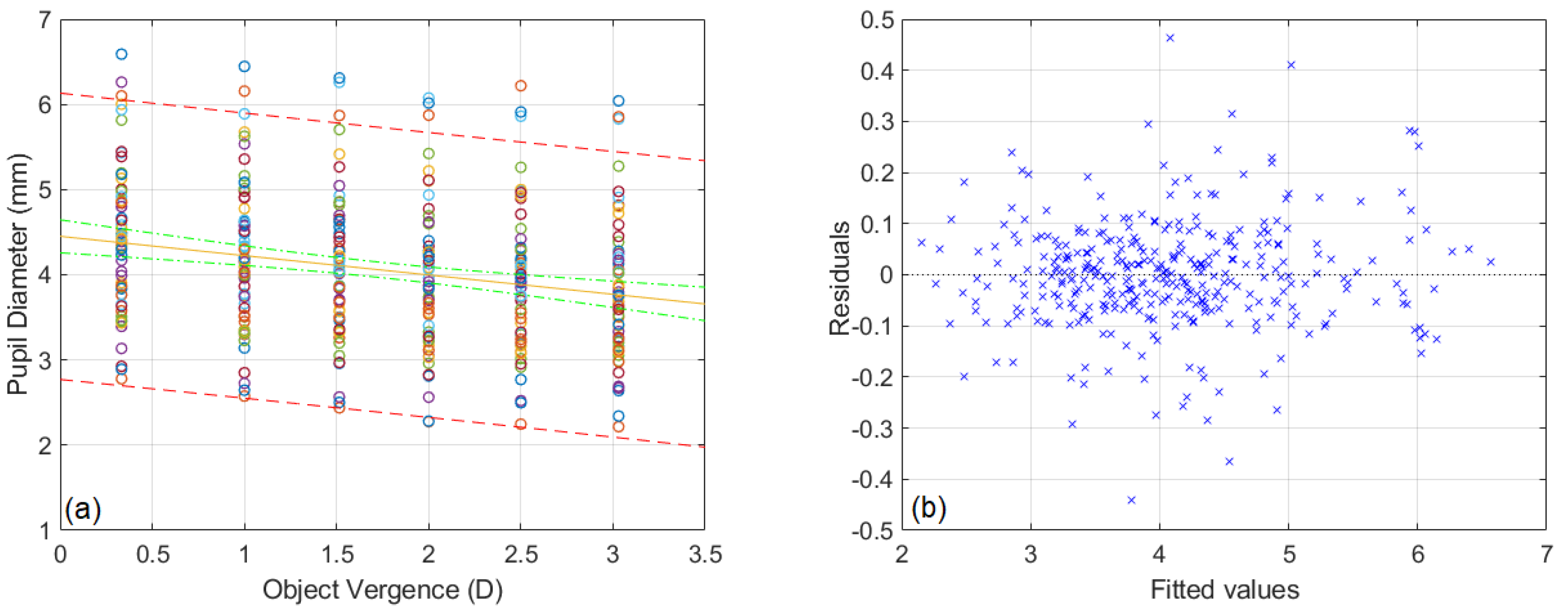
2.3. Pupil Size Statistical Modeling
2.4. Optical Performance Modeling
3. Results
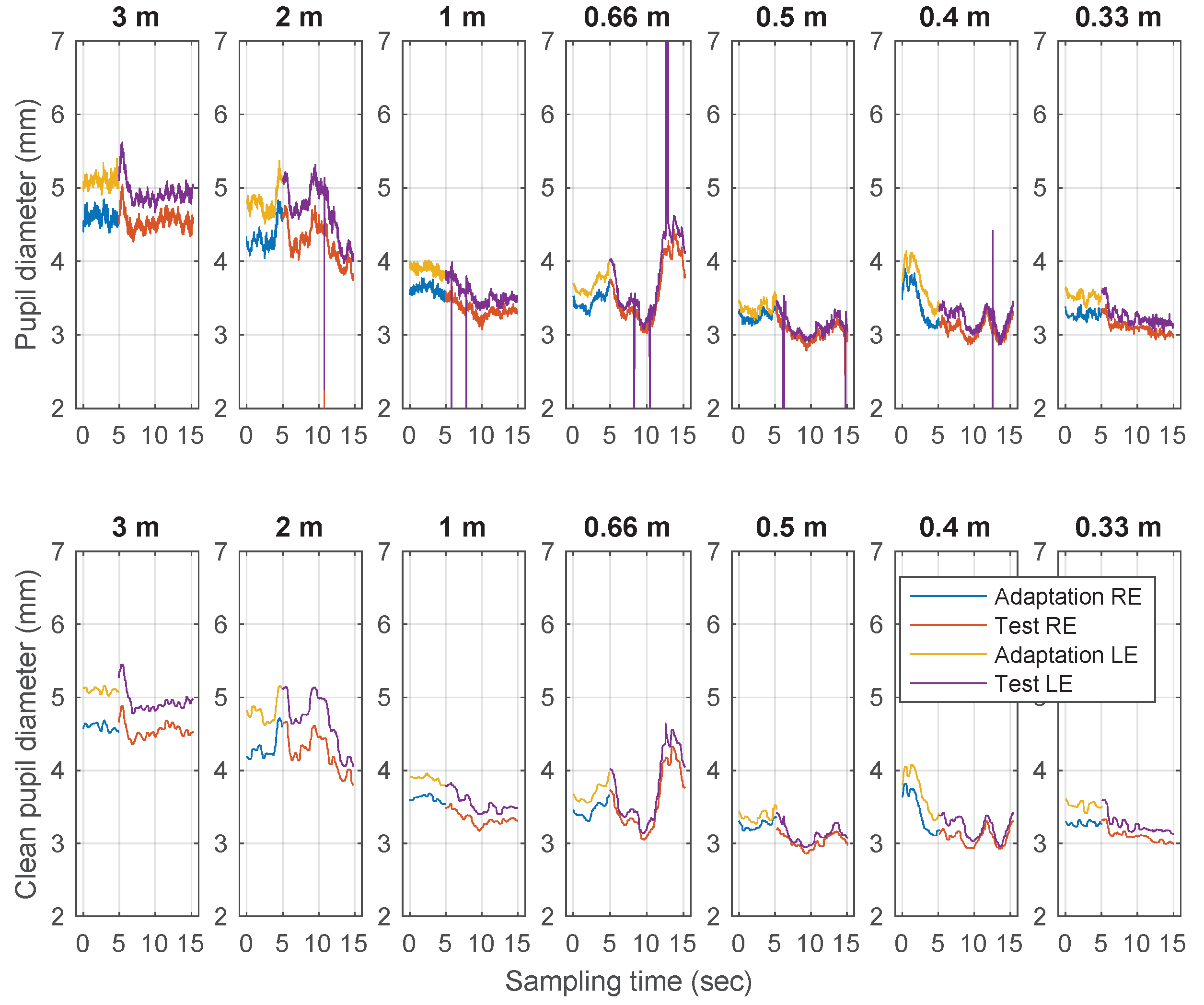
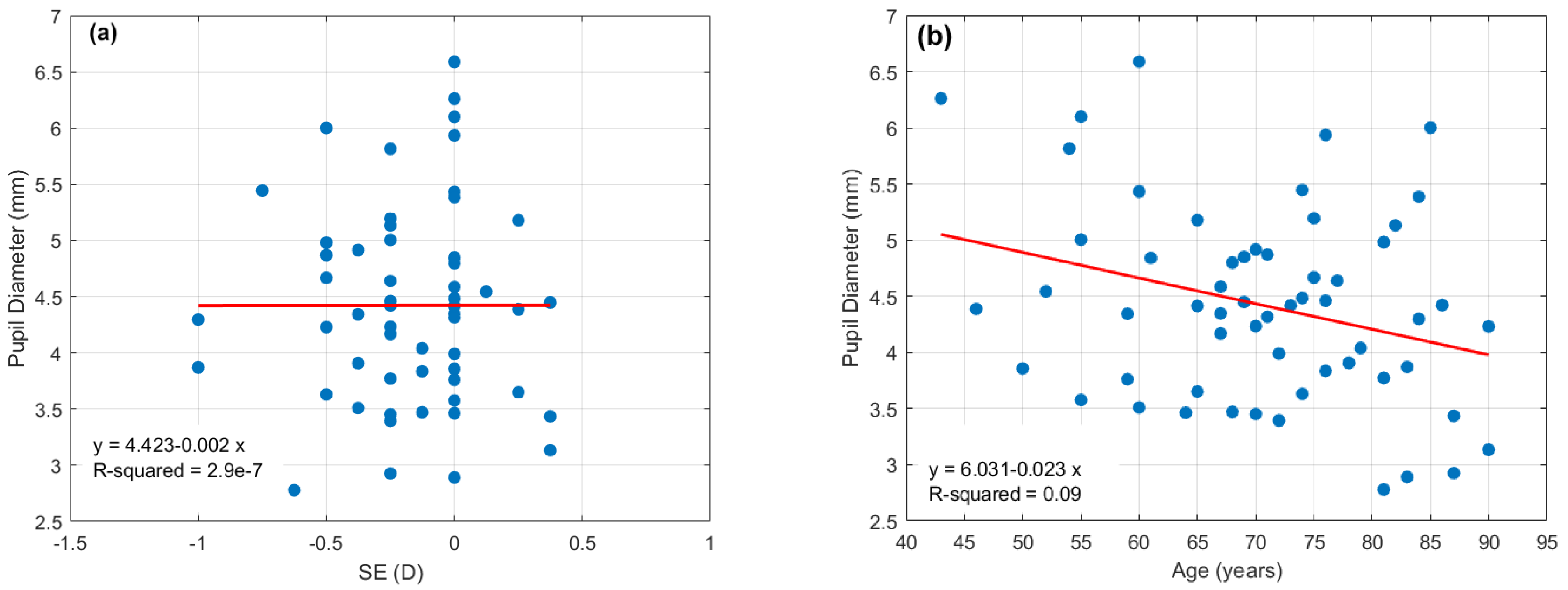
3.1. Pupillary near Response
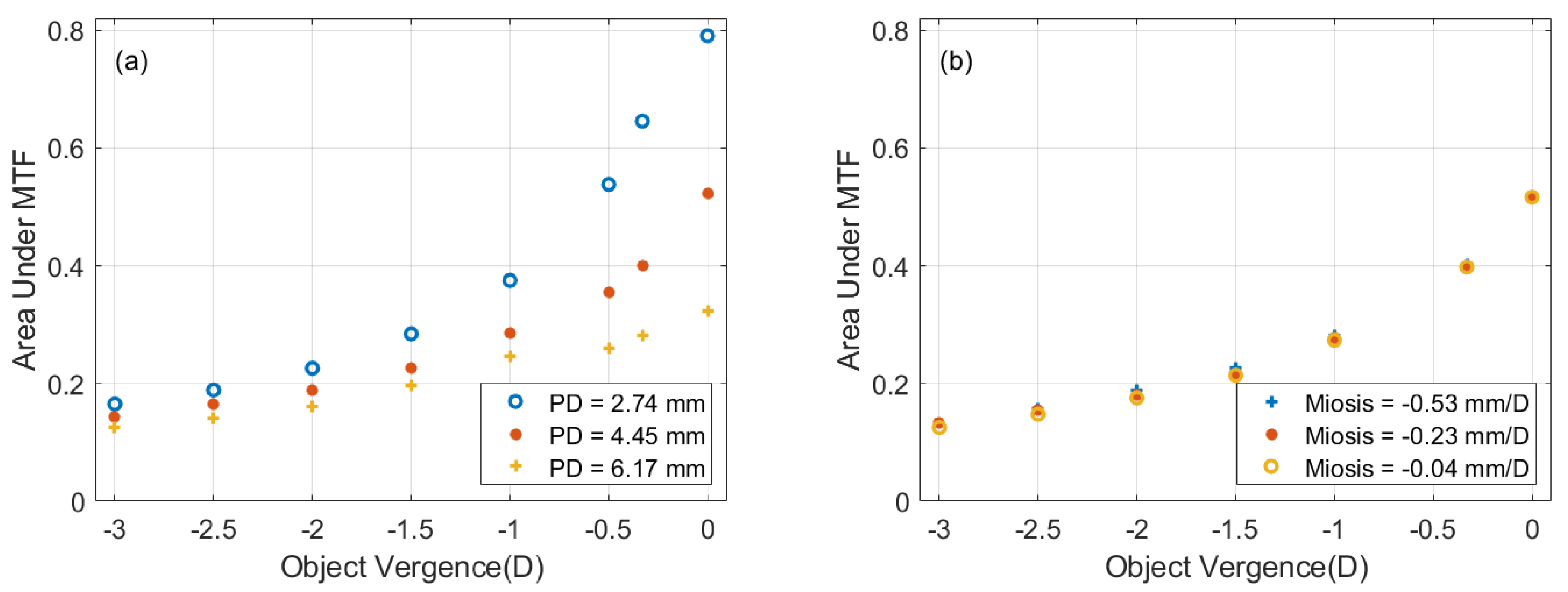
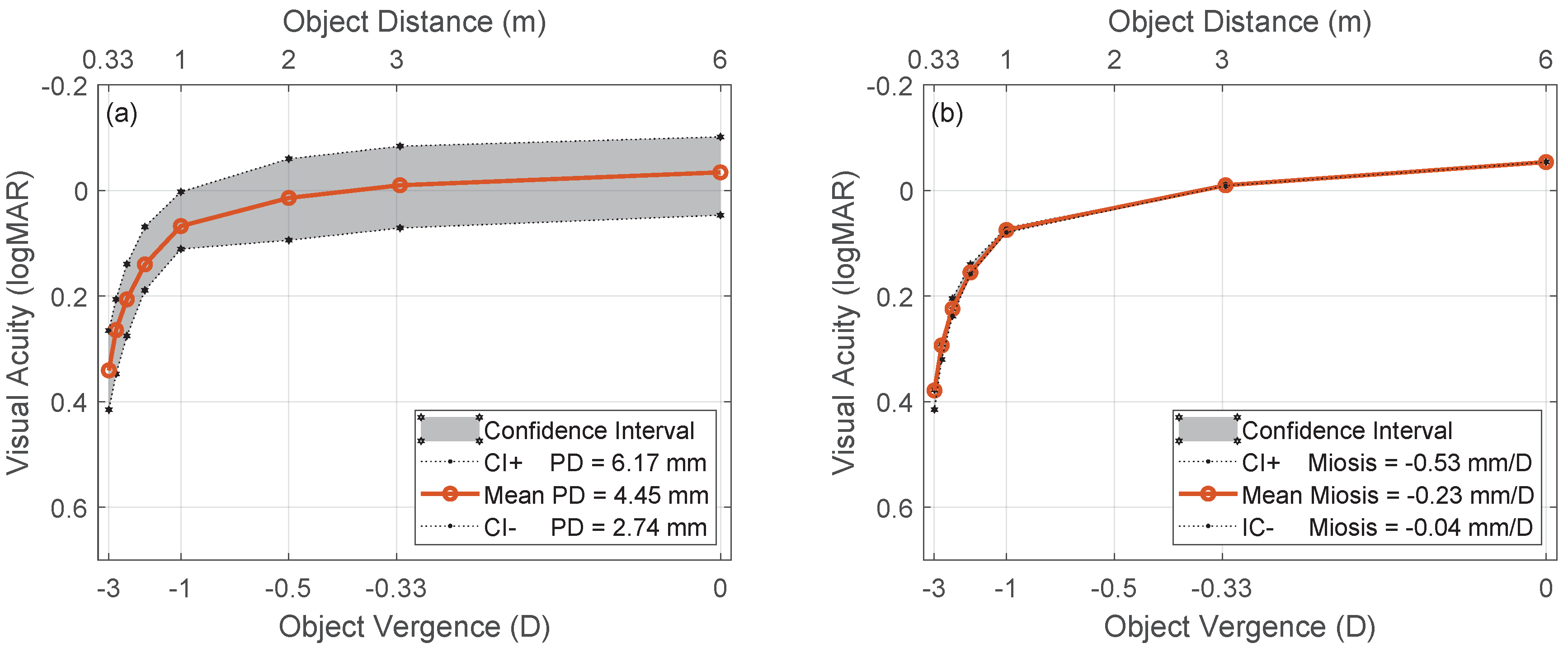
3.2. Optical Performance
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Burd, H.J.; Judge, S.J.; Flavell, M.J. Mechanics of accommodation of the human eye. Vis. Res. 1999, 39, 1591–1595. [Google Scholar] [CrossRef]
- Chateau, N.; De, J.B.; Bouchard, F.; Molenaar, H. Infrared pupillometry in presbyopes fitted with soft contact lenses. Optom. Vis. Sci. 1996, 73, 733–741. [Google Scholar] [CrossRef]
- Marchini, G.; Pedrotti, E.; Modesti, M.; Visentin, S.; Tosi, R. Anterior segment changes during accommodation in eyes with a monofocal intraocular lens: High-frequency ultrasound study. J. Cataract Refract. Surg. 2008, 34, 949–956. [Google Scholar] [CrossRef]
- Modesti, M.; Pasqualitto, G.; Appolloni, R.; Pecorella, I.; Sourdille, P. Preoperative and postoperative size and movements of the lens capsular bag: Ultrasound biomicroscopy analysis. J. Cataract Refract. Surg. 2011, 37, 1775–1784. [Google Scholar] [CrossRef]
- Findl, O.; Kiss, B.; Petternel, V.; Menapace, R.; Georgopoulos, M.; Rainer, G.; Drexler, W. Intraocular lens movement caused by ciliary muscle contraction. J. Cataract Refract. Surg. 2003, 29, 669–676. [Google Scholar] [CrossRef]
- Marcos, S.; Ortiz, S.; Pérez-Merino, P.; Birkenfeld, J.; Durán, S.; Jiménez-Alfaro, I. Three-dimensional evaluation of accommodating intraocular lens shift and alignment in vivo. Ophthalmology 2014, 121, 45–55. [Google Scholar] [CrossRef]
- Elder, M.J.; Murphy, C.; Sanderson, G.F. Apparent accommodation and depth of field in pseudophakia. J. Cataract Refract. Surg. 1996, 22, 615–619. [Google Scholar] [CrossRef]
- Langenbucher, A.; Seitz, B.; Huber, S.; Nguyen, N.X.; Küchle, M. Theoretical and measured pseudophakic accommodation after implantation of a new accommodative posterior chamber intraocular lens. Arch. Ophthalmol. 2003, 121, 1722–1727. [Google Scholar] [CrossRef]
- Nakazawa, M.; Ohtsuki, K. Apparent accommodation in pseudophakic eyes after implantation of posterior chamber intraocular lenses. Am. J. Ophthalmol. 1983, 96, 435–438. [Google Scholar] [CrossRef]
- Nakazawa, M.; Ohtsuki, K. Apparent accommodation in pseudophakic eyes after implantation of posterior chamber intraocular lenses: Optical analysis. Investig. Ophthalmol. Vis. Sci. 1984, 25, 1458–1460. [Google Scholar] [CrossRef]
- Hayashi, K.; Hayashi, H.; Nakao, F.; Hayashi, F. Aging changes in apparent accommodation in eyes with a monofocal intraocular lens. Am. J. Ophthalmol. 2003, 135, 432–436. [Google Scholar] [CrossRef]
- Trindade, F.; Oliveira, A.; Frasson, M. Benefit of against-the-rule astigmatism to uncorrected near acuity. J. Cataract Refract. Surg. 1997, 23, 82–85. [Google Scholar] [CrossRef]
- Oshika, T.; Mimura, T.; Tanaka, S.; Amano, S.; Fukuyama, M.; Yoshitomi, F.; Maeda, N.; Fujikado, T.; Hirohara, Y.; Mihashi, T. Apparent accommodation and corneal wavefront aberration in pseudophakic eyes. Investig. Ophthalmol. Vis. Sci. 2002, 43, 2882–2886. [Google Scholar]
- Nishi, T.; Nawa, Y.; Ueda, T.; Masuda, K.; Taketani, F.; Hara, Y. Effect of total higher-order aberrations on accommodation in pseudophakic eyes. J. Cataract Refract. Surg. 2006, 32, 1643–1649. [Google Scholar] [CrossRef]
- Fukuyama, M.; Oshika, T.; Amano, S.; Yoshitomi, F. Relationship between apparent accommodation and corneal multifocality in pseudophakic eyes. Ophthalmology 1999, 106, 1178–1181. [Google Scholar] [CrossRef]
- Kamiya, K.; Kawamorita, T.; Uozato, H.; Kasugai, H.; Shimizu, K. Effect of astigmatism on apparent accommodation in pseudophakic eyes. Optom. Vis. Sci. 2012, 89, 148–154. [Google Scholar] [CrossRef]
- Serra, P.N. The Effect of Meridional Blur in Pseudoaccommodation. Ph.D. Thesis, University of Bradford: Bradford School of Optometry and Vision Sciences, Bradford, UK, 2013. [Google Scholar]
- Atchison, D.A.; Smith, G. Optics of the Human Eye, 1st ed.; Butterworth-Heinemann: Edinburgh, UK, 2000. [Google Scholar]
- Kasthurirangan, S.; Glasser, A. Age related changes in the characteristics of the near pupil response. Vis. Res. 2006, 46, 1393–1403. [Google Scholar] [CrossRef]
- Winn, B.; Whitaker, D.; Elliott, D.B.; Phillips, N.J. Factors affecting light-adapted pupil size in normal human subjects. Investig. Ophthalmol. Vis. Sci. 1994, 35, 1132–1137. [Google Scholar]
- Artigas, J.M.; Menezo, J.L.; Peris, C.; Felipe, A.; Díaz-Llopis, M. Image quality with multifocal intraocular lenses and the effect of pupil size: Comparison of refractive and hybrid refractive–diffractive designs. J. Cataract Refract. Surg. 2007, 33, 2111–2117. [Google Scholar] [CrossRef]
- Alfonso, J.F.; Fernández-Vega, L.; Baamonde, M.B.; Montés-Micó, R. Correlation of pupil size with visual acuity and contrast sensitivity after implantation of an apodized diffractive intraocular lens. J. Cataract Refract. Surg. 2007, 33, 430–438. [Google Scholar] [CrossRef]
- Radhakrishnan, H.; Neil Charman, W. Age-related changes in static accommodation and accommodative miosis. Ophthalmic Physiol. Opt. 2007, 27, 342–352. [Google Scholar] [CrossRef]
- Almutairi, M.S.; Altoaimi, B.H.; Bradley, A. Accommodation and pupil behaviour of binocularly viewing early presbyopes. Ophthalmic Physiol. Opt. 2017, 37, 128–140. [Google Scholar] [CrossRef]
- Wachler, B.S.B. Effect of pupil size on visual function under monocular and binocular conditions in LASIK and non-LASIK patients. J. Cataract Refract. Surg. 2003, 29, 275–278. [Google Scholar] [CrossRef]
- Nakamura, K.; Bissen-Miyajima, H.; Oki, S.; Onuma, K. Pupil sizes in different Japanese age groups and the implications for intraocular lens choice. J. Cataract Refract. Surg. 2009, 35, 134–138. [Google Scholar] [CrossRef]
- Schäfer, W.; Weale, R. The influence of age and retinal illumination on the pupillary near reflex. Vis. Res. 1970, 10, 179–191. [Google Scholar] [CrossRef]
- Watson, A.B.; Yellott, J.I. A unified formula for light-adapted pupil size. J. Vis. 2012, 12, 12. [Google Scholar] [CrossRef]
- Fonseca, E.S.; Fiadeiro, P.T.; Gomes, R.; Trancon, A.S.; Baptista, A.M.; Serra, P. Influence of pupil function in pseudophakia. In Proceedings of the Fourth International Conference on Applications of Optics and Photonics, Lisbon, Portugal, 31 May–4 June 2019; Volume 11207, p. 112071N. [Google Scholar]
- Lindstrom, M.J.; Bates, D.M. Nonlinear mixed effects models for repeated measures data. Biometrics 1990, 46, 673–687. [Google Scholar] [CrossRef]
- Pinheiro, J.C.; Bates, D.M.; Lindstrom, M.J. Model Building for Nonlinear Mixed Effects Models; University of Wisconsin, Department of Biostatistics Madison: Madison, WI, USA, 1995. [Google Scholar]
- Akaike, H. Akaike, H. A new look at the statistical model identification. In Selected Papers of Hirotugu Akaike; Springer: New York, NY, USA, 1974; pp. 215–222. [Google Scholar]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Liou, H.L.; Brennan, N.A. Anatomically accurate, finite model eye for optical modeling. J. Opt. Soc. Am. A 1997, 14, 1684–1695. [Google Scholar] [CrossRef]
- Eppig, T.; Scholz, K.; Löffler, A.; Meßner, A.; Langenbucher, A. Effect of decentration and tilt on the image quality of aspheric intraocular lens designs in a model eye. J. Cataract Refract. Surg. 2009, 35, 1091–1100. [Google Scholar] [CrossRef]
- Thibos, L.N.; Hong, X.; Bradley, A.; Applegate, R.A. Accuracy and precision of objective refraction from wavefront aberrations. J. Vis. 2004, 4, 325–351. [Google Scholar] [CrossRef]
- Campbell, F.; Green, D. Optical and retinal factors affecting visual resolution. J. Physiol. 1965, 181, 576–593. [Google Scholar] [CrossRef]
- Alarcon, A.; Canovas, C.; Rosen, R.; Weeber, H.; Tsai, L.; Hileman, K.; Piers, P. Preclinical metrics to predict through-focus visual acuity for pseudophakic patients. Biomed. Opt. Express 2016, 7, 1877–1888. [Google Scholar] [CrossRef]
- Thibos, L.N.; Applegate, R.A.; Schwiegerling, J.T.; Webb, R. Standards for reporting the optical aberrations of eyes. J. Refract. Surg. 2002, 18, S652–S660. [Google Scholar]
- MacRae, S.; Holladay, J.T.; Glasser, A.; Calogero, D.; Hilmantel, G.; Masket, S.; Stark, W.; Tarver, M.E.; Nguyen, T.; Eydelman, M. Special report: American academy of ophthalmology task force consensus statement for extended depth of focus intraocular lenses. Ophthalmology 2017, 124, 139–141. [Google Scholar] [CrossRef]
- Xu, R.; Wang, H.; Jaskulski, M.; Kollbaum, P.; Bradley, A. Small-pupil versus multifocal strategies for expanding depth of focus of presbyopic eyes. J. Cataract Refract. Surg. 2019, 45, 647–655. [Google Scholar] [CrossRef]
- Xu, R.; Wang, H.; Thibos, L.N.; Bradley, A. Interaction of aberrations, diffraction, and quantal fluctuations determine the impact of pupil size on visual quality. J. Opt. Soc. Am. A 2017, 34, 481–492. [Google Scholar] [CrossRef]
- Hess, E.H.; Polt, J.M. Pupil size in relation to mental activity during simple problem-solving. Science 1964, 143, 1190–1192. [Google Scholar] [CrossRef]
- Hoeks, B.; Levelt, W.J. Pupillary dilation as a measure of attention: A quantitative system analysis. Behav. Res. Methods Instrum. Comput. 1993, 25, 16–26. [Google Scholar] [CrossRef]
- Kasthurirangan, S.; Glasser, A. Characteristics of pupil responses during far-to-near and near-to-far accommodation. Ophthalmic Physiol. Opt. 2005, 25, 328–339. [Google Scholar] [CrossRef]
- Barbur, J.L. Learning from the pupil-studies of basic mechanisms and clinical applications. Vis. Neurosci. 2004, 1, 641–656. [Google Scholar]
- Crawford, B. The dependence of pupil size upon external light stimulus under static and variable conditions. Proc. R. Soc. Lond. Ser. B Biol. Sci. 1936, 121, 376–395. [Google Scholar]
- Atchison, D.A.; Girgenti, C.C.; Campbell, G.M.; Dodds, J.P.; Byrnes, T.M.; Zele, A.J. Influence of field size on pupil diameter under photopic and mesopic light levels. Clin. Exp. Optom. 2011, 94, 545–548. [Google Scholar] [CrossRef]
- Guillon, M.; Dumbleton, K.; Theodoratos, P.; Gobbe, M.; Wooley, C.B.; Moody, K. The effects of age, refractive status, and luminance on pupil size. Optom. Vis. Sci. 2016, 93, 1093. [Google Scholar] [CrossRef]
- Birren, J.E.; Casperson, R.C.; Botwinick, J. Age changes in pupil size. J. Gerontol. 1950, 5, 216–221. [Google Scholar] [CrossRef]
- Kumnick, L.S. Aging and the efficiency of the pupillary mechanism. J. Gerontol. 1956, 11, 160–164. [Google Scholar] [CrossRef]
- Shentu, X.; Tang, X.; Yao, K. Spherical aberration, visual performance and pseudoaccommodation of eyes implanted with different aspheric intraocular lens. Clin. Exp. Ophthalmol. 2008, 36, 620–624. [Google Scholar] [CrossRef]
- Pieh, S.; Kellner, C.; Hanselmayer, G.; Lackner, B.; Schmidinger, G.; Walkow, T.; Sticker, M.; Weghaupt, H.; Fercher, A.F.; Skorpik, C. Comparison of visual acuities at different distances and defocus curves. J. Cataract Refract. Surg. 2002, 28, 1964–1967. [Google Scholar] [CrossRef]
- Rocha, K.M.; Soriano, E.S.; Chamon, W.; Chalita, M.R.; Nosé, W. Spherical aberration and depth of focus in eyes implanted with aspheric and spherical intraocular lenses: A prospective randomized study. Ophthalmology 2007, 114, 2050–2054. [Google Scholar] [CrossRef]
- Nanavaty, M.A.; Spalton, D.J.; Boyce, J.; Saha, S.; Marshall, J. Wavefront aberrations, depth of focus, and contrast sensitivity with aspheric and spherical intraocular lenses: Fellow-eye study. J. Cataract Refract. Surg. 2009, 35, 663–671. [Google Scholar] [CrossRef]
- Moon, P.; Spencer, D.E. On the stiles-crawford effect. J. Opt. Soc. Am. 1944, 34, 319–329. [Google Scholar] [CrossRef]
- Atchison, D.A.; Smith, G.; Efron, N. The effect of pupil size on visual acuity in uncorrected and corrected myopia. Am. J. Optom. Physiol. Opt. 1979, 56, 315–323. [Google Scholar] [CrossRef]
- Sheedy, J.E.; Bailey, I.L.; Raasch, T.W. Visual acuity and chart luminance. Am. J. Optom. Physiol. Opt. 1984, 61, 595–600. [Google Scholar] [CrossRef]
| Surface | Radius (mm) | Thickness (mm) | Conic Constant | |
|---|---|---|---|---|
| Anterior cornea | ||||
| Posterior Cornea | ||||
| Iris | ∞ | − | ||
| Anterior IOL | − | |||
| Posterior IOL | − | |||
| Retina | − | − |
| Object Vergence (D) | |||||||
|---|---|---|---|---|---|---|---|
| 0.33 | 1.00 | 1.50 | 2.00 | 2.50 | 3.00 | ||
| Pupil Size (mm) | Mean | 4.44 | 4.24 | 4.10 | 3.99 | 3.91 | 3.84 |
| SD | 0.87 | 0.90 | 0.88 | 0.87 | 0.86 | 0.86 | |
| Parameter | First Model | Second Model | |
|---|---|---|---|
| Fixed parameters | |||
| Variance components | |||
| Goodness -of-fit |
| Model | DF | AIC | BIC | Loglikelihood | LRT | p-Value |
|---|---|---|---|---|---|---|
| 1 | 6 | |||||
| 2 | 8 |
| Study | Distance m | Intermediate m | Near m | |
|---|---|---|---|---|
| Shentu et al., 2001 [52] | − | |||
| Pieh et al., 2002 [53] | ||||
| Rocha et al., 2007 [54] | ||||
| Navavaty et al., 2009 [55] | − | |||
| Present study |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fonseca, E.; Fiadeiro, P.; Gomes, R.; Sanchez Trancon, A.; Baptista, A.; Serra, P. Pupil Function in Pseudophakia: Proximal Miosis Behavior and Optical Influence. Photonics 2019, 6, 114. https://doi.org/10.3390/photonics6040114
Fonseca E, Fiadeiro P, Gomes R, Sanchez Trancon A, Baptista A, Serra P. Pupil Function in Pseudophakia: Proximal Miosis Behavior and Optical Influence. Photonics. 2019; 6(4):114. https://doi.org/10.3390/photonics6040114
Chicago/Turabian StyleFonseca, Elsa, Paulo Fiadeiro, Renato Gomes, Angel Sanchez Trancon, António Baptista, and Pedro Serra. 2019. "Pupil Function in Pseudophakia: Proximal Miosis Behavior and Optical Influence" Photonics 6, no. 4: 114. https://doi.org/10.3390/photonics6040114
APA StyleFonseca, E., Fiadeiro, P., Gomes, R., Sanchez Trancon, A., Baptista, A., & Serra, P. (2019). Pupil Function in Pseudophakia: Proximal Miosis Behavior and Optical Influence. Photonics, 6(4), 114. https://doi.org/10.3390/photonics6040114








