Surface Lattice Resonances in THz Metamaterials
Abstract
1. Introduction
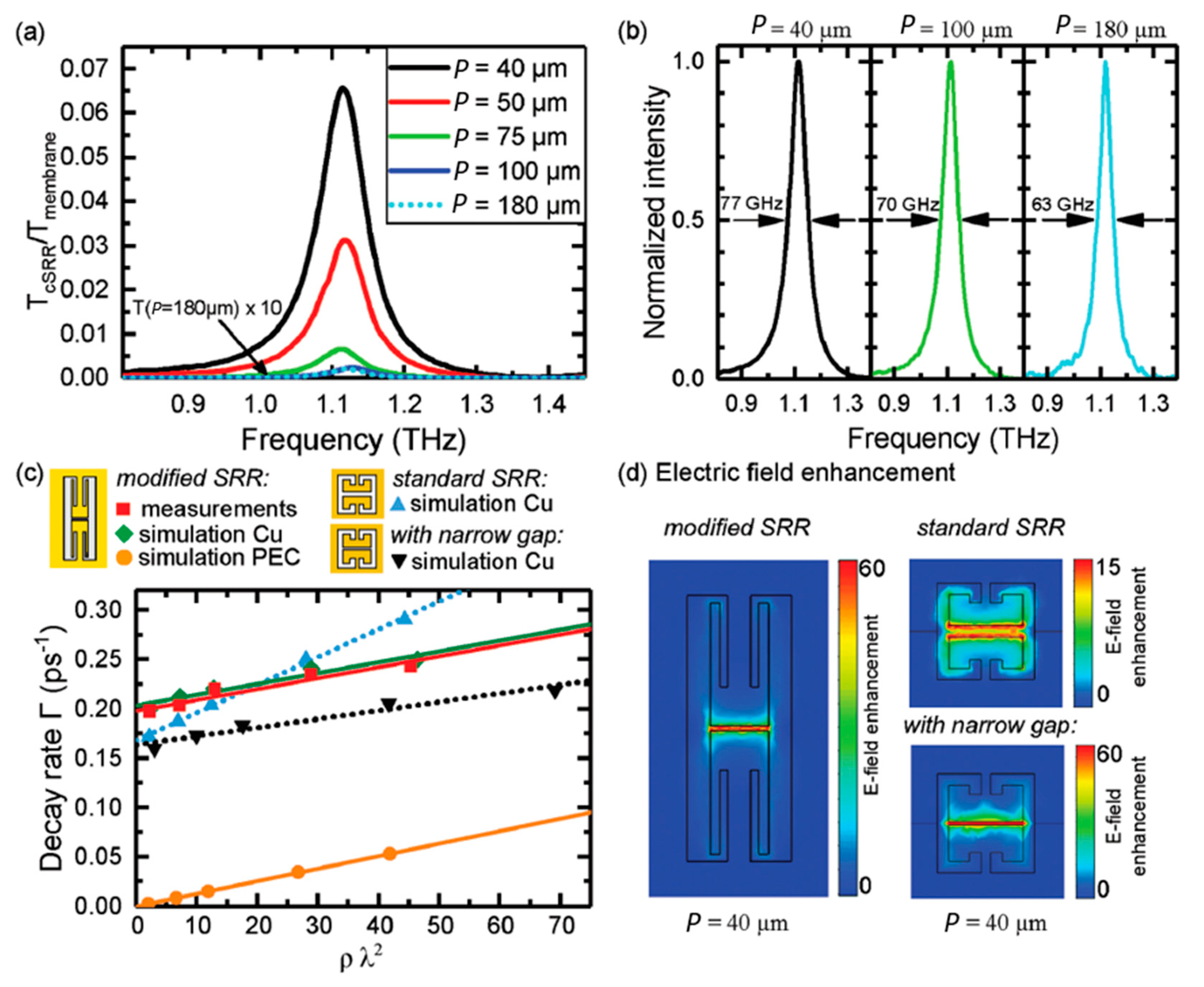
2. Effects of Packing Densities in Metamaterials
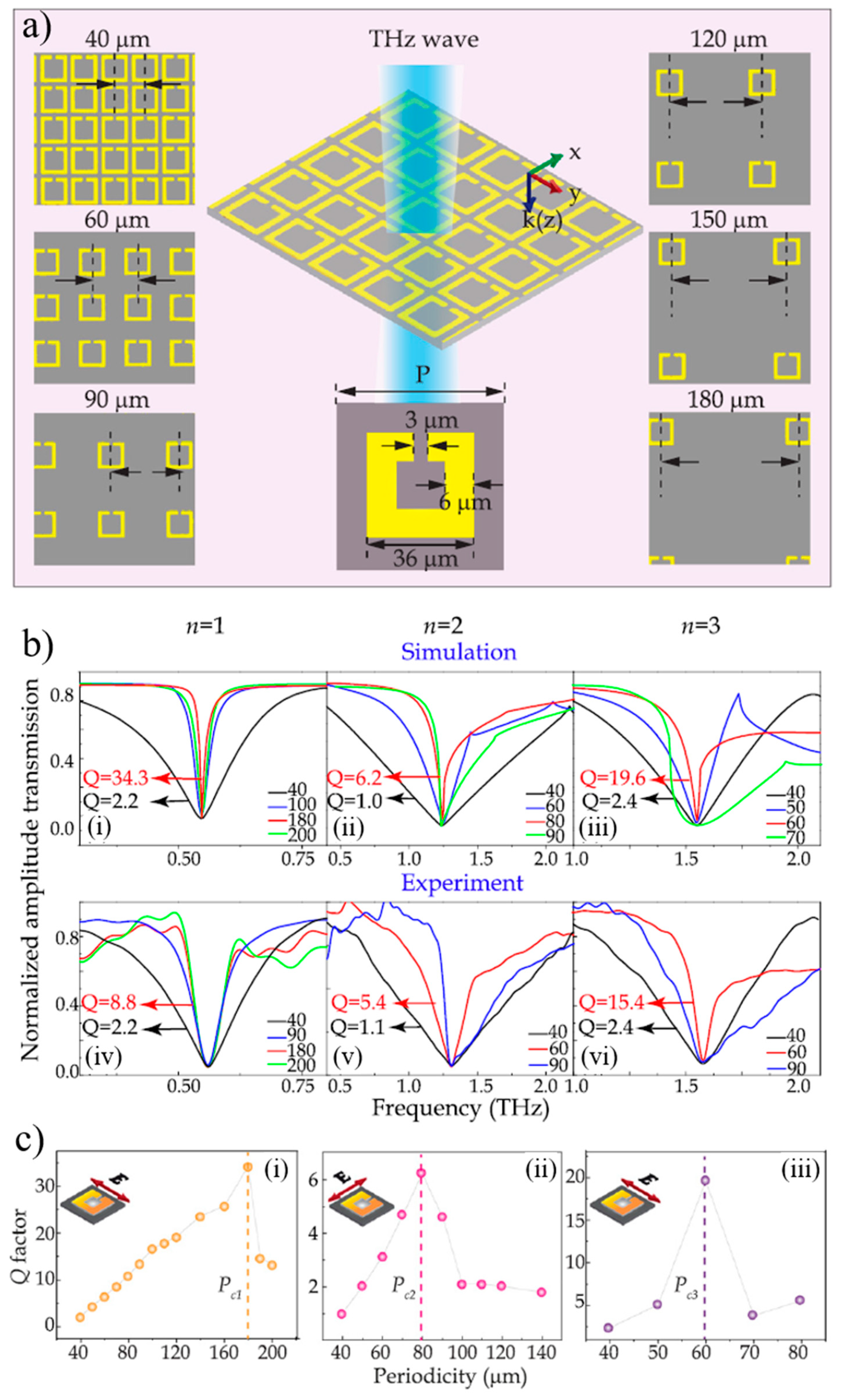
3. High-Q Resonances
3.1. Fundamental Resonances (Dipole and LC)
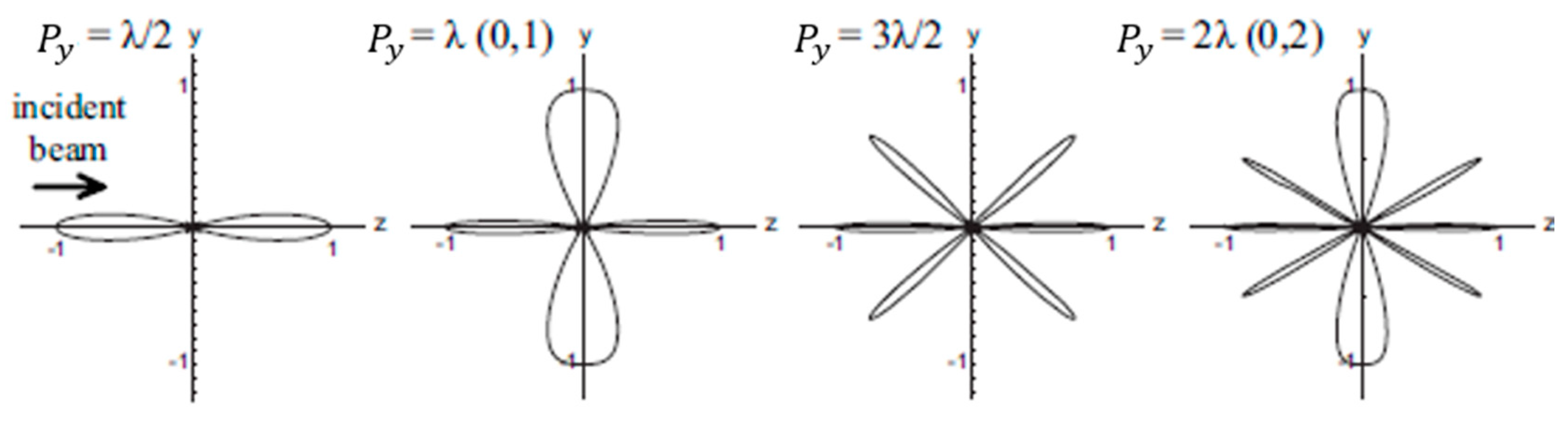
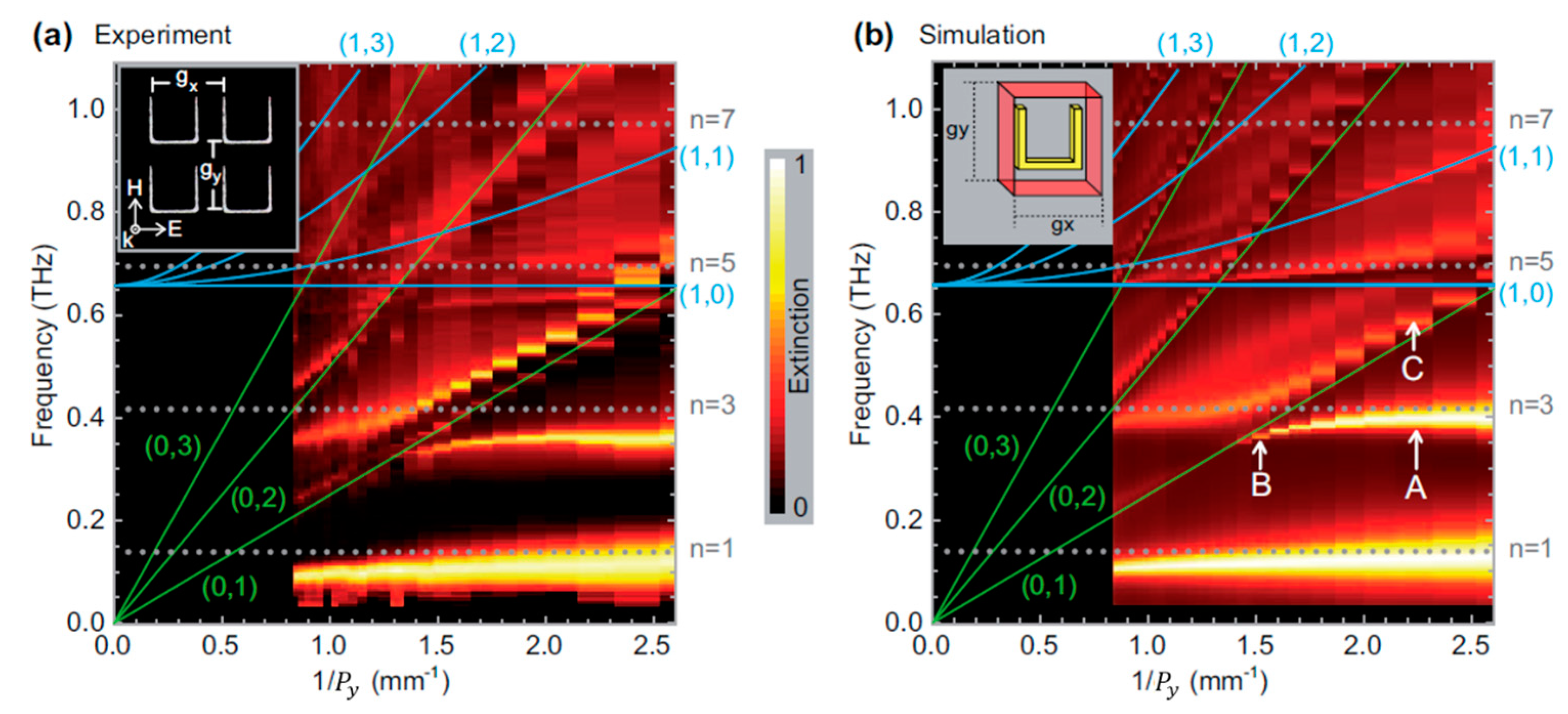
3.2. Hybridized Resonances
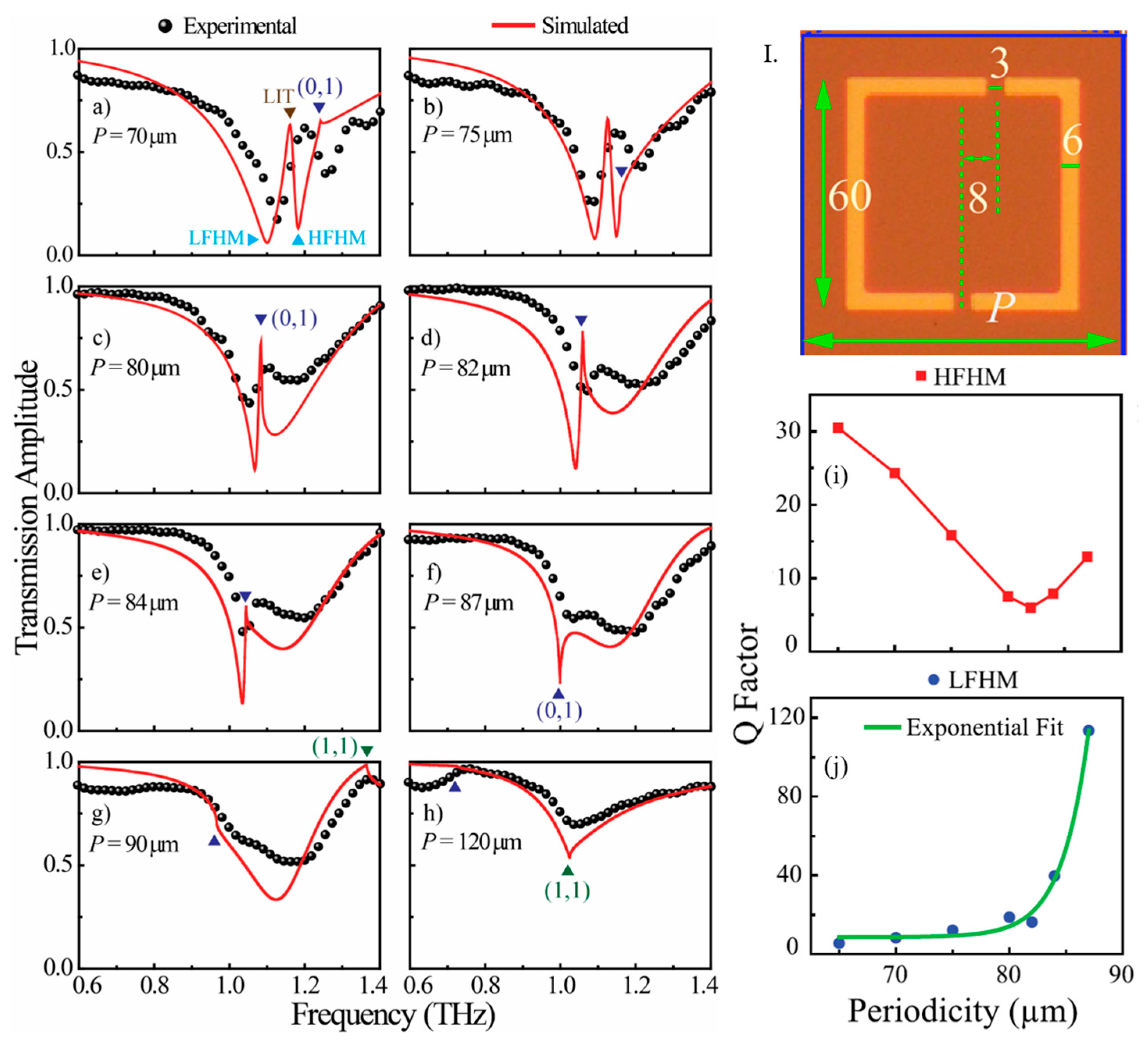
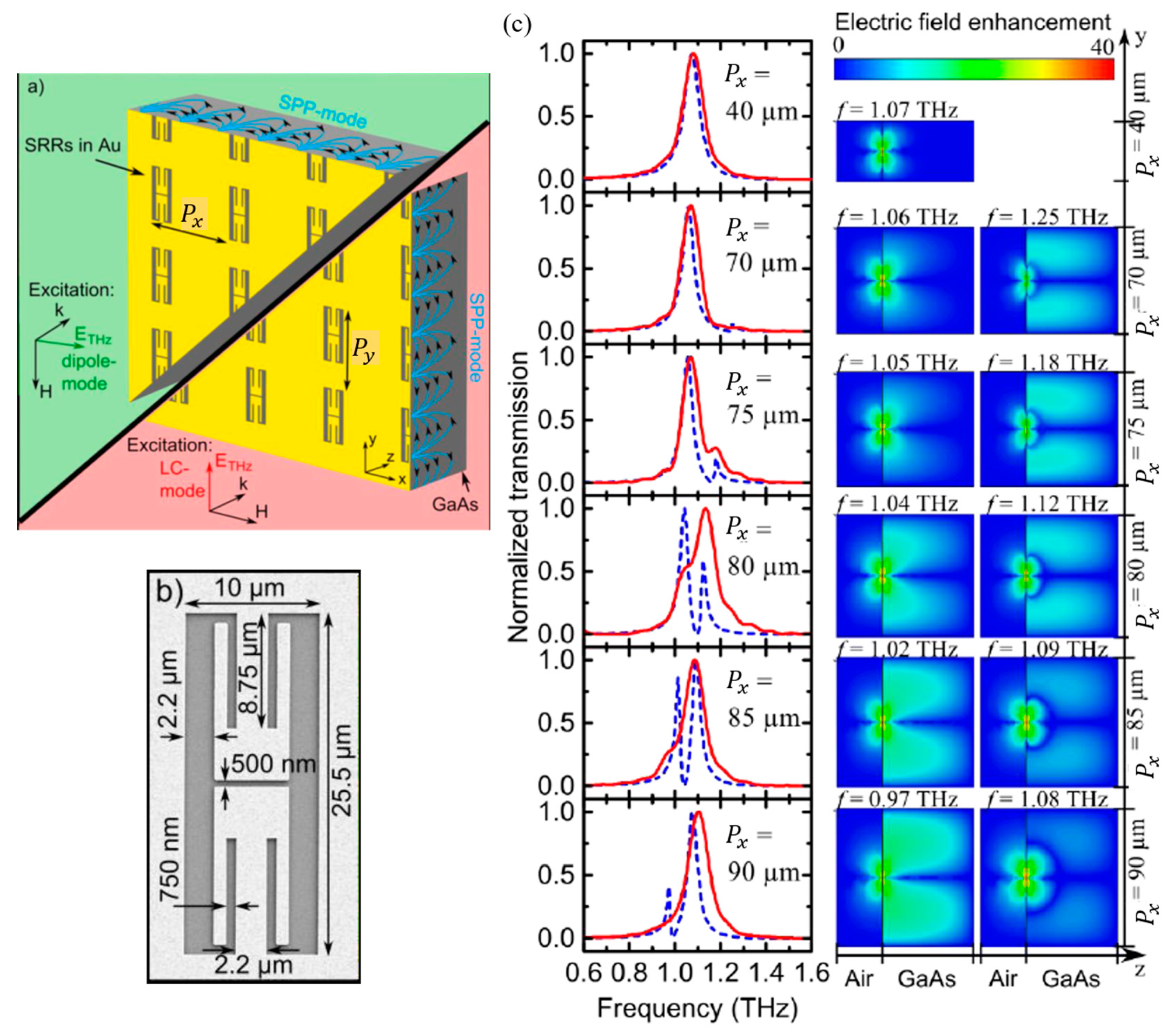
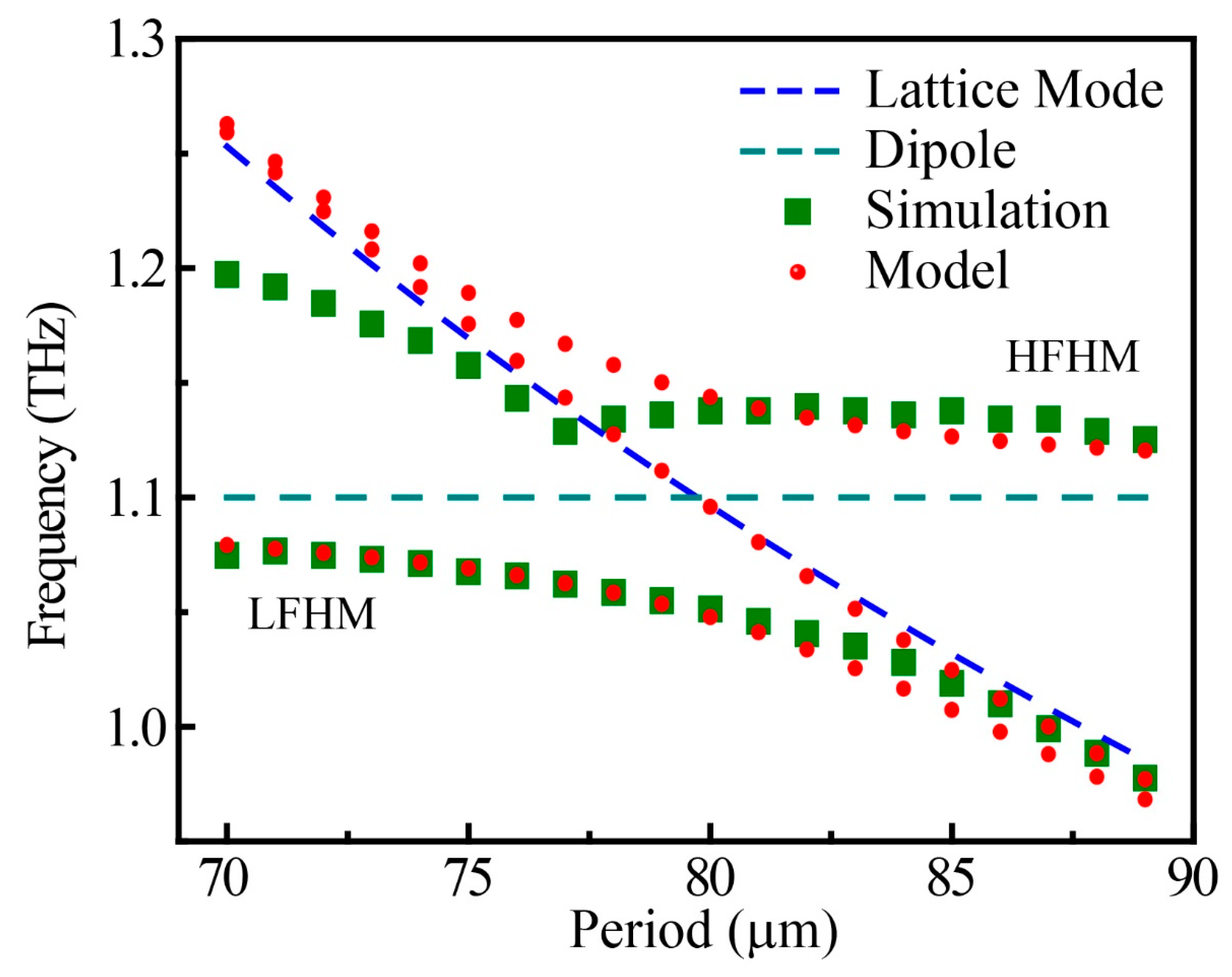
4. Lattice-Induced Transparency (LIT)
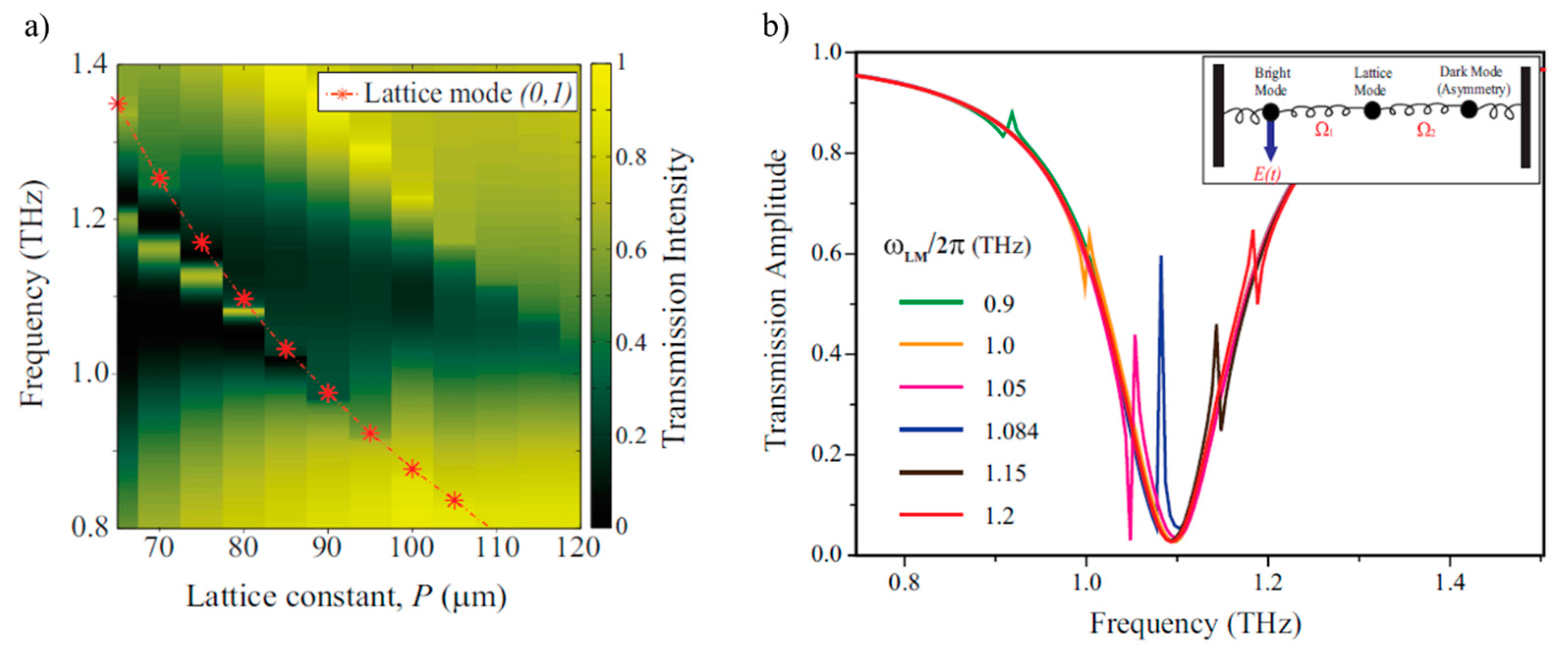
5. Lattice-Mediated Strong Coupling in Metamaterials
6. Future Outlook
6.1. Engineering Resonance Linewidths
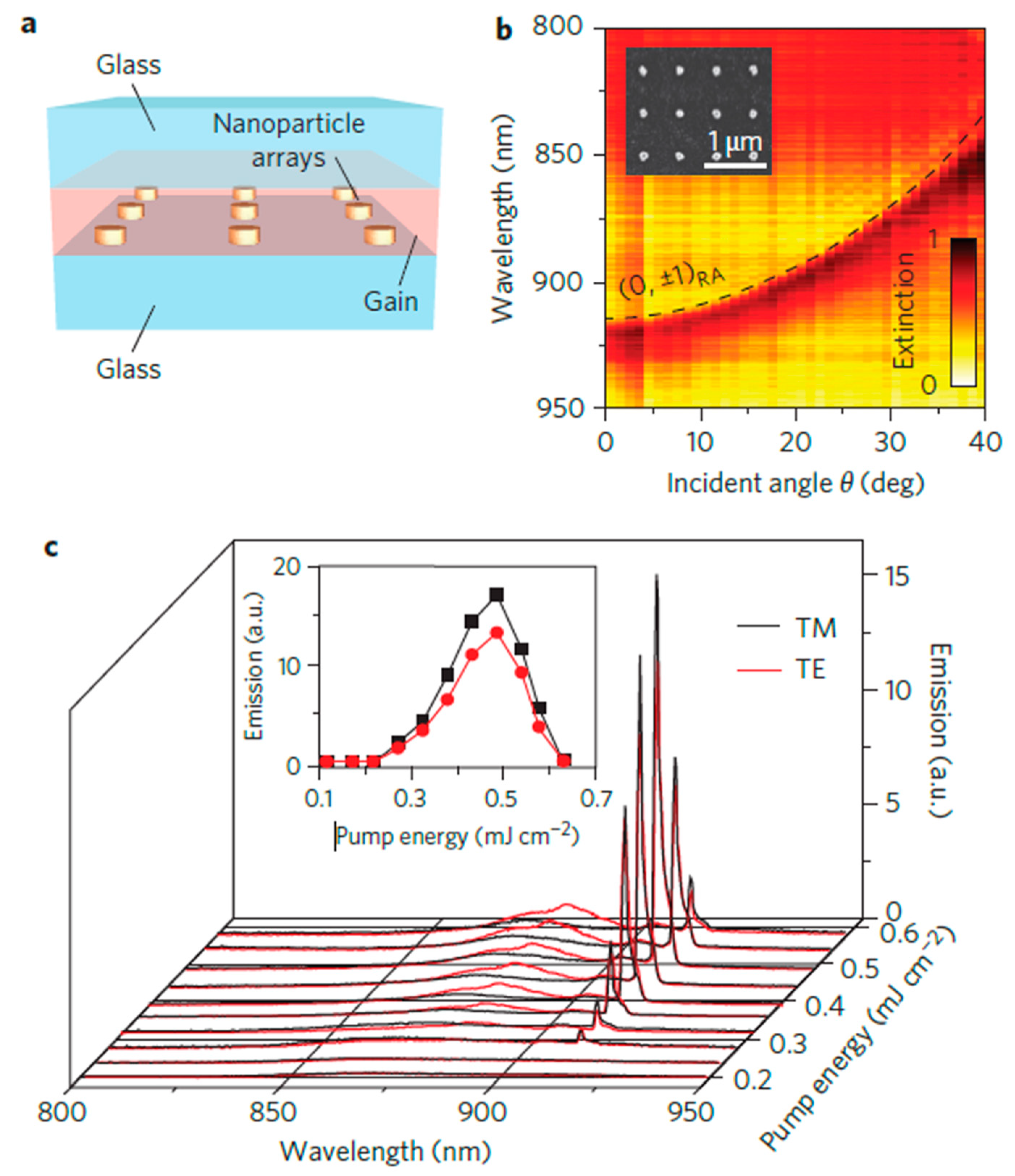
6.2. Low-Threshold Micro/Nano Lasers
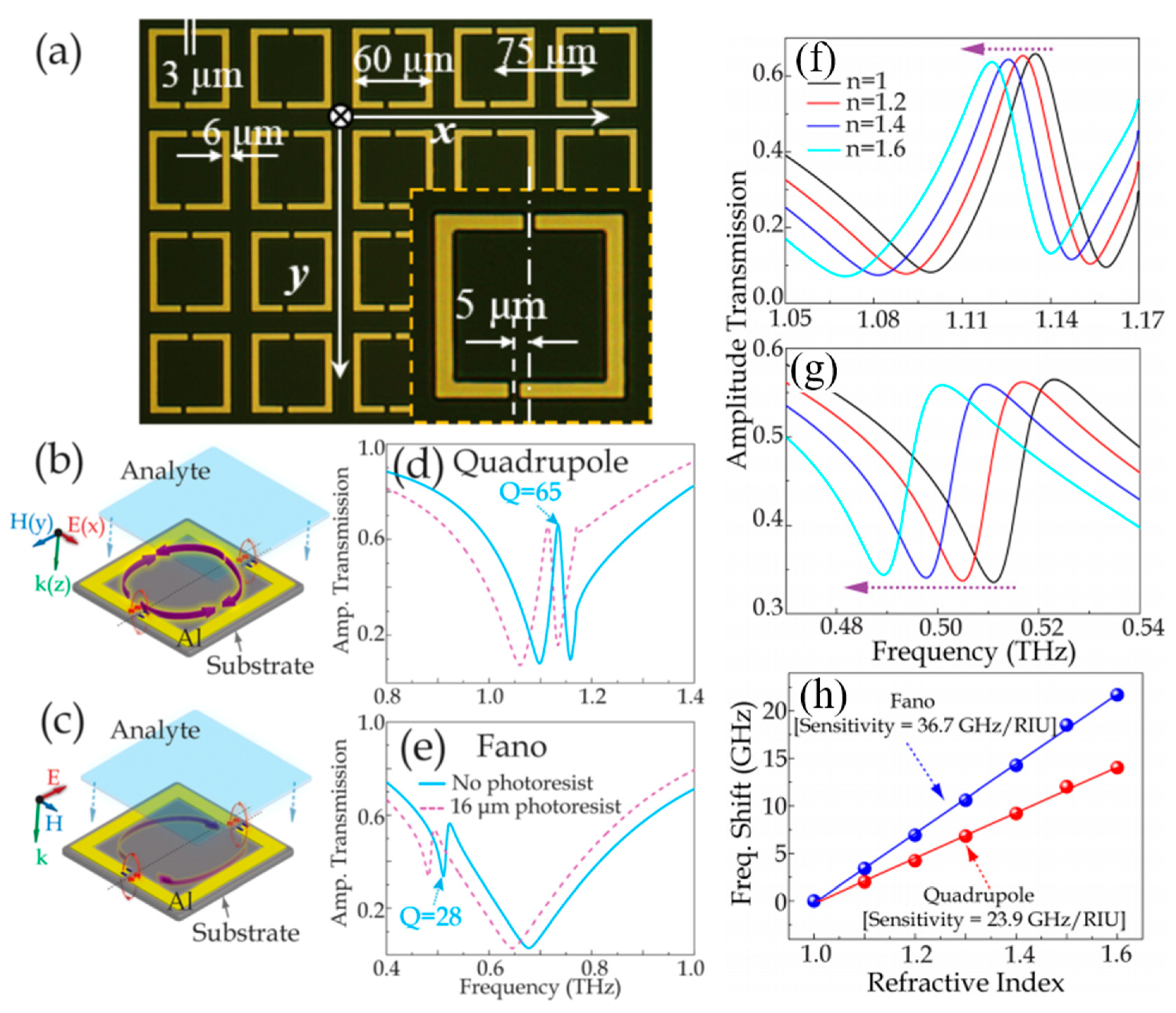
6.3. Sensing
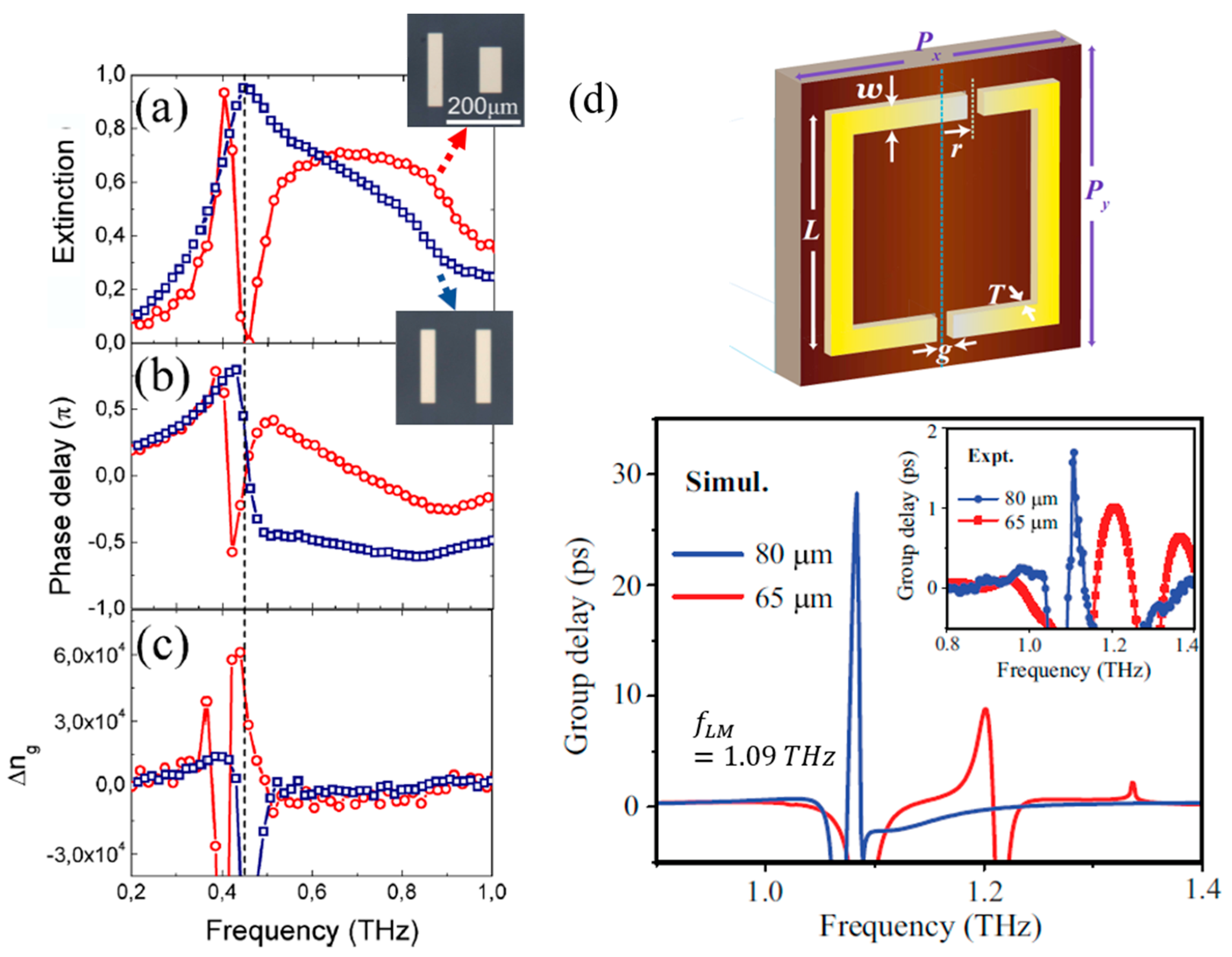
6.4. Slow Light
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wood, R.W., XLII. On a remarkable case of uneven distribution of light in a diffraction grating spectrum. Philos. Mag. 1902, 4, 396–402. [Google Scholar] [CrossRef]
- Rayleigh, L. On the dynamical theory of gratings. Proc. R. Soc. Lond. Ser. A 1907, 79, 399–416. [Google Scholar] [CrossRef]
- Rayleigh, L., III. Note on the remarkable case of diffraction spectra described by Prof. Wood. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1907, 14, 60–65. [Google Scholar] [CrossRef]
- Christ, A.; Zentgraf, T.; Kuhl, J.; Tikhodeev, S.G.; Gippius, N.A.; Giessen, H. Optical properties of planar metallic photonic crystal structures: Experiment and theory. Phys. Rev. B 2004, 70, 125113. [Google Scholar] [CrossRef]
- Gadsdon, M.R.; Hooper, I.R.; Sambles, J.R. Optical resonances on sub-wavelength silver lamellar gratings. Opt. Express 2008, 16, 22003–22028. [Google Scholar] [CrossRef] [PubMed]
- Gomez-Medina, R.; Laroche, M.; Sáenz, J.J. Extraordinary optical reflection from sub-wavelength cylinder arrays. Opt. Express 2006, 14, 3730–3737. [Google Scholar] [CrossRef] [PubMed]
- Lochbihler, H. Enhanced transmission of TE polarized light through wire gratings. Phys. Rev. B 2009, 79, 245427. [Google Scholar] [CrossRef]
- Natarov, D.M.; Byelobrov, V.O.; Sauleau, R.; Benson, T.M.; Nosich, A.I. Periodicity-induced effects in the scattering and absorption of light by infinite and finite gratings of circular silver nanowires. Opt. Express 2011, 19, 22176–22190. [Google Scholar] [CrossRef]
- Schider, G.; Krenn, J.R.; Gotschy, W.; Lamprecht, B.; Ditlbacher, H.; Leitner, A.; Aussenegg, F.R. Optical properties of Ag and Au nanowire gratings. J. Appl. Phys. 2001, 90, 3825–3830. [Google Scholar] [CrossRef]
- Alù, A.; D’Aguanno, G.; Mattiucci, N.; Bloemer, M.J. Plasmonic Brewster Angle: Broadband Extraordinary Transmission through Optical Gratings. Phys. Rev. Lett. 2011, 106, 123902. [Google Scholar] [CrossRef]
- Caglayan, H.; Bulu, I.; Ozbay, E. Extraordinary grating-coupled microwave transmission through a subwavelength annular aperture. Opt. Express 2005, 13, 1666–1671. [Google Scholar] [CrossRef] [PubMed]
- Porto, J.A.; García-Vidal, F.J.; Pendry, J.B. Transmission Resonances on Metallic Gratings with Very Narrow Slits. Phys. Rev. Lett. 1999, 83, 2845–2848. [Google Scholar] [CrossRef]
- Schröter, U.; Heitmann, D. Surface-plasmon-enhanced transmission through metallic gratings. Phys. Rev. B 1998, 58, 15419–15421. [Google Scholar] [CrossRef]
- Wasserman, D.; Shaner, E.A.; Cederberg, J.G. Midinfrared doping-tunable extraordinary transmission from sub-wavelength Gratings. Appl. Phys. Lett. 2007, 90, 191102. [Google Scholar] [CrossRef]
- Fano, U. The Theory of Anomalous Diffraction Gratings and of Quasi-Stationary Waves on Metallic Surfaces (Sommerfeld’s Waves). J. Opt. Soc. Am. 1941, 31, 213–222. [Google Scholar] [CrossRef]
- Barnes, W.L.; Dereux, A.; Ebbesen, T.W. Surface plasmon subwavelength optics. Nature 2003, 424, 824–830. [Google Scholar] [CrossRef] [PubMed]
- Kawata, S.; Inouye, Y.; Verma, P. Plasmonics for near-field nano-imaging and superlensing. Nat. Photonics 2009, 3, 388–394. [Google Scholar] [CrossRef]
- Lal, S.; Link, S.; Halas, N.J. Nano-optics from sensing to waveguiding. Nat. Photonics 2007, 1, 641–648. [Google Scholar] [CrossRef]
- Anker, J.N.; Hall, W.P.; Lyandres, O.; Shah, N.C.; Zhao, J.; Van Duyne, R.P. Biosensing with plasmonic nanosensors. Nat. Mater. 2008, 7, 442–453. [Google Scholar] [CrossRef]
- Kabashin, A.V.; Evans, P.; Pastkovsky, S.; Hendren, W.; Wurtz, G.A.; Atkinson, R.; Pollard, R.; Podolskiy, V.A.; Zayats, A.V. Plasmonic nanorod metamaterials for biosensing. Nat. Mater. 2009, 8, 867–871. [Google Scholar] [CrossRef]
- Kravets, V.G.; Schedin, F.; Jalil, R.; Britnell, L.; Gorbachev, R.V.; Ansell, D.; Thackray, B.; Novoselov, K.S.; Geim, A.K.; Kabashin, A.V.; et al. Singular phase nano-optics in plasmonic metamaterials for label-free single-molecule detection. Nat. Mater. 2013, 12, 304–309. [Google Scholar] [CrossRef] [PubMed]
- Sreekanth, K.V.; Alapan, Y.; ElKabbash, M.; Ilker, E.; Hinczewski, M.; Gurkan, U.A.; De Luca, A.; Strangi, G. Extreme sensitivity biosensing platform based on hyperbolic metamaterials. Nat. Mater. 2016, 15, 621–627. [Google Scholar] [CrossRef] [PubMed]
- Fang, N.; Lee, H.; Sun, C.; Zhang, X. Sub–Diffraction-Limited Optical Imaging with a Silver Superlens. Science 2005, 308, 534–537. [Google Scholar] [CrossRef] [PubMed]
- Pendry, J.B. Negative Refraction Makes a Perfect Lens. Phys. Rev. Lett. 2000, 85, 3966–3969. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.-J.; Kim, J.; Chen, H.-Y.; Wu, C.; Dabidian, N.; Sanders, C.E.; Wang, C.-Y.; Lu, M.-Y.; Li, B.-H.; Qiu, X.; et al. Plasmonic Nanolaser Using Epitaxially Grown Silver Film. Science 2012, 337, 450–453. [Google Scholar] [CrossRef] [PubMed]
- Suh, J.Y.; Kim, C.H.; Zhou, W.; Huntington, M.D.; Co, D.T.; Wasielewski, M.R.; Odom, T.W. Plasmonic Bowtie Nanolaser Arrays. Nano Lett. 2012, 12, 5769–5774. [Google Scholar] [CrossRef]
- Mayer, K.M.; Hafner, J.H. Localized Surface Plasmon Resonance Sensors. Chem. Rev. 2011, 111, 3828–3857. [Google Scholar] [CrossRef]
- Ritchie, R.H.; Eldridge, H.B. Optical Emission from Irradiated Foils. I. Phys. Rev. 1962, 126, 1935–1947. [Google Scholar] [CrossRef]
- Stern, E.A.; Ferrell, R.A. Surface Plasma Oscillations of a Degenerate Electron Gas. Phys. Rev. 1960, 120, 130–136. [Google Scholar] [CrossRef]
- Heitmann, D. Radiative decay of surface plasmons excited by fast electrons on periodically modulated silver surfaces. J. Phys. C Solid State Phys. 1977, 10, 397–405. [Google Scholar] [CrossRef]
- Kretschmann, E.; Raether, H. Radiative Decay of Non Radiative Surface Plasmons Excited by Light. Z. Nat. A 1968, 23, 2135–2136. [Google Scholar] [CrossRef]
- Maradudin, A.A.; Simonsen, I.; Polanco, J.; Fitzgerald, R.M. Rayleigh and Wood anomalies in the diffraction of light from a perfectly conducting reflection grating. J. Opt. 2016, 18, 024004. [Google Scholar] [CrossRef]
- Qu, D.; Grischkowsky, D.; Zhang, W. Terahertz transmission properties of thin, subwavelength metallic hole arrays. Opt. Lett. 2004, 29, 896–898. [Google Scholar] [CrossRef] [PubMed]
- Kravets, V.G.; Kabashin, A.V.; Barnes, W.L.; Grigorenko, A.N. Plasmonic Surface Lattice Resonances: A Review of Properties and Applications. Chem. Rev. 2018, 118, 5912–5951. [Google Scholar] [CrossRef] [PubMed]
- Manjappa, M.; Srivastava, Y.K.; Singh, R. Lattice-induced transparency in planar metamaterials. Phys. Rev. B 2016, 94, 161103. [Google Scholar] [CrossRef]
- Tan, T.C.; Srivastava, Y.K.; Manjappa, M.; Plum, E.; Singh, R. Lattice induced strong coupling and line narrowing of split resonances in metamaterials. Appl. Phys. Lett. 2018, 112, 201111. [Google Scholar] [CrossRef]
- Xu, N.; Singh, R.; Zhang, W. High-Q lattice mode matched structural resonances in terahertz metasurfaces. Appl. Phys. Lett. 2016, 109, 021108. [Google Scholar] [CrossRef]
- Bitzer, A.; Wallauer, J.; Helm, H.; Merbold, H.; Feurer, T.; Walther, M. Lattice modes mediate radiative coupling in metamaterial arrays. Opt. Express 2009, 17, 22108–22113. [Google Scholar] [CrossRef]
- Keller, J.; Maissen, C.; Haase, J.; Paravicini-Bagliani, G.L.; Valmorra, F.; Palomo, J.; Mangeney, J.; Tignon, J.; Dhillon, S.S.; Scalari, G.; et al. Coupling Surface Plasmon Polariton Modes to Complementary THz Metasurfaces Tuned by Inter Meta-Atom Distance. Adv. Opt. Mater. 2017, 5, 1600884. [Google Scholar] [CrossRef]
- Klarskov, P.; Tarekegne, A.T.; Iwaszczuk, K.; Zhang, X.C.; Jepsen, P.U. Amplification of resonant field enhancement by plasmonic lattice coupling in metallic slit arrays. Sci. Rep. 2016, 6, 37738. [Google Scholar] [CrossRef]
- Schaafsma, M.C.; Bhattacharya, A.; Rivas, J.G. Diffraction Enhanced Transparency and Slow THz Light in Periodic Arrays of Detuned and Displaced Dipoles. ACS Photonics 2016, 3, 1596–1603. [Google Scholar] [CrossRef]
- Yu, L.; Wang, Q.; Hu, F.; Huang, Y.; Liu, C.; Zhang, L.; Xu, X. Coupling Between Metamolecular Modes and Lattice Diffraction Modes of Metamaterials in Terahertz Region. Plasmonics 2018, 13, 961–969. [Google Scholar] [CrossRef]
- Kravets, V.G.; Schedin, F.; Grigorenko, A.N. Extremely Narrow Plasmon Resonances Based on Diffraction Coupling of Localized Plasmons in Arrays of Metallic Nanoparticles. Phys. Rev. Lett. 2008, 101, 087403. [Google Scholar] [CrossRef] [PubMed]
- Tonouchi, M. Cutting-edge terahertz technology. Nat. Photonics 2007, 1, 97–105. [Google Scholar] [CrossRef]
- Koenig, S.; Lopez-Diaz, D.; Antes, J.; Boes, F.; Henneberger, R.; Leuther, A.; Tessmann, A.; Schmogrow, R.; Hillerkuss, D.; Palmer, R.; et al. Wireless sub-THz communication system with high data rate. Nat. Photonics 2013, 7, 977–981. [Google Scholar] [CrossRef]
- Danciu, M.; Alexa-Stratulat, T.; Stefanescu, C.; Dodi, G.; Tamba, I.B.; Mihai, T.C.; Stanciu, D.G.; Luca, A.; Spiridon, A.I.; Ungureanu, B.L.; et al. Terahertz Spectroscopy and Imaging: A Cutting-Edge Method for Diagnosing Digestive Cancers. Materials 2019, 12, 1519. [Google Scholar] [CrossRef] [PubMed]
- Siegel, P.H. Terahertz technology in biology and medicine. IEEE Trans. Microw. Theory Tech. 2004, 52, 2438–2447. [Google Scholar] [CrossRef]
- Smye, S.W.; Chamberlain, J.M.; Fitzgerald, A.J.; Berry, E. The interaction between Terahertz radiation and biological tissue. Phys. Med. Biol. 2001, 46, R101–R112. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Zhao, X.; Yang, K.; Liu, Y.; Liu, Y.; Fu, W.; Luo, Y. Biomedical Applications of Terahertz Spectroscopy and Imaging. Trends Biotechnol. 2016, 34, 810–824. [Google Scholar] [CrossRef] [PubMed]
- Yu, C.; Fan, S.; Sun, Y.; Pickwell-MacPherson, E. The potential of terahertz imaging for cancer diagnosis: A review of investigations to date. Quant. Imaging Med. Surg. 2012, 2, 33–45. [Google Scholar] [PubMed]
- Fedotov, V.A.; Papasimakis, N.; Plum, E.; Bitzer, A.; Walther, M.; Kuo, P.; Tsai, D.P.; Zheludev, N.I. Spectral Collapse in Ensembles of Metamolecules. Phys. Rev. Lett. 2010, 104, 223901. [Google Scholar] [CrossRef] [PubMed]
- Jenkins, S.D.; Ruostekoski, J. Cooperative resonance linewidth narrowing in a planar metamaterial. New J. Phys. 2012, 14, 103003. [Google Scholar] [CrossRef][Green Version]
- Jenkins, S.D.; Ruostekoski, J. Resonance linewidth and inhomogeneous broadening in a metamaterial array. Phys. Rev. B 2012, 86, 205128. [Google Scholar] [CrossRef]
- Jenkins, S.D.; Ruostekoski, J. Metamaterial Transparency Induced by Cooperative Electromagnetic Interactions. Phys. Rev. Lett. 2013, 111, 147401. [Google Scholar] [CrossRef] [PubMed]
- Keller, J.; Haase, J.; Appugliese, F.; Rajabali, S.; Wang, Z.; Paravicini-Bagliani, G.L.; Maissen, C.; Scalari, G.; Faist, J. Superradiantly Limited Linewidth in Complementary THz Metamaterials on Si-Membranes. Adv. Opt. Mater. 2018, 6, 1800210. [Google Scholar] [CrossRef]
- Singh, R.; Rockstuhl, C.; Zhang, W. Strong influence of packing density in terahertz metamaterials. Appl. Phys. Lett. 2010, 97, 241108. [Google Scholar] [CrossRef]
- Boltasseva, A.; Atwater, H.A. Low-Loss Plasmonic Metamaterials. Science 2011, 331, 290–291. [Google Scholar] [CrossRef] [PubMed]
- Güney, D.Ö.; Koschny, T.; Soukoulis, C.M. Reducing ohmic losses in metamaterials by geometric tailoring. Phys. Rev. B 2009, 80, 125129. [Google Scholar] [CrossRef]
- Khurgin, J.B. How to deal with the loss in plasmonics and metamaterials. Nat. Nanotechnol. 2015, 10, 2–6. [Google Scholar] [CrossRef]
- Khlopin, D.; Laux, F.; Wardley, W.P.; Martin, J.; Wurtz, G.A.; Plain, J.; Bonod, N.; Zayats, A.V.; Dickson, W.; Gérard, D. Lattice modes and plasmonic linewidth engineering in gold and aluminum nanoparticle arrays. J. Opt. Soc. Am. B 2017, 34, 691–700. [Google Scholar] [CrossRef]
- Rodriguez, S.R.K.; Abass, A.; Maes, B.; Janssen, O.T.A.; Vecchi, G.; Gómez Rivas, J. Coupling Bright and Dark Plasmonic Lattice Resonances. Phys. Rev. X 2011, 1, 021019. [Google Scholar] [CrossRef]
- Swiecicki, S.D.; Sipe, J.E. Surface-lattice resonances in two-dimensional arrays of spheres: Multipolar interactions and a mode analysis. Phys. Rev. B 2017, 95, 195406. [Google Scholar] [CrossRef]
- Li, S.-Q.; Zhou, W.; Bruce Buchholz, D.; Ketterson, J.B.; Ocola, L.E.; Sakoda, K.; Chang, R.P.H. Ultra-sharp plasmonic resonances from monopole optical nanoantenna phased arrays. Appl. Phys. Lett. 2014, 104, 231101. [Google Scholar] [CrossRef]
- Meinzer, N.; Barnes, W.L.; Hooper, I.R. Plasmonic meta-atoms and metasurfaces. Nat. Photonics 2014, 8, 889–898. [Google Scholar] [CrossRef]
- Thackray, B.D.; Thomas, P.A.; Auton, G.H.; Rodriguez, F.J.; Marshall, O.P.; Kravets, V.G.; Grigorenko, A.N. Super-Narrow, Extremely High Quality Collective Plasmon Resonances at Telecom Wavelengths and Their Application in a Hybrid Graphene-Plasmonic Modulator. Nano Lett. 2015, 15, 3519–3523. [Google Scholar] [CrossRef] [PubMed]
- Zilio, P.; Malerba, M.; Toma, A.; Zaccaria, R.P.; Jacassi, A.; Angelis, F.D. Hybridization in Three Dimensions: A Novel Route toward Plasmonic Metamolecules. Nano Lett. 2015, 15, 5200–5207. [Google Scholar] [CrossRef] [PubMed]
- Danilov, A.; Tselikov, G.; Wu, F.; Kravets, V.G.; Ozerov, I.; Bedu, F.; Grigorenko, A.N.; Kabashin, A.V. Ultra-narrow surface lattice resonances in plasmonic metamaterial arrays for biosensing applications. Biosens. Bioelectron. 2018, 104, 102–112. [Google Scholar] [CrossRef] [PubMed]
- Auguié, B.; Barnes, W.L. Collective Resonances in Gold Nanoparticle Arrays. Phys. Rev. Lett. 2008, 101, 143902. [Google Scholar] [CrossRef] [PubMed]
- Zou, S.; Janel, N.; Schatz, G.C. Silver nanoparticle array structures that produce remarkably narrow plasmon lineshapes. J. Chem. Phys. 2004, 120, 10871–10875. [Google Scholar] [CrossRef] [PubMed]
- Rajeeva, B.B.; Lin, L.; Zheng, Y. Design and applications of lattice plasmon resonances. Nano Res. 2018, 11, 4423–4440. [Google Scholar] [CrossRef]
- Ross, M.B.; Mirkin, C.A.; Schatz, G.C. Optical Properties of One-, Two-, and Three-Dimensional Arrays of Plasmonic Nanostructures. J. Phys. Chem. C 2016, 120, 816–830. [Google Scholar] [CrossRef]
- Wang, W.; Ramezani, M.; Väkeväinen, A.I.; Törmä, P.; Rivas, J.G.; Odom, T.W. The rich photonic world of plasmonic nanoparticle arrays. Mater. Today 2018, 21, 303–314. [Google Scholar] [CrossRef]
- Fedotov, V.A.; Rose, M.; Prosvirnin, S.L.; Papasimakis, N.; Zheludev, N.I. Sharp Trapped-Mode Resonances in Planar Metamaterials with a Broken Structural Symmetry. Phys. Rev. Lett. 2007, 99, 147401. [Google Scholar] [CrossRef] [PubMed]
- Ekmekci, E.; Strikwerda, A.C.; Fan, K.; Keiser, G.; Zhang, X.; Turhan-Sayan, G.; Averitt, R.D. Frequency tunable terahertz metamaterials using broadside coupled split-ring resonators. Phys. Rev. B 2011, 83, 193103. [Google Scholar] [CrossRef]
- Powell, D.A.; Lapine, M.; Gorkunov, M.V.; Shadrivov, I.V.; Kivshar, Y.S. Metamaterial tuning by manipulation of near-field interaction. Phys. Rev. B 2010, 82, 155128. [Google Scholar] [CrossRef]
- Shi, J.H.; Plum, E.; Fedotov, V.A.; Zheludev, N.I. Tuning trapped-mode resonances in a planar metamaterial. In Proceedings of the Progress in Electromagnetics Research Symposium (PIERS 2011), Marrakesh, Morocco, 20–23 March 2011; pp. 567–571. [Google Scholar]
- Boller, K.J.; Imamoğlu, A.; Harris, S.E. Observation of electromagnetically induced transparency. Phys. Rev. Lett. 1991, 66, 2593–2596. [Google Scholar] [CrossRef]
- Fleischhauer, M.; Imamoglu, A.; Marangos, J.P. Electromagnetically induced transparency: Optics in coherent media. Rev. Mod. Phys. 2005, 77, 633–673. [Google Scholar] [CrossRef]
- Papasimakis, N.; Fedotov, V.A.; Zheludev, N.I.; Prosvirnin, S.L. Metamaterial Analog of Electromagnetically Induced Transparency. Phys. Rev. Lett. 2008, 101, 253903. [Google Scholar] [CrossRef] [PubMed]
- Tassin, P.; Zhang, L.; Koschny, T.; Economou, E.N.; Soukoulis, C.M. Low-Loss Metamaterials Based on Classical Electromagnetically Induced Transparency. Phys. Rev. Lett. 2009, 102, 053901. [Google Scholar] [CrossRef]
- Bai, Q.; Liu, C.; Chen, J.; Cheng, C.; Kang, M.; Wang, H.-T. Tunable slow light in semiconductor metamaterial in a broad terahertz regime. J. Appl. Phys. 2010, 107, 093104. [Google Scholar] [CrossRef]
- Lu, C.; Hu, X.; Shi, K.; Hu, Q.; Zhu, R.; Yang, H.; Gong, Q. An actively ultrafast tunable giant slow-light effect in ultrathin nonlinear metasurfaces. Light Sci. Amp Appl. 2015, 4, e302. [Google Scholar] [CrossRef]
- Panahpour, A.; Silani, Y.; Farrokhian, M.; Lavrinenko, A.V.; Latifi, H. Coupled plasmon-exciton induced transparency and slow light in plexcitonic metamaterials. J. Opt. Soc. Am. B 2012, 29, 2297–2308. [Google Scholar] [CrossRef]
- Harris, S.E.; Hau, L.V. Nonlinear Optics at Low Light Levels. Phys. Rev. Lett. 1999, 82, 4611–4614. [Google Scholar] [CrossRef]
- Liu, N.; Langguth, L.; Weiss, T.; Kastel, J.; Fleischhauer, M.; Pfau, T.; Giessen, H. Plasmonic analogue of electromagnetically induced transparency at the Drude damping limit. Nat. Mater. 2009, 8, 758–762. [Google Scholar] [CrossRef] [PubMed]
- Liu, N.; Weiss, T.; Mesch, M.; Langguth, L.; Eigenthaler, U.; Hirscher, M.; Sönnichsen, C.; Giessen, H. Planar Metamaterial Analogue of Electromagnetically Induced Transparency for Plasmonic Sensing. Nano Lett. 2010, 10, 1103–1107. [Google Scholar] [CrossRef]
- Novotny, L. Strong coupling, energy splitting, and level crossings: A classical perspective. Am. J. Phys. 2010, 78, 1199–1202. [Google Scholar] [CrossRef]
- Zhang, S.; Genov, D.A.; Wang, Y.; Liu, M.; Zhang, X. Plasmon-Induced Transparency in Metamaterials. Phys. Rev. Lett. 2008, 101, 047401. [Google Scholar] [CrossRef]
- Manjappa, M.; Chiam, S.-Y.; Cong, L.; Bettiol, A.A.; Zhang, W.; Singh, R. Tailoring the slow light behavior in terahertz metasurfaces. Appl. Phys. Lett. 2015, 106, 181101. [Google Scholar] [CrossRef]
- Gu, J.; Singh, R.; Liu, X.; Zhang, X.; Ma, Y.; Zhang, S.; Maier, S.A.; Tian, Z.; Azad, A.K.; Chen, H.-T.; et al. Active control of electromagnetically induced transparency analogue in terahertz metamaterials. Nat. Commun. 2012, 3, 1151. [Google Scholar] [CrossRef]
- Chen, X.; Fan, W. Ultrasensitive terahertz metamaterial sensor based on spoof surface plasmon. Sci. Rep. 2017, 7, 2092. [Google Scholar] [CrossRef]
- Islam, M.; Rao, S.J.M.; Kumar, G.; Pal, B.P.; Roy Chowdhury, D. Role of Resonance Modes on Terahertz Metamaterials based Thin Film Sensors. Sci. Rep. 2017, 7, 7355. [Google Scholar] [CrossRef] [PubMed]
- Zheludev, N.I.; Prosvirnin, S.L.; Papasimakis, N.; Fedotov, V.A. Lasing spaser. Nat. Photonics 2008, 2, 351–354. [Google Scholar] [CrossRef]
- Väkeväinen, A.I.; Moerland, R.J.; Rekola, H.T.; Eskelinen, A.P.; Martikainen, J.P.; Kim, D.H.; Törmä, P. Plasmonic Surface Lattice Resonances at the Strong Coupling Regime. Nano Lett. 2014, 14, 1721–1727. [Google Scholar] [CrossRef] [PubMed]
- Zhou, W.; Dridi, M.; Suh, J.Y.; Kim, C.H.; Co, D.T.; Wasielewski, M.R.; Schatz, G.C.; Odom, T.W. Lasing action in strongly coupled plasmonic nanocavity arrays. Nat. Nanotechnol. 2013, 8, 506–511. [Google Scholar] [CrossRef] [PubMed]
- Vasa, P.; Pomraenke, R.; Schwieger, S.; Mazur, Y.I.; Kunets, V.; Srinivasan, P.; Johnson, E.; Kihm, J.E.; Kim, D.S.; Runge, E.; et al. Coherent Exciton–Surface-Plasmon-Polariton Interaction in Hybrid Metal-Semiconductor Nanostructures. Phys. Rev. Lett. 2008, 101, 116801. [Google Scholar] [CrossRef] [PubMed]
- Neubrech, F.; Pucci, A.; Cornelius, T.W.; Karim, S.; García-Etxarri, A.; Aizpurua, J. Resonant Plasmonic and Vibrational Coupling in a Tailored Nanoantenna for Infrared Detection. Phys. Rev. Lett. 2008, 101, 157403. [Google Scholar] [CrossRef] [PubMed]
- Neubrech, F.; Weber, D.; Enders, D.; Nagao, T.; Pucci, A. Antenna Sensing of Surface Phonon Polaritons. J. Phys. Chem. C 2010, 114, 7299–7301. [Google Scholar] [CrossRef]
- Shelton, D.J.; Brener, I.; Ginn, J.C.; Sinclair, M.B.; Peters, D.W.; Coffey, K.R.; Boreman, G.D. Strong Coupling between Nanoscale Metamaterials and Phonons. Nano Lett. 2011, 11, 2104–2108. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, K.; Plum, E.; Ou, J.Y.; Uchino, T.; Zheludev, N.I. Multifold Enhancement of Quantum Dot Luminescence in Plasmonic Metamaterials. Phys. Rev. Lett. 2010, 105, 227403. [Google Scholar] [CrossRef] [PubMed]
- Van Beijnum, F.; van Veldhoven, P.J.; Geluk, E.J.; de Dood, M.J.; Gert, W.; van Exter, M.P. Surface Plasmon Lasing Observed in Metal Hole Arrays. Phys. Rev. Lett. 2013, 110, 206802. [Google Scholar] [CrossRef]
- Singh, R.; Cao, W.; Al-Naib, I.; Cong, L.; Withayachumnankul, W.; Zhang, W. Ultrasensitive terahertz sensing with high-Q Fano resonances in metasurfaces. Appl. Phys. Lett. 2014, 105, 171101. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, T.C.; Plum, E.; Singh, R. Surface Lattice Resonances in THz Metamaterials. Photonics 2019, 6, 75. https://doi.org/10.3390/photonics6030075
Tan TC, Plum E, Singh R. Surface Lattice Resonances in THz Metamaterials. Photonics. 2019; 6(3):75. https://doi.org/10.3390/photonics6030075
Chicago/Turabian StyleTan, Thomas CaiWei, Eric Plum, and Ranjan Singh. 2019. "Surface Lattice Resonances in THz Metamaterials" Photonics 6, no. 3: 75. https://doi.org/10.3390/photonics6030075
APA StyleTan, T. C., Plum, E., & Singh, R. (2019). Surface Lattice Resonances in THz Metamaterials. Photonics, 6(3), 75. https://doi.org/10.3390/photonics6030075




