The Theoretical Concept of Polarization Reflectometric Interference Spectroscopy (PRIFS): An Optical Method to Monitor Molecule Adsorption and Nanoparticle Adhesion on the Surface of Thin Films
Abstract
1. Introduction
2. Methods
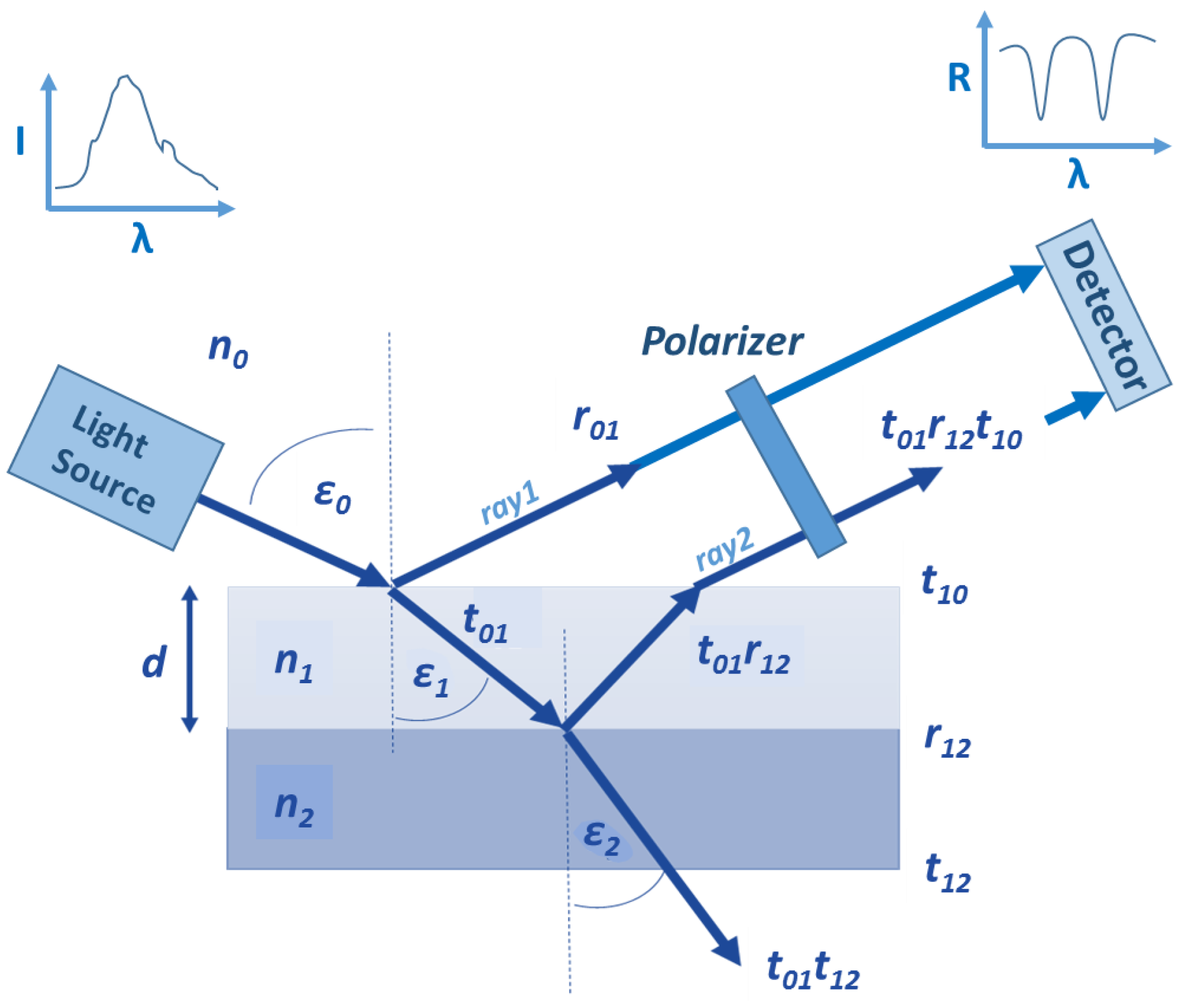
2.1. The Reflectometric Interference Spectroscopy Principle
2.2. The Polarization Reflectometric Interference Spectroscopy Principle
3. Results and Discussion
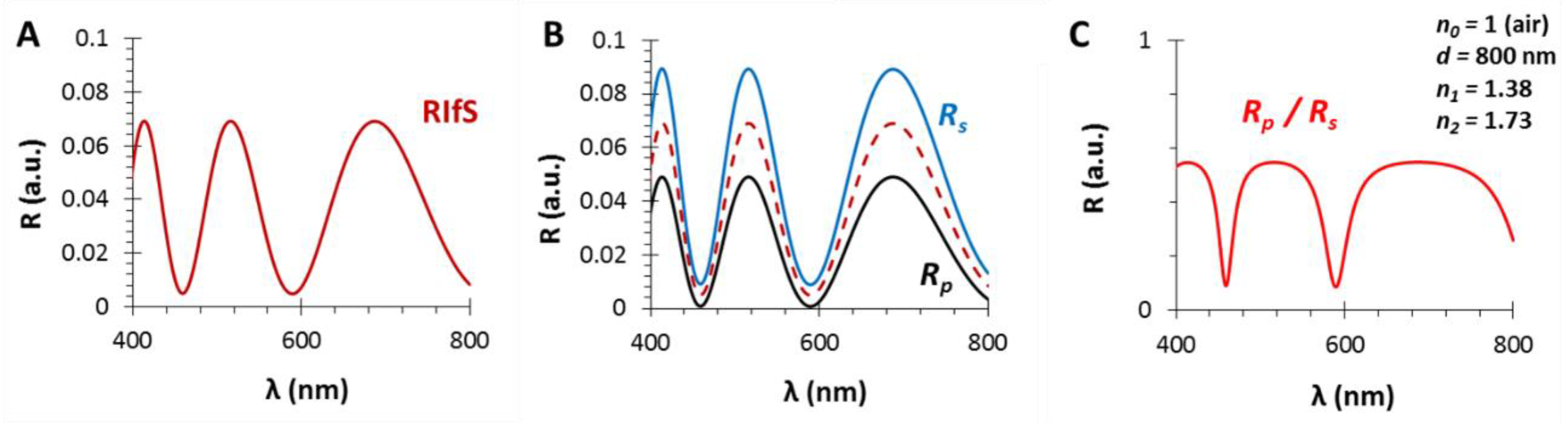
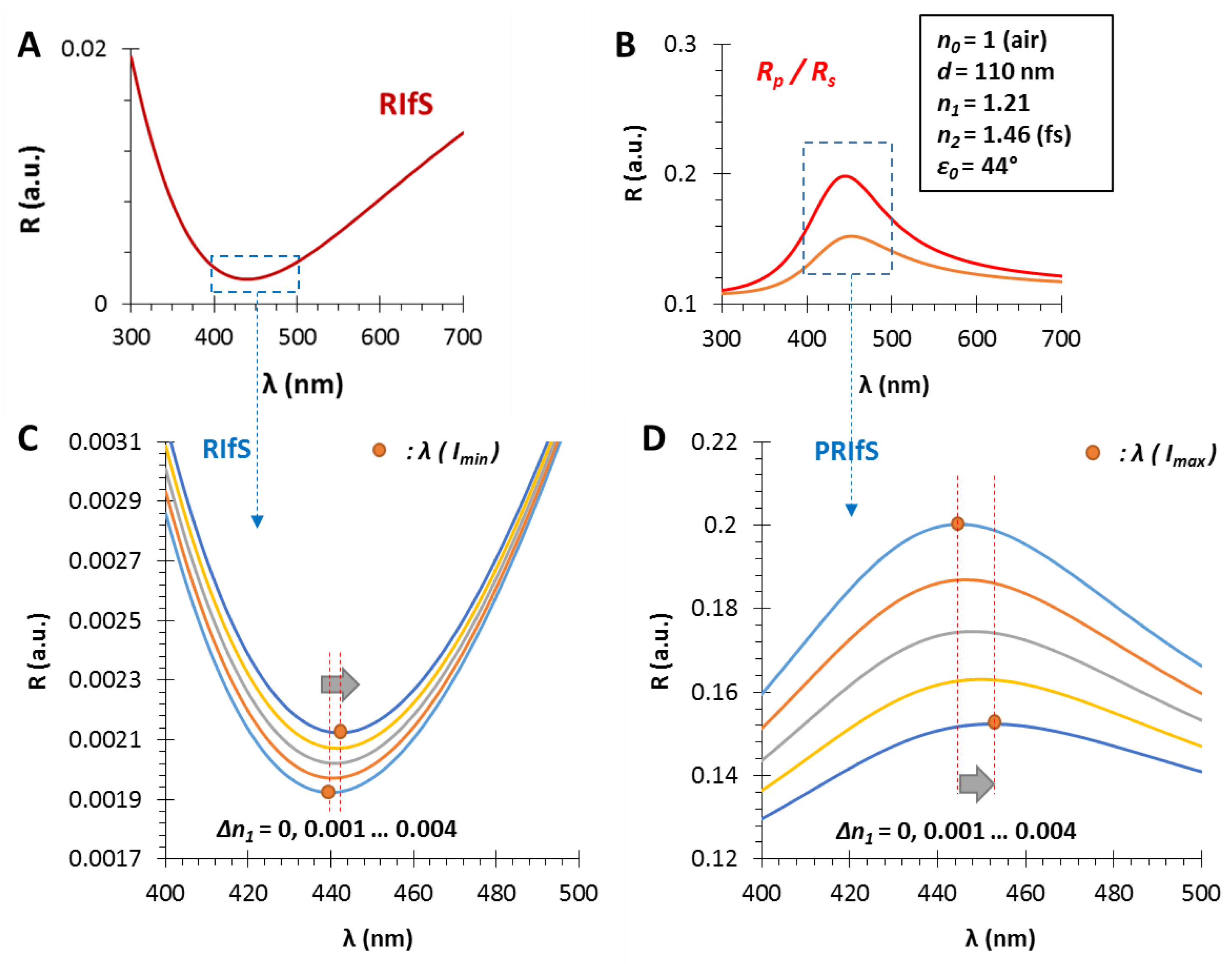
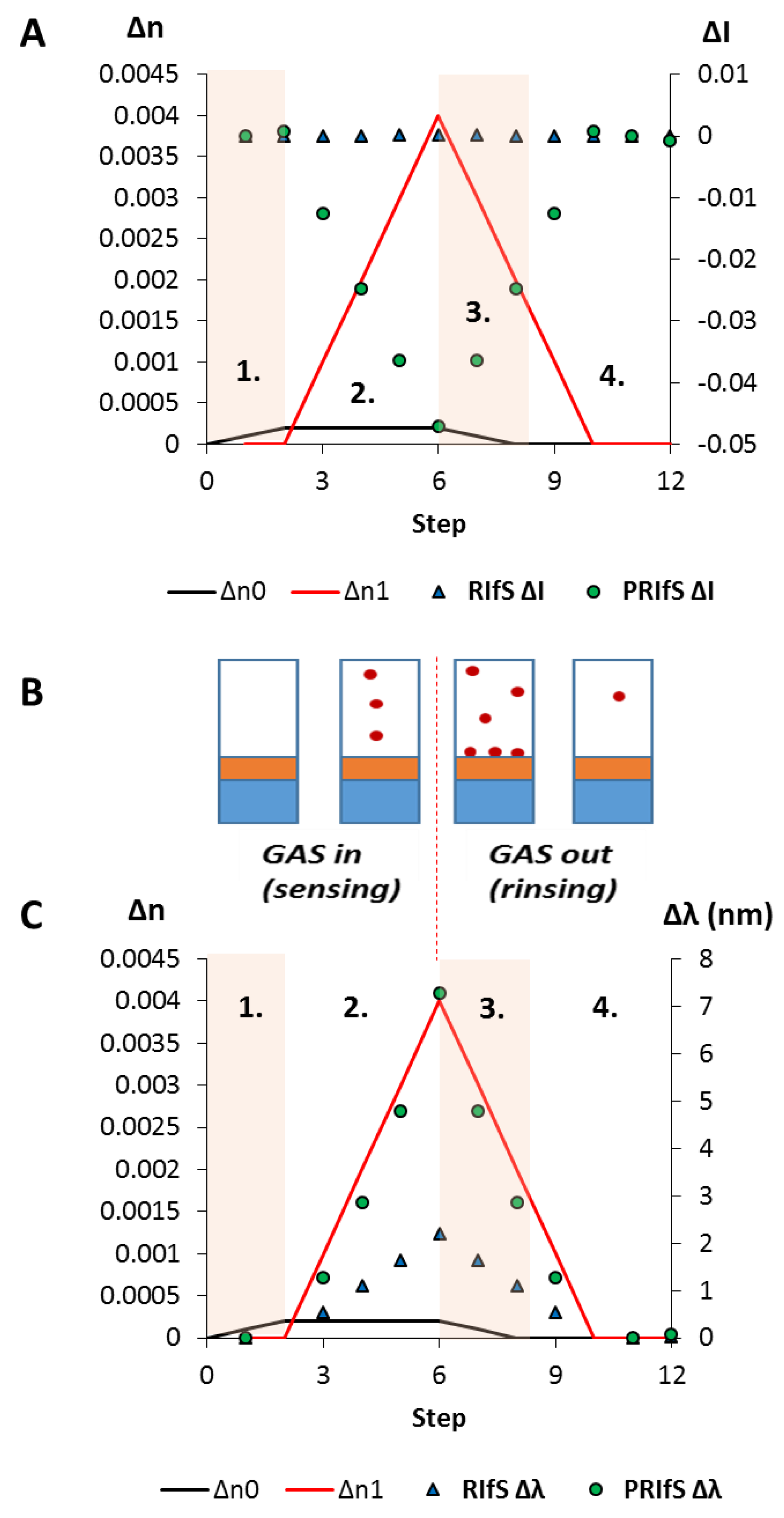
3.1. The Film Thickness (d)
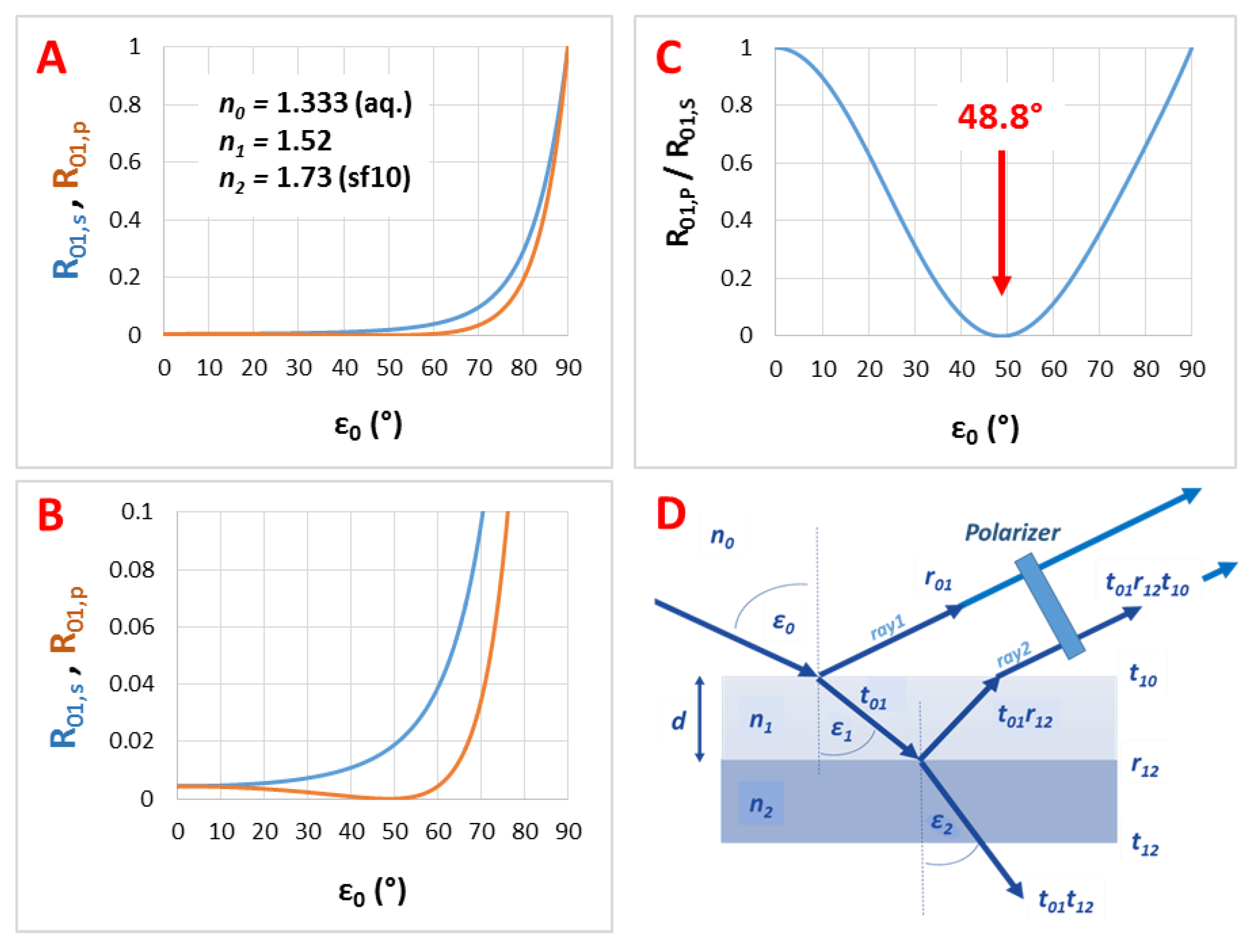
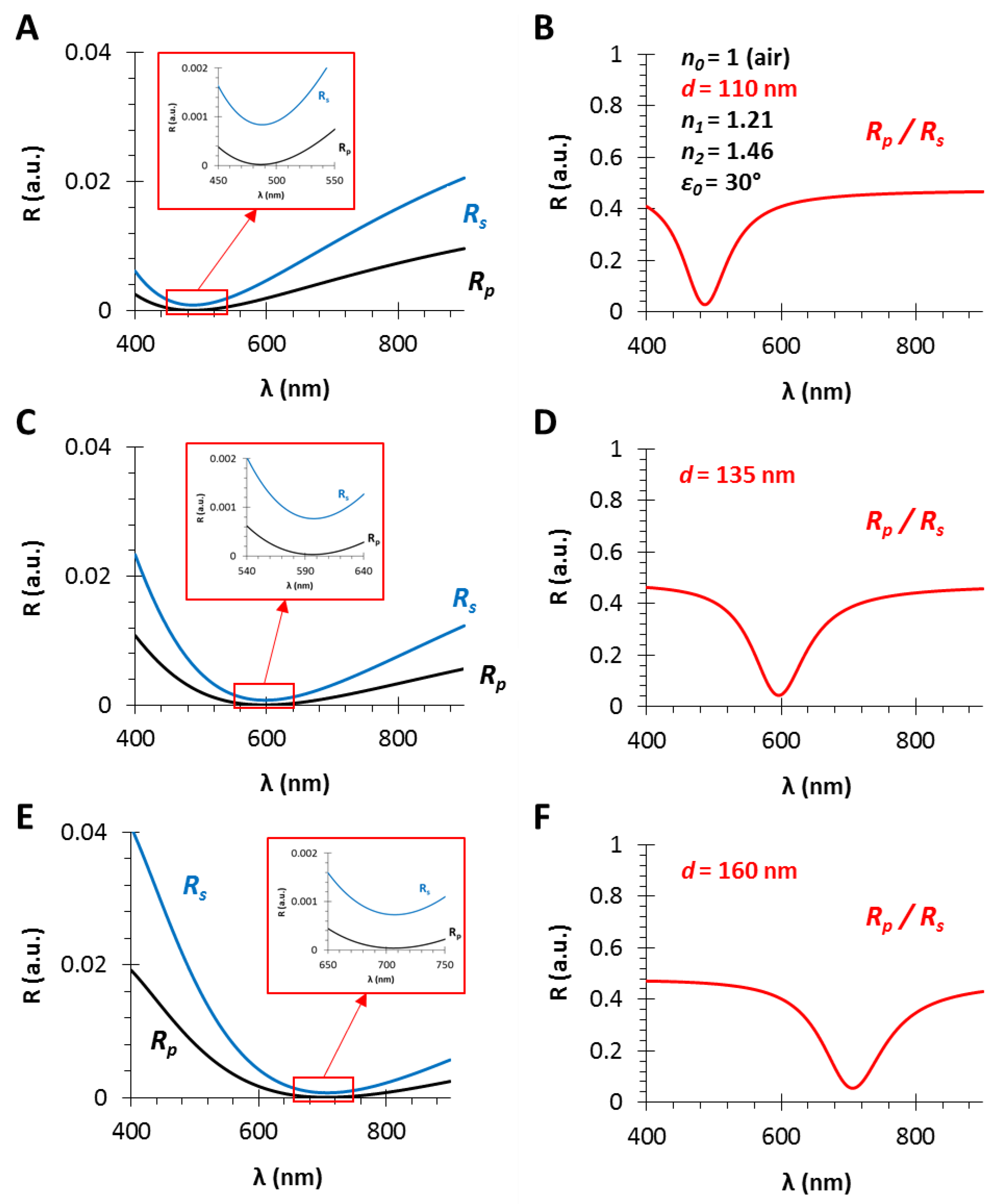
3.2. The Refractive Index of the Medium (n0), the Thin Film (n1) and the Substrate (n2)
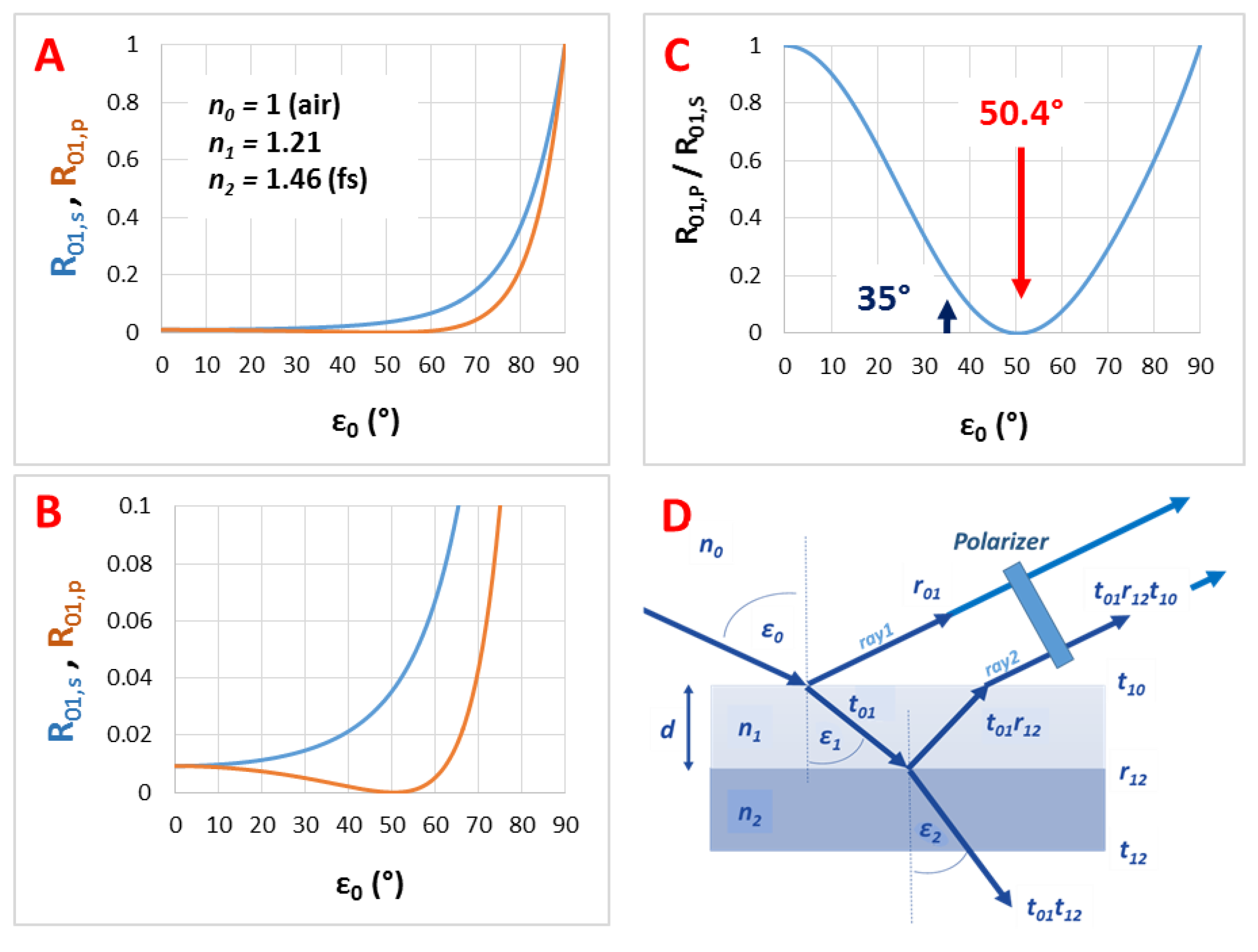
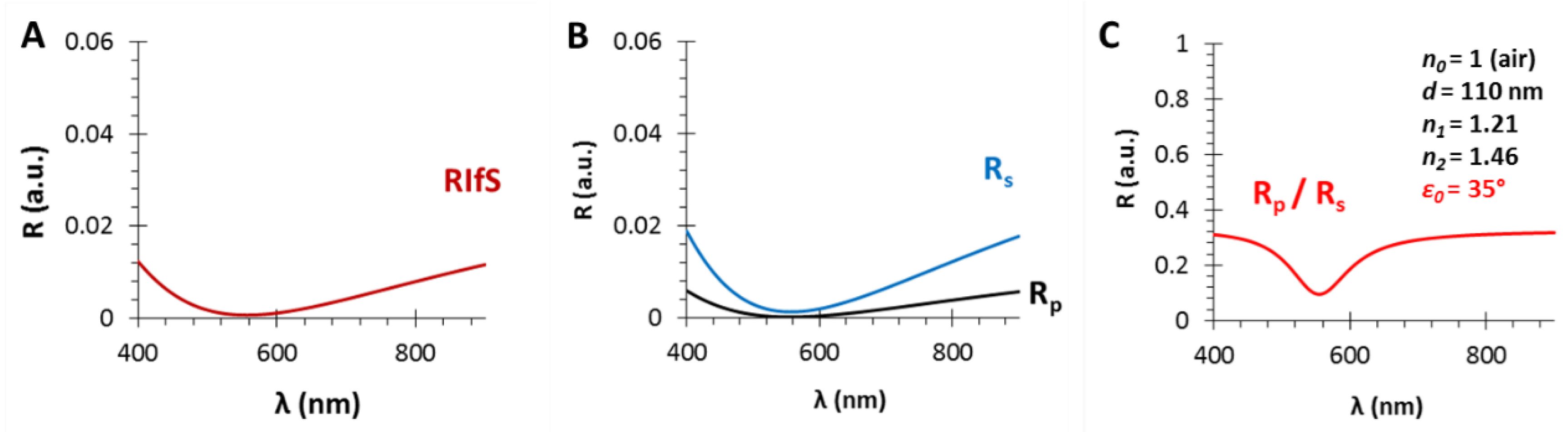
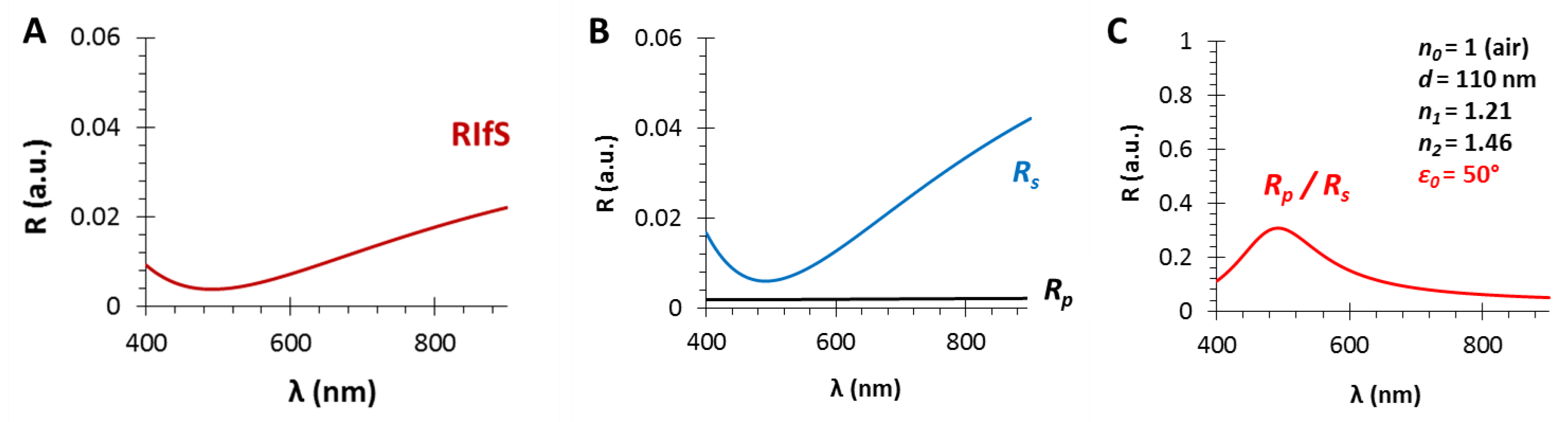
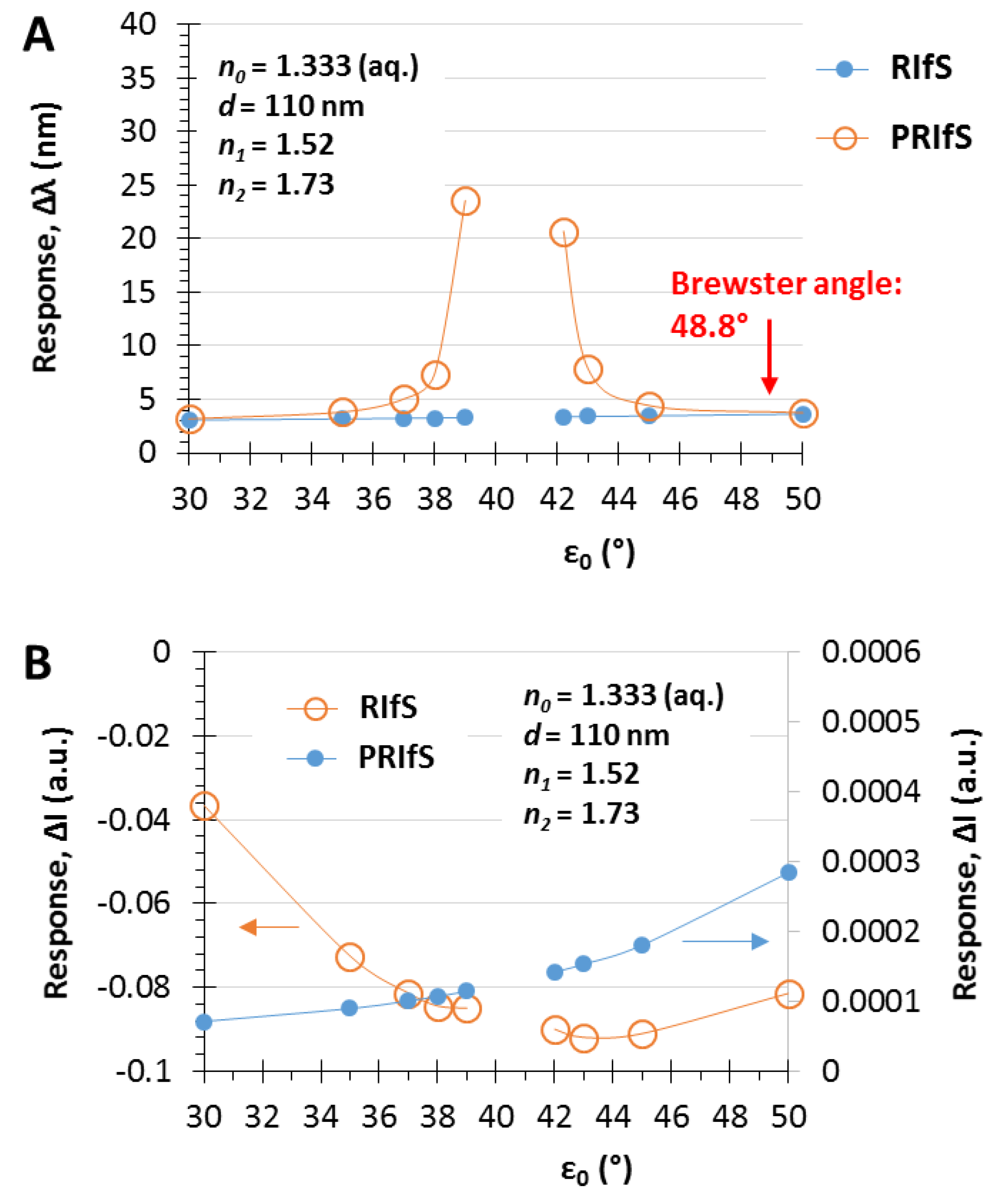
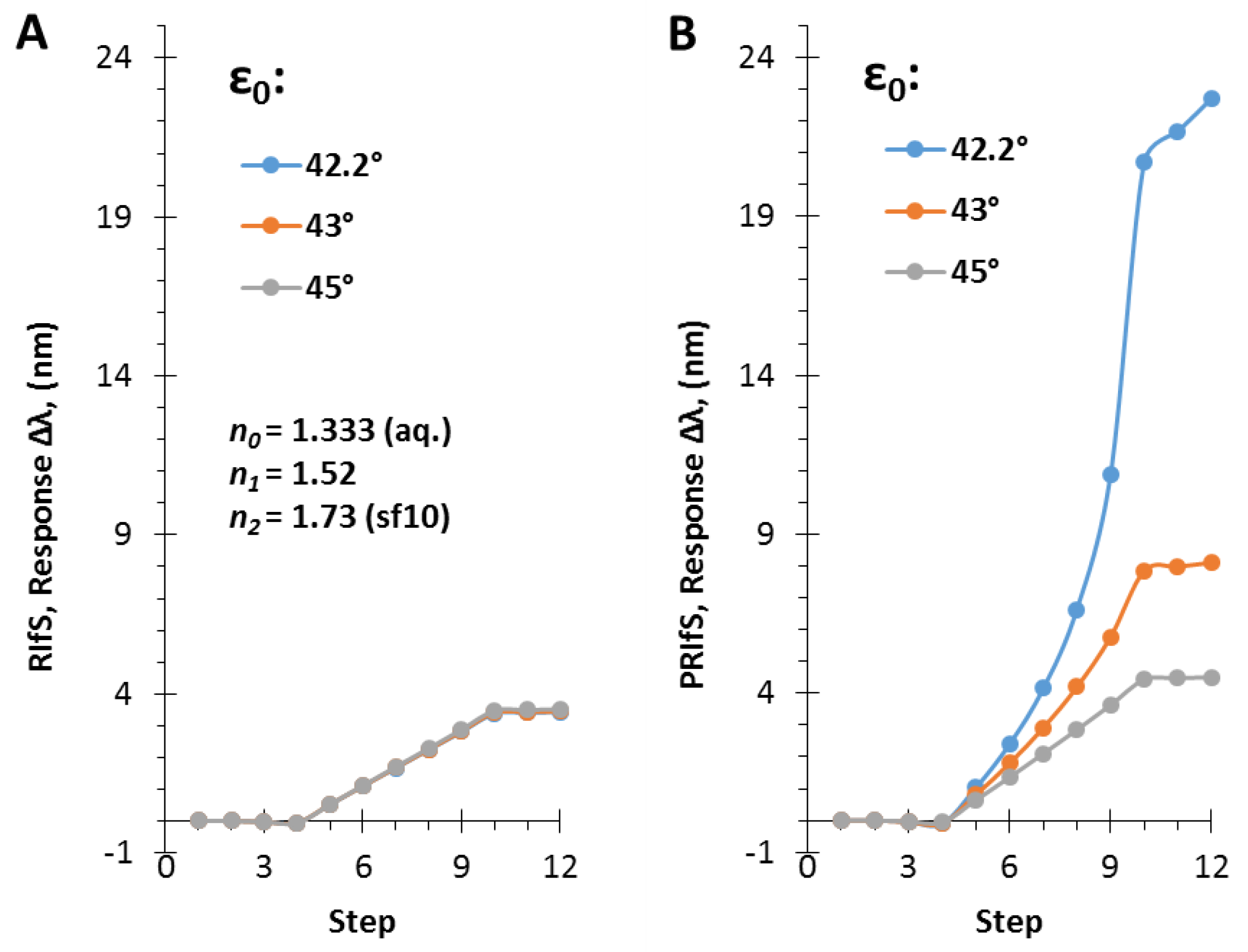
3.3. The Angle of Incidence (ε0)
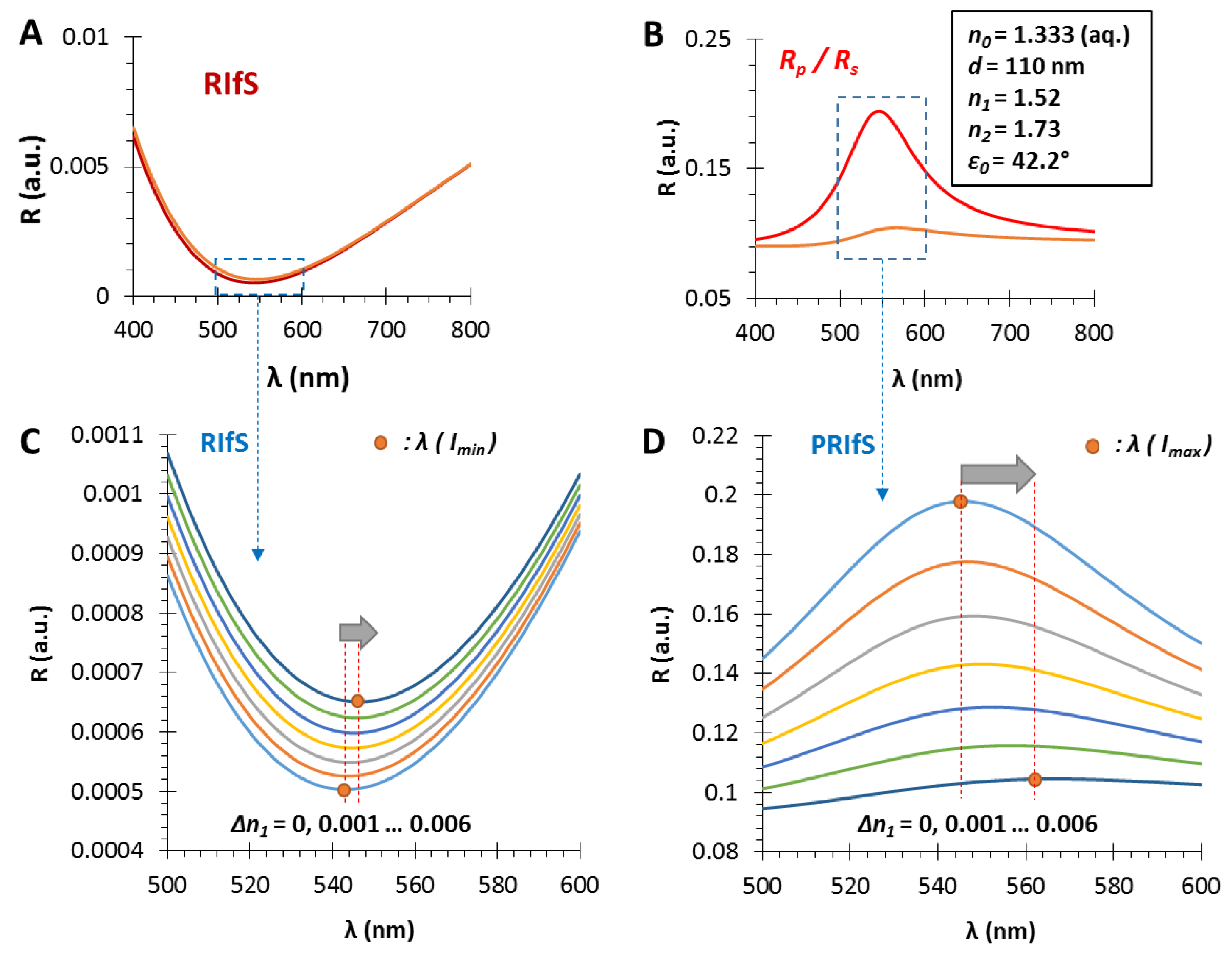
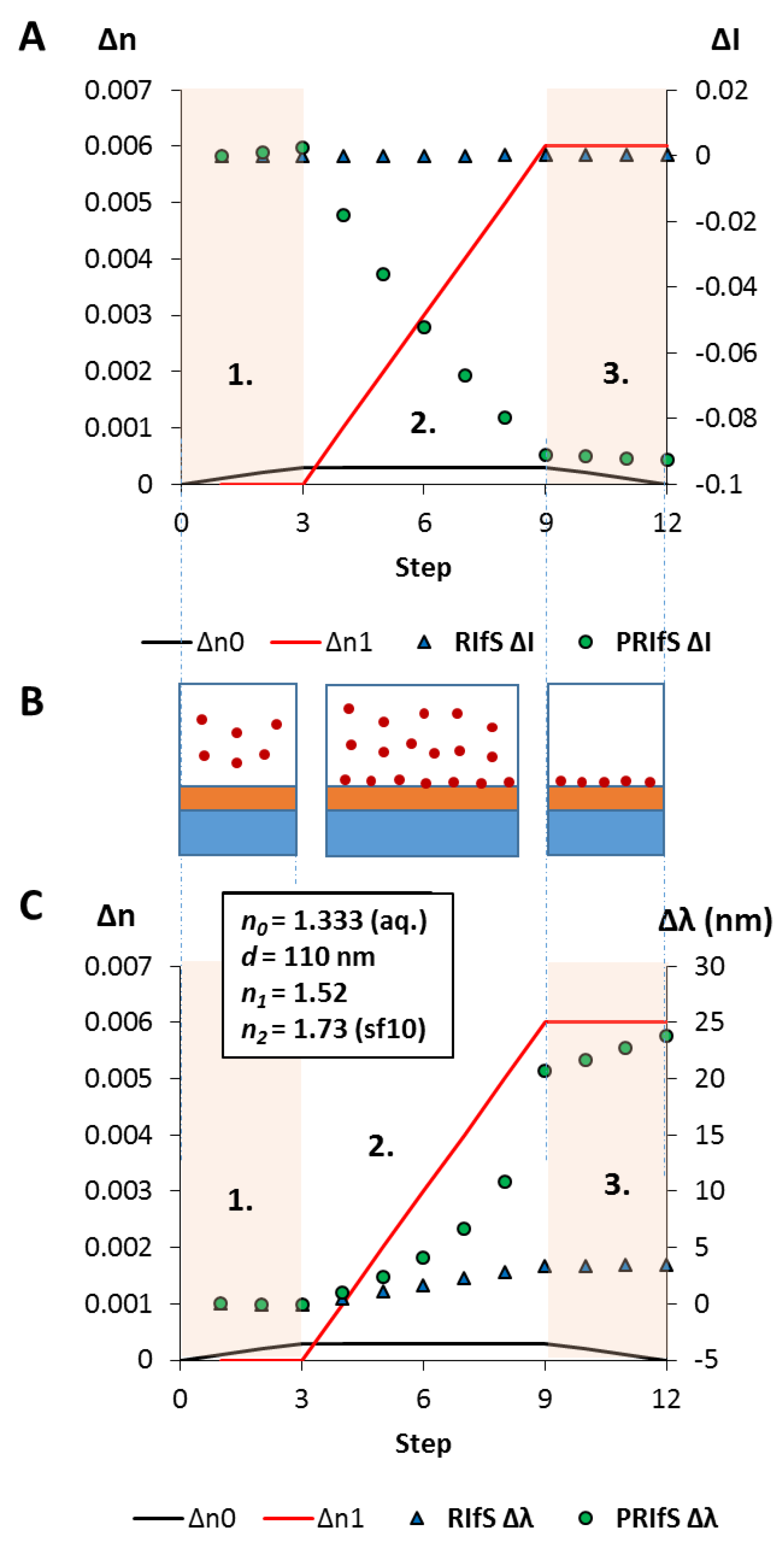
3.4. Simulating an Immobilization Measurement in Aqueous Phase
3.5. Simulating an Absorption Measurement in Gas Phase
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Zhu, Z.; Kao, C.-T.; Wu, R.-J. A highly sensitive ethanol sensor based on Ag@TiO2 nanoparticles at room temperature. Appl. Surf. Sci. 2014, 320, 348–355. [Google Scholar] [CrossRef]
- Renitta, A.; Vijayalakshmi, K. A novel room temperature ethanol sensor based on catalytic Fe activated porous WO3 microspheres. Catal. Commun. 2016, 73, 58–62. [Google Scholar] [CrossRef]
- Hazra, A.; Dutta, K.; Bhowmik, B.; Bhattacharyya, P. Repeatable low-ppm ethanol sensing characteristics of p-TiO2-based resistive devices. IEEE Sens. J. 2015, 15, 408–416. [Google Scholar] [CrossRef]
- Li, X.J.; Chen, S.J.; Feng, C.Y. Characterization of silicon nanoporous pillar array as room-temperature capacitive ethanol gas sensor. Sens. Actuators B Chem. 2007, 123, 461–465. [Google Scholar] [CrossRef]
- Hosseini, M.S.; Zeinali, S.; Sheikhi, M.H. Fabrication of capacitive sensor based on Cu-BTC (MOF-199) nanoporous film for detection of ethanol and methanol vapors. Sens. Actuators B Chem. 2016, 230, 9–16. [Google Scholar] [CrossRef]
- Sebők, D.; Janovák, L.; Kovács, D.; Sápi, A.; Dobó, D.G.; Kukovecz, Á.; Kónya, Z.; Dékány, I. Room temperature ethanol sensor with sub-ppm detection limit: Improving the optical response by using mesoporous silica foam. Sens. Actuators B Chem. 2017, 243, 1205–1213. [Google Scholar] [CrossRef]
- Reichl, D.; Krage, R.; Krummel, C.; Gauglitz, G. Sensing of Volatile Organic Compounds Using a Simplified Reflectometric Interference Spectroscopy Setup. Appl. Spectrosc. 2000, 54, 583–586. [Google Scholar] [CrossRef]
- Špačková, B.; Wrobel, P.; Bocková, M.; Homola, J. Optical biosensors based on plasmonic nanostructures: A review. Proc. IEEE 2016, 104, 2380–2408. [Google Scholar] [CrossRef]
- Csapó, E.; Juhász, Á.; Varga, N.; Sebők, D.; Hornok, V.; Janovák, L.; Dékány, I. Thermodynamic and kinetic characterization of pH-dependent interactions between bovine serum albumin and ibuprofen in 2D and 3D systems. Colloids Surf. A 2016, 504, 471–478. [Google Scholar] [CrossRef]
- Vaisocherová, H.; Víšová, I.; Bocková, M.; Špringer, T.; Ermini, M.L.; Song, X.; Krejčík, Z.; Chrastinová, L.; Pastva, O.; Pimková, K.; et al. Rapid and sensitive detection of multiple MicroRNAs in cell lysate by low-fouling surface plasmon resonance biosensor. Biosens. Bioelectron. 2015, 70, 226–231. [Google Scholar] [CrossRef]
- Horváth, R.; Pedersen, H.C.; Skivesen, N.; Selmeczi, D.; Larsen, N.B. Optical waveguide sensor for on-line monitoring of bacteria. Opt. Lett. 2003, 28, 1233–1235. [Google Scholar] [CrossRef] [PubMed]
- Höök, F.; Vörös, J.; Rodahl, M.; Kurrat, R.; Böni, P.; Ramsden, J.J.; Textor, M.; Spencer, N.D.; Tengvall, P.; Gold, J.; et al. A comparative study of protein adsorption on titanium oxide surfaces using in situ ellipsometry, optical waveguide lightmode spectroscopy, and quartz crystal microbalance/dissipation. Colloids Surf. B 2002, 24, 155–170. [Google Scholar] [CrossRef]
- Sebők, D.; Szendrei, K.; Szabó, T.; Dékány, I. Optical properties of zinc oxide ultrathin hybrid films on silicon wafer prepared by layer-by-layer method. Thin Solid Films 2008, 516, 3009–3014. [Google Scholar] [CrossRef]
- Pál, E.; Sebők, D.; Hornok, V.; Dékány, I. Structural, optical, and adsorption properties of ZnO2/poly (acrylic acid) hybrid thin porous films prepared by ionic strength controlled layer-by-layer method. J. Colloid Interface Sci. 2009, 332, 173–182. [Google Scholar] [CrossRef]
- Sebők, D.; Szabó, T.; Dékány, I. Optical properties of zinc peroxide and zinc oxide multilayer nanohybrid films. Appl. Surf. Sci. 2009, 255, 6953–6962. [Google Scholar] [CrossRef]
- Sebők, D.; Janovák, L.; Dékány, I. Optical, structural and adsorption properties of zinc peroxide/hydrogel nanohybrid films. Appl. Surf. Sci. 2010, 256, 5349–5354. [Google Scholar] [CrossRef]
- Gauglitz, G.; Krause-Bonte, J.; Schlemmer, H.; Matthes, A. Spectral interference refractometry by diode array spectrometry. Anal. Chem. 1988, 60, 2609–2612. [Google Scholar] [CrossRef]
- Gauglitz, G.; Brecht, A.; Kraus, G.; Mahm, W. Chemical and biochemical sensors based on interferometry at thin (multi-) layers. Sensor. Actuators B Chem. 1993, 11, 21–27. [Google Scholar] [CrossRef]
- Sebők, D.; Dékány, I. ZnO2 nanohybrid thin film sensor for the detection of ethanol vapour at room temperature using reflectometric interference spectroscopy. Sensor. Actuators B-Chem. 2015, 206, 435–442. [Google Scholar] [CrossRef]
- Sebők, D.; Csapó, E.; Ábrahám, N.; Dékány, I. Reflectometric measurement of n-hexane adsorption on ZnO2 nanohybrid film modified by hydrophobic gold nanoparticles. Appl. Surf. Sci. 2015, 333, 48–53. [Google Scholar] [CrossRef]
- Merkl, S.; Vornicescu, D.; Dassinger, N.; Keusgen, M. Detection of whole cells using reflectometric interference spectroscopy. Phys. Status Solidi. 2014, 211, 1416–1422. [Google Scholar] [CrossRef]
- Kumeria, T.; Kurkuri, M.D.; Diener, K.R.; Parkinson, L.; Losic, D. Label-free reflectometric interference microchip biosensor based on nanoporous alumina for detection of circulating tumour cells. Biosens. Bioelectron. 2012, 35, 167–173. [Google Scholar] [CrossRef] [PubMed]
- Piehler, J.; Schreiber, G. Fast transient cytokine-receptor interactions monitored in real time by reflectometric interference spectroscopy. Anal. Biochem. 2001, 289, 173–186. [Google Scholar] [CrossRef] [PubMed]
- Kasper, M.; Busche, S.; Dieterle, F.; Belge, G.; Gauglitz, G. Quantification of quaternary mixtures of alcohols: A comparison of reflectometric interference spectroscopy and surface plasmon resonance spectroscopy. Meas. Sci. Technol. 2004, 15, 540–548. [Google Scholar] [CrossRef]
- Hänel, C.; Gauglitz, G. Comparison of reflectometric interference spectroscopy with other instruments for label-free optical detection. Anal. Bioanal. Chem. 2002, 372, 91–100. [Google Scholar] [CrossRef] [PubMed]
- Pröll, F.; Möhrle, B.; Kumpf, M.; Gauglitz, G. Label-free characterisation of oligonucleotide hybridisation using reflectometric interference spectroscopy. Anal. Bioanal. Chem. 2005, 382, 1889–1894. [Google Scholar] [CrossRef] [PubMed]
- Zimmermann, R.; Osaki, T.; Gauglitz, G.; Werner, C. Combined microslit electrokinetic measurements and reflectometric interference spectroscopy to study protein adsorption processes. Biointerphases. 2007, 2, 159–164. [Google Scholar] [CrossRef]
- Leopold, N.; Busche, S.; Gauglitz, G.; Lendl, B. IR absorption and reflectometric interference spectroscopy (RIfS) combined to a new sensing approach for gas analytes absorbed into thin polymer films. Spectrochim. Acta A 2009, 72, 994–999. [Google Scholar] [CrossRef]
- Kumeria, T.; Losic, D. Controlling interferometric properties of nanoporous anodic aluminium oxide. Nanoscale Res. Lett. 2012, 7, 88. [Google Scholar] [CrossRef]
- Kumeria, T.; Parkinson, L.; Losic, D. A nanoporous interferometric micro-sensor for biomedical detection of volatile sulphur compounds. Nanoscale Res. Lett. 2011, 6, 634. [Google Scholar] [CrossRef]
- Choi, H.W.; Takahashi, H.; Ooyaa, T.; Takeuchi, T. Label-free detection of glycoproteins using reflectometric interference spectroscopy-based sensing system with upright episcopic illumination. Anal. Methods UK 2011, 3, 1366–1370. [Google Scholar] [CrossRef]
- Kurihara, Y.; Takama, M.; Sekiya, T.; Yoshihara, Y.; Ooya, T.; Takeuchi, T. Fabrication of Carboxylated Silicon Nitride Sensor Chips for Detection of Antigen–Antibody Reaction Using Microfluidic Reflectometric Interference Spectroscopy. Langmuir 2012, 28, 13609–13615. [Google Scholar] [CrossRef] [PubMed]
- Choi, H.W.; Sakata, Y.; Kurihara, Y.; Ooya, T.; Takeuchi, T. Label-free detection of C-reactive protein using reflectometric interference spectroscopy-based sensing system. Anal. Chim. Acta 2012, 728, 64–68. [Google Scholar] [CrossRef] [PubMed]
- Heavens, O.S. Thin Film Physics, 1st ed.; Methuen: London, UK, 1972; pp. 62–66. [Google Scholar]
- Refractive Index of Fused Silica—Malitson. 1965. Available online: https://refractiveindex.info/?shelf=glass&book=fused_silica&page=Malitson (accessed on 11 May 2019).
- Refractive Index of SF10—SCHOTT. Available online: https://refractiveindex.info/?shelf=glass&book=SF10&page=SCHOTT (accessed on 11 May 2019).



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Janovák, L.; Dékány, I.; Sebők, D. The Theoretical Concept of Polarization Reflectometric Interference Spectroscopy (PRIFS): An Optical Method to Monitor Molecule Adsorption and Nanoparticle Adhesion on the Surface of Thin Films. Photonics 2019, 6, 76. https://doi.org/10.3390/photonics6030076
Janovák L, Dékány I, Sebők D. The Theoretical Concept of Polarization Reflectometric Interference Spectroscopy (PRIFS): An Optical Method to Monitor Molecule Adsorption and Nanoparticle Adhesion on the Surface of Thin Films. Photonics. 2019; 6(3):76. https://doi.org/10.3390/photonics6030076
Chicago/Turabian StyleJanovák, László, Imre Dékány, and Dániel Sebők. 2019. "The Theoretical Concept of Polarization Reflectometric Interference Spectroscopy (PRIFS): An Optical Method to Monitor Molecule Adsorption and Nanoparticle Adhesion on the Surface of Thin Films" Photonics 6, no. 3: 76. https://doi.org/10.3390/photonics6030076
APA StyleJanovák, L., Dékány, I., & Sebők, D. (2019). The Theoretical Concept of Polarization Reflectometric Interference Spectroscopy (PRIFS): An Optical Method to Monitor Molecule Adsorption and Nanoparticle Adhesion on the Surface of Thin Films. Photonics, 6(3), 76. https://doi.org/10.3390/photonics6030076





