Tuning Plasmon Induced Reflectance with Hybrid Metasurfaces †
Abstract
:1. Introduction
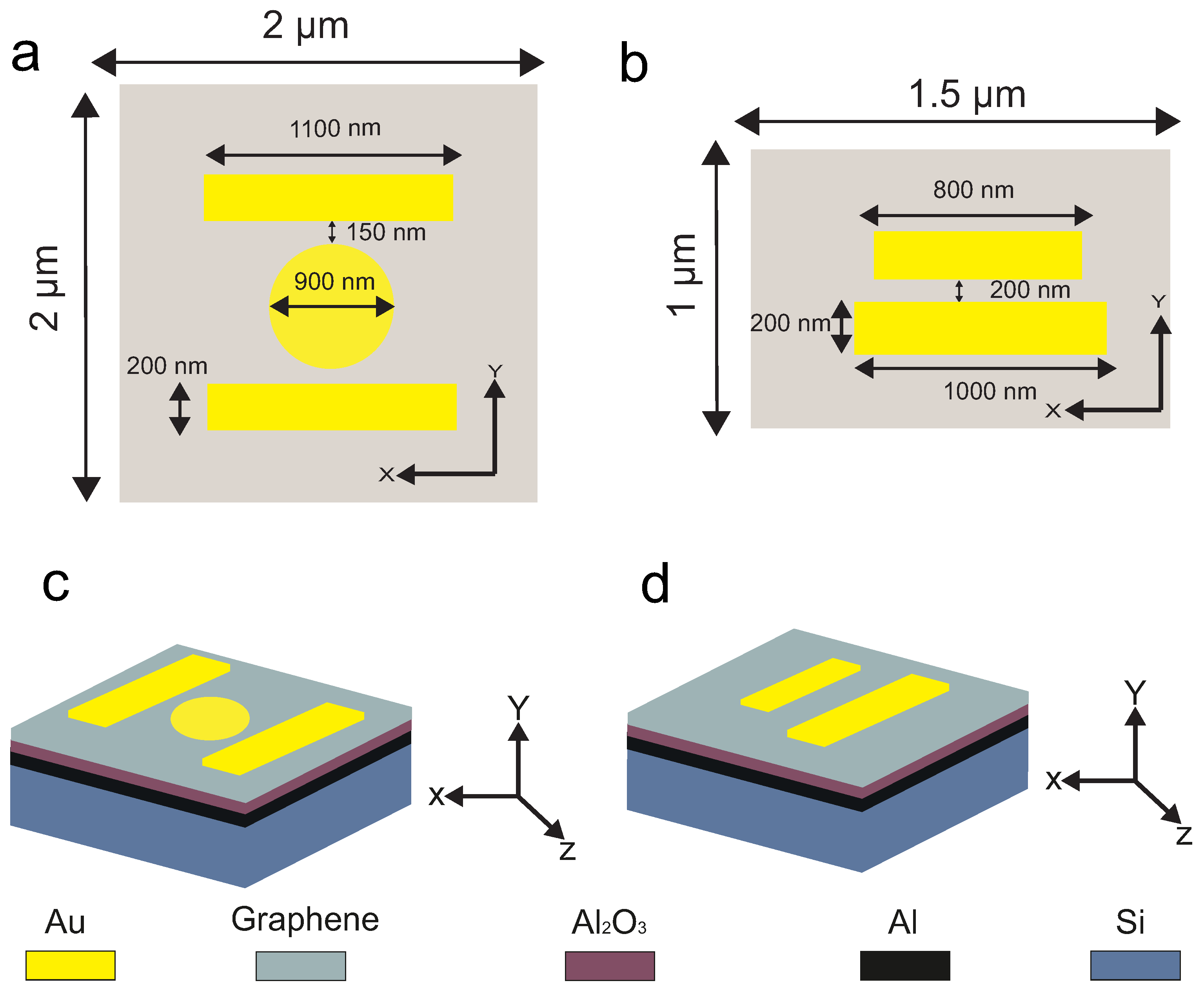
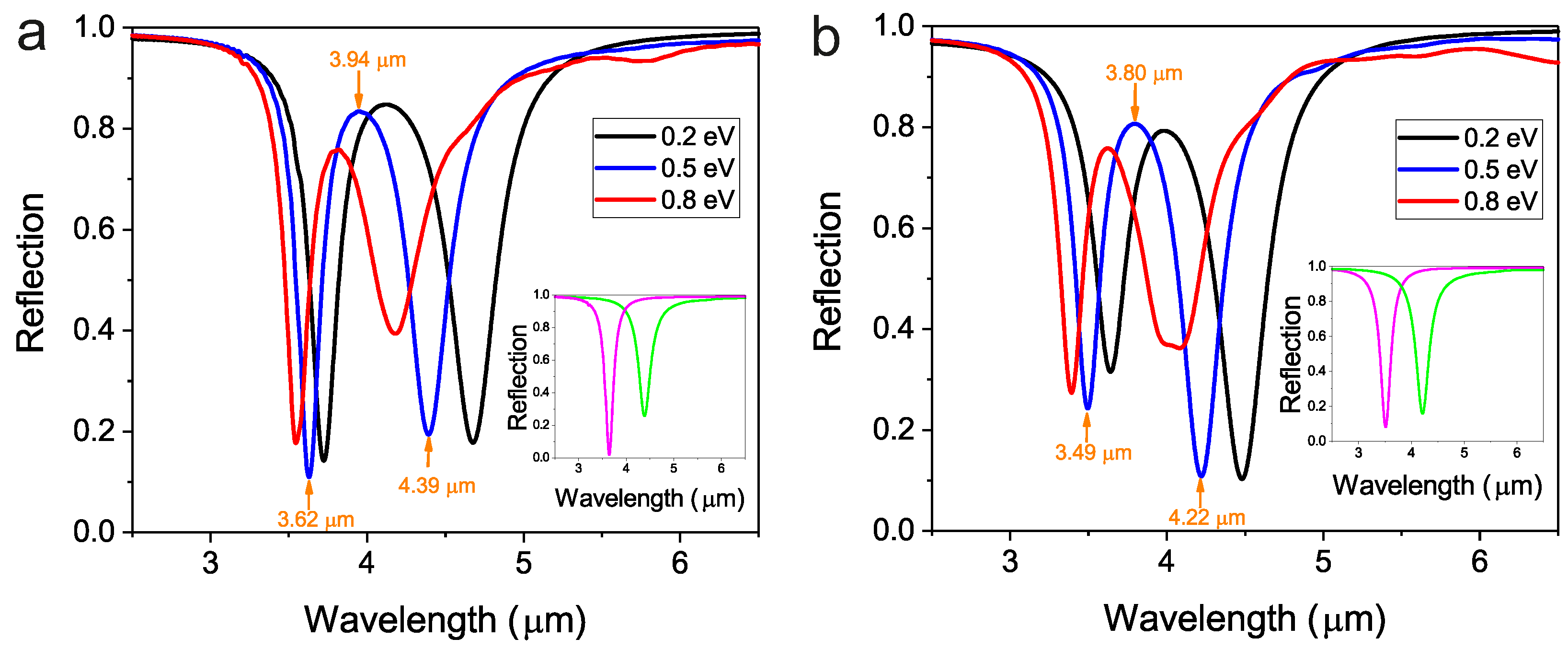
2. Numerical Investigation
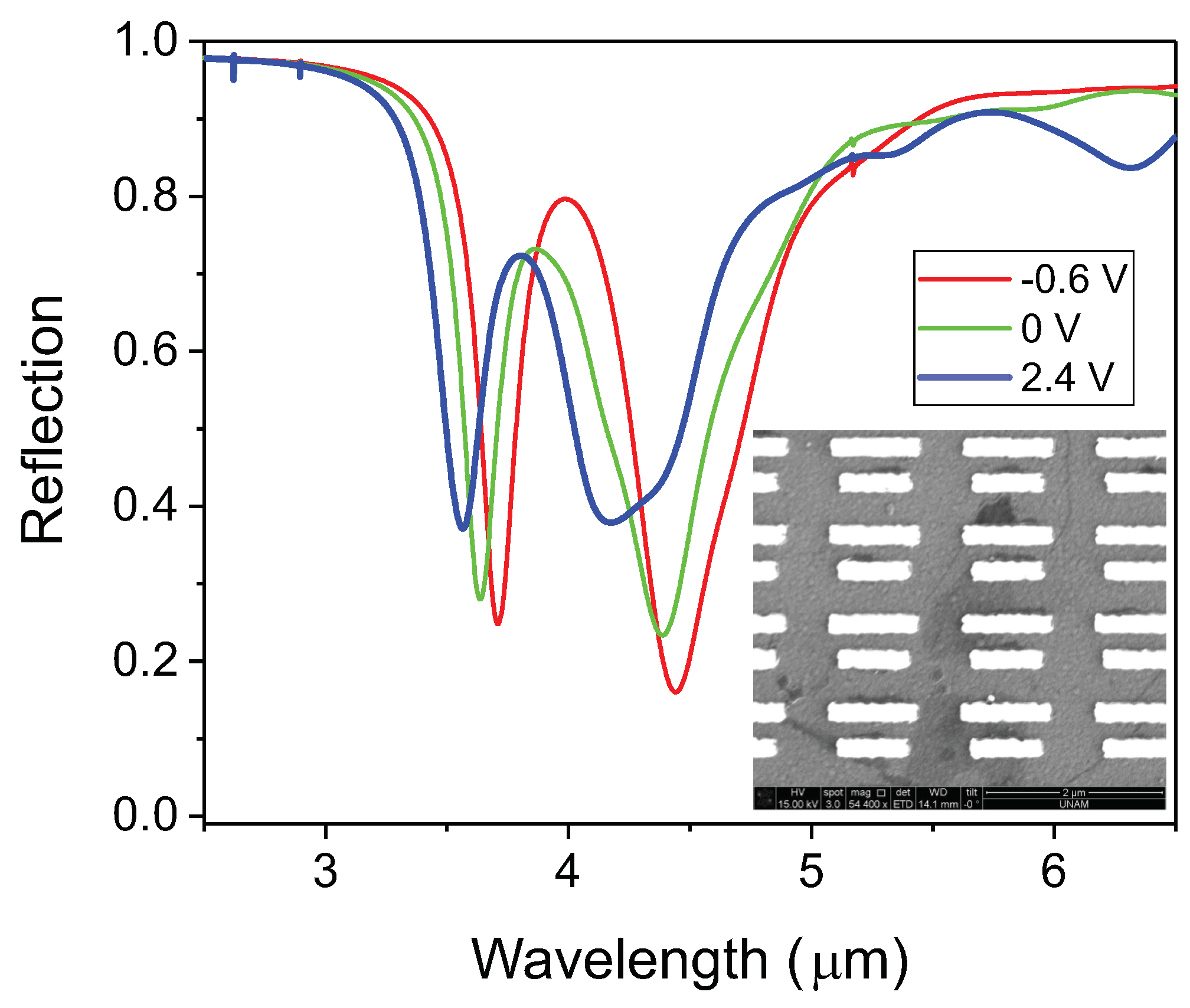
3. Experimental Investigation
4. Discussion
5. Materials and Methods
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Boller, K.J.; Imamoğlu, A.; Harris, S.E. Observation of electromagnetically induced transparency. Phys. Rev. Lett. 1991, 66, 2593. [Google Scholar] [CrossRef] [PubMed]
- Marangos, J.P. Electromagnetically induced transparency. J. Mod. Opt. 1998, 45, 471–503. [Google Scholar] [CrossRef]
- Kasapi, A.; Jain, M.; Yin, G.; Harris, S.E. Electromagnetically induced transparency: Propagation dynamics. Phys. Rev. Lett. 1995, 74, 2447. [Google Scholar] [CrossRef]
- Harris, S.; Field, J.; Kasapi, A. Dispersive properties of electromagnetically induced transparency. Phys. Rev. A 1992, 46, R29. [Google Scholar] [CrossRef] [PubMed]
- Krauss, T.F. Why do we need slow light? Nat. Photonics 2008, 2, 448. [Google Scholar] [CrossRef]
- Vafapour, Z.; Hajati, Y.; Hajati, M.; Ghahraloud, H. Graphene-based mid-infrared biosensor. JOSA B 2017, 34, 2586–2592. [Google Scholar] [CrossRef]
- Vafapour, Z. Near infrared biosensor based on Classical Electromagnetically Induced Reflectance (Cl-EIR) in a planar complementary metamaterial. Opt. Commun. 2017, 387, 1–11. [Google Scholar] [CrossRef]
- Novikova, I.; Walsworth, R.L.; Xiao, Y. Electromagnetically induced transparency-based slow and stored light in warm atoms. Laser Photonics Rev. 2012, 6, 333–353. [Google Scholar] [CrossRef]
- Chen, J.; Wang, P.; Chen, C.; Lu, Y.; Ming, H.; Zhan, Q. Plasmonic EIT-like switching in bright-dark-bright plasmon resonators. Opt. Express 2011, 19, 5970–5978. [Google Scholar] [CrossRef] [PubMed]
- Fleischhauer, M.; Imamoglu, A.; Marangos, J.P. Electromagnetically induced transparency: Optics in coherent media. Rev. Mod. Phys. 2005, 77, 633. [Google Scholar] [CrossRef]
- Amin, M.; Farhat, M.; Baǧcı, H. A dynamically reconfigurable Fano metamaterial through graphene tuning for switching and sensing applications. Sci. Rep. 2013, 3, 2105. [Google Scholar] [CrossRef]
- Habib, M.; Rashed, A.R.; Ozbay, E.; Caglayan, H. Graphene-based tunable plasmon induced transparency in gold strips. Opt. Mater. Express 2018, 8, 1069–1074. [Google Scholar] [CrossRef]
- Liu, N.; Langguth, L.; Weiss, T.; Kästel, J.; Fleischhauer, M.; Pfau, T.; Giessen, H. Plasmonic analogue of electromagnetically induced transparency at the Drude damping limit. Nat. Mater. 2009, 8, 758. [Google Scholar] [CrossRef]
- Zhu, Y.; Hu, X.; Fu, Y.; Yang, H.; Gong, Q. Ultralow-power and ultrafast all-optical tunable plasmon-induced transparency in metamaterials at optical communication range. Sci. Rep. 2013, 3, 2338. [Google Scholar] [CrossRef]
- Hokmabadi, M.P.; Philip, E.; Rivera, E.; Kung, P.; Kim, S.M. Plasmon-induced transparency by hybridizing concentric-twisted double split ring resonators. Sci. Rep. 2015, 5, 15735. [Google Scholar] [CrossRef]
- Vlasov, Y.A.; O’boyle, M.; Hamann, H.F.; McNab, S.J. Active control of slow light on a chip with photonic crystal waveguides. Nature 2005, 438, 65. [Google Scholar] [CrossRef]
- Rohde, C.; Hasegawa, K.; Deutsch, M. Plasmon-assisted transparency in metal-dielectric microspheres. Opt. Lett. 2007, 32, 415–417. [Google Scholar] [CrossRef] [PubMed]
- Yannopapas, V.; Paspalakis, E.; Vitanov, N.V. Electromagnetically induced transparency and slow light in an array of metallic nanoparticles. Phys. Rev. B 2009, 80, 035104. [Google Scholar] [CrossRef]
- Zhang, J.; Bai, W.; Cai, L.; Xu, Y.; Song, G.; Gan, Q. Observation of ultra-narrow band plasmon induced transparency based on large-area hybrid plasmon-waveguide systems. Appl. Phys. Lett. 2011, 99, 181120. [Google Scholar] [CrossRef]
- Zhang, Z.; Fan, Y.; Long, Y.; Yin, P. Theoretical realization of dynamically tunable double plasmonically induced transparency in a graphene-based waveguide structure. Opt. Mater. 2017, 72, 632–636. [Google Scholar] [CrossRef]
- Xu, J.; Fan, Y.; Yang, R.; Fu, Q.; Zhang, F. Realization of switchable EIT metamaterial by exploiting fluidity of liquid metal. Opt. Express 2019, 27, 2837–2843. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.; Hu, X.; Yang, H.; Gong, Q. On-chip plasmon-induced transparency based on plasmonic coupled nanocavities. Sci. Rep. 2014, 4, 3752. [Google Scholar] [CrossRef] [PubMed]
- Fan, Y.; Shen, N.H.; Koschny, T.; Soukoulis, C.M. Tunable terahertz meta-surface with graphene cut-wires. Acs Photonics 2015, 2, 151–156. [Google Scholar] [CrossRef]
- Fan, Y.; Shen, N.H.; Zhang, F.; Zhao, Q.; Wei, Z.; Zhang, P.; Dong, J.; Fu, Q.; Li, H.; Soukoulis, C.M. Photoexcited graphene metasurfaces: Significantly enhanced and tunable magnetic resonances. ACS Photonics 2018, 5, 1612–1618. [Google Scholar] [CrossRef]
- Tao, H.; Padilla, W.J.; Zhang, X.; Averitt, R.D. Recent progress in electromagnetic metamaterial devices for terahertz applications. IEEE J. Sel. Top. Quantum Electron. 2011, 17, 92–101. [Google Scholar] [CrossRef]
- Pendry, J.B.; Schurig, D.; Smith, D.R. Controlling electromagnetic fields. Science 2006, 312, 1780–1782. [Google Scholar] [CrossRef] [PubMed]
- Ozbay, E. Plasmonics: Merging photonics and electronics at nanoscale dimensions. Science 2006, 311, 189–193. [Google Scholar] [CrossRef] [PubMed]
- Balci, O.; Kakenov, N.; Karademir, E.; Balci, S.; Cakmakyapan, S.; Polat, E.O.; Caglayan, H.; Özbay, E.; Kocabas, C. Electrically switchable metadevices via graphene. Sci. Adv. 2018, 4, eaao1749. [Google Scholar] [CrossRef]
- Fan, Y.; Shen, N.H.; Zhang, F.; Wei, Z.; Li, H.; Zhao, Q.; Fu, Q.; Zhang, P.; Koschny, T.; Soukoulis, C.M. Electrically tunable Goos–Hänchen effect with graphene in the terahertz regime. Adv. Opt. Mater. 2016, 4, 1824–1828. [Google Scholar] [CrossRef]
- Fan, Y.; Qiao, T.; Zhang, F.; Fu, Q.; Dong, J.; Kong, B.; Li, H. An electromagnetic modulator based on electrically controllable metamaterial analogue to electromagnetically induced transparency. Sci. Rep. 2017, 7, 40441. [Google Scholar] [CrossRef]
- Kim, T.T.; Kim, H.D.; Zhao, R.; Oh, S.S.; Ha, T.; Chung, D.S.; Lee, Y.H.; Min, B.; Zhang, S. Electrically tunable slow light using graphene metamaterials. ACS Photonics 2018, 5, 1800–1807. [Google Scholar] [CrossRef]
- Cakmakyapan, S.; Caglayan, H.; Ozbay, E. Coupling enhancement of split ring resonators on graphene. Carbon 2014, 80, 351–355. [Google Scholar] [CrossRef]
- Ozdemir, O.; Aygar, A.M.; Balci, O.; Kocabas, C.; Caglayan, H.; Ozbay, E. Enhanced tunability of V-shaped plasmonic structures using ionic liquid gating and graphene. Carbon 2016, 108, 515–520. [Google Scholar] [CrossRef]
- Aygar, A.M.; Balci, O.; Cakmakyapan, S.; Kocabas, C.; Caglayan, H.; Ozbay, E. Comparison of back and top gating schemes with tunable graphene fractal metasurfaces. ACS Photonics 2016, 3, 2303–2307. [Google Scholar] [CrossRef]
- Goldflam, M.; Driscoll, T.; Chapler, B.; Khatib, O.; Marie Jokerst, N.; Palit, S.; Smith, D.; Kim, B.J.; Seo, G.; Kim, H.T.; et al. Reconfigurable gradient index using VO2 memory metamaterials. Appl. Phys. Lett. 2011, 99, 044103. [Google Scholar] [CrossRef]
- Urzhumov, Y.; Lee, J.S.; Tyler, T.; Dhar, S.; Nguyen, V.; Jokerst, N.M.; Schmalenberg, P.; Smith, D.R. Electronically reconfigurable metal-on-silicon metamaterial. Phys. Rev. B 2012, 86, 075112. [Google Scholar] [CrossRef]
- Zheludev, N.I.; Kivshar, Y.S. From metamaterials to metadevices. Nat. Mater. 2012, 11, 917. [Google Scholar] [CrossRef] [PubMed]
- Shin, D.; Urzhumov, Y.; Jung, Y.; Kang, G.; Baek, S.; Choi, M.; Park, H.; Kim, K.; Smith, D.R. Broadband electromagnetic cloaking with smart metamaterials. Nat. Commun. 2012, 3, 1213. [Google Scholar] [CrossRef] [PubMed]
- Stockman, M.I.; Faleev, S.V.; Bergman, D.J. Localization versus delocalization of surface plasmons in nanosystems: Can one state have both characteristics? Phys. Rev. Lett. 2001, 87, 167401. [Google Scholar] [CrossRef]
- Zhang, H.; Cao, Y.; Liu, Y.; Li, Y.; Zhang, Y. A novel graphene metamaterial design for tunable terahertz plasmon induced transparency by two bright mode coupling. Opt. Commun. 2017, 391, 9–15. [Google Scholar] [CrossRef]
- Habib, M.; Ozbay, E.; Caglayan, H. Tunable reflection type plasmon induced transparency with graphene. In Proceedings of the IEEE 12th International Congress on Artificial Materials for Novel Wave Phenomena (Metamaterials), Espoo, Finland, 27 August–1 September 2018; pp. 170–172. [Google Scholar]
- Xiao, F.; Zhu, W.; Shang, W.; Mei, T.; Premaratne, M.; Zhao, J. Electrical control of second harmonic generation in a graphene-based plasmonic Fano structure. Opt. Express 2015, 23, 3236–3244. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Liu, P.; Yang, C.; Lin, Y.; Liu, H. Analogue of dual-controlled electromagnetically induced transparency based on graphene metamaterial. Carbon 2018, 142, 354–362. [Google Scholar] [CrossRef]
- He, X.; Yang, X.; Lu, G.; Yang, W.; Wu, F.; Yu, Z.; Jiang, J. Implementation of selective controlling electromagnetically induced transparency in terahertz graphene metamaterial. Carbon 2017, 123, 668–675. [Google Scholar] [CrossRef]
- Ding, C.-F.; Zhang, Y.-T.; Yao, J.-Q.; Sun, C.-L.; Xu, D.-G.; Zhang, G.-Z. Reflection-type electromagnetically induced transparency analogue in terahertz metamaterials. Chin. Phys. B 2014, 23, 124203. [Google Scholar] [CrossRef]
- Liu, Y.; Dai, Y.; Feng, Q.; Shan, Y.; Du, L.; Xia, Y.; Lu, G.; Liu, F.; Du, G.; Tian, C.; et al. Enhanced light-matter interactions in graphene-covered dielectric magnetic mirrors. Opt. Express 2017, 25, 30754–30763. [Google Scholar] [CrossRef]
- Gao, L.; Ren, W.; Liu, B.; Saito, R.; Wu, Z.S.; Li, S.; Jiang, C.; Li, F.; Cheng, H.M. Surface and interference coenhanced Raman scattering of graphene. ACS Nano 2009, 3, 933–939. [Google Scholar] [CrossRef]
- Fang, Z.; Liu, Z.; Wang, Y.; Ajayan, P.M.; Nordlander, P.; Halas, N.J. Graphene-antenna sandwich photodetector. Nano Lett. 2012, 12, 3808–3813. [Google Scholar] [CrossRef]
- Xia, F.; Mueller, T.; Lin, Y.m.; Valdes-Garcia, A.; Avouris, P. Ultrafast graphene photodetector. Nat. Nanotechnol. 2009, 4, 839. [Google Scholar] [CrossRef]
- Furchi, M.; Urich, A.; Pospischil, A.; Lilley, G.; Unterrainer, K.; Detz, H.; Klang, P.; Andrews, A.M.; Schrenk, W.; Strasser, G.; et al. Microcavity-integrated graphene photodetector. Nano Lett. 2012, 12, 2773–2777. [Google Scholar] [CrossRef]
- Mak, K.F.; Ju, L.; Wang, F.; Heinz, T.F. Optical spectroscopy of graphene: From the far infrared to the ultraviolet. Solid State Commun. 2012, 152, 1341–1349. [Google Scholar] [CrossRef]
- Hanson, G.W. Dyadic Green’s functions and guided surface waves for a surface conductivity model of graphene. J. Appl. Phys. 2008, 103, 064302. [Google Scholar] [CrossRef]
- Zhu, W.; Xiao, F.; Kang, M.; Sikdar, D.; Premaratne, M. Tunable terahertz left-handed metamaterial based on multi-layer graphene-dielectric composite. Appl. Phys. Lett. 2014, 104, 051902. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, Y.; Tian, C.; Girit, C.; Zettl, A.; Crommie, M.; Shen, Y.R. Gate-variable optical transitions in graphene. Science 2008, 320, 206–209. [Google Scholar] [CrossRef] [PubMed]
- Habib, M.; Gokbayrak, M.; Ozbay, E.; Caglayan, H. Electrically controllable plasmon induced reflectance in hybrid metamaterials. Appl. Phys. Lett. 2018, 113, 221105. [Google Scholar] [CrossRef]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Habib, M.; Ozbay, E.; Caglayan, H. Tuning Plasmon Induced Reflectance with Hybrid Metasurfaces. Photonics 2019, 6, 29. https://doi.org/10.3390/photonics6010029
Habib M, Ozbay E, Caglayan H. Tuning Plasmon Induced Reflectance with Hybrid Metasurfaces. Photonics. 2019; 6(1):29. https://doi.org/10.3390/photonics6010029
Chicago/Turabian StyleHabib, Mohsin, Ekmel Ozbay, and Humeyra Caglayan. 2019. "Tuning Plasmon Induced Reflectance with Hybrid Metasurfaces" Photonics 6, no. 1: 29. https://doi.org/10.3390/photonics6010029
APA StyleHabib, M., Ozbay, E., & Caglayan, H. (2019). Tuning Plasmon Induced Reflectance with Hybrid Metasurfaces. Photonics, 6(1), 29. https://doi.org/10.3390/photonics6010029




