Terahertz Field Confinement in Nonlinear Metamaterials and Near-Field Imaging
Abstract
1. Introduction
2. Field Confinement and Applications in Terahertz and Infrared Metamaterial Devices
2.1. Background
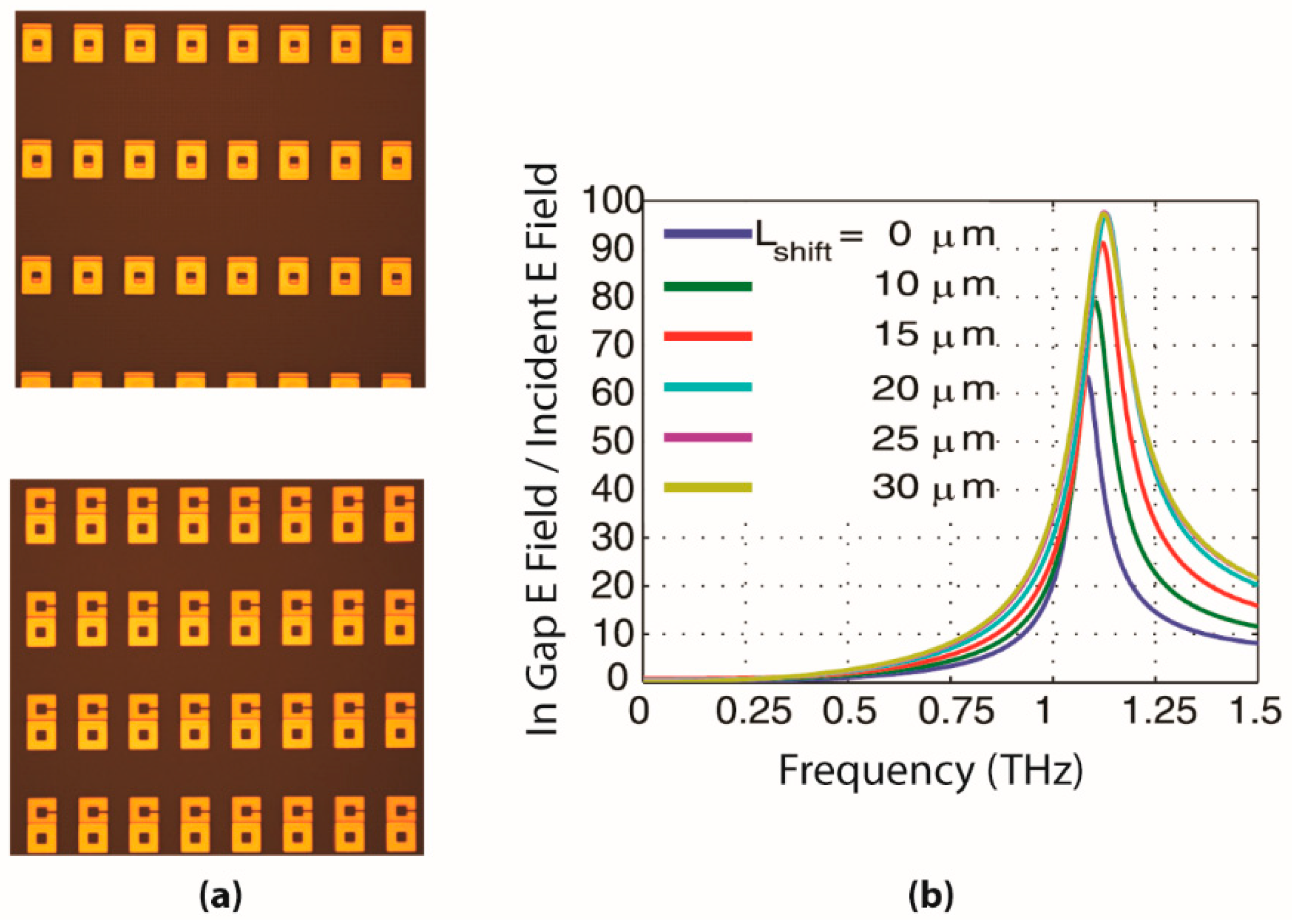
2.2. Active Control and Turning of Field Confinement in Metamaterials
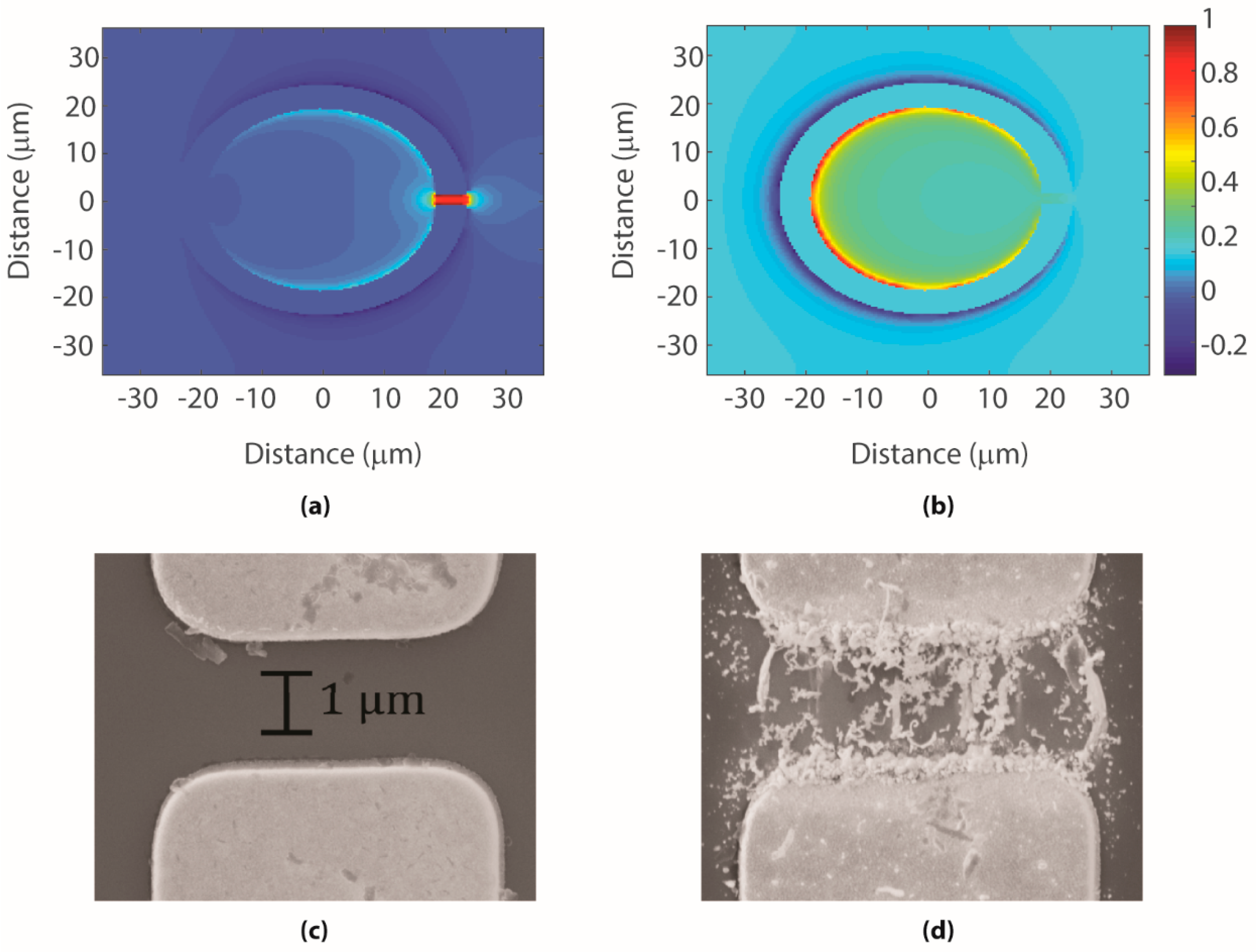
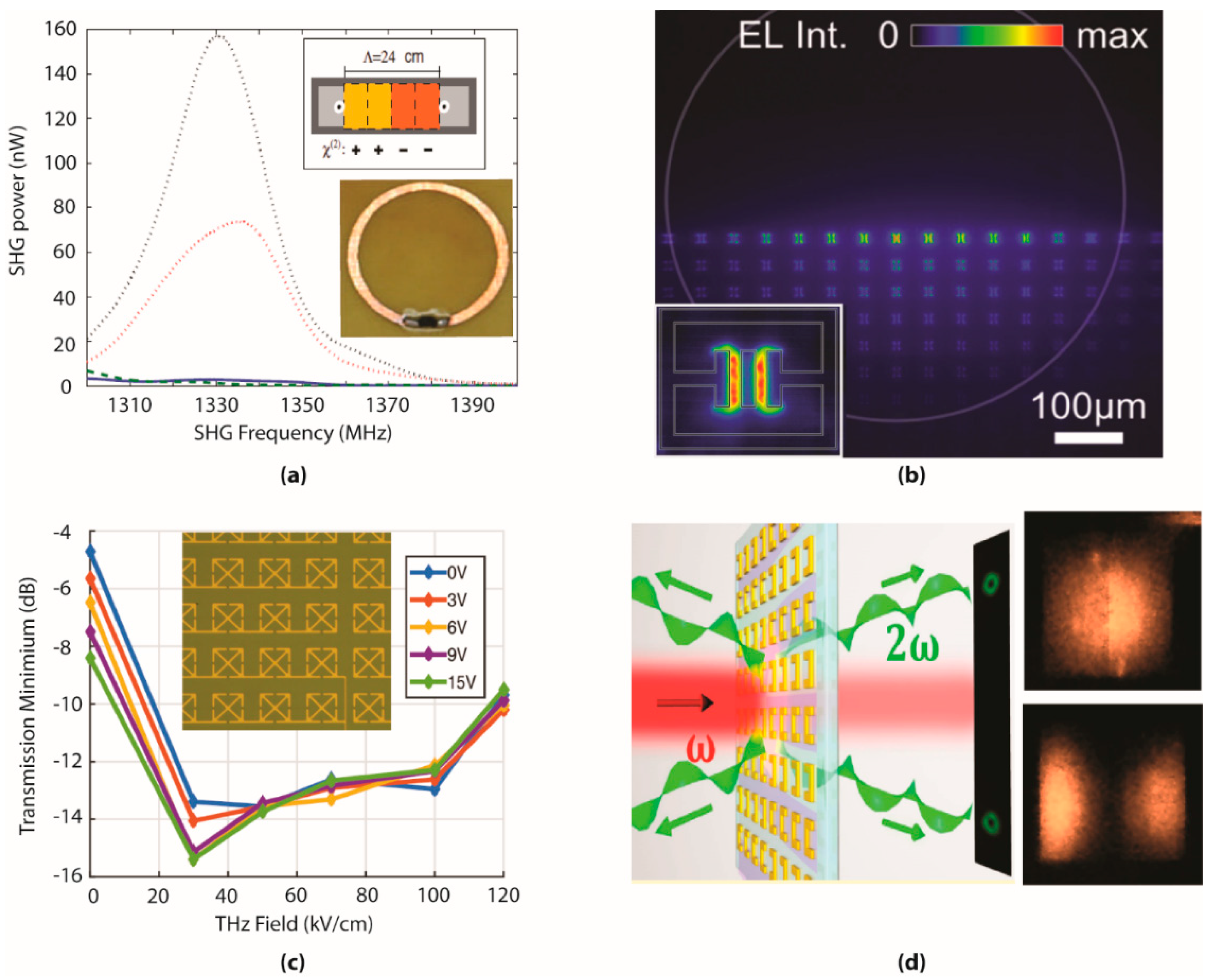
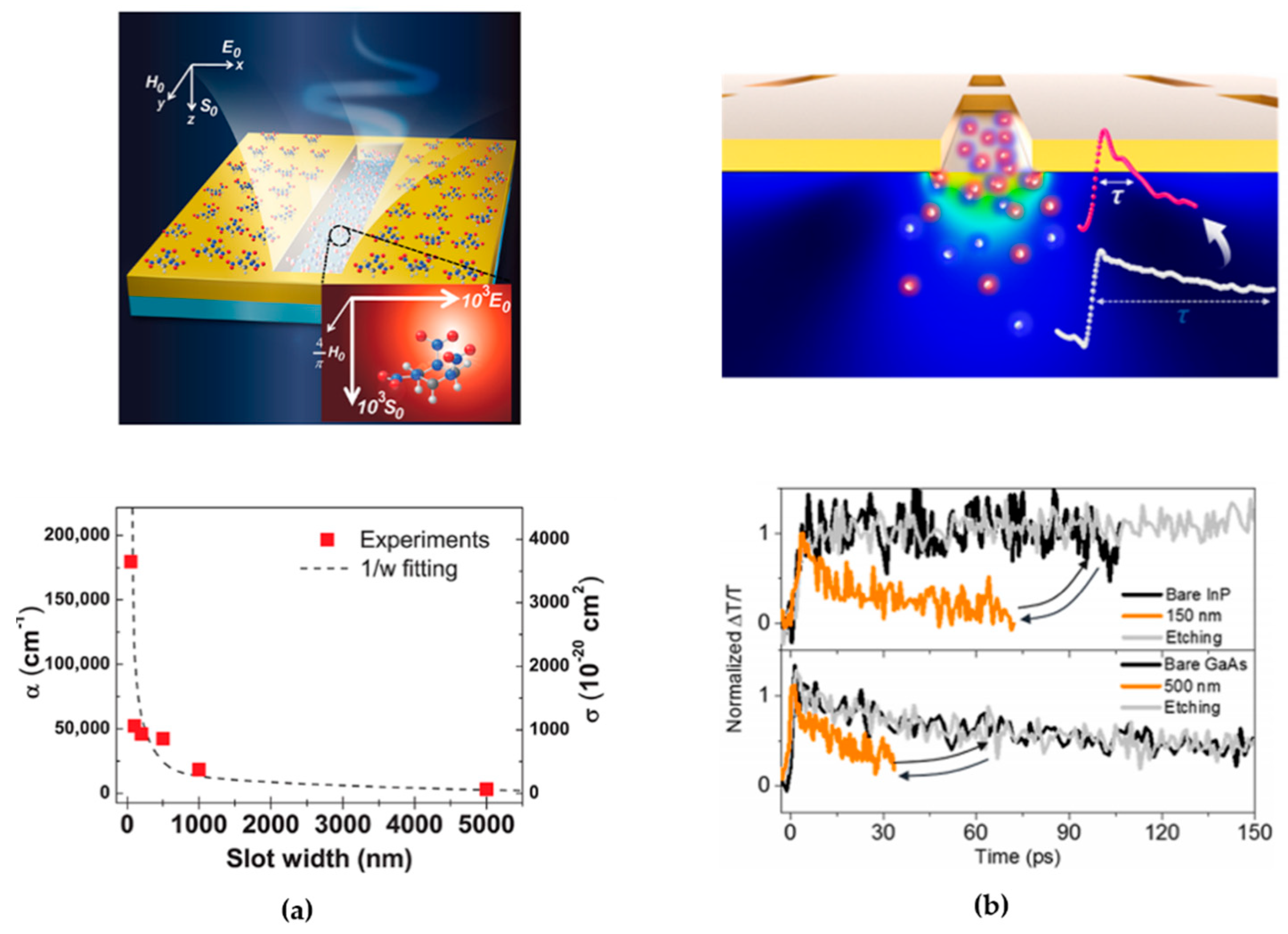
2.3. Field Confinement Applications in Nonlinear Metamaterial Devices
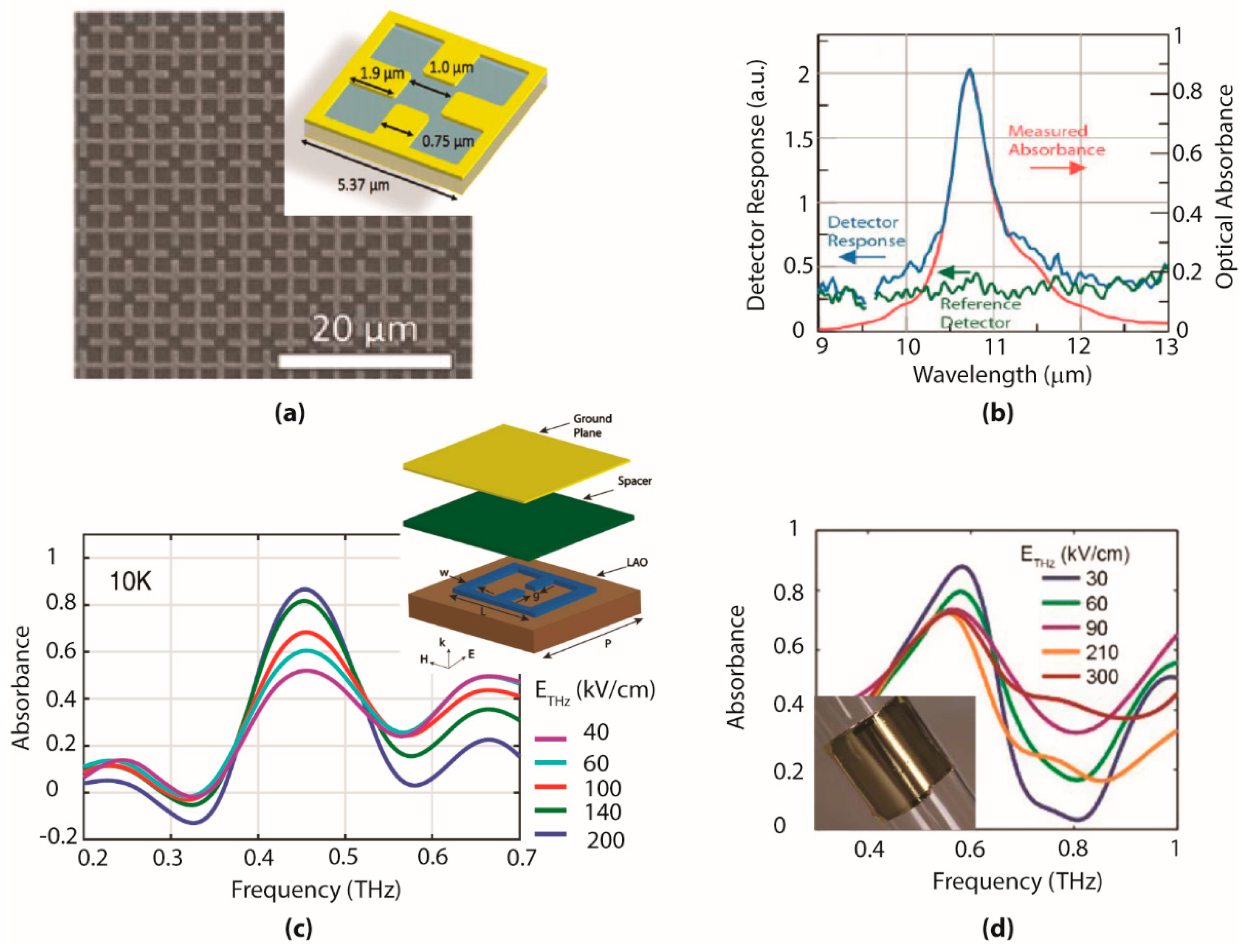
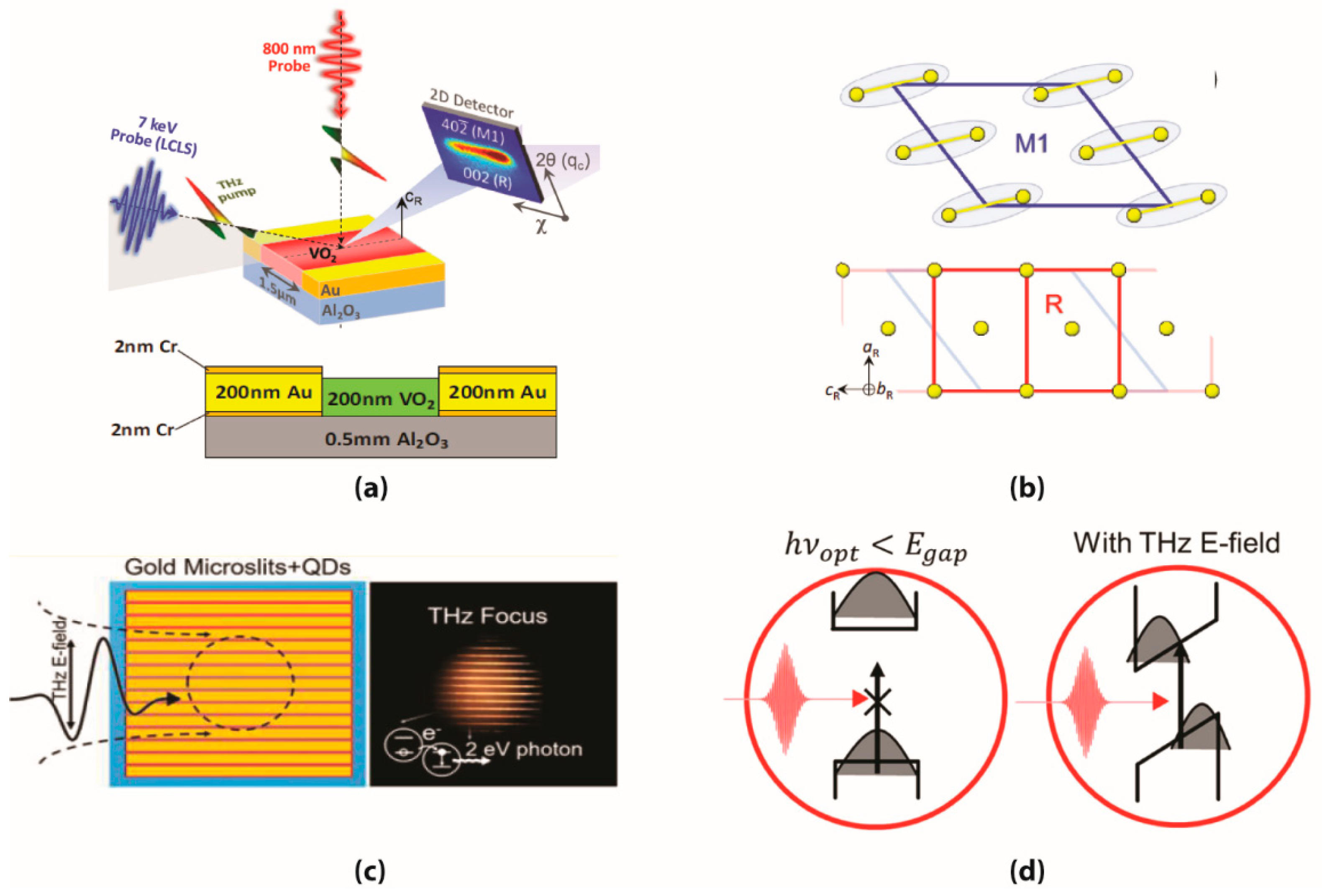
2.4. Field Confinement Applications in Nonlinear Spectroscopy
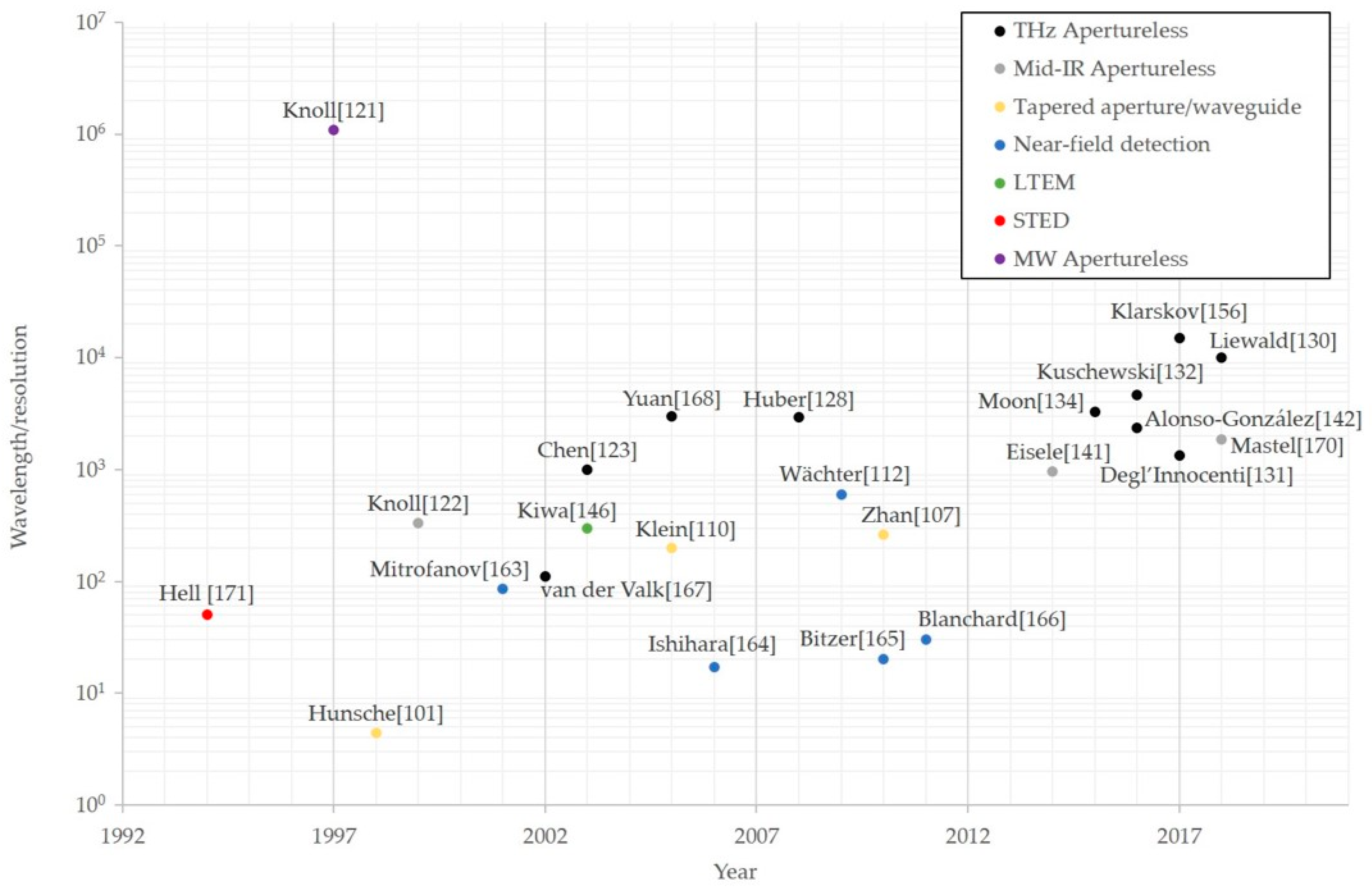
3. Field Confinement for Sub-Wavelength Imaging at Terahertz Frequencies
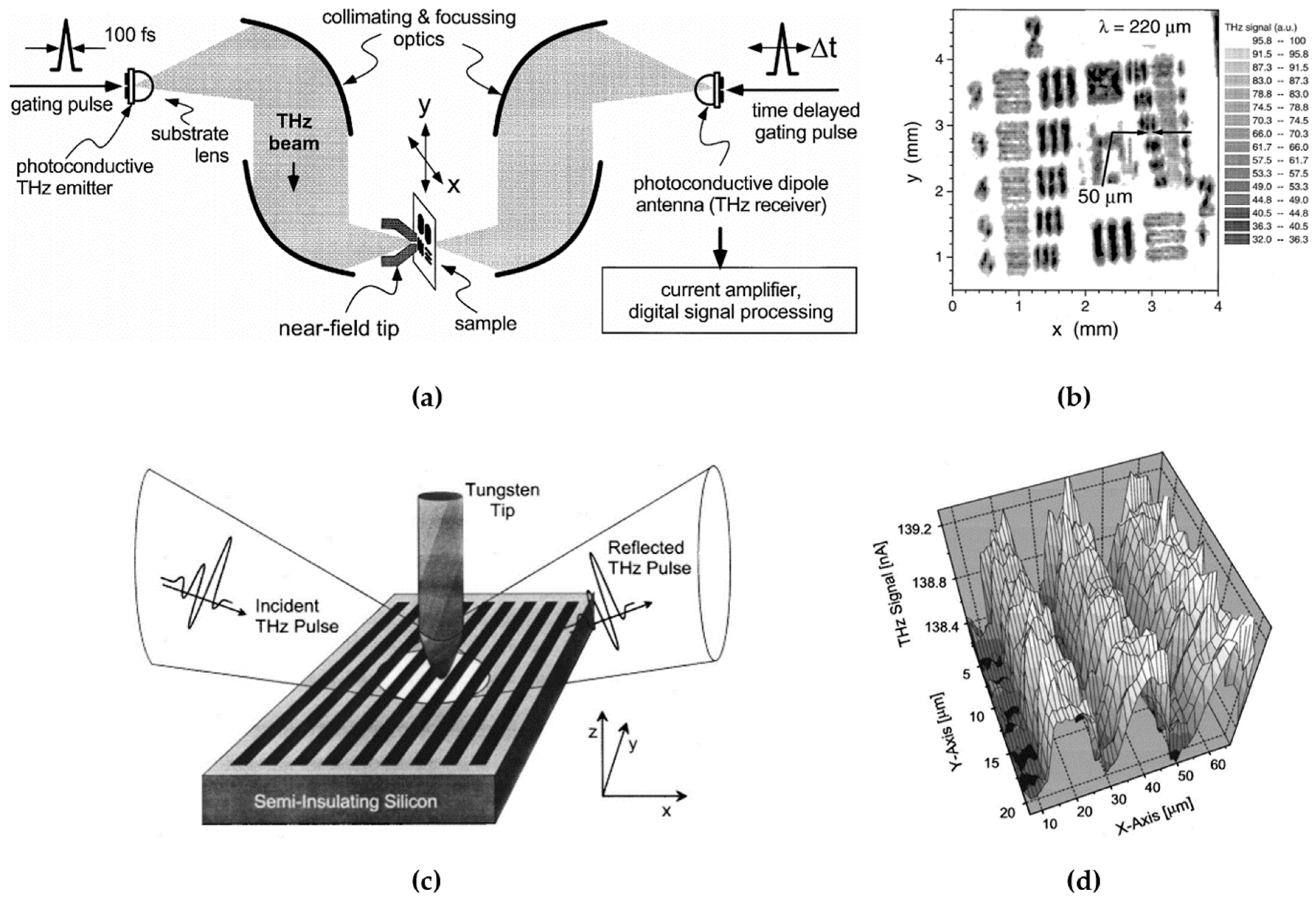
3.1. Early Work in Sub-Wavelength THz Imaging
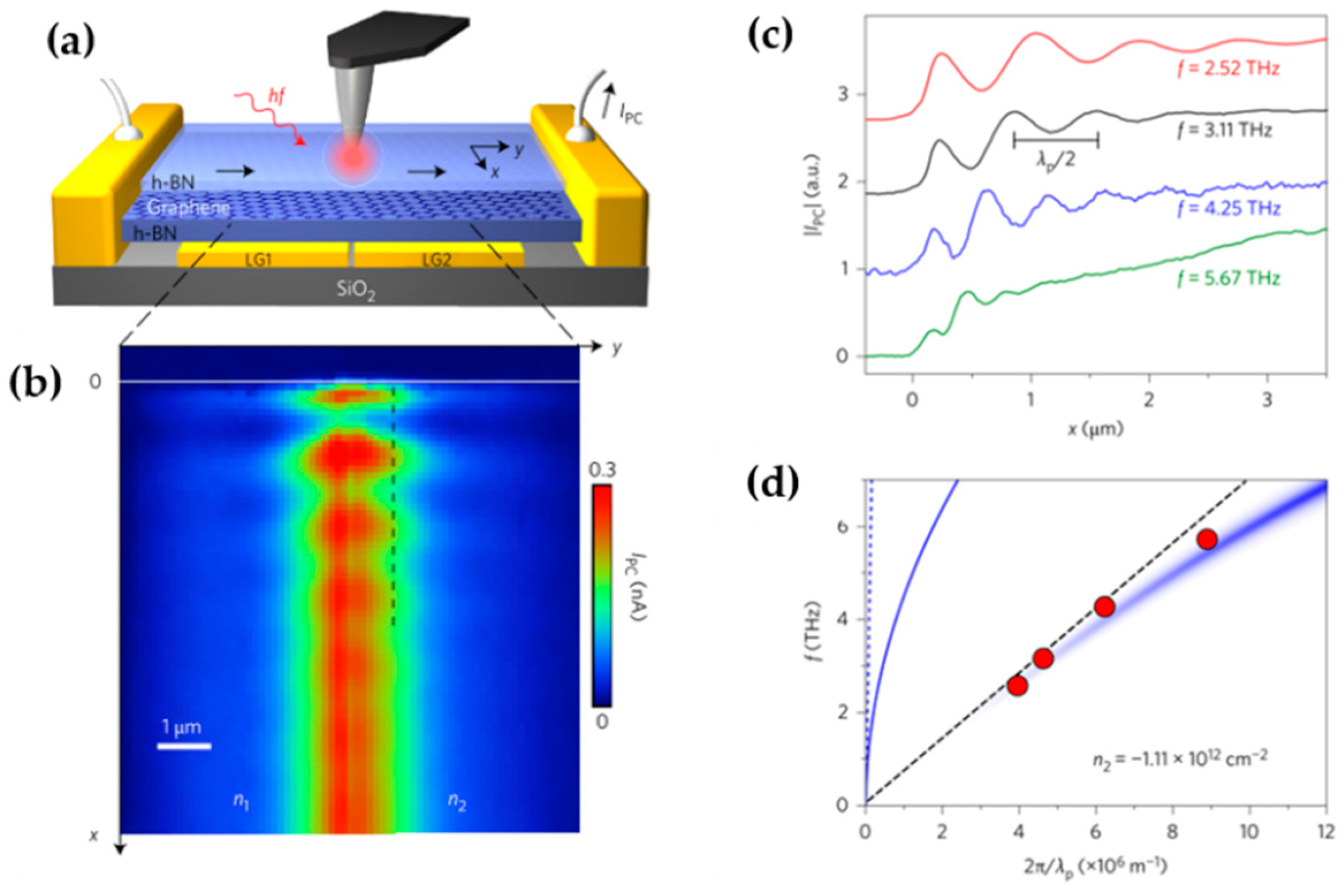
3.2. THz Imaging with s-SNOM
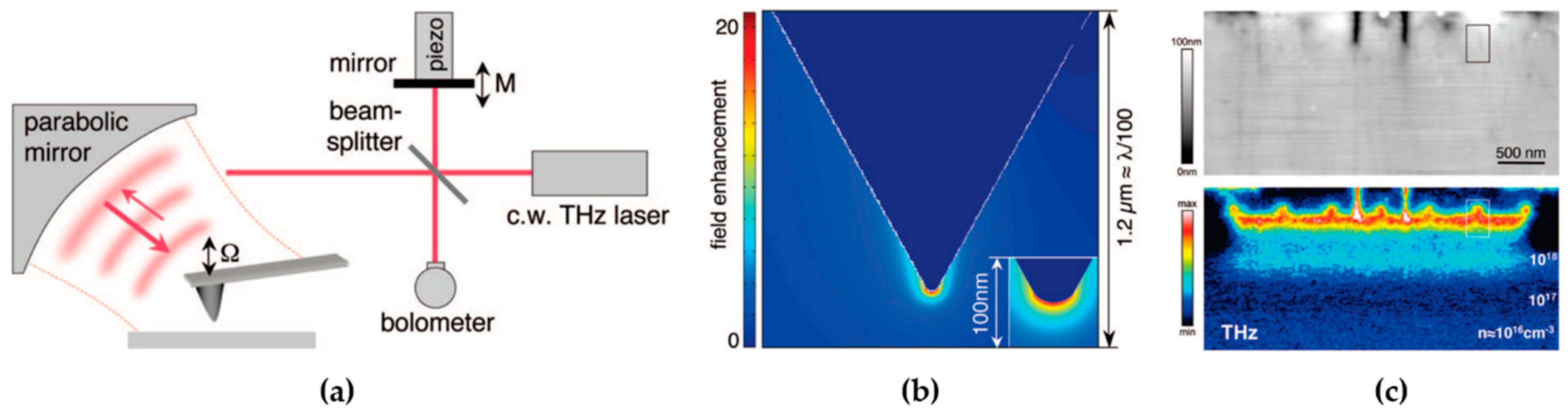
3.3. s-SNOM with CW and Pulsed THz Sources
3.4. Variations of s-SNOM Configuration for THz Imaging
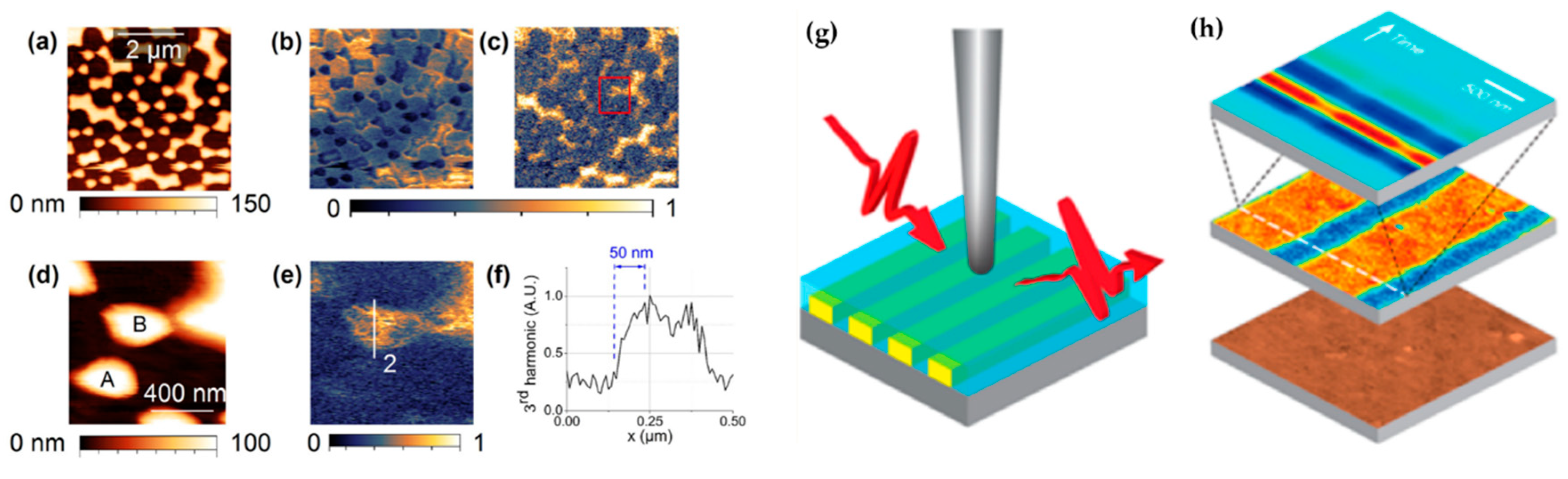
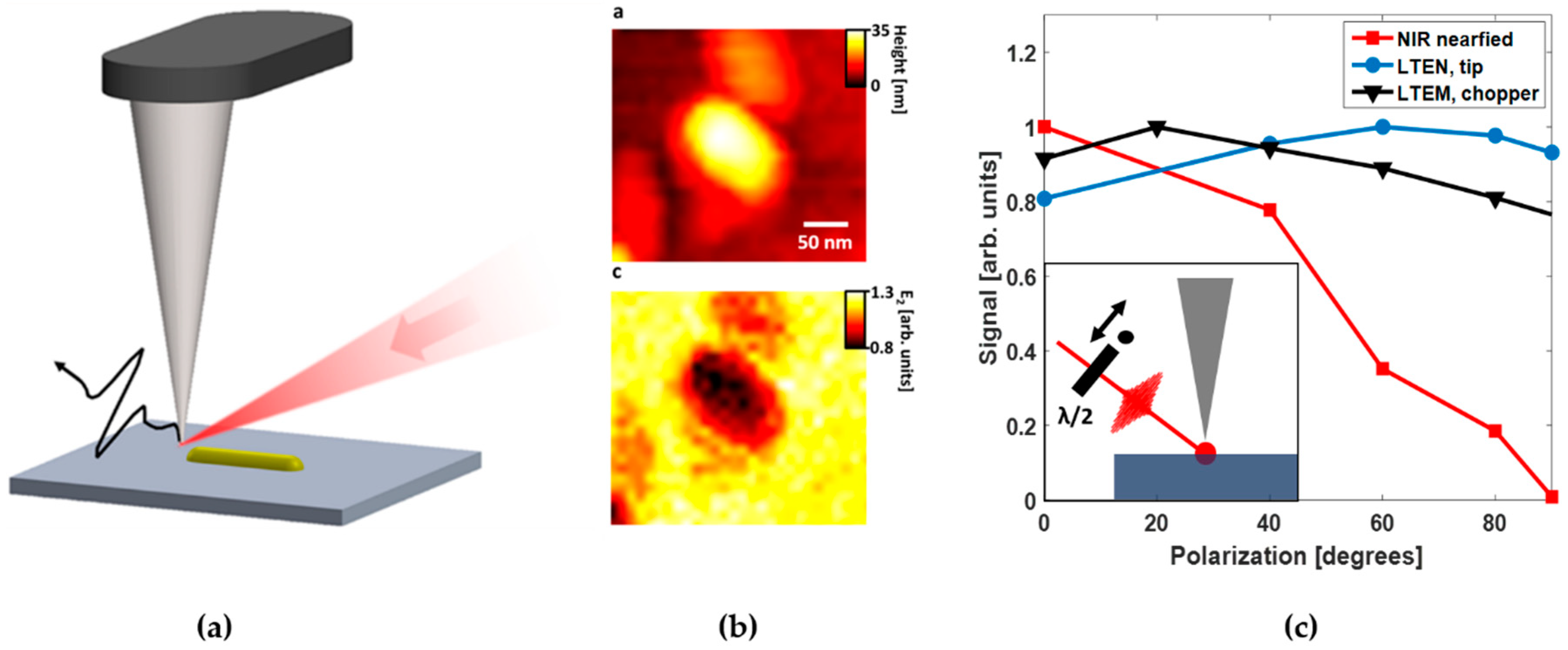
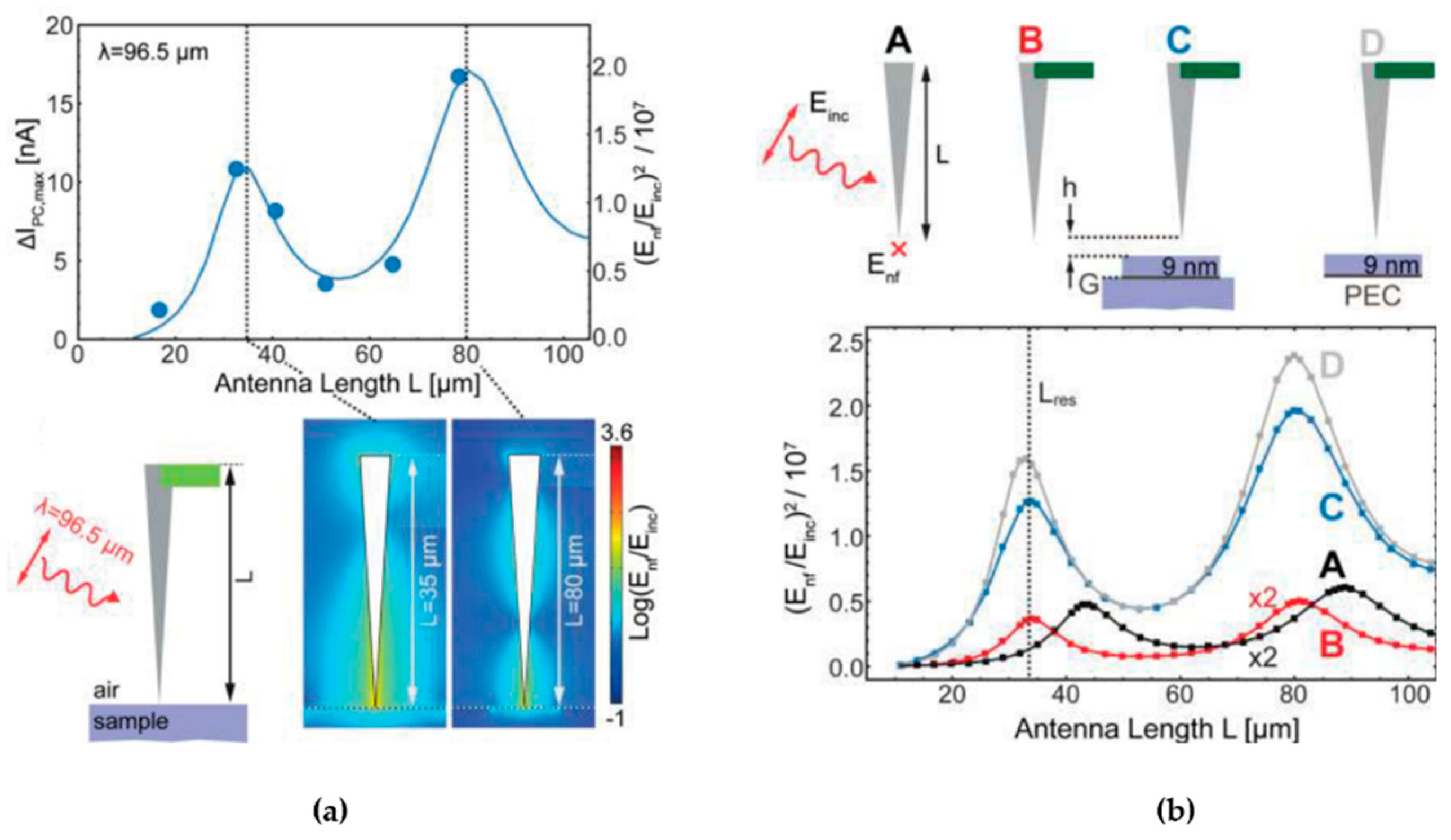
3.5. AFM Probes for THz Nanoscopy
3.6. Evolution of Sub-Wavelength THz Imaging
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sitori, C. Applied physics: Bridge for the terahertz gap. Nature 2002, 417, 132. [Google Scholar] [CrossRef] [PubMed]
- Mittleman, D.M. Perspective: Terahertz science and technology. J. Appl. Phys. 2017, 122, 230901. [Google Scholar] [CrossRef]
- Ma, J.; Shrestha, R.; Moeller, L.; Mittleman, D.M. Invited Article: Channel performance for indoor and outdoor terahertz wireless links. APL Photonics 2018, 3, 051601. [Google Scholar] [CrossRef]
- Yeh, K.; Hoffmann, M.; Hebling, J.; Nelson, K.A. Generation of 10 J ultrashort terahertz pulses by optical rectification. Appl. Phys. Lett. 2007, 90, 171121. [Google Scholar] [CrossRef]
- Hirori, H.; Doi, A.; Blanchard, F.; Tanaka, K. Single-cycle terahertz pulses with amplitudes exceeding 1 MV/cm generated by optical rectification in LiNbO3. Appl. Phys. Lett. 2011, 98, 091106. [Google Scholar] [CrossRef]
- Hebling, J.; Yeh, K.-L.; Hoffmann, M.C.; Nelson, K.A. High-Power THz Generation, THz Nonlinear Optics, and THz Nonlinear Spectroscopy. IEEE J. Sel. Top. Quantum Electron. 2008, 14, 345–353. [Google Scholar] [CrossRef]
- Cook, D.J.; Hochstrasser, R.M. Intense terahertz pulses by four-wave rectification in air. Opt. Lett. 2000, 25, 1210–1212. [Google Scholar] [CrossRef] [PubMed]
- Jepsen, P.U.; Cooke, D.G.; Koch, M. Terahertz spectroscopy and imaging—Modern techniques and applications. Laser Photonics Rev. 2011, 5, 124–166. [Google Scholar] [CrossRef]
- Merbold, H.; Bitzer, A.; Feurer, T. Second harmonic generation based on strong field enhancement in nanostructured THz materials. Opt. Express 2011, 19, 7262–7273. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Hwang, H.Y.; Tao, H.; Strikwerda, A.C.; Fan, K.; Keiser, G.R.; Sternbach, A.J.; West, K.G.; Kittiwatanakul, S.; Lu, J.; et al. Terahertz-field-induced insulator-to-metal transition in vanadium dioxide metamaterial. Nature 2012, 487, 345–348. [Google Scholar] [CrossRef] [PubMed]
- Herink, G.; Wimmer, L.; Ropers, C. Field emission at terahertz frequencies: AC-tunneling and ultrafast carrier dynamics. New J. Phys. 2014, 16, 123005. [Google Scholar] [CrossRef]
- Cocker, T.L.; Jelic, V.; Gupta, M.; Molesky, S.J.; Burgess, J.A.J.; Reyes, G.D.L.; Titova, L.V.; Tsui, Y.Y.; Freeman, M.R.; Hegmann, F.A. An ultrafast terahertz scanning tunnelling microscope. Nat. Photonics 2013, 7, 620–625. [Google Scholar] [CrossRef]
- Jelic, V.; Iwaszczuk, K.; Nguyen, P.H.; Rathje, C.; Hornig, G.J.; Sharum, H.M.; Hoffman, J.R.; Freeman, M.R.; Hegmann, F.A. Ultrafast terahertz control of extreme tunnel currents through single atoms on a silicon surface. Nat. Phys. 2017, 13, 591–598. [Google Scholar] [CrossRef]
- Cocker, T.L.; Peller, D.; Yu, P.; Repp, J.; Huber, R. Tracking the ultrafast motion of a single molecule by femtosecond orbital imaging. Nature 2016, 539, 263–267. [Google Scholar] [CrossRef] [PubMed]
- Pendry, J.B.; Holden, A.J.; Robbins, D.J.; Stewart, W.J. Magnetism from conductors and enhanced nonlinear phenomena. IEEE Trans. Microw. Theory Tech. 1999, 47, 2075–2084. [Google Scholar] [CrossRef]
- Pendry, J.B. Negative Refraction Makes a Perfect Lens. Phys. Rev. Lett. 2000, 85, 3966–3969. [Google Scholar] [CrossRef] [PubMed]
- Smith, D.R.; Padilla, W.J.; Vier, D.C.; Nemat-Nasser, S.C.; Schultz, S. Composite Medium with Simultaneously Negative Permeability and Permittivity. Phys. Rev. Lett. 2000, 84, 4184–4187. [Google Scholar] [CrossRef] [PubMed]
- Schurig, D.; Mock, J.J.; Justice, B.J.; Cummer, S.A.; Pendry, J.B.; Starr, A.F.; Smith, D.R. Metamaterial Electromagnetic Cloak at Microwave Frequencies. Science 2006, 314, 977–980. [Google Scholar] [CrossRef] [PubMed]
- Driscoll, T.; Kim, H.-T.; Chae, B.-G.; Kim, B.-J.; Lee, Y.-W.; Jokerst, N.M.; Palit, S.; Smith, D.R.; Di Ventra, M.; Basov, D.N. Memory Metamaterials. Science 2009, 325, 1518–1521. [Google Scholar] [CrossRef] [PubMed]
- Landy, N.I.; Sajuyigbe, S.; Mock, J.J.; Smith, D.R.; Padilla, W.J. Perfect Metamaterial Absorber. Phys. Rev. Lett. 2008, 100, 207402. [Google Scholar] [CrossRef] [PubMed]
- Tao, H.; Bingham, C.M.; Strikwerda, A.C.; Pilon, D.; Shrekenhamer, D.; Landy, N.I.; Fan, K.; Zhang, X.; Padilla, W.J.; Averitt, R.D. Highly flexible wide angle of incidence terahertz metamaterial absorber: Design, fabrication, and characterization. Phys. Rev. B 2008, 78, 241103. [Google Scholar] [CrossRef]
- Tao, H.; Strikwerda, A.C.; Fan, K.; Padilla, W.J.; Zhang, X.; Averitt, R.D. Reconfigurable Terahertz Metamaterials. Phys. Rev. Lett. 2009, 103, 147401. [Google Scholar] [CrossRef] [PubMed]
- Strikwerda, A.C.; Zalkovskij, M.; Lund Lorenzen, D.; Krabbe, A.; Lavrinenko, A.V.; Uhd Jepsen, P. Metamaterial composite bandpass filter with an ultra-broadband rejection bandwidth of up to 240 terahertz. Appl. Phys. Lett. 2014, 104, 191103. [Google Scholar] [CrossRef]
- Strikwerda, A.C.; Fan, K.; Tao, H.; Pilon, D.V.; Zhang, X.; Averitt, R.D. Comparison of birefringent electricsplit-ring resonator and meanderlinestructures as quarter-wave plates atterahertz frequencies. Opt. Express 2009, 17, 136–149. [Google Scholar] [CrossRef] [PubMed]
- Karl, N.; Reichel, K.; Chen, H.-T.; Taylor, A.J.; Brener, I.; Benz, A.; Reno, J.L.; Mendis, R.; Mittleman, D.M. An electrically driven terahertz metamaterial diffractive modulator with more than 20 dB of dynamic range. Appl. Phys. Lett. 2014, 104, 091115. [Google Scholar] [CrossRef]
- Chen, H.-T.; Padilla, W.J.; Cich, M.J.; Azad, A.K.; Averitt, R.D.; Taylor, A.J. A metamaterial solid-state terahertz phase modulator. Nat. Photonics 2009, 3, 148–151. [Google Scholar] [CrossRef]
- Marques, R.; Mesa, F.; Martel, J.; Medina, F. Comparative analysis of edge- and broadside-coupled split ring resonators for metamaterial design-theory and experiments. IEEE Trans. Antennas Propag. 2003, 51, 2572–2581. [Google Scholar] [CrossRef]
- Zhou, L.; Chui, S.T. Eigenmodes of metallic ring systems: A rigorous approach. Phys. Rev. B 2006, 74, 035419. [Google Scholar] [CrossRef]
- Strikwerda, A.C.; Zalkovskij, M.; Iwaszczuk, K.; Lorenzen, D.L.; Jepsen, P.U. Permanently reconfigured metamaterials due to terahertz induced mass transfer of gold. Opt. Express 2015, 23, 11586–11599. [Google Scholar] [CrossRef] [PubMed]
- Werley, C.A.; Fan, K.; Strikwerda, A.C.; Teo, S.M.; Zhang, X.; Averitt, R.D.; Nelson, K.A. Time-resolved imaging of near-fields in THz antennas and direct quantitative measurement of field enhancements. Opt. Express 2012, 20, 8551–8567. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Zhao, X.; Fan, K.; Wang, X.; Zhang, G.-F.; Geng, K.; Zhang, X.; Averitt, R.D. Terahertz radiation-induced sub-cycle field electron emission across a split-gap dipole antenna. Appl. Phys. Lett. 2015, 107, 231101. [Google Scholar] [CrossRef]
- Chen, H.-T.; O’Hara, J.F.; Taylor, A.J.; Averitt, R.D.; Highstrete, C.; Lee, M.; Padilla, W.J. Complementary planar terahertz metamaterials. Opt. Express 2007, 15, 1084–1095. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.-T.; Padilla, W.J.; Zide, J.M.O.; Gossard, A.C.; Taylor, A.J.; Averitt, R.D. Active terahertz metamaterial devices. Nature 2006, 444, 597–600. [Google Scholar] [CrossRef] [PubMed]
- Fu, Y.H.; Liu, A.Q.; Zhu, W.M.; Zhang, X.M.; Tsai, D.P.; Zhang, J.B.; Mei, T.; Tao, J.F.; Guo, H.C.; Zhang, X.H.; et al. A Micromachined Reconfigurable Metamaterial via Reconfiguration of Asymmetric Split-Ring Resonators. Adv. Funct. Mater. 2011, 21, 3589–3594. [Google Scholar] [CrossRef]
- Zhao, X.; Fan, K.; Zhang, J.; Keiser, G.R.; Duan, G.; Averitt, R.D.; Zhang, X. Voltage-tunable dual-layer terahertz metamaterials. Microsyst. Nanoeng. 2016, 2, 16025. [Google Scholar] [CrossRef]
- Keiser, G.R.; Seren, H.R.; Strikwerda, A.C.; Zhang, X.; Averitt, R.D. Structural control of metamaterial oscillator strength and electric field enhancement at terahertz frequencies. Appl. Phys. Lett. 2014, 105, 081112. [Google Scholar] [CrossRef]
- Shadrivov, I.V.; Kozyrev, A.B.; van der Weide, D.W.; Kivshar, Y.S. Tunable transmission and harmonic generation in nonlinear metamaterials. Appl. Phys. Lett. 2008, 93, 161903. [Google Scholar] [CrossRef]
- Shadrivov, I.V.; Kozyrev, A.B.; van der Weide, D.W.; Kivshar, Y.S. Nonlinear magnetic metamaterials. Opt. Express 2008, 16, 20266–20271. [Google Scholar] [CrossRef] [PubMed]
- Powell, D.A.; Shadrivov, I.V.; Kivshar, Y.S. Nonlinear electric metamaterials. Appl. Phys. Lett. 2009, 95, 084102. [Google Scholar] [CrossRef]
- Lapine, M.; Shadrivov, I.V.; Kivshar, Y.S. Colloquium: Nonlinear metamaterials. Rev. Mod. Phys. 2014, 86, 1093–1123. [Google Scholar] [CrossRef]
- Rose, A.; Larouche, S.; Huang, D.; Poutrina, E.; Smith, D.R. Nonlinear parameter retrieval from three- and four-wave mixing in metamaterials. Phys. Rev. E 2010, 82, 036608. [Google Scholar] [CrossRef] [PubMed]
- Larouche, S.; Smith, D.R. A retrieval method for nonlinear metamaterials. Opt. Commun. 2010, 283, 1621–1627. [Google Scholar] [CrossRef]
- Huang, D.; Rose, A.; Poutrina, E.; Larouche, S.; Smith, D.R. Wave mixing in nonlinear magnetic metacrystal. Appl. Phys. Lett. 2011, 98, 204102. [Google Scholar] [CrossRef]
- Larouche, S.; Rose, A.; Poutrina, E.; Huang, D.; Smith, D.R. Experimental determination of the quadratic nonlinear magnetic susceptibility of a varactor-loaded split ring resonator metamaterial. Appl. Phys. Lett. 2010, 97, 011109. [Google Scholar] [CrossRef]
- Hannam, K.E.; Powell, D.A.; Shadrivov, I.V.; Kivshar, Y.S. Tuning the nonlinear response of coupled split-ring resonators. Appl. Phys. Lett. 2012, 100, 081111. [Google Scholar] [CrossRef]
- Lapine, M.; Gorkunov, M.; Ringhofer, K.H. Nonlinearity of a metamaterial arising from diode insertions into resonant conductive elements. Phys. Rev. E 2003, 67, 065601. [Google Scholar] [CrossRef] [PubMed]
- Lapine, M.; Shadrivov, I.V.; Powell, D.A.; Kivshar, Y.S. Magnetoelastic metamaterials. Nat. Mater. 2012, 11, 30–33. [Google Scholar] [CrossRef] [PubMed]
- Rose, A.; Huang, D.; Smith, D.R. Controlling the Second Harmonic in a Phase-Matched Negative-Index Metamaterial. Phys. Rev. Lett. 2011, 107, 063902. [Google Scholar] [CrossRef] [PubMed]
- Lange, C.; Maag, T.; Hohenleutner, M.; Baierl, S.; Schubert, O.; Edwards, E.R.J.; Bougeard, D.; Woltersdorf, G.; Huber, R. Extremely Nonperturbative Nonlinearities in GaAs Driven by Atomically Strong Terahertz Fields in Gold Metamaterials. Phys. Rev. Lett. 2014, 113, 227401. [Google Scholar] [CrossRef] [PubMed]
- Keiser, G.R.; Karl, N.; Liu, P.Q.; Tulloss, C.; Chen, H.-T.; Taylor, A.J.; Brener, I.; Reno, J.L.; Mittleman, D.M. Nonlinear terahertz metamaterials with active electrical control. Appl. Phys. Lett. 2017, 111, 121101. [Google Scholar] [CrossRef]
- Fan, K.; Hwang, H.Y.; Liu, M.; Strikwerda, A.C.; Sternbach, A.; Zhang, J.; Zhao, X.; Zhang, X.; Nelson, K.A.; Averitt, R.D. Nonlinear Terahertz Metamaterials via Field-Enhanced Carrier Dynamics in GaAs. Phys. Rev. Lett. 2013, 110, 217404. [Google Scholar] [CrossRef] [PubMed]
- Darrow, J.T.; Zhang, X.; Auston, D.H.; Morse, J.D. Saturation properties of large-aperture photoconducting antennas. IEEE J. Quantum Electron. 1992, 28, 1607–1616. [Google Scholar] [CrossRef]
- Nuss, M.C.; Auston, D.H.; Capasso, F. Direct Subpicosecond Measurement of Carrier Mobility of Photoexcited Electrons in Gallium Arsenide. Phys. Rev. Lett. 1987, 58, 2355–2358. [Google Scholar] [CrossRef] [PubMed]
- Anderson, C.L.; Crowell, C.R. Threshold Energies for Electron-Hole Pair Production by Impact Ionization in Semiconductors. Phys. Rev. B 1972, 5, 2267–2272. [Google Scholar] [CrossRef]
- Keren-Zur, S.; Avayu, O.; Michaeli, L.; Ellenbogen, T. Nonlinear Beam Shaping with Plasmonic Metasurfaces. ACS Photonics 2016, 3, 117–123. [Google Scholar] [CrossRef]
- Weis, P.; Garcia-Pomar, J.L.; Beigang, R.; Rahm, M. Hybridization Induced Transparency in Composites of Metamaterials and Atomic Media. Opt. Express 2011, 19, 23573–23580. [Google Scholar] [CrossRef] [PubMed]
- Withayachumnankul, W.; Lin, H.; Serita, K.; Shah, C.M.; Sriram, S.; Bhaskaran, M.; Tonouchi, M.; Fumeaux, C.; Abbott, D. Sub-diffraction thin-film sensing with planar terahertz metamaterials. Opt. Express 2012, 20, 3345–3352. [Google Scholar] [CrossRef] [PubMed]
- Singh, R.; Al-Naib, I.A.I.; Koch, M.; Zhang, W. Sharp Fano Resonances in THz Metamaterials. Opt. Express 2011, 19, 6312–6319. [Google Scholar] [CrossRef] [PubMed]
- Singh, R.; Cao, W.; Al-Naib, I.; Cong, L.; Withayachumnankul, W.; Zhang, W. Ultrasensitive terahertz sensing with high-Q Fano resonances in metasurfaces. Appl. Phys. Lett. 2014, 105, 171101. [Google Scholar] [CrossRef]
- Yahiaoui, R.; Strikwerda, A.C.; Jepsen, P.U. Terahertz Plasmonic Structure with Enhanced Sensing Capabilities. IEEE Sens. J. 2016, 16, 2484–2488. [Google Scholar] [CrossRef]
- Suen, J.Y.; Fan, K.; Montoya, J.; Bingham, C.; Stenger, V.; Sriram, S.; Padilla, W.J. Multifunctional metamaterial pyroelectric infrared detectors. Optica 2017, 4, 276–279. [Google Scholar] [CrossRef]
- Keiser, G.R.; Zhang, J.; Zhao, X.; Zhang, X.; Averitt, R.D. Terahertz saturable absorption in superconducting metamaterials. J. Opt. Soc. Am. B 2016, 33, 2649–2655. [Google Scholar] [CrossRef]
- Zhao, X.; Zhang, J.; Fan, K.; Duan, G.; Metcalfe, G.D.; Wraback, M.; Zhang, X.; Averitt, R.D. Nonlinear terahertz metamaterial perfect absorbers using GaAs. Photonics Res. 2016, 4, A16–A21. [Google Scholar] [CrossRef]
- Haus, H. Theory of mode locking with a slow saturable absorber. IEEE J. Quantum Electron. 1975, 11, 736–746. [Google Scholar] [CrossRef]
- Haus, H.A. Theory of mode locking with a fast saturable absorber. J. Appl. Phys. 1975, 46, 3049–3058. [Google Scholar] [CrossRef]
- Watts, C.M.; Liu, X.; Padilla, W.J. Metamaterial Electromagnetic Wave Absorbers. Adv. Mater. 2012, 24, OP98–OP120. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.-T. Interference theory of metamaterial perfect absorbers. Opt. Express 2012, 20, 7165–7172. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Chowdhury, D.R.; Ramani, S.; Reiten, M.T.; Luo, S.-N.; Azad, A.K.; Taylor, A.J.; Chen, H.-T. Impact of resonator geometry and its coupling with ground plane on ultrathin metamaterial perfect absorbers. Appl. Phys. Lett. 2012, 101, 101102. [Google Scholar] [CrossRef]
- Gu, J.; Singh, R.; Tian, Z.; Cao, W.; Xing, Q.; He, M.; Zhang, J.W.; Han, J.; Chen, H.-T.; Zhang, W. Terahertz superconductor metamaterial. Appl. Phys. Lett. 2010, 97, 071102. [Google Scholar] [CrossRef]
- Ricci, M.; Orloff, N.; Anlage, S.M. Superconducting metamaterials. Appl. Phys. Lett. 2005, 87, 034102. [Google Scholar] [CrossRef]
- Ricci, M.C.; Hua, X.; Prozorov, R.; Zhuravel, A.P.; Ustinov, A.V.; Anlage, S.M. Tunability of Superconducting Metamaterials. IEEE Trans. Appl. Supercond. 2007, 17, 918–921. [Google Scholar] [CrossRef]
- Anlage, S.M. The physics and applications of superconducting metamaterials. J. Opt. 2011, 13, 024001. [Google Scholar] [CrossRef]
- Jung, P.; Ustinov, A.V.; Anlage, S.M. Progress in superconducting metamaterials. Supercond. Sci. Technol. 2014, 27, 073001. [Google Scholar] [CrossRef]
- Kunchur, M.N.; Christen, D.K.; Klabunde, C.E.; Phillips, J.M. Pair-breaking effect of high current densities on the superconducting transition in YBaC3O7-δ. Phys. Rev. Lett. 1994, 72, 752–755. [Google Scholar] [CrossRef] [PubMed]
- Glossner, A.; Zhang, C.; Kikuta, S.; Kawayama, I.; Murakami, H.; Müller, P.; Tonouchi, M. Cooper pair breakup in YBCO under strong terahertz fields. arXiv, 2012; arXiv:1205.1684. [Google Scholar]
- Geier, A.; Schön, G. Response of a superconductor to a supercritical current pulse. J. Low Temp. Phys. 1982, 46, 151–160. [Google Scholar] [CrossRef]
- Hu, T.; Strikwerda, A.C.; Fan, K.; Bingham, C.M.; Padilla, W.J.; Xin, Z.; Averitt, R.D. Terahertz metamaterials on free-standing highly-flexible polyimide substrates. J. Phys. D Appl. Phys. 2008, 41, 232004. [Google Scholar]
- Vitiello, M.S.; Scalari, G.; Williams, B.; De Natale, P. Quantum cascade lasers: 20 years of challenges. Opt. Express 2015, 23, 5167–5182. [Google Scholar] [CrossRef] [PubMed]
- Vitiello, M.S.; Scamarcio, G.; Spagnolo, V.; Dhillon, S.S.; Sirtori, C. Terahertz quantum cascade lasers with large wall-plug efficiency. Appl. Phys. Lett. 2007, 90, 191115. [Google Scholar] [CrossRef]
- Hwang, H.Y.; Fleischer, S.; Brandt, N.C.; Perkins, B.G.; Liu, M.; Fan, K.; Sternbach, A.; Zhang, X.; Averitt, R.D.; Nelson, K.A. A review of non-linear terahertz spectroscopy with ultrashort tabletop-laser pulses. J. Mod. Opt. 2014, 62, 1447–1479. [Google Scholar] [CrossRef]
- Goodenough, J.B. The two components of the crystallographic transition in VO2. J. Solid State Chem. 1971, 3, 490–500. [Google Scholar] [CrossRef]
- Cavalleri, A.; Dekorsy, T.; Chong, H.H.W.; Kieffer, J.C.; Schoenlein, R.W. Evidence for a structurally-driven insulator-to-metal transition in VO2: A view from the ultrafast timescale. Phys. Rev. B 2004, 70, 161102. [Google Scholar] [CrossRef]
- Laverock, J.; Kittiwatanakul, S.; Zakharov, A.A.; Niu, Y.R.; Chen, B.; Wolf, S.A.; Lu, J.W.; Smith, K.E. Direct Observation of Decoupled Structural and Electronic Transitions and an Ambient Pressure Monocliniclike Metallic Phase of VO2. Phys. Rev. Lett. 2014, 113, 216402. [Google Scholar] [CrossRef] [PubMed]
- Gray, A.X.; Hoffmann, M.C.; Jeong, J.; Aetukuri, N.P.; Zhu, D.; Hwang, H.Y.; Brandt, N.C.; Wen, H.; Sternbach, A.J.; Bonetti, S.; et al. Ultrafast terahertz field control of electronic and structural interactions in vanadium dioxide. Phys. Rev. B 2018, 98, 045104. [Google Scholar] [CrossRef]
- Pein, B.C.; Chang, W.; Hwang, H.Y.; Scherer, J.; Coropceanu, I.; Zhao, X.; Zhang, X.; Bulović, V.; Bawendi, M.; Nelson, K.A. Terahertz-Driven Luminescence and Colossal Stark Effect in CdSe–CdS Colloidal Quantum Dots. Nano Lett. 2017, 17, 5375–5380. [Google Scholar] [CrossRef] [PubMed]
- Empedocles, S.A.; Bawendi, M.G. Quantum-Confined Stark Effect in Single CdSe Nanocrystallite Quantum Dots. Science 1997, 278, 2114. [Google Scholar] [CrossRef] [PubMed]
- Hoffmann, M.C.; Monozon, B.S.; Livshits, D.; Rafailov, E.U.; Turchinovich, D. Terahertz electro-absorption effect enabling femtosecond all-optical switching in semiconductor quantum dots. Appl. Phys. Lett. 2010, 97, 231108. [Google Scholar] [CrossRef]
- Kyoung, J.; Seo, M.; Park, H.; Koo, S.; Kim, H.S.; Park, Y.; Kim, B.J.; Ahn, K.; Park, N.; Kim, H.T.; et al. Giant nonlinear response of terahertz nanoresonators on VO2 thin film. Opt. Express 2010, 18, 16452–16459. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.Y.; Kang, B.J.; Park, J.; Bahk, Y.M.; Kim, W.T.; Rhie, J.; Jeon, H.; Rotermund, F.; Kim, D.S. Terahertz Quantum Plasmonics of Nanoslot Antennas in Nonlinear Regime. Nano Lett. 2015, 15, 6683–6688. [Google Scholar] [CrossRef] [PubMed]
- Ryu, Y.S.; Lee, D.K.; Kang, J.H.; Lee, S.H.; Yu, E.S.; Seo, M. Ultrasensitive terahertz sensing of gold nanoparticles inside nano slot antennas. Opt. Express 2017, 25, 30591–30597. [Google Scholar] [CrossRef] [PubMed]
- Seo, M.A.; Park, H.R.; Koo, S.M.; Park, D.J.; Kang, J.H.; Suwal, O.K.; Choi, S.S.; Planken, P.C.M.; Park, G.S.; Park, N.K.; et al. Terahertz field enhancement by a metallic nano slit operating beyond the skin-depth limit. Nat. Photonics 2009, 3, 152–156. [Google Scholar] [CrossRef]
- Klarskov, P.; Tarekegne, A.T.; Iwaszczuk, K.; Zhang, X.C.; Jepsen, P.U. Amplification of resonant field enhancement by plasmonic lattice coupling in metallic slit arrays. Sci. Rep. 2016, 6, 37738. [Google Scholar] [CrossRef] [PubMed]
- Park, H.R.; Ahn, K.J.; Han, S.; Bahk, Y.M.; Park, N.; Kim, D.S. Colossal absorption of molecules inside single terahertz nanoantennas. Nano Lett. 2013, 13, 1782–1786. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.-K.; Kim, G.; Kim, C.; Jhon, Y.M.; Kim, J.H.; Lee, T.; Son, J.-H.; Seo, M. Ultrasensitive Detection of Residual Pesticides Using THz Near-Field Enhancement. IEEE Trans. Terahertz Sci. Technol. 2016, 6, 389–395. [Google Scholar] [CrossRef]
- Lee, D.K.; Kang, J.H.; Lee, J.S.; Kim, H.S.; Kim, C.; Kim, J.H.; Lee, T.; Son, J.H.; Park, Q.H.; Seo, M. Highly sensitive and selective sugar detection by terahertz nano-antennas. Sci. Rep. 2015, 5, 15459. [Google Scholar] [CrossRef] [PubMed]
- Choi, G.; Bahk, Y.M.; Kang, T.; Lee, Y.; Son, B.H.; Ahn, Y.H.; Seo, M.; Kim, D.S. Terahertz Nanoprobing of Semiconductor Surface Dynamics. Nano Lett. 2017, 17, 6397–6401. [Google Scholar] [CrossRef] [PubMed]
- Bitzer, A.; Wallauer, J.; Helm, H.; Merbold, H.; Feurer, T.; Walther, M. Lattice modes mediate radiative coupling in metamaterial arrays. Opt. Express 2009, 17, 22108–22113. [Google Scholar] [CrossRef] [PubMed]
- Tan, T.C.; Srivastava, Y.K.; Manjappa, M.; Plum, E.; Singh, R. Lattice induced strong coupling and line narrowing of split resonances in metamaterials. Appl. Phys. Lett. 2018, 112, 201111. [Google Scholar] [CrossRef]
- Adam, A.J.L. Review of Near-Field Terahertz Measurement Methods and Their Applications. J. Infrared Millim. Terahertz Waves 2011, 32, 976–1019. [Google Scholar] [CrossRef]
- Mittleman, D.M. Twenty years of terahertz imaging. Opt. Express 2018, 26, 9417. [Google Scholar] [CrossRef] [PubMed]
- Hunsche, S.; Koch, M.; Brener, I.; Nuss, M.C. THz near-field imaging. Opt. Commun. 1998, 150, 22–26. [Google Scholar] [CrossRef]
- Liu, S.; Mitrofanov, O.; Nahata, A. Near-field terahertz imaging using sub-wavelength apertures without cutoff. Opt. Express 2016, 24, 2728–2736. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.D.; Vardeny, Z.V.; Nahata, A. Concentration of terahertz radiation through a conically tapered aperture. Opt. Express 2010, 18, 25441–25448. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.H.; Lee, E.S.; Ji, Y.B.; Jeon, T.I. Improvement of THz coupling using a tapered parallel-plate waveguide. Opt. Express 2010, 18, 1289–1295. [Google Scholar] [CrossRef] [PubMed]
- Theuer, M.; Harsha, S.S.; Grischkowsky, D. Flare coupled metal parallel-plate waveguides for high resolution terahertz time-domain spectroscopy. J. Appl. Phys. 2010, 108, 113105. [Google Scholar] [CrossRef]
- Macfaden, A.J.; Reno, J.L.; Brener, I.; Mitrofanov, O. 3 μm aperture probes for near-field terahertz transmission microscopy. Appl. Phys. Lett. 2014, 104, 011110. [Google Scholar] [CrossRef]
- Zhan, H.; Mendis, R.; Mittleman, D.M. Superfocusing terahertz waves below lambda/250 using plasmonic parallel-plate waveguides. Opt. Express 2010, 18, 9643–9650. [Google Scholar] [CrossRef] [PubMed]
- Iwaszczuk, K.; Andryieuski, A.; Lavrinenko, A.; Zhang, X.C.; Jepsen, P.U. Terahertz field enhancement to the MV/cm regime in a tapered parallel plate waveguide. Opt. Express 2012, 20, 8344–8355. [Google Scholar] [CrossRef] [PubMed]
- Reichel, K.S.; Iwaszczuk, K.; Jepsen, P.U.; Mendis, R.; Mittleman, D.M. In situ spectroscopic characterization of a terahertz resonant cavity. Optica 2014, 1, 272–275. [Google Scholar] [CrossRef]
- Klein, N.; Lahl, P.; Poppe, U.; Kadlec, F.; Kužel, P. A metal-dielectric antenna for terahertz near-field imaging. J. Appl. Phys. 2005, 98, 014910. [Google Scholar] [CrossRef]
- Tuniz, A.; Kaltenecker, K.J.; Fischer, B.M.; Walther, M.; Fleming, S.C.; Argyros, A.; Kuhlmey, B.T. Metamaterial fibres for subdiffraction imaging and focusing at terahertz frequencies over optically long distances. Nat. Commun. 2013, 4, 2706. [Google Scholar] [CrossRef] [PubMed]
- Wächter, M.; Nagel, M.; Kurz, H. Tapered photoconductive terahertz field probe tip with subwavelength spatial resolution. Appl. Phys. Lett. 2009, 95, 041112. [Google Scholar] [CrossRef]
- Rusina, A.; Durach, M.; Nelson, K.A.; Stockman, M.I. Nanoconcentration of terahertz radiation in plasmonic waveguides. Opt. Express 2008, 16, 18576–18589. [Google Scholar] [CrossRef] [PubMed]
- Atkin, J.M.; Berweger, S.; Jones, A.C.; Raschke, M.B. Nano-optical imaging and spectroscopy of order, phases, and domains in complex solids. Adv. Phys. 2012, 61, 745–842. [Google Scholar] [CrossRef]
- Berweger, S.; Atkin, J.M.; Olmon, R.L.; Raschke, M.B. Light on the Tip of a Needle: Plasmonic Nanofocusing for Spectroscopy on the Nanoscale. J. Phys. Chem. Lett. 2012, 3, 945–952. [Google Scholar] [CrossRef] [PubMed]
- Qazilbash, M.M.; Brehm, M.; Chae, B.G.; Ho, P.C.; Andreev, G.O.; Kim, B.J.; Yun, S.J.; Balatsky, A.V.; Maple, M.B.; Keilmann, F.; et al. Mott transition in VO2 revealed by infrared spectroscopy and nano-imaging. Science 2007, 318, 1750–1753. [Google Scholar] [CrossRef] [PubMed]
- Fei, Z.; Andreev, G.O.; Bao, W.; Zhang, L.M.; Alexander, S.M.; Wang, C.; Stewart, M.K.; Zhao, Z.; Dominguez, G.; Thiemens, M.; et al. Infrared nanoscopy of dirac plasmons at the graphene-SiO2 interface. Nano Lett. 2011, 11, 4701–4705. [Google Scholar] [CrossRef] [PubMed]
- Zenhausern, F.; Martin, Y.; Wickramasinghe, H.K. Scanning Interferometric Apertureless Microscopy: Optical Imaging at 10 Angstrom Resolution. Science 1995, 269, 1083–1085. [Google Scholar] [CrossRef] [PubMed]
- Fei, Z.; Foley IV, J.J.; Gannett, W.; Liu, M.K.; Dai, S.; Ni, G.X.; Zettl, A.; Fogler, M.M.; Wiederrecht, G.P.; Gray, S.K.; et al. Ultraconfined Plasmonic Hotspots inside Graphene Nanobubbles. Nano Lett. 2016, 16, 7842–7848. [Google Scholar] [CrossRef] [PubMed]
- Huber, M.A.; Mooshammer, F.; Plankl, M.; Viti, L.; Sandner, F.; Kastner, L.Z.; Frank, T.; Fabian, J.; Vitiello, M.S.; Cocker, T.L.; et al. Femtosecond photo-switching of interface polaritons in black phosphorus heterostructures. Nat. Nanotechnol. 2017, 12, 207–211. [Google Scholar] [CrossRef] [PubMed]
- Knoll, B.; Keilmann, F.; Kramer, A.; Guckenberger, R. Contrast of microwave near-field microscopy. Appl. Phys. Lett. 1997, 70, 2667–2669. [Google Scholar] [CrossRef]
- Knoll, B.; Keilmann, F. Near-field probing of vibrational absorption for chemical microscopy. Nature 1999, 399, 20154. [Google Scholar] [CrossRef]
- Chen, H.-T.; Kersting, R.; Cho, G.C. Terahertz imaging with nanometer resolution. Appl. Phys. Lett. 2003, 83, 3009–3011. [Google Scholar] [CrossRef]
- Keilmann, F.; Hillenbrand, R. Near-field microscopy by elastic light scattering from a tip. Philos. Trans. A Math. Phys. Eng. Sci. 2004, 362, 787–805. [Google Scholar] [CrossRef] [PubMed]
- Knoll, B.; Keilmann, F. Enhanced dielectric contrast in scattering-type scanning near-field optical microscopy. Opt. Commun. 2000, 182, 321–328. [Google Scholar] [CrossRef]
- Cvitkovic, A.; Ocelic, N.; Hillenbrand, R. Analytical model for quantitative prediction of material contrasts in scattering-type near-field optical microscopy. Opt. Express 2007, 15, 8550–8565. [Google Scholar] [CrossRef] [PubMed]
- Govyadinov, A.A.; Amenabar, I.; Huth, F.; Carney, P.S.; Hillenbrand, R. Quantitative Measurement of Local Infrared Absorption and Dielectric Function with Tip-Enhanced Near-Field Microscopy. J. Phys. Chem. Lett. 2013, 4, 1526–1531. [Google Scholar] [CrossRef] [PubMed]
- Huber, A.J.; Keilmann, F.; Wittborn, J.; Aizpurua, J.; Hillenbrand, R. Terahertz Near-Field Nanoscopy of Mobile Carriers in Single Semiconductor Nanodevices. Nano Lett. 2008, 8, 3766–3770. [Google Scholar] [CrossRef] [PubMed]
- Giordano, M.C.; Mastel, S.; Liewald, C.; Columbo, L.L.; Brambilla, M.; Viti, L.; Politano, A.; Zhang, K.; Li, L.; Davies, A.G.; et al. Phase-resolved terahertz self-detection near-field microscopy. Opt. Express 2018, 26, 18423–18435. [Google Scholar] [CrossRef] [PubMed]
- Liewald, C.; Mastel, S.; Hesler, J.; Huber, A.J.; Hillenbrand, R.; Keilmann, F. All-electronic terahertz nanoscopy. Optica 2018, 5, 159. [Google Scholar] [CrossRef]
- Degl’Innocenti, R.; Wallis, R.; Wei, B.; Xiao, L.; Kindness, S.J.; Mitrofanov, O.; Braeuninger-Weimer, P.; Hofmann, S.; Beere, H.E.; Ritchie, D.A. Terahertz Nanoscopy of Plasmonic Resonances with a Quantum Cascade Laser. ACS Photonics 2017, 4, 2150–2157. [Google Scholar] [CrossRef]
- Kuschewski, F.; von Ribbeck, H.G.; Döring, J.; Winnerl, S.; Eng, L.M.; Kehr, S.C. Narrow-band near-field nanoscopy in the spectral range from 1.3 to 8.5 THz. Appl. Phys. Lett. 2016, 108, 113102. [Google Scholar] [CrossRef]
- Kehr, S.C.; Döring, J.; Gensch, M.; Helm, M.; Eng, L.M. FEL-Based Near-Field Infrared to THz Nanoscopy. Synchrotron Radiat. News 2017, 30, 31–35. [Google Scholar] [CrossRef]
- Moon, K.; Park, H.; Kim, J.; Do, Y.; Lee, S.; Lee, G.; Kang, H.; Han, H. Subsurface nanoimaging by broadband terahertz pulse near-field microscopy. Nano Lett. 2015, 15, 549–552. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; Mittleman, D.M.; van der Valk, N.C.J.; Planken, P.C.M. Antenna effects in terahertz apertureless near-field optical microscopy. Appl. Phys. Lett. 2004, 85, 2715–2717. [Google Scholar] [CrossRef]
- Wang, K.; Barkan, A.; Mittleman, D.M. Propagation effects in apertureless near-field optical antennas. Appl. Phys. Lett. 2004, 84, 305–307. [Google Scholar] [CrossRef]
- Zhan, H.; Astley, V.; Hvasta, M.; Deibel, J.A.; Mittleman, D.M.; Lim, Y.-S. The metal-insulator transition in VO2 studied using terahertz apertureless near-field microscopy. Appl. Phys. Lett. 2007, 91, 162110. [Google Scholar] [CrossRef]
- Moon, K.; Do, Y.; Lim, M.; Lee, G.; Kang, H.; Park, K.-S.; Han, H. Quantitative coherent scattering spectra in apertureless terahertz pulse near-field microscopes. Appl. Phys. Lett. 2012, 101, 011109. [Google Scholar] [CrossRef]
- Zhang, J.W.; Chen, X.Z.; Mills, S.; Ciavatti, T.; Yao, Z.H.; Mescall, R.; Hu, H.; Semenenko, V.; Fei, Z.; Li, H.; et al. Terahertz Nanoimaging of Graphene. ACS Photonics 2018, 5, 2645–2651. [Google Scholar] [CrossRef]
- Krutokhvostov, R.; Govyadinov, A.A.; Stiegler, J.M.; Huth, F.; Chuvilin, A.; Carney, P.S.; Hillenbrand, R. Enhanced resolution in subsurface near-field optical microscopy. Opt. Express 2012, 20, 593–600. [Google Scholar] [CrossRef] [PubMed]
- Eisele, M.; Cocker, T.L.; Huber, M.A.; Plankl, M.; Viti, L.; Ercolani, D.; Sorba, L.; Vitiello, M.S.; Huber, R. Ultrafast multi-terahertz nano-spectroscopy with sub-cycle temporal resolution. Nat. Photonics 2014, 8, 841–845. [Google Scholar] [CrossRef]
- Alonso-Gonzalez, P.; Nikitin, A.Y.; Gao, Y.; Woessner, A.; Lundeberg, M.B.; Principi, A.; Forcellini, N.; Yan, W.; Velez, S.; Huber, A.J.; et al. Acoustic terahertz graphene plasmons revealed by photocurrent nanoscopy. Nat. Nanotechnol. 2017, 12, 31–35. [Google Scholar] [CrossRef] [PubMed]
- Lundeberg, M.B.; Gao, Y.; Woessner, A.; Tan, C.; Alonso-González, P.; Watanabe, K.; Taniguchi, T.; Hone, J.; Hillenbrand, R.; Koppens, F.H.L. Thermoelectric detection and imaging of propagating graphene plasmons. Nat. Mater. 2016, 16, 204–207. [Google Scholar] [CrossRef] [PubMed]
- Woessner, A.; Alonso-González, P.; Lundeberg, M.B.; Gao, Y.; Barrios-Vargas, J.E.; Navickaite, G.; Ma, Q.; Janner, D.; Watanabe, K.; Cummings, A.W.; et al. Near-field photocurrent nanoscopy on bare and encapsulated graphene. Nat. Commun. 2016, 7, 10783. [Google Scholar] [CrossRef] [PubMed]
- Murakami, H.; Uchida, N.; Inoue, R.; Kim, S.; Kiwa, T.; Tonouchi, M. Laser Terahertz Emission Microscope. Proc. IEEE 2007, 95, 1646–1657. [Google Scholar] [CrossRef]
- Kiwa, T.; Tonouchi, M.; Yamashita, M.; Kawase, K. Laser terahertz-emission microscope for inspecting electrical faults in integrated circuits. Opt. Lett. 2003, 28, 2058–2060. [Google Scholar] [CrossRef] [PubMed]
- Tonouchi, M.; Yamashita, M.; Hangyo, M. Terahertz radiation imaging of supercurrent distribution in vortex-penetrated YBa2Cu3O7−δ thin film strips. J. Appl. Phys. 2000, 87, 7366–7375. [Google Scholar] [CrossRef]
- Suzuki, M.; Tonouchi, M.; Fujii, K.-I.; Ohtake, H.; Hirosumi, T. Excitation wavelength dependence of terahertz emission from semiconductor surface. Appl. Phys. Lett. 2006, 89, 091111. [Google Scholar] [CrossRef]
- Rana, D.S.; Takahashi, K.; Mavani, K.R.; Kawayama, I.; Murakami, H.; Tonouchi, M. Visualization of photoassisted polarization switching and its consequences in BiFeO3 thin films probed by terahertz radiation. Appl. Phys. Lett. 2007, 91, 031909. [Google Scholar] [CrossRef]
- Nakanishi, H.; Fujiwara, S.; Takayama, K.; Kawayama, I.; Murakami, H.; Tonouchi, M. Imaging of a Polycrystalline Silicon Solar Cell Using a Laser Terahertz Emission Microscope. Appl. Phys. Express 2012, 5, 112301. [Google Scholar] [CrossRef]
- Kushnir, K.; Wang, M.; Fitzgerald, P.D.; Koski, K.J.; Titova, L.V. Ultrafast Zero-Bias Photocurrent in GeS Nanosheets: Promise for Photovoltaics. ACS Energy Lett. 2017, 2, 1429–1434. [Google Scholar] [CrossRef]
- Sanjuan, F.; Gaborit, G.; Coutaz, J.L. Sub-wavelength terahertz imaging through optical rectification. Sci. Rep. 2018, 8, 13492. [Google Scholar] [CrossRef] [PubMed]
- Sano, Y.; Kawayama, I.; Tabata, M.; Salek, K.A.; Murakami, H.; Wang, M.; Vajtai, R.; Ajayan, P.M.; Kono, J.; Tonouchi, M. Imaging molecular adsorption and desorption dynamics on graphene using terahertz emission spectroscopy. Sci. Rep. 2014, 4, 6046. [Google Scholar] [CrossRef] [PubMed]
- Sakai, Y.; Kawayama, I.; Nakanishi, H.; Tonouchi, M. Visualization of GaN surface potential using terahertz emission enhanced by local defects. Sci. Rep. 2015, 5, 13860. [Google Scholar] [CrossRef] [PubMed]
- Mochizuki, T.; Ito, A.; Mitchell, J.; Nakanishi, H.; Tanahashi, K.; Kawayama, I.; Tonouchi, M.; Shirasawa, K.; Takato, H. Probing the surface potential of oxidized silicon by assessing terahertz emission. Appl. Phys. Lett. 2017, 110, 163502. [Google Scholar] [CrossRef]
- Klarskov, P.; Kim, H.; Colvin, V.L.; Mittleman, D.M. Nanoscale Laser Terahertz Emission Microscopy. ACS Photonics 2017, 4, 2676–2680. [Google Scholar] [CrossRef]
- Liu, K.; Xu, J.; Yuan, T.; Zhang, X.C. Terahertz radiation from InAs induced by carrier diffusion and drift. Phys. Rev. B 2006, 73, 155330. [Google Scholar] [CrossRef]
- Huber, M.A.; Plankl, M.; Eisele, M.; Marvel, R.E.; Sandner, F.; Korn, T.; Schuller, C.; Haglund, R.F., Jr.; Huber, R.; Cocker, T.L. Ultrafast Mid-Infrared Nanoscopy of Strained Vanadium Dioxide Nanobeams. Nano Lett. 2016, 16, 1421–1427. [Google Scholar] [CrossRef] [PubMed]
- Huth, F.; Chuvilin, A.; Schnell, M.; Amenabar, I.; Krutokhvostov, R.; Lopatin, S.; Hillenbrand, R. Resonant antenna probes for tip-enhanced infrared near-field microscopy. Nano Lett. 2013, 13, 1065–1072. [Google Scholar] [CrossRef] [PubMed]
- Mastel, S.; Lundeberg, M.B.; Alonso-Gonzalez, P.; Gao, Y.; Watanabe, K.; Taniguchi, T.; Hone, J.; Koppens, F.H.L.; Nikitin, A.Y.; Hillenbrand, R. Terahertz Nanofocusing with Cantilevered Terahertz-Resonant Antenna Tips. Nano Lett. 2017, 17, 6526–6533. [Google Scholar] [CrossRef] [PubMed]
- Siday, T.; Natrella, M.; Wu, J.; Liu, H.; Mitrofanov, O. Resonant terahertz probes for near-field scattering microscopy. Opt. Express 2017, 25, 27874–27885. [Google Scholar] [CrossRef] [PubMed]
- Kalkbrenner, T.; Ramstein, M.; Mlynek, J.; Sandoghdar, V. A single gold particle as a probe for apertureless scanning near-field optical microscopy. J. Microsc. 2001, 202, 72–76. [Google Scholar] [CrossRef] [PubMed]
- Mitrofanov, O.; Lee, M.; Hsu, J.W.P.; Brener, I.; Harel, R.; Federici, J.F.; Wynn, J.D.; Pfeiffer, L.N.; West, K.W. Collection-mode near-field imaging with 0.5-THz pulses. IEEE J. Sel. Top. Quantum Electron. 2001, 7, 600–607. [Google Scholar] [CrossRef]
- Ishihara, K.; Ohashi, K.; Ikari, T.; Minamide, H.; Yokoyama, H.; Shikata, J.-I.; Ito, H. Terahertz-wave near-field imaging with subwavelength resolution using surface-wave-assisted bow-tie aperture. Appl. Phys. Lett. 2006, 89, 201120. [Google Scholar] [CrossRef]
- Bitzer, A.; Ortner, A.; Walther, M. Terahertz near-field microscopy with subwavelength spatial resolution based on photoconductive antennas. Appl. Opt. 2010, 49, E1–E6. [Google Scholar] [CrossRef] [PubMed]
- Blanchard, F.; Doi, A.; Tanaka, T.; Hirori, H.; Tanaka, H.; Kadoya, Y.; Tanaka, K. Real-time terahertz near-field microscope. Opt. Express 2011, 19, 8277–8284. [Google Scholar] [CrossRef] [PubMed]
- van der Valk, N.C.J.; Planken, P.C.M. Electro-optic detection of subwavelength terahertz spot sizes in the near field of a metal tip. Appl. Phys. Lett. 2002, 81, 1558–1560. [Google Scholar] [CrossRef]
- Yuan, T.; Park, H.; Xu, J.; Han, H.; Zhang, X.C. THz Wave Near-Field Emission Microscope. In Ultrafast Phenomena XIV; Kobayashi, T., Okada, T., Kobayashi, T., Nelson, K.A., De Silvestri, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; Volume 79, pp. 759–761. [Google Scholar]
- Knoll, B.; Keilmann, F. Mid-infrared scanning near-field optical microscope resolves 30 nm. J. Microsc. 1999, 194, 512–515. [Google Scholar] [CrossRef] [PubMed]
- Mastel, S.; Govyadinov, A.A.; Maissen, C.; Chuvilin, A.; Berger, A.; Hillenbrand, R. Understanding the Image Contrast of Material Boundaries in IR Nanoscopy Reaching 5 nm Spatial Resolution. ACS Photonics 2018, 5, 3372–3378. [Google Scholar] [CrossRef]
- Hell, S.W.; Wichmann, J. Breaking the diffraction resolution limit by stimulated emission: Stimulated-emission-depletion fluorescence microscopy. Opt. Lett. 1994, 19, 780–782. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Keiser, G.R.; Klarskov, P. Terahertz Field Confinement in Nonlinear Metamaterials and Near-Field Imaging. Photonics 2019, 6, 22. https://doi.org/10.3390/photonics6010022
Keiser GR, Klarskov P. Terahertz Field Confinement in Nonlinear Metamaterials and Near-Field Imaging. Photonics. 2019; 6(1):22. https://doi.org/10.3390/photonics6010022
Chicago/Turabian StyleKeiser, George R., and Pernille Klarskov. 2019. "Terahertz Field Confinement in Nonlinear Metamaterials and Near-Field Imaging" Photonics 6, no. 1: 22. https://doi.org/10.3390/photonics6010022
APA StyleKeiser, G. R., & Klarskov, P. (2019). Terahertz Field Confinement in Nonlinear Metamaterials and Near-Field Imaging. Photonics, 6(1), 22. https://doi.org/10.3390/photonics6010022




