A Novel Hexahedron Photonic Crystal Fiber in Terahertz Propagation: Design and Analysis
Abstract
:1. Introduction
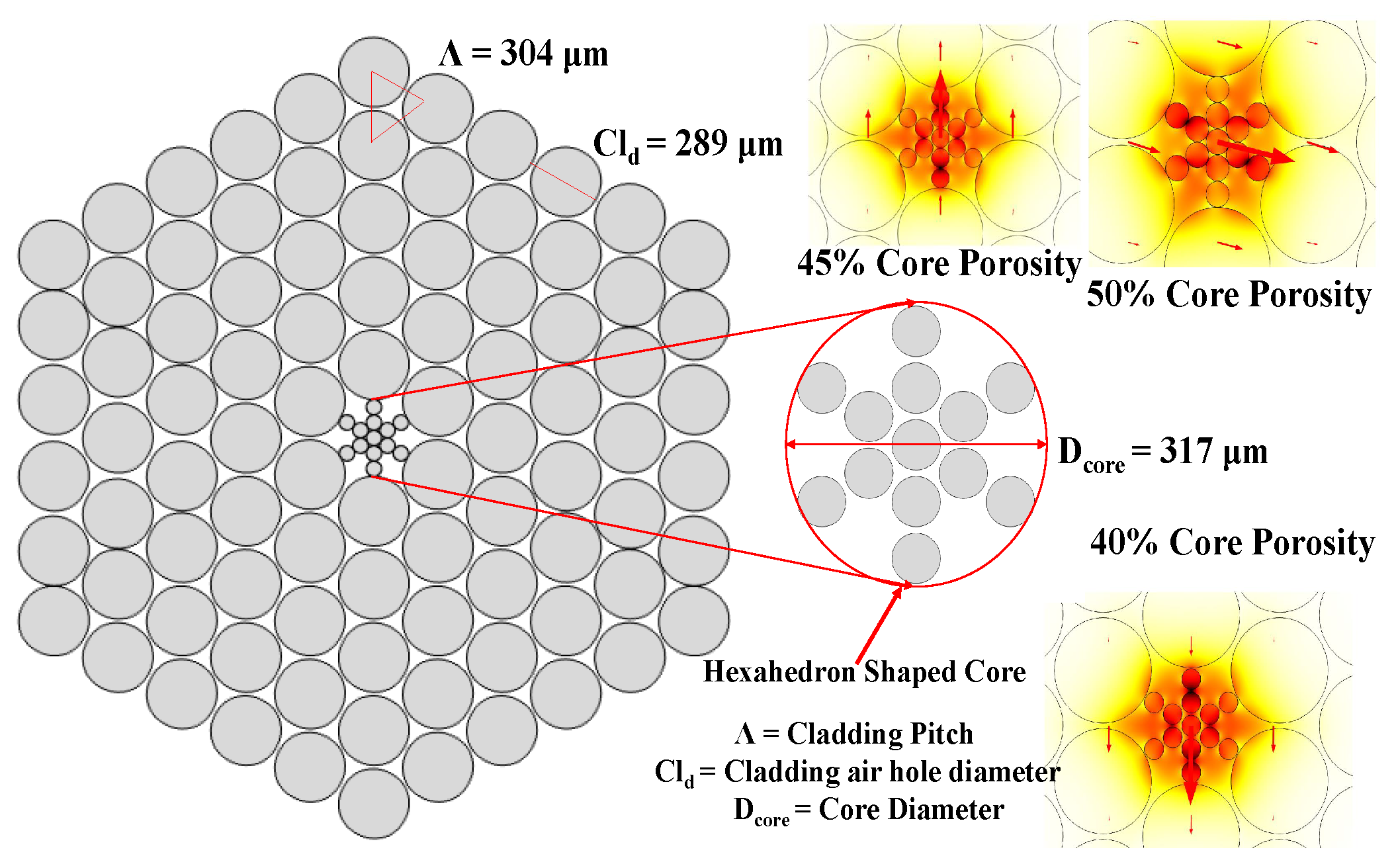
2. Design Methodology and Numerical Methods
3. Numerical Analysis
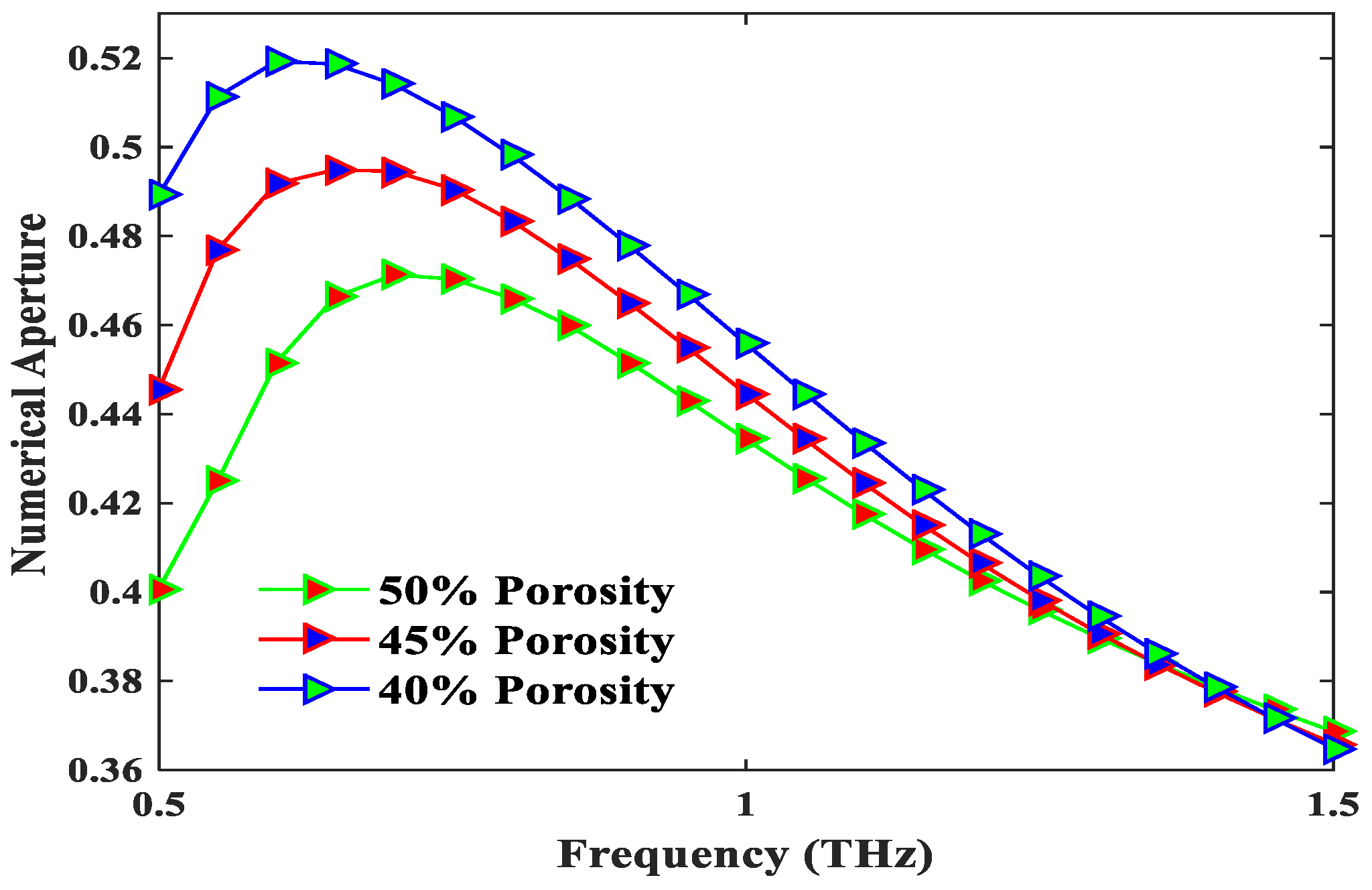
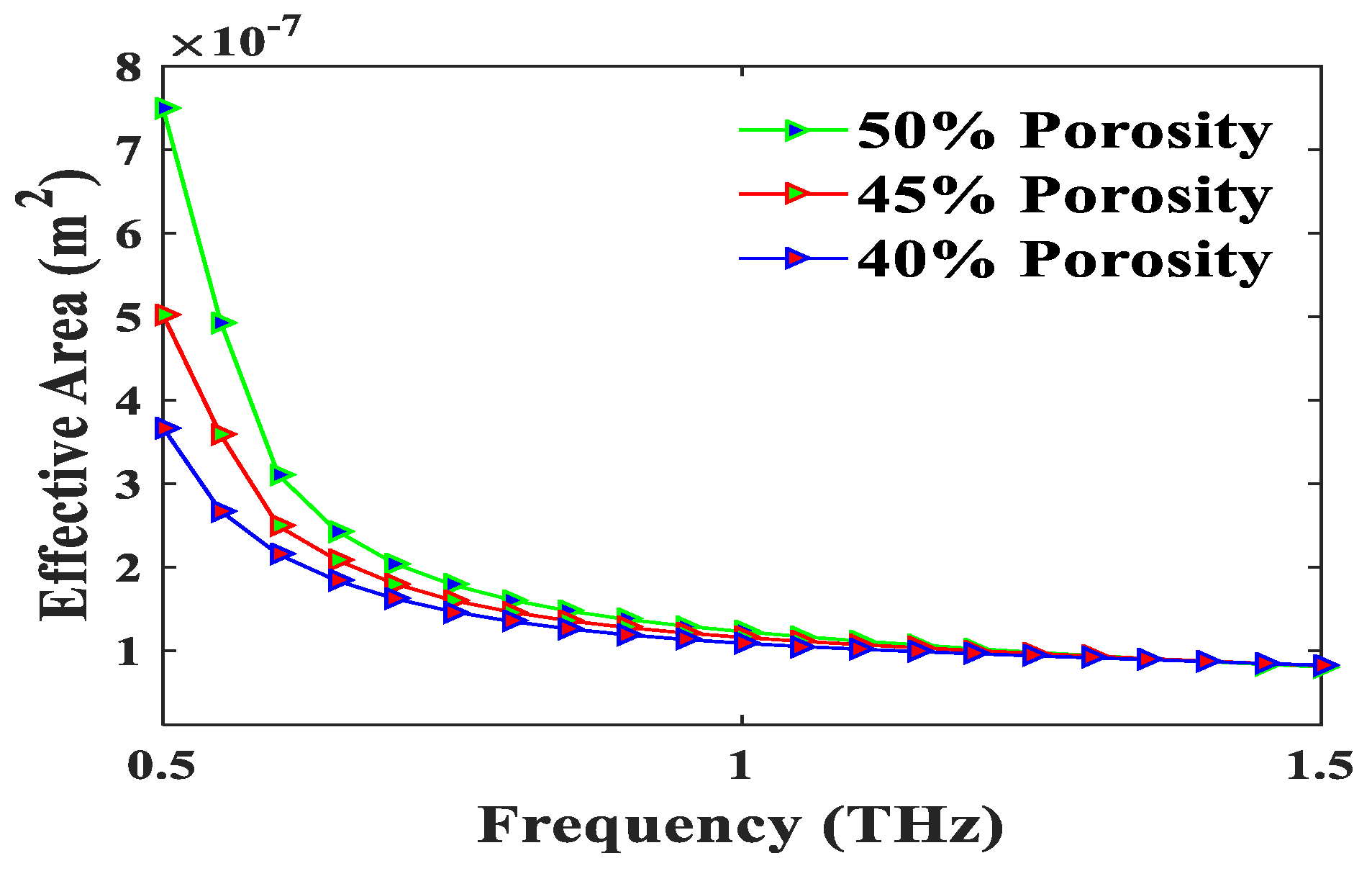
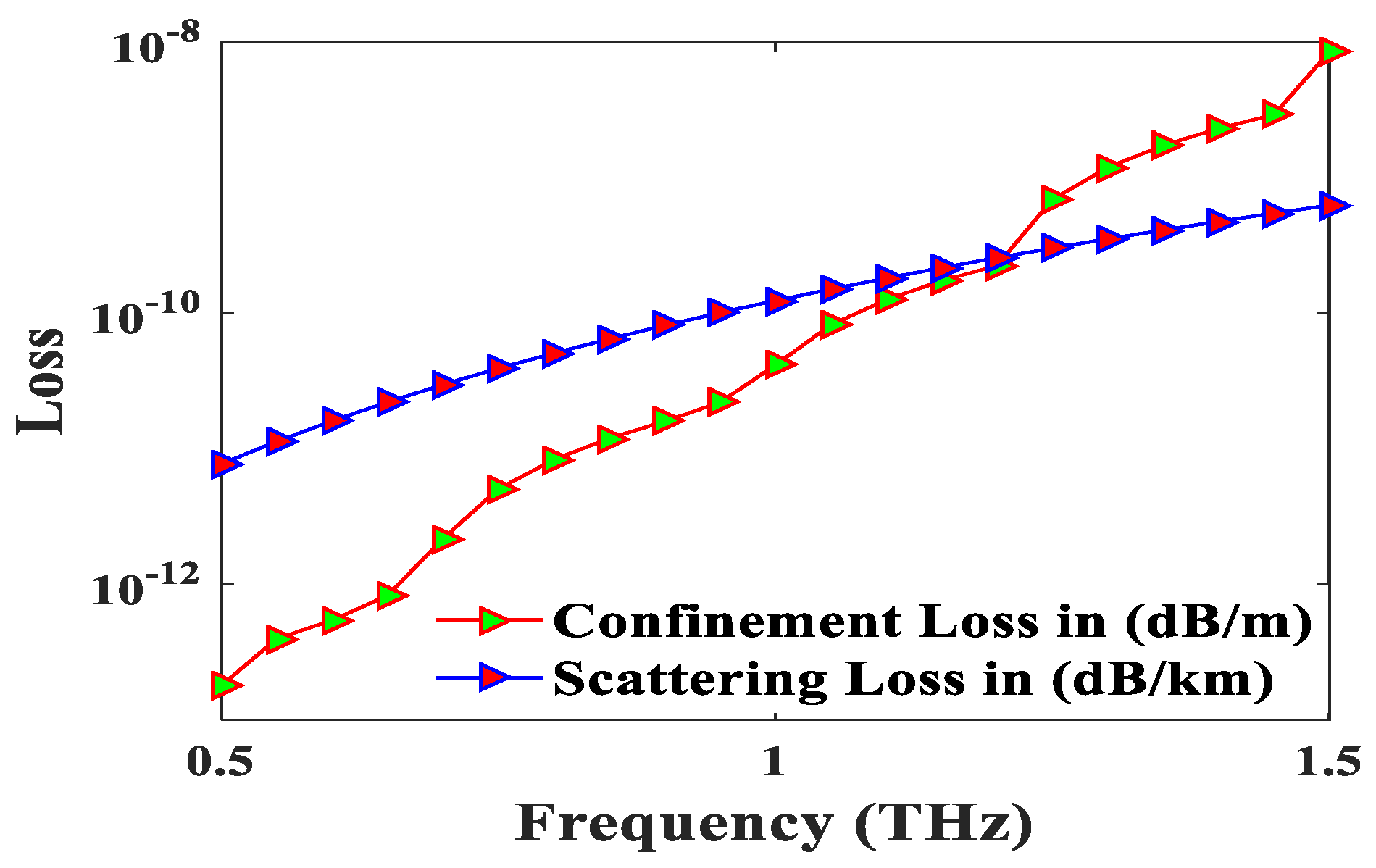
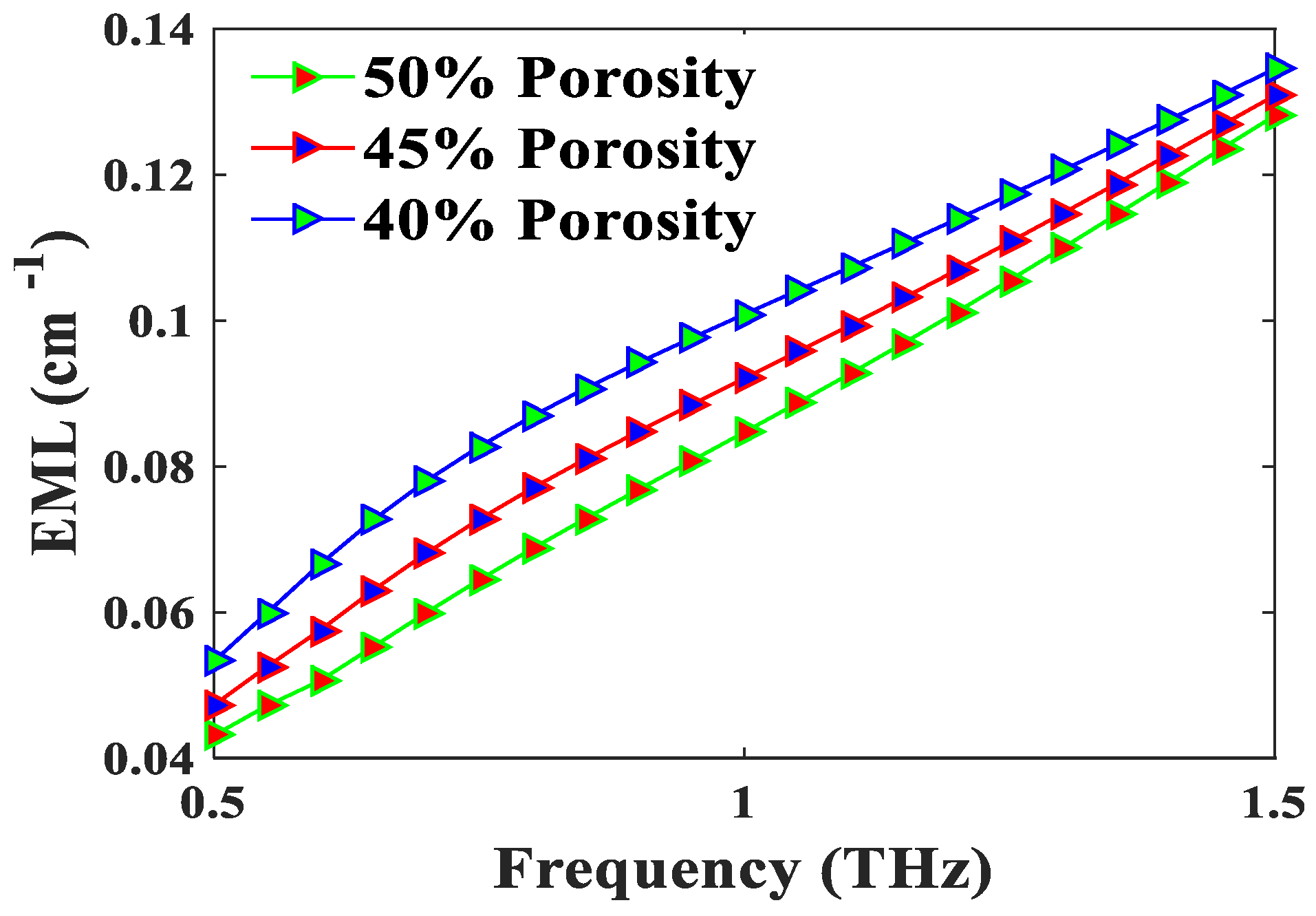
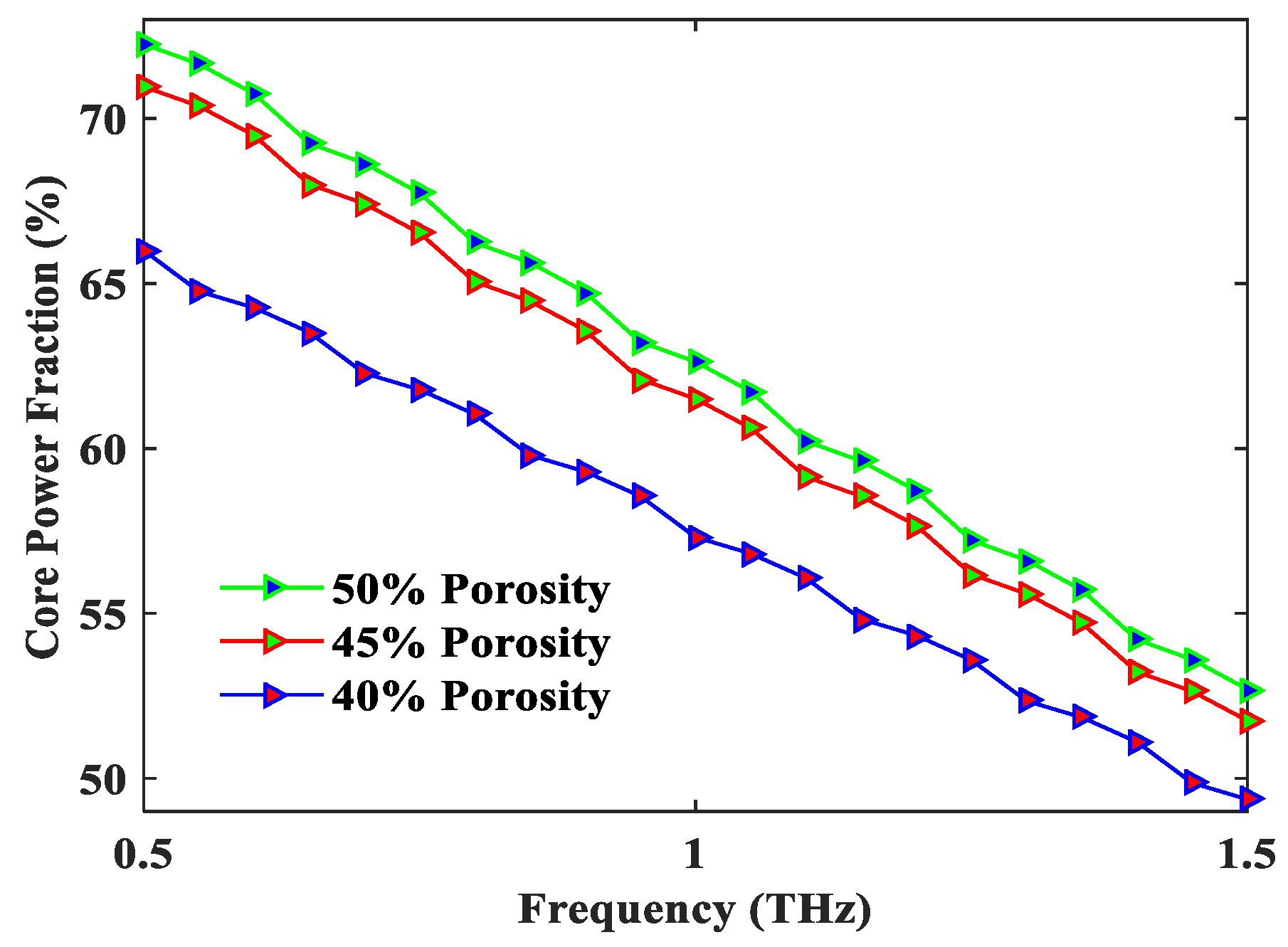
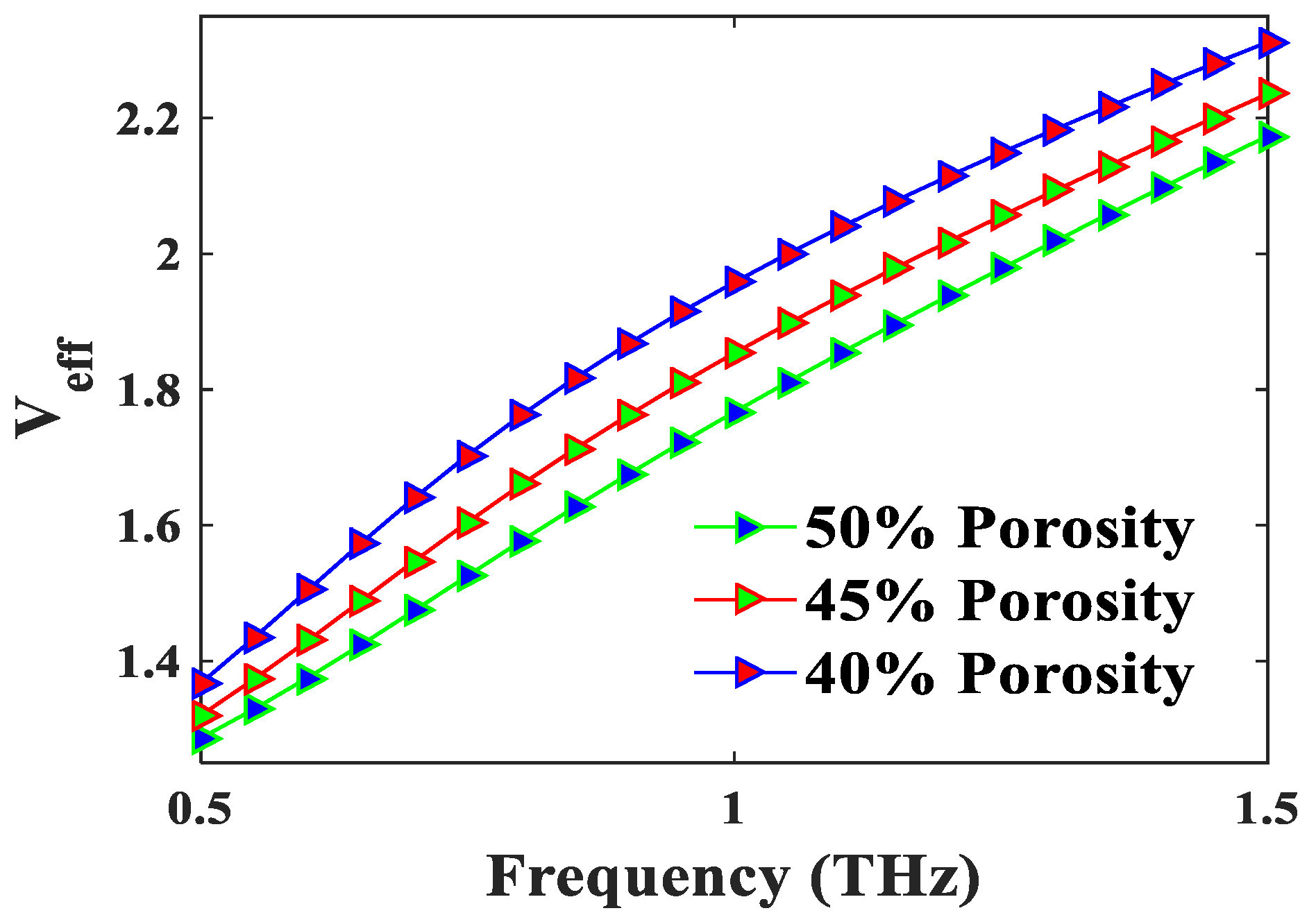
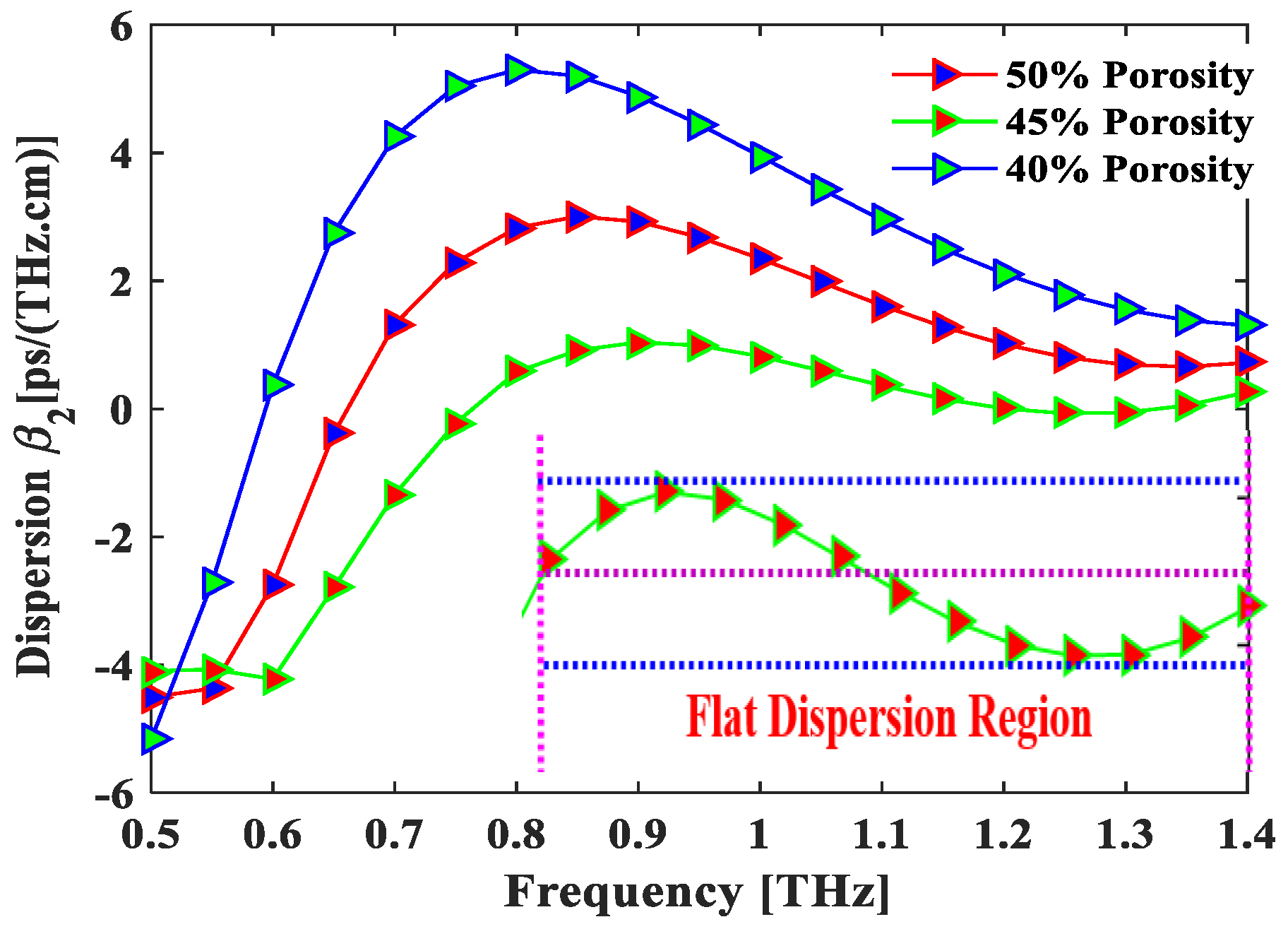
4. Result and Discussion
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Pawar, A.Y.; Sonawane, D.D.; Erande, K.B.; Derle, D.V. Terahertz technology and its applications. Drug Invent. Today 2013, 5, 157–163. [Google Scholar] [CrossRef]
- Sen, S.; Islam, M.S.; Paul, B.K.; Islam, M.I.; Chowdhury, S.; Ahmed, K.; Hasan, M.R.; Uddin, M.S.; Asaduzzaman, S. Ultra-low loss with single mode polymer-based photonic crystal fiber for THz waveguide. J. Opt. Commun. 2017. [Google Scholar] [CrossRef]
- Ahmed, K.; Paul, B.K.; Chowdhury, S.; Sen, S.; Islam, M.I.; Islam, M.S.; Hasan, M.R.; Asaduzzaman, S. Design of a single-mode photonic crystal fibre with ultra-low material loss and large effective mode area in THz regime. IET Optoelectron. 2017, 11, 265–271. [Google Scholar] [CrossRef]
- Ahmed, K.; Chowdhury, S.; Paul, B.K.; Islam, M.S.; Sen, S.; Islam, M.I.; Asaduzzaman, S. Ultrahigh birefringence ultra low material loss porous core single-mode fiber for terahertz wave guidance. Appl. Opt. 2017, 56, 3477–3483. [Google Scholar] [CrossRef] [PubMed]
- Hoo, Y.L.; Jin, W.; Shi, C.; Ho, H.L.; Wang, D.N.; Ruan, S.C. Design and modeling of a photonic crystal fiber gas sensor. Appl. Opt. 2003, 42, 3509–3515. [Google Scholar] [CrossRef] [PubMed]
- Islam, M.S.; Paul, B.K.; Ahmed, K.; Asaduzzaman, S.; Islam, M.I.; Chowdhury, S.; Sen, S.; Bahar, A.N. Liquid-infiltrated photonic crystal fiber for sensing purpose: Design and analysis. Alex. Eng. J. 2018, 57, 1459–1466. [Google Scholar] [CrossRef]
- Osório, J.H.; Hayashi, J.G.; Espinel, Y.A.; Franco, M.A.; Andrés, M.V.; Cordeiro, C.M. Photonic-crystal fiber-based pressure sensor for dual environment monitoring. Appl. Opt. 2014, 53, 668–3672. [Google Scholar] [CrossRef] [PubMed]
- Amiri, I.S.; Paul, B.K.; Ahmed, K.; Aly, A.H.; Zakaria, R.; Yupapin, P.; Vigneswaran, D. Tri-core photonic crystal fiber based refractive index dual sensor for salinity and temperature detection. Microw. Opt. Technol. Lett. 2019, 61, 847–852. [Google Scholar] [CrossRef]
- Hameed, M.F.O.; Obayya, S.S.A.; Wiltshire, R.J. Multiplexer–demultiplexer based on nematic liquid crystal photonic crystal fiber coupler. Opt. Quantum Electron. 2009, 41, 315–326. [Google Scholar] [CrossRef]
- Dadabayev, R.; Shabairou, N.; Zalevsky, Z.; Malka, D. A visible light RGB wavelength demultiplexer based on silicon-nitride multicore PCF. Opt. Laser Technol. 2019, 111, 411–416. [Google Scholar] [CrossRef]
- Malka, D.; Katz, G. An Eight-Channel C-Band Demux Based on Multicore Photonic Crystal Fiber. Nanomaterials 2018, 8, 845. [Google Scholar] [CrossRef] [PubMed]
- Malka, D.; Peled, A. Power splitting of 1 × 16 in multicore photonic crystal fibers. Appl. Surf. Sci. 2017, 417, 34–39. [Google Scholar] [CrossRef]
- Wang, G.; Li, S.; An, G.; Wang, X.; Zhao, Y.; Zhang, W. Design of a polarized filtering photonic-crystal fiber with gold-coated air holes. Appl. Opt. 2015, 54, 8817–8820. [Google Scholar] [CrossRef] [PubMed]
- Islam, R.; Rana, S.; Ahmad, R.; Kaijage, S.F. Bend-insensitive and low-loss porous core spiral terahertz fiber. IEEE Photon. Technol. Lett. 2015, 27, 2242–2245. [Google Scholar] [CrossRef]
- Rana, S.; Hasanuzzaman, G.K.M.; Habib, M.S.; Kaijage, S.F.; Islam, R. Proposal for a low loss porous core octagonal photonic crystal fiber for T-ray wave guiding. Opt. Eng. 2014, 53, 115107. [Google Scholar] [CrossRef]
- Hasan, M.R.; Islam, M.A.; Anower, M.S.; Razzak, S.M.A. Low-loss and bend-insensitive terahertz fiber using a rhombic-shaped core. Appl. Opt. 2016, 55, 8441–8447. [Google Scholar] [CrossRef] [PubMed]
- Hasan, M.R.; Islam, M.A.; Rifat, A.A. A single mode porous-core square lattice photonic crystal fiber for THz wave propagation. J. Eur. Opt. Soc.-Rapid Publ. 2016, 12, 15. [Google Scholar] [CrossRef]
- Sultana, J.; Islam, M.S.; Islam, M.R.; Abbott, D. High numerical aperture, highly birefringent novel photonic crystal fibre for medical imaging applications. Electron. Lett. 2017, 54, 61–62. [Google Scholar] [CrossRef]
- Chowdhury, S.; Sen, S.; Ahmed, K.; Asaduzzaman, S. Design of highly sensible porous shaped photonic crystal fiber with strong confinement field for optical sensing. Opt.-Int. J. Light Electron Opt. 2017, 142, 541–549. [Google Scholar] [CrossRef]
- Ahmed, K.; Islam, M.I.; Paul, B.K.; Islam, M.S.; Sen, S.; Chowdhury, S.; Uddin, M.S.; Asaduzzaman, S.; Bahar, A.N. Effect of photonic crystal fiber background materials in sensing and communication applications. Mater. Discov. 2017, 7, 8–14. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar Paul, B.; Haque, M.A.; Ahmed, K.; Sen, S. A Novel Hexahedron Photonic Crystal Fiber in Terahertz Propagation: Design and Analysis. Photonics 2019, 6, 32. https://doi.org/10.3390/photonics6010032
Kumar Paul B, Haque MA, Ahmed K, Sen S. A Novel Hexahedron Photonic Crystal Fiber in Terahertz Propagation: Design and Analysis. Photonics. 2019; 6(1):32. https://doi.org/10.3390/photonics6010032
Chicago/Turabian StyleKumar Paul, Bikash, Md. Ashraful Haque, Kawsar Ahmed, and Shuvo Sen. 2019. "A Novel Hexahedron Photonic Crystal Fiber in Terahertz Propagation: Design and Analysis" Photonics 6, no. 1: 32. https://doi.org/10.3390/photonics6010032
APA StyleKumar Paul, B., Haque, M. A., Ahmed, K., & Sen, S. (2019). A Novel Hexahedron Photonic Crystal Fiber in Terahertz Propagation: Design and Analysis. Photonics, 6(1), 32. https://doi.org/10.3390/photonics6010032





