Silicon-Based Multimode Complex Bragg Gratings for Spectra-Tailored Filter

Abstract

Multimode waveguide Bragg gratings (MWBGs) provide significant advantages over traditional single-mode counterparts through their mode-coupling operations. Nevertheless, flexible spectral response design methodologies for MWBG-based filter remain less studied. This work introduces a spectral tailoring methodology enabling physically realizable complex responses in MWBGs. We demonstrate silicon-based multi-channel Gaussian-shaped MWBGs using lateral phase delay modulation (LPDM) apodization. Experimental results confirm close conformance between measured spectral responses and target design specifications.

1. Introduction

Silicon Bragg gratings have become an essential component of integrated photonic devices, finding applications in optical filters, sensors, WDM networks, optical signal processing, dispersion compensation, microwave photonics, and so on [1,2,3,4,5,6,7,8]. To date, most of the research has focused on traditional Bragg gratings fabricated on single-mode waveguides. As a two-port device, Bragg gratings typically require an additional 3 dB optical coupler or a circulator to obtain the reflected light. Nevertheless, using a 3 dB coupler can introduce an additional 6 dB loss at the drop port as the reflected signal must pass through the coupler twice, and a circulator is difficult to be integrated on SOI platform due to the lack of CMOS-compatible magneto-optic materials.

Multimode waveguide Bragg gratings (MWBGs) have recently attracted significant attention, as they can address the limitations of traditional Bragg gratings and offer additional advantages [9,10]. A MWBG with a specifically designed grating period can couple the forward TE0 mode to a backward higher-order mode at the target wavelength. The reflected higher-order mode is then converted to the fundamental mode and efficiently dropped via an adiabatic coupler. Therefore, the need for an extra 3 dB optical coupler or circulators is eliminated. A MWBG and a pair of adiabatic couplers form a four-port device, thereby functioning as an add-drop filter. However, previous studies on MWBGs have primarily focused on controlling specific spectral characteristics, such as increasing the sidelobe suppression ratio, sharpening the edges of the reflection response, and narrowing the operational bandwidth [11,12,13]. In these efforts, the grating strength was modulated along the grating by adjusting the depths or positions of the sidewall grating corrugations. This technique is well known as apodization. However, exclusive modulation of the grating length is insufficient for realizing complex target spectra.

The synthesis of Bragg gratings has been first studied in the field of fiber optics. Several kinds of mathematical models and algorithms have been proposed for finding the grating structure (the grating strength and phase) from a specified, complex spectrum for fiber Bragg grating [14,15,16]. Recently, complex spectral tailoring for sidelobe-suppressed filters, multi-channel filters and microwave photonics Hilbert transformers has been realized on the traditional Bragg gratings and Grating-assisted contra-directional couplers [17,18,19]. However, the spectral tailoring of MWBGs has not been proposed and demonstrated on a silicon-on-insulator (SOI) platform.

In this work, we present a methodology aimed at engineering the complex spectral response of silicon MWBGs. We demonstrate the efficacy of the methodology through the experimental validation of multi-channel Gaussian spectral shaping. This study enables flexible manipulation of spectral characteristics in the integrated silicon MWBG-based devices, positioning them as promising candidates for reconfigurable photonic components including couplers, wavelength-selective switches, and add-drop multiplexers with customized spectral functionalities [8,20,21,22].

2. Design Methodology

This paper presents a fundamental design methodology for realizing an arbitrary complex spectral response using a silicon-based MWBG, in which implementing a multi-channel Gaussian-shaped filter serves as an example. The design process begins with the determination of a target complex spectral response. However, the initial target response is often not physically realizable and must be modified to become physically realizable before proceeding with the subsequent grating design. Once the physically realizable response is achieved, the discrete layer-peeling algorithm (DLPA) can be utilized to accurately calculate the grating strength and phase profiles required to meet the target response. In the next step, several fundamental parameters of the MWBG (including waveguide width, grating corrugation width, corrugation shape and grating period) are defined. Subsequently, the grating structure is established by modulating both the grating strength and phase along its length, in accordance with their respective calculated target profiles. Once the complete grating structure is created, its spectral response should be simulated to verify consistency with the realizable target response. Finally, the designed gratings are fabricated and experimentally characterized. The measured results are compared with the realizable target spectrum, enabling the iterative refinement of the design process.

2.1. Formation the Target Spectrum

Typically, the ideal objective is to achieve a specific reflection spectral response. For a multi-channel dispersionless Gaussian spectral MWBG, the target spectrum r(λ) can be expressed as

$$r(\lambda )={\displaystyle \sum _{i=1}^n{r}_i(\lambda )}=A_1\exp [-4\ln 2({\displaystyle \frac{\lambda -{\lambda }_{c1}}{\mathsf{\Delta }{\lambda }_1}}{)}^2]+A_2\exp [-4\ln 2({\displaystyle \frac{\lambda -{\lambda }_{c2}}{\mathsf{\Delta }{\lambda }_2}}{)}^2]$$

(1)

where r_i(λ) represents the reflectance of the i-th Gaussian peak at wavelength λ, A_i represents the peak reflectance, λ_c is the central wavelength, and Δλ denotes the 3 dB bandwidth. It should be noted that a larger number of channels is enabled by setting n as ≥3.

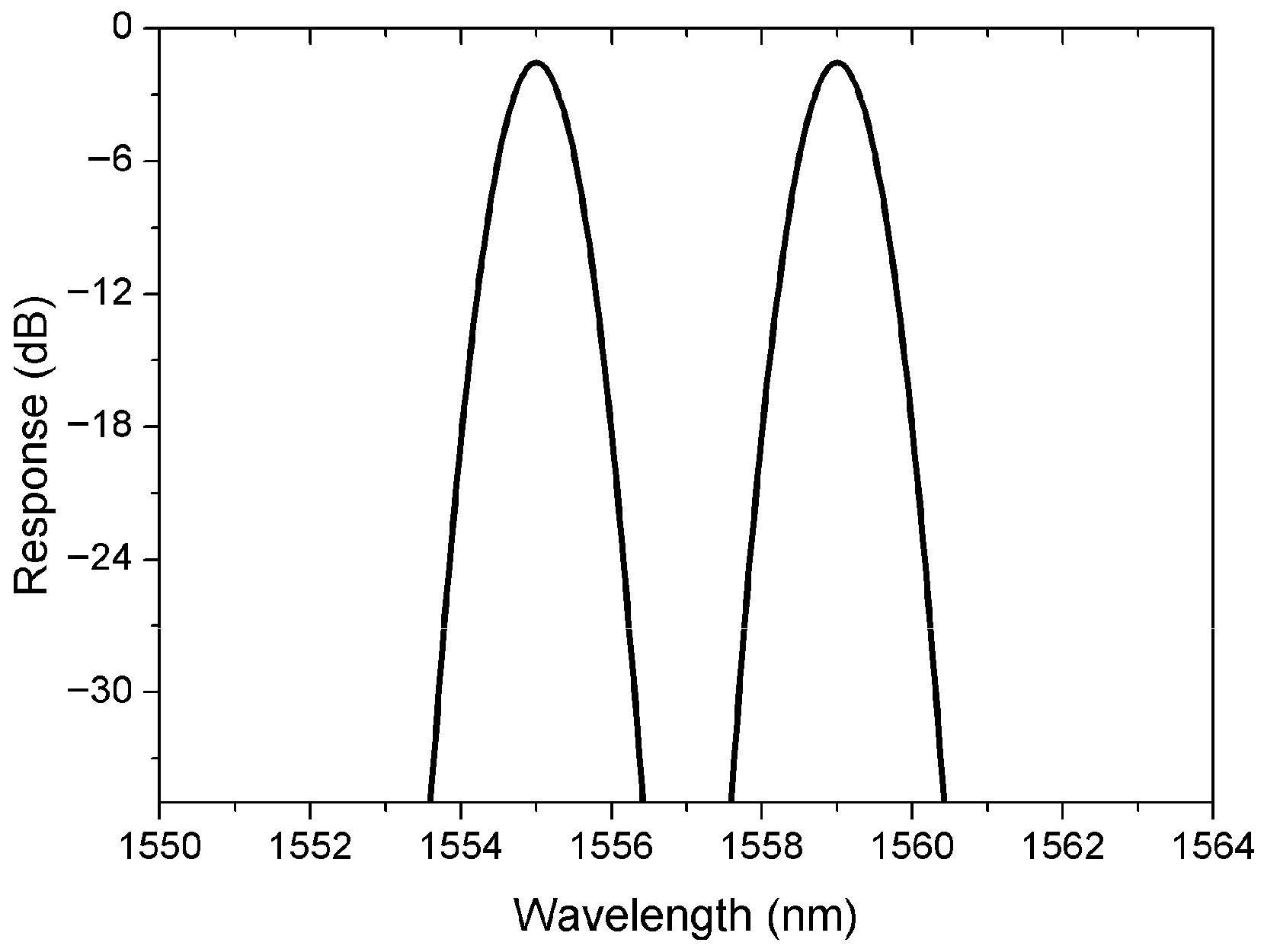
Figure 1 illustrates the target multi-channel MWBG spectrum with Gaussian profiles, showing a channel separation of 4 nm. The peak wavelengths are 1555 nm and 1559 nm, respectively. Each channel’s excess loss is 1.8 dB at the peak wavelength, and the 3 dB bandwidth of each channel is 1 nm.

As shown in Figure 2a, the original impulse response of the target spectrum is infinite in length and non-causal (i.e., it extends into the negative spatial domain). To address this, the target spectral response must be converted into a physically realizable form. We modify it by first truncating the original impulse response and then shifting the truncated response into the positive spatial domain. The resulting modified impulse response, shown in Figure 2b, is finite in length and causal.

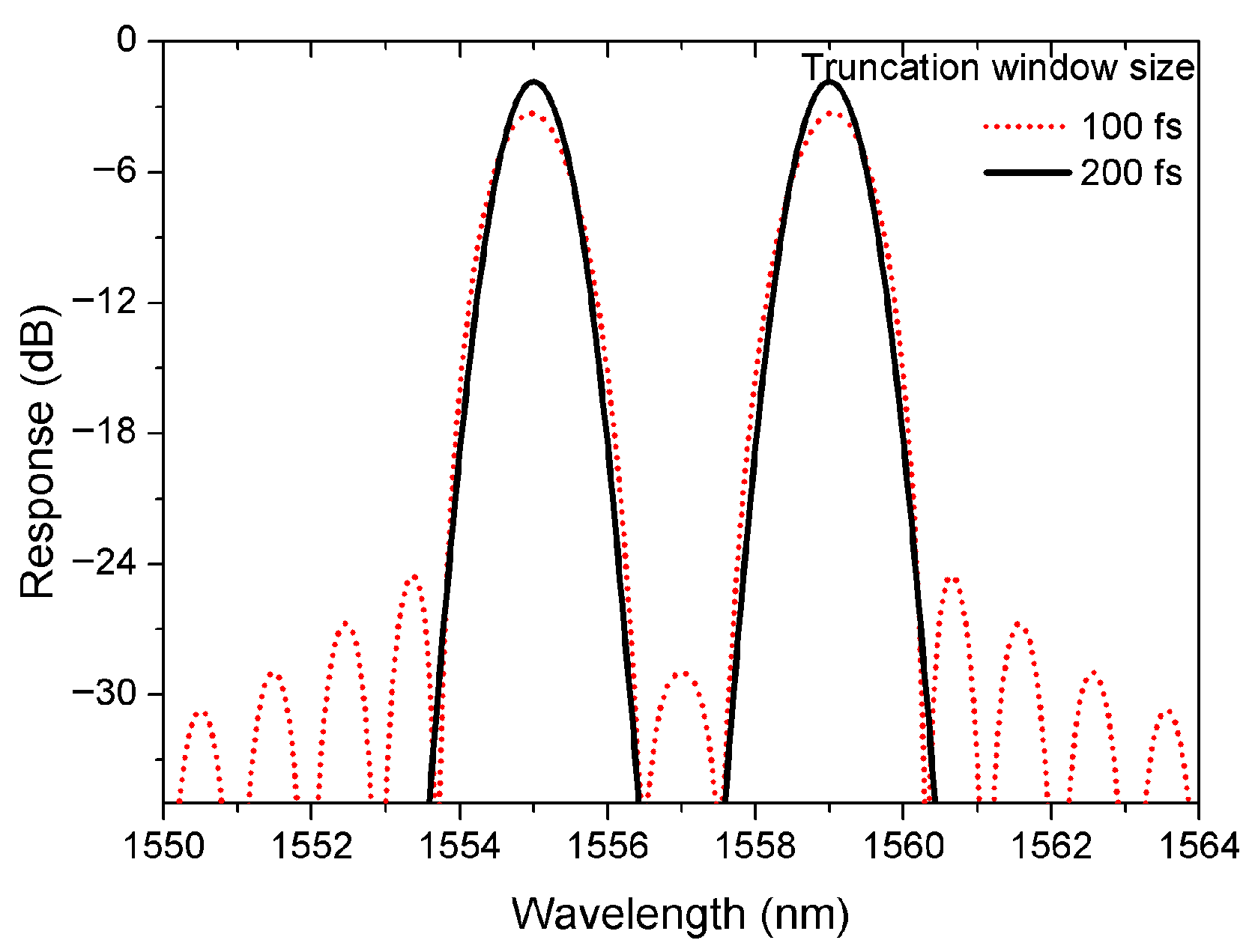
The physically realizable target response is obtained by applying the inverse Fourier transform to the modified impulse response. As shown in Figure 3, the realizable spectral response with a truncation window size of 100 fs (range 50 fs to 150 fs in Figure 2b) exhibits apparent degradation. Although the peak wavelengths match the designed spectral response, each channel suffers from 3.2 dB of excess loss, 1.2 nm of 3 dB bandwidth, and prominent sidelobes. This degradation is primarily caused by the insufficient truncation window size, which directly results in inadequate grating length. When the truncation window size increases to 200 fs (Figure 2b), the realizable spectral response closely matches the designed spectrum.

2.2. Calculating the Complex Coupling Coefficient

The DLPA is a computationally efficient inverse scattering method that has been widely adopted for fiber Bragg grating synthesis. Its principle relies on solving the coupled-mode equations using piecewise scattering and a propagation matrix approach. When the piecewise section length is sufficiently small, the grating’s leading section can be determined solely by the impulse response’s leading edge. Thus, the grating structure can be reconstructed sequentially layer by layer, while the complex coupling coefficient (including the grating strength κ(z) and phase φ(z) distribution along the grating) is directly obtained via the DLPA method. Figure 4 shows the grating strength and phase distribution synthesized derived from the realizable target spectral response. The κ(z) profile exhibits significantly greater complexity than conventional MWBGs. Meanwhile, the required φ(z) distribution manifests discrete π-phase shifts, corresponding to a dispersionless MWBG configuration [18]. These structural characteristics necessitate a high-performance and reliable apodization technique for reliable grating realization.

2.3. Structure Design

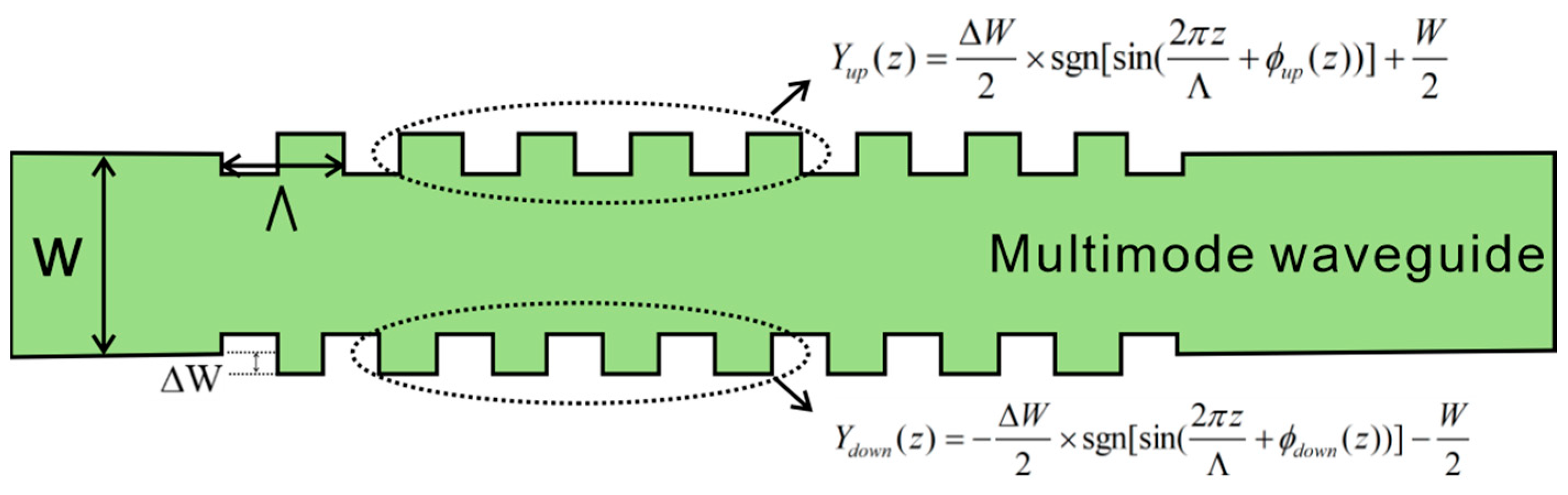
The structure of the complex-synthesized MWBG proposed is schematically illustrated in Figure 5. The 220 nm-thick silicon waveguide is embedded in a 2-μm buried oxide layer with a 2.2-μm silicon dioxide upper cladding. The multimode waveguide width W in the MWBG is configured at 850 nm to enable simultaneous propagation of both TE0 and TE1 modes. This grating structure employs rectangular sidewall modulations along the waveguide to achieve contra-directional coupling from the TE0 mode to the TE1 mode at selected wavelengths. For the target peak wavelength, the grating period Λ is determined as 314 nm via the phase matching condition.

The spectral response engineering hinges on the precise spatial modulation of both κ and φ of the grating, as defined by their respective distributions κ(z) and φ(z). A uniform MWBG can be treated as a superposition of two identical sub-gratings formed on either side of the multimode waveguide with a fixed phase offset of ∆ϕ. To achieve precise κ modulation, the lateral phase delay modulation (LPDM) method is implemented. This establishes the relationship between κ and ∆ϕ through the equation:

$$\kappa (\mathsf{\Delta }\varphi )={\kappa }_{\max }\left|\sin (\mathsf{\Delta }\varphi /2)\right|$$

(2)

where κ_max is the maximum coupling efficient when ∆ϕ is π. The phase shift distribution ∆ϕ(z) is then determined by the equation:

$$\mathsf{\Delta }\varphi (z)=2{\sin }^{-1}({\kappa }_n(z))$$

(3)

where κ_n(z) is the normalized κ(z).

The phase components of the spatial functions of the top and bottom sub-gratings are formed by the superposition of the phase delay term and φ(z):

$${\varphi }_{up}(z)=\mathsf{\Delta }\varphi (z)/2+\phi (z)$$

(4)

$${\varphi }_{down}(z)=-\mathsf{\Delta }\varphi (z)/2+\phi (z)$$

(5)

Therefore, the spatial edge functions of the two sides of the MWBG can be expressed as follows:

$$Y_{up}(z)={\displaystyle \frac{\mathsf{\Delta }W}{2}}\times \mathrm{sgn}[\sin ({\displaystyle \frac{2\pi z}{\mathsf{\Lambda }}}+{\varphi }_{up}(z))]+{\displaystyle \frac{W}{2}}$$

(6)

$$Y_{down}(z)=-{\displaystyle \frac{\mathsf{\Delta }W}{2}}\times \mathrm{sgn}[\sin ({\displaystyle \frac{2\pi z}{\mathsf{\Lambda }}}+{\varphi }_{down}(z))]-{\displaystyle \frac{W}{2}}$$

(7)

where ∆W is the grating corrugation width.

The spectral response of the designed MWBG was calculated using a three-dimensional (3D) finite-difference time-domain (FDTD) tool [20]. The designed MWBG features a grating length of 587.76 μm (truncation window size: 200 fs) and a corrugation width of 10 nm, targeting a maximum coupling coefficient κ_max of 80 cm⁻¹. The calculated drop-port response, shown in Figure 6, exhibits good agreement with the realizable target spectral response presented in Figure 2.

3. Experiment Result

The filter was fabricated on a commercial SOI wafer via electron-beam lithography (EBL) and plasma etching. Optical characterization employed a fiber probe station with a tunable laser source for signal injection and optical power sensors for output detection. Figure 7a schematically shows the characterization circuit for the designed MWBG-based filter. An adiabatic coupler was designed to convert the backward-propagating TE1 mode into the TE0 mode at the drop port. Figure 7b shows a scanning electron microscope (SEM) image of the fabricated MWBG.

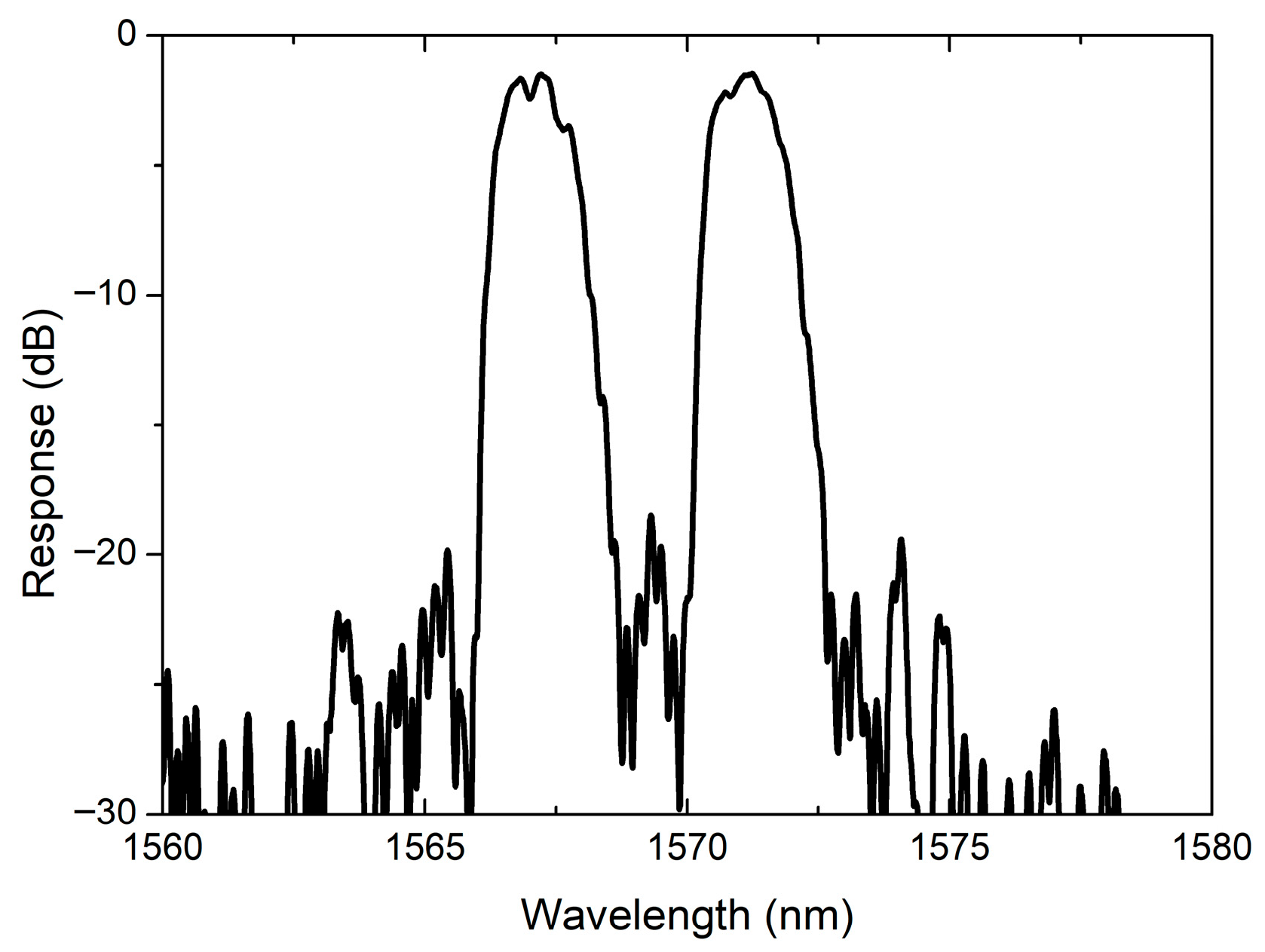
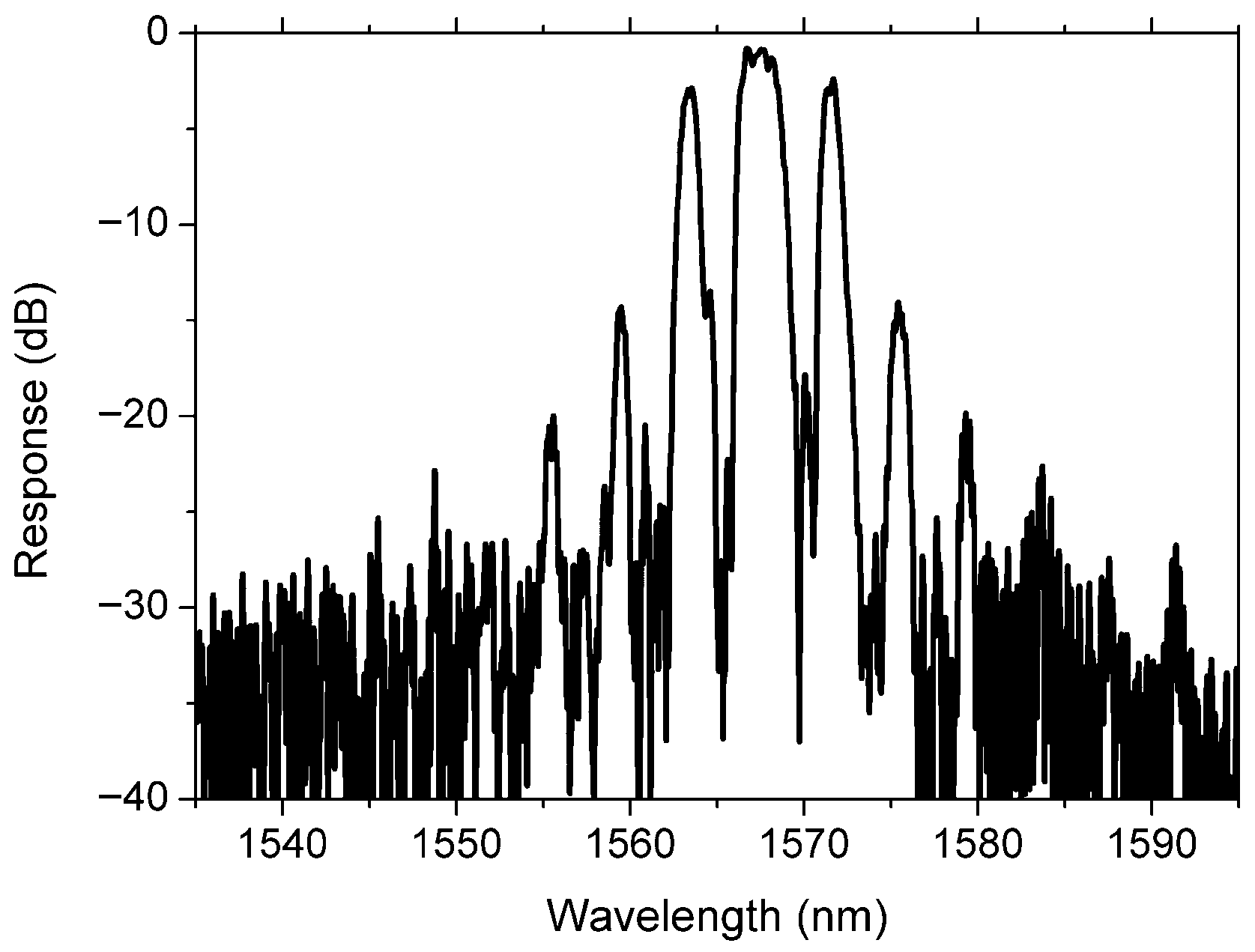
Figure 8 shows the measured normalized spectral response after calibrating out the insertion losses of the input and output grating couplers (GCs). The response exhibits a multi-channel Gaussian profile consistent with the target response with the designed 4 nm channel separation achieved. However, the measured peak wavelengths (1567 nm and 1571 nm) exhibit a redshift relative to design values, and the 3 dB bandwidth of each channel (1.3 nm) is slightly wider than intended. Based on the Bragg condition, the redshift primarily results from an increase in the effective refractive index. Our further analysis, supported by SEM measurements, indicates that the unintended enlargement of the waveguide width during fabrication is the dominant factor contributing to the redshift. The sidelobe suppression ratio of 18 dB and the excess loss of 1.4 dB are also measured.

To investigate the influence of the grating strength κ(z) and phase φ(z), we also fabricated two MWBG variants: (1) grating maintaining κ(z) while with φ(z) = 0 and (2) grating with enhanced κ(z) while preserving φ(z).

Figure 9 presents the measured normalized spectral response of a MWBG with identical κ(z) to that in Figure 4a but with φ(z) = 0. The resulting spectrum exhibits seven channels showing non-uniform bandwidths and insertion losses, demonstrating significant differences from the target spectral response. This confirms that the simultaneous engineering of both grating strength and phase distributions is essential to achieve specific reflection spectral responses.

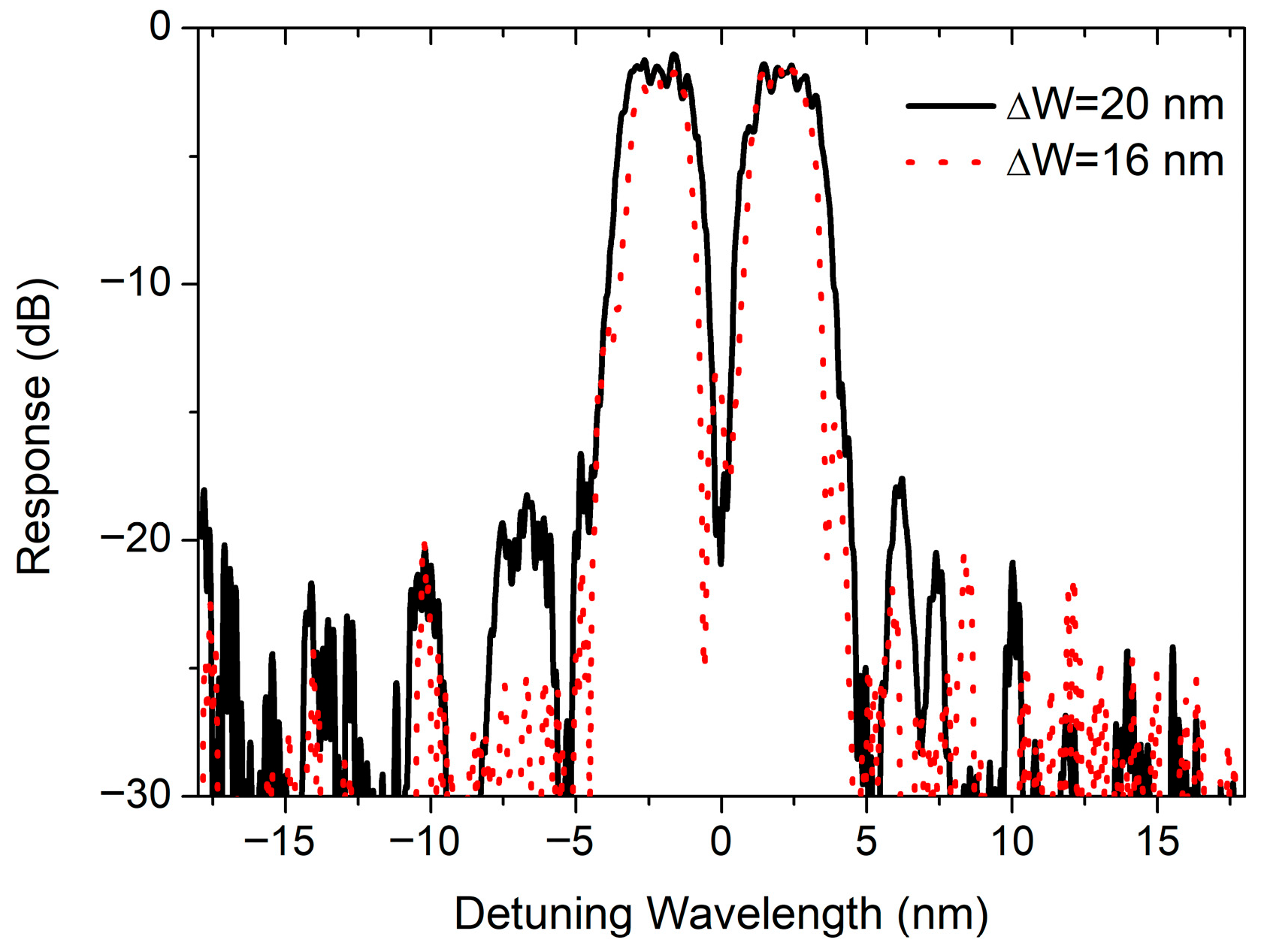
To enhance κ(z), the corrugation width was increased to 16 nm and 20 nm in two respective MWBGs, while maintaining the φ(z) profile identical to that in Figure 4b. As shown in Figure 10, the measured normalized spectra for both devices exhibited the targeted multi-channel Gaussian profile. The measured 3 dB bandwidths are 2.6 nm and 2.0 nm, respectively, with channel separations of 4.1 nm. Although the stronger grating strength broadens the spectra compared with Figure 8, it does not alter the spectral profile shape. Consequently, adjusting ∆W provides a means to mitigate the influence of fabrication errors.

4. Conclusions

In summary, we have presented a methodology for tailoring the complex responses of MWBGs. The comprehensive design flow is introduced, demonstrating its effectiveness through the realization of a multi-channel Gaussian-shaped SOI-based MWBG filter by implementing LPDM apodization. This approach enables flexible control over the complex responses of MWBG-based devices, such as couplers, switches, and add-drop multiplexers, allowing for the implementation of customized spectral functionalities.