Photonics-Enabled High-Sensitivity and Wide-Bandwidth Microwave Phase Noise Analyzers
Abstract
1. Introduction
2. Basic Phase Noise Measurement Methods
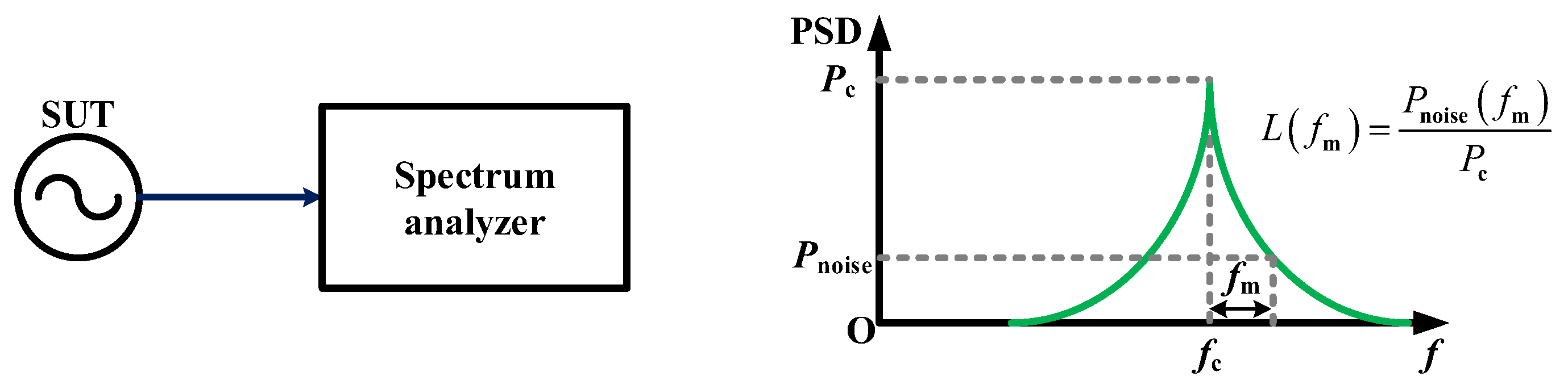
2.1. Direct Spectrum Method
- (1)
- Negligible amplitude noise in the SUT;
- (2)
- Compliance with the small-angle approximation, requiring: root mean square value of the phase fluctuations φ(t) is less than 0.01 rad, and peak magnitude of φ(t) do not exceed 0.2 rad.
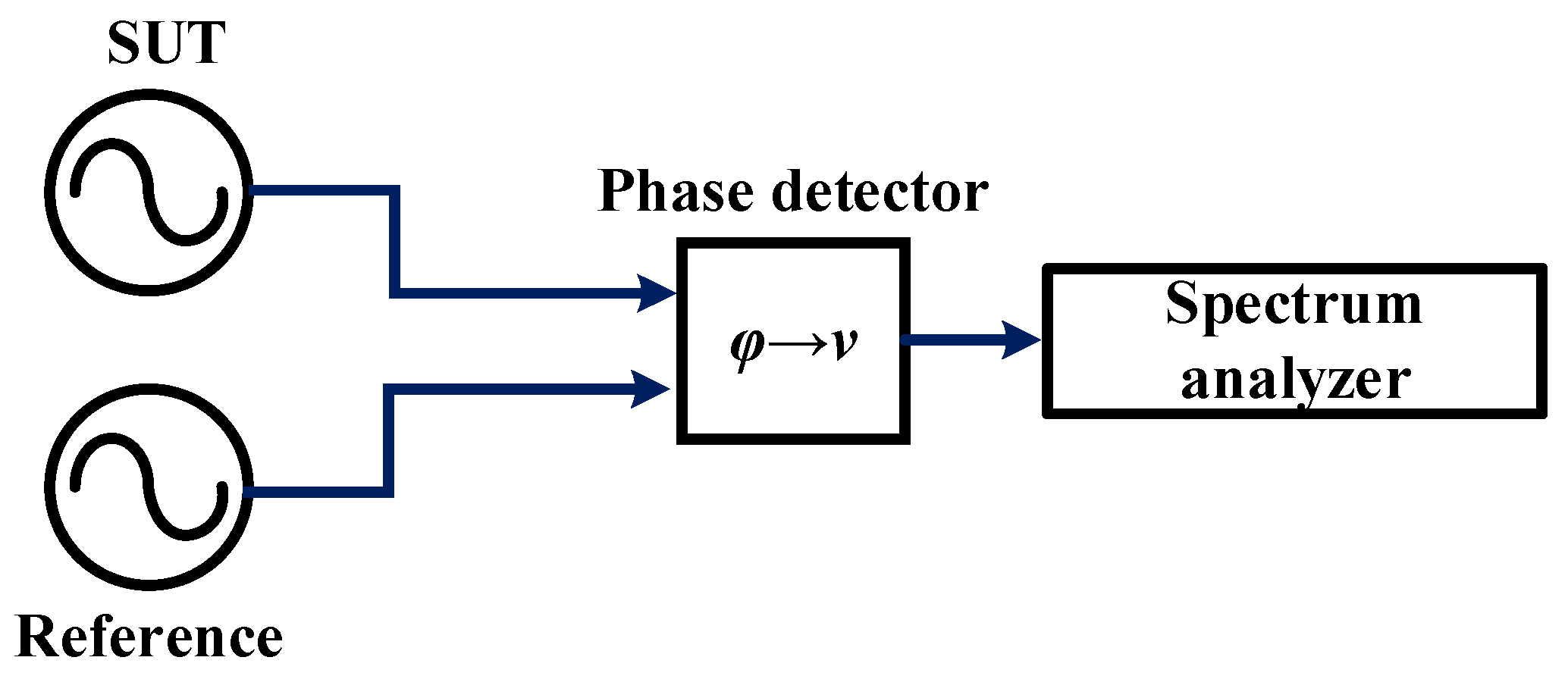
2.2. Phase Detection Method
2.3. Frequency Discrimination Method
2.4. Dual-Channel Cross-Correlation Method
3. MWP Phase-Detection-Based PNAs
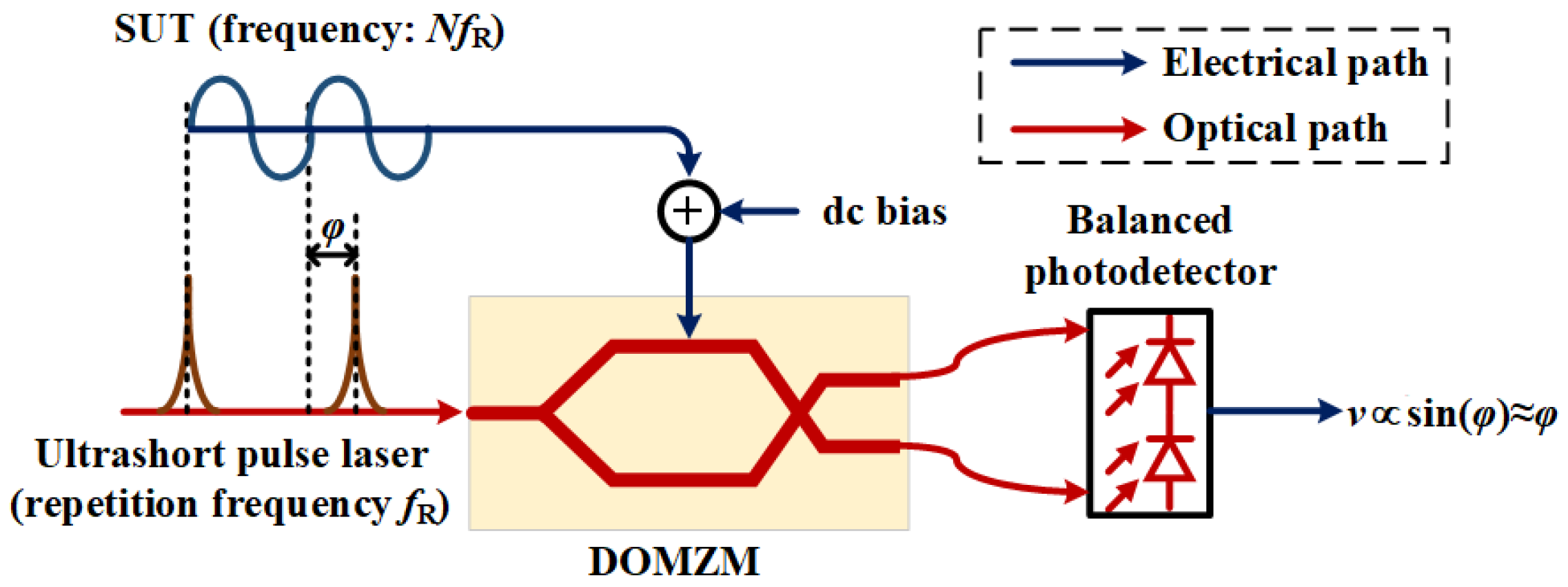
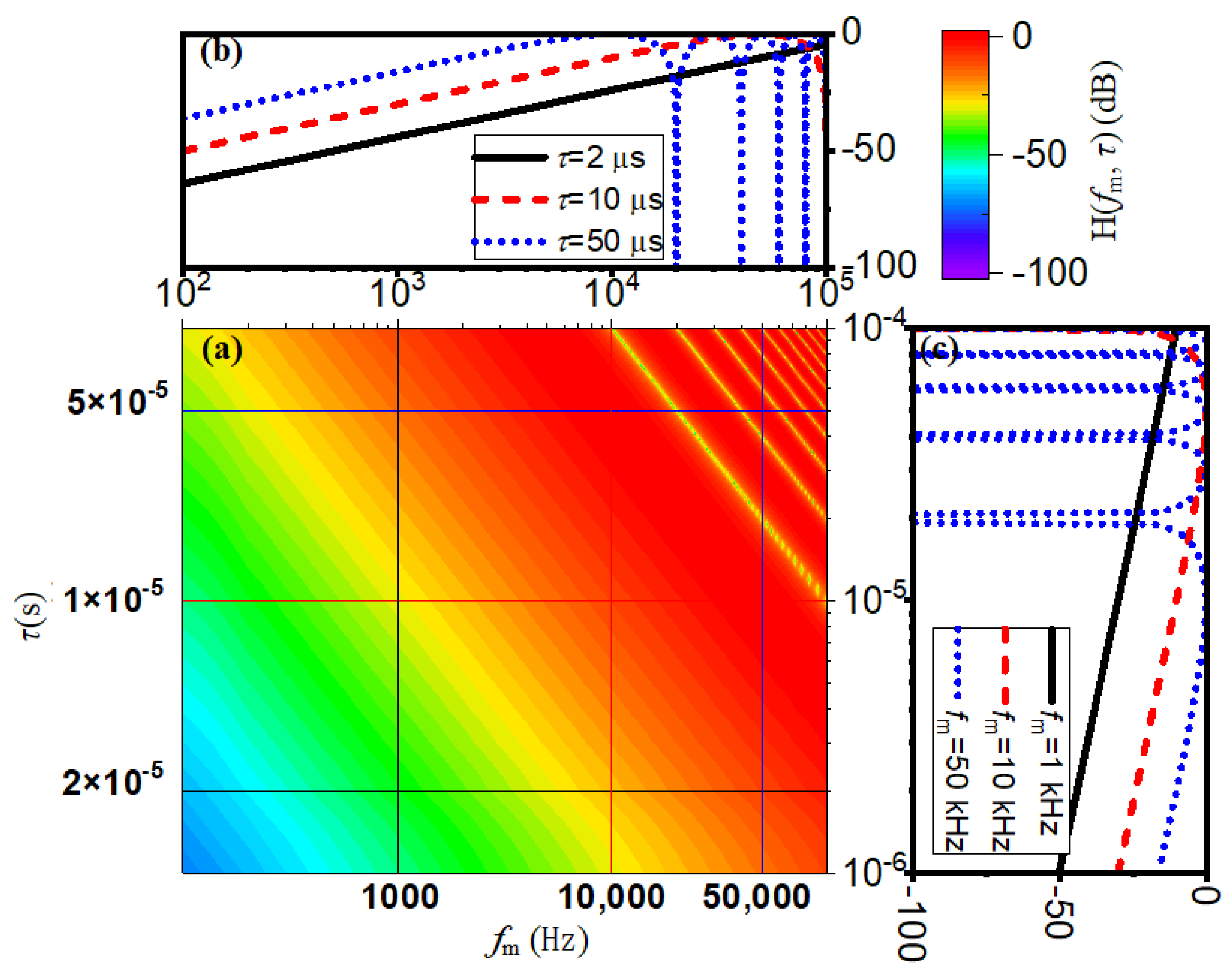
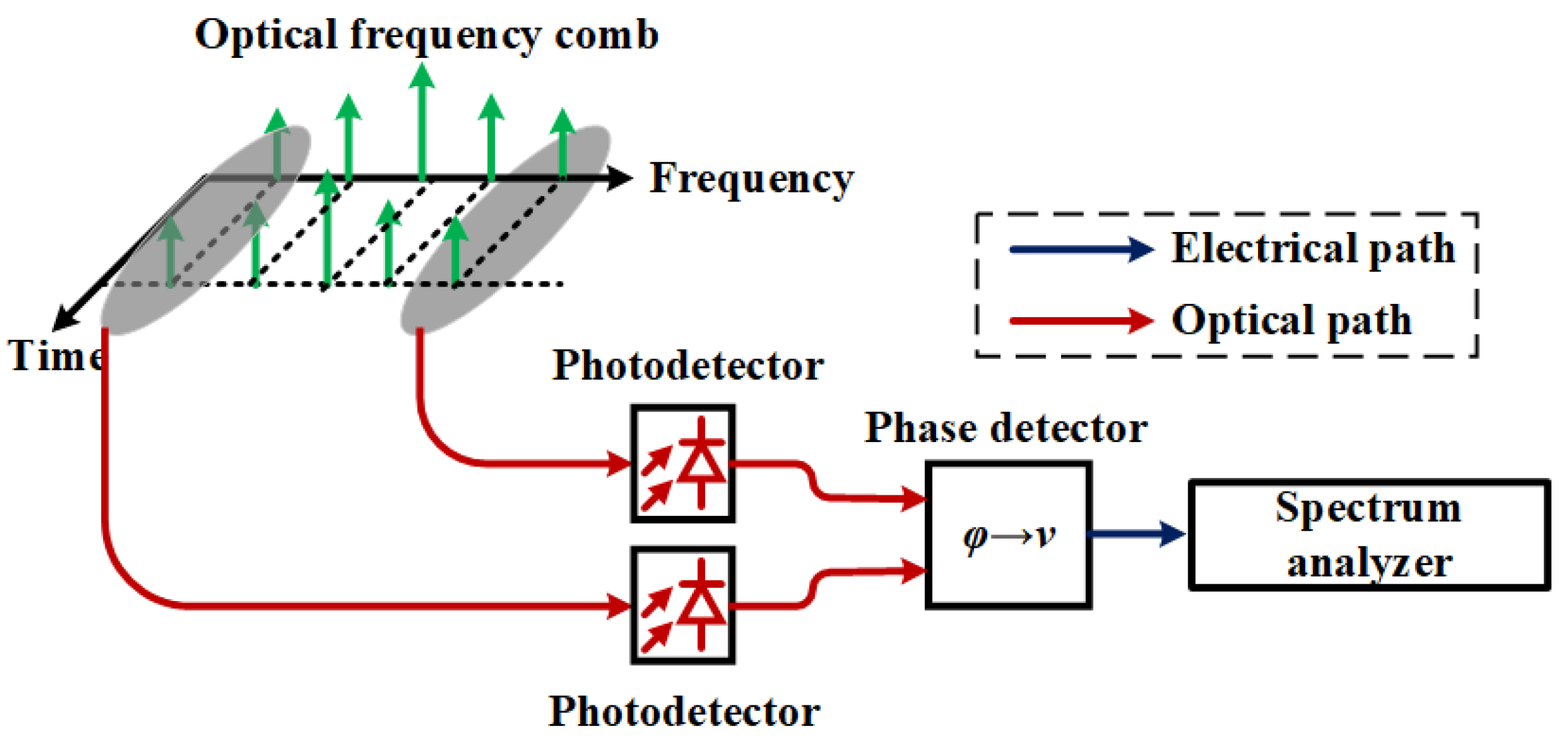
3.1. MWP PNA with Ultra-Short-Pulse Lasers
3.2. MWP PNA with OEO
4. MWP Frequency-Discrimination-Based PNAs
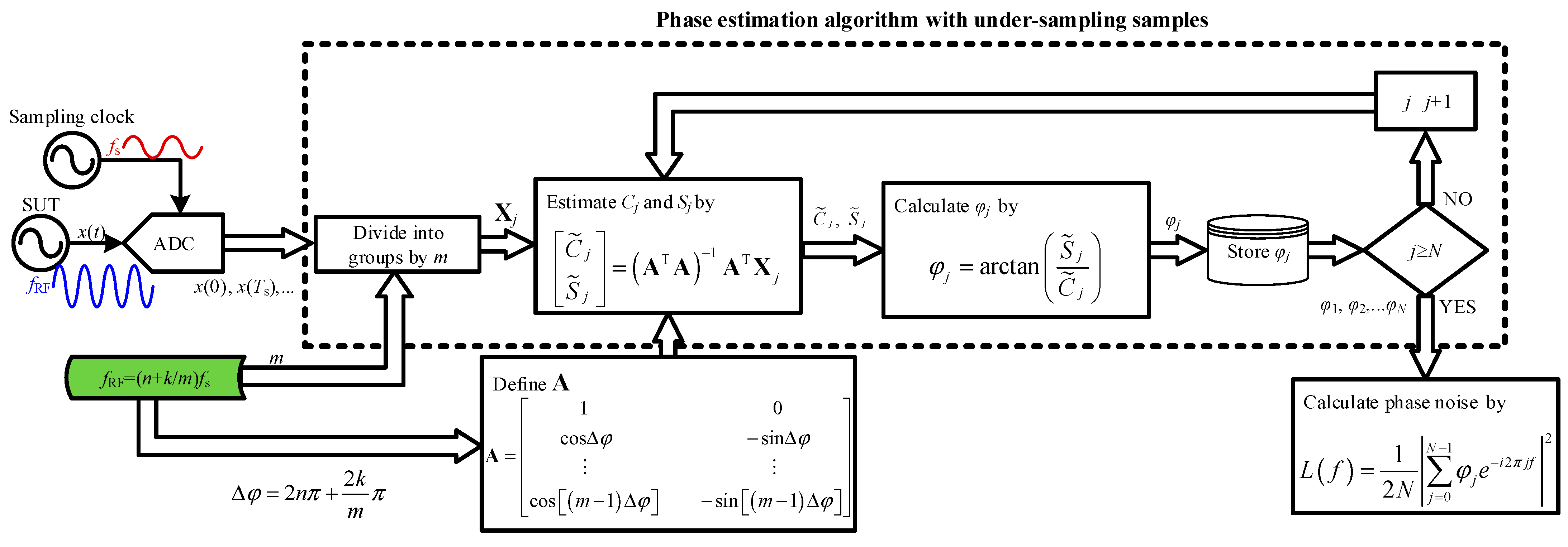
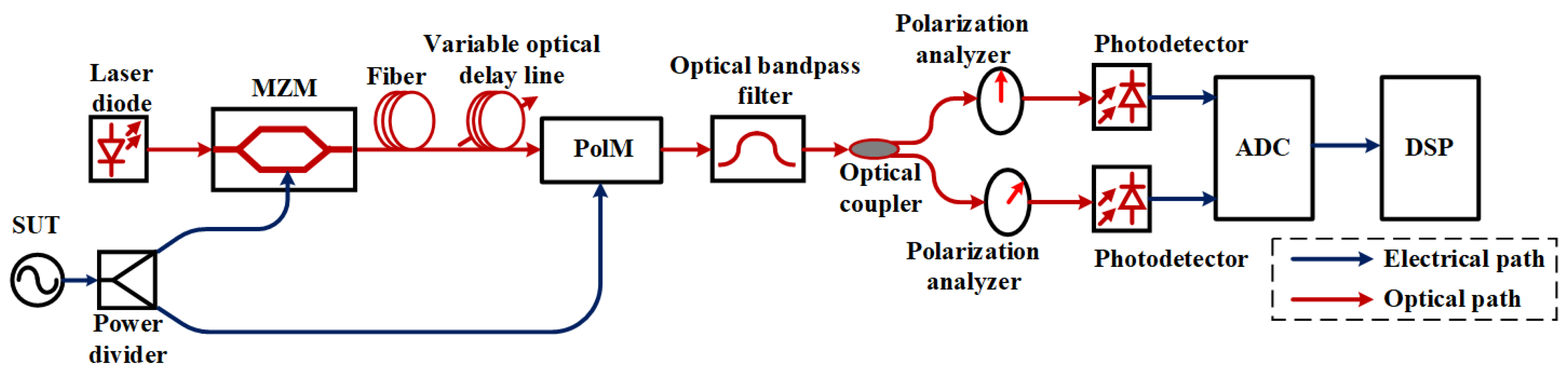
4.1. Photonic-Substitution-Type PNAs
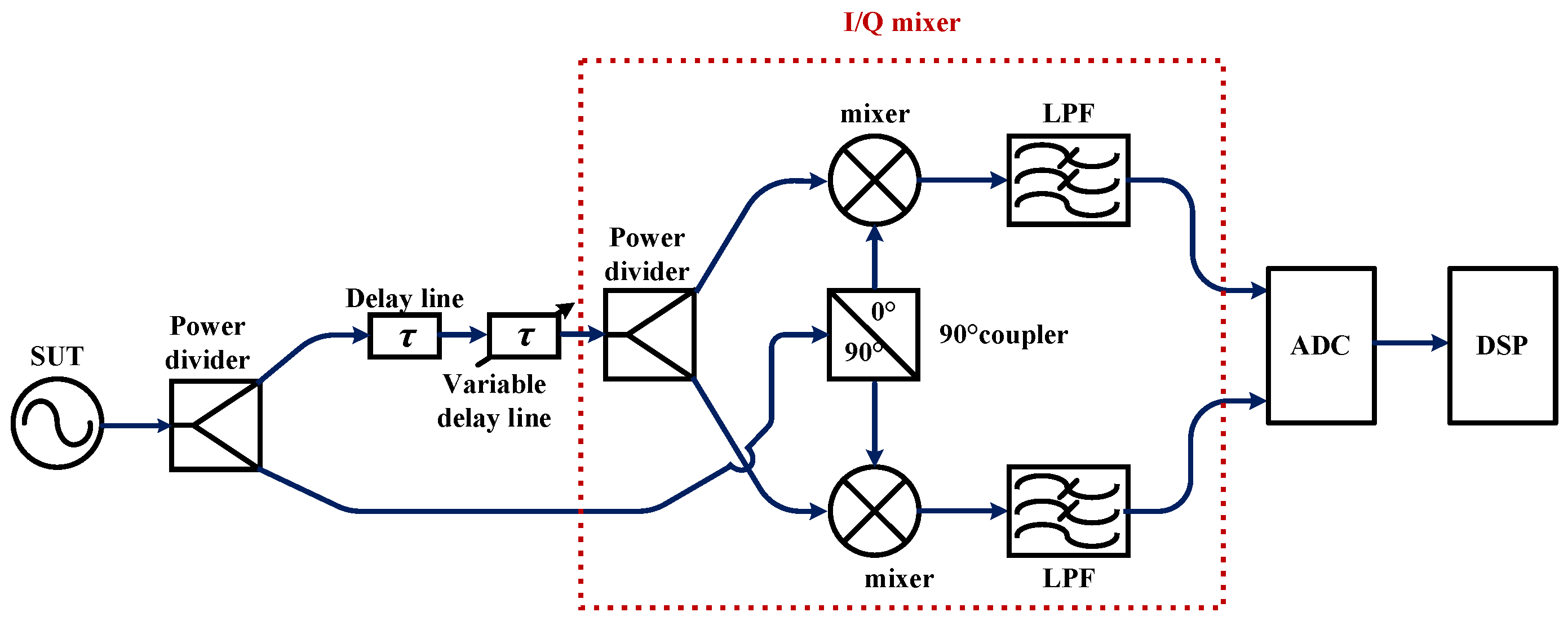
4.2. MWP Quadrature-Frequency-Discrimination-Based PNAs
5. Conclusions
- (1)
- Phase noise measurement for complex microwave signals
- (2)
- Instantaneous phase noise measurement
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| PNA | Phase noise analyzer |
| MWP | Microwave photonic |
| PSD | Power spectral density |
| SUT | Signal under test |
| MZM | Mach-Zehnder modulator |
| DOMZM | Dual-output Mach-Zehnder modulator |
| OEO | Optoelectronic oscillator |
| ADC | Analog-to-digital converter |
| I/Q | In-phase and quadrature |
| DDS | Direct digital synthesizer |
| DSP | Digital signal processing |
| DMZM | Dual-drive Mach-Zehnder modulator |
References
- Rubiola, E.; Vernotte, F. The companion of Enrico’s chart for phase noise and two-sample variances. IEEE Trans. Microw. Theory Tech. 2023, 71, 2996–3025. [Google Scholar] [CrossRef]
- Leeson, D.B. Oscillator phase noise: A 50-year review. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2016, 63, 1208–1225. [Google Scholar] [CrossRef] [PubMed]
- IEEE Std 2414™-2020; IEEE Standard for Jitter and Phase Noise. IEEE Instrumentation & Measurement Society: New York, NY, USA, 2020; pp. 1–42.
- Ayhan, S.; Scherr, S.; Bhutani, A.; Fischbach, B.; Pauli, M.; Zwick, T. Impact of frequency ramp nonlinearity, phase noise, and SNR on FMCW radar accuracy. IEEE Trans. Microw. Theory Tech. 2016, 64, 3290–3301. [Google Scholar] [CrossRef]
- Rebeyrol, E.; Macabiau, C.; Ries, L.; Issler, J.-L.; Bousquet, M.; Boucheret, M.-L. Phase noise in GNSS transmission/reception system. In Proceedings of the 2006 National Technical Meeting of the Institute of Navigation, Monterey, CA, USA, 18–20 January 2006; pp. 698–708. [Google Scholar]
- Mathecken, P.; Riihonen, T.; Werner, S.; Wichman, R. Performance analysis of OFDM with Wiener phase noise and frequency selective fading channel. IEEE Trans. Commun. 2011, 59, 1321–1331. [Google Scholar] [CrossRef]
- Maleki, L. The optoelectronic oscillator. Nat. Photonics 2011, 5, 728–730. [Google Scholar] [CrossRef]
- Pan, S.; Yao, J. Photonics-based broadband microwave measurement. J. Light. Technol. 2016, 35, 3498–3513. [Google Scholar] [CrossRef]
- Zou, X.; Lu, B.; Pan, W.; Yan, L.; Stöhr, A.; Yao, J. Photonics for microwave measurements. Laser Photonics Rev. 2016, 10, 711–734. [Google Scholar] [CrossRef]
- Yao, J. Microwave photonics. J. Light. Technol. 2009, 27, 314–335. [Google Scholar] [CrossRef]
- Seeds, A.J.; Williams, K.J. Microwave photonics. J. Light. Technol. 2006, 24, 4628–4641. [Google Scholar] [CrossRef]
- Rohde, U.L.; Poddar, A.K.; Apte, A.M. Getting its measure: Oscillator phase noise measurement techniques and limitations. IEEE Microw. Mag. 2013, 14, 73–86. [Google Scholar] [CrossRef]
- Lance, A.L.; Seal, W.D.; Labaar, F. Phase noise and AM noise measurements in the frequency domain. Infrared Millim. Waves 1984, 11, 239–289. [Google Scholar]
- Kim, J.; Kaertner, F.X. Attosecond-precision ultrafast photonics. Laser Photonics Rev. 2010, 4, 432–456. [Google Scholar] [CrossRef]
- Kim, J.; Cox, J.A.; Chen, J.; Kärtner, F.X. Drift-free femtosecond timing synchronization of remote optical and microwave sources. Nat. Photonics 2008, 2, 733–736. [Google Scholar] [CrossRef]
- Kim, J.; Song, Y. Ultralow-noise mode-locked fiber lasers and frequency combs: Principles, status, and applications. Adv. Opt. Photonics 2016, 8, 465–540. [Google Scholar] [CrossRef]
- Jung, K.; Kim, J. Subfemtosecond synchronization of microwave oscillators with mode-locked Er-fiber lasers. Opt. Lett. 2012, 37, 2958–2960. [Google Scholar] [CrossRef]
- Jung, K.; Shin, J.; Kim, J. Ultralow phase noise microwave generation from mode-locked Er-fiber lasers with subfemtosecond integrated timing jitter. IEEE Photonics J. 2013, 5, 5500906. [Google Scholar] [CrossRef]
- Kim, J.; Kärtner, F.X.; Perrott, M.H. Femtosecond synchronization of radio frequency signals with optical pulse trains. Opt. Lett. 2004, 29, 2076–2078. [Google Scholar] [CrossRef]
- Lessing, M.; Margolis, H.S.; Brown, C.T.A.; Gill, P.; Marra, G. Suppression of amplitude-to-phase noise conversion in balanced optical-microwave phase detectors. Opt. Express 2013, 21, 27057–27062. [Google Scholar] [CrossRef]
- Kim, J.; Kärtner, F.X.; Ludwig, F. Balanced optical–microwave phase detectors for optoelectronic phase-locked loops. Opt. Lett. 2006, 31, 3659–3661. [Google Scholar] [CrossRef]
- Peng, M.Y.; Kalaydzhyan, A.; Kärtner, F.X. Balanced optical-microwave phase detector for sub-femtosecond optical-RF synchronization. Opt. Express 2014, 22, 27102–27111. [Google Scholar] [CrossRef]
- Endo, M.; Shoji, T.D.; Schibli, T.R. High-sensitivity optical to microwave comparison with dual-output Mach-Zehnder modulators. Sci. Rep. 2018, 8, 4388. [Google Scholar] [CrossRef] [PubMed]
- Shi, J.; Hua, S.; Ge, J.; Zhu, D.; Zhang, F.; Wang, Y. RF Phase Noise Analyzer Based on Phase Estimation Algorithm With Undersampling Samples. IEEE Trans. Microw. Theory Tech. 2023, 72, 1118–1125. [Google Scholar] [CrossRef]
- Maleki, L. The opto-electronic oscillator (OEO): Review and recent progress. In Proceedings of the 2012 European Frequency and Time Forum, Gothenburg, Sweden, 23–27 April 2012; pp. 497–500. [Google Scholar]
- Peng, H.; Xu, Y.; Guo, R.; Du, H.; Chen, J.; Chen, Z. High sensitivity microwave phase noise analyzer based on a phase locked optoelectronic oscillator. Opt. Express 2019, 27, 18910–18927. [Google Scholar] [CrossRef]
- Rubiola, E.; Salik, E.; Huang, S.; Yu, N.; Maleki, L. Photonic-delay technique for phase-noise measurement of microwave oscillators. J. Opt. Soc. Am. B 2005, 22, 987–997. [Google Scholar] [CrossRef]
- Onillon, B.; Constant, S.; Liopis, O. Optical links for ultra low phase noise microwave oscillators measurement. In Proceedings of the 2005 IEEE International Frequency Control Symposium and Exposition, Vancouver, BC, Canada, 29–31 August 2005; 6p. [Google Scholar]
- Zhu, D.; Zhang, F.; Zhou, P.; Zhu, D.; Pan, S. Wideband phase noise measurement using a multifunctional microwave photonic processor. IEEE Photonics Technol. Lett. 2014, 26, 2434–2437. [Google Scholar] [CrossRef]
- Pan, S.; Zhang, Y. Tunable and wideband microwave photonic phase shifter based on a single-sideband polarization modulator and a polarizer. Opt. Lett. 2012, 37, 4483–4485. [Google Scholar] [CrossRef]
- Wang, W.; Liu, J.G.; Mei, H.; Sun, W.; Zhu, N. Photonic-assisted wideband phase noise analyzer based on optoelectronic hybrid units. J. Light. Technol. 2016, 34, 3425–3431. [Google Scholar] [CrossRef]
- Zhu, D.; Zhang, F.; Zhou, P.; Pan, S. Phase noise measurement of wideband microwave sources based on a microwave photonic frequency down-converter. Opt. Lett. 2015, 40, 1326–1329. [Google Scholar] [CrossRef]
- Zhang, F.; Zhu, D.; Pan, S. Photonic-assisted wideband phase noise measurement of microwave signal sources. Electron. Lett. 2015, 51, 1272–1274. [Google Scholar] [CrossRef]
- Zhou, P.; Jiang, Z.; Tang, Z.; Li, N.; Pan, S. Microwave phase noise analyzer based on photonic delay-matched frequency translation. IEEE Trans. Microw. Theory Tech. 2024, 72, 5498–5506. [Google Scholar] [CrossRef]
- Salik, E.; Yu, N.; Maleki, L.; Rubiola, E. Dual photonic-delay line cross correlation method for phase noise measurement. In Proceedings of the 2004 IEEE International Frequency Control Symposium and Exposition, Montreal, QC, Canada, 23–27 August 2004; pp. 303–306. [Google Scholar]
- Eliyahu, D.; Seidel, D.; Maleki, L. Phase noise of a high performance OEO and an ultra low noise floor cross-correlation microwave photonic homodyne system. In Proceedings of the 2008 IEEE International Frequency Control Symposium, Honolulu, HI, USA, 19–21 May 2008; pp. 811–814. [Google Scholar]
- Fan, Z.; Qiu, Q.; Su, J.; Zhang, T.; Yang, N. Photonic-delay line cross correlation method based on DWDM for phase noise measurement. IEEE Photonics J. 2018, 10, 1–9. [Google Scholar] [CrossRef]
- Fan, Z.; Qiu, Q.; Su, J.; Zhang, T.; Lin, Y. Phase noise measurement of an optoelectronic oscillator based on the photonic-delay line cross-correlation method. Opt. Lett. 2019, 44, 1992–1995. [Google Scholar] [CrossRef]
- Kuse, N.; Fermann, M. Electro-optic comb based real time ultra-high sensitivity phase noise measurement system for high frequency microwaves. Sci. Rep. 2017, 7, 2847. [Google Scholar] [CrossRef]
- Shi, J.; Zhang, F.; Pan, S. High-sensitivity phase noise measurement of RF sources by photonic-delay line and digital phase demodulation. In Proceedings of the 2017 16th International Conference on Optical Communications and Networks (ICOCN), Wuzhen, China, 7–10 August 2017; pp. 1–3. [Google Scholar]
- Shi, J.; Zhang, F.; Pan, S. Phase noise measurement of RF signals by photonic time delay and digital phase demodulation. IEEE Trans. Microw. Theory Tech. 2018, 66, 4306–4315. [Google Scholar] [CrossRef]
- Zhang, F.; Shi, J.; Pan, S. Wideband microwave phase noise measurement based on photonic-assisted I/Q mixing and digital phase demodulation. Opt. Express 2017, 25, 22760–22768. [Google Scholar] [CrossRef] [PubMed]
- Shi, J.; Zhang, F.; Ben, D.; Pan, S. Wideband microwave phase noise analyzer based on an all-optical microwave I/Q mixer. J. Light. Technol. 2018, 36, 4319–4325. [Google Scholar] [CrossRef]
- Zhang, F.; Shi, J.; Zhang, Y.; Ben, D.; Sun, L.; Pan, S. Self-calibrating and high-sensitivity microwave phase noise analyzer applying an optical frequency comb generator and an optical-hybrid-based I/Q detector. Opt. Lett. 2018, 43, 5029–5032. [Google Scholar] [CrossRef]
- Samarasekera, A.C.J.; Feger, R.; Bechter, J.; Stelzer, A. Phase noise measurements in chirped FMCW radar signals. In Proceedings of the 2020 IEEE MTT-S International Conference on Microwaves for Intelligent Mobility (ICMIM), Linz, Austria, 23 November 2020; pp. 1–4. [Google Scholar]
- Gerstmair, M.; Melzer, A.; Wagner, M.; Lang, O.; Huemer, M. Phase noise monitoring in cascaded systems for high-resolution automotive radar sensors. IEEE Trans. Microw. Theory Tech. 2021, 69, 5072–5085. [Google Scholar] [CrossRef]
- Birkenhauer, C.; Tschapek, P.; Vossiek, M. Over-the-Air Phase Noise Spectral Density Measurement for FMCW Radar Sensors. IEEE J. Microw. 2024, 4, 733–741. [Google Scholar] [CrossRef]
- Nouri, M.; Mivehchy, M.; Sabahi, M. Target recognition based on phase noise of received signal. Electron. Lett. 2017, 53, 808–810. [Google Scholar] [CrossRef]
- Shi, J.; Zhang, F.; Ben, D.; Pan, S. Photonic-assisted single system for microwave frequency and phase noise measurement. Chin. Opt. Lett. 2020, 18, 092501. [Google Scholar] [CrossRef]









| Types | Advantages | Limitations | Sensitivity | Bandwidth | |
|---|---|---|---|---|---|
| MWP Phase-Detection-Based PNAs | MWP PNA With Ultra-Short Pulse Lasers | Ultra-high sensitivity | Measurement frequency limitation imposed by laser repetition rate | −167 dBc/Hz @ 10 kHz @ 1 GHz [23] (with dual-channel cross-correlation) | Integer multiples of 1 GHz [23] |
| MWP PNA With OEO | High sensitivity | Bandwidth Limitation Caused by Poor Tunability of the OEO | −140 dBc/Hz @ 10 kHz @ 10 GHz [26] | 9–11 GHz [26] | |
| MWP Frequency-Discrimination-Based PNAs | Photonic-Substitution-Type PNAs | Wide bandwidth | Complicated calibration; Poor sensitivity at low-frequency offsets | −137 dBc/Hz @ 10 kHz @ 10 GHz [32] | 5–40 GHz [32] |
| MWP Quadrature-Frequency-Discrimination-Based PNAs | Simplified calibration; Wide bandwidth | Poor sensitivity at low-frequency offsets | −136 dBc/Hz @ 10 kHz @ 10 GHz [43] | 5–50 GHz [43] | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, J.; Tu, B.; Wang, Y. Photonics-Enabled High-Sensitivity and Wide-Bandwidth Microwave Phase Noise Analyzers. Photonics 2025, 12, 691. https://doi.org/10.3390/photonics12070691
Shi J, Tu B, Wang Y. Photonics-Enabled High-Sensitivity and Wide-Bandwidth Microwave Phase Noise Analyzers. Photonics. 2025; 12(7):691. https://doi.org/10.3390/photonics12070691
Chicago/Turabian StyleShi, Jingzhan, Baojin Tu, and Yiping Wang. 2025. "Photonics-Enabled High-Sensitivity and Wide-Bandwidth Microwave Phase Noise Analyzers" Photonics 12, no. 7: 691. https://doi.org/10.3390/photonics12070691
APA StyleShi, J., Tu, B., & Wang, Y. (2025). Photonics-Enabled High-Sensitivity and Wide-Bandwidth Microwave Phase Noise Analyzers. Photonics, 12(7), 691. https://doi.org/10.3390/photonics12070691






