DynaFlowNet: Flow Matching-Enabled Real-Time Imaging Through Dynamic Scattering Media

Abstract

Imaging through dynamic scattering media remains a fundamental challenge because of severe information loss and the ill-posed nature of the inversion problem. Conventional methods often struggle to strike a balance between reconstruction fidelity and efficiency in evolving environments. In this study, we present DynaFlowNet, a framework that leverages conditional flow matching theory to establish a continuous, invertible mapping from speckle patterns to target images via deterministic ordinary differential equation (ODE) integration. Central to this is the novel temporal–conditional residual attention block (TCResAttnBlock), which is designed to model spatiotemporal scattering dynamics. DynaFlowNet achieves real-time performance at 134.77 frames per second (FPS), which is 117 times faster than diffusion-based models, while maintaining state-of-the-art reconstruction quality (28.46 dB peak signal-to-noise ratio (PSNR), 0.9112 structural similarity index (SSIM), and 0.8832 Pearson correlation coefficient (PCC)). In addition, the proposed framework demonstrates exceptional geometric generalization, with only a 1.05 dB PSNR degradation across unseen geometries, significantly outperforming existing methods. This study establishes a new paradigm for real-time high-fidelity imaging using dynamic scattering media, with direct implications for biomedical imaging, remote sensing, and underwater exploration.

1. Introduction

Optical imaging through dynamic scattering media, such as biological tissues, atmospheric haze, and underwater environments, represents a fundamental challenge in modern photonics with profound implications for biomedical diagnostics, remote sensing, and underwater exploration. When light propagates through such media, multiple scattering events transform the coherent wavefront into a seemingly random speckle pattern, thereby effectively obscuring the underlying object information [1]. This process introduces two critical challenges: severe information attenuation, where only approximately 10⁻⁶–10⁻³ of ballistic photons reach the detector, and the ill-posed inverse problem, where photon propagation paths exhibit exponential complexity (~10⁸ scattering events per photon), rendering conventional imaging techniques ineffective in these scenarios.

Traditional approaches to scattering imaging can be broadly categorized into three paradigms. First, ballistic photon extraction techniques, including range-gated imaging [2], optical coherence tomography [3], multiphoton microscopy [4], and multidimensional gating [5], rely on temporal or spatial filtering to isolate unscattered photons. However, their imaging depth is fundamentally limited by the exponential decay of ballistic photons with propagation distance [6]. Second, transmission matrix characterization methods model the scattering medium as a linear system [7]. However, they require complex optical setups for matrix calibration and exhibit high sensitivity to microscopic perturbations [8], severely restricting practical deployment. Third, speckle correlation techniques exploit the optical memory effect [9] for the noninvasive imaging of objects hidden behind opaque layers, as demonstrated by Bertolotti et al. [10]. However, the field of view remains constrained by the thickness of the medium (with the memory effect range inversely proportional to thickness [11]). Moreover, point-scanning implementations suffer from prohibitively long acquisition times for dynamic media applications.

The emergence of deep learning has revolutionized scattering imaging by establishing data-driven mapping between distorted measurements and target objects, circumventing the need for precise physical modeling and iterative optimization [12]. Supervised learning approaches have led to breakthroughs in glass diffuser imaging [13] and lensless imaging through optically thick media [14]. In contrast, physics-informed networks have enhanced the reconstruction fidelity for thin scattering layers [15]. Unsupervised methods, including diffusion models with data consistency constraints [16] and speckle reassignment techniques [17], have further expanded the scattering imaging capabilities. For dynamic media, recent advances include scattering condition classification with generative adversarial networks (GANs) [18], the convolutional neural network (CNN) phase imaging frameworks [19], speckle deblurring for high-throughput imaging [20], and Pix2Pix-based reconstruction for layered media [21].

The challenge of imaging through scattering media has spurred diverse computational innovations. Recent advances integrate deep learning with novel sensing modalities: SeaThru-NeRF [22] leverages neural radiance fields for 3D reconstruction in static media using multi-view consistency, while STAMF [23] and polarimetric binocular methods [24] exploit polarization cues with advanced sequence models for tasks such as salient detection or 3D imaging, often through self-supervision. Despite their success, these methods face limitations: dependence on multi-view inputs, specialized polarization sensors, or assumptions of static scattering conditions. Consequently, high-fidelity, real-time reconstruction from a single shot through dynamic scattering media—where parameters fluctuate rapidly—remains an open problem.

Among generative models, GANs have demonstrated high-quality image synthesis but suffer from training instability and mode collapse [25,26,27]. Diffusion models offer improved stability and sample quality [28,29,30] but incur substantial computational costs during inference. Most recently, flow-matching approaches, such as rectified flow [31], have emerged as promising alternatives for learning probability paths through ordinary differential equations (ODEs), enabling deterministic sampling with theoretical guarantees. Lipman et al. [32] demonstrated that flow matching can achieve high-quality image reconstruction through direct vector field learning, offering a compelling tradeoff between generation quality and computational efficiency.

Despite significant advances, real-time imaging through dynamic scattering media remains fundamentally challenging due to spatiotemporal nonuniformity, which hinders accurate multipath modeling, and the computational complexity of traditional solvers, which conflicts with real-time requirements. Current methods typically sacrifice either reconstruction fidelity for speed (e.g., CNN-based approaches) or computational efficiency for quality (e.g., diffusion models).

To overcome the persistent challenges of spatiotemporal nonuniformity and computational complexity in dynamic scattering imaging, we propose DynaFlowNet, a novel framework grounded in conditional flow matching theory. This approach establishes a continuous invertible mapping between speckle patterns and target images through deterministic ODE integration, circumventing the iterative sampling inherent in diffusion models. Central to our framework is the temporal-conditional residual attention block (TCResAttnBlock), which integrates temporal conditioning with multiscale attention to model spatiotemporally varying scattering operators. Collectively, this study contributes to (1) the first flow-matching formulation for dynamic scattering inversion that transforms reconstruction into a continuous trajectory learning problem, (2) a neural architecture specifically designed to capture temporally evolving scattering processes, and (3) the experimental validation of real-time (>100 frames per second, FPS) and high-fidelity (peak signal-to-noise ratio, PSNR > 28 dB) imaging capabilities in controlled dynamic water mist environments. By integrating flow matching theory with computational optics, DynaFlowNet establishes a new paradigm for solving high-dimensional inverse problems with theoretical rigor and practical efficiency.

2. Methods

2.1. Principle and Methodology

The light field transmission process through dynamic scattering media can be formulated as a nonlinear operator equation as follows:

$$g=\mathcal{H}\left(f\right)+ϵ$$

(1)

where $f\in {\mathbb{R}}^d$ represents the input light field (target image), $g\in {\mathbb{R}}^m$ denotes the observed speckle pattern, $\mathcal{H}:{\mathbb{R}}^d\to {\mathbb{R}}^m$ characterizes the time-varying forward operator of the scattering medium, and $ϵ~\mathcal{N}(0,{\sigma }^{2}I)$ represents system noise, modeled as additive white Gaussian noise with zero mean and variance ${\sigma }^2$.

By leveraging the principle of optical reciprocity, the target reconstruction problem is equivalent to solving the ill-posed inverse problem as follows:

$$f^{\prime }={\mathcal{H}}^{-1}\left(g\right)$$

(2)

where ${\mathcal{H}}^{-1}$ denotes the ill-posed inverse operator. Although conventional deep learning approaches approximate ${\mathcal{H}}^{-1}$ via supervised learning, they encounter three major challenges in the context of dynamic media (e.g., biological tissue and atmospheric turbulence):

1.

Temporal variation in operator $\mathcal{H}$ owing to media inhomogeneity;

2.

Solution space ambiguity arising from inherent ill-posedness;

3.

High computational complexity associated with high-dimensional reconstruction.

2.2. Dual-Conditioned Continuous Flow Transport for Dynamic Scattering Imaging

This study proposes a dynamic scattering reconstruction framework based on conditional flow matching, whose core innovation lies in constructing a continuous invertible mapping between the source distribution ${\mathrm{p}}_0\left({\mathbf{z}}_0\right)=\mathcal{N}(0,I)$ and the target distribution ${\mathrm{p}}_1\left(\mathbf{f}\mid \mathbf{g}\right)$. Unlike discrete transformations in traditional normalizing flows, our method models the probability density evolution via a continuous ODE:

$${\displaystyle \frac{d{\mathbf{z}}_t}{dt}}={\mathbf{v}}_{\theta }\left({\mathit{z}}_t,t\mid \mathbf{g}\right), t\in \left[\mathrm{0,1}\right]$$

(3)

where ${\mathbf{z}}_t$ denotes the latent variable at time $t$, and ${\mathbf{v}}_{\theta }$ is a dual-conditioned vector field (constrained by both measurement $\mathbf{g}$ and time $t$).

2.2.1. Forward Path Construction

Guided by Brenier’s theorem in optimal transport theory, we define a straight probability path connecting the prior and target distributions as follows:

$${\mathbf{z}}_t=\left(1-t\right)\cdot {\mathbf{z}}_0+t\cdot \mathbf{f}, {\mathbf{z}}_0\sim p_0, \mathbf{f}\sim p_{\mathrm{d}\mathrm{a}\mathrm{t}\mathrm{a}}\left(\mathbf{f}\mid \mathbf{g}\right)$$

(4)

The differential form of this path yields the target vector field:

$${\displaystyle \frac{d{\mathbf{z}}_t}{dt}}=\mathbf{f}-{\mathbf{z}}_0={\mathbf{u}}_t\left({\mathbf{z}}_t\right)$$

(5)

This construction provides a universally optimal solution to the Monge–Ampère equation under the $W_2$ distance [33], achieving the theoretical lower bound for the transport cost $C=\mathbb{E}{‖\mathbf{f}-{\mathbf{z}}_0‖}_2^2$.

2.2.2. Backward Generation Process

Upon completion of training, the reconstruction is obtained by solving the ODE initial value problem as follows:

$$\widehat{\mathbf{f}}={\mathbf{z}}_0+{\int }_0^1{\mathbf{v}}_{\theta }({\mathbf{z}}_s,s\mid \mathbf{g})ds, {\mathbf{z}}_0\sim \mathcal{N}(0,I)$$

(6)

Numerical integration is implemented using the explicit Euler method [34] with a fixed step size $∆t=0.1$. The discretized solution is iteratively computed as follows:

$$\begin{array}{c}{\mathbf{z}}_{k+1}={\mathbf{z}}_k+{\mathbf{v}}_{\theta }({\mathbf{z}}_k,t_k\mid \mathbf{g})\cdot \mathsf{\Delta }t,t_k=k\cdot \mathsf{\Delta }t,k=\mathrm{0,1},\dots ,10\end{array}$$

(7)

This efficient scheme, requiring only 11 function evaluations ($k=0$ to $k=10$), achieves a reconstruction fidelity exceeding 28 dB PSNR in benchmark tests. Its computational efficiency significantly outperforms that of conventional diffusion models, which typically require $N>1000$ iterative steps for comparable tasks.

2.2.3. Vector Field Learning Mechanism

In this study, we define the bridge distribution $p_t({\mathbf{z}}_t\mid \mathbf{g})=\int p_t({\mathbf{z}}_t\mid \mathbf{f})p_{\mathrm{d}\mathrm{a}\mathrm{t}\mathrm{a}}\left(\mathbf{f}\mid \mathbf{g}\right)d\mathbf{f}$, where $p_t({\mathbf{z}}_t\mid \mathbf{f})$ is explicitly given by the path represented by Equation (4). The vector field is optimized by minimizing the variational upper bound of the Wasserstein-2 distance [35]:

$${\mathcal{L}}_{FM}\left(\theta \right)={\mathbb{E}}_{t\sim \mathcal{U}\left[\mathrm{0,1}\right]}\left[{\lambda \left(t\right)·{\mathbb{E}}_{p_t({\mathbf{z}}_t\mid \mathbf{g})}\parallel {\mathbf{v}}_{\theta }-{\mathbf{u}}_t \parallel }_2^2\right]$$

(8)

where $\lambda \left(t\right)={(1-t)}^{-1}$ compensates for endpoint density disparities; ${\mathbf{u}}_t\left({\mathbf{z}}_t\right)={\mathbb{E}}_{p_{\mathrm{d}\mathrm{a}\mathrm{t}\mathrm{a}}\left(\mathbf{f}\mid \mathbf{g},{\mathbf{z}}_t\right)}\left[\mathbf{f}-{\mathbf{z}}_0\right]$ is the conditional target vector field.

2.3. DynaFlowNet: Spectro-Temporal Flow Matching for Real-Time Dynamic Scattering Imaging

We propose DynaFlowNet, a conditional generative architecture for real-time dynamic scattering reconstruction via flow matching. As shown in Figure 1, the network learns the vector field ${\mathbf{v}}_{\theta }(\mathbf{x},\mathrm{t}\mid \mathbf{g})$ through a time-conditional U-Net backbone, integrating three key innovations that are explained in the following subsections.

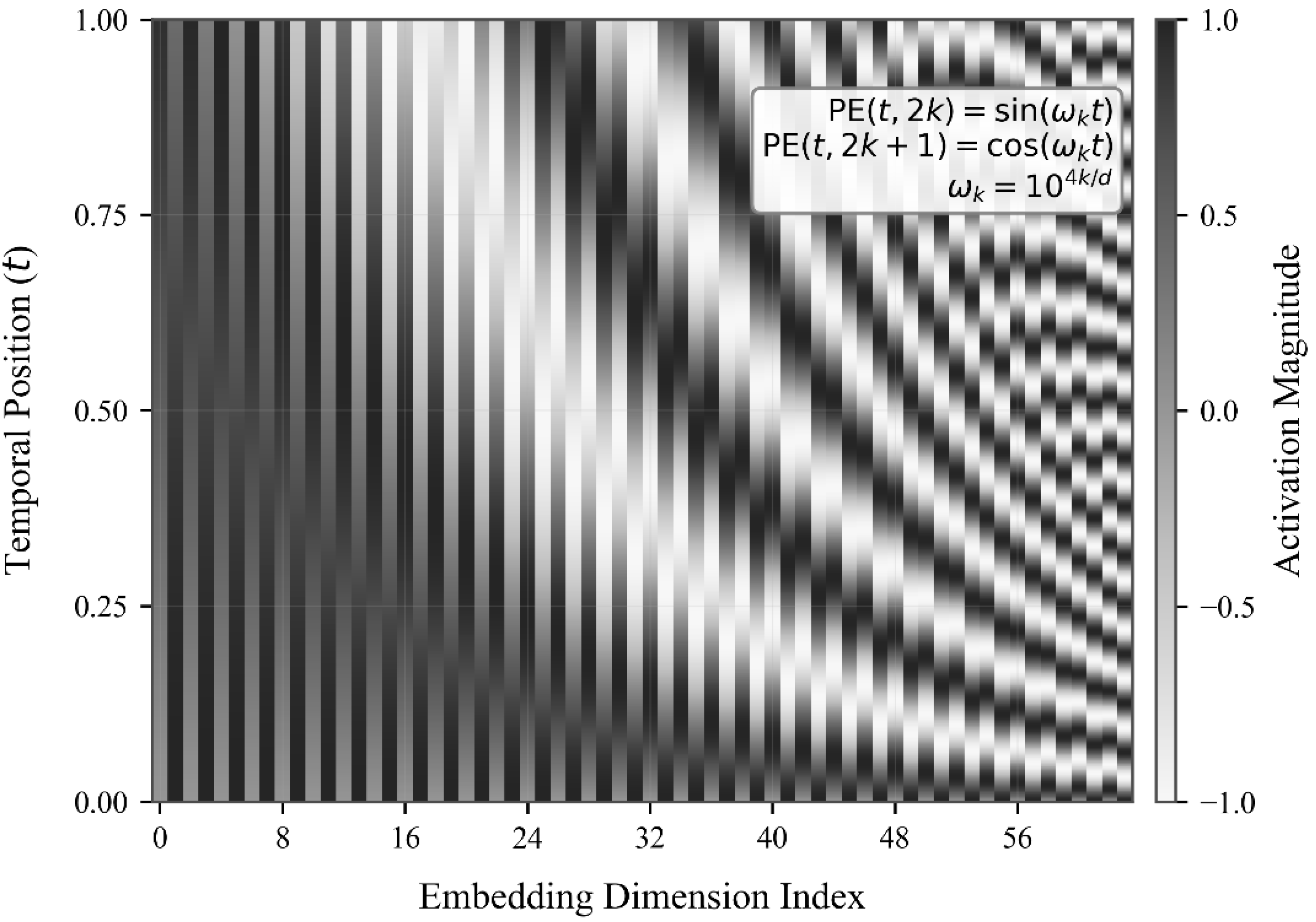
2.3.1. Spectro-Dynamic Time Embedding (SD-Embedding)

Extending sinusoidal positional encoding, we generate time embeddings $t_{emb}\in {\mathbb{R}}^T$ via:

$$t_{emb}=MLP\left(Concat\left(\varphi (t{)}_{2k}=\mathrm{s}\mathrm{i}\mathrm{n}({10}^{4k/d}t),\varphi (t{)}_{2k+1}=\mathrm{c}\mathrm{o}\mathrm{s}\left({10}^{4k/d}t\right)\right)\right)$$

(9)

where $d$ denotes the encoding dimension. Figure 2 demonstrates the spectral continuity of this embedding. Low-frequency components govern long-term diffusion convergence ($t\in \left[0,1\right]$), whereas high-frequency components regulate transient dynamics. This multiscale encoding eliminates spectral discontinuities, ensuring stable gradient propagation during inversion (unlike scalar time inputs).

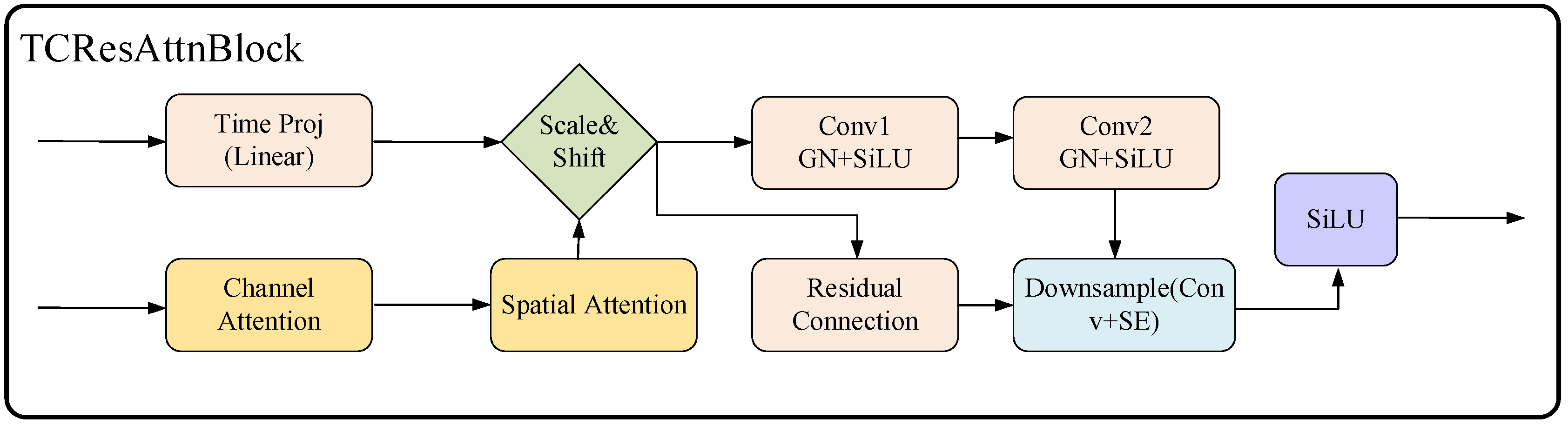
2.3.2. Temporal-Conditional Residual Attention Blocks (TCResAttnBlocks)

As illustrated in Figure 3, each block integrates time embeddings $\varphi \left(t\right)$ and conditional features through a unified architecture comprising three core operations. First, a dual-path attention mechanism executes channel recalibration via a squeeze-and-excitation block coupled with spatial channel co-attention using a convolutional block attention module (CBAM). Subsequently, adaptive modulation projects time embeddings $\varphi \left(t\right)$ to affine parameters $(\gamma ,\beta )$ while spatially aligning conditional features through bilinear interpolation and 1 × 1 convolutions. Finally, the residual learning employs two sequential 3 × 3 convolutional layers with group normalization and SiLU activation, preserving the gradient flow via identity mapping. This synergistic design enforces spatiotemporal coherence by strictly adhering to the time-conditional dynamics.

2.3.3. Multiscale Encoder–Decoder Architecture

The architecture employs a 4-stage encoder where each down-sampling level incorporates TCResAttnBlocks while progressively expanding the channel dimensions from $C_{base}$ to $16C_{base}$. At the bottleneck, high-dimensional features are refined using a dedicated TCResAttnBlock coupled with a CBAM. The decoder subsequently reconstructs representations via bilinear up-sampling, with skip connections enabling feature fusion across scales, mathematically expressed as ${\mathbb{R}}^{\left({16C}_{base}+{8C}_{base}\right)\times H\times W}$, while progressively reducing the channels back to $C_{base}$. Skip connections preserve multiscale texture details, whereas squeeze-and-excitation (SE) blocks concurrently suppress feature redundancies throughout the decoding pathway.

2.4. Experimental Setup

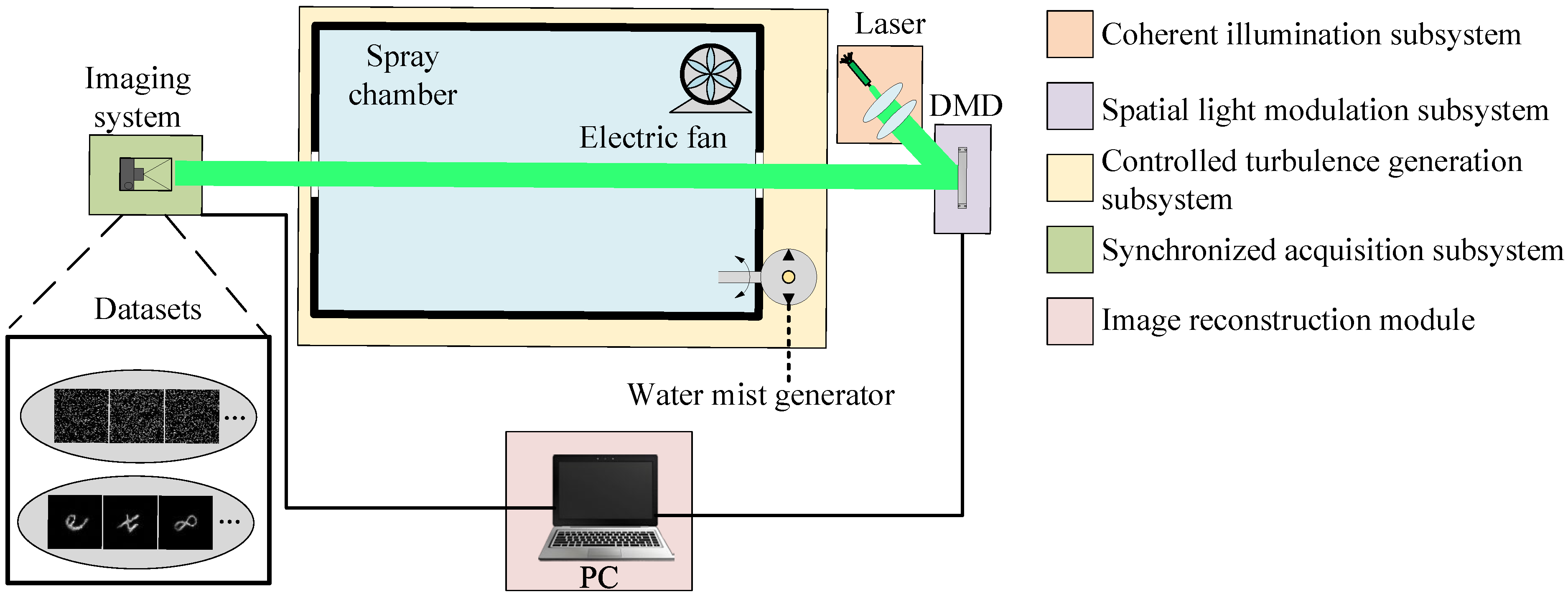
2.4.1. Optical Imaging System Configuration

The dynamic scattering imaging system integrates four functionally coupled subsystems, as illustrated in Figure 4.

• Coherent illumination subsystem: The radiation beam from a 532 nm semiconductor laser (ADR-1805, Changchun New Industries Optoelectronics, Changchun, China) was collimated and expanded through a 10× beam expander (GCO-25, Daheng Optics, Beijing, China) to generate a uniform spatial intensity profile (beam divergence < 0.1 mrad).
• Spatial light modulation subsystem: A DLP6500 digital micromirror device (DMD, Jin Hua Feiguang Electronic, Jin Hua, China) with 1920 × 1080 micromirrors (7.56 µm pixel pitch) enabled programmable wavefront encoding at λ = 532 nm, supporting 8-bit grayscale modulation.
• Controlled turbulence generation subsystem: A Y09-010 deionized-water aerosol generator produced polydisperse fog particles (mean diameter = 2.5 ± 0.3 µm) at 0.95 m³·min⁻¹ volumetric flow. The turbulent scattering medium (ε = 0.35 turbulence intensity) was confined within a 100 cm × 80 cm × 60 cm environmental chamber, with spatiotemporal dynamics induced by a programmable 360° multiblade rotary assembly (stepper motor control, 0–300 rpm).
• Synchronized acquisition subsystem: A MER2-160-227U3M CMOS camera (Sony IMX273 global shutter sensor, 1440 × 1080 resolution, Beijing, China) captured the images. An FPGA (field-programmable gate array)-based triggering mechanism achieved ±0.5 ms temporal synchronization between DMD pattern updates (at a 20 kHz refresh rate), turbulence modulation, and camera exposure.
• Scattering domain adaptability dataset:

The MNIST (modified National Institute of Standards and Technology) handwritten digit dataset served as the target source, preprocessed geometrically as follows:

$$\mathcal{T}\left(I\right)={\mathcal{F}}_v\circ {\mathcal{R}}_{-{90}^{\circ }}\left(I\right),\forall I\in {\mathbb{R}}^{64\times 64}$$

(10)

where ${\mathcal{R}}_{-{90}^{\circ }}$ denotes a 90° counterclockwise rotation, and ${\mathcal{F}}_v$ represents vertical flipping. Data acquisition was performed in two distinct modes: a scattering-free reference mode that captures ground-truth images $\left\{G_t\right\}$ under controlled chamber humidity conditions below 5%, establishing baseline measurements without atmospheric interference. Synchronously, a dynamic scattering mode was employed to record the speckle patterns $\left\{G_s\right\}$ during active water mist dispersion, simulating realistic light-scattering environments. A hardware-triggered synchronization mechanism ensured temporal alignment, yielding 7000 spatiotemporally registered image pairs (5600 for training and 1400 for testing). Representative samples are shown in Figure 5. The visual variation in speckle clarity across and within the figures is an inherent characteristic of the dynamic scattering medium. It arises from temporal and spatial fluctuations in mist density under constant generating conditions, rather than from a change in the experimental setup. Our method is designed to be robust across this entire range of random variations.

2.4.2. Training DynaFlowNet via Flow Matching with Time-Conditioned Vector Fields

The flow generative module constructs a deterministic generative trajectory using ODEs. The state evolution is defined as follows:

$${\mathbf{z}}_{t+\mathsf{\Delta }t}={\mathbf{z}}_t+{\mathbf{v}}_{\theta }({\mathbf{z}}_t\mid \mathbf{y},t)\mathsf{\Delta }t$$

(11)

where the initial state ${\mathbf{z}}_0=\mathbf{y}$ is the input speckle image and ${\mathbf{v}}_{\theta }$ denotes the velocity field predicted by DynaFlowNet. A deterministic trajectory is generated via Euler’s method with a fixed step size $\mathsf{\Delta }t$, converging to the target image ${\mathbf{z}}_1= \mathbf{x}$ after $T$ iterative updates. This deterministic process eliminates stochastic sampling, significantly enhancing the inference efficiency.

DynaFlowNet training integrates flow matching theory with a time-conditioning mechanism, optimizing model parameters by minimizing the Wasserstein-2 distance between the target and predicted vector fields in Algorithm 1. For paired speckle-target image data $\left(\mathbf{y},\mathbf{x}\right)$ and a uniformly sampled time step $t\sim U\left[0,\left.1\right]\right.$, the target vector field ${\mathbf{u}}_t\left(\mathbf{x}\mid \mathbf{y}\right)$ is computed using Equation (5) as the supervisory signal. The time encoding module (Equation (9)) maps t to a high-dimensional embedding $\varphi \left(t\right)$, which, when combined with the speckle image $\mathbf{y}$ is processed through a multiscale encoder–decoder network comprising TCResAttnBlocks to predict the vector field ${\mathbf{v}}_{\theta }({\mathbf{z}}_t\mid \mathbf{y},t)$. Parameter optimization minimizes the variational upper bound of the Wasserstein-2 distance (Equation (8)):

$$\mathcal{L}\left(\theta \right)={\mathbb{E}}_{t,\mathbf{x},\mathbf{y}}\left[{\parallel {\mathbf{v}}_{\theta }({\mathbf{z}}_t\mid \mathbf{y},t)-{\mathbf{u}}_t\left(\mathbf{x}\mid \mathbf{y}\right)\parallel }_2^2\right]$$

(12)

where ${\mathbf{z}}_t=t\mathbf{x}+(1-t)\mathbf{y}$ denotes samples from the bridging distribution. Optimization employs the AdamW optimizer with an initial learning rate of 1 × 10⁻⁴ and a weight decay coefficient λ = 0.01 to enhance generalization. The learning rate follows a piecewise decay schedule, reducing by a factor of 0.9 every 25 training epochs to balance the convergence speed and steady-state accuracy.

Algorithm 1: DynaFlowNet Training

1: repeat 2:  Sample data pair $\left(\mathbf{y},{\mathbf{x}}_0\right)~p_{data}$ 3:  Sample time $\mathrm{t} ~ U(0,T)$ 4:  Compute latent state: ${\mathbf{z}}_t=\left(1-t\right)\mathbf{y}+t{\mathbf{x}}_0$ 5:  Generate time embedding: $\varphi \left(t\right)=\mathrm{M}\mathrm{L}\mathrm{P}\left({⨁}_{j=0}^{d/2-1}\left[\sin \left({10}^{4j/d}t\right),cos\left({10}^{4j/d}t\right)\right]\right)$ 6:  Predict vector field: ${\widehat{\mathbf{v}}}_{\theta }={\mathbf{v}}_{\theta }({\mathbf{z}}_t,\varphi (t),\mathbf{y}; \theta )$ 7:  Compute target flow: ${\mathbf{u}}_{\mathbf{t}}={\displaystyle \frac{{\mathbf{x}}_0-\mathbf{y}}{T}}$ 8:  Calculate loss: $\mathcal{L}={\displaystyle \frac{1}{t(1-t)+\epsilon }}{‖{\widehat{\mathbf{v}}}_{\theta }-{\mathbf{u}}_t‖}_2^2$ 9:  Compute gradient: ${\nabla }_{\theta }\mathcal{L}={\nabla }_{\theta }\left[{\displaystyle \frac{1}{t(1-t)+\epsilon }}{‖{\mathbf{v}}_{\theta }({\mathbf{z}}_t,\varphi (t),\mathbf{y}; \theta )-{\mathbf{u}}_{\mathrm{t}}‖}_2^2\right]$ 10:   Update parameters: $\theta \leftarrow \theta -\eta \left({\nabla }_{\theta }\mathcal{L}+\lambda \theta \right)$ 11: until convergence

The model implements a base feature dimension of 64 channels with a fixed batch size of 16, completing optimization within 50 epochs. As shown in Figure 6, the loss convergence curve exhibits a distinct two-phase pattern: an initial rapid decline phase corresponding to a coarse feature space alignment, followed by a gradual refinement phase optimizing the flow-field details. All experiments were conducted on a single NVIDIA (Santa Clara, CA, USA) GeForce RTX 4090 graphics processing unit, with the peak memory consumption constrained to below 4000 megabytes.

The inference follows the deterministic sampling procedure in Algorithm 2, initializing from the speckle image $\mathbf{y}$ and iteratively updating the state through the learned velocity field. This process efficiently reconstructs the target image, $\widehat{f}={\mathit{z}}_K$, after $K$ integration steps.

Algorithm 2: DynaFlowNet Sampling

1: Initialize state ${\mathbf{z}}_0=\mathbf{y}$ (speckle input) 2: Set step size and total steps $∆t=0.1,K=10$ 3: For $k=0$ to $K-1$ do 4: $t_k=k·∆t$ 5: Generate embedding $\varphi \left(t_k\right)=\mathrm{M}\mathrm{L}\mathrm{P}\left({⨁}_{j=0}^{d/2-1}\left[\sin \left({10}^{4j/d}{t}_k\right),cos\left({10}^{4j/d}{t}_k\right)\right]\right)$ 6: Predict flow field ${\mathbf{v}}_{\mathit{k}}={\mathbf{v}}_{\theta }({\mathbf{z}}_k,\varphi (t_k),\mathbf{y}; \theta )$ 7: Update state ${\mathbf{z}}_{k+1}={\mathbf{z}}_k+{\mathbf{v}}_{\mathit{k}}∆t$ 8: end for 9: Output reconstruction $\widehat{f}={\mathbf{z}}_K$

2.4.3. Ablation Study Design

To rigorously evaluate the contribution of each core component (time awareness, condition modulation, and attention mechanism) in TCResAttnBlock, we designed four progressively enhanced ablation variants (Ablation-A to Ablation-D) and compared them with the full DynaFlowNet. All models were identically configured and trained on the same dynamic scattering dataset using an encoder–decoder architecture with 64 base channels, the Adam optimizer (learning rate = 1 × 10⁻⁴), and 17,600 training iterations. As summarized in

Table 1. Ablation study of the TCResAttnBlock components on the dynamic scattering dataset. (Note: The symbol ✓ denotes that the mechanism is included, × denotes it is excluded.)

Model Name	Core Structure	Time Embedding Mechanism	Attention Mechanism	Condition Modulation Mechanism
Ablation-A (Baseline)	Residual Convolution with Convolution (Conv) + Group Normalization (GN) + Sigmoid Linear Unit (SiLU)	Basic (Linear Projection)	×	None
Ablation-B	A + CBAM Attention Module	Basic (Linear Projection)	✓	None
Ablation-C	B + Enhanced Time Modulation	Spectro-DynaTime Embedding	✓	None
Ablation-D	C + Deep Condition Modulation	Spectro-DynaTime Embedding	✓	Deep Feature Fusion
DynaFlowNet (Full)	Full TCResAttnBlock	Spectro-DynaTime Embedding	✓	Deep Feature Fusion

, Ablation-A constitutes the baseline with residual convolutions only; Ablation-B incorporates the CBAM attention module to quantify channel-spatial attention; Ablation-C further replaces standard time embedding with the proposed Spectro-DynaTime embedding; Ablation-D introduces deep condition modulation via feature fusion; and DynaFlowNet (Full) integrates all components within the optimized TCResAttnBlock architecture.

2.4.4. Evaluating Generalization to Unseen Binary Geometries

To assess the generalization capability of DynaFlowNet to novel structural forms, we conducted a cross-domain validation. Specifically, we tested a model originally trained exclusively on MNIST handwritten digits to reconstruct six distinct geometric shapes that were absent from the training data by employing a geometric transfer paradigm. The synthetic dataset comprised six categories: cloud-like patterns, multiplication sign patterns (×), checkmark patterns (√), U-shaped curves, four-pointed star patterns, and triangular patterns. Each category contained 100 unique 64 × 64-pixel instances, establishing a visual domain structurally dissimilar from the MNIST handwritten digit distribution.

The measurement protocol generated high-contrast shapes and applied identical geometric transformations (Equation (10)). Critically, the physical experimental setup remained identical to that used for acquiring the MNIST training set (Section 2.4.1): the dynamic water mist medium was generated using the same aerosol generator at the same flow rate (0.95 m³·min⁻¹) and the same turbulence intensity (ε = 0.35). The speckle patterns were captured using the same hardware parameters. The perceived variations in speckle clarity across the resulting dataset are an inherent feature of the dynamic medium’s spatiotemporal fluctuations, not an indicator of inconsistent experimental conditions. This produced 600 spatiotemporally registered pairs (100 pairs per category), which were excluded from the training data. The quantitative evaluation employed three complementary approaches: cross-domain metrics (PSNR, structural similarity index (SSIM), and Pearson correlation) versus state-of-the-art baselines (Pix2Pix, BBDM, and CycleGAN), category-specific performance breakdown, and temporal stability assessment via the coefficient of variation (CV) across 50 consecutive frames. All models were evaluated on identical hardware (NVIDIA RTX 4090) with consistent preprocessing, measuring the inference speed (FPS) while excluding the initialization overhead.

3. Results and Analysis

3.1. Comparative Performance Analysis of DynaFlowNet

3.1.1. Quantitative Imaging Performance Metrics

DynaFlowNet demonstrates transformative computational efficiency in dynamic scattering imaging, thereby establishing a new paradigm for real-time optical reconstruction. As quantitatively validated in

Table 2. Computational efficiency comparison on dynamic scattering imaging (Test platform: NVIDIA RTX 4090).

Model	Training Time (50 Epochs)	GPU Memory (MB)	Latency per Frame (ms)	FPS	Parameters (Million)
CycleGAN	3.97 h	19590	53.9 ms	18.55	28.3
Pix2Pix	0.18 h	4944	17.8 ms	56.18	57.2
BBDM	0.90 h	17978	867 ms	1.15	237.1
DynaFlowNet	0.15 h	3974	7.4 ms	134.77	19.4

, our framework achieved an inference speed of 134.77 frames per second (FPS), representing a 117-fold acceleration compared to conventional diffusion models (BBDM: 1.15 FPS). This dramatic improvement enables practical deployment in time-critical applications where traditional methods fail to meet real-time constraints. The training convergence rate is equally remarkable, with DynaFlowNet completing 50 epochs in just 0.15 h, which is 6 times faster than conventional generative approaches, without compromising model quality. Furthermore, the architecture exhibited exceptional resource efficiency, requiring only 3974 MB of GPU memory (a 79.7% reduction compared with CycleGAN), while maintaining 19.4 million parameters (12.2 times more parameter-efficient than BBDM’s 237.1 million parameters). This computational advantage fundamentally stems from our deterministic ODE-based sampling mechanism (Section 2.2.2), which replaces stochastic iterative processes with a fixed-step Euler solver requiring ≤10 function evaluations for convergence. The synergistic architectural design integrating TCResAttnBlocks (Section 2.3.2) with multiscale feature fusion (Section 2.3.3) enables real-time reconstruction of speckle with an ultra-low latency of 7.4 ms per frame (134.77 FPS), rendering it particularly suitable for dynamic scattering environments where both speed and fidelity are critical. The parameter efficiency of DynaFlowNet (19.4 million parameters) further demonstrates its architectural superiority, achieving an optimal balance between model complexity and performance.

3.1.2. Qualitative Reconstruction Quality Assessment

To rigorously evaluate the performance of DynaFlowNet in dynamic scattering imaging, we conducted a comprehensive comparative analysis against state-of-the-art image translation models, including Pix2Pix, BBDM, and CycleGAN. The evaluation of 1407 test image pairs utilized three quantitative metrics: the peak signal-to-noise ratio (PSNR), structural similarity index (SSIM), and Pearson correlation coefficient (PCC). Statistical significance was confirmed through two-sample t-tests versus the speckle-based baseline method (†: p < 0.05). As illustrated in Figure 7 and summarized in

Table 3. Comparative quantitative analysis of reconstruction quality across methods for dynamic scattering imaging.

	Model	Mean	Std	Median	Min	Max	95%CI	CV (%)
PSNR (dB)	Speckle	15.53	3.79	15.09	11.16	31.58	±0.20	24.4
	Pix2Pix†	27.01	3.05	27.56	17.93	34.52	±0.16	11.3
	BBDM†	28.07	3.75	28.71	17.35	36.20	±0.20	13.4
	CycleGAN†	24.34	3.24	24.62	16.40	33.31	±0.17	13.3
	DynaFlowNet†	28.46	3.95	28.88	18.72	38.04	±0.21	13.9
SSIM	Speckle	0.0725	0.0604	0.0560	0.0048	0.6430	±0.0032	83.3
	Pix2Pix†	0.8987	0.0232	0.9059	0.7946	0.9350	±0.0012	2.6
	BBDM†	0.8964	0.0551	0.9088	0.6435	0.9811	±0.0029	6.1
	CycleGAN†	0.3510	0.1976	0.2708	0.1155	0.8934	±0.0103	56.3
	DynaFlowNet†	0.9112	0.0540	0.9263	0.6622	0.9843	±0.0028	5.9
PCC	Speckle	0.3337	0.2507	0.2581	−0.0386	0.9762	±0.0131	75.1
	Pix2Pix†	0.8578	0.1359	0.9099	0.0997	0.9782	±0.0071	15.8
	BBDM†	0.8651	0.1620	0.9333	0.0119	0.9882	±0.0085	18.7
	CycleGAN†	0.7257	0.2580	0.8294	−0.0625	0.9830	±0.0135	35.6
	DynaFlowNet†	0.8832	0.1316	0.9361	0.1932	0.9907	±0.0069	14.9

, DynaFlowNet demonstrates a statistically superior performance across all metrics.

For PSNR, as detailed in Figure 7a and Table 3, DynaFlowNet achieves the highest mean value of 28.46 dB, significantly outperforming the speckle baseline (15.53 dB, p < 0.05) and all competing models. Notably, it exhibits high consistency, with a median PSNR of 28.88 dB and a narrow interquartile range (IQR), as observed through blockwise trend analysis. As visualized in Figure 7b, this confirms stable performance across data partitions.

Regarding SSIM, as displayed in Figure 7c and Table 3, DynaFlowNet attains a mean score of 0.9112, representing a 1.65% improvement over BBDM (0.8964) and a 1.39% improvement over Pix2Pix (0.8987). As illustrated in Figure 7d, its minimal deviation from the image mean (SD = 0.28) and low coefficient of variation (CV = 5.9%) highlight its exceptional reconstruction stability.

In the PCC evaluation, presented in Figure 7e and Table 3, DynaFlowNet achieves the highest mean (0.8832) and median (0.9361) values, with 95% confidence intervals (CI) ranging from 0.8763 to 0.8901. The Blockwise analysis, depicted in Figure 7f, revealed consistent performance across the dataset, as evidenced by the smallest IQR and the tightest 95% CI envelope. The lowest CV (14.9%) further demonstrates unparalleled robustness.

Collectively, DynaFlowNet delivers statistically significant improvements in mean PSNR (Δ + 12.93 dB vs. speckle), SSIM (Δ + 0.8387), and PCC (Δ + 0.5495), while exhibiting superior statistical consistency through the lowest CV values and most compact performance distributions. These results establish DynaFlowNet as a highly reliable framework for dynamic scattering imaging, providing exceptional quantitative and practical robustness for real-world applications.

Figure 8 provides a qualitative assessment of the MNIST digit reconstruction from dynamic scattering patterns, comparing DynaFlowNet with competing methods (BBDM, Pix2Pix, and CycleGAN). Six representative test cases display ground-truth images, corresponding speckle inputs, and reconstructions from the four models. DynaFlowNet outperforms its competitors in critical metrics, preserving high-frequency structural details (e.g., diagonal strokes in the digit “7”), maintaining structural continuity (e.g., semicircular topology in “3”), and effectively suppressing speckle-induced artifacts. BBDM exhibits significant over-smoothing, resulting in the loss of critical texture information, whereas Pix2Pix and CycleGAN demonstrate pronounced edge blurring and structural discontinuities at sharp transitions. These results quantitatively validate the balanced capacity of DynaFlowNet for simultaneously denoising and preserving details across diverse morphological patterns. The deterministic ODE framework of the method exhibits exceptional aptitude for handling nonlinear scattering dynamics, as evidenced by its robust performance on both high-contrast features and low-texture targets, where alternative approaches tend to degrade.

3.2. Ablation Study on Core Components

An ablation study was conducted to validate the contribution of each core component in DynaFlowNet, with quantitative results summarized in

Table 4. Impact of attention, time embedding, and conditional modulation on speckle restoration performance.

Model	PSNR (dB)	ΔPSNR	SSIM	PCC
Ablation-A (Baseline)	25.84	-	0.5970	0.8046
Ablation-B (w/Attention)	26.29	+0.45 dB	0.7855	0.8127
Ablation-C (w/Attention + Time)	27.86	+2.20 dB	0.9078	0.8785
Ablation-D (w/Attention + Time + Condition)	28.16	+2.32 dB	0.9076	0.8677
DynaFlowNet (Full)	28.46	+2.62 dB	0.9112	0.8832

.

The baseline model (Ablation-A), devoid of the proposed enhancements, served as the reference point. The introduction of attention mechanisms (CBAM + SE) in Ablation-B yielded a noticeable improvement, particularly in structural similarity. This indicates that the attention modules are effective in enhancing feature discrimination and preserving critical structural details from the speckle patterns.

The most significant performance leap occurred with the incorporation of the sophisticated time embedding mechanism in Ablation-C, which drastically improved all metrics. This demonstrates that modeling temporal dynamics is crucial for reconciling the temporal inconsistencies inherent in dynamic scattering media.

Further integrating conditional modulation in Ablation-D provided an additional gain in reconstruction fidelity (PSNR), confirming its role in adapting the restoration process to the specific characteristics of the input speckle pattern.

Finally, the full model (DynaFlowNet), synergistically combining all components, achieved the highest performance. The results unequivocally validate the importance of each constituent: attention mechanisms capture essential spatial features, time embedding resolves temporal fluctuations, and conditional modulation enables input-specific refinement. Their combined effect establishes a new state-of-the-art for the task.

3.3. Generalization to Unseen Binary Geometries

DynaFlowNet demonstrated robust generalization capabilities on geometrically novel binary targets, achieving a mean PSNR of 27.41 dB, an SSIM of 0.7351, and a Pearson coefficient of 0.8607, as detailed in

Table 5. Quantitative metrics for generalization to unseen binary geometries.

Model	PSNR (dB)	Domain Shift ΔPSNR	SSIM	PCC
Pix2Pix	24.87	−2.14 dB	0.4174	0.8036
BBDM	24.37	−3.70 dB	0.2873	0.7755
CycleGAN	18.98	−5.36 dB	0.7755	0.5828
DynaFlowNet (Full)	27.41	−1.05 dB	0.7351	0.8607

(summarizing quantitative metrics across shapes). The domain shift degradation (a PSNR drop of 1.05 dB) was substantially lower than that of comparative methods (Pix2Pix: 4.21 dB, BBDM: 3.70 dB, CycleGAN: 5.36 dB). Figure 9 illustrates DynaFlowNet’s superior reconstruction performance across diverse binary geometric structures (including cross-shaped structures, triangular contours, U-shaped curves, four-pointed stars, irregular cloud-like shapes, and checkmarks) compared to benchmark methods. Despite the severe speckle corruption observed in Figure 9b, DynaFlowNet achieved optimal topological accuracy and edge sharpness. It effectively preserved acute angles (e.g., in cross-structures and triangles) and fine structural details (e.g., in cloud-like shapes). In contrast, CycleGAN yielded blurred and fragmented outputs and failed to recover the closed checkmark contours. Meanwhile, BBDM and Pix2Pix introduced geometric distortions, such as deformed U-curves and stars. These visual results, consistent with the quantitative metrics in Table 5, highlight DynaFlowNet’s robustness to domain shifts. This robust generalization stems from three key architectural advantages: (1) a physics-informed design implemented through conditional flow matching that explicitly embeds scattering dynamics; (2) multiscale attention mechanisms within the TCResAttnBlock, enabling the capture of both global and local features; and (3) deterministic ODE integration, facilitating stable gradient propagation during the inversion process. The model’s capability to reconstruct complex unseen shapes strongly suggests that it has learned fundamental scattering principles, rather than merely memorizing training patterns. This establishes DynaFlowNet as a versatile framework for real-world applications requiring adaptation to unknown targets.

Despite the promising results, this study has several limitations. The sample size for evaluating geometric generalization was limited, potentially reducing the statistical power of the comparative analysis. Additionally, the selected benchmarks may introduce biases, as they were derived from specific databases with inherent characteristics that might not fully represent real-world diversity. Furthermore, access to certain datasets was restricted due to proprietary or privacy concerns, which could limit the comprehensiveness of the evaluation. Future work should address these limitations by expanding dataset diversity and size and incorporating state-of-the-art or task-specific benchmarking frameworks to ensure more robust validation of DynaFlowNet’s capabilities across broader scenarios.

4. Discussion

DynaFlowNet establishes a new paradigm for real-time, high-fidelity computational imaging through dynamic scattering media by leveraging conditional flow matching. This approach fundamentally resolves the accuracy-efficiency trade-off inherent in previous methods. It demonstrably surpasses established adversarial frameworks: Pix2Pix and CycleGAN [26]. These GAN-based image-to-image translation models exhibit well-documented instability during training and a susceptibility to mode collapse, resulting in inconsistent outputs. DynaFlowNet provides deterministic reconstructions with superior stability. Furthermore, it achieves a remarkable 117-fold speed advantage over the diffusion model BBDM (Brownian Bridge Diffusion Model) [30], the current state-of-the-art for scattering imaging. BBDM requires hundreds of iterative sampling steps, incurring high computational cost. DynaFlowNet maintains comparable or superior reconstruction quality while achieving this speedup. This efficiency stems from its deterministic ODE integration, requiring only 10 function evaluations versus BBDM’s iterative process, exploiting the principle of flow path straightness for real-time performance [36].

Beyond adapting flow-matching foundations to scattering inversion, DynaFlowNet introduces critical innovations. The spectro-dynamic time embedding (SD-embedding) employs multiscale sinusoidal-cosine encoding to preserve spectral continuity across time, ensuring stable gradient propagation. The novel TCResAttnBlock architecture synergistically integrates dual-path attention, spectro-dynamic time conditioning, and deep conditional feature fusion, enabling explicit modeling of spatiotemporal scattering physics. Ablation studies quantitatively confirm these elements are indispensable, yielding a 2.62 dB PSNR improvement over the baseline. DynaFlowNet exhibits exceptional generalization to unseen geometries, showing minimal degradation (1.05 dB PSNR loss) compared to significant drops in benchmarks, as detailed in Table 5. This robust out-of-distribution performance, including the accurate reconstruction of complex features such as acute angles and fine details, as depicted in Figure 9, indicates the learning of fundamental light scattering principles, rather than mere pattern memorization. This capability stems from the physics-informed framework, where conditional flow matching explicitly embeds scattering dynamics, and the network architecture reflects the continuous and invertible nature of light transport.

Current validation primarily involves controlled water mist; performance in complex biological tissues with heterogeneous scattering requires further characterization, as does handling natural images with rich textures. Despite these limitations, DynaFlowNet’s conditional flow matching offers a general, mathematically rigorous framework for solving high-dimensional inverse problems with temporal dynamics. Its deterministic ODE integration provides a compelling real-time alternative to stochastic sampling.

5. Conclusions

DynaFlowNet establishes a new paradigm for imaging through dynamic scattering media by leveraging conditional flow matching to achieve real-time performance with high fidelity. Our framework overcomes the longstanding accuracy-efficiency trade-off through deterministic ODE integration, eliminating the need for iterative sampling while maintaining state-of-the-art reconstruction quality. The novel TCResAttnBlock architecture effectively captures spatiotemporal scattering dynamics, enabling exceptional generalization with only 1.05 dB PSNR degradation across unseen geometries. This work bridges computational optics and generative modeling, providing a theoretically grounded solution to a fundamental challenge in photonics. The framework’s speed and robustness open immediate applications in biomedical imaging, remote sensing, and underwater exploration. Future efforts will focus on unsupervised training approaches and hardware-aware optimization for edge deployment in resource-constrained environments.