Analysis and Optimization of Two-Dimensional Photonic Crystal Microcavity Structures for Gas Sensing
Abstract
1. Introduction
2. Research Methods and Structural Design
2.1. Research Methods
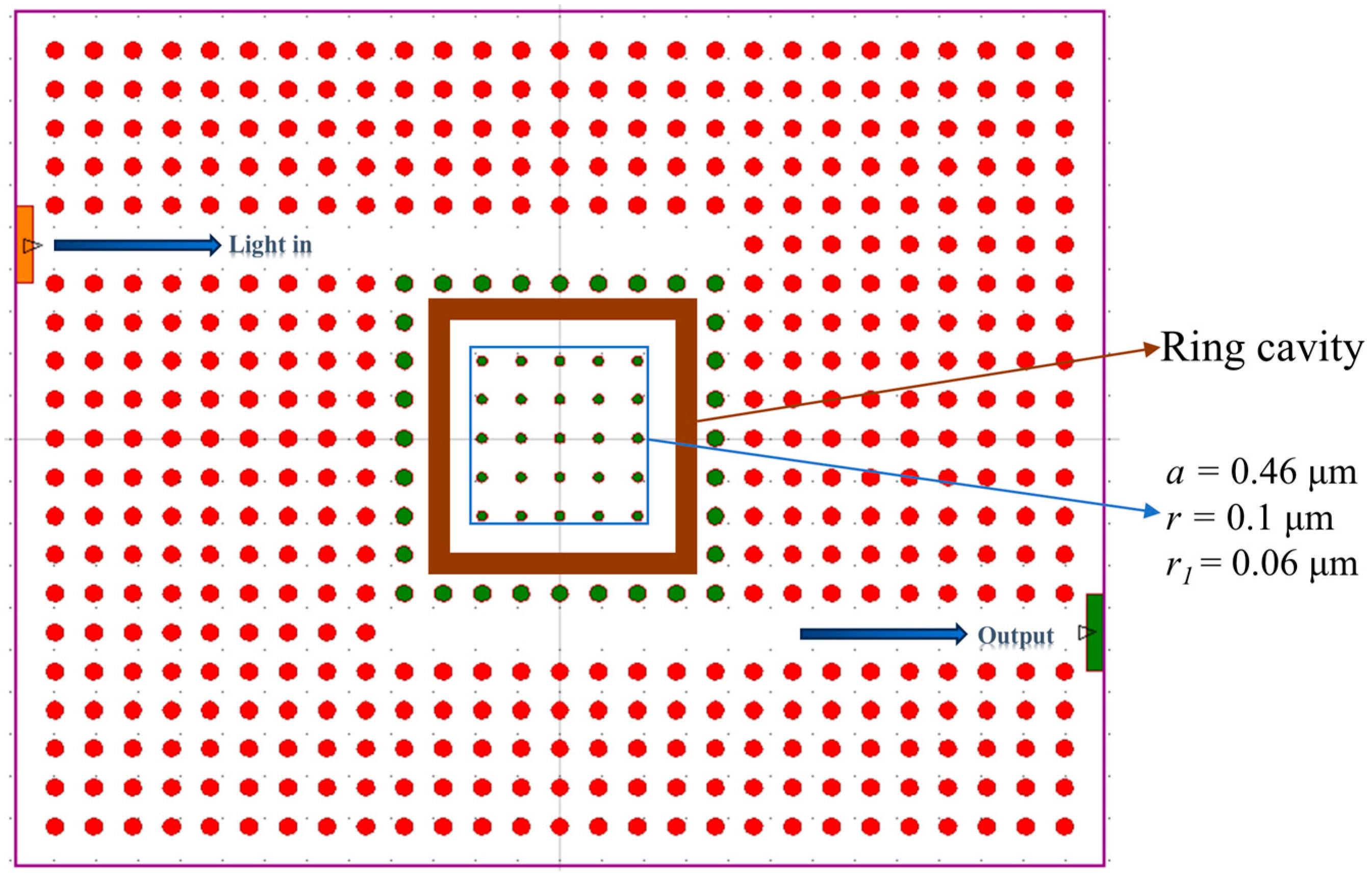
2.2. Structural Design of PhC Sensors
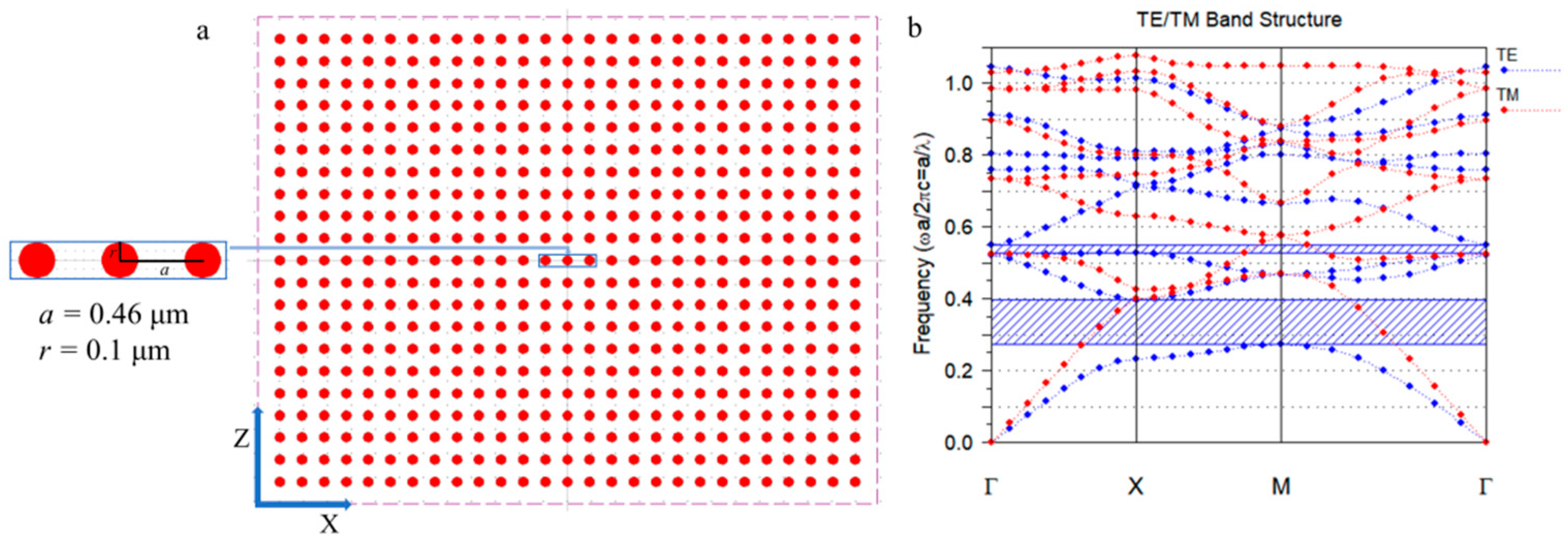
2.2.1. Simulation and Analysis of Photonic Crystal Bandgap Using Rsoft
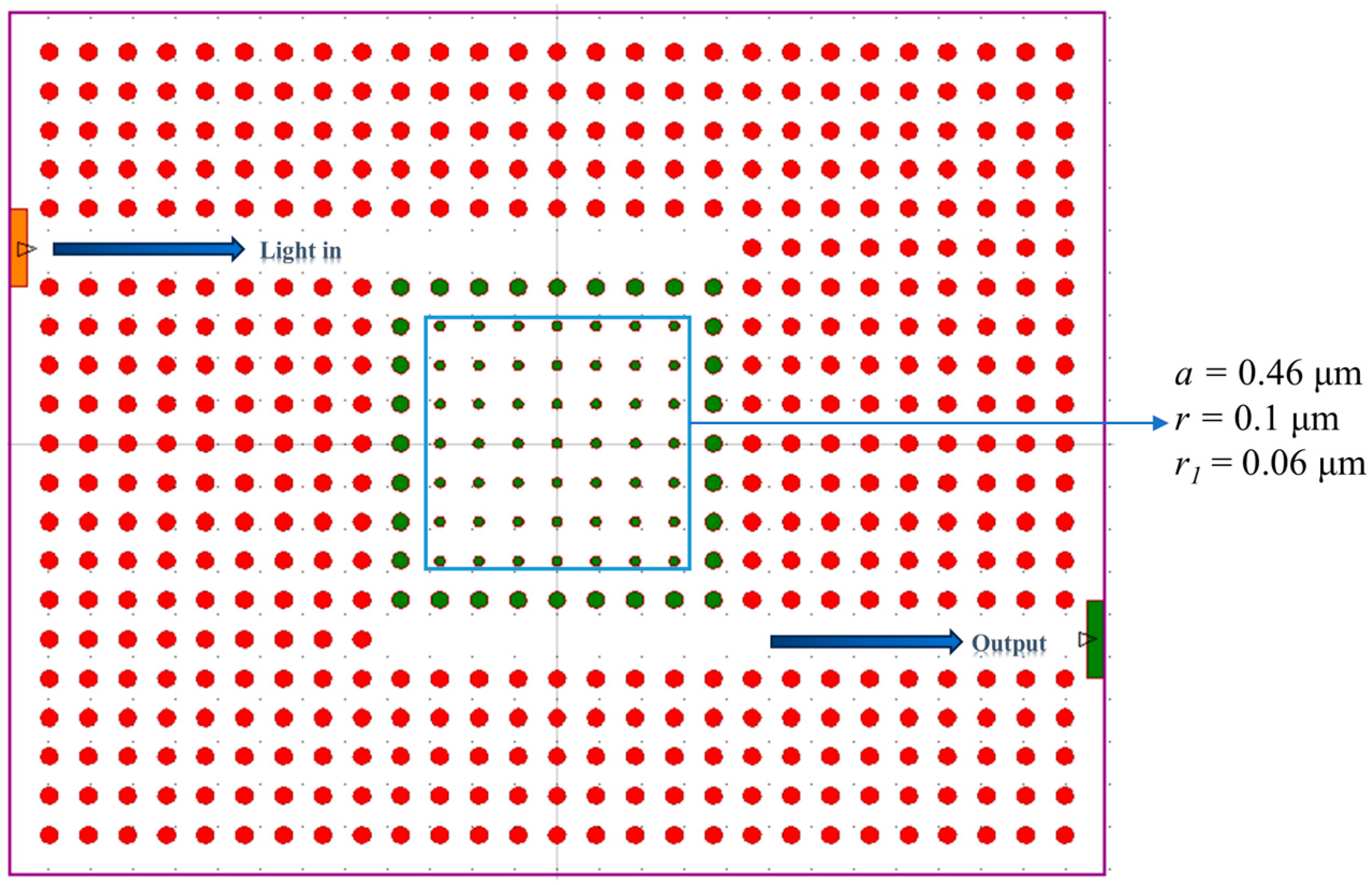
2.2.2. Introduction of Line and Point Defects for Photonic Crystal Microcavity
3. Results and Discussion
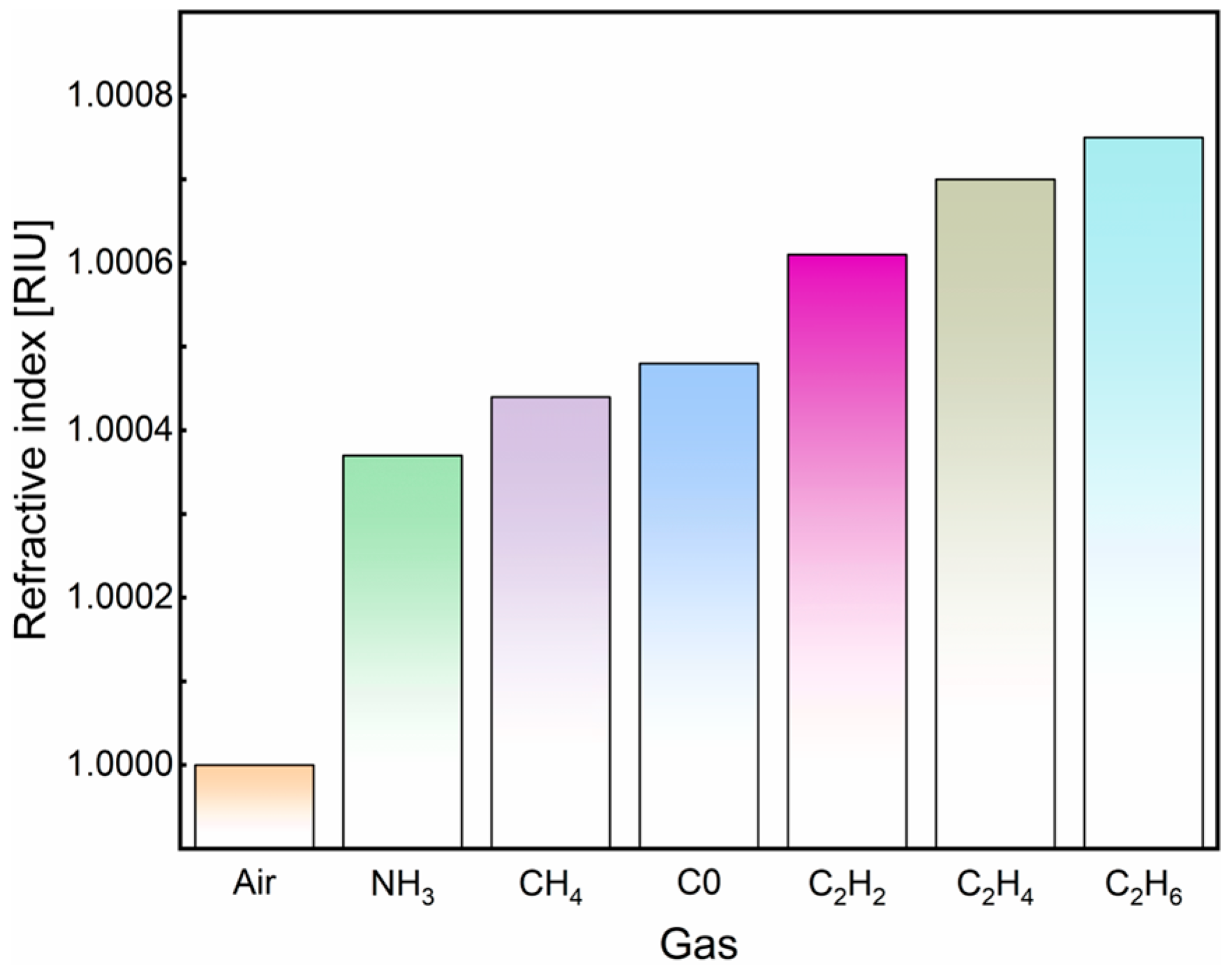
3.1. Properties of NH3, CH4, CO, C2H2, C2H4, and C2H6
3.2. Gas Detection and Sensor Performance Analysis
3.3. Performance Analysis of the Sensor with Ring Cavities
3.4. Performance Comparison of Two Sensor Designs
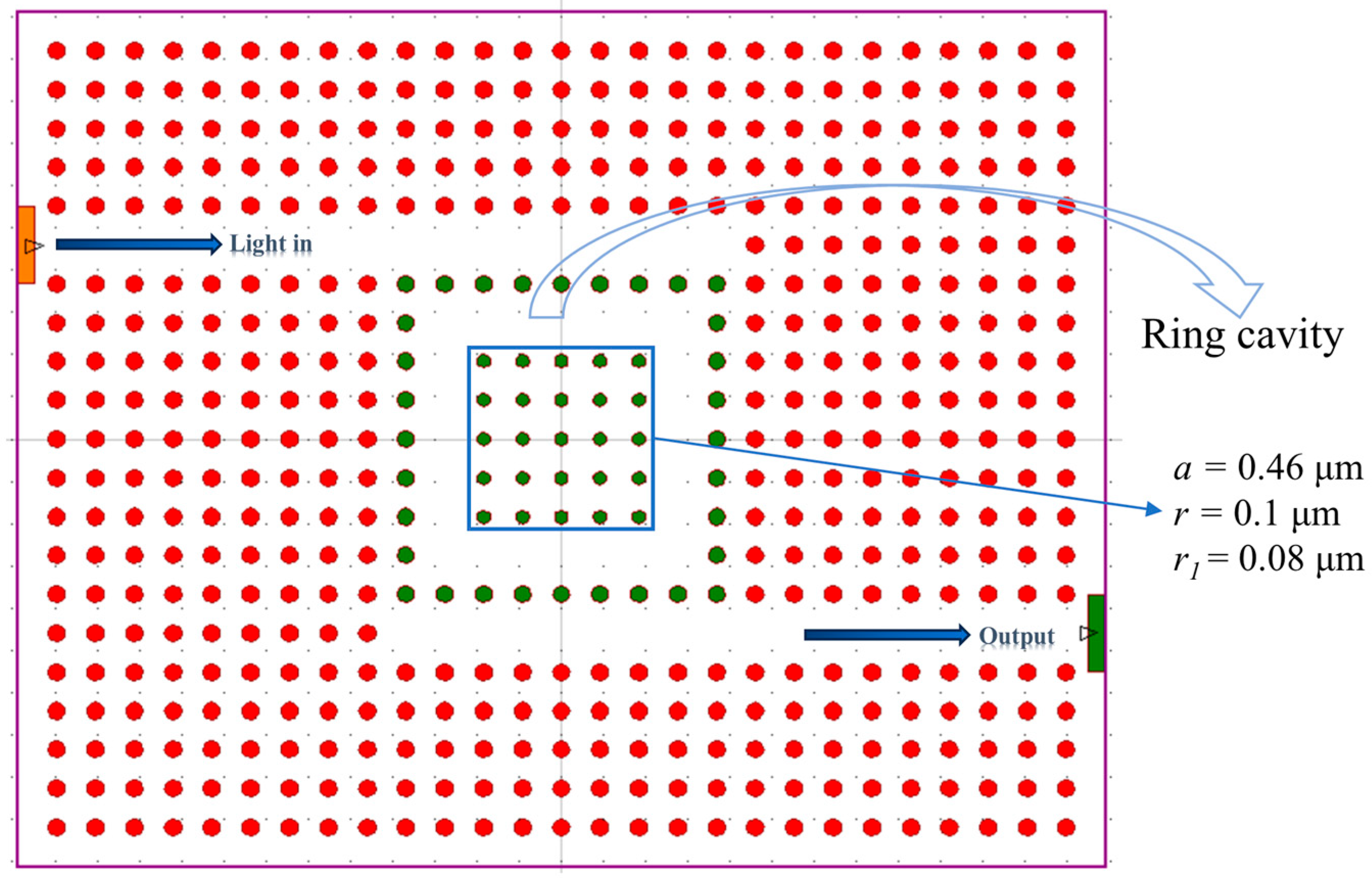
3.5. Extended Optimization and Performance Analysis of the Sensor
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Fitch, J.P.; Raber, E.; Imbro, D.R. Technology Challenges in Responding to Biological or Chemical Attacks in the Civilian Sector. Science 2003, 302, 1350–1354. [Google Scholar] [CrossRef] [PubMed]
- Lelieveld, J.; Lechtenböhmer, S.; Assonov, S.S.; Brenninkmeijer, C.A.M.; Dienst, C.; Fischedick, M.; Hanke, T. Low methane leakage from gas pipelines. Nature 2005, 434, 841–842. [Google Scholar] [CrossRef] [PubMed]
- Amann, A.; Miekisch, W.; Schubert, J.; Buszewski, B.; Ligor, T.; Jezierski, T.; Pleil, J.; Risby, T. Analysis of exhaled breath for disease detection. Annu. Rev. Anal. Chem. 2014, 7, 455–482. [Google Scholar] [CrossRef]
- Potyrailo, R.A.; Mirsky, V.M. Combinatorial and high-throughput development of sensing materials: The first 10 years. Chem. Rev. 2008, 108, 770–813. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, Y.; Liu, J.; Guo, P.; Cai, Z.; Wang, J.-J. Polymer-infiltrated SiO2 inverse opal photonic crystals for colorimetrically selective detection of xylene vapors. Sens. Actuators B-Chem. 2019, 291, 67–73. [Google Scholar] [CrossRef]
- Cai, Z.; Liu, Y.J.; Lu, X.; Teng, J. In Situ “Doping” Inverse Silica Opals with Size-Controllable Gold Nanoparticles for Refractive Index Sensing. J. Phys. Chem. C 2013, 117, 9440–9445. [Google Scholar] [CrossRef]
- John, S. Strong Localization of Photons in Certain Disordered Dielectric Superlattices. Phys. Rev. Lett. 1987, 58, 2486–2489. [Google Scholar] [CrossRef] [PubMed]
- Yablonovitch, E. Inhibited Spontaneous Emission in Solid-State Physics and Electronics. Phys. Rev. Lett. 1987, 58, 2059–2062. [Google Scholar] [CrossRef]
- Butt, M.A.; Khonina, S.N.; Kazanskiy, N.L. Recent advances in photonic crystal optical devices: A review. Opt. Laser Technol. 2021, 142, 107265. [Google Scholar] [CrossRef]
- Cai, Z.; Li, Z.; Ravaine, S.; He, M.; Song, Y.; Yin, Y.; Zheng, H.; Teng, J.; Zhang, A. From colloidal particles to photonic crystals: Advances in self-assembly and their emerging applications. Chem. Soc. Rev. 2021, 50, 5898–5951. [Google Scholar] [CrossRef]
- Quan, J.; Song, Y.; Li, H.; Zhao, F.; Zhou, L.; Cai, Z.; Wan, Y. Effects of Building Blocks and Defects on the Performance of Two-Dimensional Photonic Crystal Sensors for Black Liquor Detection. J. Anal. Test. 2025, 9, 50–60. [Google Scholar] [CrossRef]
- Meade, R.D.; Rappe, A.; Brommer, K.; Joannopoulos, J.; Alerhand, O. Accurate theoretical analysis of photonic band-gap materials. Phys. Rev. B 1993, 48, 8434. [Google Scholar] [CrossRef]
- Keller, O. On the theory of spatial localization of photons. Phys. Rep. 2005, 411, 1–232. [Google Scholar] [CrossRef]
- Fu, H.-w.; Zhao, H.; Qiao, X.-g.; Li, Y.; Zhao, D.-z.; Yong, Z. Study on a novel photonic crystal temperature sensor. Optoelectron. Lett. 2011, 7, 419–422. [Google Scholar] [CrossRef]
- Zegadi, R.; Ziet, L.; Zegadi, A. Design of High Sensitive Temperature Sensor Based on Two-Dimensional Photonic Crystal. Silicon 2020, 12, 2133–2139. [Google Scholar] [CrossRef]
- Aly, A.H.; Mohamed, B.A.; Al-Dossari, M.; Mohamed, D. A temperature sensor based on Si/PS/SiO2 photonic crystals. Sci. Rep. 2023, 13, 21560. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, D.; Tian, H.; Ji, Y. Photonic crystal stress sensor with high sensitivity in double directions based on shoulder-coupled aslant nanocavity. Sens. Actuators A-Phys. 2013, 193, 149–154. [Google Scholar] [CrossRef]
- Vijaya Shanthi, K.; Robinson, S. Two-dimensional photonic crystal based sensor for pressure sensing. Photonics Sens. 2014, 4, 248–253. [Google Scholar] [CrossRef]
- Arunkumar, R.; Suganya, T.; Robinson, S. Design and analysis of photonic crystal elliptical ring resonator based pressure sensor. Int. J. Photonics Opt. Technol. 2017, 3, 30–33. [Google Scholar]
- Kwon, S.-H.; Sünner, T.; Kamp, M.; Forchel, A. Optimization of photonic crystal cavity for chemical sensing. Opt. Express 2008, 16, 11709–11717. [Google Scholar] [CrossRef] [PubMed]
- Baker, J.E.; Sriram, R.; Miller, B.L. Two-dimensional photonic crystals for sensitive microscale chemical and biochemical sensing. Lab Chip 2015, 15, 971–990. [Google Scholar] [CrossRef]
- Cai, Z.; Smith, N.L.; Zhang, J.-T.; Asher, S.A. Two-Dimensional Photonic Crystal Chemical and Biomolecular Sensors. Anal. Chem. 2015, 87, 5013–5025. [Google Scholar] [CrossRef]
- Johnson, S.G.; Villeneuve, P.R.; Fan, S.; Joannopoulos, J.D. Linear waveguides in photonic-crystal slabs. Phys. Rev. B 2000, 62, 8212. [Google Scholar] [CrossRef]
- Jamois, C.; Wehrspohn, R.; Andreani, L.; Hermann, C.; Hess, O.; Gösele, U. Silicon-based two-dimensional photonic crystal waveguides. Photonic Nanostruct. 2003, 1, 1–13. [Google Scholar] [CrossRef]
- Zouache, T.; Hocini, A. A 2D photonic crystal indium arsenide based with dual micro-cavities coupled to a waveguide as a platform for a high sensitivity pressure sensor. Opt. Quantum Electron. 2023, 55, 238. [Google Scholar] [CrossRef]
- Sünner, T.; Stichel, T.; Kwon, S.-H.; Schlereth, T.W.; Höfling, S.; Kamp, M.; Forchel, A. Photonic crystal cavity based gas sensor. Appl. Phys. Lett. 2008, 92, 26112. [Google Scholar] [CrossRef]
- Zhang, Y.; Han, S.; Zhang, S.; Liu, P.; Shi, Y. High-Q and High-Sensitivity Photonic Crystal Cavity Sensor. IEEE Photonics J. 2015, 7, 1–6. [Google Scholar] [CrossRef]
- Fallahi, V.; Kordrostami, Z.; Hosseini, M. Sensitivity and quality factor improvement of photonic crystal sensors by geometrical optimization of waveguides and micro-ring resonators combination. Sci. Rep. 2024, 14, 2001. [Google Scholar] [CrossRef]
- Nair, R.V.; Vijaya, R. Photonic crystal sensors: An overview. Prog. Quantum Electron. 2010, 34, 89–134. [Google Scholar] [CrossRef]
- Sharma, P.; Medhekar, S. Ring resonator-based highly sensitive chemical/biochemical sensor created on holes in silicon slab 2D photonic crystal. J. Opt. 2023, 52, 2315–2322. [Google Scholar] [CrossRef]
- Painter, O.; Lee, R.K.; Scherer, A.; Yariv, A.; O’Brien, J.D.; Dapkus, P.D.; Kim, I. Two-Dimensional Photonic Band-Gap Defect Mode Laser. Science 1999, 284, 1819–1821. [Google Scholar] [CrossRef]
- Akahane, Y.; Asano, T.; Song, B.-S.; Noda, S. High-Q photonic nanocavity in a two-dimensional photonic crystal. Nature 2003, 425, 944–947. [Google Scholar] [CrossRef]
- Dorfner, D.F.; Hürlimann, T.; Zabel, T.; Frandsen, L.H.; Abstreiter, G.; Finley, J.J. Silicon photonic crystal nanostructures for refractive index sensing. Appl. Phys. Lett. 2008, 93, 181103. [Google Scholar] [CrossRef]
- Huang, L.; Tian, H.; Yang, D.; Zhou, J.; Liu, Q.; Zhang, P.; Ji, Y. Optimization of figure of merit in label-free biochemical sensors by designing a ring defect coupled resonator. Opt. Commun. 2014, 332, 42–49. [Google Scholar] [CrossRef]
- Kane, Y. Numerical solution of initial boundary value problems involving maxwell’s equations in isotropic media. IEEE Trans. Antennas Propag. 1966, 14, 302–307. [Google Scholar] [CrossRef]
- Ward, A.; Pendry, J.B. Refraction and geometry in Maxwell’s equations. J. Mod. Opt. 1996, 43, 773–793. [Google Scholar] [CrossRef]
- Bao, G.; Li, P. Maxwell’s Equations in Periodic Structures; Springer: Singapore, 2022. [Google Scholar]
- Zivanovic, S.S.; Yee, K.S.; Mei, K.K. A subgridding method for the time-domain finite-difference method to solve Maxwell’s equations. IEEE Trans. Microw. Theory Tech. 1991, 39, 471–479. [Google Scholar] [CrossRef]
- Teixeira, F.; Sarris, C.; Zhang, Y.; Na, D.-Y.; Berenger, J.-P.; Su, Y.; Okoniewski, M.; Chew, W.; Backman, V.; Simpson, J.J. Finite-difference time-domain methods. Nat. Rev. Methods Primers 2023, 3, 75. [Google Scholar] [CrossRef]
- Haar, L. Thermodynamic properties of ammonia as an ideal gas. Journal of Research of the National Bureau of Standards. Sect. A Phys. Chem. 1968, 72, 207. [Google Scholar]
- Guerra, C.; Schulman, J.H. The adsorption of CO gas by metals supported on silica. Surf. Sci. 1967, 7, 229–249. [Google Scholar] [CrossRef]
- Huang, H.; Haghighat, F.; Blondeau, P. Volatile organic compound (VOC) adsorption on material: Influence of gas phase concentration, relative humidity and VOC type. Indoor Air 2006, 16, 236–247. [Google Scholar] [CrossRef]
- Zhang, Y.-n.; Zhao, Y.; Wang, Q. Measurement of methane concentration with cryptophane E infiltrated photonic crystal microcavity. Sens. Actuators B-Chem. 2015, 209, 431–437. [Google Scholar] [CrossRef]
- Du, Z.; Mo, J.; Zhang, Y.; Li, X.; Xu, Q. Evaluation of a new passive sampler using hydrophobic zeolites as adsorbents for exposure measurement of indoor BTX. Anal. Methods 2013, 5, 3463–3472. [Google Scholar] [CrossRef]
- Pennec, Y.; Jin, Y.; Djafari-Rouhani, B. Phononic and photonic crystals for sensing applications. Adv. Appl. Mech. 2019, 52, 105–145. [Google Scholar]
- Zhang, Y.-n.; Zhao, Y.; Lv, R.-q. A review for optical sensors based on photonic crystal cavities. Sens. Actuators A-Phys. 2015, 233, 374–389. [Google Scholar] [CrossRef]
- Goyal, A.K.; Dutta, H.S.; Pal, S. Recent advances and progress in photonic crystal-based gas sensors. J. Phys. D Appl. Phys. 2017, 50, 203001. [Google Scholar] [CrossRef]
- Parandin, F.; Heidari, F.; Rahimi, Z.; Olyaee, S. Two-Dimensional photonic crystal Biosensors: A review. Opt. Laser Technol. 2021, 144, 107397. [Google Scholar] [CrossRef]
- Gao, Y.; Dong, P.; Shi, Y. Suspended slotted photonic crystal cavities for high-sensitivity refractive index sensing. Opt. Express 2020, 28, 12272–12278. [Google Scholar] [CrossRef]
- Fallahi, V.; Kordrostami, Z.; Hosseini, M. A Solution for Detection of Ethanol and Methanol With Overlapping Refractive Indexes Based on Photonic Crystal Ring Resonator Optical Sensors. IEEE Sens. J. 2023, 23, 6791–6798. [Google Scholar] [CrossRef]
- Jannesari, R.; Pühringer, G.; Stocker, G.; Grille, T.; Jakoby, B. Design of a High Q-Factor Label-Free Optical Biosensor Based on a Photonic Crystal Coupled Cavity Waveguide. Sensors 2024, 24, 193. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, S.; Biswas, P.; Palit, P.; Zhou, W.; Sun, Y. Optofluidic vapor sensing with free-space coupled 2D photonic crystal slabs. Sci. Rep. 2019, 9, 4209. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Liu, Y.; Zhao, D.; Yang, H.; Zhou, W.; Sun, Y. Optofluidic Fano resonance photonic crystal refractometric sensors. Appl. Phys. Lett. 2017, 110, 091105. [Google Scholar] [CrossRef]
- Biswas, P.; Zhang, C.; Chen, Y.; Liu, Z.; Vaziri, S.; Zhou, W.; Sun, Y. A Portable Micro-Gas Chromatography with Integrated Photonic Crystal Slab Sensors on Chip. Biosensors 2021, 11, 326. [Google Scholar] [CrossRef] [PubMed]
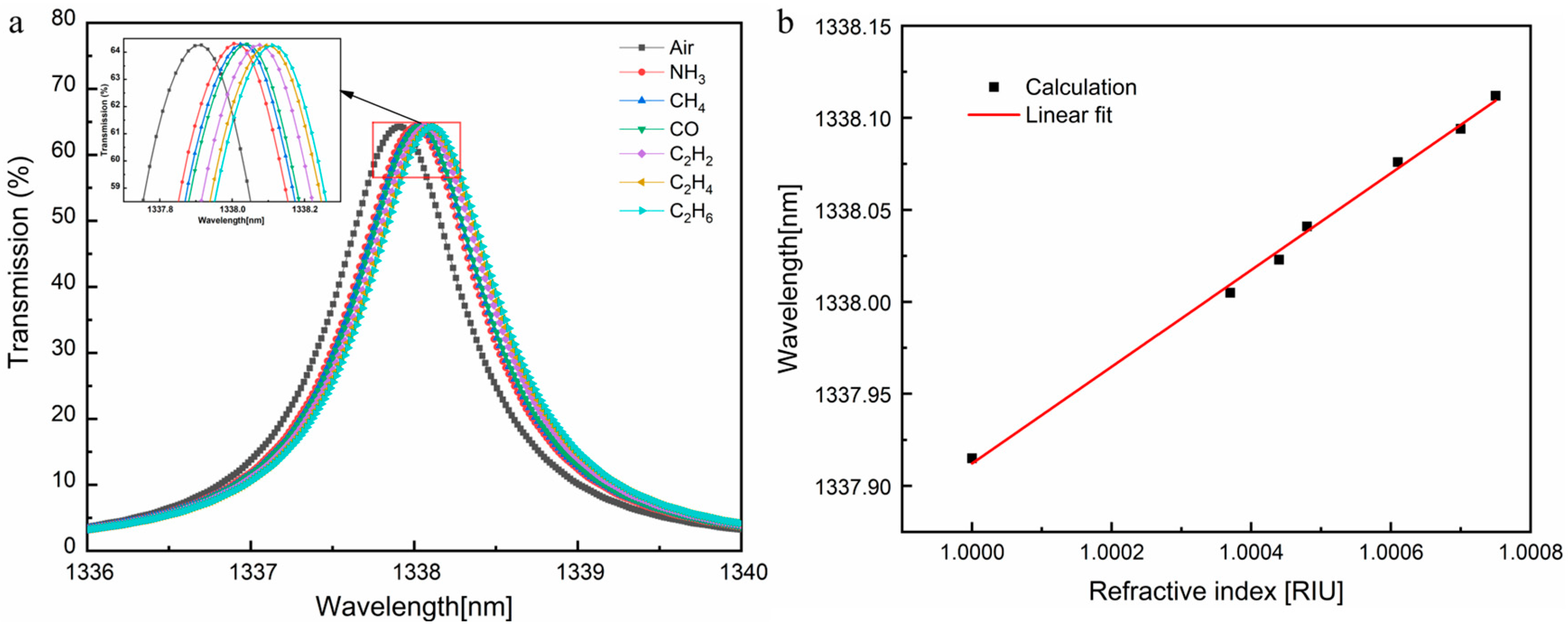
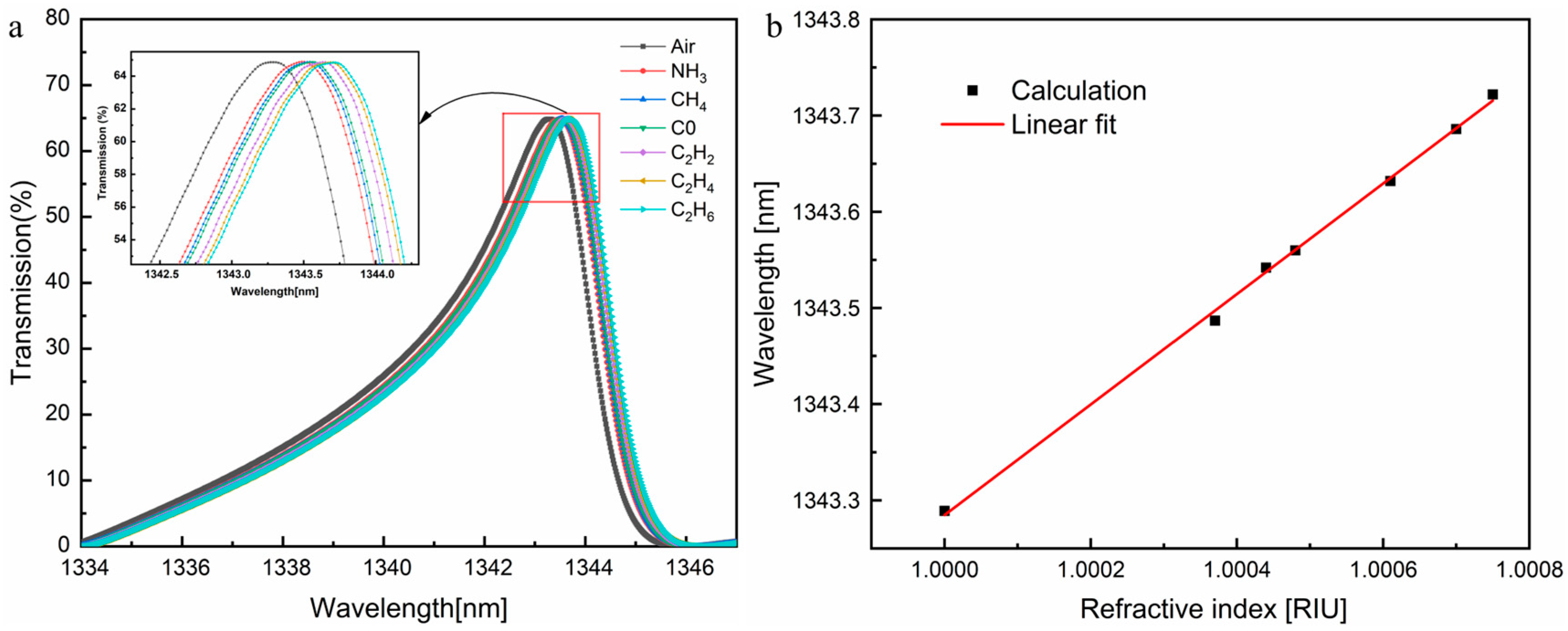

| Gas | Refractive Index | λr (nm) | TR (%) | S (nm/RIU) | Q | LoD (RIU) |
|---|---|---|---|---|---|---|
| Air | 1.00000 | 1337.915 | 64.267 | Ref | 1408.332 | Ref |
| NH3 | 1.00037 | 1338.005 | 64.319 | 243.24 | 1437.170 | 3.827 × 10−4 |
| CH4 | 1.00044 | 1338.023 | 64.303 | 245.45 | 1437.189 | 3.793 × 10−4 |
| CO | 1.00048 | 1338.041 | 64.306 | 262.50 | 1383.703 | 3.684 × 10−4 |
| C2H2 | 1.00061 | 1338.076 | 64.271 | 263.93 | 1385.172 | 3.660 × 10−4 |
| C2H4 | 1.00070 | 1338.094 | 64.256 | 255.71 | 1385.190 | 3.778 × 10−4 |
| C2H6 | 1.00075 | 1338.112 | 64.260 | 262.67 | 1385.209 | 3.678 × 10−4 |
| Gas | Refractive Index | λr (nm) | TR (%) | S (nm/RIU) | Q | LoD (RIU) |
|---|---|---|---|---|---|---|
| Air | 1.00000 | 1343.289 | 64.858 | Ref | 420.435 | Ref |
| NH3 | 1.00037 | 1343.487 | 64.882 | 535.14 | 421.156 | 5.961 × 10−4 |
| CH4 | 1.00044 | 1343.542 | 64.874 | 575.00 | 423.430 | 5.518 × 10−4 |
| CO | 1.00048 | 1343.560 | 64.871 | 564.58 | 430.628 | 5.526 × 10−4 |
| C2H2 | 1.00061 | 1343.632 | 64.860 | 562.30 | 430.651 | 5.555 × 10−4 |
| C2H4 | 1.00070 | 1343.686 | 64.853 | 567.14 | 425.756 | 5.565 × 10−4 |
| C2H6 | 1.00075 | 1343.722 | 64.830 | 577.33 | 433.179 | 5.373 × 10−4 |
| Gas | Refractive Index | λr (nm) | TR (%) | S (nm/RIU) | Q | LoD (RIU) |
|---|---|---|---|---|---|---|
| Air | 1.00000 | 1423.302 | 72.049 | Ref | 2266.404 | Ref |
| NH3 | 1.00037 | 1423.647 | 72.063 | 932.43 | 2341.525 | 6.521 × 10−5 |
| CH4 | 1.00044 | 1423.708 | 72.045 | 922.73 | 2341.625 | 6.589 × 10−5 |
| CO | 1.00048 | 1423.728 | 72.002 | 887.50 | 2267.083 | 7.076 × 10−5 |
| C2H2 | 1.00061 | 1423.850 | 72.110 | 898.36 | 2421.514 | 6.545 × 10−5 |
| C2H4 | 1.00070 | 1423.931 | 72.087 | 898.57 | 2421.651 | 6.544 × 10−5 |
| C2H6 | 1.00075 | 1423.971 | 72.055 | 892.00 | 2421.719 | 6.592 × 10−5 |
| Sensing Parameters | S (nm/RIU) | Q |
|---|---|---|
| Suspended slotted photonic crystal cavities for high-sensitivity refractive index sensing [49] | 656 | -- |
| A solution for detection of ethanol and methanol with overlapping refractive indexes based on photonic crystal ring resonator optical sensors [50] | 756 | 1092 |
| Design of a high Q-Factor label-free optical biosensor based on a photonic crystal coupled cavity waveguide [51] | 203 | 13,360 |
| This work | 932 | 2421 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Y.; Quan, J.; Li, L.; Sun, J.; Huang, X.; Meng, Z.; Zhang, J.; Cai, Z.; Wan, Y. Analysis and Optimization of Two-Dimensional Photonic Crystal Microcavity Structures for Gas Sensing. Photonics 2025, 12, 875. https://doi.org/10.3390/photonics12090875
Song Y, Quan J, Li L, Sun J, Huang X, Meng Z, Zhang J, Cai Z, Wan Y. Analysis and Optimization of Two-Dimensional Photonic Crystal Microcavity Structures for Gas Sensing. Photonics. 2025; 12(9):875. https://doi.org/10.3390/photonics12090875
Chicago/Turabian StyleSong, Yu, Jiajia Quan, Linying Li, Jincheng Sun, Xinyi Huang, Zhili Meng, Jun Zhang, Zhongyu Cai, and Yong Wan. 2025. "Analysis and Optimization of Two-Dimensional Photonic Crystal Microcavity Structures for Gas Sensing" Photonics 12, no. 9: 875. https://doi.org/10.3390/photonics12090875
APA StyleSong, Y., Quan, J., Li, L., Sun, J., Huang, X., Meng, Z., Zhang, J., Cai, Z., & Wan, Y. (2025). Analysis and Optimization of Two-Dimensional Photonic Crystal Microcavity Structures for Gas Sensing. Photonics, 12(9), 875. https://doi.org/10.3390/photonics12090875






