Efficient Single-Exposure Holographic Imaging via a Lightweight Distilled Strategy
Abstract
1. Introduction
2. Theoretical Framework and Network Design
2.1. Theoretical Framework
2.2. Teacher Model Architecture (Lnet)
2.3. Student Model Architecture
2.4. Knowledge Training Framework
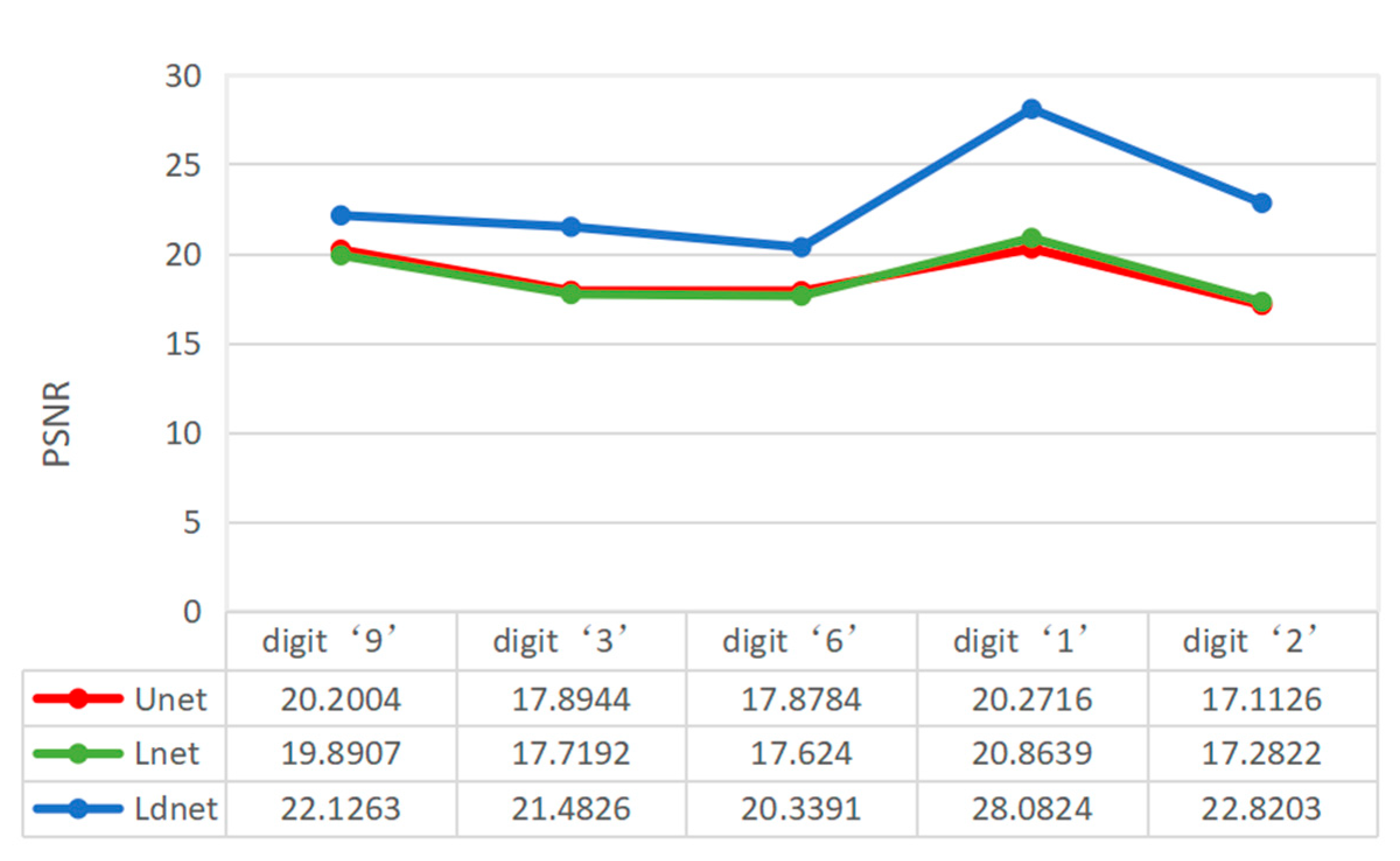
3. Analysis and Verification of Experimental Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Javidi, B.; Carnicer, A.; Anand, A.; Barbastathis, G.; Chen, W.; Ferraro, P.; Goodman, J.W.; Horisaki, R.; Khare, K.; Kujawinska, M. Roadmap on digital holography. Opt. Express 2021, 29, 35078–35118. [Google Scholar] [CrossRef] [PubMed]
- Tan, J.; Liu, J.; Wang, X.; He, Z.; Su, W.; Huang, T.; Xie, S. Large depth range binary-focusing projection 3D shape reconstruction via unpaired data learning. Opt. Lasers Eng. 2024, 181, 108442. [Google Scholar] [CrossRef]
- Anand, A.; Javidi, B. Digital holographic microscopy for automated 3D cell identification: An overview. Chin. Opt. Lett. 2014, 12, 060012. [Google Scholar] [CrossRef]
- Hong, J. A review of 3D particle tracking and flow diagnostics using Digital Holography. Meas. Sci. Technol. 2025, 36, 032005. [Google Scholar] [CrossRef]
- Tan, J.; Niu, H.; Su, W.; He, Z. Structured light 3D shape measurement for translucent media base on deep Bayesian inference. Opt. Laser Technol. 2025, 181, 111758. [Google Scholar] [CrossRef]
- Huang, H.; Huang, H.; Zheng, Z.; Gao, L. Insights into infrared crystal phase characteristics based on deep learning holography with attention residual network. J. Mater. Chem. A 2025, 13, 6009–6019. [Google Scholar] [CrossRef]
- Kim, M.K. Phase-Shifting Digital Holography; Springer: Berlin/Heidelberg, Germany, 2011; Volume 162, pp. 95–108. [Google Scholar] [CrossRef]
- Li, F.; Fang, H.; Jing, H.; Su, Y. Multi-image encryption based on three-step phase-shifting digital holography. J. Opt. 2025, 1–13. [Google Scholar] [CrossRef]
- Kakue, T.; Yonesaka, R.; Tahara, T.; Awatsuji, Y.; Nishio, K.; Ura, S.; Kubota, T.; Matoba, O. High-speed phase imaging by parallel phase-shifting digital holography. Opt. Lett. 2011, 36, 4131–4133. [Google Scholar] [CrossRef]
- Bai, F.; Lang, J.; Gao, X.; Zhang, Y.; Cai, J.; Wang, J. Phase shifting approaches and multi-channel interferograms position registration for simultaneous phase-shifting interferometry: A review. Photonics 2023, 10, 946. [Google Scholar] [CrossRef]
- Rivenson, Y.; Wu, Y.; Ozcan, A. Deep learning in holography and coherent imaging. Light Sci. Appl. 2019, 8, 85. [Google Scholar] [CrossRef]
- Li, J.; Wu, B.; Liu, T.; Zhang, Q. URNet: High-quality single-pixel imaging with untrained reconstruction network. Opt. Lasers Eng. 2023, 166, 107580. [Google Scholar] [CrossRef]
- Zhang, Z.; Zheng, Y.; Xu, T.; Upadhya, A.; Lim, Y.J.; Mathews, A.; Xie, L.; Lee, W.M. Holo-UNet: Hologram-to-hologram neural network restoration for high fidelity low light quantitative phase imaging of live cells. Biomed. Opt. Express 2020, 11, 5478–5487. [Google Scholar] [CrossRef] [PubMed]
- Ren, Z.; Xu, Z.; Lam, E.Y. Learning-based nonparametric autofocusing for digital holography. Optica 2018, 5, 337–344. [Google Scholar] [CrossRef]
- Nagahama, Y. Phase retrieval using hologram transformation with U-Net in digital holography. Opt. Contin. 2022, 1, 1506–1515. [Google Scholar] [CrossRef]
- Kang, J.W.; Park, B.S.; Kim, J.K.; Kim, D.W.; Seo, Y.H. Deep-learning-based hologram generation using a generative model. Appl. Opt. 2021, 60, 7391–7399. [Google Scholar] [CrossRef]
- Huang, L.; Liu, T.; Yang, X.; Luo, Y.; Rivenson, Y.; Ozcan, A. Holographic image reconstruction with phase recovery and autofocusing using recurrent neural networks. ACS Photonics 2021, 8, 1763–1774. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, Q.; Liu, T.; Li, J. Single-pixel deep phase-shifting incoherent digital holography. Opt. Express 2024, 32, 35939–35951. [Google Scholar] [CrossRef]
- Xu, G.; Feng, J.; Lyu, J.Y.; Dian, S.; Jin, B.; Liu, P. A coarse-to-fine attention-guided autofocusing for holography under high noisy scenes with explainable neural network. Opt. Lasers Eng. 2025, 190, 108945. [Google Scholar] [CrossRef]
- Mehta, S.; Rastegari, M. Mobilevit: Light-Weight, General-Purpose, and Mobile-Friendly Vision Transformer. arXiv 2021, arXiv:2110.02178. [Google Scholar] [CrossRef]
- Liu, Y.; Xue, J.; Li, D.; Zhang, W.; Chiew, T.K.; Xu, Z. Image recognition based on lightweight convolutional neural network: Recent advances. Image Vis. Comput. 2024, 146, 105037. [Google Scholar] [CrossRef]
- Zeng, T.; So, H.K.-H.; Lam, E.Y. RedCap: Residual encoder-decoder capsule network for holographic image reconstruction. Opt. Express 2020, 28, 4876–4887. [Google Scholar] [CrossRef] [PubMed]
- An, Q.; Liu, X.; Men, G.; Dou, J.; Di, J. Frequency-domain learning-driven lightweight phase recovery method for in-line holography. Opt. Express 2025, 33, 5890–5899. [Google Scholar] [CrossRef]
- Hinton, G.; Vinyals, O.; Dean, J. Distilling the Knowledge in a Neural Network. arXiv 2015, arXiv:1503.02531. [Google Scholar] [CrossRef]
- Xiang, J.; Colburn, S.; Majumdar, A.; Shlizerman, E. Knowledge distillation circumvents nonlinearity for optical convolutional neural networks. Appl. Opt. 2022, 61, 2173–2183. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the 18th International Conference on Medical Image Computing and Computer-Assisted Intervention (MICCAI 2015), Munich, Germany, 5–9 October 2015; Proceedings, Part III 18. pp. 234–241. [Google Scholar]








| Network | Params (M) | Flops (G) | Model Size (MB) | FPS (Frames/s)(cpu) |
|---|---|---|---|---|
| Unet | 31.03 | 54.53 | 118.37 | 2.98 |
| Lnet | 5.99 | 28 | 22.84 | 3.52 |
| Ldnet | 1.69 | 8.23 | 6.44 | 8.17 |
| Index | Network | Digit ‘9’ | Digit ‘3’ | Digit ‘6’ |
|---|---|---|---|---|
| PSNR (dB) | Ldnet_half | 19.02 | 20.45 | 18.37 |
| Ldnet | 22.13 | 21.48 | 20.34 | |
| SSIM | Ldnet_half | 0.8946 | 0.9109 | 0.8822 |
| Ldnet | 0.9259 | 0.9129 | 0.8983 | |
| MAE | Ldnet_half | 7.42 | 6.29 | 8.34 |
| Ldnet | 5.14 | 5.89 | 6.85 |
| Index | Network | Digit ‘4’ | Digit ‘0’ | Digit ‘1’ |
|---|---|---|---|---|
| PSNR (dB) | Lnet_onlyDS | 16.38 | 16.17 | 21.20 |
| Lnet | 19.06 | 17.83 | 22.70 | |
| SSIM | Lnet_onlyDS | 0.8584 | 0.8121 | 0.9254 |
| Lnet | 0.8747 | 0.8329 | 0.9307 | |
| MAE | Lnet_onlyDS | 11.39 | 14.08 | 5.06 |
| Lnet | 8.39 | 11.19 | 4.33 |
| Noise Level | Without Noise | 1% | 2% | 5% | 10% | 15% |
|---|---|---|---|---|---|---|
| PSNR (dB) | 17.39 | 15.36 | 15.34 | 15.31 | 15.31 | 14.90 |
| SSIM | 0.8739 | 0.803 | 0.8024 | 0.8029 | 0.8044 | 0.8008 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Liu, H.; Lai, Z.; Chen, Y.; Shan, C.; Zhang, S.; Liu, Y.; Huang, T.; Ma, Q.; Zhang, Q. Efficient Single-Exposure Holographic Imaging via a Lightweight Distilled Strategy. Photonics 2025, 12, 708. https://doi.org/10.3390/photonics12070708
Li J, Liu H, Lai Z, Chen Y, Shan C, Zhang S, Liu Y, Huang T, Ma Q, Zhang Q. Efficient Single-Exposure Holographic Imaging via a Lightweight Distilled Strategy. Photonics. 2025; 12(7):708. https://doi.org/10.3390/photonics12070708
Chicago/Turabian StyleLi, Jiaosheng, Haoran Liu, Zeyu Lai, Yifei Chen, Chun Shan, Shuting Zhang, Youyou Liu, Tude Huang, Qilin Ma, and Qinnan Zhang. 2025. "Efficient Single-Exposure Holographic Imaging via a Lightweight Distilled Strategy" Photonics 12, no. 7: 708. https://doi.org/10.3390/photonics12070708
APA StyleLi, J., Liu, H., Lai, Z., Chen, Y., Shan, C., Zhang, S., Liu, Y., Huang, T., Ma, Q., & Zhang, Q. (2025). Efficient Single-Exposure Holographic Imaging via a Lightweight Distilled Strategy. Photonics, 12(7), 708. https://doi.org/10.3390/photonics12070708





