A Preliminary Study on the Principle of Linear Effect Scaling Laws for Laser Atmospheric Transmission

Abstract

Numerical simulations were performed to rapidly predict and evaluate laser beam expansion caused by linear atmospheric transmission effects, such as turbulence and jitter, thereby enhancing the accuracy of the scaling law. Simulation results indicate that the turbulence term coefficient in the beam expansion calibration expression correlates linearly with the initial beam mass and inversely with the transmission distance. By fitting a nonlinear surface, the relationship between the turbulence term coefficient, initial beam mass, and transmission distance was established. Additionally, under turbulence-free conditions, a calibration expression relating initial beam mass to transmission distance was derived. The tracking jitter-term coefficient was determined to be 3.69, effectively characterizing beam expansion due to system jitter error. Based on simulation outcomes, a scaling law model for beam expansion induced by linear atmospheric transmission effects was clearly established. The model closely matched the simulation data, with a root mean square error (RMSE) of 3.88. Compared with existing scaling law simulations, the proposed calibration expression significantly enhances the accuracy in predicting and evaluating beam expansion caused by linear atmospheric transmission effects. It also provides a more precise characterization of variations in beam expansion during laser transmission.

1. Introduction

Lasers, as critical light sources, have attracted significant attention due to their atmospheric transmission characteristics. When laser beams propagate through the atmosphere, they experience linear effects including absorption, scattering, and turbulence, as well as nonlinear thermal halo effects, all leading to beam spot expansion [1,2,3]. This expansion degrades the beam quality, significantly affecting performance in laser-based atmospheric applications such as communications, remote sensing, and range measurements. Understanding and modeling laser atmospheric transmission requires fundamental physical principles, mathematical models, complex numerical simulations, and experimental verification. By establishing accurate calibration relationships, researchers can quickly predict and evaluate laser beam expansion under varying environmental conditions.

In recent years, with the development of computer technology, based on the fluctuating optics theory, the numerical simulation method has become an important research tool for studying the variation in the quality of laser beams transmitted in the atmosphere. Although fluctuating optics simulations can accurately reproduce the spatial and temporal variations in atmospheric beam transmission, they require consideration of multiple factors, such as initial beam quality, atmospheric conditions, system jitter, and blocking ratio [4,5]. Consequently, their slow computational speed limits their practicality for real-world applications [6]. Based on the analysis method of mean square and radius [7], domestic scholars have successively proposed a variety of calibration laws, including the atmospheric transmission calibration law of focused Gaussian beam [8] and focused platform beam [9,10,11,12,13], the calibration law of genetic algorithm optimization [6], and the improved numerical model of the calibration law [6,14], etc., which mainly use the control variables to analyze, one by one, the change in expression coefficients induced by the change in individual parameters. On the basis of determining the coefficients of one expression, the value of the coefficients of another expression is further determined by changing other parameters, and the calibration expression is finally determined. A limitation of this method is its inability to traverse multiple parameter combinations, thereby failing to accurately characterize laser transmission under diverse atmospheric conditions. If expression coefficients are merely averaged from specific scenarios, broader applicability and enhanced accuracy of the calibration expressions become challenging to achieve [14,15]. Additionally, comparisons of previous research results indicate significant variations in the calibration expression coefficients depending on parameters such as beam type, initial beam quality, transmission distance, and system jitter error [10]. Thus, employing constant values to characterize these coefficients does not accurately reflect actual conditions.

This study utilizes the mean square sum relationship to analyze linear effects in atmospheric transmission. Numerical simulations were conducted by systematically varying parameter combinations to investigate laser transmission characteristics under diverse atmospheric conditions. Relationships between the calibration expression coefficients and variables including initial beam quality, transmission distance, and system jitter error were established. This approach significantly enhances the accuracy of calibration expressions describing linear effects in laser atmospheric transmission.

2. Theoretical Analysis

Typically, changes in laser beam quality in the far field after atmospheric transmission can be assessed using parameters such as the beam quality factor, which quantifies beam expansion at the focal plane. It is commonly assumed that the various perturbation sources contributing to beam expansion act independently [12]. When considering linear effects such as laser system jitter, atmospheric absorption, scattering, and turbulence, it is typically assumed these effects combine at the beam’s focal plane. Specifically, the squared spot radius equals the sum of the squares of the effective radii from each individual effect, satisfying the mean square sum relationship:

$${\beta }^2={\beta }_0^2+{\beta }_T^2+{\beta }_J^2,$$

(1)

where $\beta$ is the beam quality factor after beam expansion due to linear effects of laser transmission, ${\beta }_0$ is the beam quality factor characterizing expansion due to diffraction, ${\beta }_T$ is the beam quality factor characterizing expansion due to turbulence, and ${\beta }_J$ is the beam quality factor characterizing expansion due to tracking jitter.

According to the literature [1,11], Equation (1) can be written as follows:

$${\beta }^2={\beta }_0^2+A{(D/r_0)}^2+B{({\sigma }_i/{\sigma }_0)}^2,$$

(2)

where $D$ is the laser emission aperture; ${\sigma }_i$ is the system tracking jitter error; ${\sigma }_0$ is the diffraction angle of the emission system; and $r_0$ is the atmospheric coherence length. The first and second terms on the right side of the equal sign in Equation (2) characterize beam expansion due to diffraction and turbulence [4], while the third term characterizes beam expansion due to tracking jitter.

The diffraction angle ${\sigma }_0$ of the emitting system is given by the following:

$${\sigma }_0=1.22\lambda /D,$$

(3)

The expression for the atmospheric correlation length $r_0$ is given by the following:

$$r_0={\left[0.423k^2{\displaystyle {\int }_0^L{C}_n^2(z){(1-z/L)}^{5/3}\mathrm{d}z}\right]}^{-3/5},$$

(4)

where $\lambda$ is the emitted laser wavelength, $k$ is the wave number, and $C_n^2$ is the refractive index structure constant.

Since it is not very reasonable to characterize the beam expansion rate with a constant, a relational equation for the beam expansion law of laser atmospheric transmission containing linear effects such as diffraction, turbulence, and tracking jitter is proposed:

$${\beta }^2={\beta }_0^2+A_m{(D/r_0)}^2+B_m{({\sigma }_i/{\sigma }_0)}^2,$$

(5)

where $A_m$ and $B_m$ take values as a function of parameters related to the laser transmission distance $L$ and initial beam quality ${\beta }_0$, among others. For the proposed calibration relation (5), a numerical simulation is performed using a four-dimensional program to verify its feasibility and accuracy.

3. Numerical Simulation Results and Analysis

In the numerical simulation calculation, the wavelength is a truncated Gaussian beam of 1 μm, the laser emission aperture is 0.5 m to 1m, the initial beam quality is 1 to 10, the horizontal atmospheric transmission distance is 1 km to 9 km, the tracking jitter error of the laser system is 2.5 μrad, 5 μrad, and 7.5 μrad, and the refractive index structural constant takes values in the range of 1 × 10⁻¹⁶ m^−2/3 to 1 × 10⁻¹⁴ m^−2/3. The average wind speed is 2 m/s, the laser transmission time is 10 s, phase screen generation is performed via the spectral inversion method [16,17], the number of phase screen calculation grids is 256 × 256, the number of transmission steps, i.e., the number of phase screens, is 50, and the statistical results are taken from 30 laser transmission long exposures.

Without considering system jitter conditions, the beam expansion satisfies the calibration relation ${\beta }^2={\beta }_0^2+A_m{(D/r_0)}^2$, and the variation in the expansion multiple ${\beta }^2-{\beta }_0^2$ with the turbulence term ${(D/r_0)}^2$ for 63.2% of the ring-envelope energy radius in the focal plane caused by the turbulence effect is given in Figure 1. The variation in the turbulence term ${(D/r_0)}^2$ in the figure is calculated by changing the parameters of the initial beam quality ${\beta }_0$, transmission distance L, and turbulence intensity (${\mathrm{C}}_n^2$), where $D/r_0$ takes the value in the range of 0.866–19.295 and is fitted with a $k$ value of about 1 using the linear expression $y=k\cdot x$, so that A_m ≈ 1. In this paper, the main simulation input parameters are transmission distance, initial beam quality, and atmospheric turbulence intensity, etc. These will be traversed in combinations; i.e., all laser transmission situations under the setup conditions are considered, totaling 1800 combinations. Because the initial beam quality ${\beta }_0$ changes will not cause the atmospheric correlation length to change, and under the same atmospheric turbulence intensity conditions, the transmission distance is determined, the size of the ${(D/r_0)}^2$ term remains unchanged, while ${\beta }^2$ increases with the increase of ${\beta }_0^2$. Consequently, Figure 1 appears with ${(D/r_0)}^2$ taking a certain value, where ${\beta }^2-{\beta }_0^2$ corresponds to a number of groups of values. The value of this phenomenon is mainly due to the value of ${\beta }_0$ caused by the different value of the phenomenon.

The Amplitude Scintillation parameter, A_m ≈ 1, can characterize the trend of spot expansion caused by the turbulence effect, but there is a large error, which is mainly manifested in the large difference in the A_m values obtained from the fits with different initial beam qualities ${\beta }_0$ or different transmission distances L. To observe the difference in the A_m values obtained from the fits more intuitively, we take ${\beta }_0$ = 1 and 8, and L = 1 km and 9 km, respectively. 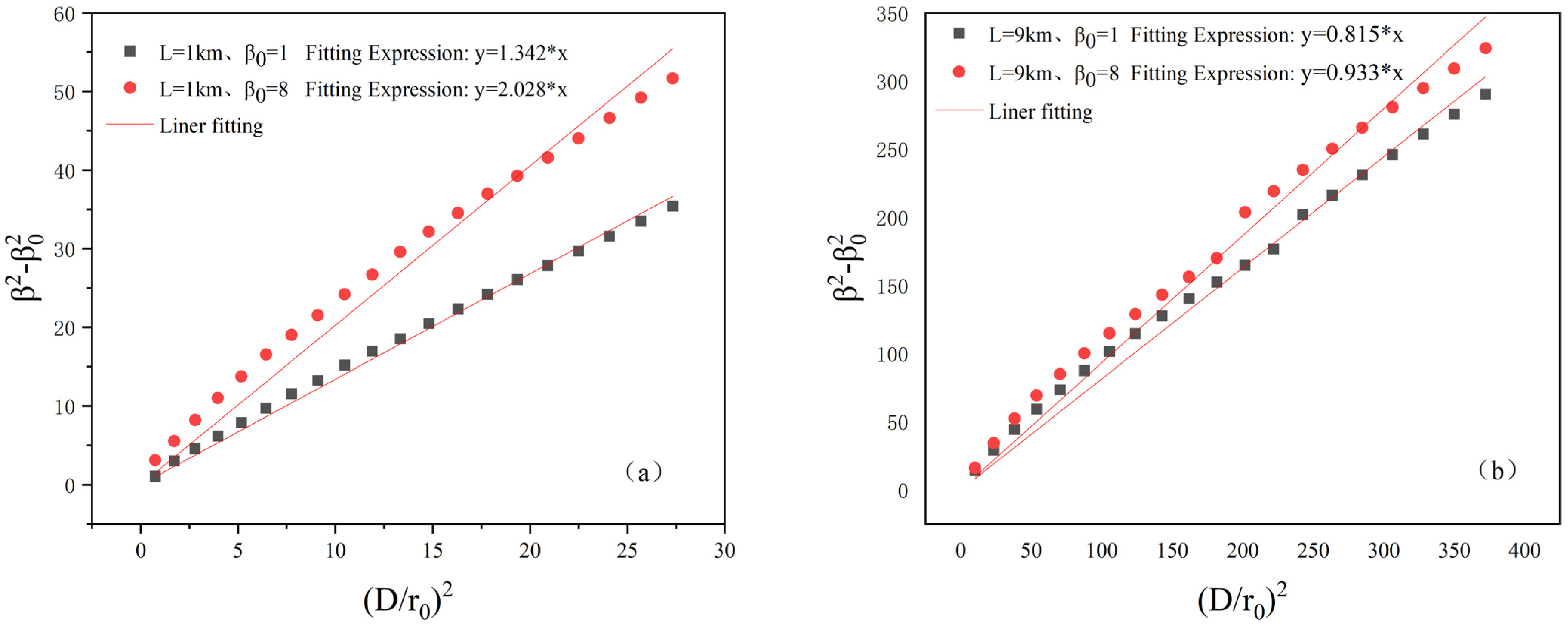By changing the turbulence strength, the variation relationship of the expansion multiplier ${\beta }^2-{\beta }_0^2$, with the turbulence term ${(D/r_0)}^2$, is obtained as shown in Figure 2a,b, and the fitting results are shown in

Table 1. The fitting values of coefficient A_m for ${\beta }_0$ and L under different value conditions.

Am	${\mathit{\beta }}_0=1$	${\mathit{\beta }}_0=8$
L = 1 km	1.34	2.03
L = 9 km	0.81	0.93

.

When the initial beam quality ${\beta }_0$ is 1 and the transmission distance L is 1 km, the fitting coefficient A_m is 1.34. As ${\beta }_0$ increases to 8, Am decreases to 2.03, indicating that A_m increases with ${\beta }_0$ under the same distance conditions. When ${\beta }_0$ is 8 and L is 9 km, A_m is 0.93. As L decreases to 1 km, A_m increases to 2.03, indicating that A_m increases with decreasing L under the same initial beam quality conditions. Additionally, for initial beam qualities of 1 and 8 and laser atmospheric transmissions of 1 and 9 km, the A_m coefficient values range from about 0.814 to 2.03, with a difference of about 2.5 times between the maximum and minimum values. Using A_m ≈ 1 to characterize the values of A_m in this range would result in a large error.

The coefficient A_m characterizes the rate of change in the turbulence term ${(D/r_0)}^2$ from expression ${\beta }^2={\beta }_0^2+A_m{(D/r_0)}^2$. Comparing Figure 2a,b, A_m decreases with increasing ${\beta }_0$ and increases with decreasing transmission distance L. Therefore, the magnitude of A_m is related to the values of ${\beta }_0$ and L. To better understand the relationship between A_m, ${\beta }_0$, and L, under the same wavelength and aperture conditions, we traverse the initial beam quality ${\beta }_0$ and transmission distance L, taking a value combination. Adjusting the intensity of atmospheric turbulence, with these parameters as input, we simulate the coefficient A_m and obtain the corresponding relationships of ${\beta }_0$ and L. 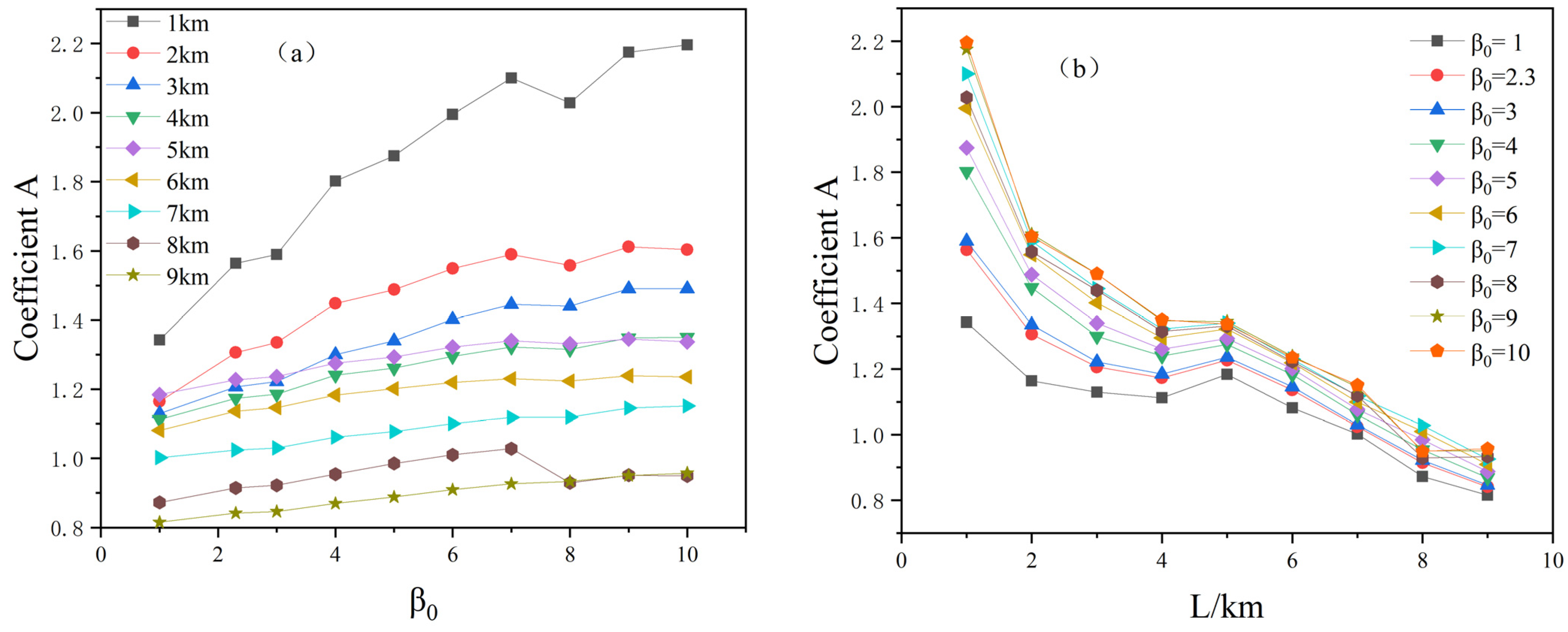In Figure 3, we show the coefficient A_m and its corresponding relationship with ${\beta }_0$, and in Figure 4, we show the coefficient A_m and its corresponding relationship with L.

Beam quality is typically characterized by parameters such as beam divergence, divergence angle, M² factor (aberration), and beam quality factor. All factors affecting near-field beam quality also impact far-field beam quality [18]. A laser beam with high beam quality ensures a small beam waist and long Rayleigh length, enabling transmission over longer distances [19]. As expressed by ${\beta }^2={\beta }_0^2+A_m{(D/r_0)}^2$, the coefficient A_m mainly characterizes the rate of change in the turbulence term ${(D/r_0)}^2$. When the initial beam quality is small and the beam divergence is low with a small cross-sectional area, the beam expansion caused by the turbulence effect is reduced to a certain extent, protecting the energy density in the beam center and maintaining it constant during propagation or slowly decreasing. The turbulence effect induced by beam expansion changes slowly, with the coefficient A_m being smaller. When the initial beam quality is larger, the beam divergence is higher, and the cross-sectional area is larger; the beam is more susceptible to turbulence during transmission, resulting in increased beam expansion, deteriorated beam quality, and rapidly changing beam expansion induced by the turbulence effect, with the coefficient A_m increasing. As shown in Figure 3, with the increase of ${\beta }_0$, the turbulence-induced beam expansion is intensified, corresponding to the increasing coefficient A_m and the overall linearly increasing relationship, satisfying A_m ∝ ${\beta }_0$, which can be expressed as

$$A_m=a+b\cdot {\beta }_0$$

(6)

which characterizes the changing relationship between A_m and ${\beta }_0$, and a and b are the fitting parameters.

Furthermore, as the transmission distance increases, the laser beam experiences more turbulence effects, and the beam expansion caused by the turbulence effect accumulates; at this time, it is difficult to cause a rapid change in the total cumulative effect of the turbulence effect by changing the characteristic parameter $D/r_0$ of the turbulence effect; i.e., after long-distance transmission, the rate of change in the beam expansion caused by the turbulence effect decreases gradually. Combined with Figure 4, it can be seen that under different initial beam qualities ${\beta }_0$, the coefficient A_m decreases with the increase in the transmission distance L, and the overall relationship is an inverse proportional decreasing relationship, satisfying A_m ∝ $1/L^n$ (n > 0), which can be expressed as

$$A_m=c/L^n(n>0)$$

(7)

which characterizes the changing relationship between Am and L, and c is the fitting parameter.

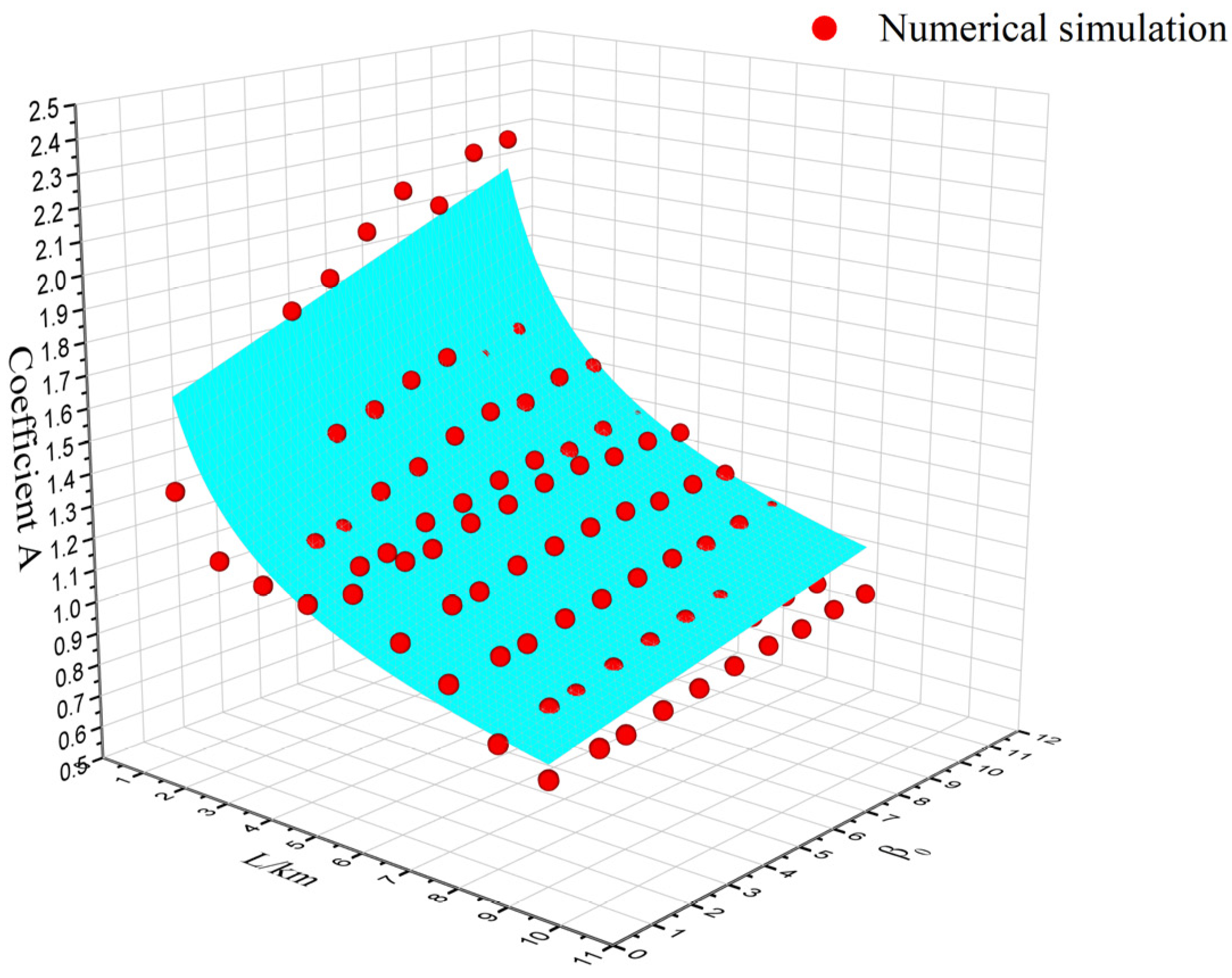
On this basis, a new expression can be constructed:

$$A_m={\displaystyle \frac{a+b\cdot {\beta }_0}{L^n}},n>0$$

(8)

It describes the functional relationship between the coefficient A_m and the initial beam quality ${\beta }_0$, and the transmission distance L. By nonlinear surface fitting, the fitting results are obtained as shown in Figure 4. The fitting coefficient of determination, R² = 0.91, indicates that there is a high degree of agreement between the distribution of data points and the fitted surface, providing a good explanation of the model.

Based on the fitting results depicted in Figure 4, the fitted expression is obtained as follows:

$$A_m={\displaystyle \frac{1.58+0.052\cdot {\beta }_0}{L^{0.291}}}$$

(9)

The fitting parameters are as follows: a = 1.58, b = 0.052, n = 0.291, and the length scale L in kilometers.

Considering the system tracking jitter error, the turbulence intensity is set to 0; i.e., the influence of turbulence is not considered, and the numerical simulation results use the statistical values of 30 laser transmission long exposures. From Equation (3), it can be seen that the system tracking jitter error caused by the beam expansion term calculation is mainly related to the wavelength and launching aperture, and is not related to the transmission distance. Therefore, ${\sigma }_0$ can be calculated to be 1.622 μrad under the conditions of a wavelength of 1 μm and a launching aperture of 0.7 m. The simulation calculates the initial beam quality ${\beta }_0$ to be 1, 3, 5, 7, and 9, and the tracking jitter error ${\sigma }_j$ to be 2.5 μrad, 5 μrad, and 7.5 μrad under far-field beam quality conditions. Fitting these results yields different values for coefficient B, as shown in

Table 2. The fitting values of coefficient B_m for ${\beta }_0$ and ${\sigma }_j$ under different value conditions.

${\mathit{\sigma }}_{\mathit{i}}$/μrad		2.5	5	7.5
Bm	β0 = 1	3.265	3.270	3.285	${\overline{B}}_m=$ 3.69
	β0 = 3	3.980	3.702	3.491
	β0 = 5	3.532	3.737	3.684
	β0 = 7	3.639	3.825	3.773
	β0 = 9	4.338	3.996	3.877

. The average value of B is 3.69.

As demonstrated in Table 2, under identical initial beam quality conditions, the rate of beam extension variation induced by system tracking jitter error remains nearly constant. This observation suggests a steady growth pattern of beam extension caused by the jitter. Notably, although an increase in initial beam quality leads to a gradual rise in the beam expansion rate, the fluctuation range of this rate remains centered around 3.69, indicating minimal sensitivity to initial beam quality. Furthermore, under turbulence-free conditions with a fixed system tracking jitter error (e.g., 2.5 μrad), the relative contribution of beam expansion attributed to this error decreases significantly—from 88.6% to 11.3%—as the initial beam quality increases from 1 to 9. This inverse relationship implies that higher initial beam quality diminishes the proportional impact of jitter-induced beam extension on the total expansion. When turbulence effects are considered, the influence of the error coefficient B becomes even less pronounced. Consequently, the parameter ${\overline{\mathrm{B}}}_m$ = 3.69 effectively characterizes the beam expansion dynamics governed by system jitter error.

In conclusion, the linear atmospheric propagation effects on beam spreading at the 1/e² intensity contour demonstrate quantifiable scaling relationships for λ = 1 μm laser systems. Through systematic parametric analysis (D = 0.7 m transmitter aperture, L = 1–9 km propagation distance, ${\beta }_0$ = 1–10 initial beam quality factor), experimental measurements confirm that the radial spread satisfies the dimensionless calibration model:

$${\beta }^2={\displaystyle \frac{1.58+0.052{\beta }_0}{L^{0.291}}}(D/r_0{)}^2+3.69{({\sigma }_j/{\sigma }_0)}^2$$

(10)

This finding aligns with the turbulence-independent scaling law proposed by Andrews et al. [20] while extending its applicability to low-coherence beams (${\beta }_0$ > 5) through modified terms.

To validate the predictive accuracy of Equation (10), we conducted numerical simulations using a Monte Carlo approach (N = 500 iterations) with the following constrained parameters: propagation distance L = 2 km, initial beam quality factor ${\beta }_0$ = 5, and pointing jitter ${\sigma }_j$ = 2.5 μrad. The simulated beam spreading characteristics were systematically compared with both the proposed calibration model and established scaling laws from Refs. [1,14], please refer to Appendix A. Under strong turbulence conditions, the laser beam undergoes breakup into multiple sub-spots, whose statistical properties are governed by the turbulence inner scale ($l_0$) and non-Kolmogorov spectral characteristics. If discrepancies exist in the phase screen generation algorithms or the truncation of scattering orders (e.g., neglecting higher-order scattering terms), the turbulence-induced beam breakup effect will be underestimated, thereby introducing deviations in the simulated beam spreading and intensity statistics.

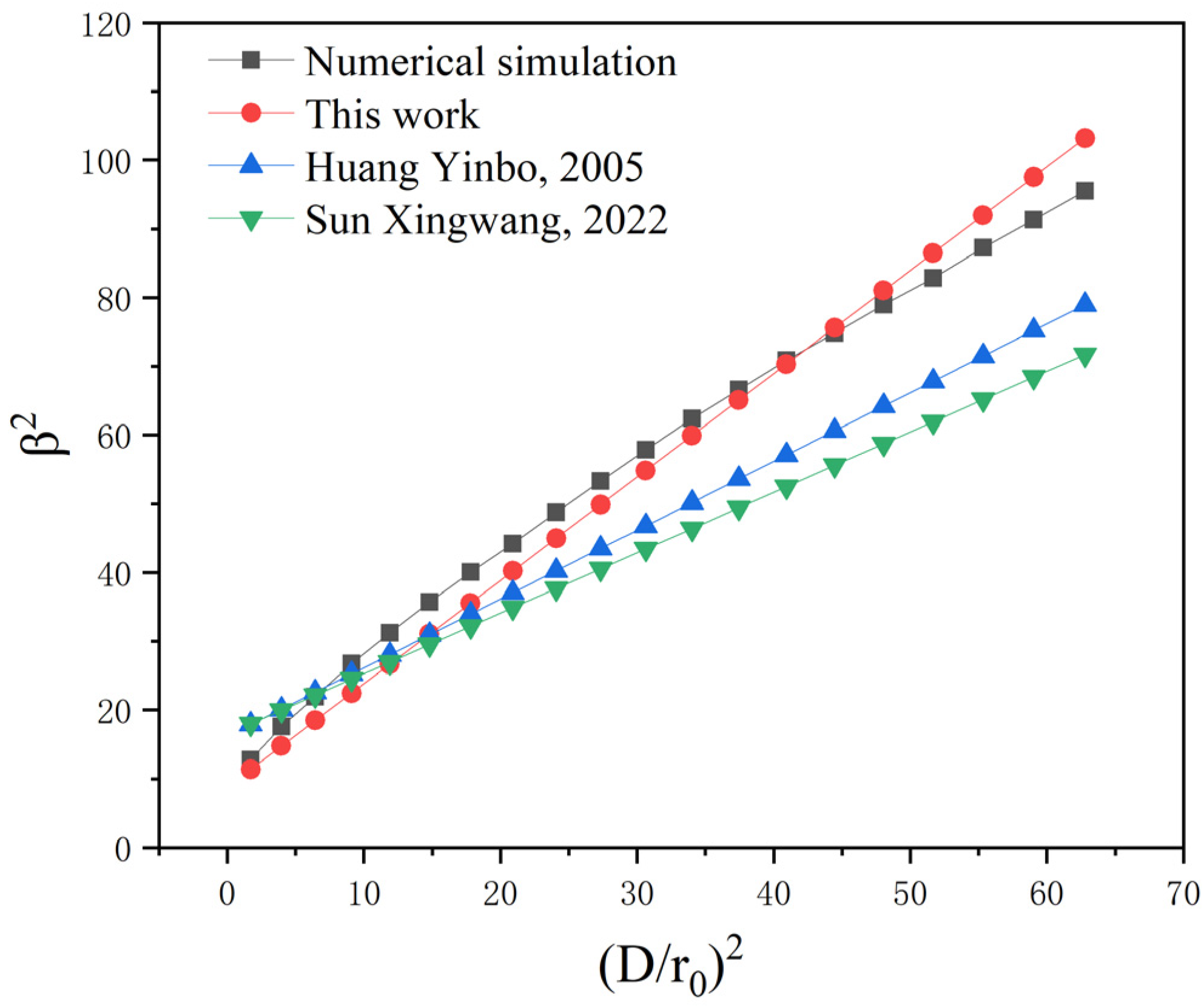
As evidenced in Figure 5, both Equation (10) and the calibration models from Refs. [1,14] demonstrate satisfactory agreement with numerical simulations. Specifically, Equation (10) achieves the minimal deviation from simulated results with a root mean square error (RMSE) of 3.88. With increasing turbulence intensity (${\mathrm{C}}_n^2$ > 10⁻¹⁴ m^−2/3), the prediction accuracy of Refs. [1,14] deteriorates significantly, yielding RMSE values of 10.91 and 14.87, respectively. This comparative analysis confirms that the proposed calibration formalism in Equation (10) enhances prediction accuracy for laser beam spreading by 64.4% and 73.8% relative to Refs. [1,14], achieved through systematic parameter space exploration (L ∈ [0.5, 10] km, ${\beta }_0$ ∈ [1, 10], ${\mathrm{C}}_n^2$ ∈ [10⁻¹⁶, 10⁻¹³] m^−2/3). The improved fidelity originates from optimized weight coefficients in the generalized scaling law, which effectively minimizes overfitting through global sensitivity analysis across 1800 parameter combinations.

4. Conclusions

This study systematically investigates laser beam spreading dynamics caused by linear atmospheric effects, including diffraction, turbulence, and jitter, through detailed numerical simulations. Quantitative analysis demonstrates how beam expansion varies parametrically with initial beam quality (M² = 1–10) and propagation distance (L = 1–9 km), given a fixed transmitter aperture (D = 0.5–1 m) at a wavelength of λ = 1 μm. A generalized calibration model was established through global optimization across 1800 parameter combinations, resulting in excellent agreement with simulated beam profiles within the 1/e² intensity contour. Comparative validations show a 64.2% reduction in root mean square deviation (RMSE = 3.88) compared to established models [1,14]. This improvement is especially significant under strong turbulence conditions (Cn² > 10⁻¹⁴ m⁻²/³), where previous formulations exhibit a 12–22% overestimation.

Although this study focuses on horizontal propagation paths to isolate turbulence effects, two critical extensions are proposed: (1) implementation of slant-path transmission models incorporating altitude-dependent profiles consistent with the Hufnagel–Valley (HV) atmospheric model; and (2) integration of nonlinear thermal blooming effects via a coupled solution of wave propagation and heat diffusion equations.