Image-Based Laser-Beam Diagnostics Using Statistical Analysis and Machine Learning Regression
Abstract
1. Introduction
2. Methodology
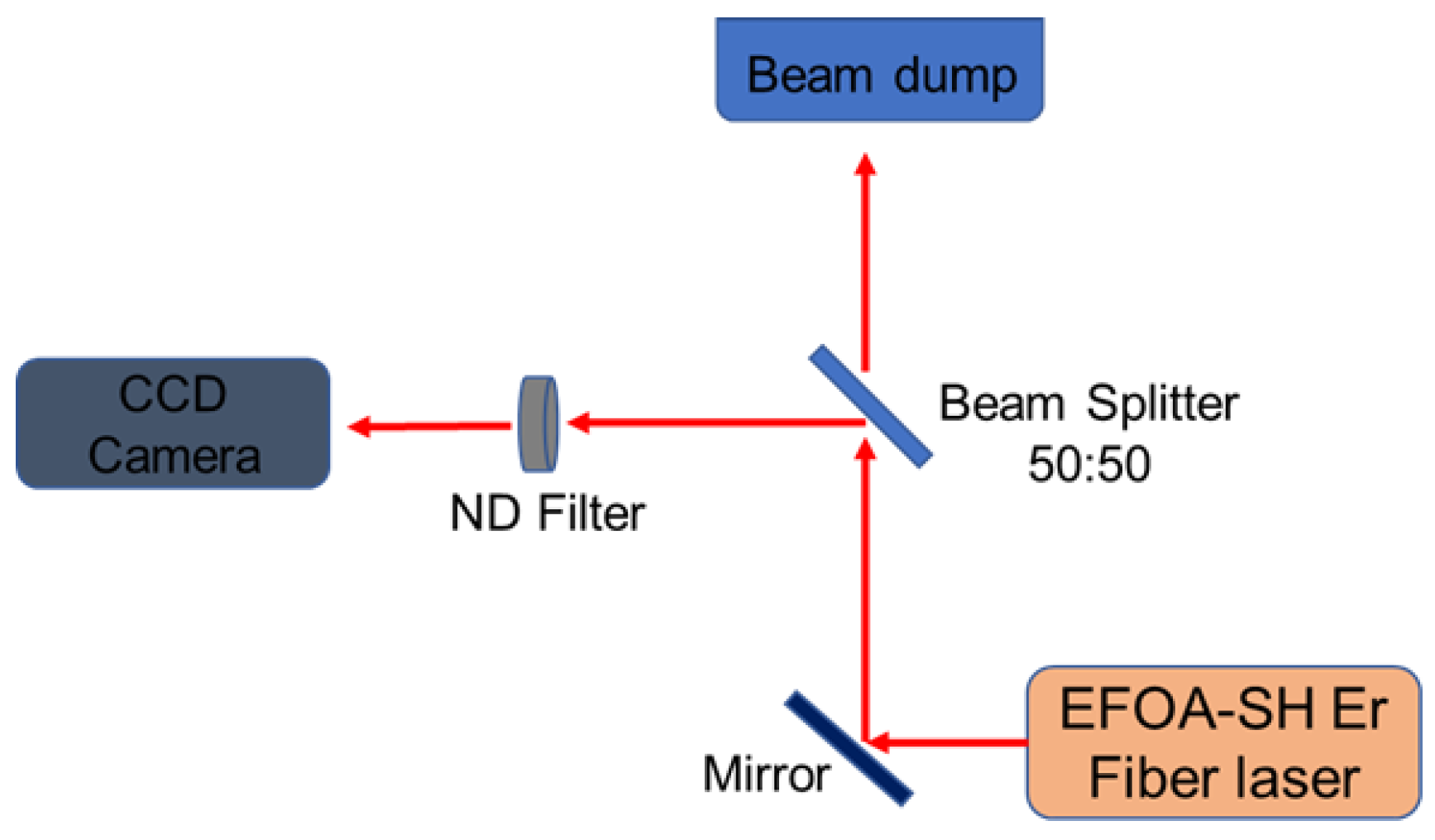
2.1. Image Data Acquisition and Preprocessing
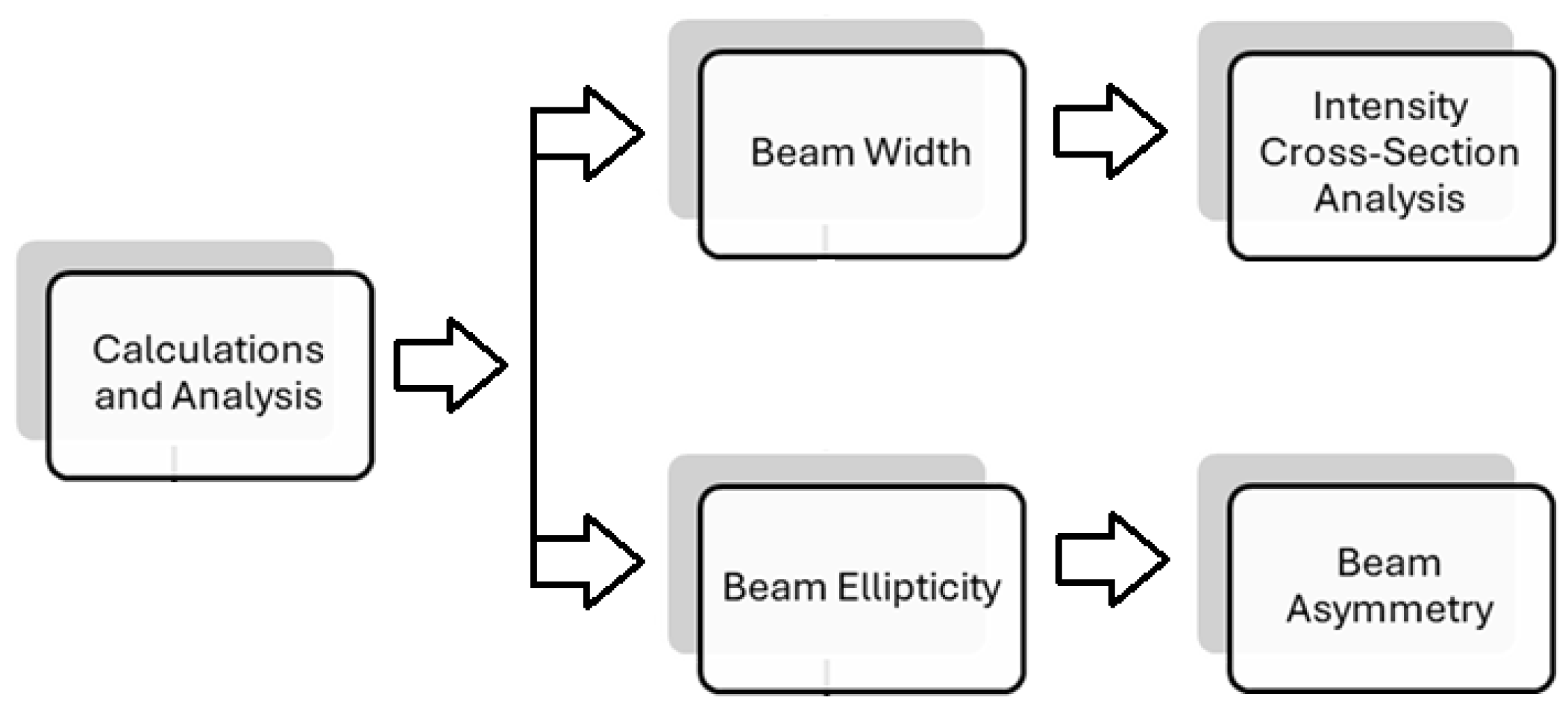
2.2. Statistical and Numerical Calculations and Analysis
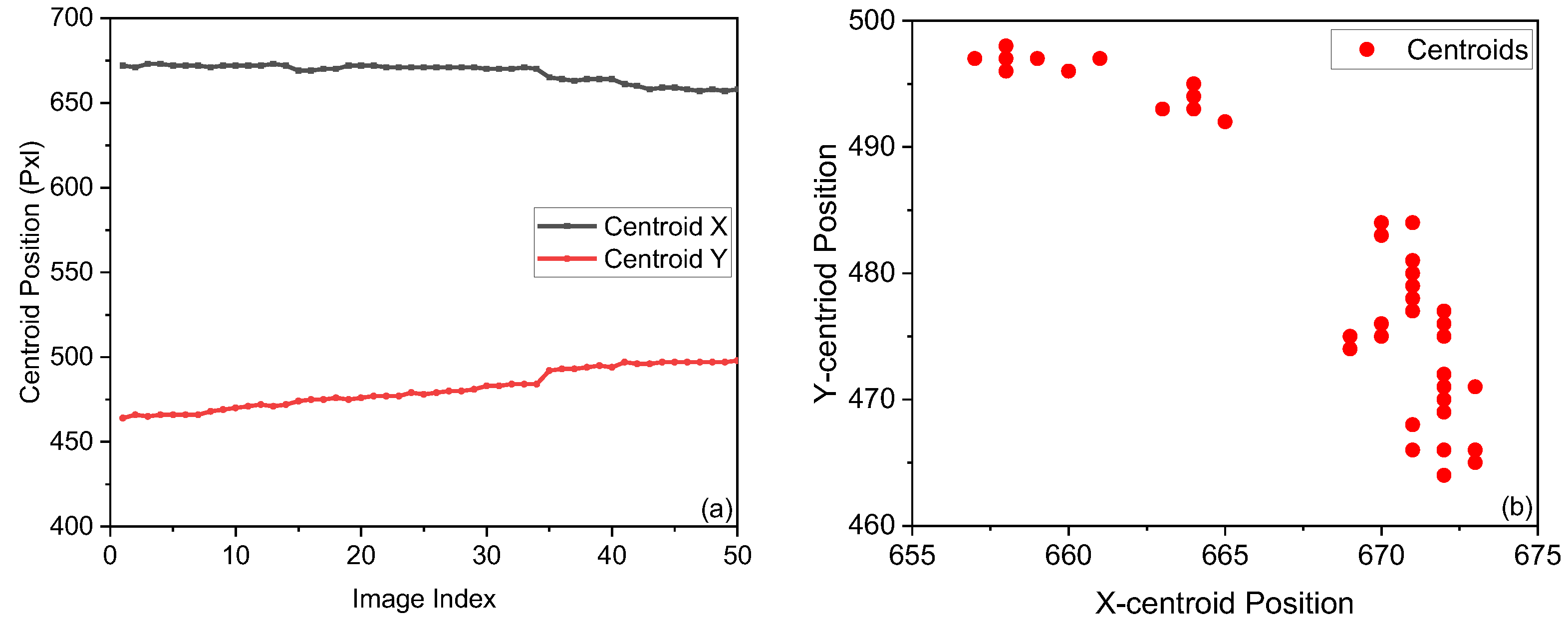
2.2.1. Beam Centroid Calculation and Analysis
2.2.2. Beam Width Estimation Using Full Width at Half Maximum (FWHM)
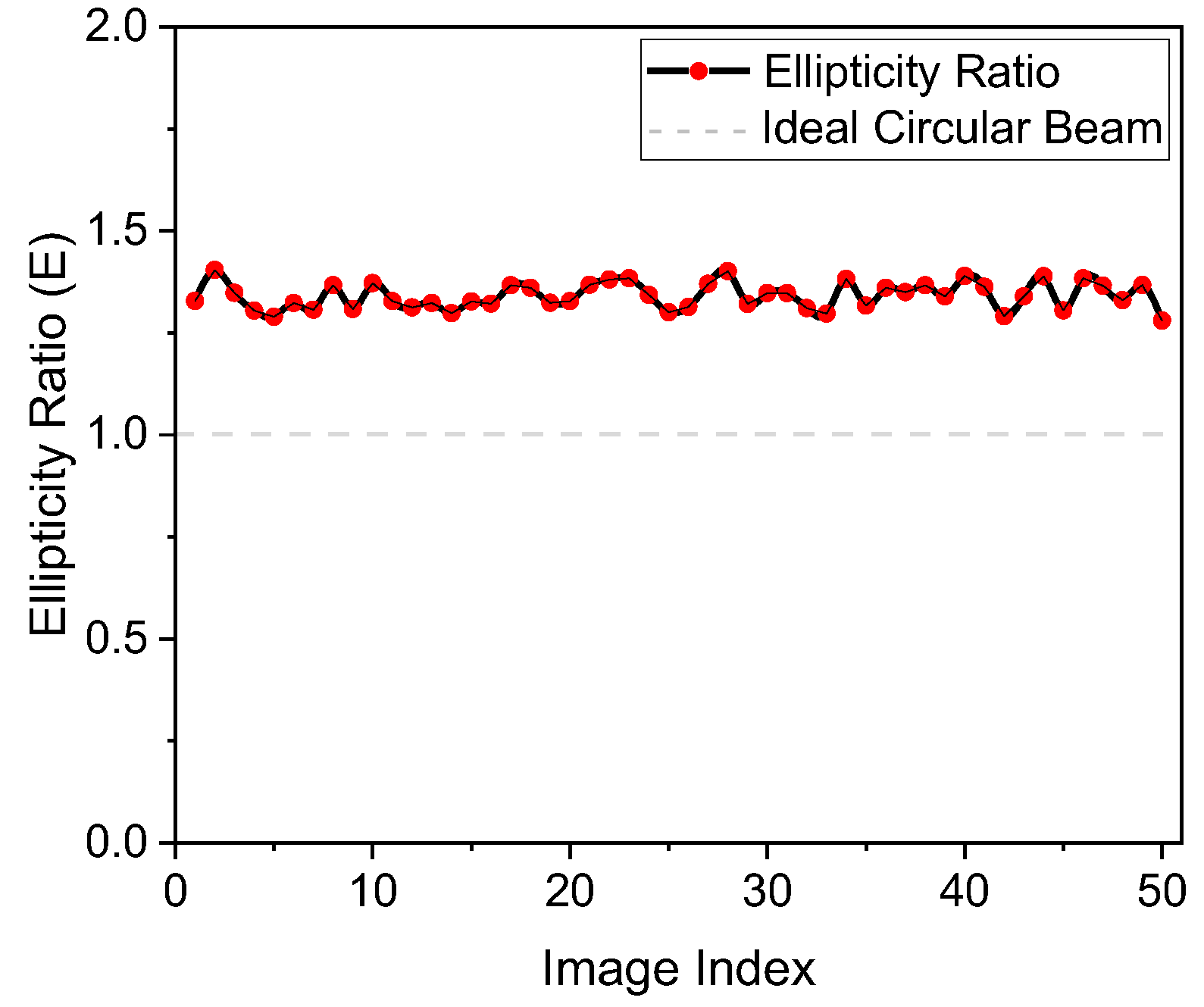
2.2.3. Beam Ellipticity Estimation Using FWHM Ratio Analysis
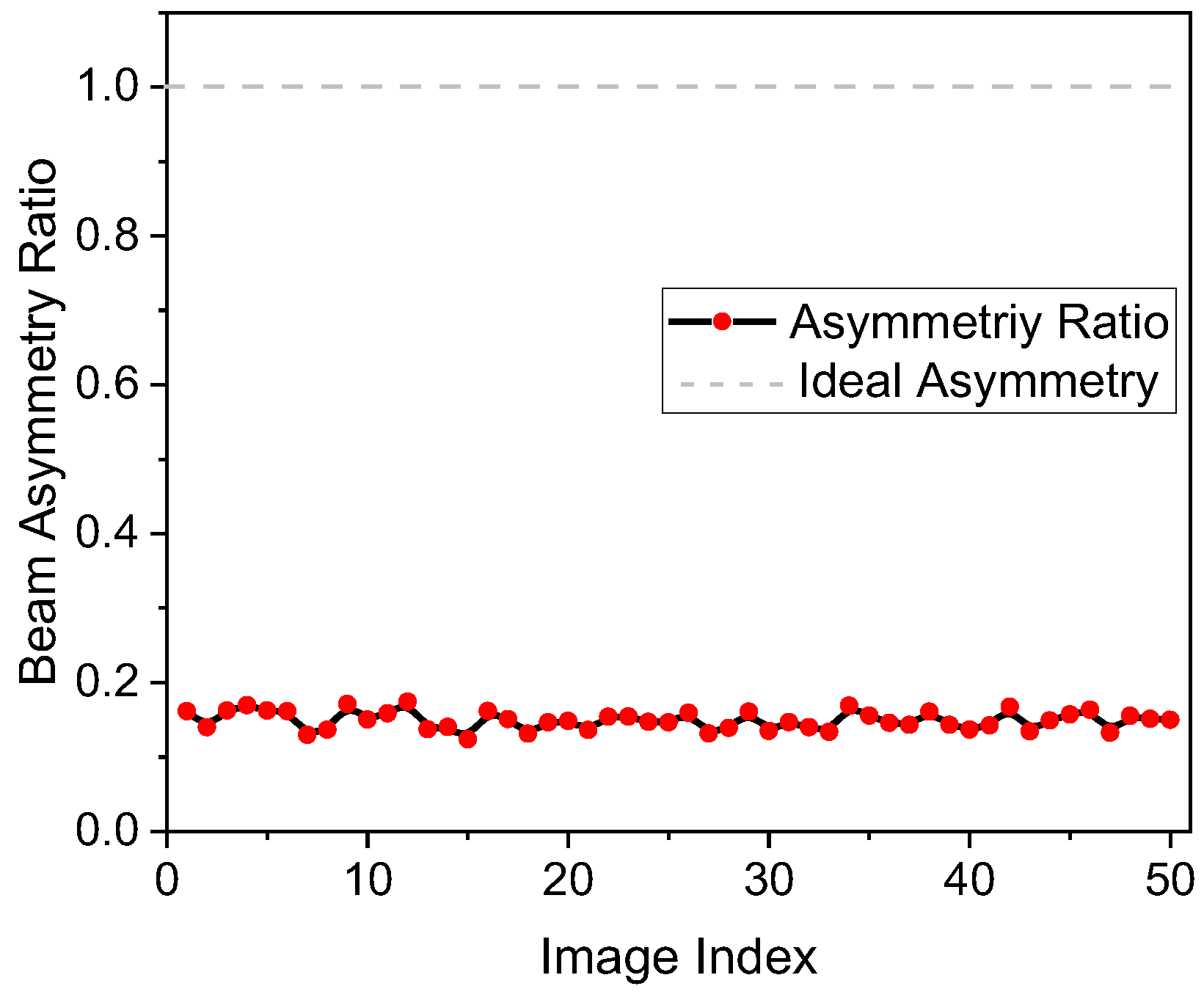
2.2.4. Beam Asymmetry Evaluation Using Directional FWHM Ratio Analysis
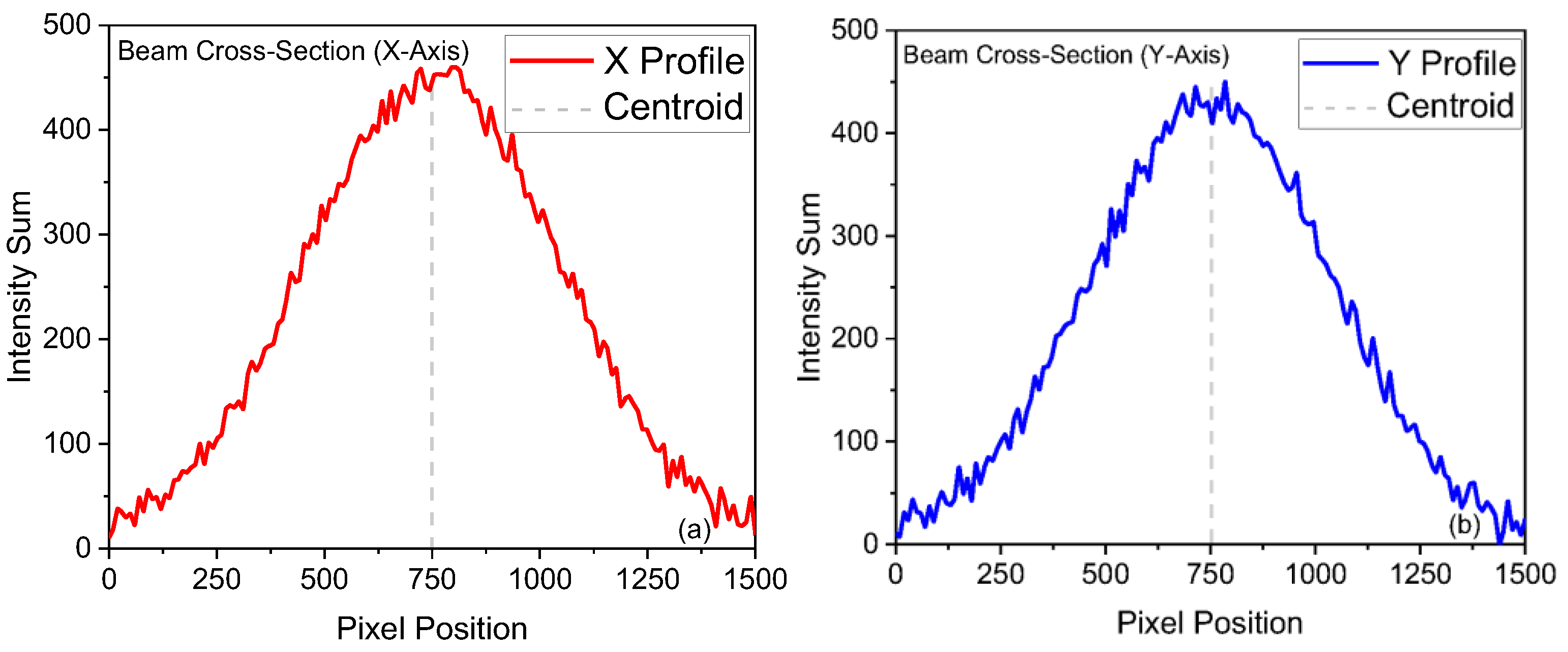
2.2.5. Intensity Cross-Sectional Analysis
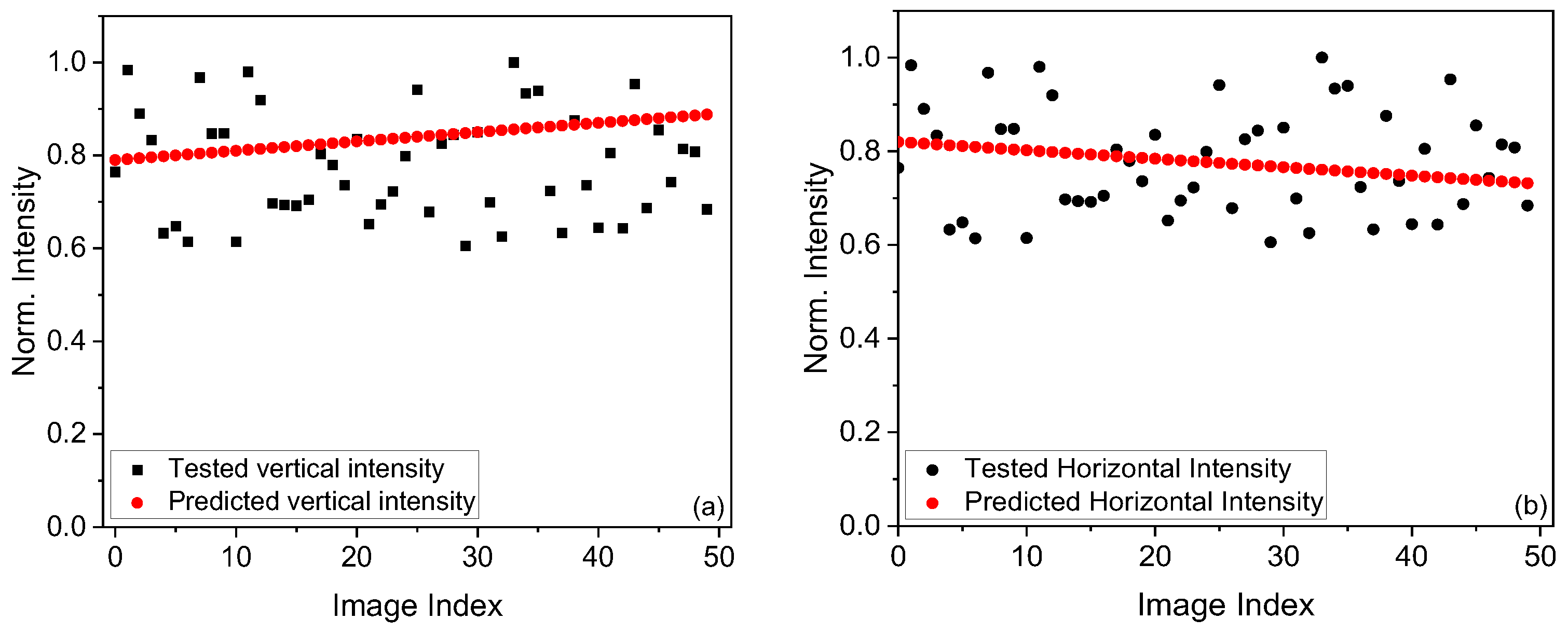
2.3. Predictive Modeling
Linear Regression
3. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Blecher, J.; Palmer, T.A.; Kelly, S.M.; Martukanitz, R.P. Identifying performance differences in transmissive and reflective laser optics using beam diagnostic tools. Weld. J. 2012, 91, 204S–214S. [Google Scholar]
- Chouffani, K.; Harmon, F.; Wells, D.; Jones, J.; Lancaster, G. Laser-Compton scattering as a tool for electron beam diagnostics. Laser Part. Beams 2006, 24, 411–419. [Google Scholar] [CrossRef]
- Dubey, A.K.; Yadava, V. Laser beam machining—A review. Int. J. Mach. Tools Manuf. 2008, 48, 609–628. [Google Scholar] [CrossRef]
- Bolton, P.R.; Borghesi, M.; Brenner, C.; Carroll, D.C.; De Martinis, C.; Fiorini, F.; Flacco, A.; Floquet, V.; Fuchs, J.; Gallegos, P.; et al. Instrumentation for diagnostics and control of laser-accelerated proton (ion) beams. Phys. Medica 2014, 30, 255–270. [Google Scholar] [CrossRef]
- Yang, G.; Liu, L.; Jiang, Z.; Guo, J.; Wang, T. The effect of beam quality factor for the laser beam propagation through turbulence. Optik 2018, 156, 148–154. [Google Scholar] [CrossRef]
- Verhaeghe, G.; Hilton, P. The effect of spot size and laser beam quality on welding performance when using high-power continuous wave solid-state lasers. In ICALEO 2005: 24th International Congress on Laser Materials Processing and Laser Microfabrication; AIP Publishing: Melville, NY, USA, 2005. [Google Scholar]
- Peng, W.; Jin, P.; Li, F.; Su, J.; Lu, H.; Peng, K. A review of the high-power all-solid-state single-frequency continuous-wave laser. Micromachines 2021, 12, 1426. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.; Rolt, S.; Maropoulos, P.G. Modelling and optimization of novel laser multilateration schemes for high-precision applications. Meas. Sci. Technol. 2005, 16, 2541. [Google Scholar] [CrossRef]
- Tan, Y.; Lin, F.; Ali, M.; Su, Z.; Wong, H. Development of a novel beam profiling prototype with laser self-mixing via the knife-edge approach. Opt. Lasers Eng. 2023, 169, 107696. [Google Scholar] [CrossRef]
- Schäfer, B.; Lübbecke, M.; Mann, K. Hartmann-Shack wave front measurements for real time determination of laser beam propagation parameters. Rev. Sci. Instrum. 2006, 77, 053103. [Google Scholar] [CrossRef]
- Zhang, Y.; Gao, Z.; Jin, R.; Zhao, W.; Zhu, L.; Ye, H.; Zhang, Y.; Yang, P.; Wang, S. Multi-line-of-sight Hartmann-Shack wavefront sensing based on image segmentation and K-means sorting. Opt. Express 2024, 32, 15336–15357. [Google Scholar] [CrossRef]
- Kwee, P.; Seifert, F.; Willke, B.; Danzmann, K. Laser beam quality and pointing measurement with an optical resonator. Rev. Sci. Instrum. 2007, 78, 073103. [Google Scholar] [CrossRef]
- Schuhmann, K.; Kirch, K.; Nez, F.; Pohl, R.; Antognini, A. Thin-disk laser scaling limit due to thermal lens induced misalignment instability. Appl. Opt. 2016, 55, 9022–9032. [Google Scholar] [CrossRef]
- Shah, B.K.; Kedia, V.; Raut, R.; Ansari, S.; Shroff, A. Evaluation and comparative study of edge detection techniques. IOSR J. Comput. Eng. 2020, 22, 6–15. [Google Scholar]
- Hernandez-Gonzalez, M.; Jimenez-Lizarraga, M.A. Real-time laser beam stabilization by sliding mode controllers. Int. J. Adv. Manuf. Technol. 2017, 91, 3233–3242. [Google Scholar] [CrossRef]
- Imran, T.; Naeem, M.; Hussain, M. An experimental study of intensity-phase characterization of femtosecond laser pulses propagated through a polymethyl methacrylate. Microw. Opt. Technol. Lett. 2024, 66, e34217. [Google Scholar] [CrossRef]
- Gu, W.; Ruan, D.; Zou, W.; Dong, L.; Sheng, K. Linear energy transfer weighted beam orientation optimization for intensity-modulated proton therapy. Med. Phys. 2021, 48, 57–70. [Google Scholar] [CrossRef] [PubMed]
- Allegre, O.J. Laser Beam Measurement and Characterization Techniques. In Handbook of Laser Micro- and Nano-Engineering; Springer International Publishing: Cham, Switzerland, 2021; pp. 1885–1925. [Google Scholar]
- Rondepierre, A.; Oumbarek Espinos, D.; Zhidkov, A.; Hosokai, T. Propagation and focusing dependency of a laser beam with its aberration distribution: Understanding of the halo induced disturbance. Opt. Contin. 2023, 2, 1351–1367. [Google Scholar] [CrossRef]
- Liu, J.; Tian, X.; Chu, C.; Sui, H.; Zhang, Z.; Liang, D.; Zhang, N.; Lin, L.; Liu, W. Effect of beam ellipticity on femtosecond laser multi-filamentation regulated by π-phase plate. Laser Phys. Lett. 2020, 17, 085402. [Google Scholar] [CrossRef]
- Wellburn, D.; Shang, S.; Wang, S.Y.; Sun, Y.Z.; Cheng, J.; Liang, J.; Liu, C.S. Variable beam intensity profile shaping for layer uniformity control in laser hardening applications. Int. J. Heat Mass Transf. 2014, 79, 189–200. [Google Scholar] [CrossRef]
- Imran, T. Anomaly Detection in ELI-NP Front-end Laser Energy Data Using an Optimized Moving Average Method. Rom. J. Phys. 2025, 70, 902. [Google Scholar]
- Maulud, D.; Abdulazeez, A.M. A review on linear regression comprehensive in machine learning. J. Appl. Sci. Technol. Trends 2020, 1, 140–147. [Google Scholar] [CrossRef]
- Ostertagová, E. Modelling using polynomial regression. Procedia Eng. 2012, 48, 500–506. [Google Scholar] [CrossRef]
- Srilakshmi, U.; Manikandan, J.; Velagapudi, T.; Abhinav, G.; Kumar, T.; Saideep, D. A new approach to computationally-successful linear and polynomial regression analytics of large data in medicine. J. Comput. Allied Intell. 2024, 2, 35–48. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Imran, T.; Naeem, M. Image-Based Laser-Beam Diagnostics Using Statistical Analysis and Machine Learning Regression. Photonics 2025, 12, 504. https://doi.org/10.3390/photonics12050504
Imran T, Naeem M. Image-Based Laser-Beam Diagnostics Using Statistical Analysis and Machine Learning Regression. Photonics. 2025; 12(5):504. https://doi.org/10.3390/photonics12050504
Chicago/Turabian StyleImran, Tayyab, and Muddasir Naeem. 2025. "Image-Based Laser-Beam Diagnostics Using Statistical Analysis and Machine Learning Regression" Photonics 12, no. 5: 504. https://doi.org/10.3390/photonics12050504
APA StyleImran, T., & Naeem, M. (2025). Image-Based Laser-Beam Diagnostics Using Statistical Analysis and Machine Learning Regression. Photonics, 12(5), 504. https://doi.org/10.3390/photonics12050504





