Generation of Longitudinal Bessel Beam Based on Complex Amplitude Metasurface

Abstract

Bessel beams occupy an important position in optical research due to their characteristics of long focal depth, self-healing ability, and diffraction-free propagation. Traditional methods for generating Bessel beams suffer from complexity, a large size, low uniformity, and limited NA. Metasurfaces are considered to be a new technology for the miniaturization of optical devices due to their ability to regulate optical fields at subwavelength scales flexibly. Here, we generated Bessel beams by a complex-amplitude (CA) metasurface. The polarization conversion efficiency was controlled by the geometric size, while the phase value from 0 to 2π was manipulated based on the Pancharatnam–Berry (PB) phase. This approach enabled precise control over the axial intensity distribution of the optical field, which facilitated the generation of sub-millimeter-scale Bessel beams. Axial light field control based on CA metasurfaces has great potential for applications in a variety of fields, such as particle manipulation, large-depth-of-field imaging, and laser processing.

1. Introduction

In 1987, Durnin [1] first put forward Bessel beams as an exact solution for the propagation-invariant mode of the Helmholtz equation. Then, the concept sparked extensive research interest. Zero-order Bessel beams are a fundamental type of non-diffraction beams. Its main characteristic is a bright central spot surrounded by multiple concentric rings. The zero-order Bessel beam maintains its shape during long-distance propagation in free space, with minimal diffraction or distortion. A higher-order Bessel beam is a vortex beam with a helical wavefront and orbital angular momentum. Due to its non-diffracting and self-healing characteristics, the Bessel beam has found extensive applications in optical trapping and particle manipulation [2,3], optical microscopic imaging [4], micro–nano fabrication [5], and femtosecond laser processing [6]. Furthermore, Bessel beams demonstrate potential applications in spatiotemporal light bullets, beam alignment, and plasma channels [7]. Traditionally, Bessel beams are generated using axicon prisms [8,9], diffractive optics [10], three-dimensional phase plates [11], computer-generated holograms [12], or spatial light modulators [13]. For axicon prisms, the full width at half maximum (FWHM) of the generated Bessel beam is inherently constrained. Additionally, due to the effects of total internal reflection and fabrication limitations, these lenses typically exhibit a low numerical aperture (NA). Diffractive optics, typically designed for a specific wavelength, suffer efficiency losses when operated outside their designated range. Three-dimensional phase plates demand high-precision fabrication, which is both costly and time-consuming. Computer-generated holograms introduce additional diffraction orders, leading to noise and an unwanted background that degrade the beam quality and accuracy. While spatial light modulators offer greater flexibility in generating Bessel beams, their performance is constrained by the inherent pixel spacing and relatively large pixel size. In conclusion, these conventional optical components are usually systematically complex and bulky, inefficient, and difficult to fabricate with high precision, which seriously affects the miniaturization and integration of optics and limits the further application of Bessel beams.

Metasurfaces are artificial ultrathin materials composed of two-dimensional arrays of subwavelength structures. Their lightweight, compact design; ease of integration; and flexible programmability have garnered widespread attention. A metasurface composed of single-layer subwavelength metal/dielectric antennas shows great potential for realizing the full control of light, such as modulating the amplitude [14], phase [15], polarization [16], and orbital angular momentum [17,18]. Metasurfaces offer precise and flexible control over optical fields at the subwavelength scale, making them highly promising for applications in holography [19], metalenses [20,21,22], information encryption [23], and nonlinear optics [24].

So far, most studies have focused on metasurfaces that can only modulate the phase or amplitude. In contrast, complex-amplitude metasurfaces have attracted widespread interest due to their ability to independently and flexibly manipulate both the amplitude and phase. Dielectric metasurfaces composed of hybrid meta-atoms or multilayered meta-atom designs based on subwavelength nanostructures have been shown to effectively and independently modulate both the amplitude and phase [25,26,27]. These metasurfaces have been extensively studied for applications in holographic displays, flexible diffraction order manipulation, and anti-counterfeiting [28,29,30]. In Bessel beam generation, the absence of suitable complex-amplitude modulation devices necessitates encoding the computed complex-amplitude optical field into either amplitude or phase information. However, Bessel beam generation using simple phase- or amplitude-only metasurfaces [31,32,33] suffers from drawbacks, such as a reduced beam uniformity and efficiency, as well as limited beam-shaping capabilities. Therefore, exploring Bessel beam generation techniques based on complex amplitude modulation is essential to overcoming these limitations.

Here, we propose and demonstrate a Bessel beam generation device based on a complex amplitude metasurface. The complex amplitude modulation is realized through cross-shaped meta-atoms, with the amplitude regulated by varying the width of one rod and the phase controlled by rotating the meta-atoms in the plane. The encoded complex amplitudes are designed using an optimized Fourier coding method. To achieve precise encoding of the desired complex-amplitude optical field using meta-atoms, a particle swarm optimization (PSO) algorithm was employed to determine the meta-atom distribution that minimized the encoding error. This process was conducted after establishing a library of meta-atom optical responses. The effectiveness of the complex-amplitude-modulated metasurface in generating Bessel beams was then verified through a simulation. In this work, a single cross-shaped meta-atom was used to encode complex amplitude values, simplifying the system design while mitigating the issue of the uneven light intensity distribution caused by phase-only modulation. This approach ensured the generation of higher-quality Bessel beams.

2. Methods and Design

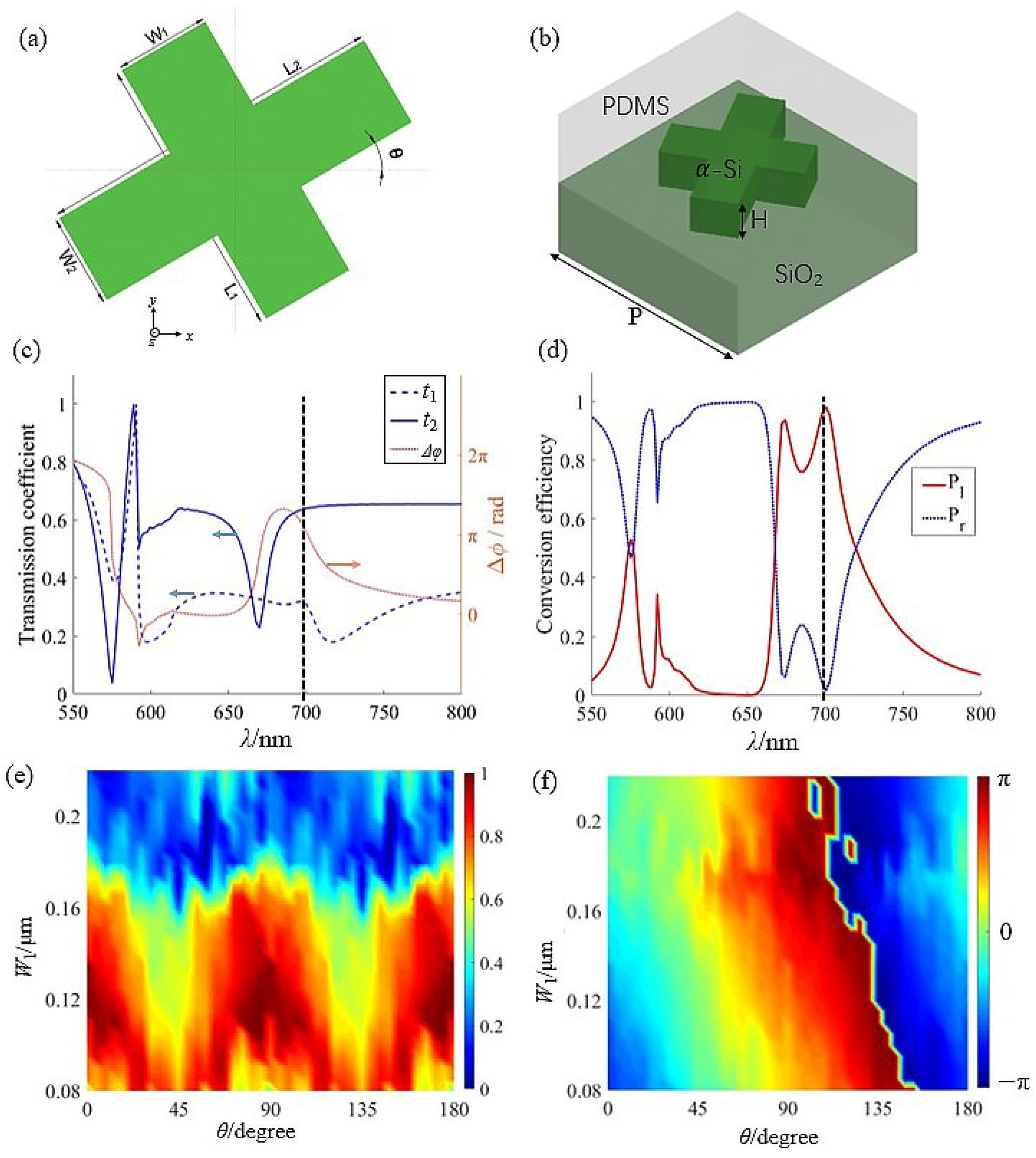
In this paper, we propose an ultra-thin dielectric metasurface with a cross-shaped structure that can independently and simultaneously manipulate arbitrary amplitudes and phases in the visible region. Two amorphous silicon (α-Si) blocks perpendicular to each other were embedded in polydimethylsiloxane (PDMS), with silica as the substrate, as shown in Figure 1a,b. The PDMS layer served two key functions. First, it maintained a significant refractive index contrast (~2.9) between the α-Si meta-atoms and the background material, which facilitated the excitation of higher-order modes to satisfy the Kerker condition and enhance forward scattering. Second, the PDMS layer protected the microstructures from damage caused by dust and scratches.

The modulation of the optical field by the proposed cross-shaped structure can be elucidated by the Jones matrix. As shown in Figure 1a, the local orthogonal coordinate system is assigned as uov, the global coordinate system is xoy, and the angle between u and x is θ. Define the transmission coefficient as $t=A{e}^{\mathrm{i}\phi }$, where A is the amplitude and $\phi$ is the phase. For the meta-atom with circularly polarized basis vectors proposed in this study, the Jones matrix can be expressed as [34]

$$J=\left[\begin{array}{cc}{t}_{RR}& t_{RL}\\ t_{LR}& t_{LL}\end{array}\right]=\left[\begin{array}{cc}{t}_u{\cos }^2\theta +t_v{\sin }^2\theta & (t_u-t_v)(\sin 2\theta )/2\\ (t_u-t_v)(\sin 2\theta )/2& t_u{\sin }^2\theta +t_v{\cos }^2\theta \end{array}\right]$$

(1)

where $t_{RR}$ and $t_{LL}$ represent the transmission coefficients of the right- and left-circularly polarized states, respectively, while $t_{RL}$ and $t_{LR}$ represent the transmission coefficients of the corresponding cross-polarized polarization states $t_u=t_1\exp (j{\phi }_1)$ and $t_v=t_2\exp (j{\phi }_2)$. The output light field of the meta-atom under the irradiation of left- or right-circularly polarized light can be expressed as

$$\left[\begin{array}{c}{E}_{R\mathrm{out}}\\ E_{L\mathrm{out}}\end{array}\right]=J\left[\begin{array}{c}{E}_{R\mathrm{in}}\\ E_{L\mathrm{in}}\end{array}\right]=\left[\begin{array}{cc}{t}_{RR}& t_{RL}{e}^{\mathrm{i}2\theta }\\ t_{LR}{e}^{-\mathrm{i}2\theta }& t_{LL}\end{array}\right]\left[\begin{array}{c}{E}_{R\mathrm{in}}\\ E_{L\mathrm{in}}\end{array}\right]$$

(2)

where $E_{R\mathrm{in}}$ and $E_{L\mathrm{in}}$ represent the RCP/LCP optical input, while the corresponding output light is $E_{R\mathrm{out}}$ and $E_{L\mathrm{out}}$. The amplitude of the transmitted cross-polarized light is governed by the dimensions of the meta-atom, whereas the phase depends on both its size and rotation angle. The incident light is assumed to be left-circularly polarized (LCP), i.e., $E_{R\mathrm{in}}=0$. To achieve the maximum polarization conversion efficiency, $t_{RL}$ needs to be maximized. This requires $t_u=-t_v$, i.e., $t_1=-t_2$ and ${\phi }_1-{\phi }_2=2m\pi +\pi$. To this end, we achieved this goal by optimizing the geometric dimensions of the meta-atom. The optimized structural parameters were L₂ = 300 nm, W₂ = 80 nm, L₁ = 150 nm, W₁ = 90 nm, period P = 420 nm, and height H = 110. We obtained the transmittance and phase difference of the two orthogonal arms, as well as the polarization conversion efficiency (PCE), as shown in Figure 1c,d. It can be seen that the PCE reached its maximum value at a wavelength of 699 nm, at which time the transmittance coefficients of the two arms differed very little, and the phase difference was close to 0.

By adjusting the length and width of these two rectangular elements, the multipole resonances shift gradually, leading to changes in both the PCE and the phase response of the meta-atoms [35]. When W₁ changes from 80 to 220 nm, the phase of the scattered field also changes. This is because the PCE of the atoms gradually deviates from the Kerker condition as the geometry changes [35]. To further achieve decoupled control of the amplitude and phase, the Pancharatnam–Berry (PB) phase is introduced as compensation. Theoretically, this approach enables arbitrary phase control without affecting the PCE. This method realizes the mapping relation for arbitrary complex amplitude control in a simpler and easier way than other structures.

To establish a database of complex amplitude responses, the geometrical parameters were scanned using the FDTD method to extract the polarization conversion efficiency and phase response of the outgoing cross-polarized light under circularly polarized illumination with an incident plane wave with a wavelength of 699 nm while varying the meta-atoms’ width and orientation angle. As shown in Figure 1e,f, the polarization conversion efficiency exhibited an almost monotonic variation from 0 to 1 as W₁ varied. At the same time, in the process of rotating the antenna, the phase changed almost linearly with θ. Although theoretically, the PB phase has no effect on the polarization conversion efficiency, in fact, because each meta-atom of the rotation is not an ideal line without width, its rotation more or less causes fluctuations in the polarization conversion efficiency. When encoding the computed complex amplitude distribution, flexible modulation of arbitrary complex amplitudes can be achieved by finding combinations of the amplitude and phase in Figure 1e,f.

By utilizing a Durnin ring in combination with spatial spectrum optimization, axial beam modulation can be achieved [36]. As shown in Figure 2a, a quasi-Bessel beam is generated near the back focal plane of the lens when a sharp, transparent ring-shaped Durnin mask with radius R is placed in the front focal plane, allowing the incident beam to pass through. This beam exhibits an approximately Gaussian intensity distribution along the z-axis.

Within a cylindrical coordinate framework, the light field associated with any axial intensity profile $I(z)=E{(z)}^2$ can be expressed as a superposition of orthogonal Bessel spatial spectrum components, with each defined by a distinct propagation constant kz:

$$E(r=0,z)={\displaystyle {\int }_0^{k}U\left(\sqrt{k^2-k_z^2},z\right)\exp (i{k}_z}z)k_{z}d{k}_z$$

(3)

Here, $E(r=0,z)$ represents the predefined amplitude function on the axis. $k=2\pi /\lambda$ is the wave number in free space. $U(\cdot )$ denotes the Bessel spectral coefficient.

In order to generate a quasi-Bessel beam with the desired axial envelope profile, it is first necessary to generate the corresponding spatial spectrum. According to the inverse Fourier transform of Equation (3), the spatial spectrum based on the ideal Bessel beam can be expressed as

$$U\left(\sqrt{k^2-k_z^2},z=0\right)={\displaystyle \frac{1}{2\pi k_z}}{\mathcal{F}}^{-1}\left\{E\left(z\right)\exp \left(i{k}_{z0}z\right)\right\}$$

(4)

Here, $k_{z0}$ represents the propagation constant corresponding to the main space spectrum and ${\mathcal{F}}^{-1}$ is the Fourier inverse transform operator. Given the Fourier transform relationship between the Bessel function and the delta function, the complex coefficient in Equation (4) characterizes the complex amplitude distribution in the Fourier spectrum plane, effectively replacing the idealized sharp transparent ring. By setting $E(r=0,z)=\mathrm{rect}(z/a)$ and the width of the rectangular function to a = 1 mm, the rectangular function represents a predefined intensity profile along the axis, which is introduced to indicate that the function is effective only within a finite spatial region. The transmission profile of the corresponding mask is illustrated in Figure 3a. In order to remove the Fourier transform lens in Figure 2a and further reduce the size of the Bessel beam generation device, the Fourier transform operation can be superimposed onto the Durnin ring plane. A schematic of the metasurface assembly is presented in Figure 2b.

To implement the Fourier transform function of the metasurface, we replaced the complex amplitude function at the front focal plane (Equation (4)) with a transfer function. This function accounts for the propagation from the focal plane to the lens surface. The propagation process is modeled by Fresnel diffraction, as described in Equation (4):

$$\begin{array}{l}U\left(x,y\right)=T(x,y){\mathrm{e}}^{i{\phi }_{\mathrm{c}}(x,y)}\\ \propto \mathcal{F}\left\{{\displaystyle \frac{1}{2\pi k_z}}{\mathcal{F}}^{-1}\left\{E\left(z\right)\exp (i{k}_{z0}z)\right\}\exp \left(ik{\displaystyle \frac{x_0^2+y_0^2}{2f}}\right)\right\}\end{array}$$

(5)

where $T\left(x,y\right)$ and ${\phi }_c\left(x,y\right)$ are the transmission amplitude and phase of the metasurface, respectively. $f$ is the focal length and its value was 0.25 mm. Figure 3b,c show the amplitude and phase distributions of the optimized complex amplitude.

The light field distribution loaded on the metasurface is a combination of the complex amplitude distribution of the optimized mask and the phase of the Fourier lens. The optimized mask is calculated according to Equation (5). Assuming that the focal point of the Fourier transform lens is $f$, the phase profile of the lens can be expressed as $\varphi =2\pi (f-\sqrt{r^2+f^2})/\lambda$. By applying this phase function to the complex amplitude, the final complex amplitude $T\cdot \exp [\mathrm{i}({\phi }_c+\varphi )]$ is obtained, as illustrated in Figure 4. To accurately find the meta-atom that can encode the required complex amplitude in the scanned meta-atom library, we used the particle swarm optimization (PSO) algorithm [37]. PSO is a global optimization technique based on swarm intelligence and is known for its easy implementation and high search efficiency. Compared with traditional gradient-based methods, PSO does not rely on derivative information and is more effective at avoiding local optimality. This optimization process minimizes the matching error by selecting from a precomputed database containing the complex-amplitude responses of scanned meta-atoms. To achieve precise control over both the amplitude and phase of the transmitted light, it is essential to accurately engineer the complex transmission coefficient of each unit cell. Therefore, the optimization must simultaneously account for both the amplitude and phase errors, rather than addressing them separately. In this work, the PSO algorithm was utilized to minimize the complex amplitude difference between the target and searched values, with the objective function defined as |A_texp(iφ_t) − A_sexp(iφ_s)|, where A_t and φ_t represent the target amplitude and phase, and A_s and φ_s correspond to the amplitude and phase of the selected meta-atom. The amplitude and phase distributions that minimized the matching error searched in the meta-atoms library are shown in Figure 4. It can be seen that the complex amplitude values mapped to the search parameter $A_s\exp ({\phi }_s)$ were very close to the theoretical value $A_t\exp ({\phi }_t)$, and the errors between the searched amplitude (phase) values and the actual amplitude (phase) values were mostly around zero.

3. Results and Discussion

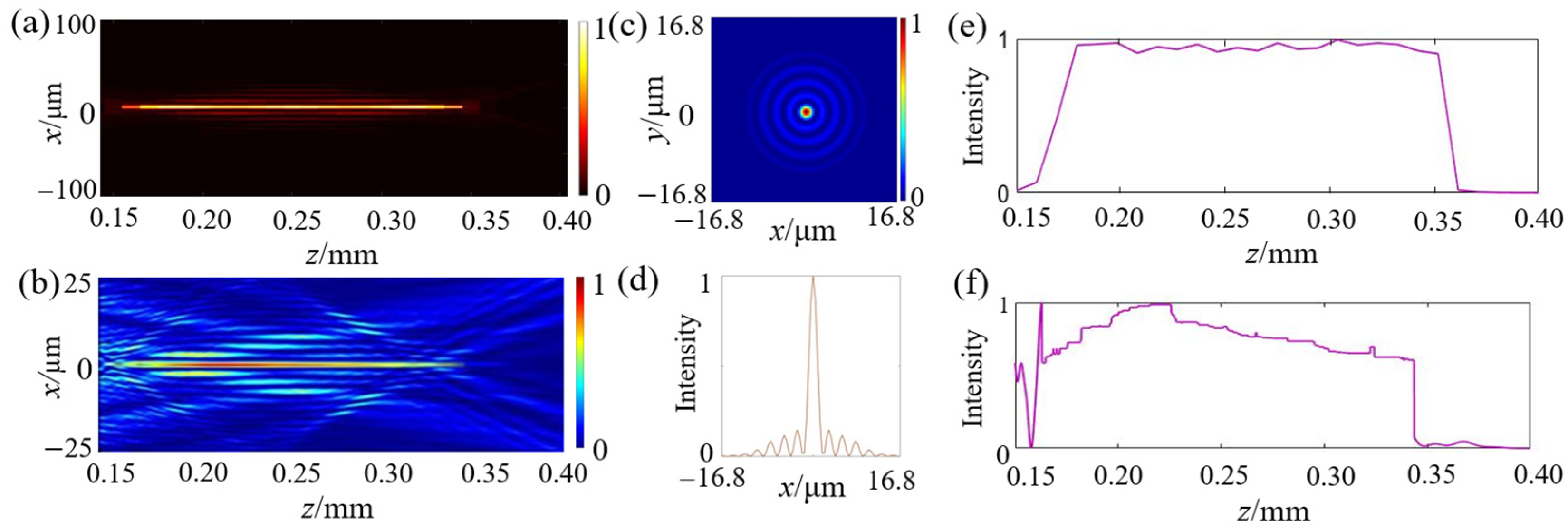
To verify the effectiveness of the proposed complex-amplitude metasurface for generating Bessel beams, we computed and encoded 600 × 600 meta-atoms. Using Fresnel diffraction, the complex amplitude response optimized by the PSO algorithm was propagated to the specified distance, which yielded the intensity distributions in both the xz- and xy-planes, as shown in Figure 5. The corresponding calculated and simulated axial intensity distributions are also depicted. In the range of z = 0.15 mm to 0.35 mm, the beam showed almost no diffraction transmission and presented a uniform intensity distribution. The beams appeared uniform, but there were still some fluctuations. This perturbation primarily arose from the truncation of higher-order spatial frequency components. The finite aperture of the metasurface lens limited the transmission of Bessel beam components with large transverse wavevectors, thereby restricting the constructive interference required for proper beam formation and reducing the uniformity of the intensity distribution. Therefore, in the design of metasurfaces, it is crucial to consider the role of the aperture in modulating the angular spectrum to optimize the beam quality and enhance the stability. To mitigate the adverse effects caused by a limited aperture, several strategies may be adopted. The most straightforward approach is to enlarge the physical size of the metasurface, enabling it to support a broader range of spatial frequencies, and thus, accommodate more high-order spectral components critical for beam shaping. In addition, spatial-frequency-selective absorption or gradient modulation mechanisms can be introduced into the structural design. Furthermore, applying spectral-domain pre-compensation in the complex-amplitude calculation stage is another viable solution. By enhancing or weighting high-frequency components during the target field inversion process, the adverse effects of spectral truncation can be partially compensated, thereby improving the quality of the reconstructed beam.

Conventional Fourier spectral masks typically respond only to the amplitude or phase [36,38], which limits their ability to be used in complex light field modulation. In contrast, the optimized mask is capable of controlling both the amplitude and phase, thus improving the efficiency of the optical transmission. This can be seen from the comparison of the region with non-zero amplitude shown in Figure 3a and Figure 4, where the optimized mask significantly enlarged the transmission region. Additionally, complex-amplitude modulation using the metasurface offers a compact solution. For example, compared with the longitudinal beam generation method that relies on a Durnin ring and Fourier lens, as shown in Figure 2, the metasurface integrates both functions into a single device, thereby achieving the functionality of two separate elements in one. Amplitude-modulated metasurfaces can control the intensity of the transmitted light but lack phase control, which limits their ability to precisely shape or focus a beam. As a result, they are typically less efficient and less stable, making them less ideal for applications that require tightly focused beams. Phase modulation metasurfaces can shape the transmitted wavefront, enabling the generation of specific beams, but they often produce beams with a non-uniform intensity and weaker overall performance, limiting their efficiency and practical applicability. In contrast, complex-amplitude metasurfaces enable simultaneous control of both the amplitude and phase, offering greater flexibility and precision in Bessel beam generation. This dual modulation leads to beams with higher intensity, sharper focus, and more stable propagation, significantly outperforming amplitude-only and phase-only metasurfaces. As a result, the generated Bessel beams maintain a superior shape and intensity over longer distances, enhancing their applicability in advanced optical systems.

The previous validation of the quality of the generated Bessel beam based on the searched complex amplitude did not take into account the coupling and crosstalk between the individual nanopillars in the metasurface device. Here, we used the time-domain finite-difference method (FDTD) for the full-wave simulation to verify the quality of the generated Bessel beam. In simulations, the more pixels contained in the metasurface used, the better the distribution of the generated Bessel beam, but this poses a challenge for computational resources. Note that the complex amplitude distribution calculated in Figure 4 is circularly symmetric, so we can only took the middle column of meta-atoms for the simulation. When the boundary conditions were set, the y-axis direction was set as periodic boundary conditions, and the x-axis direction was set as PML conditions. Figure 5b shows the intensity distribution of the simulated x–z cross-section, and Figure 5c,d correspond to the intensity distribution of the xy-plane at z = 0.25 mm and the intensity distribution along the x-axis, respectively, which conformed to the characteristics of Bessel beam. The subwavelength characteristics of the generated Bessel beam were further evaluated by calculating the full width at half maximum (FWHM) of the intensity distribution at the focal plane using numerical simulations, which resulted in a FWHM of approximately 1.765 μm. The generated Bessel beam maintained good focusing performance within a certain distance and the wavefront remained relatively flat. The Bessel beam obtained from the FDTD simulation exhibited energy attenuation due to medium properties and boundary conditions, which resulted in a reduction in the main lobe intensity compared with the ideal case. However, it still retained high intensity in the far-field region. Future improvements can be made by optimizing the PML absorbing boundary and the computational grid resolution to minimize errors and enhance the beam quality.

4. Conclusions

In conclusion, we present a complex-amplitude modulation method based on a metasurface for the efficient generation of high-quality Bessel beams. By combining the cross-shaped meta-atoms with PB phase modulation, independent and precise control of the optical field amplitude and phase was achieved. The simulation results demonstrate that the generated beam exhibited excellent non-diffraction characteristics. Compared with conventional optical elements, complex-amplitude metasurface designs exhibit the advantages of small size, high integration, and high flexibility. The use of meta-atoms with higher degrees of freedom is expected to offer greater flexibility for more complex optical field modulations, such as polarization-correlation longitudinal optical field modulation and achromatic longitudinal optical field modulation. The results demonstrate that the proposed method not only significantly enhances the imaging efficiency and quality of Bessel beams but also provides a novel approach for generating complex optical fields, positioning it as a promising technology for applications in optical trapping, laser processing, optical communications, and precision imaging. Furthermore, by optimizing the multi-dimensional light field control characteristics of complex-amplitude meta-atoms combined with inverse design algorithms, such as neural networks, it can be extended to the customized generation of higher-order Bessel beams.