Ultra-Compact Multimode Micro-Racetrack Resonator Based on Cubic Spline Curves
Abstract
1. Introduction
2. Design and Simulation
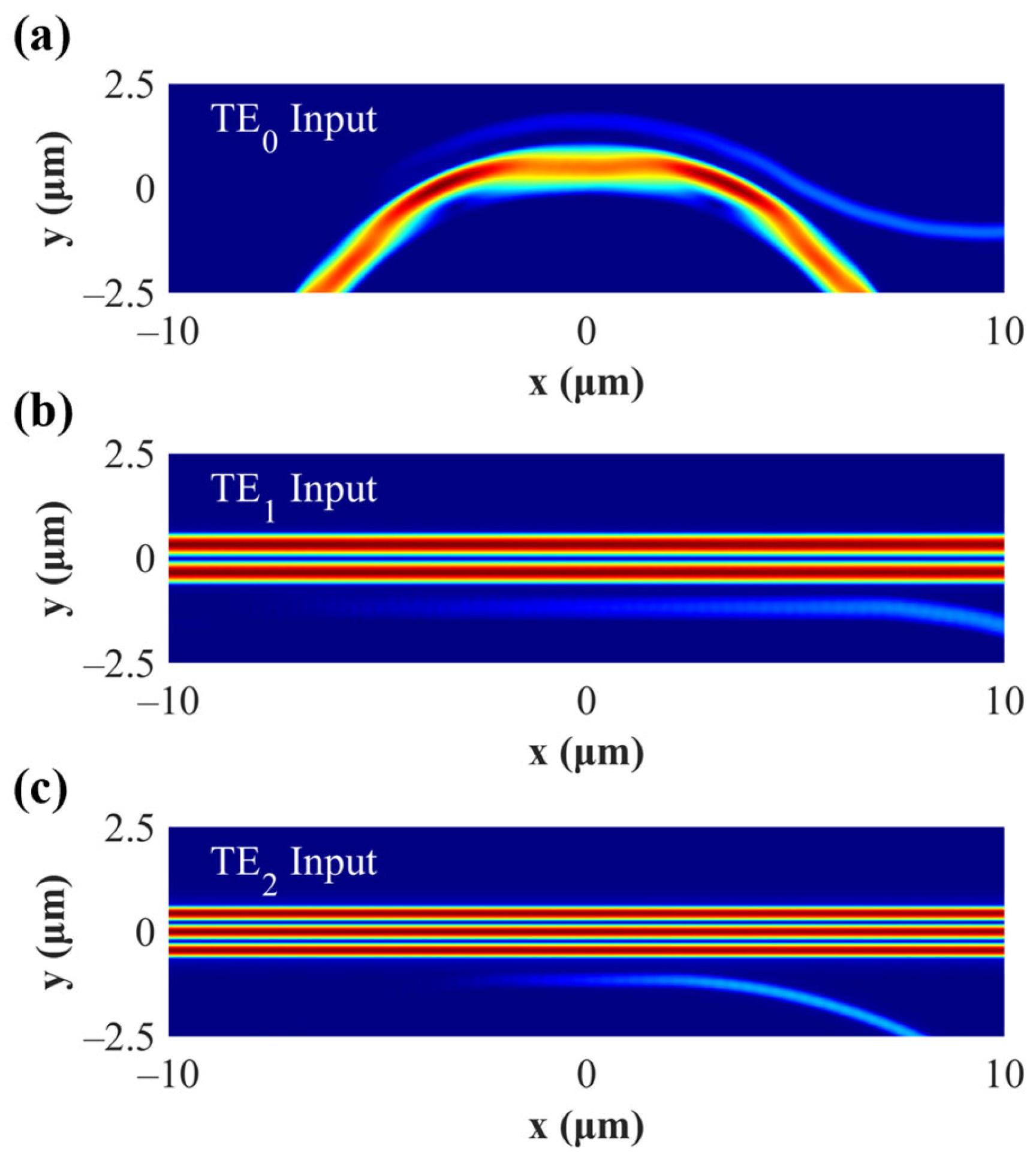
2.1. The Design of Multimode Waveguide Bend (MWB)
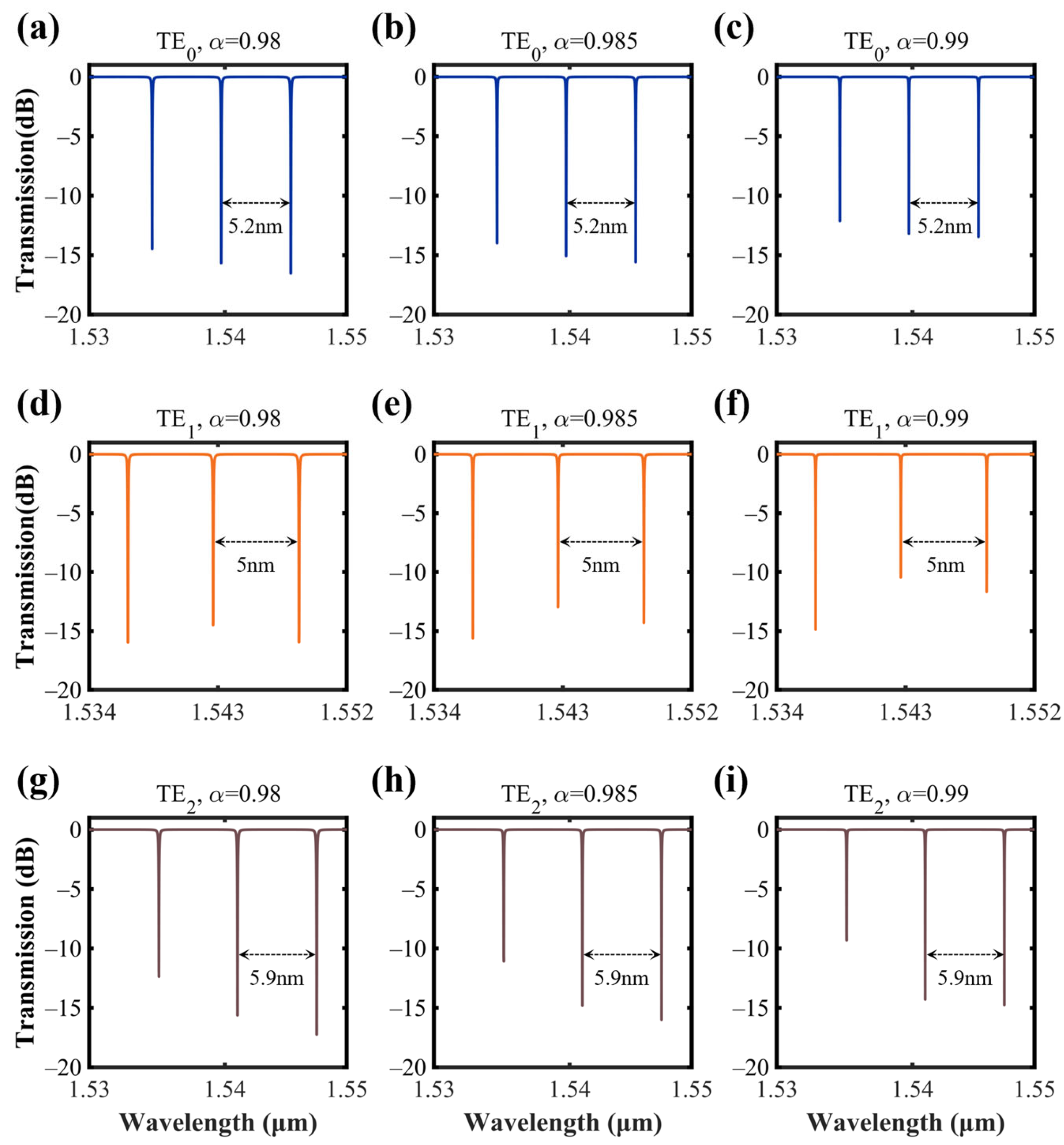
2.2. The Design of Multimode Micro-Racetrack Resonator (MMRR)
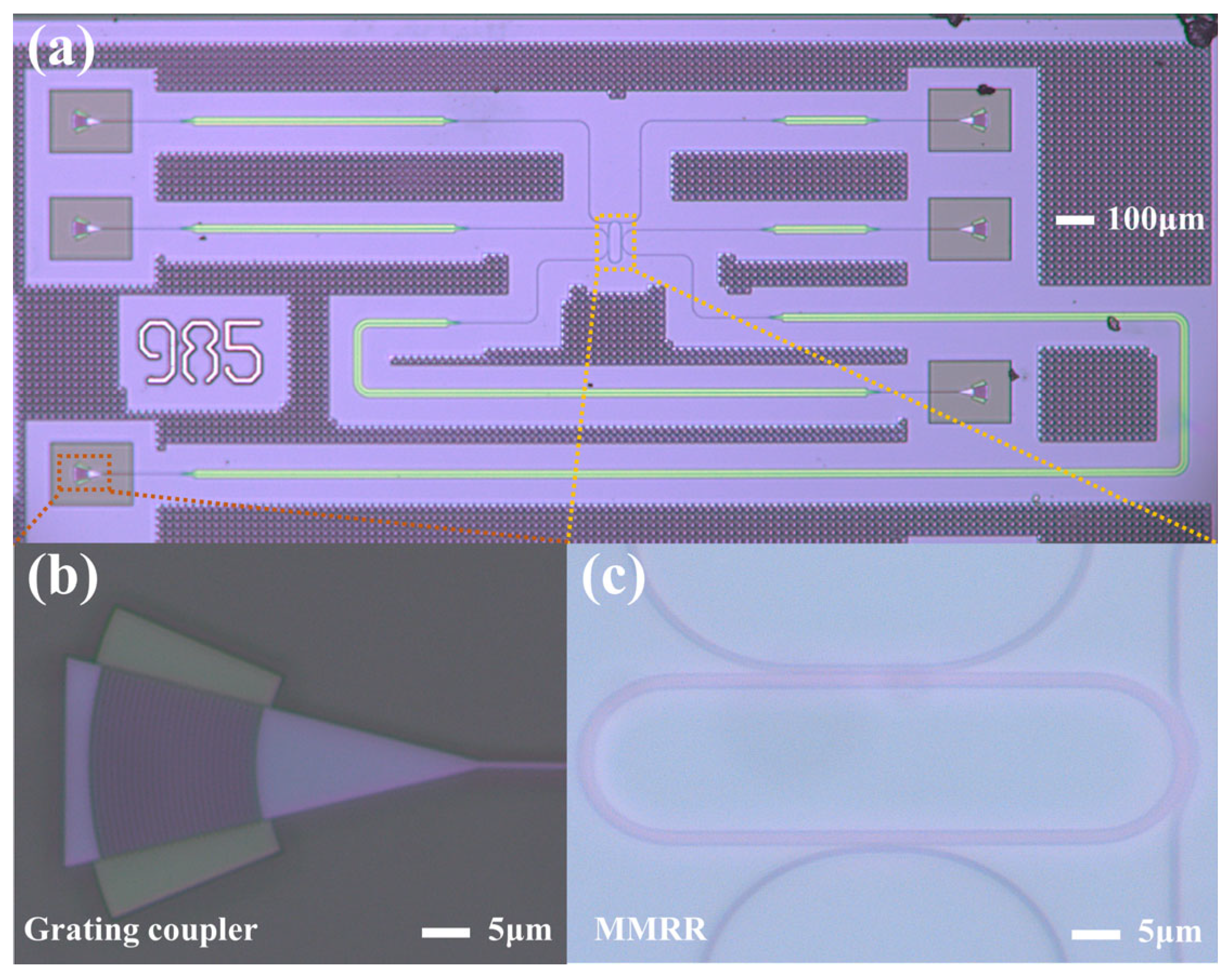
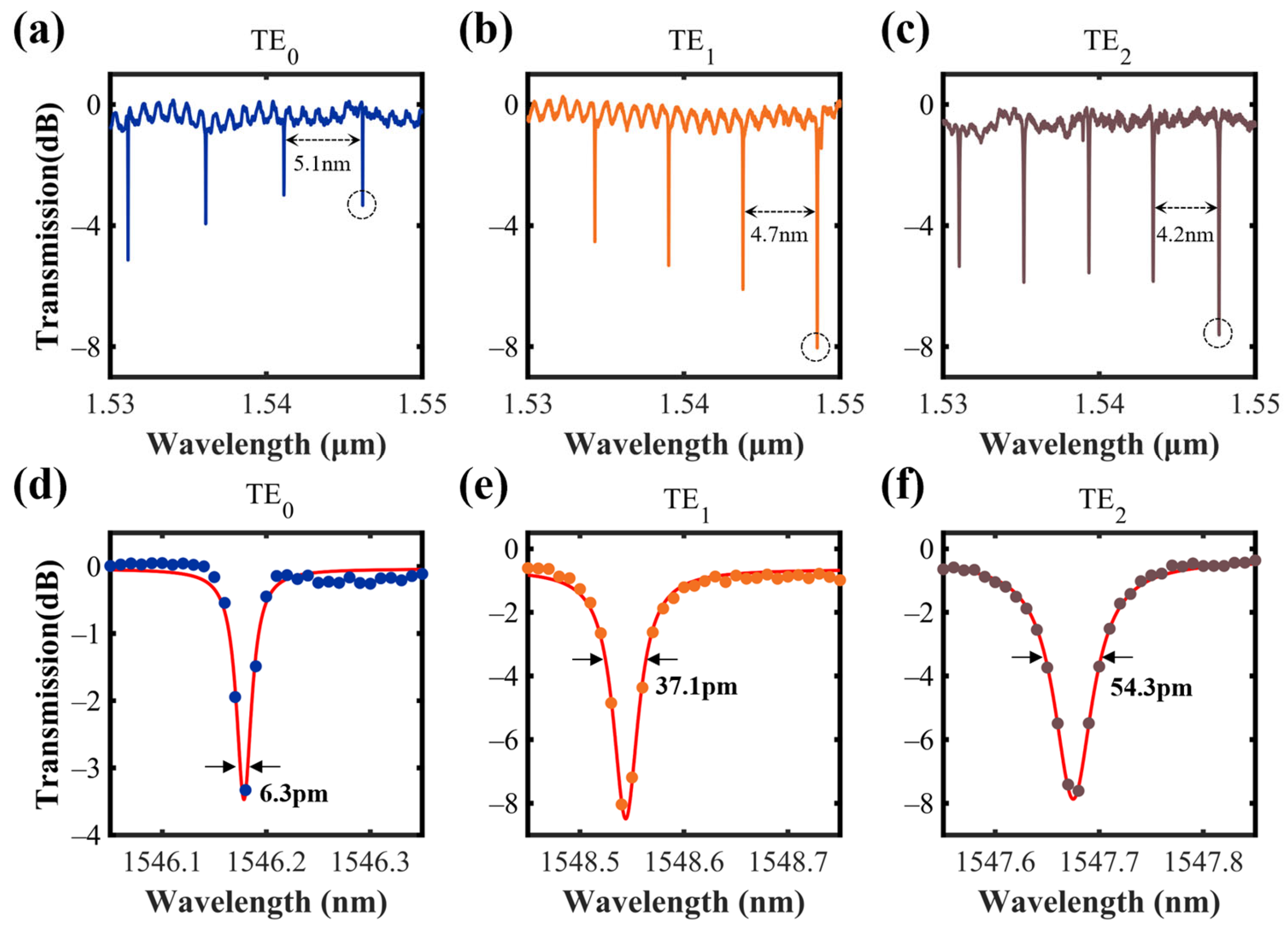
3. Fabrication and Characterization
4. Discussions
4.1. Performance Comparison
4.2. Loaded Q Factor
4.3. Fabrication Errors
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MMRR | multimode micro-racetrack resonator |
| MWB | multimode waveguide bend |
| ADC | asymmetric directional coupler |
| FSR | free spectral range |
| MDM | mode division multiplexing |
| SWG | subwavelength grating |
| IL | insertion loss |
| TIR | total internal reflection |
| SOI | silicon-on-insulator |
| FOM | figure-of-merit |
| FDTD | finite-difference time-domain |
| ER | extinction ratio |
| EBL | electron beam lithography |
| LNOI | lithium-niobate-on-insulator |
| AlGaAsOI | AlGaAs-on-insulator |
| MSMMR | multiple single mode micro-racetracks |
| OSA | optical spectrum analyzer |
| ASE | amplified spontaneous emission |
| TO | transformation optics |
References
- Yao, J.; Capmany, J. Microwave Photonics. Sci. China Inf. Sci. 2022, 65, 221401. [Google Scholar] [CrossRef]
- Marpaung, D.; Yao, J.; Capmany, J. Integrated Microwave Photonics. Nat. Photon. 2019, 13, 80–90. [Google Scholar] [CrossRef]
- Eppenberger, M.; Messner, A.; Bitachon, B.I.; Heni, W.; Blatter, T.; Habegger, P.; Destraz, M.; De Leo, E.; Meier, N.; Del Medico, N.; et al. Resonant Plasmonic Micro-Racetrack Modulators with High Bandwidth and High Temperature Tolerance. Nat. Photon. 2023, 17, 360–367. [Google Scholar] [CrossRef]
- Kashi, A.A.; Van Der Tol, J.J.G.M.; Lebby, M.S.; Zhang, X.; Williams, K.; Jiao, Y. Ring-Assisted Mach-Zehnder Modulator on the InP Membrane on Silicon Platform. J. Light. Technol. 2024, 42, 4553–4562. [Google Scholar] [CrossRef]
- Green, W.M.J.; Lee, R.K.; DeRose, G.A.; Scherer, A.; Yariv, A. Hybrid InGaAsP-InP Mach-Zehnder Racetrack Resonator for Thermooptic Switching and Coupling Control. Opt. Express 2005, 13, 1651–1659. [Google Scholar] [CrossRef]
- Xu, H.-H.; Huang, Q.-Z.; Li, Y.-T.; Yu, Y.-D.; Yu, J.-Z. Sub-Nanosecond Optical Switch Based on Silicon Racetrack Resonator. Chin. Phys. B 2010, 19, 084210. [Google Scholar] [CrossRef]
- Tao, Z.; Tao, Y.; Jin, M.; Qin, J.; Chen, R.; Shen, B.; Wu, Y.; Shu, H.; Yu, S.; Wang, X. Highly Reconfigurable Silicon Integrated Microwave Photonic Filter towards Next-Generation Wireless Communication. Photon. Res. 2023, 11, 682. [Google Scholar] [CrossRef]
- Yan, H.; Xie, Y.; Zhang, L.; Dai, D. Wideband-Tunable on-Chip Microwave Photonic Filter with Ultrahigh-Q U-Bend-Mach–Zehnder-Interferometer-Coupled Microring Resonators. Laser Photonics Rev. 2023, 17, 2300347. [Google Scholar] [CrossRef]
- Zhao, W.; Peng, Y.; Cao, X.; Zhao, S.; Liu, R.; Wei, Y.; Liu, D.; Yi, X.; Han, S.; Wan, Y.; et al. 96-Channel on-Chip Reconfigurable Optical Add-Drop Multiplexer for Multidimensional Multiplexing Systems. Nanophotonics 2022, 11, 4299–4313. [Google Scholar] [CrossRef]
- James, A.; Novick, A.; Rizzo, A.; Parsons, R.; Jang, K.; Hattink, M.; Bergman, K. Scaling Comb-Driven Resonator-Based DWDM Silicon Photonic Links to Multi-Tb/s in the Multi-FSR Regime. Optica 2023, 10, 832. [Google Scholar] [CrossRef]
- Yi, X.; Zhao, W.; Li, C.; Zhang, L.; Xiang, Y.; Liu, C.; Shi, Y.; Liu, L.; Dai, D. Reconfigurable Optical Add-Drop Multiplexers for Hybrid Mode-/Wavelength-Division-Multiplexing Systems. Adv. Photon. Nexus 2023, 2, 066004. [Google Scholar] [CrossRef]
- Mojaver, K.R.; Safaee, S.M.R.; Morrison, S.S.; Liboiron-Ladouceur, O. Recent Advancements in Mode Division Multiplexing for Communication and Computation in Silicon Photonics. J. Light. Technol. 2024, 42, 7860–7870. [Google Scholar] [CrossRef]
- Li, C.; Liu, D.; Dai, D. Multimode Silicon Photonics. Nanophotonics 2019, 8, 227–247. [Google Scholar] [CrossRef]
- Wu, X.; Huang, C.; Xu, K.; Shu, C.; Tsang, H.K. Mode-Division Multiplexing for Silicon Photonic Network-on-Chip. J. Light. Technol. 2017, 35, 3223–3228. [Google Scholar] [CrossRef]
- Dai, D.; Li, C.; Wang, S.; Wu, H.; Shi, Y.; Wu, Z.; Gao, S.; Dai, T.; Yu, H.; Tsang, H. 10-Channel Mode (de)Multiplexer with Dual Polarizations. Laser Photonics Rev. 2018, 12, 1700109. [Google Scholar] [CrossRef]
- Zhao, W.; Yi, X.; Peng, Y.; Zhang, L.; Chen, H.; Dai, D. Silicon Multimode Waveguide Crossing Based on Anisotropic Subwavelength Gratings. Laser Photonics Rev. 2022, 16, 2100623. [Google Scholar] [CrossRef]
- Chang, W.; Zhang, M. Silicon-Based Multimode Waveguide Crossings. J. Phys. Photonics 2020, 2, 022002. [Google Scholar] [CrossRef]
- Liu, R.; Lu, L.; Zhang, P.; Chang, W.; Liu, D.; Zhang, M. Integrated Dual-Mode 3-dB Power Splitter Based on Multimode Interference Coupler. IEEE Photon. Technol. Lett. 2020, 32, 883–886. [Google Scholar] [CrossRef]
- Sun, S.; Fu, Y.; Li, S.; Ning, X.; Zhou, Z.; Zhang, D.; Wang, X. Ultra-Broadband Multimode Fiber-to-Chip Edge Coupler Based on Periodically Segmented Waveguides. Opt. Lett. 2024, 49, 6061. [Google Scholar] [CrossRef]
- Zhang, R.; Li, X.; He, Y.; Chen, G.; Xiong, L.; Chen, H.; Fontaine, N.K.; Zhang, Y.; Xie, W.; Su, Y. Ultra-High Bandwidth Density and Power Efficiency Chip-To-Chip Multimode Transmission through a Rectangular Core Few-Mode Fiber. Laser Photonics Rev. 2023, 17, 2200750. [Google Scholar] [CrossRef]
- Dai, D.; Bowers, J.E. Silicon-Based on-Chip Multiplexing Technologies and Devices for Peta-Bit Optical Interconnects. Nanophotonics 2014, 3, 283–311. [Google Scholar] [CrossRef]
- Jiang, X.; Wu, H.; Dai, D. Low-Loss and Low-Crosstalk Multimode Waveguide Bend on Silicon. Opt. Express 2018, 26, 17680–17689. [Google Scholar] [CrossRef] [PubMed]
- Sun, C.; Yu, Y.; Chen, G.; Zhang, X. Ultra-Compact Bent Multimode Silicon Waveguide with Ultralow Inter-Mode Crosstalk. Opt. Lett. 2017, 42, 3004. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Li, C.; Song, L.; Tsang, H.-K.; Bowers, J.E.; Dai, D. Ultra-Sharp Multimode Waveguide Bends with Subwavelength Gratings. Laser Photonics Rev. 2019, 13, 1800119. [Google Scholar] [CrossRef]
- Li, W.; Chen, J.; Zhu, M.; Dai, D.; Shi, Y. Ultra-Compact Multimode Waveguide Bend With Optimized Dual Bezier Contours. IEEE Photon. Technol. Lett. 2023, 35, 1131–1134. [Google Scholar] [CrossRef]
- Li, S.; Cai, L.; Gao, D.; Dong, J.; Hou, J.; Yang, C.; Chen, S.; Zhang, X. Compact and Broadband Multimode Waveguide Bend by Shape-Optimizing with Transformation Optics. Photon. Res. 2020, 8, 1843. [Google Scholar] [CrossRef]
- Sun, S.; Dong, P.; Zhang, F.; Wang, J.; Zhu, N.; Shi, Y. Inverse Design of Ultra-Compact Multimode Waveguide Bends Based on the Free-Form Curves. Laser Photonics Rev. 2021, 15, 2100162. [Google Scholar] [CrossRef]
- Sun, S.; Yang, Z.; Wang, J.; Zhang, R.; Zhang, F.; Zhu, N.; Wan, L.; Li, Z. Ultra-Sharp Silicon Multimode Waveguide Bends Based on Double Free-Form Curves. Photonics Res. PRJ 2022, 10, 1484–1490. [Google Scholar] [CrossRef]
- Tan, J.; Xiao, H.; Ma, M.; Zhou, X.; Yuan, M.; Dubey, A.; Boes, A.; Nguyen, T.G.; Ren, G.; Su, Y.; et al. Arbitrary Access to Optical Carriers in Silicon Photonic Mode/Wavelength Hybrid Division Multiplexing Circuits. Opt. Lett. 2022, 47, 3531. [Google Scholar] [CrossRef]
- Cai, L.; Gao, D.; Dong, J.; Hou, J.; Yang, C.; Chen, S.; Zhang, X. Compact and High Q-Factor Multimode Racetrack Ring Resonator Based on Transformation Optics. Opt. Express 2022, 30, 15766. [Google Scholar] [CrossRef]
- Chen, Z.; Ye, M.; Zhang, L.; Zhang, Q. Compact mode-insensitive ring resonator based on SWG coupler and Euler bends. In Proceedings of the AOPC 2021: Micro-Optics and MOEMS, Beijing, China, 20–22 June 2021; Volume 12066, pp. 144–149. [Google Scholar]
- Wei, C.; Li, J.; Jia, Q.; Li, D.; Liu, J. Ultrahigh-Q Lithium Niobate Microring Resonator with Multimode Waveguide. Opt. Lett. 2023, 48, 2465. [Google Scholar] [CrossRef] [PubMed]
- Ye, C.; Liu, Y.; Zhou, Y.; Zhao, Y.; Zheng, Y.; Kim, C.; Oxenløwe, L.K.; Yvind, K.; Pu, M. Multimode AlGaAs-on-Insulator Microring Resonators for Nonlinear Photonics. IEEE J. Sel. Top. Quantum Electron. 2024, 30, 1–11. [Google Scholar] [CrossRef]
- Ye, M.; Sun, C.; Yu, Y.; Ding, Y.; Zhang, X. Silicon Integrated Multi-Mode Ring Resonator. Nanophotonics 2021, 10, 1265–1272. [Google Scholar] [CrossRef]
- Yang, S.; Jia, H.; Niu, J.; Fu, X.; Yang, L. CMOS-Compatible Ultra-Compact Silicon Multimode Waveguide Bend Based on Inverse Design Method. Opt. Commun. 2022, 523, 128733. [Google Scholar] [CrossRef]
- Dou, T.; Yue, S.; Hou, Y.; Wang, R.; Shi, H.; Li, Y.; Feng, Y.; Zhang, Z. Ultra-Sharp Multimode Waveguide Bends Based on Superellipse Curves and Shallowly Etched Nanoslots Designed by an Intelligent Algorithm. J. Light. Technol. 2024, 42, 5249–5261. [Google Scholar] [CrossRef]
- Liao, J.; Tian, Y.; Yang, Z.; Xu, H.; Dai, T.; Zhang, X.; Kang, Z. Broadband and Compact Silicon Multimode Waveguide Bends Based on Hybrid Shape Optimization. J. Light. Technol. 2024, 42, 4882–4891. [Google Scholar] [CrossRef]
- Zhang, E.; Yang, S.; Zhang, L. General Waveguide Bend Design Based on Cubic Spline Interpolation and Inverse Design. J. Light. Technol. 2024, 42, 4614–4625. [Google Scholar] [CrossRef]
- Lalau-Keraly, C.M.; Bhargava, S.; Miller, O.D.; Yablonovitch, E. Adjoint Shape Optimization Applied to Electromagnetic Design. Opt. Express 2013, 21, 21693. [Google Scholar] [CrossRef]
- Georgieva, N.K.; Glavic, S.; Bakr, M.H.; Bandler, J.W. Feasible Adjoint Sensitivity Technique for EM Design Optimization. IEEE Trans. Microw. Theory Tech. 2002, 50, 2751–2758. [Google Scholar] [CrossRef]
- Cheng, C.; Yang, S.; Liu, W.; Liu, S.; Huo, Y.; Fu, X.; Yang, L. Ultra-Compact Inverse Designed Multimode Waveguide Bend Based on Levelset Method. IEEE Photonics Technol. Lett. 2024, 36, 571–574. [Google Scholar] [CrossRef]
- Teytaud, O.; Bennet, P.; Moreau, A. Discrete Global Optimization Algorithms for the Inverse Design of Silicon Photonics Devices. Photonics Nanostruct.-Fundam. Appl. 2022, 52, 101072. [Google Scholar] [CrossRef]
- Haus, H.A.; Huang, W. Coupled-Mode Theory. Proc. IEEE 1991, 79, 1505–1518. [Google Scholar] [CrossRef]
- Dai, D.; Bowers, J.E. Novel Ultra-Short and Ultra-Broadband Polarization Beam Splitter Based on a Bent Directional Coupler. Opt. Express 2011, 19, 18614–18620. [Google Scholar] [CrossRef]
- McKinnon, W.R.; Xu, D.X.; Storey, C.; Post, E.; Densmore, A.; Delâge, A.; Waldron, P.; Schmid, J.H.; Janz, S. Extracting Coupling and Loss Coefficients from a Ring Resonator. Opt. Express 2009, 17, 18971. [Google Scholar] [CrossRef]





| α | θ (Degree) | (μm) | (μm) |
|---|---|---|---|
| 0.98 | 62.57 | 12.74 | 3.27 |
| 0.985 | 51.4 | 10.57 | 2.3 |
| 0.99 | 42.86 | 8.03 | 1.28 |
| Ref. | Method | Radius (μm) | FSR (nm) | Loaded Q | Modes | Fabrication | Platform |
|---|---|---|---|---|---|---|---|
| [29] | MSMMR | Rmax = 1000, Rmin = 30 * | 1.34 | \ | 3 TE | EBL | SOI |
| [30] | TO | 15 | 3.7 | 5.9 × 104 | 3 TE | EBL | SOI |
| [31] | SWG | Rmax = 600, Rmin = 10 * | 3.8 | \ | 2 TE | \ | SOI |
| [32] | Euler curve | Rmax = 250, Rmin = 130 * | 0.45 | 4.1 × 106 | 1 TE | EBL | LNOI |
| [33] | Taper waveguide | 25 | 2.1 | 7.8 × 105 | 2 TE | EBL | AlGaAsOI |
| [34] | TIR | \ | 6.65 | 7300 | 4 TE | EBL | SOI |
| This work | Cubic spline curve | 8 | 5.1 | 2.3 × 105 | 3 TE | Lithography | SOI |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Cheng, C.; Fu, X.; Yang, L. Ultra-Compact Multimode Micro-Racetrack Resonator Based on Cubic Spline Curves. Photonics 2025, 12, 326. https://doi.org/10.3390/photonics12040326
Li Z, Cheng C, Fu X, Yang L. Ultra-Compact Multimode Micro-Racetrack Resonator Based on Cubic Spline Curves. Photonics. 2025; 12(4):326. https://doi.org/10.3390/photonics12040326
Chicago/Turabian StyleLi, Zhen, Chuang Cheng, Xin Fu, and Lin Yang. 2025. "Ultra-Compact Multimode Micro-Racetrack Resonator Based on Cubic Spline Curves" Photonics 12, no. 4: 326. https://doi.org/10.3390/photonics12040326
APA StyleLi, Z., Cheng, C., Fu, X., & Yang, L. (2025). Ultra-Compact Multimode Micro-Racetrack Resonator Based on Cubic Spline Curves. Photonics, 12(4), 326. https://doi.org/10.3390/photonics12040326




