VCSELs with Stable Linear Polarization Emission Induced by Dielectric Columnar Thin Film Mirrors

Abstract

We propose and analyze numerically new approaches to force the laser emission from VCSELs in a well-defined linear polarization independent of the existing phase and amplitude anisotropies by using dielectric columnar thin-film (CTF) layers in the distributed Bragg reflector (DBR). In one approach, we have demonstrated CTF-VCSELs with top DBR consisting of two alternating CTF layers grown in orthogonally oriented planes and with high and low refractive index for one linear polarization while having the same value of the refractive index value for the orthogonal linear polarization. Such CTF-VCSELs have large dichroism of the mirror losses for two orthogonal linear polarizations. We have also shown DBR designs with parallel columnar orientations of the two CTF dielectric materials. In a second approach, we implement only one CTF layer in the dielectric DBR chosen in such a way that only one linearly polarized longitudinal mode is resonant in the CTF-VCSEL while light with the orthogonally oriented linear polarization is out of resonance and thus cannot lase. Simple estimation of the polarization mode suppression ratio for the different exemplary designs of CTF-VCSELs based on $Ti{O}_2$ and $Ta{O}_2$ dielectric CTFs results in values as high as 80 dB, which compares favorably to the existing alternative approaches.

1. Introduction

Vertical-Cavity Surface-Emitting Lasers (VCSELs) are notorious for their unstable polarization emission. In fact, as first reported in [1] VCSELs typically emit a linear polarization (LP) at the threshold but switch abruptly to the orthogonal LP as the current is increased [2,3]. Higher order transverse modes also appear in orthogonal polarization to the principle one of the fundamental mode [1]. Polarization instabilities occur in VCSELs due to the surface emission perpendicular to the active quantum wells, making conduction band to heavy hole band transitions dominant with the same transition matrix element for any LP direction in the quantum well plane [4,5]. In addition, the cylindrical symmetry of the VCSELs removes the waveguiding and reflectivity anisotropies. Due to the lack of strong polarization anisotropy, several physical mechanisms can lead to polarization instabilities, such as the relative change of the net modal gains and losses with the injection current [2], spatial hole burning [6] or microscopic spin-flip processes in the presence of birefringence and linewidth enhancement factor [5,7] (for a review see [3]).

A great deal of work has been devoted to stabilizing VCSEL polarization by introducing polarization-dependent gain or loss. These include etching of rectangular or elliptical mesas [8,9,10], fabricating anisotropic apertures [11,12], introducing anisotropic mechanical strain [13,14], etching metal-dielectric grating [15] or subwavelength grating [16], growth on misoriented substrates [17], intracavity patterning [18], etc. Most of these approaches are usually rather difficult to implement and often provide limited enhancement of polarization stabilization.

Herein, we propose a new type of VCSEL with stable LP emission independent of the existing phase and amplitude anisotropies and transverse modal structure by using columnar thin-film (CTF) layers in the VCSEL dielectric distributed Bragg mirror (DBR). The birefringent multilayer CTF structure allows great flexibility in controlling the polarization dependence of the VCSEL resonator finesse and hence the threshold gain for two orthogonal LPs. The paper is organized as follows: in Section 2 we introduce the notion of VCSEL with a dielectric columnar thin-film mirror: CTF-VCSEL. To this aim, we first describe the design of CTF-VCSEL in Section 2.1. In Section 2.2 we briefly describe the optics of the anisotropic columnar thin films and present the empirical formulas for determining their refractive indices. Then we investigate in detail two cases of different orientations of the pair of two columnar thin films with high and low refractive indices in the laser DBR: in two orthogonal to each other planes in Section 2.3 and in the same plane in Section 2.4. In Section 3 we take a different approach to the problem of polarization stabilization of VCSELs, namely, we utilize the polarization-dependent phase-change on reflection from the CTF distributed Bragg mirrors for creating a preferable orientation of one linear polarization. In Section 4, we quantify the results of polarization stabilization of VCSELs by our CTF technique by introducing the polarization mode suppression ratio (MSR) as a measure. We then compare our results with published results from alternative techniques. As this section makes it clear, our CTF VCSEL designs compare very favorably with the alternative approaches, achieving a much higher polarization MSR of around 80 dB. We also describe briefly the experimental approach to manufacturing CTF VCSELs. Finally, in Section 5 we summarize our results on CTF-VCSELs.

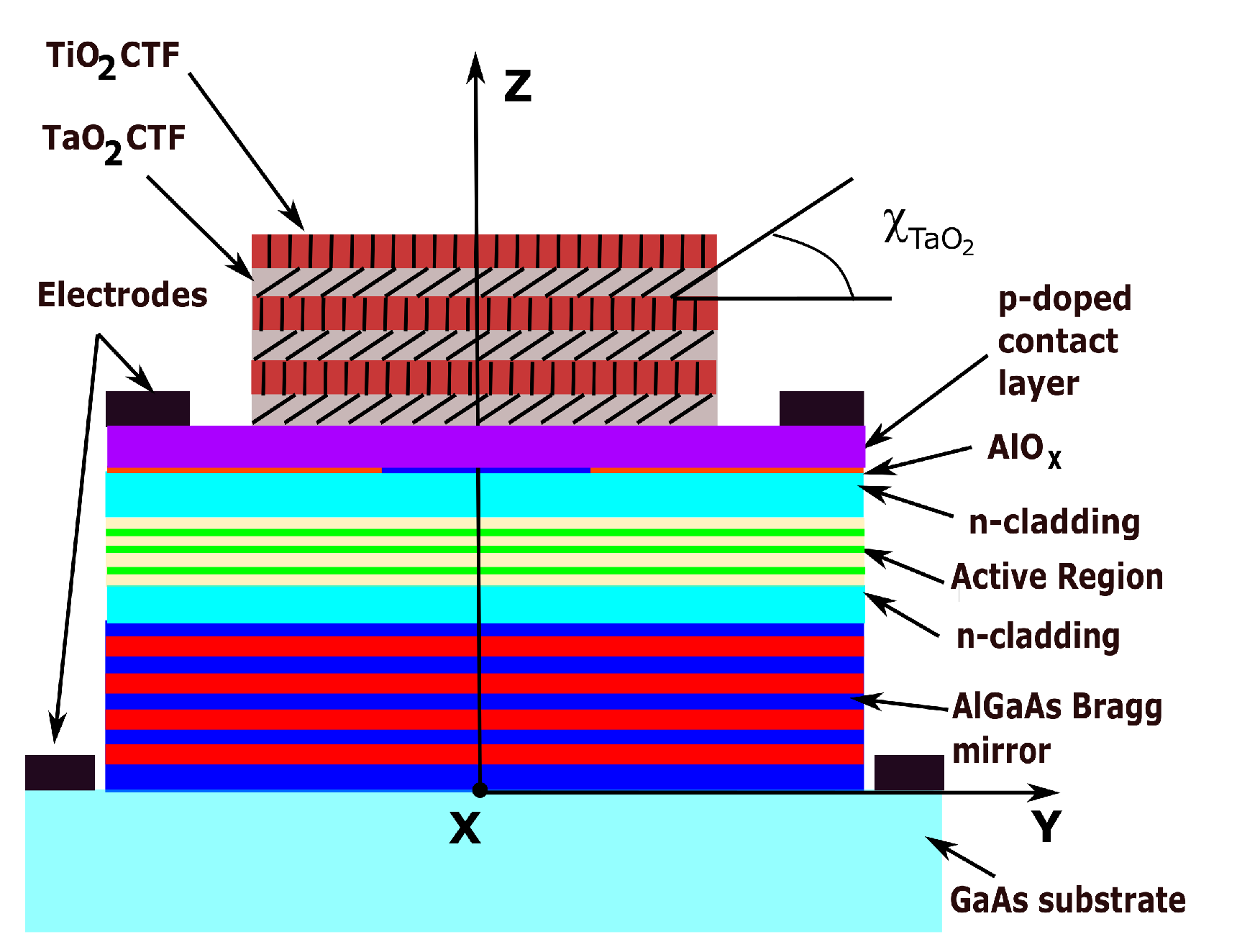
2. VCSEL with a Dielectric Columnar Thin-Film Mirror

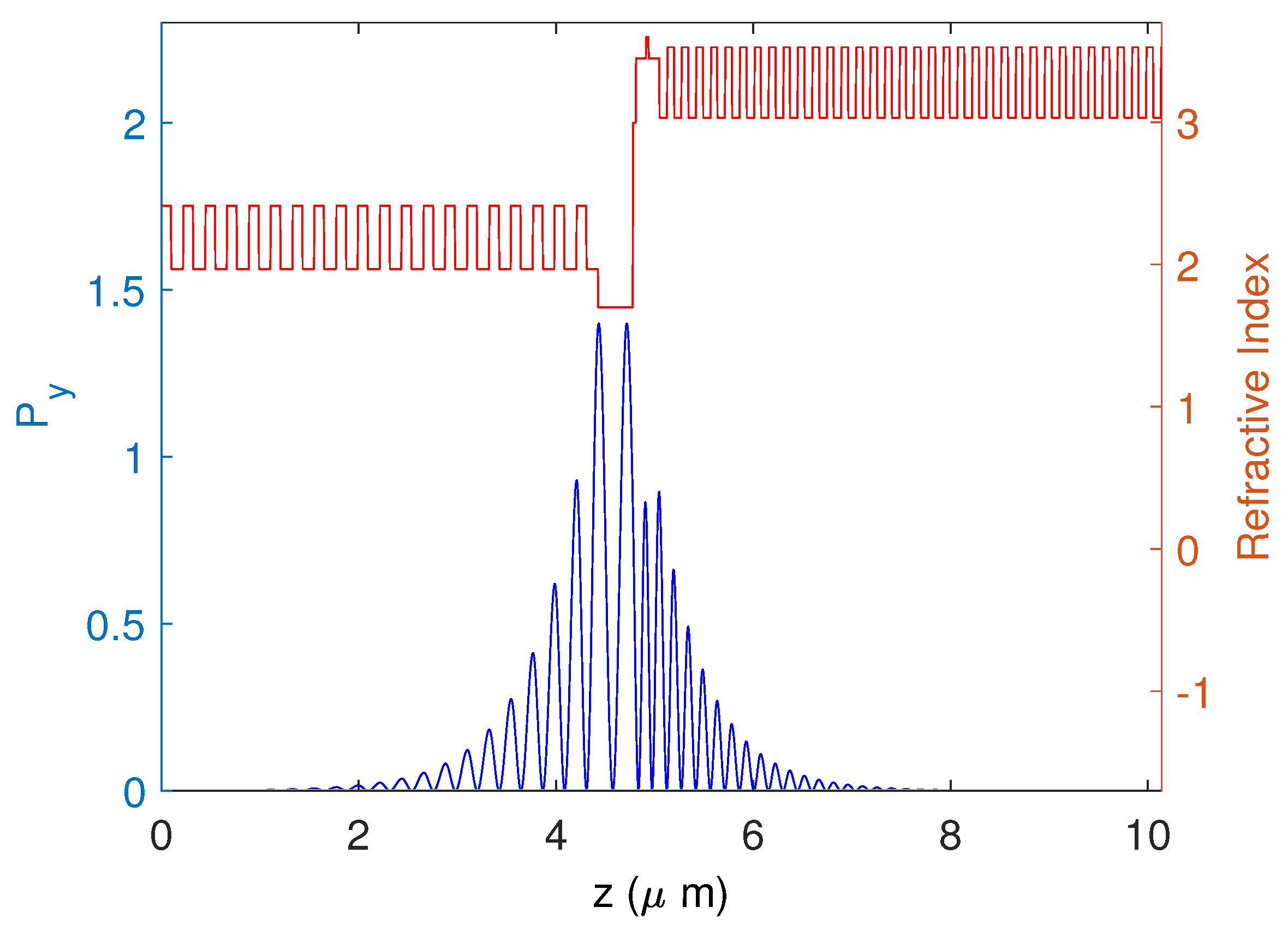
2.1. Design of CTF-VCSEL

The proposed CTF-VCSEL is independent of the specific material system as the only change in the VCSEL structure is the inclusion of the dielectric DBR with CTF layers, i.e., it is independent of the VCSEL emission wavelength. As an example, we consider a standard GaAs-based VCSEL structure designed for emission at 0.96 $\mathsf{\mu }$m, but replacing its AlGaAs-based top mirror with a dielectric one. The schematic of the CTF-VCSEL structure is shown in Figure 1. The standard half-VCSEL structure consists of 35 pairs of N-doped $A{l}_{0.12}G{a}_{0.88}As$ and $A{l}_{0.9}G{a}_{0.1}As$$\lambda /4$ layers forming the bottom DBR; a $\lambda$ thick cavity with 3 $InGaAs$ quantum wells topped by a 30 nm $A{l}_{0.98}G{a}_{0.02}As$ layer for lateral oxidation confinement and a p-doped layer for intracavity contact. For specificity, we consider titanium oxide ($Ti{O}_2$) and tantalum oxide ($Ta{O}_2$) for the CTF dielectric DBR. The pair of $Ti{O}_2$ and $Ta{O}_2$ CTF layers are deposited at an angle ${\chi }_v$ to form the top DBR. These layers and the orientation of the columnar stacks are shown schematically in Figure 1, which illustrates the case where the vapor evaporation angles are in two orthogonal planes: $yz$ for $Ta{O}_2$ and $xz$ for $Ti{O}_2$.

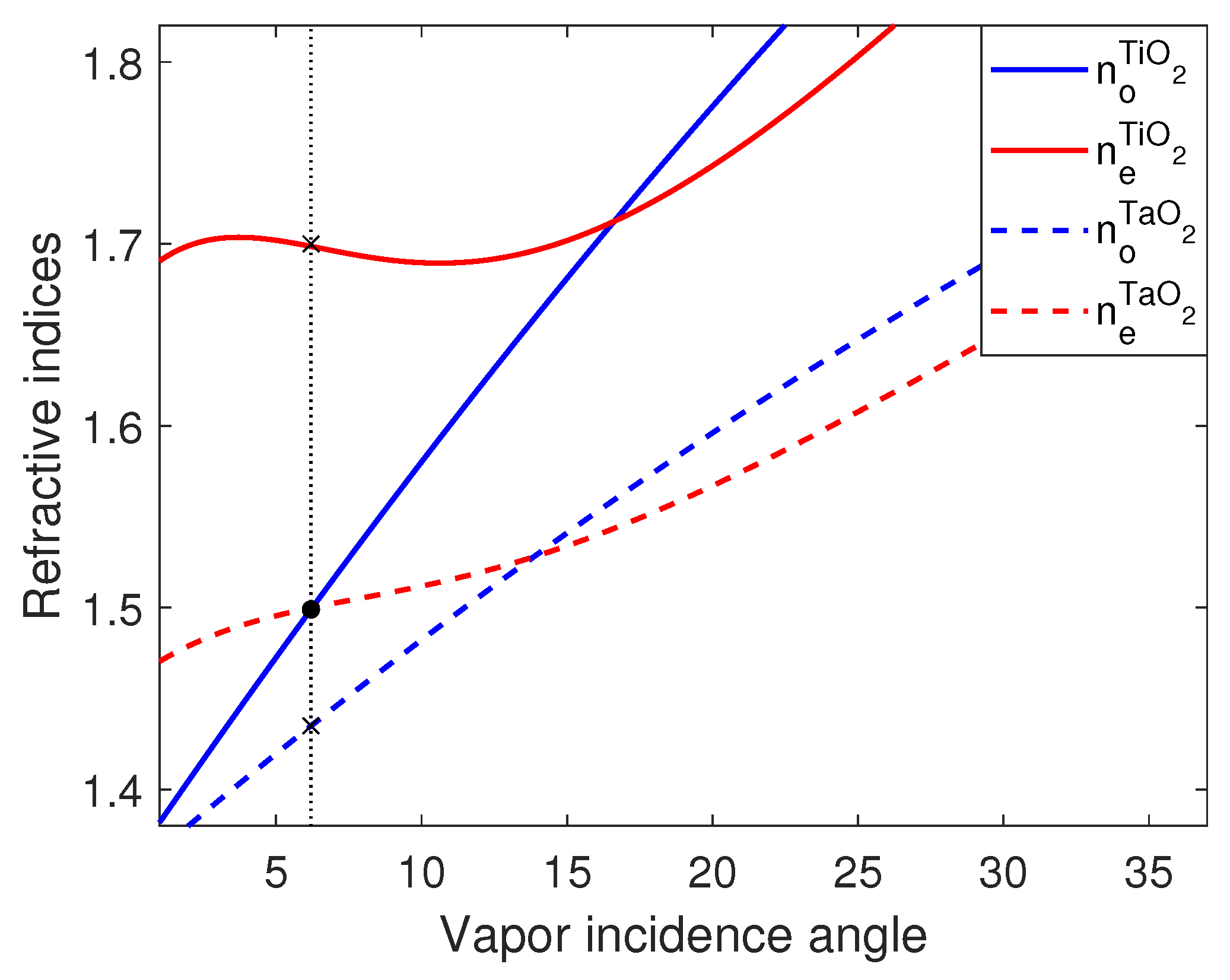
2.2. Columnar Thin Films

The actual orientation of the CTF columnar structures is tilted in the corresponding planes by angles $\chi$ which are related to the vapor deposition angle ${\chi }_v$ by [19,20,21,22].

$${\chi }_i=arctan[M_{t,i}·tan\left({\chi }_{v,i}\right)],$$

(1)

with $i=Ti{O}_2,Ta{O}_2$. For the case of $Ta{O}_2$ CTF, whose vapor incidence plane (also called morphologically significant plane) is the $yz$ plane, the angle ${\chi }_{Ta{O}_2}$ is shown in Figure 1. Similarly, the $Ti{O}_2$ columns, whose vapor incidence plane is the $xz$ plane, make an angle ${\chi }_{Ti{O}_2}$ with the x-axis. The CTF layers are characterized by three main dielectric susceptibilities ${ϵ}_{a,b,c}$ given by the following empirical expressions [21,22]

$$\begin{array}{ccc}\hfill {ϵ}_a& =& a_0+a_1\ast v+a_2\ast v^2,\hfill \\ \hfill {ϵ}_b& =& b_0+b_1\ast v+b_2\ast v^2,\hfill \\ \hfill {ϵ}_c& =& c_0+c_1\ast v+c_2\ast v^2.\hfill \end{array}$$

(2)

Here, $v={\chi }_v/(\pi /2)$ and $a_i$,$b_i$ and $c_i$, ($i=1,2,3$) are empirically determined constants for the specific dielectric materials—see

Table 1. $Ti{O}_2$ and $Ta{O}_2$ CTF parameters [21,22].

Parameter	${\mathit{TiO}}_2$	${\mathit{TaO}}_2$
$a_0$	$1.0443$	$1.1961$
$a_1$	$2.7394$	$1.5439$
$a_2$	$-1.3697$	$-0.7719$
$b_0$	$1.6765$	$1.4600$
$b_1$	$1.5649$	$1.0400$
$b_2$	$-0.7825$	$-0.5200$
$c_0$	$1.3586$	$1.3532$
$c_1$	$2.1109$	$1.2296$
$c_2$	$-1.0554$	$-0.6148$
$M_t$	$2.8818$	$3.1056$

.

In general, light propagation in a medium with biaxial dielectric susceptibility according to Equation (2) is mathematically described by the 4 × 4 transfer matrix method [23]. However, when the light propagates in the morphologically significant planes $xz$ and $xy$, the 4 × 4 matrices are decomposed into two 2 × 2 matrices for light polarized in the x and y directions [22]. Furthermore, for normal incidence, as in our case of Figure 1, the eigenvalues of the 2 × 2 matrix take a very simple form and give the conventional ordinary and extraordinary refractive indices given by

$$\begin{array}{ccc}\hfill n_o& =& \sqrt{{ϵ}_c},\hfill \\ \hfill n_e& =& \sqrt{{ϵ}_d},\hfill \end{array}$$

(3)

with

$${ϵ}_d={\displaystyle \frac{{ϵ}_a{ϵ}_b}{{ϵ}_a{cos}^2\chi +{ϵ}_b{sin}^2\chi }}.$$

(4)

Here, $n_o$ ($n_e$) refers to linearly polarized light with the electric vector perpendicular (parallel) to the morphologically significant plane.

Figure 2 shows the ordinary and extraordinary refractive indices of $Ti{O}_2$ and $Ta{O}_2$ as a function of the vapor incidence angle ${\chi }_v$, calculated by Equations (1)–(4). Remarkably, the curves of $n_o^{Ti{O}_2}$ (solid blue line) and $n_e^{Ta{O}_2}$ (dashed red line) cross for ${\chi }_v=6.{25}^{\circ }$. Therefore, for a multilayer structure evaporated at such angles, light linearly polarized in the x-direction propagating along the z-axis will not see abrupt interfaces at the boundaries of the two different CTF media. However, light of wavelength $\lambda$ polarized along the y direction will see a DBR if the layer thicknesses are $d^{Ti{O}_2}=\lambda /\left(4n_o^{Ti{O}_2}\right)$ and $d^{Ta{O}_2}=\lambda /\left(4n_e^{Ta{O}_2}\right)$.

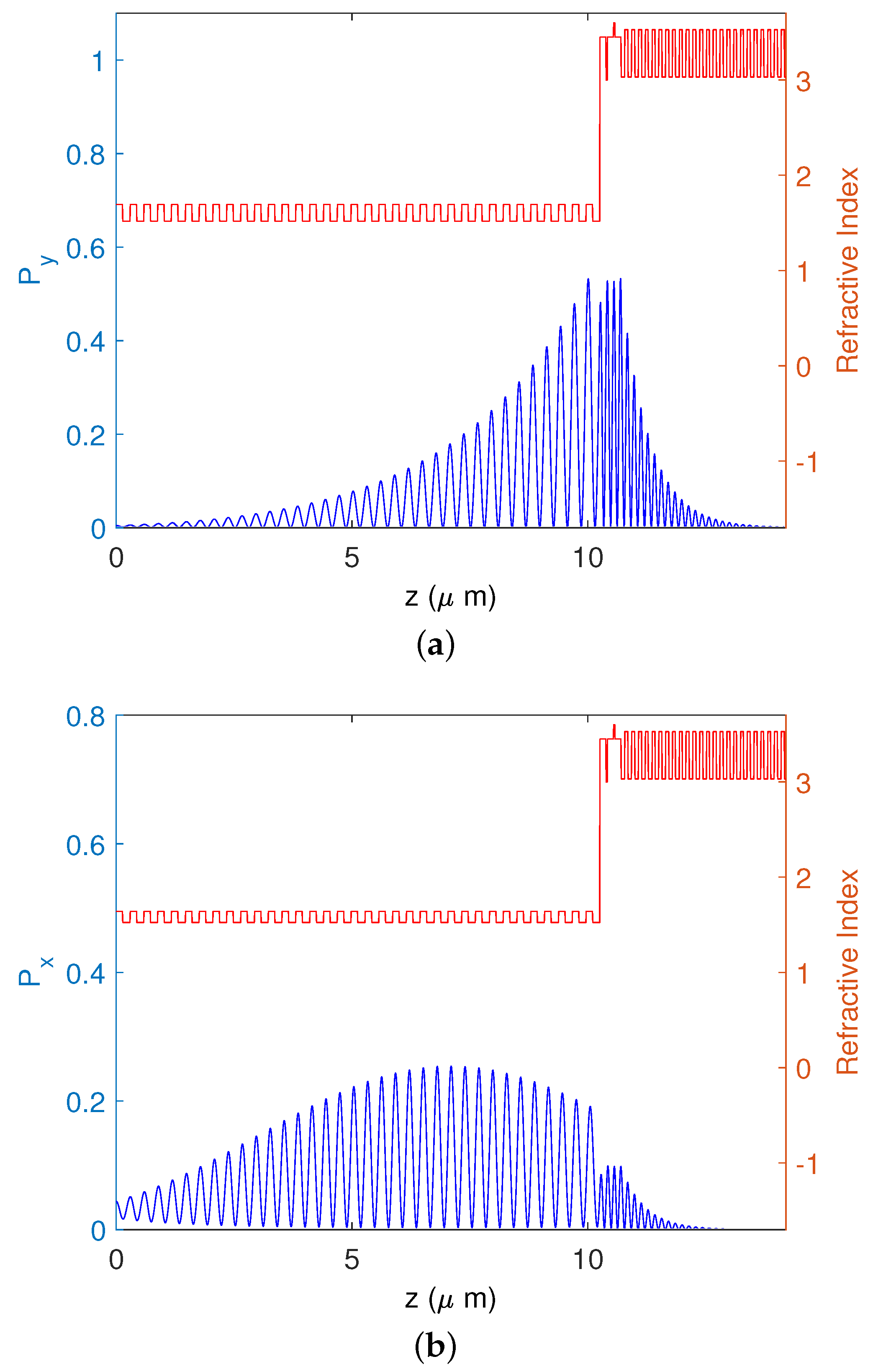
2.3. VCSEL with Orthogonally Oriented Pair of Columnar Thin-Film Layers

Due to the significant simplification of the problem of light propagation in the CTF-DBR as given by Equations (3) and (4), our procedure for finding the longitudinal resonance wavelengths of the CTF-VCSEL and their corresponding threshold gains is based on the 2 × 2 transfer matrix method [24]. An implicit characteristic equation is obtained by imposing the condition that there is no incident field on the whole CTF-VCSEL multilayer structure [25]. The complex implicit characteristic equation is then solved for two variables, namely the resonant wavelength and the optical gain in the quantum wells [25].

First, we consider the case where the vapor evaporation angles of the two quarter-wave layers with high and low refractive indices are made of CTF materials with columnar tilt angles lying in two orthogonal planes. Figure 1 schematically shows these layers and the orientation of their columnar stacks: $yz$ for $Ta{O}_2$ and $xz$ for $Ti{O}_2$. Figure 3 shows the calculated normalized optical power distribution along the CTF-VCSEL structure for two orthogonally polarized resonant modes for the case of ${\chi }_v=6.2^{\circ }$ (the black dashed vertical line in Figure 2) for 30 pairs of $Ti{O}_2$ and $Ta{O}_2$ CTF layers. Figure 3a shows the case of y polarization with a resonance wavelength of ${\lambda }_y=0.967$ μm and a quite reasonable threshold gain of $g_y^{th}=712$ cm⁻¹. In this case, the refractive indices of the constituent layers of the CTF multilayer are different, namely $n_e^{Ti{O}_2}=1.6986$ and $n_e^{Ta{O}_2}=1.4356$, and the resulting top DBR confines the light well in the CTF-VCSEL. Figure 3b shows the case of x polarization with a resonance wavelength of ${\lambda }_x=0.9787$ $\mathsf{\mu }$m and a huge threshold gain of $g_x^{th}=140,958$ cm⁻¹. In this case, the refractive indices of the $Ti{O}_2$ and $Ta{O}_2$ layers in the CTF stack are the same, namely $n_o^{Ti{O}_2}=n_e^{To{O}_2}=1.5$, and the light does not see the top DBR of the CTF-VCSEL, but rather a thick homogeneous layer. The huge difference in the threshold gains for the two orthogonal LPs reflects the huge dichroism in their mirror losses: clearly only the y polarized light will be generated in the CTF-VCSEL designed in this way, even in the presence of amplitude and phase anisotropies. Furthermore, this extremely large dichroism will also affect the polarization of the higher-order transverse modes.

In fact, one does not need as large a dichroism as discussed so far to produce polarization-stable emission. Figure 2 suggests that with increasing ${\chi }_v$ away from the intersection at ${\chi }_v={6.2}^{\circ }$ a difference $n_o^{Ti{O}_2}-n_e^{To{O}_2}$ appears and increases (see the solid blue line and the dashed red line), but it is considerably smaller than the difference $n_e^{Ti{O}_2}-n_o^{Ta{O}_2}$, i.e., the contrast of the refractive indices of the CTF layers will still be much higher for the y polarized light. Therefore, one expects to be able to produce large mirror loss dichroism even if the crossing point condition is not strictly maintained. Indeed, we confirm this conjecture in Figure 4a,b, which are calculated for an increased vapor incidence angle to ${\chi }_v={13}^{\circ }$. As the refractive index contrast of the $Ti{O}_2$ and $Ta{O}_2$ layers decreases, we also increase the number of CTF pairs in the upper DBR to $n_{top}=35$. The calculated threshold gains for the x and y linearly polarized light in Figure 4a,b are $g_x^{th}=54,141$ cm⁻¹ and $g_x^{th}=1298$ cm⁻¹, respectively. Such a large difference in threshold gain reflects the still quite large mirror loss dichroism that is produced even when the crossing point condition is not strictly maintained.

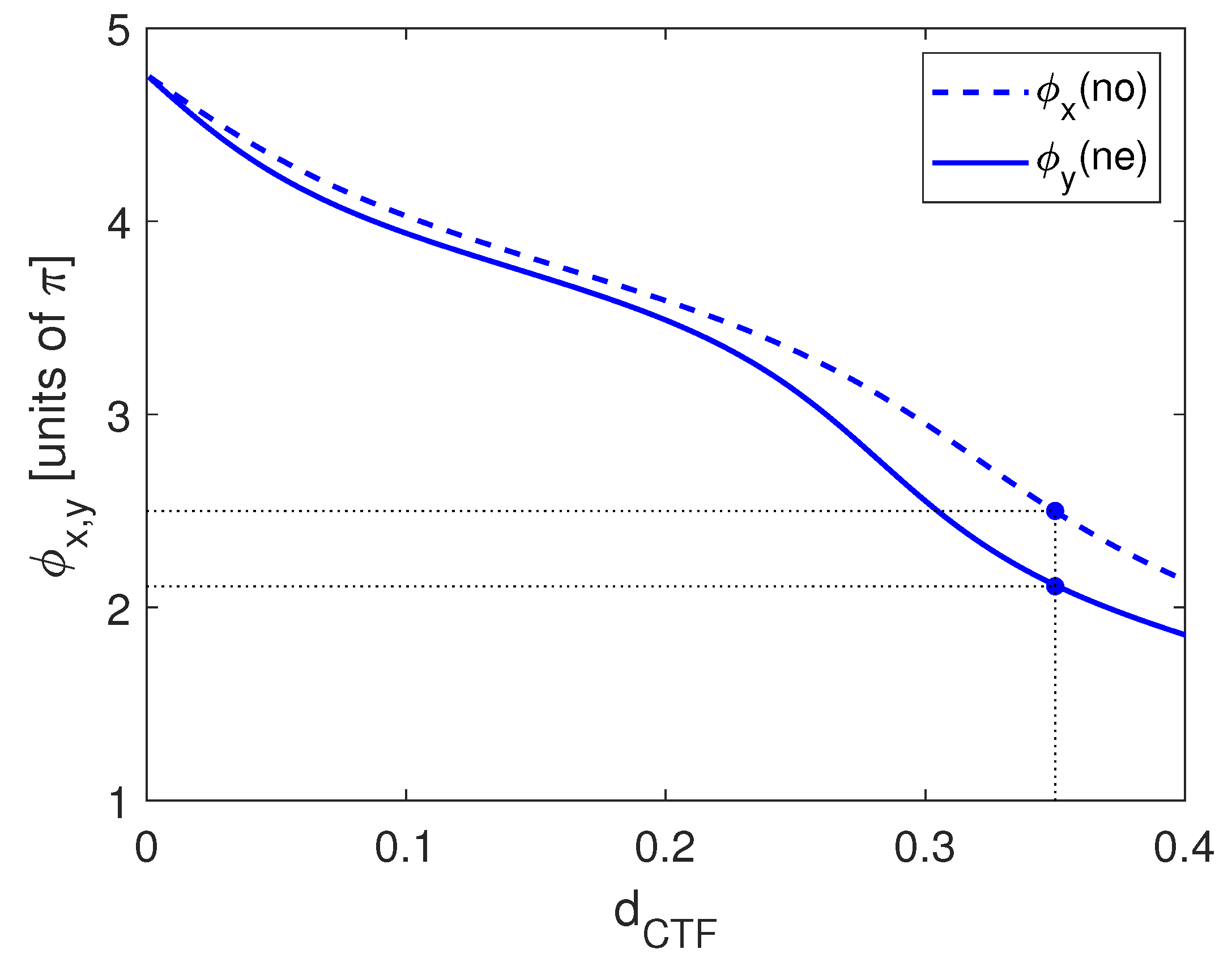
2.4. VCSEL with Pair of Columnar Thin-Film Layers Oriented in the Same Plane

Another interesting feature of Figure 2 is that the difference of the ordinary refractive indices $n_o^{Ti{O}_2}-n_o^{Ta{O}_2}$, i.e., the distance between the two blue curves, decreases strongly with decreasing ${\chi }_v$, while the difference $n_e^{Ti{O}_2}-n_e^{Ta{O}_2}$ remains large. This suggests that it is still possible to produce large dichroism without depositing the CTF layers in such a way that their columnar structures are tilted in two orthogonal planes. This means that the CTF deposition process can be simplified: there is no need to rotate the substrate at ${90}^{\circ }$ each time when switching between the $Ti{O}_2$ and $Ta{O}_2$ materials and vice versa. In terms of Figure 1 this means that all the columns shown schematically in the CTF DBR (the short black lines) will point in the same direction, e.g., along the angle ${\chi }_{Ta{O}_2}$. We illustrate these considerations in Figure 5a,b. The $Ti{O}_2$ and $Ta{O}_2$ materials in the CTF DBR have now been deposited so that their columnar structures are inclined in the same plane. The vapor incidence angle is ${\chi }_v={10}^{\circ }$. The calculated threshold gains for the x and y linearly polarized light in Figure 5a,b are $g_x^{th}=\mathrm{75,307}$ cm⁻¹ and $g_y^{th}=285$ cm⁻¹, respectively. This large threshold gain difference, i.e., the large mirror loss dichroism, confirms that polarization-stable CTF-VCSELs can be fabricated with CTF DBRs whose columnar structures of the constituent layer pair are tilted in the same plane.

3. Polarization Stable VCSEL by Phase-Change Effect

So far, our approach to induce large dichroism in the CTF-VCSELs has been to modify the absolute reflectivity of the CTF mirror for two orthogonal LP directions. In this way, the fineness of the active VCSEL cavity is very high for one LP and low for the orthogonal LP, resulting in much higher mirror losses. We now take a different approach, namely to use the phase change on reflection from the CTF DBR to modify the Fabry–Perot resonance conditions for the active VCSEL cavity for the two LPs. For example, if y LP is in resonance, ${\varphi }_y=m\pi$, but x LP is out of resonance, ${\varphi }_x=(m+1/2)\pi$, where m is an integer, a stable y LP emission is expected from such a CTF-VCSEL. Equation (5) list the phase changes for a round trip in the VCSEL active cavity for x and y polarized light

$$\begin{array}{c}\hfill {\varphi }_x={\displaystyle \frac{2\pi }{\lambda }}{n}_{cav}{d}_{cav}+{\varphi }_{top,x}^{DBR}({\chi }_v,n_o,d_{CTF})+{\varphi }_{bot}^{DBR},\\ \hfill {\varphi }_y={\displaystyle \frac{2\pi }{\lambda }}{n}_{cav}{d}_{cav}+{\varphi }_{top,y}^{DBR}({\chi }_v,n_e,d_{CTF})+{\varphi }_{bot}^{DBR}.\end{array}$$

(5)

As an example, we consider a top dielectric DBR consisting of $n_{top}=20$ pairs of isotropic $Ti{O}_2$ and $Ta{O}_2$$\lambda /4$ layers (i.e., layers deposited at ${\chi }_v={90}^{\circ }$) with an additional single $Ti{O}_2$ CTF layer (deposited at an angle ${\chi }_v=6^{\circ }$) of thickness $d_{CTF}$ adjacent to the VCSEL active cavity. Figure 6 shows the calculated dependence of ${\varphi }_x$ and ${\varphi }_y$ on the length $d_{CTF}$ of the CTF layer. At $d_{CTF}=0.35$ $\mathsf{\mu }$m the phase change for y LP light is nearly integer ${\varphi }_y$≈ 2 while ${\varphi }_x$≈ 2.5. This means that the CTF-VCSEL is in resonance for the y LP light while it is out of resonance for the x LP light, which is indeed confirmed in Figure 7 where we see a well-confined y LP mode with a very low threshold gain of $g_y^{th}=201$ cm⁻¹. At the same time, we find no well-confined mode for x LP light.

4. Discussion

We have shown various ways of utilizing dielectric columnar thin films in the VCSEL multi-layered structure for creating large dichroism for two orthogonal directions of light linear polarization and thus for stabilizing very efficiently the polarization of the generated light. When growing the VCSEL top DBR by two quaterwavelength CTF materials of low and high refractive indices chosen at the crossing point of their refractive indices as a function of the vapor incidence angle one creates a high-reflectivity mirror for linearly polarized light in one direction while light polarized in the orthogonal direction sees a single isotropic layer with a very low reflection. Thus, the mirror losses of the VCSEL cavity become highly anisotropic resulting in a huge difference in the threshold laser gains: for the specific case considered in Figure 3 the threshold gains differ by hundreds of thousand cm⁻¹.

However, such design somewhat constrains the choice of the CTF materials and the conditions for their growth. We have, therefore, shown that one can still create very large mirror loss dichroism even when the angle of the vapor incidence when growing the CTF layers is different from the one at the crossing point. In that case, the light of orthogonal linear polarization sees DBR with different contrasts of the refractive indices of the two constituent materials as illustrated by the red curves in Figure 4. This refractive index contrast and consequently the mirror losses and threshold gain dichroism can be manipulated by the choice of the vapor incidence angle, for the specific case of $Ti{O}_2$ and $Ta{O}_2$ materials and ${\chi }_v={13}^{\circ }$ the calculated threshold gains difference is tens of thousands of inverse centimeters.

Looking at simplifying the manufacturing of the CTF-VCSEL we investigated the case when the two CTF materials are evaporated with columnar structure inclination angle in the same plane. This means that the CTF deposition process is simplified as the substrate is not rotated at ${90}^{\circ }$ each time when switching between the $Ti{O}_2$ and $Ta{O}_2$ materials and vice versa. In that case, the refractive index contrast is given by $n_o^{Ti{O}_2}-n_o^{Ta{O}_2}$ for one linear polarization and by $n_e^{Ti{O}_2}-n_e^{Ta{O}_2}$ for the orthogonal linear polarization, i.e., there is a large difference by properly choosing ${\chi }_v$. As shown in Figure 5, the calculated threshold gains difference is tens of thousands of inverse centimeters.

Finally, we have shown that one can stabilize CTF-VCSEL polarization even with a single CTF layer in the VCSEL dielectric top mirror. To this end, we have taken a different approach, namely we use the phase change on reflection from the CTF DBR to modify the Fabry–Perot resonance conditions for the active VCSEL cavity for the two orthogonal linear polarizations: one to be in resonance and the other one to be out of resonance—see Figure 7.

It is also important to note that our approach to polarization stabilization of VCSELs is fully compatible with the semiconductor technology used to grow and process VCSELs. To fabricate CTF VCSELs, one can use either molecular beam epitaxy or metal-organic chemical vapor deposition to grow the VCSEL bottom DBR, the cavity spacer, the active region consisting of either quantum wells or quantum dots, the top cavity spacer and the oxide aperture layer(s), as is conveniently conducted in VCSEL technology. The VCSEL wafers can then be processed in the usual and well-established way of VCSEL manufacturing. Finally, the dielectric CTF DBR is deposited by placing the laser wafer in a vacuum chamber, fixing it at an oblique angle ${\chi }_v$ to the evaporation sources as described in the paper, and depositing the CTF multilayer structures by electron beam evaporation. For some of the first two CTF VCSEL structures considered here, it is necessary to rotate the wafer by 90° with respect to the substrate normal when switching between the high and low refractive index CTF materials. The evaporation process is somewhat simplified for the other structures considered, as no such rotation is required.

We now compare our approach of stabilizing VCSEL polarization to the alternative techniques demonstrated in the literature. To this end, we have to estimate the polarization mode suppression ratio (MSR) for the different designs of CTF-VCSELs. As shown in [4] MSR is proportional to the ratio of the difference of the mirror losses $\Delta {\alpha }_m$ and modal gains $\Delta g$ to the net modal gain of the main mode ${\delta }_G$, i.e., MSR (dB) $\sim 10$log₁₀$\left[(\Delta {\alpha }_m+\Delta g)/{\delta }_G\right]$. The value of the net modal gain of the main mode depends on the injection current and is estimated for typical semiconductor laser parameters as ${\delta }_G\sim {10}^{-3}{I}_{th}/(I-I_{th})$[4], i.e., for twice the threshold current ${\delta }_G\sim {10}^{-3}$. Then the polarization MSR for the different VCSEL designs will be of the order of 80 dB, 77 dB and 76 dB for the cases of Figure 3, Figure 4 and Figure 5, respectively. We also estimated polarization MSR of the order of 80 dB for the CTF-VCSEL based on the phase change on reflection from the CTF DBR.

In [8,9,10] the loss dichroism is created by anisotropic transverse laser cavity geometries of etched air-post VCSELs. Such dichroism is not large, for example, in [8] a linearly polarized emission is only obtained up to twice the threshold current for rhombus-shaped cavities, while a polarization suppression ratio of only 14 dB is demonstrated for dumbbell-shaped cavities.

In [11,12] the loss dichroism is created by fabricating anisotropic oxide apertures. Similarly, the etched air-post VCSELs dichroism is not large. In [11] polarization suppression ratio of only 18 dB is obtained at an injection current of 2.5 mA where the peak light output power is attained. In [12] where the selectively-oxidized current aperture is of rhomboidal shape the polarization suppression ratio is about 20 dB.

In [13] thermally stressed epitaxial layers including an active region are made anisotropic by an elliptically etched substrate structure. Although the polarization MSR is not measured, this stress-induced anisotropy in the optical gain is not large: polarization control with about 80% reproducibility is obtained by employing a thick gold film or polyimide as a stress-enhancing material.

In [14] well controlled technique for applying external mechanical stress to the VCSEL is developed by bending the metal plate of the laser package on which the VCSEL wafer is glued. This geometry introduces a tensile strain in the laser along one direction of the holder and a compressive strain in the orthogonal direction. A higher polarization mode suppression ratio of up to about 26 dB is demonstrated depending on the applied mechanical stress.

In [15] the loss dichroism is created by etching metal-dielectric grating terminating the top DBR and serving as a polarizer. A reflectivity difference of about 9% for light polarization along and perpendicular to the grating grooves at the cavity resonance is obtained resulting in a gain difference of about 500 cm⁻¹. This is much less than the one estimated for the CTF-VCSEL designs.

In [16] the loss dichroism is created by etching a subwavelength grating which also serves as a high reflectivity mirror replacing a large part of the top DBR. A polarization mode suppression ratio of about 20 dB is demonstrated.

Growing the VCSEL structure on a misoriented semiconductor substrate results in an intrinsic gain anisotropy and, therefore, in intrinsic polarization selectivity. It has the advantage that the VCSEL fabrication process is the same as that for fabrication on (100) substrates. Such an approach has been taken in [17] by a VCSEL growth on (311) B misoriented substrates and the anisotropic optical gain resulted in a polarization MSR of about 13 dB.

In [18] an intra-cavity patterning of wafer-fused VCSELs emitting at 1310 nm wavelength, i.e., etching two symmetrically arranged arcs above the gain structure within the laser cavity is used to introduce both birefringence and dichroism. The patterning helps to fix the polarization angle at the threshold with respect to the crystal axes; however, it only leads to an increase in the polarization switching current without avoiding the switching. Although the polarization MSR ratio is not measured, the maintained presence of polarization switching signifies that the polarization MSR ratio is low and not sufficient for avoiding the switching.

5. Conclusions

In summary, we have demonstrated columnar thin-film CTF-VCSELs of different designs with large polarization dichroism capable of emitting light with well-defined linear polarization. In one approach, we have demonstrated CTF-VCSELs with dielectric DBR consisting of two alternating CTF layers grown in orthogonally oriented planes and having a high and low refractive index for one linear polarization, while having the same refractive index value for the orthogonal linear polarizations. Such CTF-VCSELs have very large dichroism of the mirror losses for these two orthogonal linear polarizations. We have also shown CTF-VCSEL designs with parallel orientations of the CTFs in the dielectric DBR. In a second approach, we use the phase change on reflection from the CTF DBR to modify the Fabry–Perot resonance conditions for the active VCSEL cavity for the two orthogonal linear polarizations. For this purpose, we implement only one CTF layer in the dielectric DBR, chosen in such a way that only one linearly polarized mode is resonant in the CTF-VCSEL, while the light with orthogonally oriented linear polarization is out of resonance and thus cannot lase. To quantify the results of polarization stabilization of VCSELs, we use the polarization mode suppression ratio (MSR) as a measure and show that all our CTF VCSEL designs compare very favorably with the alternative approaches, achieving a much higher polarization MSR of around 80 dB. Finally, we emphasize that the experimental approach to fabricating CTF VCSELs is fully compatible with the existing and well-established technology of VCSEL epitaxial growth and processing.