Improved Res-UNet Network for Phase Unwrapping of Interferometric Gear Tooth Flank Measurements

Abstract

This article introduces an improved deep learning network, GRU-Net, designed to facilitate direct and precise phase unwrapping of wrapped phase measurements in gear tooth surface interferometry. GRU-Net incorporates a Gram matrix within each down-sampling process to compute style loss, thereby capturing essential stripe structure information features. This network exhibits enhanced capability in handling larger and more intricate gear tooth interferograms, particularly in scenarios involving pronounced noise and aliasing, while still yielding favorable outcomes. A comparative evaluation was conducted, contrasting GRU-Net with the Res-UNet network and other conventional methods. The results demonstrate that GRU-Net surpasses the alternative approaches in terms of unwrapping accuracy, noise resilience, and anti-aliasing capabilities, with accuracy improved by at least 24%, exhibiting significantly superior performance. Additionally, in contrast to the Res-UNet network, GRU-Net demonstrates accelerated learning speed and generates more compact models.

1. Introduction

In many fields that utilize interferometric principles for measurement, indirect measurement of the measured physical quantity is usually achieved through phase information, such as synthetic aperture radar [1], magnetic resonance imaging [2], structured light projection measurement [3], phase-shifting interferometry measurement [4], etc. Therefore, the precise extraction of phase information is a crucial step in achieving high-precision measurement. During the measurement process, due to the correlation between the measured physical quantity and the measured wavelength, the measured changes usually cause a phase change of more than, resulting in phase ambiguity problems. When using the inverse trigonometric function to extract phase, the wrapped phase is limited too, and phase unwrapping is the process of removing these discontinuous phases to restore the desired continuous true phase. However, in the actual phase unwrapping process, external noise, local shadows and stripe breaks, under-sampling [5], and other issues introduced by the external environment still make phase unwrapping a challenging problem.

Scholars have attempted to address the common issues in this interferometric measurement from different perspectives. Usually, these traditional unwrapping methods can be roughly divided into three categories: path-tracking methods [6], optimization-based methods [7], and phase map preprocessing-based methods [8]. The path tracking method divides the path or quality map to plan a better integration path and avoid the accumulation of errors in abnormal phase points, such as the branch cutting method [9] and quality map-guided method [10]; based on optimization methods, the resulting process is transformed into a global optimization problem for solution, such as weighted least squares method [11]; based on filtering methods, efforts are made to improve the reliability of the original wrapped phase and reduce the difficulty of unwrapping, such as the unwrapping method based on Kalman filtering [12].

As can be seen, the main idea of traditional classical unwrapping methods is to improve the quality of the original phase through approaches such as optimizing the integration path or other global optimization methods to avoid the influence of unreliable phase points as much as possible. However, in situations such as noise, severe discontinuity points, and aliasing points introduced by the measurement object itself, the effectiveness of traditional methods becomes very limited. The development and application of deep learning technology in various fields has enabled tremendous advantages in the field of image processing. Jin et al. [13] first applied deep learning technology to solve pathological problems in image processing, bringing new technological implementation paths for phase unwrapping under the extreme conditions mentioned above. At present, phase unwrapping methods based on deep learning can be divided into two categories [14]. The first category uses deep learning networks to transform the phase unwrapping problem into a multi-classification recognition problem with the number of phase packages. For example, Time Phase Unwrapping (TPU) is crucial for recovering unambiguous phases of discontinuous surfaces or spatially isolated objects in fringe projection profilometry. Guo [15] integrates TPU into deep learning to mitigate the influence of noise and significantly enhance the reliability of phase unwrapping, and the Multi-Frequency Time Phase Unwrapping (MF-TPU) method, as a classical phase unwrapping algorithm in Fringe Projection Profilometry (FPP), can eliminate phase ambiguity even in the presence of surface discontinuities or spatially isolated objects. Wei [16] combined MF-TPU with multi-scale deep neural networks to eliminate phase ambiguity and improve measurement accuracy. The architecture proposed by Spoorthi [17] includes a convolutional encoder network and corresponding decoder network, followed by a pixel-by-by-pixel classification layer; the second type directly learns the mapping relationship between wrapped phase and absolute phase through neural networks, treating phase unwrapping as a regression problem. For example, Zhang [18] proposed a DCNN architecture, DeepLabV3+fast, and a robust two-dimensional phase unwrapping method, DCNN is first used to perform semantic segmentation to obtain segmentation results of the wrapped phase map. Then, combine the wrapped phase map with the segmentation results to generate the unwrapped phase. Zhu [19] proposed a deep learning based Inertial Constrained Fusion (ICF) target interference graphic packet algorithm and demonstrated a method for generating ICF target measurement system datasets, Wang [20] combined U-Net and Res-Net to form a new network, Res-Unet, which was successful in phase unwrapping. The Res-U-net exhibits excellent anti-noise and anti-aliasing capabilities compared to classical methods, and Qin [21] proposed a novel deep neural network VUR-Net which combined U-Net, Res-Net, and VGG to achieve direct and accurate phase unwrapping; Although the effectiveness of the above methods has been confirmed, most of them only have reliability in simulations or specific test objects. For the gear tooth flank interferogram obtained by laser phase-shifting interference measurement, the above methods cannot obtain satisfactory results directly, and its specific application scenarios require more specific preprocessing [22] and post-processing [23] steps.

This article proposes a novel deep neural network for phase unwrapping of gear tooth flanks, named GRU-Net. This network is inspired by U-Net, Resnet, and Gram matrices [24]. GRU-Net adds Gram matrix operations to each layer and captures the style information of each layer. We will demonstrate that, after appropriate training, despite the presence of noise, under-sampling, and aliasing, the proposed GRU-Net network can achieve very high accuracy in the phase unwrapping results of gear tooth flanks. We compared our method with the original Res-UNet network and some commonly used traditional algorithms and found that it exhibited astonishing advantages in accuracy, training speed, and model size on the same dataset. On the basis of improving accuracy, the model can also be lightweight. The results indicate that GRU-Net can meet the real-time application of phase unwrapping of gear tooth flanks. In Section 2, we provide a detailed introduction to the GRU-Net algorithm, explaining its core Gram matrix and the network’s composition. In Section 3, we conduct simulation experiments, demonstrating that GRU-Net maintains strong unwrapping capabilities even for wrapped images containing background regions. In Section 4, we present experimental validation, confirming GRU-Net’s effective phase unwrapping ability for gear tooth surface interferograms. Afterward, we discussed the advantages and disadvantages of the network, as well as the preprocessing and postprocessing of the experiments. Finally, we summarize the entire paper, affirming that GRU-Net is a high-performance network.

2. Principles of Algorithms

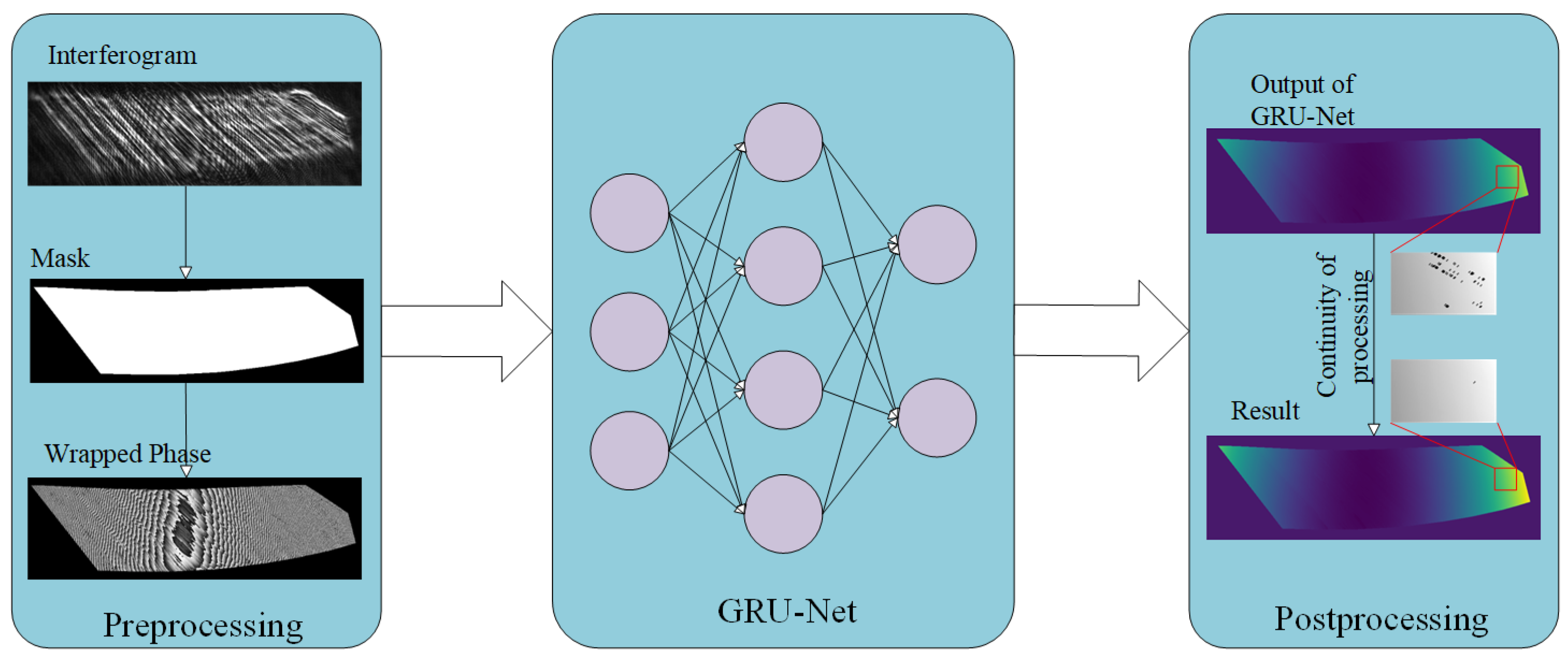
As shown in Figure 1, the data processing procedure of the phase unwrapping method proposed in this paper for gear interferometry is divided into three steps: preprocessing, wrapped phase unwrapping, and postprocessing. The entire algorithm workflow is shown in Figure 1. During the preprocessing stage, four gear tooth surface interference fringe images are obtained using the four-step phase-shifting method. Then, the background regions in the interference images are removed using the adaptive foreground region extraction method we previously proposed in the literature [22]. The wrapped phase map of the measured tooth surface can be obtained through the least squares method. The obtained wrapped phase map is processed using the GRU-Net proposed in this paper to achieve the unwrapped results. After applying some postprocessing to the unwrapped results, the final results can be obtained.

2.1. Preprocessing

In the preprocessing stage, we first obtain interference images using the phase-shifting interferometry method. Phase-shifting interferometry introduces an additional phase modulation to the reference wave. We use a four-step equally spaced phase-shifting method to acquire four interference fringe images of the gear tooth surface I₁, I₂, I_3, and I₄, with phase shifts of 0, $\pi$, $\pi /2$ and $3\pi /2$.

In gear interferometry, the phase shift is performed in fixed steps each time, resulting in a periodic variation in the grayscale of the phase-shifted interference fringes. When the phase shifts are 0, $\pi$, $\pi /2$, and $3\pi /2$, the grayscale difference at the same pixel point on the measured tooth surface interference fringes reaches its maximum, while the grayscale of the background region pixels does not significantly change with the phase shift. Therefore, the grayscale difference of the pixel points at different phases can be utilized to extract the foreground region.

The interference differential images at different phase shifts can be calculated using Equations (1) and (2).

$${Gray}_i\left(x,y\right)=\left|\begin{array}{l}{\phi }_{i+1}\left(x,y\right)\sin \left(i\pi /2\right)+\\ {\phi }_{i+3}\left(x,y\right)\sin \left[\left(i+2\right)\pi /2\right]\end{array}\right|i=1$$

(1)

$${Gray}_i\left(x,y\right)=\left|\begin{array}{l}{\phi }_i\left(x,y\right)\sin \left[\left(i-1\right)\pi /2\right]+\\ {\phi }_{i+2}\left(x,y\right)\sin \left[\left(i+1\right)\pi /2\right]\end{array}\right|i=1$$

(2)

where:

$Gra{y}_i\left(x,y\right)$—Grayscale value of the target pixel in the (i)th processed image;

${\phi }_i\left(x,y\right)$—Grayscale value of the target pixel in the (i)th phase-shifted interference image.

Using the threshold segmentation method proposed by [22], a binary mask of the foreground region can be obtained. This mask can be used to acquire the gear tooth surface interference fringe images I_s1, I_s2, I_s3, and I_s4, without the background region. Using Equation (3), the wrapped phase map of the gear can be obtained.

$$\phi (x,y)=-\arctan {\displaystyle \frac{{\displaystyle \sum _{i=1,}^N{I}_{si}(x,y)\sin {\delta }_i}}{{\displaystyle \sum _{i=1}^N{I}_{si}(x,y)\cos {\delta }_i}}}$$

(3)

where (N) is the number of phase-shifting steps, which in this case is 4.

2.2. Network Architecture

The model initially undergoes a sequence of four down-sampling modules, each comprising a residual module and a max pooling layer. Within each down-sampling module, the input data size is halved, while the number of features is doubled. Notably, a Gram matrix is generated by each down-sampling block to capture style information at the current level.

Each residual module consists of five branches, encompassing a convolutional layer, a batch normalization layer, and a Gram matrix. The outputs of these branches are interconnected, added to the original input, and subsequently subjected to a non-linear transformation via the LeakyReLU activation function.

Following the down-sampling phase, the model reconstructs the feature maps using four up-sampling modules. Each up-sampling module comprises an up-sampling operation (employing bilinear interpolation or transposed convolution), a convolutional layer, and a residual module. Within each up-sampling module, the feature map size is doubled, while the number of features is halved.

Finally, the last layer converts the output of the decoder into the final output image and adjusts its dimensions to match those of the input through bilinear interpolation.

Additionally, the model calculates the Gram matrix on the output of each module, primarily utilized for computing Style Loss. The entire network progressively extracts features via an encoder, while the bottleneck section further processes these features. Subsequently, the decoder gradually restores the spatial dimensions of the feature map, ultimately generating an output of the identical size as the input. Throughout this process, each block generates a Gram matrix that effectively captures and leverages the style information inherent in the image.

As shown in Figure 2, GRU-Net includes an encoder and a decoder. The figures clearly show the changes in image resolution during the network learning process. After a series of preprocessing, the interferogram is wrapped in a phase map, which is learned by the network and output. After certain post-processing, high-precision unwrapping results can be obtained.

2.3. Res-Net Residual Connection

The main function of Res-Net is to introduce residual connections or skip connections, which solves the problem of gradient vanishing in deep neural networks.

In traditional deep neural networks, the output of each layer is obtained by multiplying the input data with a weight matrix and then performing nonlinear transformations through activation functions. However, as the depth of the network increases, this approach may lead to gradient vanishing problems, where the value of the gradient becomes very small during backpropagation, making weight updates very difficult.

Res-Net introduces residual connections, allowing the network to directly transmit input data to subsequent layers. When the network deteriorates, shallow networks can achieve better training results than deep networks. If we transfer low-level features to higher layers, the effect should not be worse than shallow networks. Therefore, we add a mapping between shallow and deep layers to ensure that the (n + 1)th layer networks can contain more information than nth layer networks. Here, we introduce Res-Net networks to improve network performance.

Assuming we have an input x that is transformed into H(x) through identity mapping, but through such learning, deeper layers cannot achieve better results. If we can make it learn the residual F(x), that is H(x) = F(x) + x, even if F(x) = 0, it can ensure that the network performance does not decrease. However, in reality, the residual cannot be 0, so the network will inevitably have better performance.

The expression formula for residual blocks is:

$$x_{l+1}=x_l+F\left(x_l,W_l\right)$$

(4)

where $x_{l+1}$ denotes the output of the residual block, i.e., the output feature map of the current residual block, $F\left(x_l,W_l\right)$ denotes the nonlinear transformation function inside the residual block, and $x_l$ denotes the input feature map of the residual block, which is the output of the previous layer. $W_l$ denotes the parameters inside the residual block, usually the weights of the convolution kernel.

By recursion, any number of layers can be expressed as

$$x_L=x_l+{\displaystyle \sum _{i=l}^{L-1}F\left(x_i,W_i\right)}$$

(5)

where L denotes deeper layers of the net, Obtained through recursion from previous layers.

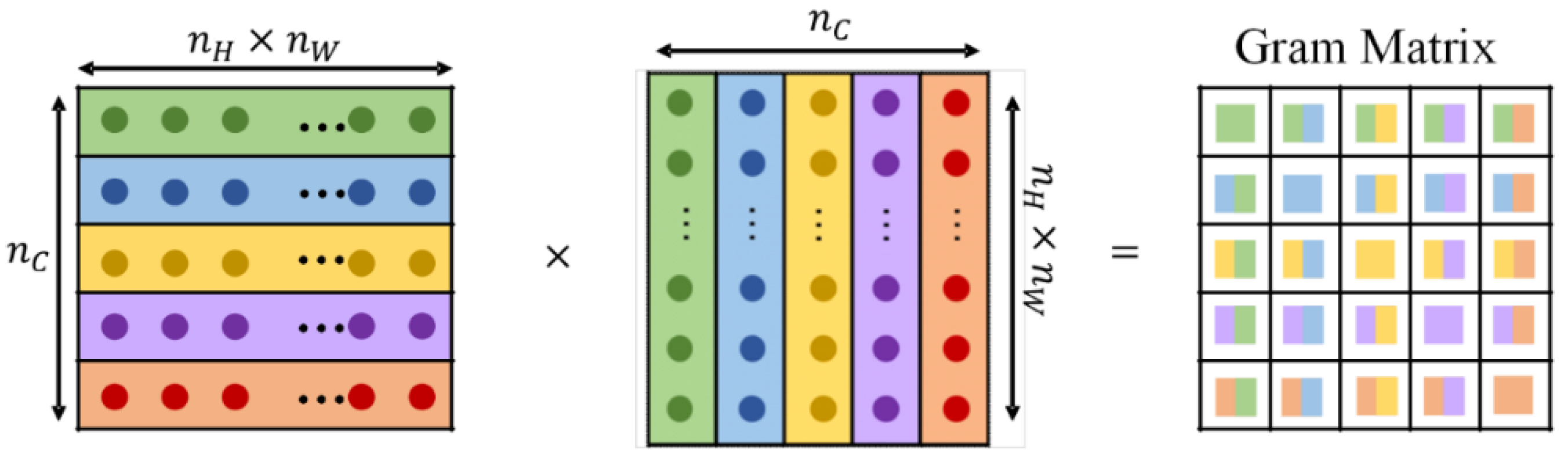
2.4. Gram Matrix

Gram matrix is an important concept in linear algebra and has wide applications in deep learning and computer vision. The definition of a Gram matrix is a symmetric matrix composed of the inner product of a set of vectors. For a set of vectors, the element Gij of the Gram matrix G is the inner product of the sum. The formula is as follows:

$$\Delta \left({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_k\right)=\left(\begin{array}{cccc}\left({\alpha }_1,{\alpha }_1\right)& \left({\alpha }_1,{\alpha }_2\right)& \dots & \left({\alpha }_1,{\alpha }_k\right)\\ \left({\alpha }_2,{\alpha }_1\right)& \left({\alpha }_2,{\alpha }_2\right)& \dots & \left({\alpha }_2,{\alpha }_k\right)\\ \dots & \dots & \dots & \dots \\ \left({\alpha }_k,{\alpha }_1\right)& \left({\alpha }_k,{\alpha }_2\right)& \dots & \left({\alpha }_k,{\alpha }_k\right)\end{array}\right)$$

(6)

In broad terms, shallow networks primarily extract localized and detailed texture features, whereas deep networks excel at capturing more abstract information such as contours and sizes. Within the realm of deep learning, Gram matrices are frequently employed to quantify feature styles. This is owing to the Gram matrix’s ability to capture correlations between features. To compute the Gram matrix, a feature matrix undergoes a flattening process, transforming it into a one-dimensional vector. Subsequently, the inner product is calculated between all feature vectors, yielding the Gram matrix. Throughout this procedure, the Gram matrix encapsulates feature correlations while disregarding their spatial distribution. This property renders the Gram matrix a powerful tool for characterizing feature styles. The calculation of the Gram matrix is illustrated in Figure 3. The inner product calculation process of the Gram matrix can be seen in Figure 3.

$$G_{ij}^l={\displaystyle \sum _k{F}_{ik}^l}{F}_{jk}^l$$

(7)

where l denotes the layers and i denotes the feature map of channel i; j denotes the feature map of channel j. k denotes multiplying 1 − k inner products.

In the context of this article’s phase unwrapping problem pertaining to gears, a particular type of image necessitates the extraction of foreground information from a substantial background while effectively capturing stripe structure information with heightened sensitivity. In light of these requirements, the feature style description provided by the Gram matrix offers a means to capture the stripe structure information present in the image. Leveraging the Gram matrix facilitates enhanced accuracy in the unwrapping process, enabling more precise acquisition of stripe structure information even within intricate stripe patterns.

2.5. Post-Processing

Upon obtaining the unwrapping stage through the utilization of the GRU-Net network, subsequent continuity processing assumes paramount importance in rectifying errors and attaining more precise unwrapping outcomes. Empirical investigations have demonstrated that image quality, comprising factors such as inherent noise interference and hardware accuracy issues, can give rise to the emergence of pixel block defect areas within the wrapped phase map, commonly denoted as discontinuous areas. The existence of these discontinuous regions exerts an adverse influence on the ensuing phase unwrapping process, therefore post-processing of the unwrapping result is necessary. We have elected to utilize a two-dimensional 5 × 5 median filter as the post-processing methodology. This selection ensures the preservation of a larger number of pixels without introducing distortions, while simultaneously smoothing only the truly discontinuous pixels. Such a post-processing strategy is deemed to be more methodical and readily implementable.

3. Simulation

To substantiate the superior performance and enhanced unwrapping capability of the GRU-Net network in contrast to the original network, we devised the present simulation.

3.1. Models and Tools

This simulation was conducted on a computing platform equipped with Windows 11 as the operating system, a Xeon(R) Platinum 8352V as the processor, and an NVIDIA GeForce RTX 3080Ti GPU as the graphics card, complemented by 32 GB of RAM. The algorithm operates within an environment consisting of PyTorch 1.11.0 and CUDA 11.3. With such a robust GPU at its disposal, the procedure not only ensures the precision of data unpacking but also notably enhances the speed.

3.2. Experimental Design and Dataset Production

In the simulation phase, 20,000 sets of 128 × 128 package images are used as the training set, and 2000 sets of 128 × 128 package images are used as the testing set. During the generation of the dataset, we first generated phase unwrapping maps using Zernike polynomials and GAN networks, as Ground Truth (GT). Then, using the arctangent and sine-cosine method, we obtained the simulated unwrapped phase maps with phase values in the range of $\left(-\pi ,\pi \right]$. In this way, we obtained the training dataset. Under the testing of this dataset, ensure that the GRU-Net network can unpack correctly and test whether it has stronger performance compared to the original network.

$$\varphi (x,y)={\displaystyle {\sum }_{i=1}^s}{c}_i{Z}_i(x,y)$$

(8)

where $Z_i(x,y)$ represents the i-th Zernike polynomial defined within the unit circle, $c_i$ denotes its corresponding coefficient, and s indicates the total number of polynomials.

In this paper, we used MAE (Mean Absolute Error) as the loss function to calculate the average absolute error between the predicted values and the true values. Using MAE as the loss function in this research has several advantages: it converges more stably, is relatively simple to compute, and can improve the unwrapping speed.

$$MAE={\displaystyle \frac{1}{n}}{{\displaystyle {\sum }_{i=1}^n(y_i-{\stackrel{⌢}{y}}_i)}}^2$$

(9)

where $y_i$ represents the ground truth, and ${\stackrel{⌢}{y}}_i$ represents the output model value.

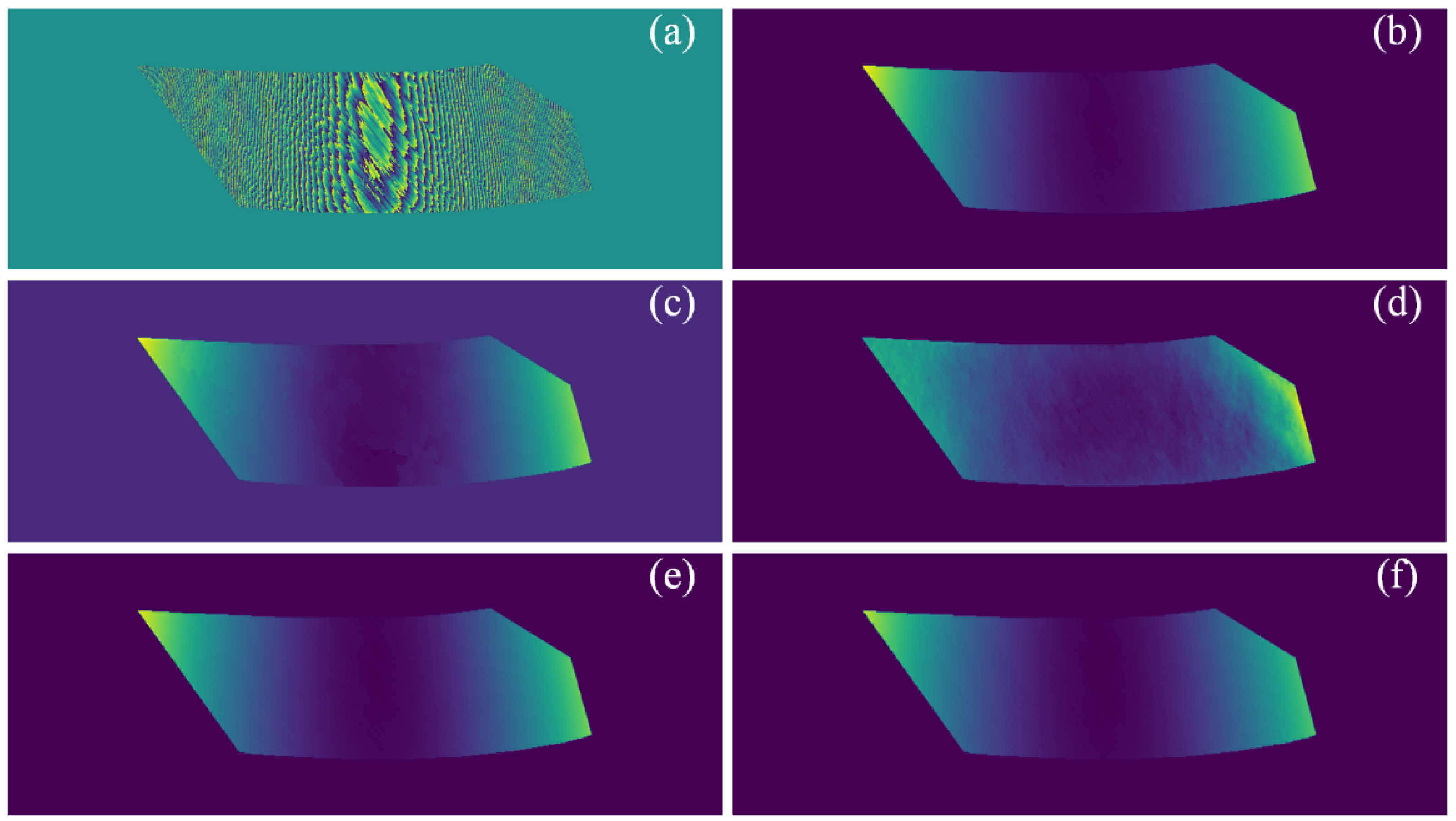
According to the comparison of the four sets of images in Figure 4, it can be found that the GRU-Net network is better at wrapped phase images of 128 × 128 size. In order to more intuitively demonstrate the difference between the two algorithms, root mean square error can be used to discuss the relationship between them. In Figure 4, we can compare the error maps, namely d and f, for each set of images to assess the unwrapping accuracy of the two networks. From d and f in Group 1, we can see that the PV error of Res-Unet reached 8, with a maximum error value of −7, while GRU-Net’s PV error was 5, with a maximum error value of −3, indicating relatively smaller errors. In Group 2, the PV error of Res-Unet was 8, with a maximum error value of −7, whereas GRU-Net’s PV error was 7, with a maximum error value of 4, again showing smaller errors compared to Res-Unet. In Groups 3 and 4, the PV errors of Res-Unet were 6 and 4, respectively, while those of GRU-Net were 6 and 5, showing similar results. However, the maximum error values for Res-Unet were −5 and −4, which are greater than GRU-Net’s 3 and −3. Comparing the error maps, it is evident that the unwrapping accuracy of the GRU-Net network is superior to that of Res-Unet. Next, we use RMSE for a more quantitative comparison.

According to the following formula:

$$RMSE=\sqrt{MSE}=\sqrt{{\displaystyle \frac{SSE}{n}}}=\sqrt{{\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^m(y_i-{\widehat{y}}_i}{)}^2}$$

(10)

This formula is used to evaluate the mean square error of corresponding points between unwrapping phase and real phase.

According to

Table 1. The RMSE of Res-UNet and GRU-Net.

	RSME/Rad	Group 1	Group 2	Group 3	Group 4
Method
Res-UNet		2.4153	2.5674	2.1070	1.5999
GRU-Net		0.4674	0.5319	0.4171	0.3348

, it can be found that when processing wrapped images with a size of 128 × 128, the improved network has a smaller RSME value, indicating higher accuracy. This proves that the improved network performance improved significantly.

In Figure 5, we specifically chose the 100th row from a collection of outcomes and conducted a comparative analysis with the ground truth (GT). The comparison reveals that GRU-Net exhibits a higher degree of proximity to GT when juxtaposed with Res-UNet, thereby attesting to its heightened accuracy. Consequently, it becomes evident that the incorporation and refinement of the Gram matrix within this network enhancement and upgrade yielded a remarkably commendable effect, significantly augmenting the precision in packet interpretation.

However, the unwrapping of gears presents an even greater challenge due to their irregular shape, complex stripe structure, and the absence of a guarantee to obtain a 128 × 128 size wrapping image that encompasses relevant information throughout the entire image. To accommodate varying gear wrapping image sizes, we expanded the dataset dimensions to 512 × 2048. While this size can accommodate different wrapping image sizes, it may also include numerous extraneous backgrounds. In the new simulation, it is imperative to assess whether the Res-UNet network can effectively discriminate between the background and foreground within such large-scale images, and accurately unpack the foreground gear wrapping image. This places exceptionally high demands on the network’s segmentation and unwrapping capabilities.

Given these requirements, the primary objective is to validate the network’s ability to correctly unpack parcel images that contain a substantial number of background regions. To this end, we generated 10,000 sets of 512 × 2048 datasets, specifically designed to include numerous background regions. These datasets serve to evaluate the network’s capacity to learn effectively, unpack correctly after learning, and determine the resulting unwrapping effect.

In Figure 6, it becomes evident that both the original network and the enhanced network demonstrate proficient unwrapping capabilities for simple wrapped images encompassing numerous background regions, exhibiting commendable accuracy and robust noise resistance. However, the question of whether the Res-UNet network and GRU-Net network possess an adequate unwrapping capacity for intricate gear-phase-wrapped images remains unverified. The subsequent experimental section comprehensively examines and compares the unwrapping proficiency of the Res-UNet network and GRU-Net network when confronted with complex gear-phase-wrapped images.

4. Experimental Verification

4.1. Experimental Design

In order to verify that the GRU-Net network can still have strong unwrapping ability when dealing with irregularly shaped gear wrapping images with a large number of background regions and complex stripe structures and a lot of noise in the foreground region, which are 512 × 20,148 in size, we built an experimental platform and collected enough gear interference fringe patterns, which were wrapped and processed as a dataset. The foreground area size and shape of these datasets vary.

4.2. Data Collection and Preprocessing

To ensure dataset diversity and authenticity, we developed an experimental platform based on the Mach Zehnder interferometer model to capture gear interferograms. By processing the interference patterns, we obtained gear-wrapping images of various sizes for experimentation. Throughout the dataset processing phase, we generated a training set comprising 10,000 sets of datasets and utilized three sets of gear-wrapping diagrams of different sizes as the testing set. In the experimental preparation process, we conducted nine rounds of ten learning iterations each, with a step size of 1 applied in each learning process. Both the original network prior to improvement and the enhanced network underwent three rounds of learning, and their learning outcomes were compared. In the preprocessing stage, we extracted the foreground region using our previously developed adaptive interferogram extraction method [22], obtaining a mask in the process. This allowed the successful extraction of the foreground region. Therefore, in this experiment, although there was background present, it remained at zero intensity and did not interfere with the deep learning process.

Each training set had dimensions of 512 × 2048, occupying a storage size of 1453 KB. To assess whether the GRU-Net network exhibited superior accuracy compared to the original network, we conducted a comparative evaluation of the number of non-contiguous phase points in the experimental results. Additionally, we employed the phase diagram of the ideal gear tooth surface obtained by Wang [25] through simulation results as the Ground Truth (GT) in this experiment.

4.3. Experimental Process

After conducting ten rounds of training for two distinct networks, we observed the emergence of two models with contrasting sizes. The model generated by the GRU-Net network exhibited a notably compact size, measuring 235 MB. In contrast, the model developed by the Res-UNet network was larger, measuring 299 MB. This indicates a size reduction of approximately 21.4% for the GRU-Net model compared to the Res-UNet model. Furthermore, the GRU-Net network demonstrated a significantly reduced learning duration, requiring only about 50% of the time needed by the Res-UNet network for a single ten-round training session.

4.4. Result Display

Prior to comparing the accuracy of deep learning methods, this study opted to assess the unwrapping effects and accuracy of two well-established classical methods: the quality-guided method (TQGA) and the weighted least squares method (WLS). With TQGA, by guiding the unwrapping path with the quality map of the wrapped phase image, error propagation during the integration process is avoided. WLS transforms the phase unwrapping problem into a global optimization problem for a solution.

These methods demonstrated favorable unwrapping effects and relatively high accuracy. The gear wrapping images were subjected to testing using three distinct gear tooth surface wrapping diagrams, varying in size and complexity. Preceding the experiment, it was essential to process the interference fringe pattern of the tooth surface and convert it into a phase wrapping pattern. To mitigate interference from the background region during the experiment, established foreground region extraction methods were employed.

For the purpose of comparing the learning outcomes, three gear-wrapped phase maps of varying sizes were selected. They are Face A, Face B, and Face C, with different resolutions. Face A is an image with a resolution of 860 × 270, Face B is an image with a resolution of 1260 × 350, and Face C is an image with a resolution of 1196 × 257. The subsequent section presents the corresponding package results.

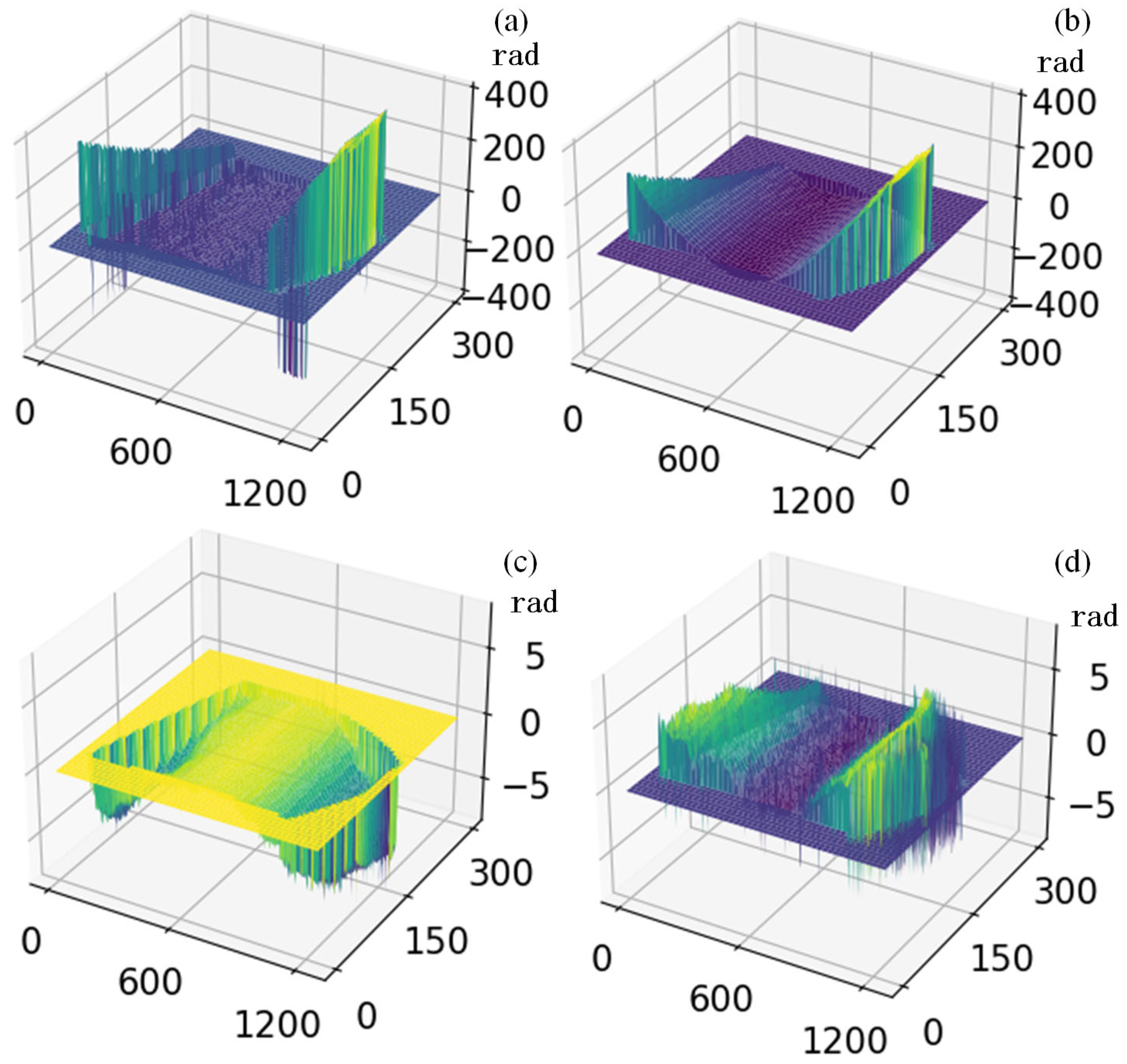
Figure 7 and Figure 8 represent the unwrapping results and error cloud maps of four different methods for Face A. Figure 9 and Figure 10 represent the unwrapping results and error cloud maps of four different methods for Face B. Figure 11 and Figure 12 represent the unwrapping results and error cloud maps of four different methods for Face C. Figure 7, Figure 9, and Figure 11 depict the unwrapping results obtained using two classical methods and two deep learning methods, considering variations in sizes, complexities, and stripe structures. It is evident that the unwrapping outcomes achieved by the classical methods are not optimal for the three gear tooth surface-phase-wrapping diagrams, which exhibit distinct sizes, complexities, and stripe structures. The accuracy of TQGA can only reach up to approximately 65%, while the accuracy of WLS can only reach up to approximately 61%. The denser the stripes, the poorer the unwrapping effect. When facing more complex wrapped phases, the accuracy of TQGA was only about 55%, while the accuracy of WLS was also only about 58%. Even when confronted with the relatively simplest stripe structure wrapping diagram in Figure 7, the performance of the classical method can be characterized as mediocre; the accuracy of TQGA was only 71%, while the accuracy of WLS was only 68%. Figure 8, Figure 10, and Figure 12 provide error cloud maps that vividly illustrate significant unwrapping errors associated with the classical method, with a majority of tooth surfaces experiencing such errors. The accuracies were all below 80%. This substantiates the inadequacy of the classical method’s unwrapping capability to meet contemporary high-precision unwrapping requirements. In contrast, a comparative analysis reveals that the deep learning methods yield exceptional unwrapping results, characterized by minimal errors and high accuracy. Their accuracies all exceeded 90%. Next, we conduct a targeted comparison of the phase unwrapping effects of deep learning methods on gear tooth surfaces.

Based on the comparison of the aforementioned three sets of graphs, it is apparent that the results obtained from the GRU-Net network and the Res-UNet network are highly similar. It is difficult to accurately compare which one has higher accuracy by only looking at the error cloud images. However, upon closer examination of the cloud images, it becomes evident that the errors in the GRU-Net network are primarily concentrated at the edges. To provide a more precise assessment of the disparity between the two networks, we selected discontinuous phase points as indicators for evaluation. By comparing the results and labels of the two networks, any point exceeding the threshold is considered a discontinuous point. Accordingly, we conducted a comparison of discontinuous phase points, as illustrated in the subsequent figure.

According to

Table 2. Table of the number of discontinuous phase points using different methods.

Method	Face A	Face B	Face C
TQGA	11847	4979	32576
WLS	26062	52401	14686
Res-UNet	2854	377	5895
GRU-Net	264	76	1536

, the number of discontinuous phase points in GRU-Net is significantly reduced compared to classical unwrapping methods. Specifically, there is a reduction of 95.3–98.5% compared to TQGA and 89.5–99.9% compared to WLS. It is evident that the accuracy of the GRU-Net algorithm is significantly higher than that of classical algorithms. In the comparison with Res-Unet, the GRU-Net network also demonstrates higher accuracy, with a reduction in the number of discontinuous phase points ranging from 73.9% to 90.7% compared to the Res-Unet network.

Table 2 provides a clear visual representation of the discrepancy in the number of non-contiguous phase points between the Res-UNet and GRU-Net networks. When processing relatively straightforward parcel plots, both networks exhibit comparable unwrapping abilities. However, the GRU-Net network surpasses the Res-UNet network in terms of accuracy. Conversely, when faced with more intricate parcel plots, the GRU-Net network demonstrates distinct advantages. A meticulous examination of the non-contiguous phase points reveals that the GRU-Net network possesses a heightened capacity for handling complex models, resulting in significantly improved unwrapping accuracy. Furthermore, the GRU-Net network exhibits expedited learning speed and generates more compact models. These findings firmly establish the comprehensive superiority of the GRU-Net network over the Res-UNet network, thereby facilitating its wider application.

5. Discussion

Currently, GRU-Net aims to address the phase unwrapping problem in gear tooth surface interferometry. The network was initially designed to fully utilize the complex interference fringe structure unique to gear tooth surfaces. In each sampling process of the Res-Unet network, the Gram matrix is integrated. The greatest advantage of the Gram matrix is its ability to better recognize fringe structure information. Therefore, in this experiment, the GRU-Net network, which integrates the Gram matrix, has a very high phase unwrapping fit for gear tooth surfaces. Experimental results showed that GRU-Net has better network performance. Although the complexity of the network increased, it still has strong performance in solving the unwrapping problem of gear tooth surfaces. For the phase unwrapping problem of gear tooth surfaces, the network has a faster training speed and a smaller model size. During the process of collecting interferograms, due to the particularity of the gear tooth surface and the larger field of view, the collected images contain a large non-tooth surface measurement area, i.e., the background area. If not processed, this can cause error propagation and reduce unwrapping accuracy. Therefore, preprocessing must be performed throughout the unwrapping process. In the post-processing stage, since the measured tooth surface is a continuous curved surface, median filtering is used to handle unsmooth points. However, not all unwrapping processes require this; the necessity of post-processing for other unwrapping remains debatable.

6. Conclusions

We proposed a phase unwrapped GRU-Net and provided a demonstration of its effectiveness and feasibility. Furthermore, we conducted a comparative analysis between the proposed GRU-Net and the Res-UNet network, as well as classical methods, highlighting the former’s efficient and robust unwrapping capability. With appropriate preprocessing and post-processing steps, the GRU-Net yielded highly accurate phase unwrapping results. In terms of accuracy, training the GRU-Net on the same dataset presented a clear advantage over both the original network and classical methods. We posit that by leveraging the support of the Gram matrix, the network can achieve enhanced feature recognition capabilities and higher accuracy. This conclusion offers novel insights for the design of future phase unwrapping networks. Additionally, despite the utilization of a substantial dataset, the GRU-Net exhibited shorter learning times and can generate lighter models under commonly employed hardware configurations, rendering it suitable for real-time applications.