Optimisation of the Transmitter Layout in a VLP System Using an Aperture-Based Receiver

Abstract

In this paper, we consider a visible light positioning (VLP) system, where an array of photo diodes combined with apertures is used as a directional receiver and a set of inexpensive and energy-efficient light-emitting diodes (LEDs) is used as transmitters. The paper focuses on the optimisation of the layout of the transmitter, i.e., the number and placement of the LEDs, to meet the wanted position estimation accuracy levels. To this end, we evaluate the Cramer–Rao bound (CRB), which is a lower bound on the mean-squared error (MSE) of the position estimate, to analyse the influence of the LEDs’ placement. In contrast to other works, where only the location of the LEDs was considered and/or the optimisation was carried out through simulations, in this work, the optimisation is carried out analytically and considers all the parameters involved in the VLP system as well as the illumination. Based on our results, we formulate simple rules of thumb with which we can determine the spacing between LEDs and the minimum number of LEDs, as well as their position on the ceiling, while also taking into account the requirements for the illumination.

1. Introduction

In the last decade, LEDs have become the main illumination source due to their excellent energy efficiency and their long lifetime. In contrast to traditional light sources, such as incandescent and fluorescent lights, LEDs can be modulated up to several MHz. Given that LEDs are typically mounted on the ceiling, an optical receiver pointing upward will experience a line-of-sight link with the LED. Due to this, LEDs are considered transmitters in visible light communication systems [1,2]. Moreover, considering that the channel gain of the LOS component is a simple function of the distance and the angle between the LED and the optical receiver, we can obtain position-related information from the received light. Therefore, visible-light LEDs are considered for indoor positioning. Several works have already investigated the accuracy of visible light positioning (VLP) systems [3,4,5], and reported an accuracy in the order of centimetres. As only a few changes need to be made to the illumination infrastructure to be able to modulate the LEDs, VLP systems can be considered as an accurate, low-cost solution for indoor positioning.

The type and amount of position-related information that can be extracted from the visible-light LEDs depends on the optical receiver that is considered. While charge-coupled device (CCD) cameras contain a large number of pixels with which not only the received signal strength (RSS) can be obtained, but also the direction from which the light is coming, a single photo diode (PD) will only be able to detect the RSS. However, due to practical problems with the CCD camera, including higher energy consumption compared to a PD and the shutter speed of the camera, which limits the modulation bandwidth of the LED, recent work has focused on VLP systems using PDs in the receiver [6,7]. As a single PD is not capable of extracting the direction of the light, several papers investigated other optical receiver structures that offer angular diversity, i.e., that are able to detect the direction of the light [8,9,10]. To make the receiver directional, in [11], a receiver with several tilted PDs was considered, while [12,13] considered PDs combined with apertures. In this paper, we consider the receiver structure from [12], consisting of an array of PDs and apertures, as this receiver offers a wide field of view (FOV) with high angular diversity.

To obtain a low-cost solution, a visible light positioning system is preferably combined with an existing illumination system. Most works on VLP focus on positioning accuracy and optimise the placement of the LEDs to improve the accuracy. However, in a VLP system that coexists with the illumination system, there are additional factors that require further analysis. Illuminance, for example, has a major effect on how people perceive and perform their visual tasks. Because of this, the illuminance levels and the illumination uniformity must be maintained in a range that ensures eye safety and comfort. In our paper [14], we analysed the placement of illumination LEDs to optimise the number of LEDs and their spacings. In this paper, we will employ our results from [14] to analyse the positioning performance of an aperture-based VLP system and to evaluate the coexistence of the VLP system with the illumination system. Our analytical approach provides a deeper insight into the impact of each of the parameters that makes up the system. This contrasts with [15], where a few scenarios were considered with a limited number of LEDs, and results were obtained after extensive experiments. To measure the positioning performance, we use the Cramer–Rao bound (CRB), which is a lower bound on the mean-squared error (MSE) of the positioning error. The results will provide useful information about the installation of LEDs used for illumination and VLP and will be shown to be applicable for rooms of various sizes.

The remainder of the paper is structured as follows. In Section 2, the system is described. Section 3 considers the derivation of the CRB and the illumination level, and the numerical results are shown in Section 4. Finally, the conclusions are given in Section 5. Furthermore, we provide in

Table 1. Summary of the main parameters of the system.

Parameter	Description
${\displaystyle X_{max}}$, ${\displaystyle Y_{max}}$, ${\displaystyle Z_{max}}$	Room size on the ${\displaystyle x}$, ${\displaystyle y}$ and ${\displaystyle z}$ coordinate axes. For rooms with square areas on the ${\displaystyle xy}$ plane, ${\displaystyle X_{max}=Y_{max}={\chi }_{max}}$.
${\displaystyle {\rho }_a}$	Scaling factor that sets the VLP-LED grid spread in the ${\displaystyle a}$ direction. For rooms with square areas on the ${\displaystyle xy}$ plane, ${\displaystyle {\rho }_x={\rho }_y=\rho }$.
${\displaystyle {\rho }_{a,I}^{min}}$	Minimum ${\displaystyle {\rho }_a}$ from the perspective of illumination.
${\displaystyle {\rho }_{a,I}^{max}}$	Maximum ${\displaystyle {\rho }_a}$ from the perspective of illumination.
${\displaystyle {\rho }_{a,V}^{opt}}$	Optimal ${\displaystyle {\rho }_a}$ from the perspective of VLP.
${\displaystyle {\delta }_{L,a}}$	Distance between VLP-LEDs in the ${\displaystyle a}$ direction. For rooms with square areas on the ${\displaystyle xy}$ plane, ${\displaystyle {\delta }_{L,x}={\delta }_{L,y}={\delta }_L}$.
${\displaystyle K_{L,a}}$	Number of VLP-LEDs placed in the ${\displaystyle a}$ direction. For rooms with square areas on the ${\displaystyle xy}$ plane, ${\displaystyle K_{L,x}=K_{L,y}=K_L}$.
${\displaystyle h_{j,i}}$	Vertical distance between LED ${\displaystyle i}$ and RE ${\displaystyle j}$.
${\displaystyle {\varphi }_{j,i}}$	Incident angle between LED ${\displaystyle i}$ and RE ${\displaystyle j}$.
${\displaystyle m_{S,i}}$	Lambertian order of the LED ${\displaystyle i}$.
${\displaystyle {\overline{\Phi }}_{e,i}}$	Average optical power of the LED ${\displaystyle i}$.
${\displaystyle {\Phi }_{v,i}}$	Luminous flux of the LED ${\displaystyle i}$.
${\displaystyle {\mathcal{U}}_t}$	Uniformity level of illumination of the task area.
${\displaystyle {\mathcal{U}}_s}$	Uniformity level of illumination of the surrounding area.
${\displaystyle {\xi }^t}$	Task area delimiter (central sub-area of the area where the receiver is assessed). This is determined during the illumination design.
${\displaystyle \zeta }$	Maximum desired accuracy level of receiver position estimation.

a list of the most important parameters examined in Section 4.

2. System Description

2.1. Transmitter

This paper considers a VLP system that uses ${\displaystyle K_L}$ VLP-LEDs attached to the ceiling. Although, for illumination purposes, LEDs are often grouped in arrays of LEDs, using multiple LEDs within one array for positioning purposes is not recommended for the following reason. Taking into account that the dimensions of an array are rather small compared to the dimensions of a room, this implies that two LEDs belonging to the same array can be considered as virtually co-located. Assuming that all LEDs within an array have the same orientation, it follows that position information that can be obtained from these two LEDs is strongly correlated, and will lead to a reduced dilution of precision (DOP) (the dilution of precision is a term used in GPS navigation to express the positional measurement precision) for a given number of VLP-LEDs. To obtain a good DOP, the LEDs need to have good spatial spreading. For this reason, when LED arrays are available for illumination, we will only use one LED per array for positioning purposes. We assume that all LEDs follow a Lambertian radiation pattern, where the Lambertian order of the VLP-LED ${\displaystyle i}$ is expressed as ${\displaystyle m_{S,i}=-\frac{ln2}{ln\left(cos\left({\Phi }_{1/2,i}\right)\right)}}$, with ${\displaystyle i=1,\dots ,K_L}$ and ${\displaystyle {\Phi }_{1/2,i}}$ as the semi-angle at which half optical power is reached.

In order to estimate the position of a receiver within the room, we define a global coordinate system (GCS), ${\displaystyle (X,Y,Z)}$, whose origin is fixed at the centre of the ceiling. Within this coordinate system, the ${\displaystyle i}$th VLP-LED has coordinates ${\displaystyle {\mathit{v}}_{L,i}}$ with ${\displaystyle {\mathit{v}}_{L,i}={\left(x_{L,i},y_{L,i},z_{L,i}\right)}^T}$. We assume that the coordinates of all LEDs are known by the receiver, and all LEDs point straight downward, i.e., their normal is ${\displaystyle {\mathit{N}}_{L,i}={(0,0,-1)}^T}$.

The receiver captures the modulated light emitted by the VLP-LEDs, the nonmodulated light from I-LEDs and background light. To separate the light from the different VLP-LEDs and the other light sources, we assume the VLP-LEDs are modulated using different orthogonal frequencies that can be separated by applying a discrete Fourier transform at the receiver.

2.2. Receiver

The receiver consists of an array of ${\displaystyle M}$ receiving elements (REs). Each RE contains a bare photo diode (PD) and an aperture in an opaque screen [16]. We assume that the aperture and the PD have the same size and shape, and that the plane of the apertures is parallel to and at a distance ${\displaystyle h_A}$ above the plane of the PDs. We restrict our attention to the case where the PDs are circular with radius ${\displaystyle R_D}$ and assume that the only light that reaches the PD is the light that enters through its aperture. Taking into account that ${\displaystyle R_D}$ is much larger than the wavelength of light, the incident light will introduce a circular light spot with radius ${\displaystyle R_D}$ in the plane of the PDs.

To determine the receiver’s position, we select a reference point, ${\displaystyle {\mathit{v}}_U={\left(x_U,y_U,z_U\right)}^T}$, in the plane of the apertures. The centre ${\displaystyle {\mathit{v}}_{AP,j}={\left(x_{AP,j},y_{AP,j},z_{AP,j}\right)}^T}$ of the aperture ${\displaystyle j}$ is located in a relative position ${\displaystyle {\mathit{v}}_{{\delta }_{AP,j}}={\left(x_{{\delta }_{AP},j},y_{{\delta }_{AP},j},z_{{\delta }_{AP},j}\right)}^T}$ from this reference point ${\displaystyle {\mathit{v}}_U}$, i.e., ${\displaystyle {\mathit{v}}_{AP,j}={\mathit{v}}_U+{\mathit{v}}_{{\delta }_{AP},j}}$, ${\displaystyle j=1,\dots ,M}$ (Figure 1). For simplicity, we assume that the receiver array points straight upward, that is, the normal of the receiver is ${\displaystyle {\mathit{N}}_R={(0,0,1)}^T}$, implying that ${\displaystyle z_{AP,j}=z_U}$ and ${\displaystyle z_{{\delta }_{AP},j}=0}$. However, the extension to the case where the receiver array or the REs within the array are tilted is straightforward.

PDs are relatively displaced compared to their apertures in order to create angular diversity [12] (see Figure 2). The centre ${\displaystyle {\mathit{v}}_{PD,j}={\left(x_{PD,j},y_{PD,j},z_{PD,j}\right)}^T}$ of PD ${\displaystyle j}$ has coordinates ${\displaystyle {\mathit{v}}_{PD,j}={\mathit{v}}_{AP,j}+\Delta {\mathit{v}}_{PD,j}}$ with ${\displaystyle \Delta {\mathit{v}}_{PD,j}={\left(d_{AP,j}cos{\alpha }_{AP,j},d_{AP,j}sin{\alpha }_{AP,j},z_{PD,j}\right)}^T}$, where ${\displaystyle z_{PD,j}=-h_A}$. The angles ${\displaystyle {\alpha }_{AP,j}=j{\displaystyle \frac{2\pi }{M}}}$ are chosen to obtain a receiver array with angular diversity, while the distance ${\displaystyle d_{AP,j}}$ and height ${\displaystyle h_A}$ can be selected to change the FOV of the receiver array [17].

2.3. Received Signal Strength

We will determine the position of the receiver by comparing the received signal strengths (RSS) in the different REs. The RSS level corresponding to the contribution from VLP-LED ${\displaystyle i}$ detected at RE ${\displaystyle j}$ mainly depends on the radiation angle at the source and the angle at which the light ray impinges on the PD, that is, the incident angle. Taking into account the assumption that the LED array and receiver array are parallel to the ceiling, this incident angle is equal to the radiation angle (see Figure 3) and can be expressed as

$${\varphi }_{j,i}=arctan\left(\frac{z_{L,i}-z_{AP,j}}{\Vert {\mathit{v}}_{L,i}-{\mathit{v}}_{AP,j}\Vert }\right).$$

(1)

where, we recall, ${\displaystyle {\mathit{v}}_{AP,j}={\mathit{v}}_U+{\mathit{v}}_{{\delta }_{AP},j}}$, i.e., the RSS levels at the different REs depend on the unknown position ${\displaystyle {\mathit{v}}_U}$ of the receiver and the known layout of the receiver and the known positions of the VLP-LEDs.

In each RE, we focus only on the contributions from the VLP-LEDs by filtering out the contributions originating from sources different from those of the VLP-LEDs. Collecting in RE ${\displaystyle j}$ the contributions of the ${\displaystyle K}$ VLP-LEDs, we obtain the vector ${\displaystyle {\mathbf{r}}_j}$, ${\displaystyle j=1,\dots ,M}$, of observations:

$${\mathbf{r}}_j\left[i\right]=R_{p,j}{h}_c^{(j,i)}{\overline{\Phi }}_{e,i}+{\tilde{N}}_j,i=1,\cdots ,K,$$

(2)

where ${\displaystyle R_{p,j}}$ is the responsivity of PD ${\displaystyle j}$, ${\displaystyle h_c^{(j,i)}}$ is the optical channel gain between LED ${\displaystyle i}$ and PD ${\displaystyle j}$, ${\displaystyle {\overline{\Phi }}_{e,i}}$ is the average transmitted optical power of LED ${\displaystyle i}$ and ${\displaystyle {\tilde{N}}_j}$ is the shot noise in RE ${\displaystyle j}$. This shot noise is modelled as a zero-mean Gaussian random variable with variance ${\displaystyle N_{0,j}=2q{R}_{p,j}{p}_{n,j}{A}_{D,j}\Delta \lambda }$ [18], with ${\displaystyle q}$ being the charge of an electron, ${\displaystyle p_{n,j}}$ the optical power obtained at PD ${\displaystyle j}$ from light sources different from the VLP-LEDs, ${\displaystyle A_{D,j}}$ the area of PD ${\displaystyle j}$ and ${\displaystyle \Delta \lambda }$ the optical bandwidth. Furthermore, following [18], the channel gain ${\displaystyle h_c^{(j,i)}}$ can be written as

$$h_c^{(j,i)}=\frac{(m_{S,i}+1)}{2\pi d_{j,i}^2}{A}_0^{(j,i)}{cos}^{m_{S,i}+1}{\varphi }_{j,i}$$

(3)

where ${\displaystyle d_{j,i}}$ is the Euclidean distance between VLP-LED ${\displaystyle i}$ and the centre ${\displaystyle {\mathit{v}}_{sp}^{(j,i)}}$ of the light spot introduced by aperture ${\displaystyle j}$ and coming from VLP-LED ${\displaystyle i}$, i.e., ${\displaystyle d_{j,i}=\Vert {\mathit{v}}_{L,i}-{\mathit{v}}_{sp}^{(j,i)}\Vert }$. In (3), ${\displaystyle A_0^{\left(j,i\right)}}$ is the surface of the overlap area between PD ${\displaystyle j}$ and the light spot with the centre ${\displaystyle {\mathit{v}}_{sp}^{(j,i)}}$. These coordinates of the centres of the light spots are given by ${\displaystyle {\mathit{v}}_{sp}^{(j,i)}={\mathit{v}}_{AP,j}+{\mathit{v}}_{{\delta }_{SP}}^{(j,i)}}$, where ${\displaystyle {\mathit{v}}_{{\delta }_{SP}}^{(j,i)}={(d_{sp}^{(j,i)}cos{\alpha }_{sp}^{(j,i)},d_{sp}^{(j,i)}sin{\alpha }_{sp}^{(j,i)},-h_A)}^T}$, with ${\displaystyle d_{sp}^{(j,i)}=h_{A}tan{\varphi }_{j,i}}$ being the horizontal distance between the centres of the light spot and aperture of RE ${\displaystyle j}$, and ${\displaystyle {\alpha }_{sp}^{(j,i)}=\pi +{\alpha }_{j,i}}$ (see Figure 2), where ${\displaystyle {\alpha }_{j,i}}$ is the azimuth angle of the incoming light. Defining the horizontal distance ${\displaystyle {\Delta }_{j,i}=h_{j,i}tan{\varphi }_{j,i}}$ between VLP-LED ${\displaystyle i}$ and the centre of aperture ${\displaystyle j}$, with ${\displaystyle h_{j,i}=z_{L,i}-z_{AP,j}}$ as the vertical distance between the VLP-LED and the receiver (see Figure 3), the azimuth angle ${\displaystyle {\alpha }_{j,i}}$ can be written as

$$cos{\alpha }_{j,i}=\frac{x_{L,i}-x_{AP,j}}{{\Delta }_{j,i}}.$$

(4)

Using the angles ${\displaystyle {\varphi }_{j,i}}$ and ${\displaystyle {\alpha }_{j,i}}$, we establish the following relationship between the RE positions and the VLP-LEDs:

$$\begin{array}{cc}{x}_{L,i}=\hfill & x_{AP,j}+(z_{L,i}-z_{AP,j})tan{\varphi }_{j,i}cos{\alpha }_{j,i}\hfill \\ y_{L,i}=\hfill & y_{AP,j}+(z_{L,i}-z_{AP,j})tan{\varphi }_{j,i}sin{\alpha }_{j,i}\hfill \end{array}.$$

(5)

Taking into account the definition of the centre ${\displaystyle {\mathit{v}}_{SP}^{(j,i)}}$ of the light spot, the overlap area ${\displaystyle A_0^{(j,i)}}$ is given by

$$A_0^{(j,i)}=\left\{\begin{array}{cc}2R_D^{2}arccos\left(\frac{{\delta }_{j,i}}{2R_D}\right)\hfill & 0\le {\delta }_{j,i}\le 2R_D\hfill \\ -\frac{{\delta }_{j,i}}{2}\sqrt{4R_D^2-{\delta }_{j,i}^2}\hfill \\ 0\hfill & {\delta }_{j,i}>2R_D\hfill \end{array}\right.,$$

(6)

where the distance ${\displaystyle {\delta }_{j,i}}$ between the centre of the light spot and the centre of PD ${\displaystyle j}$ equals

$${\delta }_{j,i}=∥{\mathit{v}}_{PD,j}-{\mathit{v}}_{sp}^{(j,i)}∥.$$

(7)

2.4. Average Transmitted Optical Power

The objective of this paper is to relate the positioning accuracy of the VLP system to the illumination level of the area. As will be shown in the next section, the positioning accuracy is a function of the average transmitted optical power ${\displaystyle {\overline{\Phi }}_{e,i}}$, ${\displaystyle i=1,\dots ,K}$ of the LEDs. This transmitted optical power is, in turn, a function of the forward current signal applied to the LED. Taking into account that the receiver must be able to distinguish the signals from the different LEDs, we assume that the different LEDs are modulated using different orthogonal frequencies. A standard technique for combining signals modulated with different carrier frequencies is orthogonal frequency division multiplexing (OFDM). However, standard OFDM is not real-valued or positive. Therefore, several real-valued positive variants of OFDM have been developed for LED modulation, e.g., DC-biased optical OFDM (DCO-OFDM), asymmetrically clipped OFDM (ACO-OFDM) and asymmetrically clipped DC-biased optical OFDM (ADO-OFDM) [19,20,21]. In these techniques, the orthogonality of the signals is affected by non-linear distortions. Therefore, the LED typically operates within the linear dynamic range of the current versus voltage (I–V) curve of the LED (see Figure 4). Assuming that each LED uses only a single subcarrier, for all OFDM variants mentioned above, the signal for LED ${\displaystyle i}$ can be written as

$$s_i\left(t\right)=K_c{A}_i\left(1+cos\left(2\pi f_{c,i}t\right)\right).$$

(8)

where the frequencies ${\displaystyle f_{c,i}}$ of the LEDs are selected to be orthogonal over a time interval ${\displaystyle T_c}$, the amplitude ${\displaystyle A_i}$ is selected so that the LED operates within the linear dynamic range of the current versus voltage (I–V) curve of the LED and ${\displaystyle K_c}$ is the slope of the linear part of the I–V curve of the LED. The OFDM system also allows us to filter out the contributions of the nonmodulated I-LEDs, implying that the presence of the I-LEDs will have no effect on the observed signals (the presence of the I-LEDs will have an influence, though, on the operation of the PD as it will generate a DC bias current that depends on the optical power of the I-LEDs. Provided that the presence of the I-LEDs does not saturate the PDs, we assume that this constant bias current is filtered out before the amplifier).

To relate the average optical power ${\displaystyle {\overline{\Phi }}_{e,i}}$ from (2) to the forward current ${\displaystyle s_i\left(t\right)}$, we need the luminous flux ${\displaystyle {\Phi }_v}$, which is also used to determine the illumination level in an area, as will be explained in the next section. This luminous flux depends not only on the electrical current ${\displaystyle s_i\left(t\right)}$, but also on factors such as thickness, combination concentration and the geometrical distribution of the material of which it is composed. This relationship is summarised through ${\displaystyle {\Phi }_{v,i}=K_{\Phi }{\Phi }_v^{typ}{s}_i\left(t\right)}$, obtained from the forward current versus normalised relative luminous flux curve contained in the LED data sheets [22], where ${\displaystyle K_{\Phi }}$ is the slope of the linear part of the curve, and ${\displaystyle {\Phi }_v^{typ}}$ is the typical value of the luminous flux tested by the manufacturer. The instantaneous optical power ${\displaystyle {\Phi }_{e,i}\left(t\right)}$, radiated by the LED ${\displaystyle i}$, is proportional to this luminous flux:

$${\Phi }_{e,i}\left(t\right)=\frac{{\Phi }_{v,i}}{{\eta }_{LER}}=\frac{K_{\Phi }{\Phi }_v^{typ}}{{\eta }_{LER}}{s}_i\left(t\right),$$

(9)

where ${\displaystyle {\eta }_{LER}}$ is the luminous efficacy of optical radiation (${\displaystyle {\eta }_{LER}}$ (lm/Watt) relates to the optical power demanded by the emitting device and should not be confused with the luminous efficiency ${\displaystyle {\eta }_{LE}}$ (lm/Watt) of a light source, which is a term widely found in the technical specifications of LEDs but expresses the electrical power demanded by the emitting device), which is obtained by considering the LED operational electrical power and the normalized relative luminous flux specified in [22]. Consequently, the average optical power ${\displaystyle {\overline{\Phi }}_{e,i}}$ from (2) is given by

$${\overline{\Phi }}_{e,i}=\kappa \underset{T\to \infty }{lim}\frac{1}{T}{\int }_0^T{s}_i\left(t\right)dt=\kappa A_i$$

(10)

where ${\displaystyle \kappa =\frac{K_{\Phi }{\Phi }_v^{typ}{K}_c}{{\eta }_{LER}}}$.

3. System Evaluation Criteria

The evaluation criterion that will be used to assess the accuracy of positioning in our VLP system is the Cramer–Rao bound [23,24], which is a lower bound on the MSE of the position estimate for unbiased estimators. In [25], it is shown that, in most cases, the bias in the position estimate is sufficiently small to be neglected, implying that the CRB is a suitable lower bound to assess the performance of practical estimators and to analyse the VLP system.

In this paper, we evaluate the CRB on the position estimate ${\displaystyle {\widehat{\mathit{v}}}_U=\left({\widehat{x}}_U,{\widehat{y}}_U,{\widehat{z}}_U\right)}$ of the receiver position ${\displaystyle {\mathit{v}}_U=\left(x_U,y_U,z_U\right)}$ to bound the MSE [24]:

$$\begin{array}{cc}MSE\hfill & =E[{(x_U-{\widehat{x}}_U)}^2+{(y_U-{\widehat{y}}_U)}^2+{(z_U-{\widehat{z}}_U)}^2]\hfill \\ \hfill & \ge \mathrm{tr}\left({\mathit{F}}_U^{-1}\right).\hfill \end{array}$$

(11)

In (11), ${\displaystyle \mathrm{tr}(·)}$ is the trace operator, and ${\displaystyle {\mathit{F}}_U}$ is the Fisher information matrix (FIM). This FIM measures the amount of information about ${\displaystyle {\mathit{v}}_U}$ that can be extracted from the observed vector ${\displaystyle \mathit{r}}$ (2) of RSS values and is given by

$${\mathit{F}}_U=E\left[({\mathbf{\nabla }}_{{\mathit{v}}_U}lnp\left(\mathit{r}\right|{\mathit{v}}_U)){({\mathbf{\nabla }}_{{\mathit{v}}_U}lnp\left(\mathit{r}\right|{\mathit{v}}_U))}^T\right],$$

(12)

where ${\displaystyle \mathit{r}={[{\mathit{r}}_1^T\dots {\mathit{r}}_M^T]}^T}$. From (2), it follows that ${\displaystyle {\mathit{r}}_j\left[i\right]|{\mathit{v}}_U}$ is Gaussian distributed with average ${\displaystyle R_{p,j}{h}_c^{(j,i)}{\overline{\Phi }}_{e,i}}$ and variance ${\displaystyle N_{0,j}}$. Substituting in (12), we find, after straightforward derivations, that ${\displaystyle {\mathit{F}}_U=2T_c{\left(F_U\right)}_{a,b}}$, with ${\displaystyle a,b\in \{x_U,y_U,z_U\}}$, where ${\displaystyle T_c}$ is the time interval over which the signal is observed and

$${\left({\mathit{F}}_U\right)}_{a,b}=\sum _{i,i^{\prime }=1}^K{\overline{\Phi }}_{e,i}{\left(\sum _{j=1}^M\frac{R_{p,j}^2}{N_{0,j}}\left(\frac{\partial }{\partial a}{h}_c^{(j,i)}\frac{\partial }{\partial b}{h}_c^{(j,i^{\prime })}\right)\right)}_{i,i^{\prime }}{\overline{\Phi }}_{e,i^{\prime }}.$$

(13)

By substituting (3) in (13), the CRB can be obtained in a straightforward way (more details regarding the derivation of the CRB-related equations can be found in the appendix in [16] and of the illuminance-related equations in [14]).

4. Numerical Results

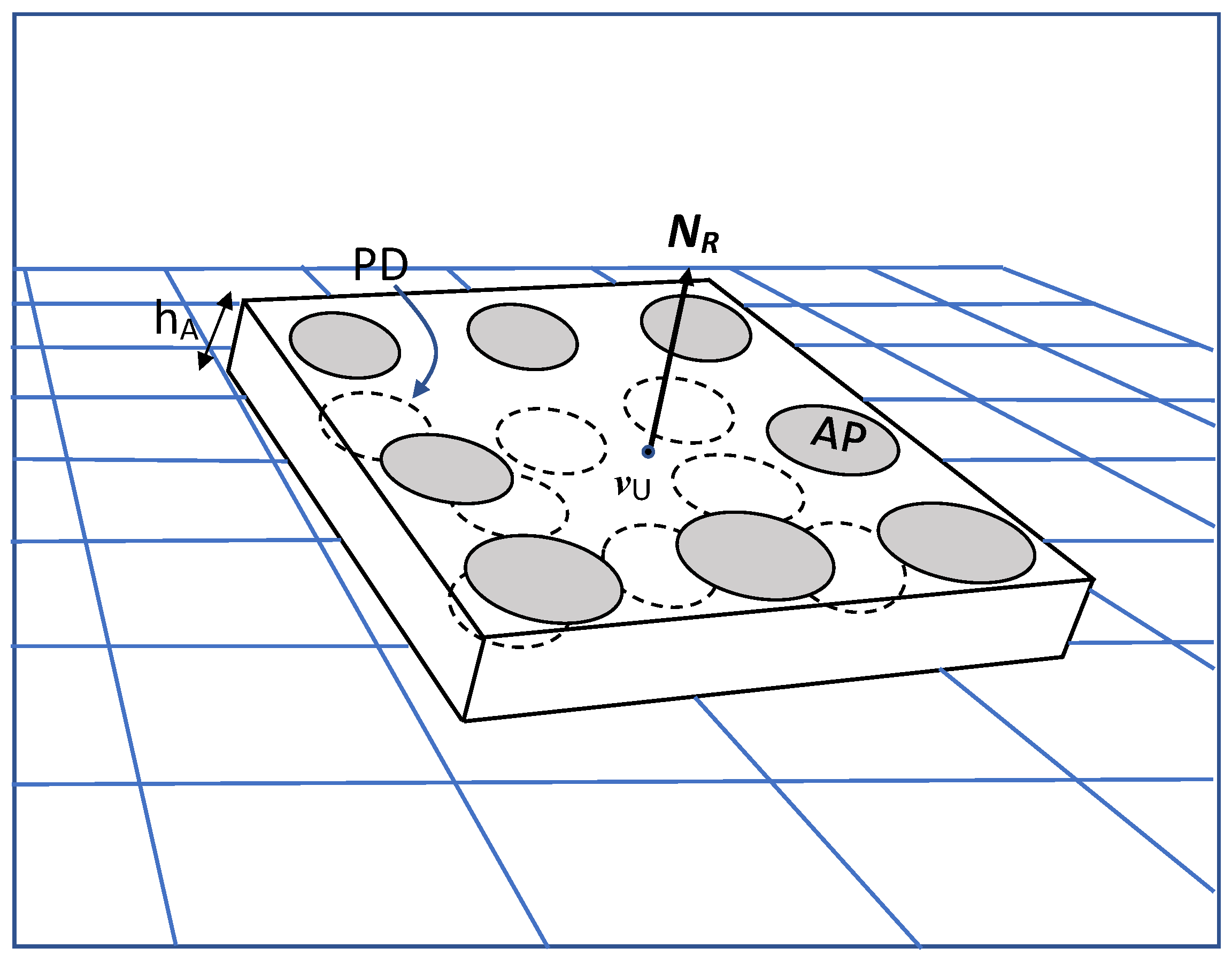
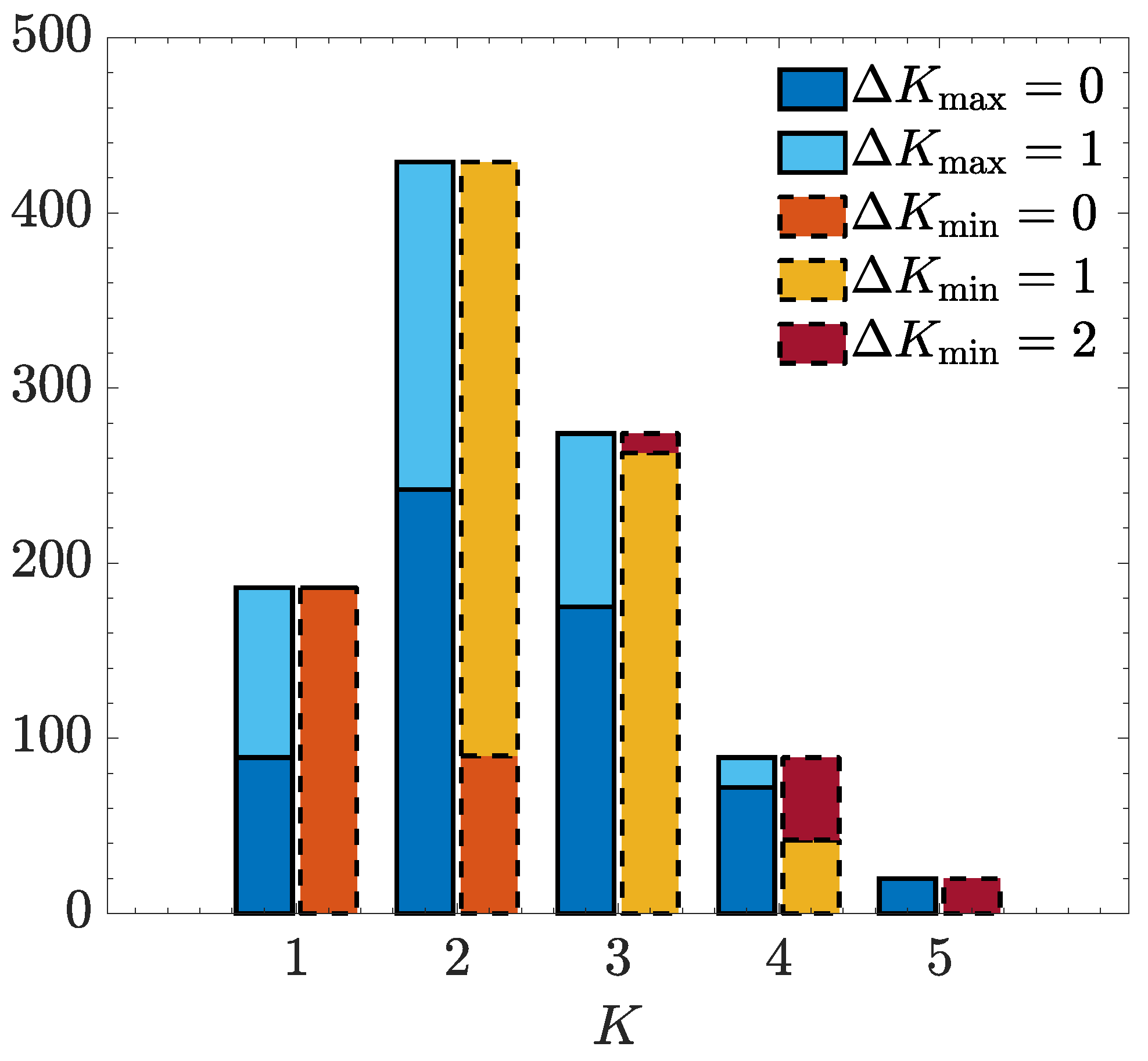In this section, we analyse the performance of the VLP system. Unless specified otherwise, we consider that both the area where the receiver is evaluated, i.e., the receiver area, and the ceiling area have dimensions ${\displaystyle X_{max}\times Y_{max}}$, with the latter located parallel and at a distance ${\displaystyle Z_{max}}$ above the first, with ${\displaystyle Z_{max}=z_{L,i}=h_{j,i}}$. We assume that the receiver contains ${\displaystyle M=8}$ REs. The relative coordinates ${\displaystyle {\mathit{v}}_{AP,j}}$ of the aperture centres with respect to the reference point ${\displaystyle {\mathit{v}}_U}$ of the receiver are given by ${\displaystyle {\mathit{v}}_{AP,j}=(x_{AP,j},y_{AP,j},z_{AP,j})}$, where ${\displaystyle {\mathit{x}}_{AP}=ϵh_A\left(\begin{array}{cccccccc}-1& 0& 1& 1& 1& 0& -1& -1\end{array}\right)}$, ${\displaystyle {\mathit{y}}_{AP}=ϵh_A(\begin{array}{cccccccc}-1& -1& -1& 0& 1& 1& 1& 0)\end{array}}$ and ${\displaystyle {\mathit{z}}_{AP}=\mathbf{0}}$, with ${\displaystyle ϵ=5}$ and ${\displaystyle h_A=}$ 1 mm. The horizontal distance ${\displaystyle ϵh_A}$ between the apertures, i.e., five times the vertical distance between the apertures and the PD, ensures that the only light that reaches the PD is the light coming through its own aperture. Furthermore, we assume that the coordinates ${\displaystyle \Delta {\mathit{v}}_{AP,j}}$ of the PD centres, relative to the aperture centres, are given by ${\displaystyle \Delta {\mathit{v}}_{AP,j}=(d_{AP,j}cos{\alpha }_{AP,j},d_{AP,j}sin{\alpha }_{AP,j},-h_A)}$, where ${\displaystyle d_{AP,j}=0.5R_D}$, with ${\displaystyle R_D=h_A}$ and ${\displaystyle {\alpha }_{AP,j}=j·\pi /4}$. The apertures and PD are positioned in such a way that they provide a large FOV to collect the light from a large number of different VLP-LEDs. To determine the level of the noise spectral density, we assume a background spectral irradiance ${\displaystyle p_n=}$ 5.8 ${\displaystyle \times }$ ${\displaystyle {10}^{-6}}$ W/cm²${\displaystyle ·}$nm [18] and PD responsivity ${\displaystyle R_{p_j}=}$ 0.4 mA/mW for all ${\displaystyle j=1,\dots ,M}$ [26]. The optical filter only passes visible light in the range 380 to 740 nm, resulting in an optical bandwidth of ${\displaystyle \Delta \lambda =}$ 360 nm. We assume that the signals transmitted by the LEDs are confined to the bandwidth ${\displaystyle B=20}$ MHz, and we observe the signals during an interval ${\displaystyle T_c=1}$ ms.

We determine the average optical transmitted power and the luminous flux based on the characteristics of the LED GW CSSRMU.CM manufactured by OSRAM Opto Semiconductors Inc. [22]. This LED has a Lambertian order ${\displaystyle m_{S,i}=1}$, which corresponds to a semi-angle ${\displaystyle {\Phi }_{1/2,i}={60}^{\circ }}$, a typical luminous flux output ${\displaystyle {\Phi }_v^{typ}=270}$ lm at forward voltage of 2.7 V and ${\displaystyle {\Phi }_{v,i}\approx 300}$ lm in the modulation zone. The luminous efficacy ${\displaystyle {\eta }_{LER}}$, which depends on the operation current and voltage, for this type of LED is ${\displaystyle {\eta }_{LER}=110}$ lm/W [27]. This allows an average optical power of ${\displaystyle {\overline{\Phi }}_e={\Phi }_{v,i}/{\eta }_{LER}=2.7}$ W.

In our analysis, we investigate the impact on the VLP system from relevant aspects such as the number and position of LEDs used as VLP transmitters.

4.1. Visible Light Positioning Light-Emitting Diodes and Receiver Area

To evaluate the influence of the placement of VLP-LEDs on the positioning performance, we assume that the VLP-LEDs are attached in a grid of ${\displaystyle K_L=K_{L,x}\times K_{L,y}}$ LEDs attached to the ceiling. We assume that the receiver is located at a distance ${\displaystyle Z_{max}=h_{j,i}=2}$ m below the ceiling in an area of size ${\displaystyle X_{max}\times Y_{max}}$ m². Further, we assume that the ${\displaystyle xy}$ coordinates of the centre of the grid correspond to the ${\displaystyle xy}$ coordinates of the centre of the receiver area. We select the positions of the VLP-LEDs to be

$$\begin{array}{cc}\hfill x_L\left({\ell }_x\right)=& \left(\frac{1}{K_{L,x}-1}({\ell }_x-1)-\frac{1}{2}\right){\rho }_x{X}_{max}\hfill \\ \hfill y_L\left({\ell }_y\right)=& \left(\frac{1}{K_{L,y}-1}({\ell }_y-1)-\frac{1}{2}\right){\rho }_y{Y}_{max}\hfill \end{array},$$

(14)

where ${\displaystyle {\ell }_x=1,\cdots ,K_{L,x}}$ and ${\displaystyle {\ell }_y=1,\cdots ,K_{L,y}}$, which corresponds to ${\displaystyle i=({\ell }_y-1)K_{L,x}+{\ell }_x}$, ${\displaystyle i=1,\cdots ,K_L}$.

The scaling factors ${\displaystyle {\rho }_x}$ and ${\displaystyle {\rho }_y}$ determine how far the grid is extended in the ${\displaystyle x}$ direction and ${\displaystyle y}$ direction. To ensure that all VLP-LEDs are contained in the ${\displaystyle X_{max}\times Y_{max}}$ m² area, the scaling factors ${\displaystyle {\rho }_x}$ and ${\displaystyle {\rho }_y}$ must satisfy ${\displaystyle 0\le {\rho }_x,{\rho }_y\le 1}$.

4.2. Optimal Ratios

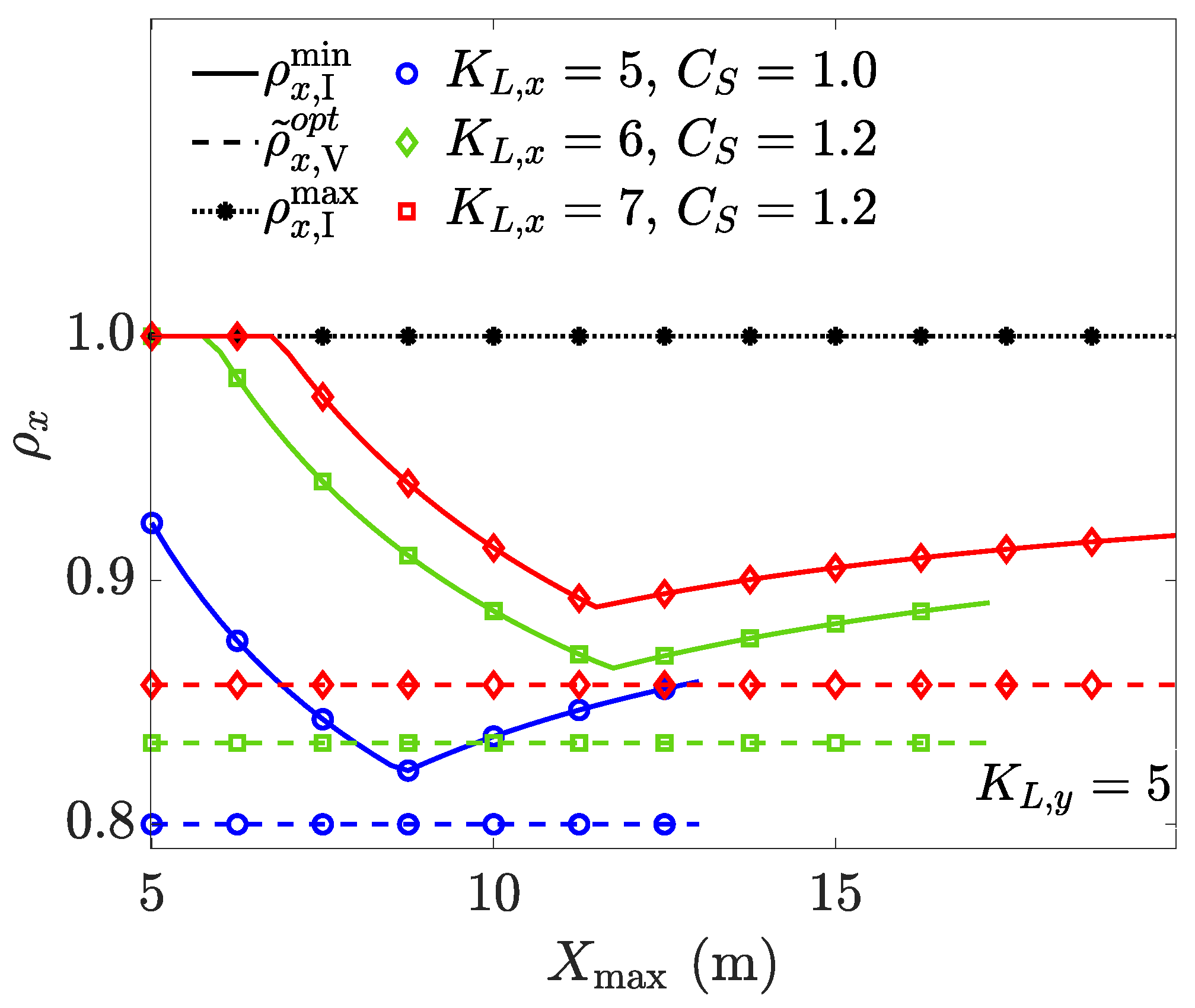
We first analyse the impact of the choice of ${\displaystyle K_{L,x}}$ and ${\displaystyle K_{L,y}}$ on the positioning performance. To this end, we assume the total number of VLP-LEDs is constant, that is, ${\displaystyle K_L=K_{L,x}{K}_{L,y}=144}$, and consider different combinations of ${\displaystyle K_{L,x}}$ and ${\displaystyle K_{L,y}}$: ${\displaystyle K_{L,i_K}=\left({\mathbf{K}}_{L,x}\left(i_K\right),{\mathbf{K}}_{L,y}\left(i_K\right)\right)}$ with ${\displaystyle {\mathbf{K}}_{L,x}=[48,36,24,18,12]}$ and ${\displaystyle {\mathbf{K}}_{L,y}=[3,4,6,8,12]}$, ${\displaystyle i_K=1,\dots ,5}$. We assume that the area has fixed size ${\displaystyle X_{max}\times Y_{max}=256}$ m², but we consider rectangular areas with different ${\displaystyle x}$ and ${\displaystyle y}$ dimensions, i.e., ${\displaystyle {\mathcal{S}}_c\left(i_s\right)=\left({\mathbf{X}}_c^T\left(i_s\right),{\mathbf{Y}}_c^T\left(i_s\right)\right)}$ with ${\displaystyle {\mathbf{X}}_c=16\left[\sqrt{\frac{47}{2}},\sqrt{\frac{35}{3}},\sqrt{\frac{23}{5}},\sqrt{\frac{17}{7}},\right]}$ m and ${\displaystyle {\mathbf{Y}}_c=16\left[\sqrt{\frac{2}{47}},\sqrt{\frac{3}{35}},\sqrt{\frac{5}{23}},\sqrt{\frac{7}{17}},\right]}$ m, ${\displaystyle i_s=1,\dots ,5}$.

To evaluate the positioning accuracy, we consider the spatial average of the square root of the CRB, i.e., ${\displaystyle \overline{\mathrm{rCRB}}}$, and the normalised standard deviation ${\displaystyle {\widehat{\sigma }}_{\mathrm{rCRB}}={\sigma }_{\overline{\mathrm{rCRB}}}/\overline{\mathrm{rCRB}}}$. While the first performance measure, ${\displaystyle \overline{\mathrm{rCRB}}}$, serves to find the configuration resulting in the most accurate average positioning performance, the second performance measure, ${\displaystyle {\widehat{\sigma }}_{\mathrm{rCRB}}}$, is an indication of the spatial uniformity of the result. For every combination of the above-mentioned area dimensions and VLP-LED layouts, we determine the optimal values ${\displaystyle {\rho }_x}$ and ${\displaystyle {\rho }_y}$ that result in the minimum value of ${\displaystyle \overline{\mathrm{rCRB}}}$. The resulting ${\displaystyle \overline{\mathrm{rCRB}}}$ is shown in Figure 5a. Similarly, we determine the values ${\displaystyle {\rho }_x}$ and ${\displaystyle {\rho }_y}$ that result in the lowest ${\displaystyle {\widehat{\sigma }}_{\mathrm{rCRB}}}$. The resulting ${\displaystyle {\widehat{\sigma }}_{\mathrm{rCRB}}}$ is shown in Figure 5b.

Although the optimal values of ${\displaystyle {\rho }_x}$ and ${\displaystyle {\rho }_y}$ differ for the two figures, because they optimise different objective functions, we can observe in Figure 5a,b that, for a given area dimension ${\displaystyle {\mathbf{X}}_c\left(i_s\right)\times {\mathbf{Y}}_c\left(i_s\right)}$, the VLP-LED layout with

$$\frac{{\mathbf{X}}_c\left(i_s\right)}{{\mathbf{Y}}_c\left(i_s\right)}=\frac{{\mathbf{K}}_{L,x}\left(i_K\right)-1}{{\mathbf{K}}_{L,y}\left(i_K\right)-1}$$

(15)

results in the smallest ${\displaystyle \overline{\mathrm{rCRB}}}$ and ${\displaystyle {\widehat{\sigma }}_{\mathrm{rCRB}}}$. In other words, ignoring the presence of the scaling factors ${\displaystyle {\rho }_x}$ and ${\displaystyle {\rho }_y}$, this corresponds to an equal spacing between the VLP-LEDs in the ${\displaystyle x}$ and ${\displaystyle y}$ direction, respectively: ${\displaystyle \frac{X_{max}}{K_{L,x}-1}=\frac{Y_{max}}{K_{L,y}-1}}$. This brings us to a first rule of thumb. Equation (15) shows us that the number of VLP-LEDs in the ${\displaystyle x}$ and ${\displaystyle y}$ direction should follow the dimensions of the receiver area.

4.3. Optimal Visible Light Positioning Light-Emitting Diode Spacing

In the previous discussion, we determined, for a given number of VLP-LEDs, the number of VLP-LEDs in each direction, i.e., ${\displaystyle K_{L,x}}$ and ${\displaystyle K_{L,y}}$. Now, we will further investigate the optimal spacing between VLP-LEDs, where the distance between VLP-LEDs in the ${\displaystyle x}$ direction, ${\displaystyle {\delta }_{L,x}}$, and in the ${\displaystyle y}$ direction, ${\displaystyle {\delta }_{L,y}}$, are derived from (14), resulting in ${\displaystyle {\delta }_{L,x}=\frac{{\rho }_x{X}_{max}}{K_{L,x}-1}}$ and ${\displaystyle {\delta }_{L,y}=\frac{{\rho }_y{Y}_{max}}{K_{L,y}-1}}$. To this end, we first restrict our attention to the case where the receiver area is square and the VLP-LEDs are placed in a square grid: ${\displaystyle {\rho }_x={\rho }_y=\rho }$, ${\displaystyle {\delta }_{L,x}={\delta }_{L,y}={\delta }_L}$, ${\displaystyle X_{max}=Y_{max}={\chi }_{max}}$ and ${\displaystyle K_{L,x}=K_{L,y}=K=\sqrt{K_L}}$. We will generalise later in this section the results to the rectangular layout. We consider three receiver areas with different sizes, i.e., with ${\displaystyle {\chi }_{max}=1}$, ${\displaystyle 4}$ and ${\displaystyle 10}$ m. The scaling factor ${\displaystyle \rho }$ with ${\displaystyle \rho \in [0,1]}$, influencing the distance between neighbouring VLP-LEDs, will be optimised.

In this optimisation, we use as an objective function the spatial average ${\displaystyle \overline{\mathrm{rCRB}}}$ over the ${\displaystyle {\chi }_{max}\times {\chi }_{max}}$ m² area of a receiver placed at a vertical distance of ${\displaystyle h_{j,i}=2}$ m below the ceiling. First, we plot ${\displaystyle \overline{\mathrm{rCRB}}}$ as a function of the scaling factor ${\displaystyle \rho }$ for different values of ${\displaystyle K_L}$. As expected, the results in Figure 6a show that increasing the number ${\displaystyle K_L=K^2}$ of VLP-LEDs leads to a lower rCRB, and thus a better positioning accuracy, as more information is available to estimate the user’s position. Further, Figure 6a reveals that the positioning accuracy first improves when ${\displaystyle \rho }$ increases but deteriorates after reaching a minimum. This can be explained as follows. When ${\displaystyle \rho }$ is small, all VLP-LEDs are concentrated above the centre of the receiver area, implying that the centre is well lit, but the edges of the area receive less light due to distance-dependent attenuation and relatively large radiation and incident angle. Hence, although the position of a receiver can be determined accurately if it is located in the centre of the receiver area, the positioning accuracy will be strongly reduced when the receiver is near the boundary of the area because of the larger distance and angle between the receiver and the VLP-LEDs. Obviously, this will also have a negative impact on the uniformity ${\displaystyle {\widehat{\sigma }}_{\mathrm{rCRB}}}$ of the positioning performance, see Figure 6b. By increasing ${\displaystyle \rho }$, the positioning accuracy near the edges will improve due to the better channel response for the closest VLP-LEDs, improving both the average positioning accuracy and the uniformity. However, when the distance becomes too large, the VLP-LEDs furthest away from the receiver start to drop out of the FOV of the receiver, implying that less information is available to determine the position, resulting in a degradation of the accuracy. The effect of ${\displaystyle \rho }$ on the position accuracy is greater when ${\displaystyle {\chi }_{max}}$ increases as the incident and radiation angles, as well as the distance between the VLP-LEDs and the receiver, increase when the area becomes larger. In Figure 6, we can observe that, in most cases, the optimal value of the spacing ${\displaystyle \rho }$ for ${\displaystyle \overline{\mathrm{rCRB}}}$ corresponds more or less to the optimal spacing for ${\displaystyle {\widehat{\sigma }}_{\mathrm{rCRB}}}$, and, in the cases where there is a discrepancy between the optimal spacing for optimising ${\displaystyle \overline{\mathrm{rCRB}}}$ and ${\displaystyle {\widehat{\sigma }}_{\mathrm{rCRB}}}$, the normalised standard deviation ${\displaystyle {\widehat{\sigma }}_{\mathrm{rCRB}}}$ is relatively small. Therefore, in the remainder of this section, we concentrate on the optimisation of ${\displaystyle \overline{\mathrm{rCRB}}}$.

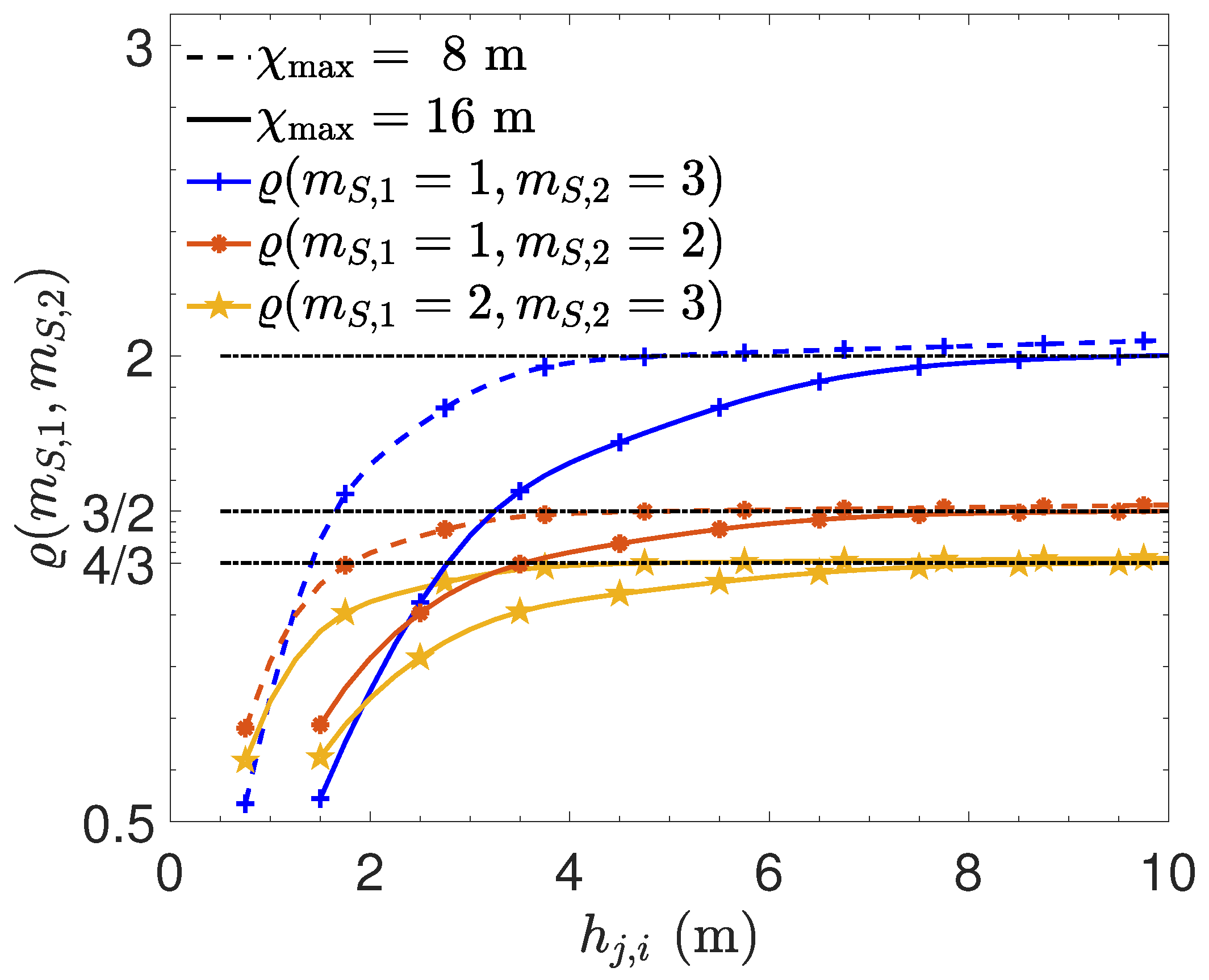
Let us look more closely at the optimal scaling factor ${\displaystyle \rho }$ and the corresponding optimal distance between the VLP-LEDs. In Figure 7a, we determine the optimal scaling factor ${\displaystyle \rho }$ that minimises ${\displaystyle \overline{\mathrm{rCRB}}}$ as a function of ${\displaystyle {\chi }_{max}}$. We observe that, when ${\displaystyle {\chi }_{max}<2}$ m, the scaling factor ${\displaystyle \rho \approx 1}$, i.e., the VLP-LEDs must be placed near the edges of the area. Due to the small area, the distance between the receiver and the VLP-LEDs is limited, as well as the radiation and incident angle, implying that the channel gain will be good for all positions of VLP-LEDs and the receiver. As the Fisher information matrix becomes closer to singular when ${\displaystyle \rho }$ is small (as the measurements from the different VLP-LEDs will be correlated strongly because the VLP-LEDs are approximately co-located), the VLP-LEDs must be placed apart as far as possible. On the other hand, when ${\displaystyle {\chi }_{max}\gg 2}$ m, we observe that ${\displaystyle \rho }$ becomes approximately independent of ${\displaystyle {\chi }_{max}}$, and the optimal distance increases with the increasing number of VLP-LEDs. In Figure 7b, we show the ratio between the ${\displaystyle \frac{{\delta }_L}{{\chi }_{max}}}$ for the cases considered in Figure 7a, and we compare the results with the level ${\displaystyle \frac{1}{K}}$. From these results, we find that the optimal spacing ${\displaystyle {\delta }_L^{opt}\left(K\right)}$ can be approximated by

$${\delta }_L^{opt}\left(K\right)\approx \frac{{\chi }_{max}}{K}\stackrel{\Delta }{=}{\tilde{\delta }}_L^{opt}\left(K\right),$$

(16)

which corresponds to

$${\tilde{\rho }}_{opt}=\frac{K-1}{K}.$$

(17)

To evaluate the positioning performance for this approximation of the optimal spacing, we compare the ${\displaystyle \overline{\mathrm{rCRB}}}$ for the spacing ${\displaystyle {\tilde{\delta }}_L^{opt}\left(K\right)}$ (16) with the performance for the true optimal spacing ${\displaystyle {\delta }_L^{opt}\left(K\right)}$ from Figure 7. The results, shown in Figure 8, reveal that the approximated spacing (16) provides a close-to-optimal positioning performance, even for small values of ${\displaystyle {\chi }_{max}}$. This can be explained by evaluating Figure 6a; for small areas, ${\displaystyle \overline{\mathrm{rCRB}}}$ is essentially independent of ${\displaystyle \rho }$, implying that, for the spacing (16), the resulting ${\displaystyle \overline{\mathrm{rCRB}}}$ will be close to the minimum.

In the above analysis, we restricted our attention to the case of a square receiver area. We now extend the results to the rectangular areas discussed earlier in this section. Using Equation (17), we extrapolate the approximation to

$$\begin{array}{cc}\hfill {\tilde{\rho }}_x^{opt}& \approx \frac{K_{L,x}-1}{K_{L,x}}\hfill \\ \hfill {\tilde{\rho }}_y^{opt}& \approx \frac{K_{L,y}-1}{K_{L,y}}\hfill \end{array}$$

(18)

and

$$\begin{array}{cc}\hfill \frac{{\delta }_{L,x}^{opt}}{{\delta }_{L,y}^{opt}}& =\frac{\frac{{\rho }_x^{opt}{X}_{max}}{K_{L,x}-1}}{\frac{{\rho }_y^{opt}{Y}_{max}}{K_{L,y}-1}}\approx \frac{\frac{{\tilde{\rho }}_x^{opt}{X}_{max}}{K_{L,x}-1}}{\frac{{\tilde{\rho }}_y^{opt}{Y}_{max}}{K_{L,y}-1}}\approx \frac{C_S}{C_L},\hfill \end{array}$$

(19)

where ${\displaystyle C_S=\frac{X_{max}}{Y_{max}}}$ and ${\displaystyle C_L=\frac{K_{L,x}}{K_{L,y}}}$. Comparing the approximation (18) with the optimal values of ${\displaystyle ({\rho }_x,{\rho }_y)}$ for the different scenarios considered in Figure 5a, we notice that ${\displaystyle {\tilde{\rho }}_x^{opt}}$ closely approximates all the values obtained for ${\displaystyle X_{max}}$. However, for the ${\displaystyle y}$ dimension, a larger deviation occurs between the optimal scaling factor ${\displaystyle {\rho }_y}$ and the approximation ${\displaystyle {\tilde{\rho }}_y^{opt}}$ for areas with a small ${\displaystyle Y_{max}}$. However, this does not imply that the approximation is not useful, as, similarly to the square area, when ${\displaystyle {\chi }_{max}}$, ${\displaystyle X_{max}}$ or ${\displaystyle Y_{max}}$ is small, the ${\displaystyle \overline{\mathrm{rCRB}}}$ becomes largely independent of ${\displaystyle \rho }$, ${\displaystyle {\rho }_x}$ or ${\displaystyle {\rho }_y}$, respectively. Hence, the approximations (17) and (18) can be used as a general rule of thumb to determine the optimal spacing between the VLP-LEDs.

4.4. Average Accuracy Level

Now that the optimal placement of the VLP-LEDs has been determined, we are interested in finding the minimum number of VLP-LEDs required to obtain a given average positioning accuracy. To this end, we show in Figure 9 the positioning accuracy that can be obtained with ${\displaystyle K_L=K^2}$ VLP-LEDs in square areas with dimensions ${\displaystyle {\chi }_{max}\times {\chi }_{max}}$ for different Lambertian orders and transmitted optical power. From these figures, we can determine the minimum number of VLP-LEDs that results in ${\displaystyle \overline{\mathrm{rCRB}}<\zeta }$ for areas up to ${\displaystyle 30\times 30}$ m². The figures reveal a linear relationship between the minimum ${\displaystyle K}$ to obtain ${\displaystyle \overline{\mathrm{rCRB}}<\zeta }$ and ${\displaystyle {\chi }_{max}}$. This linear relationship can be expressed as

$$K\ge \mathcal{S}(m_{S,i},h_{j,i},\zeta ,{\overline{\Phi }}_e){\chi }_{max}+\mathcal{B}(m_{S,i},h_{j,i},\zeta ,{\overline{\Phi }}_e),$$

(20)

where the slope ${\displaystyle \mathcal{S}}$ and bias ${\displaystyle \mathcal{B}}$ depend on the system parameters ${\displaystyle m_{S,i}}$, ${\displaystyle h_{j,i}}$ and ${\displaystyle {\overline{\Phi }}_e}$ and on the wanted accuracy level ${\displaystyle \zeta }$. Our simulations reveal that the bias ${\displaystyle \mathcal{B}}$ is very close to zero for all considered scenarios, implying that we can simplify (20) to

$$K\ge \mathcal{S}(m_{S,i},h_{j,i},\zeta ,{\overline{\Phi }}_e){\chi }_{max}.$$

(21)

This behaviour is expected because the positioning performance is mainly determined by the distance between the receiver and the nearest VLP-LEDs, indicating that, if the size of the area increases, the number of VLP-LEDs should increase accordingly to keep this distance between the nearest VLP-LEDs and the receiver constant. Combining this linear behaviour between ${\displaystyle {\chi }_{max}}$ and ${\displaystyle K}$ with (16), it follows that the optimal spacing ${\displaystyle {\delta }_L^{opt}}$ is constant for a given accuracy level and equal to the inverse of this slope. In the following, we investigate the dependency of the slope ${\displaystyle \mathcal{S}}$ on the system parameters. Let us first evaluate the slopes for the cases shown in Figure 9. The slopes of the curves and the resulting optimal spacing are listed in

Table 2. Definition of the ranges and the slopes and the resulting ${\displaystyle {\delta }_L^{opt}}$ for Figure 9.

Legend	Average Accuracy Range (in cm)	${\displaystyle {\overline{\mathbf{\Phi }}}_{\mathit{e}}=2.7}$ W		${\displaystyle {\overline{\mathbf{\Phi }}}_{\mathit{e}}=1.3}$ W		${\displaystyle {\overline{\mathbf{\Phi }}}_{\mathit{e}}=2.7}$ W
		${\displaystyle {\mathit{m}}_{\mathit{S},\mathit{i}}=\mathbf{1}}$		${\displaystyle {\mathit{m}}_{\mathit{S},\mathit{i}}=\mathbf{1}}$		${\displaystyle {\mathit{m}}_{\mathit{S},\mathit{i}}=\mathbf{3}}$
		${\displaystyle {\mathit{h}}_{\mathit{j},\mathit{i}}=\mathbf{2}}$ m		${\displaystyle {\mathit{h}}_{\mathit{j},\mathit{i}}=\mathbf{2}}$ m		${\displaystyle {\mathit{h}}_{\mathit{j},\mathit{i}}=\mathbf{2}}$ m
		Slope	${\displaystyle {\mathit{\delta }}_{\mathit{L}}^{\mathit{opt}}}$ (m)	Slope	${\displaystyle {\mathit{\delta }}_{\mathit{L}}^{\mathit{opt}}}$ (m)	Slope	${\displaystyle {\mathit{\delta }}_{\mathit{L}}^{\mathit{opt}}}$ (m)
0.025 cm	${\displaystyle 0<\overline{\mathrm{rCRB}}\le 0.025}$	0.65	1.5	1.25	0.8	0.46	2.2
0.05 cm	${\displaystyle 0.025<\overline{\mathrm{rCRB}}\le 0.05}$	0.40	2.5	0.65	1.5	0.34	2.9
0.1 cm	${\displaystyle 0.05<\overline{\mathrm{rCRB}}\le 0.1}$	0.29	3.4	0.40	2.5	0.28	3.5
0.5 cm	${\displaystyle 0.1<\overline{\mathrm{rCRB}}\le 0.5}$	0.19	5.2	0.26	3.8	0.20	5

.

Comparing Figure 9a (${\displaystyle m_{S,i}=1}$ and ${\displaystyle {\overline{\Phi }}_e=2.7}$ W) with Figure 9b (${\displaystyle m_{S,i}=1}$ and ${\displaystyle {\overline{\Phi }}_e=2.7/2}$ W) and the slopes of the curves, given in Table 2, we observe that, if we halve the transmitted optical power, this results in the curve ${\displaystyle \overline{\mathrm{rCRB}}=0.05}$ cm in Figure 9a being equivalent to the ${\displaystyle \overline{\mathrm{rCRB}}=0.1}$ cm in Figure 9b. In general, if we increase the transmitted optical power with a factor ${\displaystyle \beta }$, the side ${\displaystyle {\chi }_{max}}$ of the square area may increase with the same factor ${\displaystyle \beta }$ to obtain the same average positioning accuracy (of course, this is provided that the scaling factor ${\displaystyle \beta }$ is small enough that the VLP-LEDs do not disappear out of the field of view of the receiver and the receiver does not fall out of the field of view of the VLP-LEDs) with the same number of VLP-LEDs. The explanation can be found by verifying Equations (11) and (13); the rCRB is proportional to ${\displaystyle 1/{\overline{\Phi }}_e}$, so increasing the optical power ${\displaystyle {\overline{\Phi }}_e}$ will reduce the rCRB with the same factor. In other words, the slope ${\displaystyle \mathcal{S}}$ in (20) will be a function of the product ${\displaystyle \zeta {\overline{\Phi }}_e}$.

In Figure 9c (${\displaystyle m_{S,i}=3}$ and ${\displaystyle {\overline{\Phi }}_e=2.7}$ W), we change the Lambertian order so that ${\displaystyle m_{S,i}+1}$ is doubled compared to Figure 9a (${\displaystyle m_{S,i}=1}$ and ${\displaystyle {\overline{\Phi }}_e=2.7}$ W). The channel gain (3) depends on the Lambertian order through the prefactor ${\displaystyle m_{S,i}+1}$, but also through the exponent of the cosine of the incident angle ${\displaystyle {\varphi }_{j,i}}$. This incident angle depends on the position of the receiver, implying that the dependency of the rCRB on the Lambertian order is more complex than on the optical power. However, it is expected that, when this incident angle is sufficiently small, we can approximate ${\displaystyle cos{\varphi }_{j,i}\approx 1}$. In that case, the channel gain will depend on ${\displaystyle m_{S,i}}$ through the prefactor ${\displaystyle m_{S,i}+1}$ only, implying that the rCRB will behave approximately proportionally to ${\displaystyle 1/(m_{S,i}+1)}$. This will be the case when the height ${\displaystyle h_{j,i}}$ is sufficiently large as, when the height increases, the incidence angle will become smaller. In Figure 9c, the rCRB only roughly reduces by factor ${\displaystyle m_{S,i}+1}$, indicating that the incident angle is not small enough for this approximation to hold. In general, the slope ${\displaystyle \mathcal{S}}$ in (20) will be a complicated function of the Lambertian order ${\displaystyle m_{S,i}}$.

In Figure 9a–c, we keep the same height of VLP-LEDs, i.e., ${\displaystyle h_{j,i}=2}$ m. Changing this height will have an impact on ${\displaystyle \overline{\mathrm{rCRB}}}$ that is more complex than when changing the optical power or Lambertian order as this height is directly related to the ${\displaystyle z}$ coordinate ${\displaystyle z_U}$ of the receiver position, that is, ${\displaystyle h_{j,i}=z_{L,i}-z_U+h_A}$. This can be observed in Figure 10, where we show the impact of the receiver height ${\displaystyle h_{j,i}}$ on the ${\displaystyle \overline{\mathrm{rCRB}}}$ for ${\displaystyle K^2=49}$ VLP-LEDs with Lambertian order ${\displaystyle m_{S,i}\in \{1,2,3\}}$ and optical power ${\displaystyle {\overline{\Phi }}_e\in \{2.7,1.4\}}$ W and for two different receiver areas ${\displaystyle {\chi }_{max}\in \{8,16\}}$ m. As predicted by our analysis of Figure 9a–c, we observe in Figure 10 that, for a given ${\displaystyle {\chi }_{max}}$, the blue and red curves are parallel; doubling the transmitted optical power results in a reduction in the rCRB by a factor of two. In addition, we stated that the rCRB is approximately proportional to ${\displaystyle 1/(m_{S,i}+1)}$ when the incident angle is small. Hence, for a large ${\displaystyle h_{j,i}}$, we expect that the yellow curve will become parallel to the blue curve. This effect indeed can be observed in the figure. This is further analysed in detail in Figure 11, where we show the ratio

$$\varrho (m_{S,1},m_{S,2})=\frac{\overline{\mathrm{rCRB}}{|}_{m_{S,1}}}{\overline{\mathrm{rCRB}}{|}_{m_{S,2}}}.$$

(22)

as a function of height for ${\displaystyle m_{S,i}\in \{1,2,3\}}$ and ${\displaystyle {\chi }_{max}\in \{8,16\}}$ m. It can be observed that the curves converge to a constant for a sufficiently large ${\displaystyle h_{j,i}}$. This constant is slightly larger than ${\displaystyle \frac{m_{S,2}+1}{m_{S,1}+1}}$ as ${\displaystyle {cos}^{m_{S,2}+1}{\varphi }_{j,i}\le {cos}^{m_{S,1}+1}{\varphi }_{j,i}}$ for ${\displaystyle m_{S,2}>m_{S,1}}$, implying that the overestimation of the channel gain (underestimation of the rCRB) when approximating ${\displaystyle cos{\varphi }_{j,i}\approx 1}$ is larger for ${\displaystyle m_{S,2}}$ than for ${\displaystyle m_{S,1}}$. For a given ${\displaystyle {\chi }_{max}}$, the height ${\displaystyle h_{j,i}^{†}}$ at which ${\displaystyle \varrho (m_{S,1},m_{S,2})}$ converges is approximately independent of the value ${\displaystyle m_{S,i}}$ of the Lambertian order. Comparing the height ${\displaystyle h_{j,i}^{†}}$ for ${\displaystyle {\chi }_{max}=8}$ m and ${\displaystyle {\chi }_{max}=16}$ m, we find that the height ${\displaystyle h_{j,i}^{†}}$ for ${\displaystyle {\chi }_{max}=16}$ m is twice the height ${\displaystyle h_{j,i}^{†}}$ for ${\displaystyle {\chi }_{max}=8}$ m, that is, the height of convergence scales with ${\displaystyle {\chi }_{max}}$. To explain this, let us consider the following scenario. Consider the four LEDs surrounding the receiver and assume that the receiver is located in the centre of these four LEDs. Further, suppose that the LEDs are optimally spaced, that is, their spacing is ${\displaystyle {\delta }_L^{opt}\left(K\right)=\frac{{\chi }_{max}}{K}}$ (16). Then, the incidence angle ${\displaystyle {\varphi }_{j,i}}$ is for the four considered LEDs ${\displaystyle h_{j,i}tan{\varphi }_{j,i}=\frac{{\chi }_{max}}{\sqrt{2}K}}$. Inserting ${\displaystyle h_{j,i}^{†}=3.75}$ m for ${\displaystyle {\chi }_{max}=8}$ m (${\displaystyle h_{j,i}^{†}=7.5}$ m for ${\displaystyle {\chi }_{max}=16}$ m), the resulting incidence angle for ${\displaystyle K=7}$ approximately equals ${\displaystyle {\varphi }_{j,i}^{†}={12}^{\circ }}$. We evaluated the convergence height for various values of ${\displaystyle K}$ and ${\displaystyle {\chi }_{max}}$ and found, for all cases, that convergence occurs when the incidence angle is in the interval ${\displaystyle {\varphi }_{j,i}^{†}\in [{11}^{\circ },{14}^{\circ }]}$. This corresponds to a height ${\displaystyle h_{j,i}^{†}={\alpha }_h\frac{{\chi }_{max}}{K}}$, where ${\displaystyle {\alpha }_h\in [2.8,3.6]}$, i.e., when the height is greater than ${\displaystyle {\alpha }_h}$ times the optimal spacing ${\displaystyle \frac{{\chi }_{max}}{K}}$ between the VLP-LEDs, the rCRB will be approximately proportional to ${\displaystyle 1/(m_{S,i}+1)}$.

Until now, we have concentrated on the relative differences between the curves in Figure 10. Now, we will discuss the behaviour of the ${\displaystyle \overline{\mathrm{rCRB}}}$ as a function of height ${\displaystyle h_{j,i}}$. The figure shows that, for a small ${\displaystyle h_{j,i}}$, the ${\displaystyle \overline{\mathrm{rCRB}}}$ first decreases as a function of ${\displaystyle h_{j,i}}$, and, after reaching a minimum, it increases again. This is explained as follows. For a small ${\displaystyle h_{j,i}}$, the receiver sees only a limited number of LEDs because it falls out of the FOV of most LEDs. By increasing the height, the receiver will gradually see more LEDs, so more information will be available to determine its position, resulting in an improvement of the positioning accuracy. However, at some point, the additional information that is obtained by detecting more LEDs will be outweighed by the reduction in the channel gain because the receiver is further away from the LEDs. As the signal-to-noise ratio reduces as a result of the smaller channel gain, the position accuracy will degrade. For a large ${\displaystyle h_{j,i}}$, the rCRB increases approximately proportionally to ${\displaystyle h_{j,i}^2}$. This follows from Equation (3); when ${\displaystyle h_{j,i}}$ is large, ${\displaystyle cos{\varphi }_{j,1}\approx 1}$, and, for the nearest LEDs, ${\displaystyle d_{j,i}\approx h_{j,i}}$, implying that the channel gain approximately is proportional to ${\displaystyle 1/h_{j,i}^2}$, which leads to the rCRB being proportional to ${\displaystyle h_{j,i}^2}$.

In conclusion, the rCRB scales with the transmitted optical power ${\displaystyle {\overline{\Phi }}_e}$, and, when the incidence angle (for the four closest LEDs) is sufficiently small, the rCRB is proportional to ${\displaystyle 1/(m_{S,i}+1)}$ and ${\displaystyle h_{j,i}^2}$. This will occur when ${\displaystyle h_{j,i}\ge h_{j,i}^{†}}$, where ${\displaystyle h_{j,i}^{†}={\alpha }_h\frac{{\chi }_{max}}{K}}$ with ${\displaystyle {\alpha }_h\in [2.8,3.6]}$ and ${\displaystyle \frac{{\chi }_{max}}{K}}$ is the optimal spacing between the LEDs.

Although the above analysis gives us insight into the behaviour of the rCRB as a function of the system parameters, we are not able to find an accurate closed-form expression for the slope ${\displaystyle \mathcal{S}}$ in (21) as a function of the system parameters ${\displaystyle {\overline{\Phi }}_e}$, ${\displaystyle m_{S,i}}$ and ${\displaystyle h_{j,i}}$ and accuracy level ${\displaystyle \zeta }$. Therefore, we will derive a lower and upper bound on the minimum number ${\displaystyle K}$ of VLP-LEDs.

To find a lower bound ${\displaystyle K_{min}}$ in ${\displaystyle K}$, i.e., ${\displaystyle K\ge K_{min}}$, we analyse the FOV of the receiver. To estimate the receiver position, at least one VLP-LED must be in this FOV, otherwise the Fisher information matrix will become singular. Let us focus on the receiver position furthest from the centre of the area, i.e., in a corner, and consider the VLP-LED closest to the receiver. This VLP-LED will be in the FOV when the incident angle ${\displaystyle {\varphi }_{j,i}}$ is smaller than the FOV angle ${\displaystyle {\Phi }_{\mathrm{rec}}}$, i.e.,

$$tan\left({\Phi }_{\mathrm{rec}}\right)>tan\left({\varphi }_{j,i}\right).$$

(23)

Assuming the LEDs are optimally spaced, i.e., ${\displaystyle {\delta }_L^{opt}=\frac{{\chi }_{max}}{K}}$, the horizontal distance between the LED and the receiver in this scenario equals ${\displaystyle \Delta =\sqrt{2}\frac{{\chi }_{max}}{2K}}$, which is related to the incident angle through ${\displaystyle \Delta =h_{j,i}tan{\varphi }_{j,i}}$, leading to the lower bound

$$K_{min}=\frac{\sqrt{2}}{4tan\left({\Phi }_{\mathrm{rec}}\right)h_{j,i}}{\chi }_{max}\stackrel{\Delta }{=}{\mathcal{S}}_{min}{\chi }_{max}.$$

(24)

For the receiver structure specified at the beginning of the numerical results section, ${\displaystyle tan\left({\Phi }_{\mathrm{rec}}\right)=2.5}$. The slope ${\displaystyle {\mathcal{S}}_{min}}$ for this lower bound is independent of ${\displaystyle m_S}$ and ${\displaystyle \zeta {\overline{\Phi }}_e}$. As (24) is a strict lower bound on ${\displaystyle K}$, which implies that the slope ${\displaystyle {\mathcal{S}}_{min}}$ is a lower bound on the true slope ${\displaystyle \mathcal{S}}$, it is expected that the lower bound will become less tight when ${\displaystyle {\chi }_{max}}$ increases. This is observed in Figure 12, which shows a histogram where, as a function of ${\displaystyle K}$, the difference ${\displaystyle \Delta K_{min}=K-K_{min}}$ is depicted for 1000 scenarios, where we randomly choose for each parameter in

Table 3. Parameter ranges for the simulations of the lower and upper bound (24) and (25).

	Min.	Max.	Units
${\displaystyle h_{j,i}}$	1.5	4	m
${\displaystyle {\chi }_{max}}$	5	25	m
FoV	40	70	Deg
${\displaystyle m_{S,i}}$	0.65	4.82
${\displaystyle {\overline{\Phi }}_e}$	1	5	W
${\displaystyle \zeta }$	1	10	cm

a value within the range specified in the table. As can be observed, when ${\displaystyle K=1}$, corresponding to a small ${\displaystyle {\chi }_{max}}$, the lower bound is tight, that is, ${\displaystyle \Delta K_{min}=0}$ for all scenarios. The difference ${\displaystyle \Delta K_{min}}$ increases for increasing ${\displaystyle K}$ and, thus, ${\displaystyle {\chi }_{max}}$. For ${\displaystyle K>2}$, the difference ${\displaystyle \Delta K_{min}\ge 1}$ for all scenarios.

As the above lower bound becomes less tight for a larger ${\displaystyle {\chi }_{max}}$, we designed an approximation for the minimum number of VLP-LEDs in an empirical way. To this end, we added to the lower bound (24), a factor that depends on the parameters ${\displaystyle m_S}$, ${\displaystyle h_{j,i}}$ and ${\displaystyle \zeta {\overline{\Phi }}_e}$, and tuned the factor based on the simulations. This led to the following approximation:

$$K_{max}=⌈\frac{1}{4tan\left({\Phi }_{\mathrm{rec}}\right)}\sqrt{\frac{2}{h_{j,i}}}{\left(\frac{\zeta {\overline{\Phi }}_e}{0.175\zeta {\overline{\Phi }}_e-0.12}\right)}^{0.3}⌉{\chi }_{max}.$$

(25)

The difference ${\displaystyle \Delta K_{max}=K_{max}-K}$ between this approximation ${\displaystyle K_{max}}$ and the true minimum value ${\displaystyle K}$ is also visualised in Figure 12 for the 1000 simulated scenarios. As can be observed in the figure, for all scenarios, ${\displaystyle \Delta K_{max}=0}$ or ${\displaystyle \Delta K_{max}=1}$, implying that the approximation can serve as an upper bound on the true minimum ${\displaystyle K}$, i.e., ${\displaystyle K_{min}\le K\le K_{max}}$. We also observe in the histogram that the upper bound (25) becomes more tight when ${\displaystyle K}$ increases. This will occur when ${\displaystyle {\chi }_{max}}$ increases (for a given ${\displaystyle h_{j,i}}$) or ${\displaystyle h_{j,i}}$ reduces (for a given ${\displaystyle {\chi }_{max}}$).

In this analysis, we restricted our attention to square areas. However, the results can be extended to rectangular areas where ${\displaystyle C_S>1}$. We found that the lower and upper bounds (24) and (25) can also be used to find a lower and upper bound on ${\displaystyle K_{L,x}}$ and ${\displaystyle K_{L,y}}$ for the rectangular case by replacing in (24) and (25) ${\displaystyle {\chi }_{max}}$ with ${\displaystyle X_{max}}$ and ${\displaystyle Y_{max}}$, respectively, for the ranges indicated in Table 3 provided that ${\displaystyle \frac{C_S}{C_L}\approx 1}$ and ${\displaystyle C_S\le 2}$, i.e., ${\displaystyle X_{max}\le 2Y_{max}}$.

4.5. Illumination- versus Visible-Light-Positioning-Based Optimisation

Until now, we have focused on the placement of the VLP-LEDs in order to optimise the positioning performance without considering the primary purpose of the LEDs, i.e., illumination. In [14], we analysed the placement of LEDs to satisfy the constraints on the horizontal illuminance and uniformity of illumination according to the DIN EN 12464-1 standard [28]. Assuming that the LEDs are grouped into luminaries, in [14], we showed that the average illuminance depends mainly on the total number of LEDs contained in the luminaries, while the uniformity of the illuminance depends primarily on the placement of the luminaries. That analysis also revealed that the number and spacing of the luminaries to meet the required illuminance and uniformity of illumination depend in a complex manner on the system parameters such as the size of the room, the layout of luminaries to be used and the desired level of lighting uniformity in the lit area.

In this section, we will use the results of [14] to evaluate the feasibility of combining illumination with VLP on the same infrastructure. To this end, we assume that the illumination LEDs are grouped in luminaries and distributed on the ceiling in a rectangular grid, similarly to in [14]. Further, we assume that each luminary contains one VLP-LED placed in the centre of the luminary. Taking into account that the average illuminance depends mainly on the number of LEDs and is essentially independent of the placement of the LEDs, in our analysis, we focus on the illuminance uniformity.

We first compare the results of the optimal luminary placement obtained from [14] with the optimal VLP-LED spacing from this paper. To this end, we determine the spacing between the luminaries in order to maintain the illumination uniformity levels as prescribed in the standard [28]. Similarly to in Section 4.3, this spacing is expressed in terms of the fraction ${\displaystyle {\rho }_{x,I}\in [0,1]}$ of ${\displaystyle X_{max}}$. As the standard defines a range for the illumination level and uniformity, the value of ${\displaystyle {\rho }_{x,I}}$ for which the illumination conditions are satisfied will also belong to a range, i.e., ${\displaystyle [{\rho }_{x,I}^{min},{\rho }_{x,I}^{max}]}$. In Figure 13, we show this range of ${\displaystyle {\rho }_{x,I}}$ as a function of ${\displaystyle X_{max}}$ for different values of ${\displaystyle K_{L,x}}$ and ${\displaystyle C_S=\frac{X_{max}}{Y_{max}}}$, assuming ${\displaystyle K_{L,y}=5}$. For the parameters used in the figure, the upper bound is equal to ${\displaystyle {\rho }_{x,I}^{max}=1}$ for all values of ${\displaystyle X_{max}}$, while the lower bound ${\displaystyle {\rho }_{x,I}^{min}}$ varies as a function of ${\displaystyle X_{max}}$. In this figure, we also show the optimal spacing for the VLP-LEDs in terms of the fraction ${\displaystyle {\rho }_{x,V}^{opt}}$ of ${\displaystyle X_{max}}$. As can be observed in the figure, the optimal value ${\displaystyle {\rho }_{x,V}^{opt}}$ for the spacing of the VLP-LEDs lies below the curve of ${\displaystyle {\rho }_{x,I}^{min}}$. In other words, the minimum spacing between the luminaries according to the illumination constraints is larger than the optimal spacing between the LEDs for VLP. Hence, it is not possible to satisfy the illumination constraints and obtain optimal positioning accuracy at the same time. This implies that we need to find a compromise between the illumination and positioning constraints.

For this reason, we evaluate how the spacing resulting from the illumination conditions degrades the positioning performance, and how the spacing obtained from the VLP constraints analysed in this paper impacts the illumination levels and uniformity. In Figure 14a, we show the rCRB for the optimal spacing for VLP, i.e., corresponding to the fraction ${\displaystyle {\rho }_{x,V}^{opt}}$, and for the lower bound ${\displaystyle {\rho }_{x,I}^{min}}$ as, for all spacings satisfying the illumination constraints, this spacing is closest to the optimal spacing for VLP, implying that the degradation of the rRCB will be the smallest. As can be seen in the figure, the degradation is negligibly small for areas up to ${\displaystyle X_{max}=15}$ m. For ${\displaystyle X_{max}>15}$ m, the degradation increases but is still small. On the other hand, in Figure 14b,c, we show the uniformity for the task area (the task area is defined as the central part of the area where the illuminance uniformity should be higher, i.e., more uniform, than in the surrounding area, which is defined as the part of the area near its boundaries. For the task area, this uniformity should be ${\displaystyle {\mathcal{U}}_t\ge 0.7}$, and, for the surrounding area, ${\displaystyle {\mathcal{U}}_s\ge 0.5}$) ${\displaystyle {\mathcal{U}}_t}$ and the surrounding area ${\displaystyle {\mathcal{U}}_s}$ for different values of ${\displaystyle K_{L,x}}$ and ${\displaystyle C_S}$, assuming ${\displaystyle K_{L,y}=5}$, ${\displaystyle m_{S,i}=1}$ and ${\displaystyle {\xi }^t=0.8}$ (${\displaystyle {\xi }^t}$ defines the central sub-area of the area where the receiver is assessed, and ${\displaystyle {\xi }^t=0.8}$ means that 80% is taken in both the ${\displaystyle x}$ and ${\displaystyle y}$ directions). As can be observed in Figure 14b, for the task area, the uniformity for ${\displaystyle {\rho }_{x,I}^{min}}$ exceeds the required level of uniformity for all considered area sizes (except for ${\displaystyle K_{L,x}=5}$, where it is only met for ${\displaystyle X_{max}<18}$). For the optimum spacing for VLP, the figure shows that, for a larger ${\displaystyle X_{max}}$, the uniformity level for ${\displaystyle {\rho }_{x,V}^{opt}}$ lies above that for ${\displaystyle {\rho }_{x,I}^{min}}$. Hence, we still meet the uniformity condition. However, for smaller area sizes, i.e., ${\displaystyle X_{max}}$ < 9–11 m, we cannot satisfy the uniformity requirement for the task area when using the optimal spacing for VLP. On the other hand, as can be seen in Figure 14c, in the surrounding area, the minimum uniformity level for ${\displaystyle {\rho }_{x,I}^{min}}$ is reached for all area sizes, but this is not the case for the optimum spacing ${\displaystyle {\rho }_{x,V}^{opt}}$ for VLP. Here, only for a smaller ${\displaystyle X_{max}}$, that is, ${\displaystyle X_{max}}$ < 8–9 m, is the uniformity sufficiently large. Hence, when the optimal spacing for VLP is used, these results show that it is not possible to satisfy the illumination constraints for both the task and surrounding area.

To summarise this subsection, our results show that the optimal spacing for the VLP does not conform to the spacing range in which the illumination constraints are satisfied, implying that a compromise needs to be established between VLP and illumination. Based on our results, if one wants to design a combined illumination and positioning system, our recommendation is to retain the (minimum) spacing for illumination because, when using this spacing, the degradation of the positioning accuracy is limited, while, in the other case, when we use the optimal spacing for VLP, the uniformity of illumination will be seriously affected.

5. Conclusions

We have presented an analysis of a VLP system comprising a set of non-directional white LEDs used as transmitters and, as receiver, an aperture-based receiver with a wide FOV and high angular diversity. The receiver was evaluated in an area of ${\displaystyle X_{max}\times Y_{max}}$ m² at a vertical distance of ${\displaystyle Z_{max}}$ m below the ceiling where the VLP-LEDs were distributed in a rectangular grid. Moreover, we assumed that the LEDs were perfectly pointing downward and that the receiver was orientated parallel to the ceiling.

The performance of the VLP system was evaluated by obtaining a lower bound on the mean-squared error of the receiver position estimation, the CRB. More specifically, both the highest accuracy and the uniformity of receiver position estimation were considered in the analysis. Unlike in other studies, the simulations carried out in the optimisation process involved parameters such as the room dimension, the number of VLP-LEDs and the Lambertian order of LEDs, as well as the uniformity in the illuminance.

The results obtained allowed us to establish rules of thumb for the design of VLP systems for the optimal distance at which the VLP-LEDs should be spaced, depending mainly on the room dimensions and the number of VLP-LEDs, as well as a simple approximation for calculating the overall average receiver position estimation accuracy.

Furthermore, we further contrasted the results of the optimal spacing of VLP-LEDs with the recommendation on the optimal spacing distance between luminaries made in [14], where only the primary function of LEDs, illumination, was considered. It was found that, although the optimal spacing distance between the VLP-LEDs is below the optimal range determined in the analysis based on adequate illumination, the degradation in average positioning accuracy is negligible for small areas and of greater impact in large areas, which could be mitigated by increasing the number of VLP-LEDs.