Abstract
High directional emission and high radiative quantum efficiency are strongly needed when moving a single optical nano-emitter (such as a quantum dot) into the practical realm. However, a typical optical nano-emitter struggles to meet the requirements above, which limits its practical applications in next-generation nano-photonic devices such as single-photon sources. Here, to achieve these features simultaneously, we propose and theoretically investigate a composite plasmonic antenna consisting of a hemispherical solid immersion lens (SIL) and a bowtie plasmonic nano-antenna, wherein a high directional emission of 10° and 2.5 × 103 of Purcell factor have both been enabled. Moreover, we find that directionality and the Purcell factor can be manipulated independently in our antenna, which provides a novel platform for the optimization of single-photon sources.
1. Introduction
Classic luminescent emitters mostly have properties of relatively long luminescence lifetimes and directionless emission, which limits the development of optical devices required for next-generation quantum computation and quantum communication, such as high-speed nano-scale light emitting [1,2,3] and single-photon sources [4,5,6]. Particularly, the single-photon source is playing a fundamental role in the fields mentioned above. To move single-photon sources into the practical realm, a series of challenging requirements must be met, including a high spontaneous emission rate [7] and high radiation directionality and photon coherence (indistinguishability) [8]. However, when optimizing the performance of single-photon sources, it is difficult to improve the radiation directionality while maintaining a high spontaneous emission rate at the same time, which greatly limits the development of the single-photon source. To achieve these features simultaneously, a platform is needed for optimizing and controlling the parameters of the embedded emitters. So far, the Purcell effect, a phenomenon whereby the spontaneous lifetime of a quantum source can be influenced by its interaction with the environment, is mainly used to enhance the spontaneous emission rate. It is widely utilized in whispering gallery microcavities [9,10], photonic crystals (PCs) [11], optical nano-antennae [12,13], and metamaterials [14,15]. Optical nano-antennae, such as nano-cube antennae [16,17], single-bowtie antennae [15,18,19], and metal double-rods antennae [20], can significantly enhance the spontaneous emission rate. For example, George Kountouris’s team designed a dielectric bowtie cavity whose Purcell factor could be as high as 104 [21]. As for novel metal micro- or nano-antenna, surface plasmon polaritons (SPPs), employed in the bowtie antenna mentioned above, are electromagnetic waves that occur at the boundary between a metal and a dielectric material. Its potential applications span a wide array of fields, including quantum communication [21], energy [22], biology [23], and sensing [24], providing an excellent platform for exploring light–matter interactions. However, highly directive far-field radiation patterns are not always available in such antennae due to their compact structure. For antennae of a larger size, it is easier to realize high radiation directionality, such as with the Yagi-Uda antenna [25,26], the split ring resonator [27], the concentric-ring structure [28,29], and hemispherical solid immersion lens (SIL) [30,31,32]. For instance, Yan Chen’s team use the GaP hemispherical SIL [SIL1], and D. H. Ahn’s team use a GaAs–polymer double solid [32]. Both of their structures perform high directionality. Unfortunately, compared to nano-antennae, the micro-antenna’s larger size means that their Purcell factor struggles to reach a satisfactory value [30]. In recent years, many research teams have endeavored to enhance both the spontaneous emission rate and directionality of single-photon sources, yielding significant advancements. Zhaogang Dong’s team designed the silicon nano-antenna mix arrays, exhibiting a Purcell factor of ~47 and achieving enhanced directionality by ~2.45 fold [33]. Hamza Abudayyeh’s team suggested a composite consisting of a nano-cone and a circular Bragg grating, which achieved a Purcell factor of 20 alongside record-high directionality [34]. A. Barreda’s team studied different geometries and material combinations for a dimer of cylinders and proposed a hybrid structure composed of a gold dimer and silicon nano-particles whose Purcell factor was over 3000 and which present high radiation directionality [35]. However, as of now, there exists no research endeavor aimed at integrating the advantages of both SIL and single-bowtie antennae.
In this paper, we achieve high radiation directivity while maintaining a high spontaneous emission rate by leveraging SPPs and solid immersion lens. Our approach involves the design of a hemispherical SIL-plasmonic antenna (HSPA) consisting of a hemispherical SIL (used as an antenna) and a bowtie plasmonic nano-antenna (used as a plasmonic resonator). We calculate the resonant modes of the HSPA and study the Purcell factor and far field distribution for each resonant mode. Furthermore, we investigate the effect of structural parameters on the performance of the HSPA, revealing the properties of the individual tuning of the directional emission and the luminance of a quantum emitter.
2. Structure Description
A 3D schematic of the proposed nano-antenna is shown in Figure 1, consisting of a GaAs hemispherical solid immersion lens (SIL), a single Au bowtie plasmonic nano-antenna, and the Au metallic reflector. A quantum dot is placed at the center of the Au bowtie. Here, we choose a CdSe/ZnS quantum dot rather than InGa/GaAs QDs because of the small size of the bowtie antenna gap, which is beneficial in obtaining a large localized optical field intensity. The design of HSPA’s geometric parameters is inspired by previous works [18,19,30,36] and intended to obtain a more effective light–matter interaction. In Figure 1a, hemispherical SIL is used to improve the directionality of the radiation pattern of a quantum emitter, while plasmonic nano-antennae can increase the light–matter interaction for the emitter buried in a solid-state environment. To maximize the hemispherical SIL’s performance, we choose GaAs as the material of SIL, which exhibits a high refractive index in a 500–1500 nm wavelength range. A GaAs film with thickness h1 = 185 nm is below the hemispherical SIL. It should be mentioned that the Au bowtie is set to be embedded in the GaAs film in order to avoid the interference of lights from the emitter and reflection inside the SIL, which may be adverse to improving directionality. The radius of the GaAs hemispherical SIL is set to 500 nm. The Au bowtie plasmonic nano-antenna consists of two Au equilateral triangular prisms with 100 nm height (H) and 50 nm thickness of each triangular prism. The quantum emitter is placed at the center of two Au equilateral triangular prisms, while the nano-gap between two prisms is 10 nm. In this nano-gap, a strong enhancement of the electric field intensity and an extremely small mode volume of electric field are produced, allowing for intense interaction between the emitter and the local field. Thus, a larger Purcell factor and greater quantum efficiency can be obtained. Under the GaAs film, an Au film with thickness h2 = 200 nm performs a reflection layer with a high reflectance, while the wavelength of incident light is between 500 nm and 1500 nm. The existence of the Au mirror helps redirect light emitted downward by quantum dots back toward the positive z-axis, thus reducing energy dissipation and effectively enhancing directionality. Additionally, we have tested a thicker Au layer or multiple Au layers as the metallic reflector for the HSPA, which has no significant effect on the performance of the HSPA. The bottom is the bulk GaAs substrate, providing rigidity to the structure. The fabrication of HSPA is feasible, which can be supported by references [30,36,37,38]. Concretely, the Au layer, GaAs layer, and GaAs hemispherical SIL can be fabricated via a sequential deposition process on the GaAs substrate. The Au bowtie can be fabricated via etching and deposition processes before fabricating the SIL.
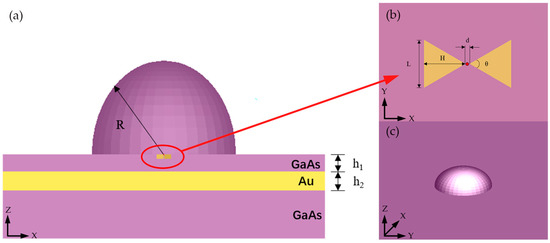
Figure 1.
(a) The schematic of the HSPA from the XZ perspective showing part of the geometric parameters of the HSPA. (b) The schematic of the Au bowtie antenna from the XY perspective showing the geometric parameters of the bowtie. The dipole source is placed in the center of the bowtie, which is represented by the red dot. The propagation direction of the dipole source is along the positive half of the z-axis, while the polarization direction is along the x-axis. (c) The 3D schematic of the HSPA.
Here, we used the finite-difference time-domain (FDTD) method to analyze the performance of HSPA. Regarding the FDTD, it replaces the solutions of the original electromagnetic field partial differential equations with solutions of discrete difference equations. The calculated results are meaningful only when the solutions of the discretized difference equations are convergent and stable. Therefore, our simulation results are robust and reliable. The materials of Au and GaAs are in keeping with the experimental results of Johnson and Christy and Palik, respectively. The quantum emitter is modeled by a dipole light source with horizontal polarization along the top angle of the prisms. The perfect match layer (PML) is used for the boundary condition of the simulation region, which can simulate an infinite space. Referring to [39,40] and taking into account practical fabrication capabilities and simulation efficiency, we set the accuracy of 3 nm × 3 nm × 3 nm for the Au bowtie and 20 nm × 20 nm × 20 nm for the rest of region. Two types of light source are used in our simulation. We first use the total-field scattered-field (TFSF) source to excite the resonant modes of HSPA. The TFSF is a plane wave source which is commonly employed for investigating the scattering of small particles illuminated by a plane wave. The TFSF is incident from above the structure at a distance of 100 nm, along the negative z-axis direction, polarized along the x-axis. Then, the “cross section” monitor is used to collect the scattering data to obtain the scattering spectrum of HSPA, which is shown in Figure 2a. Obviously, there are many resonance peaks in HSPA which have arisen from specific electric field patterns excited by the external incident plane wave. And here, we choose four of them to calculate their Purcell factor. They are marked by red dots and display a Lorentzian shape at 1162 nm, 1478 nm, 1612 nm, and 1888 nm. The full width at half height of the resonance peaks is 5 nm, 11 nm, 11 nm, and 16 nm, respectively. Next, a dipole source with horizontal polarization is used to simulate the emission of the emitter in HSPA. Figure 2b,d show the electric field distribution of the HSPA’s XZ view and the Au bowtie’s XY view, respectively. It is clear that the electric field is strongly confined in the nano-gap of the Au bowtie, while the local field in the hemispherical SIL is relatively weak. In general, a significant amount of the light will be lost and not focused on a specific desired direction due to the geometric morphology of the single-bowtie antenna. Here, a clear propagation of light along the vertical direction is observed in GaAs SIL, indicating a good directionality of HSPA. To confirm this conjecture, we calculated the far-field distribution of HSPA for each resonant peak shown in Figure 2e. It is obvious that HSPA performs good directionality in all resonant peaks, with a difference only in radiation intensity. It means that HSPA is most suitable for the collection of low-numerical-aperture optical devices, thus forming an efficient light–matter interface. This pertains to the refraction of light passing through the GaAs SIL, resulting in a spotlight effect resembling a convex lens. Then, we calculated the Purcell factor (Fp) of HSPA with an incident light range from 1000 nm to 2000 nm. The electric field intensity and distribution around the HSPA structure is then used to calculate the dyadic Green’s function according to the following equation:
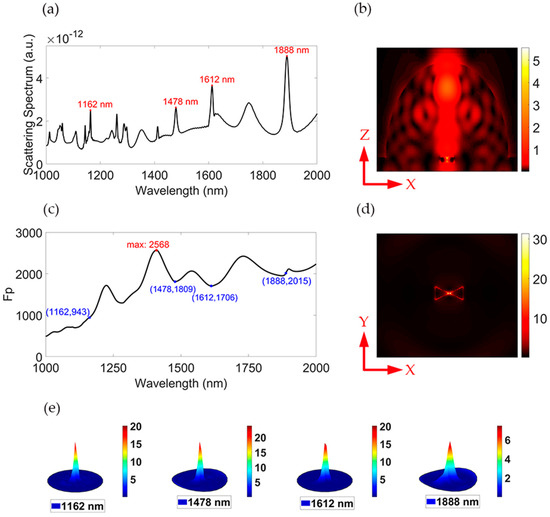
Figure 2.
(a) Scattering spectrum of the HSPA from 1000 nm to 2000 nm while R = 1000 nm and d = 10 nm. (b) Electric field distribution of the HSPA at λ = 1162 nm with 3D-FDTD in XZ view. (c) Simulation of the Purcell enhancement versus wavelength for the HSPA in TE mode while R = 1000 nm and d = 10 nm. The red dot marks the maximum of Fp, while λ = 1000~2000 nm. Bule dots mark the Fp for each resonant mode of the TE mode. (d) The electric field distribution of the HSPA at λ = 1162 nm with 3D-FDTD in XY view. (e) The 3D far-field distribution for each resonant mode.
Here, G represents the dyadic Green function, defined by the electric field at point r generated by a point source at point . denote the dipole moment and permittivity of vacuum, respectively, while is the relative dielectric constant. c is the velocity of light. Since G is a 3 × 3 symmetric matrix, each component of G can be obtained using the corresponding dipole orientation. We focus on the electric field component Gzz, which is calculated from a dipole oriented along the z direction. The local density of states (LDOS) along one direction, denoted as , can be derived from the imaginary part of the Green’s function:
where characterizes the localization and intensity of the electric field produced by the structure and is associated with the spontaneous decay rate of the quantum emitter. Considering a two-level quantum system with a transition at and decay , the spontaneous decay rate with the influence of HSPA is given by the following:
where represents the reduced Planck constant. Finally, the Purcell factor Fp is obtained as follows:
where is the vacuum spontaneous decay rate of the emitter. The Purcell factor Fp as a function of emission wavelength is shown in Figure 2c. The Fp of resonance peaks is highlighted by blue dots, and the maximum is emphasized by a red dot.
3. Results and Discussion
To demonstrate the advantage of the HSPA in addressing the limitations of bowtie nano-antenna and hemispherical SIL, we employed the FDTD method to assess the performance of each structure: a single hemispherical GaAs SIL, a single Au bowtie, and the HSPA. As depicted in Figure 3a, the 2D far-field distribution for these structures at a wavelength (λ) range of 500~1500 nm reveals distinctive patterns. The single Au bowtie exhibits an emission pattern characterized by one main lobe and two side lobes. Despite displaying a modest range of emission angles, its directionality is evidently less satisfactory compared to the others. In contrast, the HSPA produces a narrower emission pattern featuring a prominent main lobe and negligible side lobes, thus demonstrating stronger radiation directionality. For a more visual understanding, Figure 3b presents the 3D far-field distribution, showcasing geometries resembling triangular pyramids for both the SIL and the HSPA, indicating excellent directionality characteristics. Conversely, the emission pattern of the single Au bowtie, depicted as three distinct peaks, shows minimal influence on the overall emission pattern but significantly enhances the emission intensity. This enhancement is quantified in Figure 3c, which illustrates the Purcell factor (Fp) for each structure across the emission wavelength spectrum. The Fp graph highlights that both the HSPA and the single bowtie exhibit similar trends, corroborating the earlier observations. Notably, within the λ = 500~1500 nm range, their Fp values are markedly higher compared to those of the SIL. Specifically, the Fp values for the HSPA and the single bowtie can reach up to 2568, while the maximum for the SIL remains below 3.
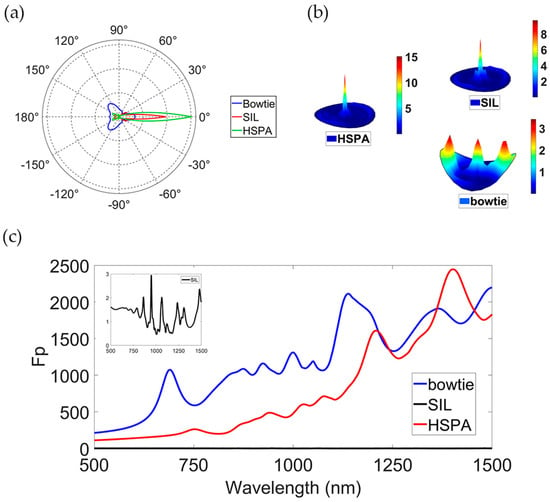
Figure 3.
(a) Two-dimensional far-field distribution for corresponding structure at . (b) Three-dimensional far-field distribution for corresponding structure at . (c) Simulation of the Purcell enhancement versus wavelength for three structures.
To investigate the impact of the structural parameters of the SIL on the spectral positioning of the HSPA resonant modes, we conducted FDTD to calculate the scattering spectrum for different radii of the SIL. Figure 4a presents the scattering spectra of the HSPA across the wavelength range of 1000 nm to 2000 nm, with the SIL radius (R) ranging from 800 to 1100 nm. The distinct scattering spectra reveal several clear resonance modes of the HSPA, each displaying a characteristic Lorentzian shape within the emission wavelength range of 1000 nm to 2000 nm. Notably, as the SIL radius (R) increases, the peak of each resonant mode, marked in Figure 4a, gradually shifts towards longer wavelengths. Taking the resonant modes at R = 1000 nm as a benchmark, let us consider the 1612 nm mode as an example. For every 100 nm increase in R, the resonant wavelength of the 1612 nm mode shifts to longer wavelengths by approximately 135 nm. This behavior can be succinctly described by the following formula: W = 1612 + 1.35(R − 1000), where W represents the resonant wavelength of the 1612 nm mode and R denotes the radius of the hemispherical SIL. Such a formula provides a useful tool for selecting desired light frequencies. Different resonant modes exhibit varying emission efficiencies. In typical hemispherical cavities, emission modes are mainly characterized by two orthogonal polarized modes—transverse electric (TE) and transverse magnetic (TM). Due to the axial symmetry of the cavity, the overall emission efficiency can be characterized by integrating the far-field power density over the spherical space for TE and TM modes, respectively. Consequently, FDTD simulations were employed to calculate Fp and far-field power density for every resonant mode within the wavelength band of 1000 nm to 2000 nm at R = 1000 nm. Figure 4b,d illustrate the simulated far-field distribution for various TE and TM modes. Particularly for TE modes, it is evident that the divergence of the highly directive far-field beam pattern of the 1162 nm mode (at R = 1000 nm) is much lower compared to other resonant modes. In contrast, the directionality of each TM mode is notably poorer than that of the TE modes, as indicated by the distinct side lobes in their far-field distributions. Figure 2e and Figure 4c further present the Fp for each TE and TM mode, respectively. While each mode exhibits a distinct Fp value, a clear trend emerges—there is a clear increase in the Fp of the corresponding modes as the wavelength increases. Additionally, it is obvious that the Fp values of TM modes are lower than those of TE modes. Therefore, TE modes demonstrate superior directionality and higher spontaneous emission rates compared to TM modes within the examined wavelength range.
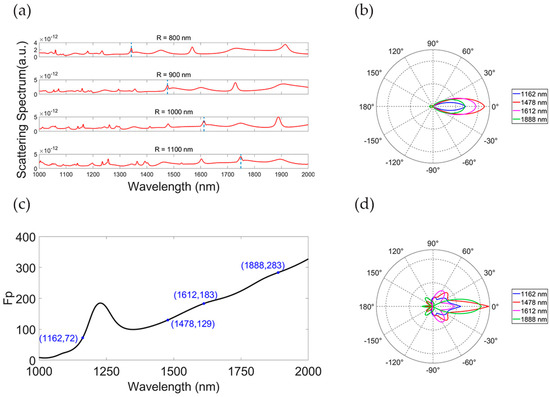
Figure 4.
(a) Reflectivity spectra between 1000 nm and 2000 nm of the HSPA with the SIL’s radius (R) varying from 800 to 1100 nm. (b) Two-dimensional far-field distribution for the HSPA while R = 1000 nm and d = 10 nm for different resonant modes in the TE mode. (c) Simulation of the Purcell enhancement versus wavelength for the HSPA in the TM mode while R = 1000 nm and d = 10 nm. Blue dots mark the Fp for each resonant mode of the TM mode. (d) Two-dimensional far-field distribution for the HSPA while R = 1000 nm and d = 10 nm for different resonant modes in the TM mode.
The variations of various structural parameters of the HSPA have different effects on its overall performance. To delve into the modulating impact of the hemispherical SIL size and the relative position of bowtie nano-antenna on the HSPA’s performance, we utilize FDTD to calculate the Purcell factor (Fp) and far-field radiation distribution of the HSPA under each parameter. This exploration aids in understanding changes in the spontaneous radiation rate and radiation directionality of the antenna. Figure 5a,b illustrate the effects of varying the radius of the hemispherical SIL on the HSPA’s performance. As depicted in Figure 5a, the Fp shows negligible change as the radius of the hemispherical SIL gradually increases, indicating that the hemispherical SIL has little effect on Fp of the HSPA. Additionally, Figure 5b reveals that within the emission wavelength band of 500–1500 nm, the radiation directionality reaches its optimum when the radius of the hemispherical SIL is set to 1000 nm. This observation provides a valuable insight into regulating the far-field radiation directionality of the HSPA. Next, Figure 5c,d demonstrate the effects of varying the gap created by the single Au bowtie on the HSPA’s performance. As shown in Figure 5d, the radiation directionality remains largely unchanged with the increase of the gap, indicating that the bowtie has little effect on the radiation directionality of the HSPA. Conversely, Figure 5c illustrates that, overall, as the gap increases, the Fp decreases due to variations in the electric field enhancement. This observation offers a means by which to modulate the HSPA’s Fp by adjusting the gap. Based on the above findings, we further investigate the impact of various structural parameters on the overall performance of HSPA at specific wavelengths. Taking λ = 1478 nm as an example, when the quantum dot in the gap emits monochromatic light at 1478 nm, we can observe significant changes in the directionality of HSPA while varying the radius of the hemispherical SIL, which is shown in Figure 5e. Simultaneously, the Purcell factor of the HSPA shows negligible change. Furthermore, the directionality reaches its optimum when R = 1000 nm. These observations align with our conclusions drawn from discussions on wavelengths ranging from 500 to 1500 nm. When we change the gap, we can also observe the same phenomenon as when discussing wavelengths of 500–1500 nm. Upon observing Figure 5f, we also noted a similar phenomenon while adjusting the gap, reinforcing our observations concerning wavelengths within the 500–1500 nm range. In summary, the simulation results presented above offer insights into regulating the far-field distribution and the Fp of the HSPA by adjusting the radius of the hemispherical SIL and the gap of the bowtie nano-antenna, respectively.
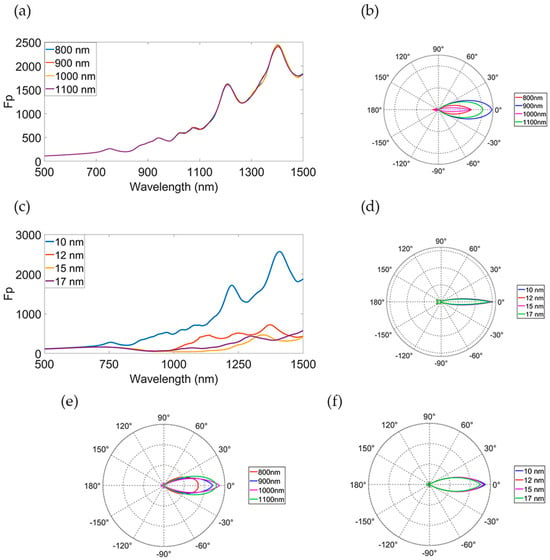
Figure 5.
(a) Simulation of the Purcell enhancement versus wavelength for various radii of hemispherical SIL at λ = 500~1500 nm. (b) Two-dimensional far-field distribution for various radii of hemispherical SIL at λ = 500~1500 nm. (c) Simulation of the Purcell enhancement versus wavelength for various gap sizes at λ = 500~1500 nm. (d) Two-dimensional far-field distribution for various gap sizes at λ = 500~1500 nm. (e) Two-dimensional far-field distribution for various radii of hemispherical SIL at λ = 1478 nm. (f) Two-dimensional far-field distribution for various gap sizes at λ = 1478 nm.
4. Conclusions
In summary, the HSPA proposed in this work is a new platform combining the advantages of both the hemispherical GaAs SIL and the single Au bowtie nano-antenna. Compared to the isolated hemispherical GaAs SIL, the HSPA enhances the Purcell factor by approximately 1000 times while maintaining high directionality. Furthermore, in comparison to the single Au bowtie nano-antenna, the HSPA overcomes the limitation of directionality while preserving a high spontaneous emission rate. Through analysis of the HSPA’s performance parameters using the FDTD method, we have shown that the radius of the hemispherical SIL significantly influences the resonant wavelengths of the HSPA. Simultaneously, the performance parameters of the HSPA in TE modes exhibit superior characteristics compared to TM modes. Moreover, we also found that the effects caused by the changes in the structural parameters and demonstrated by the radii of hemispherical SIL mainly influence the directionality and have little effect on Fp. Conversely, the effects caused by the gap of the single bowtie nano-antenna show the opposite trend. The findings of our study present a new method for optimizing the performance of single-photon sources. The HSPA’s ability to enhance the Purcell factor, maintain high directionality, and overcome the limitations of traditional structures makes it a promising candidate for applications in nano-photonics and quantum optics. Our work paves the way for further advancements in the development of efficient and high-performance single-photon sources.
Author Contributions
Conceptualization, C.X. and Y.H.; methodology, Y.M.; software, R.L.; formal analysis, C.X. and Y.H.; investigation, C.X.; resources, Y.M.; data curation, C.X. and Y.M.; writing—original draft preparation, C.X.; writing—review and editing, C.X., Y.H., R.L. and Y.M.; supervision, Y.M.; project administration, Y.H. and Y.M.; funding acquisition, R.L. and Y.M. All authors have read and agreed to the published version of the manuscript.
Funding
The work was supported by the China Electronics Technology Group Corporation 44th Research Institute Quantum Laboratory under grant 6310001-2, and the Project “Noninvasive Sensing Measurement Based on Terahertz Technology” from the Province and Ministry of Education Collaborative Innovation Centre for New Generation Information Networking and Terminals and the National Natural Science Foundation of China (62375031).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained with the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Romeira, B.; Figueiredo, J.M.; Javaloyes, J. NanoLEDs for energy-efficient and gigahertz-speed spike-based sub-λ neuromorphic nanophotonic computing. Nanophotonics 2020, 9, 4149–4162. [Google Scholar] [CrossRef]
- Ali, A.; Qasem, Z.A.; Li, Y.; Li, Q.; Fu, H.Y. All-inorganic liquid phase quantum dots and blue laser diode-based white-light source for simultaneous high-speed visible light communication and high-efficiency solid-state lighting. Opt. Express 2022, 30, 35112–35124. [Google Scholar] [CrossRef] [PubMed]
- Ren, A.; Wang, H.; Zhang, W.; Wu, J.; Wang, Z.; Penty, R.V.; White, I.H. Emerging light-emitting diodes for next-generation data communications. Nat. Electron. 2021, 4, 559–572. [Google Scholar] [CrossRef]
- Zeng, H.Z.; Ngyuen, M.A.; Ai, X.; Bennet, A.; Solntsev, A.S.; Laucht, A.; Al-Juboori, A.; Toth, M.; Mildren, R.P.; Malaney, R.; et al. Integrated room temperature single-photon source for quantum key distribution. Opt. Lett. 2022, 47, 1673–1676. [Google Scholar] [CrossRef] [PubMed]
- Somaschi, N.; Giesz, V.; De Santis, L.; Loredo, J.C.; Almeida, M.P.; Hornecker, G.; Portalupi, S.L.; Grange, T.; Anton, C.; Demory, J.; et al. Near-optimal single-photon sources in the solid state. Nat. Photonics 2016, 10, 340–345. [Google Scholar] [CrossRef]
- Zhong, H.S.; Wang, H.; Deng, Y.H.; Chen, M.C.; Peng, L.C.; Luo, Y.H.; Qin, J.; Wu, D.; Ding, X.; Hu, Y.; et al. Quantum computational advantage using photons. Science 2020, 370, 1460–1463. [Google Scholar] [CrossRef]
- Russell, K.J.; Liu, T.L.; Cui, S.; Hu, E.L. Large spontaneous emission enhancement in plasmonic nanocavities. Nat. Photonics 2012, 6, 459–462. [Google Scholar] [CrossRef]
- Hochrainer, A.; Lahiri, M.; Erhard, M.; Krenn, M.; Zeilinger, A. Quantum indistinguishability by path identity and with undetected photons. Rev. Mod. Phys. 2022, 94, 025007. [Google Scholar] [CrossRef]
- Yang, S.; Wang, Y.; Sun, H. Advances and prospects for whispering gallery mode microcavities. Adv. Opt. Mater. 2015, 3, 1136–1162. [Google Scholar] [CrossRef]
- Chiasera, A.; Dumeige, Y.; Feron, P.; Ferrari, M.; Jestin, Y.; Nunzi Conti, G.; Pelli, S.; Soria, S.; Righini, G.C. Spherical whispering-gallery-mode microresonators. Laser Photonics Rev. 2010, 4, 457–482. [Google Scholar] [CrossRef]
- Cai, Z.; Li, Z.; Ravaine, S.; He, M.; Song, Y.; Yin, Y.; Zheng, H.; Teng, J.; Zhang, A.O. From colloidal particles to photonic crystals: Advances in self-assembly and their emerging applications. Chem. Soc. Rev. 2021, 50, 5898–5951. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Q.; Roy, P.; Claude, J.B.; Wenger, J. Single photon source from a nanoantenna-trapped single quantum dot. Nano Lett. 2021, 21, 7030–7036. [Google Scholar] [CrossRef] [PubMed]
- Abudayyeh, H.; Lubotzky, B.; Blake, A.; Wang, J.; Majumder, S.; Hu, Z.; Kim, Y.; Htoon, H.; Bose, R.; Malko, A.V.; et al. Single photon sources with near unity collection efficiencies by deterministic placement of quantum dots in nanoantennas. APL Photonics 2021, 6, 036109. [Google Scholar] [CrossRef]
- Shen, L.; Lin, X.; Shalaginov, M.Y.; Low, T.; Zhang, X.; Zhang, B.; Chen, H. Broadband enhancement of on-chip single-photon extraction via tilted hyperbolic metamaterials. Appl. Phys. Rev. 2020, 7, 021403. [Google Scholar] [CrossRef]
- Bai, Y.; Liu, S. A novel dual-beam terahertz leaky-wave antenna based on spoof surface plasmon waveguide. Optoelectron. Lett. 2022, 7, 404–407. [Google Scholar] [CrossRef]
- Roy, P.; Zhu, S.; Claude, J.B.; Liu, J.; Wenger, J. Ultraviolet Resonant Nanogap Antennas with Rhodium Nanocube Dimers for Enhancing Protein Intrinsic Autofluorescence. ACS Nano 2023, 17, 22418–22429. [Google Scholar] [CrossRef] [PubMed]
- Yang, G.; Shen, Q.; Niu, Y.; Wei, H.; Bai, B.; Mikkelsen, M.H.; Sun, H.B. Unidirectional, ultrafast, and bright spontaneous emission source enabled by a hybrid plasmonic nanoantenna. Laser Photonics Rev. 2020, 14, 1900213. [Google Scholar] [CrossRef]
- Yang, J.; Kong, F.; Li, K.; Zhao, J. Optimizing the bowtie nano-antenna for enhanced purcell factor and electric field. Prog. Electromagn. Res. Lett. 2014, 44, 93–99. [Google Scholar] [CrossRef]
- Carlson, C.; Hughes, S. Dissipative modes, Purcell factors, and directional beta factors in gold bowtie nanoantenna structures. Phys. Rev. B 2020, 102, 155301. [Google Scholar] [CrossRef]
- Qian, Z.; Li, Z.; Hao, H.; Shan, L.; Zhang, Q.; Dong, J.; Gong, Q.; Gu, Y. Absorption reduction of large purcell enhancement enabled by topological state-led mode coupling. Phys. Rev. Lett. 2021, 126, 023901. [Google Scholar] [CrossRef]
- Kountouris, G.; Mørk, J.; Denning, E.V.; Kristensen, P.T. Modal properties of dielectric bowtie cavities with deep sub-wavelength confinement. Opt. Express 2022, 30, 40367–40378. [Google Scholar] [CrossRef] [PubMed]
- Weisman, D.; Carmesin, C.M.; Rozenman, G.G.; Efremov, M.A.; Shemer, L.; Schleich, W.P.; Arie, A. Diffractive guiding of waves by a periodic array of slits. Phys. Rev. Lett. 2021, 127, 014303. [Google Scholar] [CrossRef] [PubMed]
- Sayed, M.; Yu, J.; Liu, G.; Jaroniec, M. Non-noble plasmonic metal-based photocatalysts. Chem. Rev. 2022, 122, 10484–10537. [Google Scholar] [CrossRef]
- Zain, H.A.; Batumalay, M.; Rahim, H.R.; Harun, S.W. Numerical analysis of a Kretschmann surface plasmon resonance sensor with silver/TiO2/BaTiO3/silver/graphene for refractive index sensing. Optoelectron. Lett. 2023, 19, 583–586. [Google Scholar] [CrossRef]
- Kullock, R.; Ochs, M.; Grimm, P.; Emmerling, M.; Hecht, B. Electrically-driven Yagi-Uda antennas for light. Nat. Commun. 2020, 11, 115. [Google Scholar] [CrossRef] [PubMed]
- Hao, J.; Ren, J.; Du, X.; Mikkelsen, J.H.; Shen, M.; Yin, Y.Z. Pattern-reconfigurable Yagi–Uda antenna based on liquid metal. IEEE Antennas Wirel. Propag. Lett. 2021, 20, 587–591. [Google Scholar] [CrossRef]
- Chen, T.; Zhang, D.; Huang, F.; Li, Z.; Hu, F. Design of a terahertz metamaterial sensor based on split ring resonator nested square ring resonator. Mater. Res. Express 2020, 7, 095802. [Google Scholar] [CrossRef]
- Rahbany, N.; Geng, W.; Bachelot, R.; Couteau, C. Plasmon–emitter interaction using integrated ring grating–nanoantenna structures. Nanotechnology 2017, 28, 185201. [Google Scholar] [CrossRef] [PubMed]
- Jeon, W.B.; Moon, J.S.; Kim, K.Y.; Ko, Y.H.; Richardson, C.J.; Waks, E.; Kim, J.H. Plug-and-Play Single-Photon Devices with Efficient Fiber-Quantum Dot Interface. Adv. Quantum Technol. 2022, 5, 2200022. [Google Scholar] [CrossRef]
- Ma, Y.; Ballesteros, G.; Zajac, J.M.; Sun, J.; Gerardot, B.D. Highly directional emission from a quantum emitter embedded in a hemispherical cavity. Opt. Lett. 2015, 40, 2373–2376. [Google Scholar] [CrossRef]
- Chen, Y.; Zopf, M.; Keil, R.; Ding, F.; Schmidt, O.G. Highly-efficient extraction of entangled photons from quantum dots using a broadband optical antenna. Nat. Commun. 2018, 9, 2994. [Google Scholar] [CrossRef]
- Ahn, D.H.; Jang, Y.D.; Baek, J.S.; Park, S.I.; Song, J.D.; Lee, D. A broadband high-brightness quantum-dot double solid immersion lens single photon source. APL Photonics 2023, 1, 8. [Google Scholar]
- Dong, Z.; Gorelik, S.; Paniagua-Dominguez, R.; Yik, J.; Ho, J.; Tjiptoharsono, F.; Lassalle, E.; Rezaei, S.D.; Neo, D.C.; Bai, P.; et al. Silicon nanoantenna mix arrays for a trifecta of quantum emitter enhancements. Nano Lett. 2021, 21, 4853–4860. [Google Scholar] [CrossRef]
- Abudayyeh, H.; Mildner, A.; Liran, D.; Lubotzky, B.; Luder, L.; Fleischer, M.; Rapaport, R. Overcoming the rate-directionality trade-off: A room-temperature ultrabright quantum light source. Acs Nano 2021, 15, 17384–17391. [Google Scholar] [CrossRef]
- Barreda, A.; Hell, S.; Weissflog, M.A.; Minovich, A.; Pertsch, T.; Staude, I. Metal, dielectric and hybrid nanoantennas for enhancing the emission of single quantum dots: A comparative study. J. Quant. Spectrosc. Radiat. Transf. 2021, 276, 107900. [Google Scholar] [CrossRef]
- Schraml, K.; Spiegl, M.; Kammerlocher, M.; Bracher, G.; Bartl, J.; Campbell, T.; Finley, J.J.; Kaniber, M. Optical properties and interparticle coupling of plasmonic bowtie nanoantennas on a semiconducting substrate. Phys. Rev. B 2014, 90, 035435. [Google Scholar] [CrossRef]
- Santhosh, K.; Bitton, O.; Chuntonov, L.; Haran, G. Vacuum Rabi splitting in a plasmonic cavity at the single quantum emitter limit. Nat. Commun. 2016, 7, ncomms11823. [Google Scholar] [CrossRef] [PubMed]
- Kabiri, A.; Girgis, E.; Capasso, F. Buried nanoantenna arrays: Versatile antireflection coating. Nano Lett. 2013, 13, 6040–6047. [Google Scholar] [CrossRef] [PubMed]
- Morshed, M.; Li, Z.; Olbricht, B.C.; Fu, L.; Haque, A.; Li, L.; Rifat, A.A.; Rahmani, M.; Miroshnichenko, A.E.; Hattori, H.T. High fluence chromium and tungsten bowtie nano-antennas. Sci. Rep. 2019, 9, 13023. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.S.; Callegari, V.; Geisler, P.; Brüning, C.; Kern, J.; Prangsma, J.C.; Wu, X.; Feichtner, T.; Ziegler, J.; Weinmann, P.; et al. Atomically flat single-crystalline gold nanostructures for plasmonic nanocircuitry. Nat. Commun. 2010, 1, 150. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).