Photon Number States via Iterated Photon Addition in a Loop
Abstract
1. Introduction
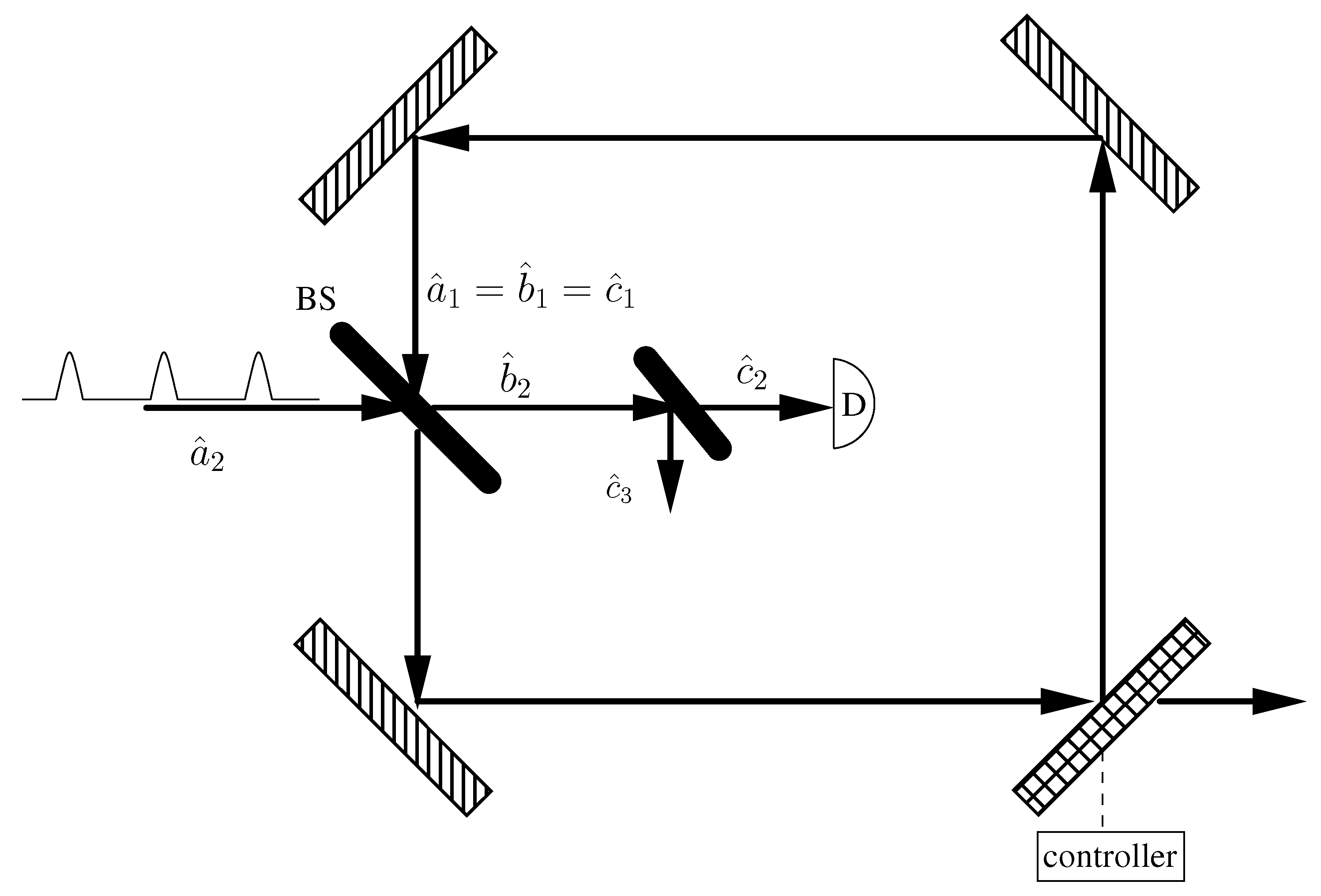
2. Methods
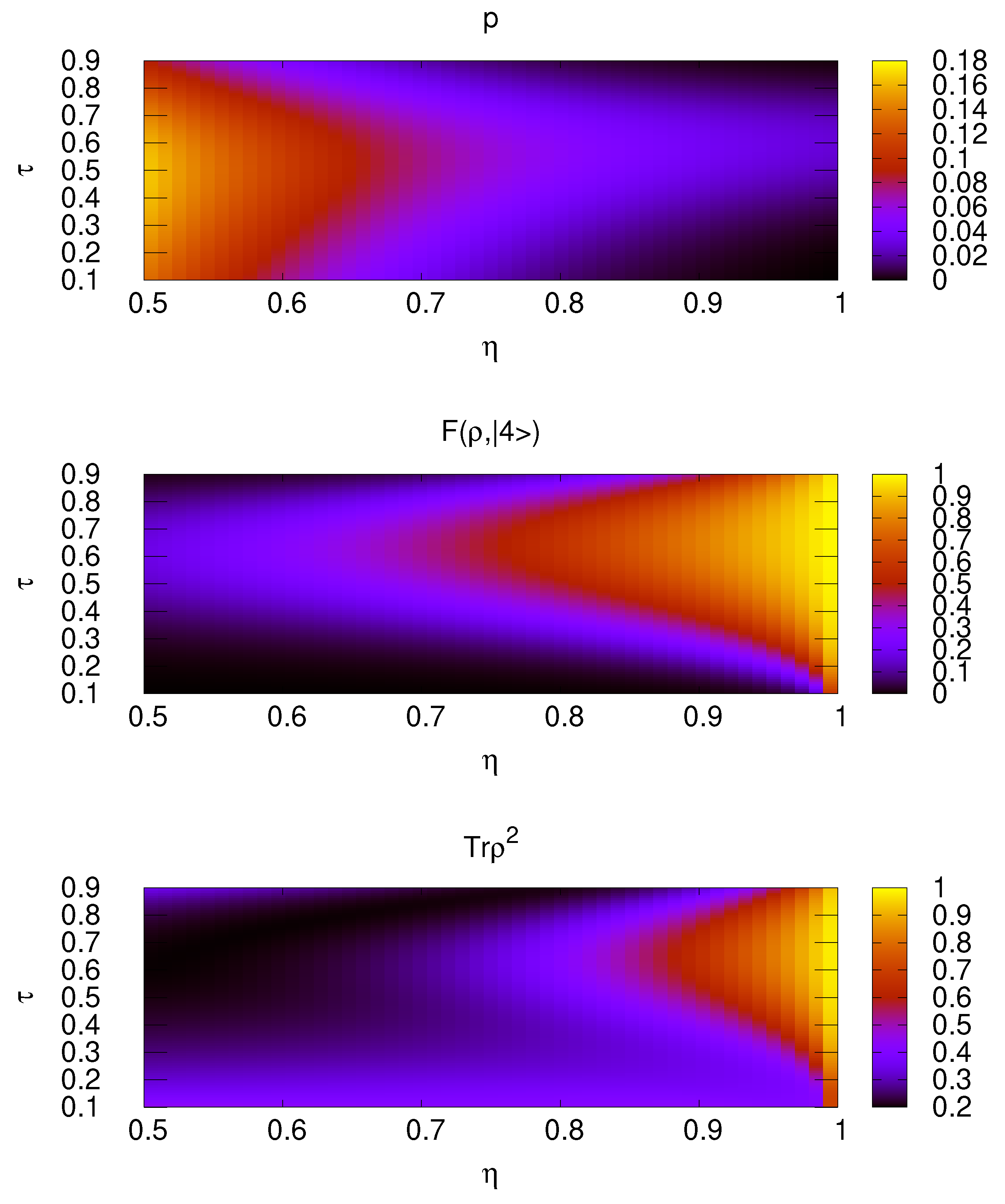
3. Results
3.1. Photon Addition with a Beam Splitter and a Detector
3.2. Iterated Photon Addition
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hong, C.K.; Ou, Z.Y.; Mandel, L. Measurement of subpicosecond time intervals between two photons by interference. Phys. Rev. Lett. 1987, 59, 2044–2046. [Google Scholar] [CrossRef] [PubMed]
- Drago, C.; Brańczyk, A.M. Hong–Ou–Mandel interference: A spectral–temporal analysis. Can. J. Phys. 2024, 102, 411–421. [Google Scholar] [CrossRef]
- Zavatta, A.; Viciani, S.; Bellini, M. Quantum-to-Classical Transition with Single-Photon-Added Coherent States of Light. Science 2004, 306, 660–662. [Google Scholar] [CrossRef] [PubMed]
- Zavatta, A.; Viciani, S.; Bellini, M. Single-photon excitation of a coherent state: Catching the elementary step of stimulated light emission. Phys. Rev. A 2005, 72, 23820. [Google Scholar] [CrossRef]
- Zavatta, A.; Parigi, V.; Bellini, M. Experimental nonclassicality of single-photon-added thermal light states. Phys. Rev. A 2007, 75, 052106. [Google Scholar] [CrossRef]
- Parigi, V.; Zavatta, A.; Kim, M.; Bellini, M. Probing Quantum Commutation Rules by Addition and Subtraction of Single Photons to/from a Light Field. Science 2007, 317, 1890–1893. [Google Scholar] [CrossRef]
- Akhtar, N.; Wu, J.; Peng, J.X.; Liu, W.M.; Gao, X. Sub-Planck structures and sensitivity of the superposed photon-added or photon-subtracted squeezed-vacuum states. Phys. Rev. A 2023, 107, 052614. [Google Scholar] [CrossRef]
- Biagi, N.; Francesconi, S.; Zavatta, A.; Bellini, M. Photon-by-photon quantum light state engineering. Prog. Quantum Electron. 2022, 84, 100414. [Google Scholar] [CrossRef]
- Holmes, C.A.; Milburn, G.J.; Walls, D.F. Photon-number-state preparation in nondegenerate parametric amplification. Phys. Rev. A 1989, 39, 2493–2501. [Google Scholar] [CrossRef]
- Dotsenko, I.; Mirrahimi, M.; Brune, M.; Haroche, S.; Raimond, J.M.; Rouchon, P. Quantum feedback by discrete quantum nondemolition measurements: Towards on-demand generation of photon-number states. Phys. Rev. A 2009, 80, 013805. [Google Scholar] [CrossRef]
- Varcoe, B.T.H.; Brattke, S.; Weidinger, M.; Walther, H. Preparing pure photon number states of the radiation field. Nature 2000, 403, 743–746. [Google Scholar] [CrossRef] [PubMed]
- Brattke, S.; Varcoe, B.T.H.; Walther, H. Generation of Photon Number States on Demand via Cavity Quantum Electrodynamics. Phys. Rev. Lett. 2001, 86, 3534–3537. [Google Scholar] [CrossRef] [PubMed]
- Sayrin, C.; Dotsenko, I.; Zhou, X.; Peaudecerf, B.; Rybarczyk, T.; Gleyzes, S.; Rouchon, P.; Mirrahimi, M.; Amini, H.; Brune, M.; et al. Real-time quantum feedback prepares and stabilizes photon number states. Nature 2011, 477, 73–77. [Google Scholar] [CrossRef] [PubMed]
- Brattke, S.; Guthöhrlein, G.R.; Keller, M.; Lange, W.; Varcoe, B.; Walther, H. Generation of photon number states on demand. J. Mod. Opt. 2003, 50, 1103–1113. [Google Scholar] [CrossRef]
- Hofheinz, M.; Weig, E.M.; Ansmann, M.; Bialczak, R.C.; Lucero, E.; Neeley, M.; O’Connell, A.D.; Wang, H.; Martinis, J.M.; Cleland, A.N. Generation of Fock states in a superconducting quantum circuit. Nature 2008, 454, 310–314. [Google Scholar] [CrossRef]
- Cosacchi, M.; Wiercinski, J.; Seidelmann, T.; Cygorek, M.; Vagov, A.; Reiter, D.E.; Axt, V.M. On-demand generation of higher-order Fock states in quantum-dot–cavity systems. Phys. Rev. Res. 2020, 2, 033489. [Google Scholar] [CrossRef]
- Waks, E.; Diamanti, E.; Yamamoto, Y. Generation of photon number states. New J. Phys. 2006, 8, 4. [Google Scholar] [CrossRef]
- Cooper, M.; Wright, L.J.; Söller, C.; Smith, B.J. Experimental generation of multi-photon Fock states. Opt. Express 2013, 21, 5309–5317. [Google Scholar] [CrossRef]
- Sonoyama, T.; Takahashi, K.; Sano, T.; Suzuki, T.; Nomura, T.; Yabuno, M.; Miki, S.; Terai, H.; Takase, K.; Asavanant, W.; et al. Generation of multi-photon Fock states at telecommunication wavelength using picosecond pulsed light. Opt. Express 2024, 32, 32387–32395. [Google Scholar] [CrossRef]
- Zhang, S.; Dong, Y.; Zou, X.; Shi, B.; Guo, G. Continuous-variable-entanglement distillation with photon addition. Phys. Rev. A 2013, 88, 32324. [Google Scholar] [CrossRef]
- Bodog, F.; Mechler, M.; Koniorczyk, M.; Adam, P. Optimization of multiplexed single-photon sources operated with photon-number-resolving detectors. Phys. Rev. A 2020, 102, 013513. [Google Scholar] [CrossRef]
- Meyer-Scott, E.; Silberhorn, C.; Migdall, A. Single-photon sources: Approaching the ideal through multiplexing. Rev. Sci. Instrum. 2020, 91, 3320. [Google Scholar] [CrossRef] [PubMed]
- Arakawa, Y.; Holmes, M.J. Progress in quantum-dot single photon sources for quantum information technologies: A broad spectrum overview. Appl. Phys. Rev. 2020, 7, 021309. [Google Scholar] [CrossRef]
- Adam, P.; Mechler, M. Single-photon sources based on incomplete binary-tree multiplexers with optimal structure. Opt. Express 2023, 31, 30194–30211. [Google Scholar] [CrossRef]
- Li, R.; Liu, F.; Lu, Q. Quantum Light Source Based on Semiconductor Quantum Dots: A Review. Photonics 2023, 10, 639. [Google Scholar] [CrossRef]
- Adam, P.; Mechler, M. Single-photon sources based on stepwise optimized binary-tree multiplexers. Opt. Express 2024, 32, 17173–17188. [Google Scholar] [CrossRef]
- Campos, R.A.; Saleh, B.E.; Teich, M.C. Quantum-mechanical lossless beam splitter: SU (2) symmetry and photon statistics. Phys. Rev. A 1989, 40, 1371. [Google Scholar] [CrossRef]
- Schreiber, A.; Cassemiro, K.N.; Potoček, V.; Gábris, A.; Mosley, P.J.; Andersson, E.; Jex, I.; Silberhorn, C. Photons Walking the Line: A Quantum Walk with Adjustable Coin Operations. Phys. Rev. Lett. 2010, 104, 050502. [Google Scholar] [CrossRef]
- Lubasch, M.; Valido, A.A.; Renema, J.J.; Kolthammer, W.S.; Jaksch, D.; Kim, M.S.; Walmsley, I.; García-Patrón, R. Tensor network states in time-bin quantum optics. Phys. Rev. A 2018, 97, 062304. [Google Scholar] [CrossRef]
- QuTiP Quantum Toolbox in Python. 2012. Available online: https://qutip.org (accessed on 5 November 2024).
- Johansson, J.; Nation, P.; Nori, F. QuTiP: An open-source Python framework for the dynamics of open quantum systems. Comput. Phys. Commun. 2012, 183, 1760–1772. [Google Scholar] [CrossRef]
- Johansson, J.; Nation, P.; Nori, F. QuTiP 2: A Python framework for the dynamics of open quantum systems. Comput. Phys. Commun. 2013, 184, 1234–1240. [Google Scholar] [CrossRef]
- Nitsche, T.; De, S.; Barkhofen, S.; Meyer-Scott, E.; Tiedau, J.; Sperling, J.; Gábris, A.; Jex, I.; Silberhorn, C. Local Versus Global Two-Photon Interference in Quantum Networks. Phys. Rev. Lett. 2020, 125, 213604. [Google Scholar] [CrossRef] [PubMed]
- Madsen, L.S.; Laudenbach, F.; Askarani, M.F.; Rortais, F.; Vincent, T.; Bulmer, J.F.F.; Miatto, F.M.; Neuhaus, L.; Helt, L.G.; Collins, M.J.; et al. Quantum computational advantage with a programmable photonic processor. Nature 2022, 606, 75–81. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mendei, B.; Koniorczyk, M.; Homa, G.; Adam, P. Photon Number States via Iterated Photon Addition in a Loop. Photonics 2024, 11, 1075. https://doi.org/10.3390/photonics11111075
Mendei B, Koniorczyk M, Homa G, Adam P. Photon Number States via Iterated Photon Addition in a Loop. Photonics. 2024; 11(11):1075. https://doi.org/10.3390/photonics11111075
Chicago/Turabian StyleMendei, Barna, Mátyás Koniorczyk, Gábor Homa, and Peter Adam. 2024. "Photon Number States via Iterated Photon Addition in a Loop" Photonics 11, no. 11: 1075. https://doi.org/10.3390/photonics11111075
APA StyleMendei, B., Koniorczyk, M., Homa, G., & Adam, P. (2024). Photon Number States via Iterated Photon Addition in a Loop. Photonics, 11(11), 1075. https://doi.org/10.3390/photonics11111075




