Research on Dual-Grating Spacing Calibration Method Based on Multiple Improved Complete Ensemble Empirical Mode Decomposition with Adaptive Noise Combined with Hilbert Transform
Abstract
1. Introduction
2. Theoretical Analysis
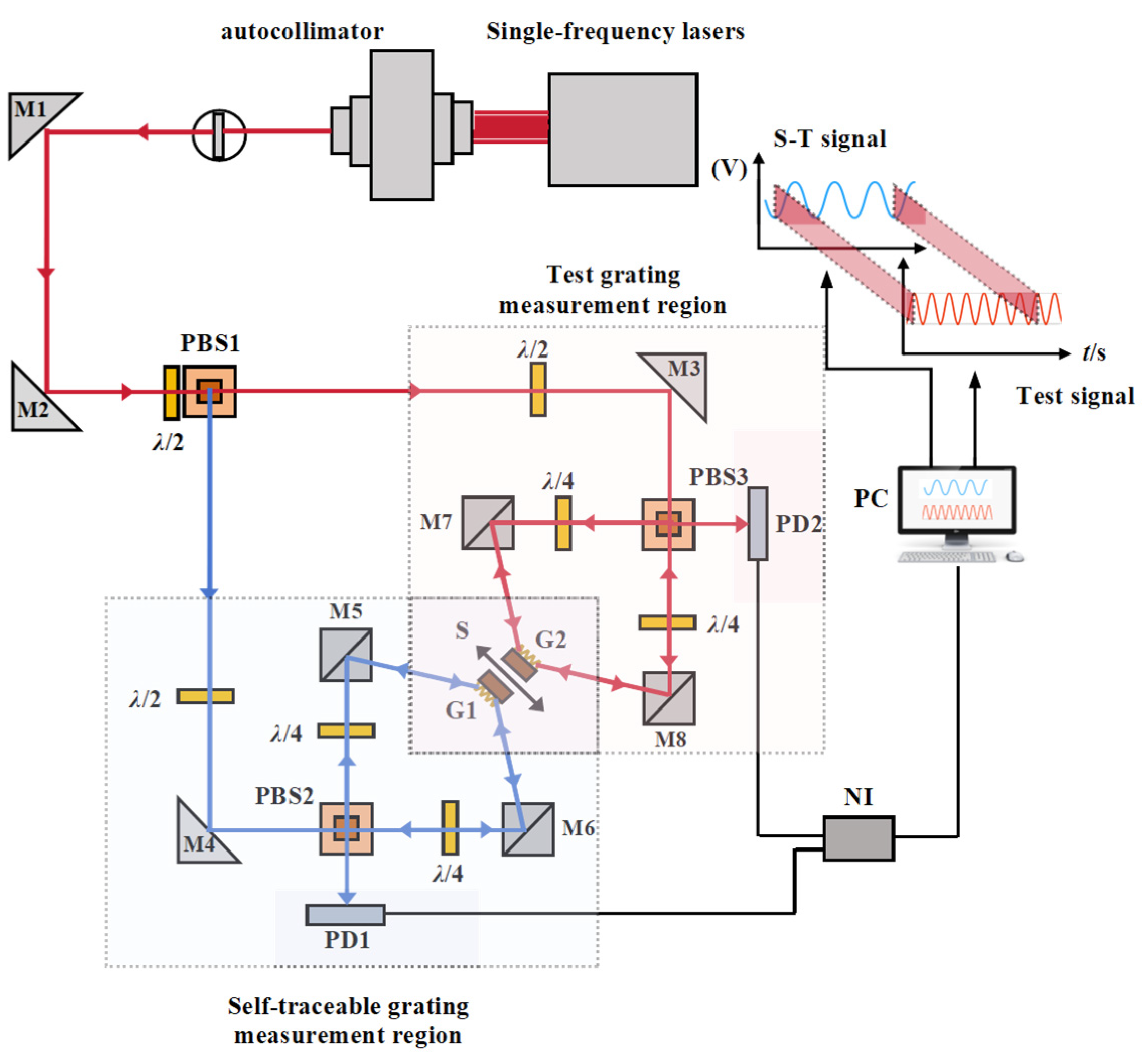
2.1. Principle of Dual-Grating Homodyne Interferometer Calibration
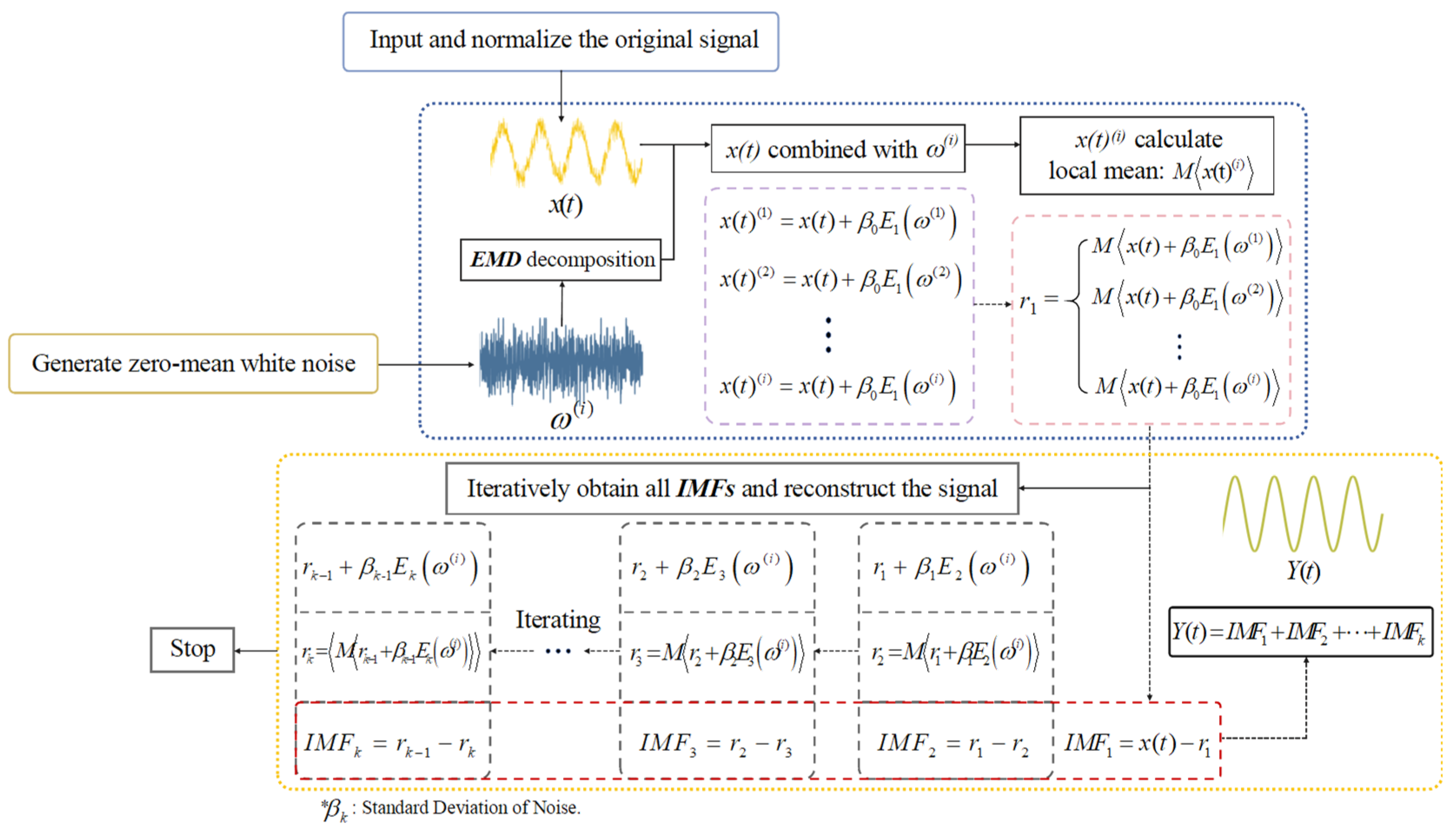
2.2. The Basic Principle of ICEEMDAN
- Firstly, define as the original signal in time series, as the signal after adding white noise, as the local mean of the signal, as the th white noise with unit variance and zero mean (), represents the standard deviation of the noise, and as the th IMF component after decomposition by EMD algorithm (where the symbol denotes the average).
- Secondly, the first Gaussian white noise is decomposed by EMD to construct the signal after adding white noise, which is expressed as , where represents the first-order white noise component. The local mean is obtained according to the formula , and then the first-order residual component can be calculated by taking the average of :
- The first-order intrinsic mode component can be obtained by subtracting the original signal from the first-order residual component, which is expressed as:
- The first-order residual component is taken as the source signal of the second-order decomposition, the second-order residual component is constructed by adding the second-order white noise , which can be expressed as . Then, the second-order modal component is obtained . The th residual is denoted as ;
- Step(4) is repeated until the maximum iteration of the SIFT algorithm or the modal component is less than the local extreme value, the values of all components are finally obtained, and the results are reconstructed into the original scale time domain signal :
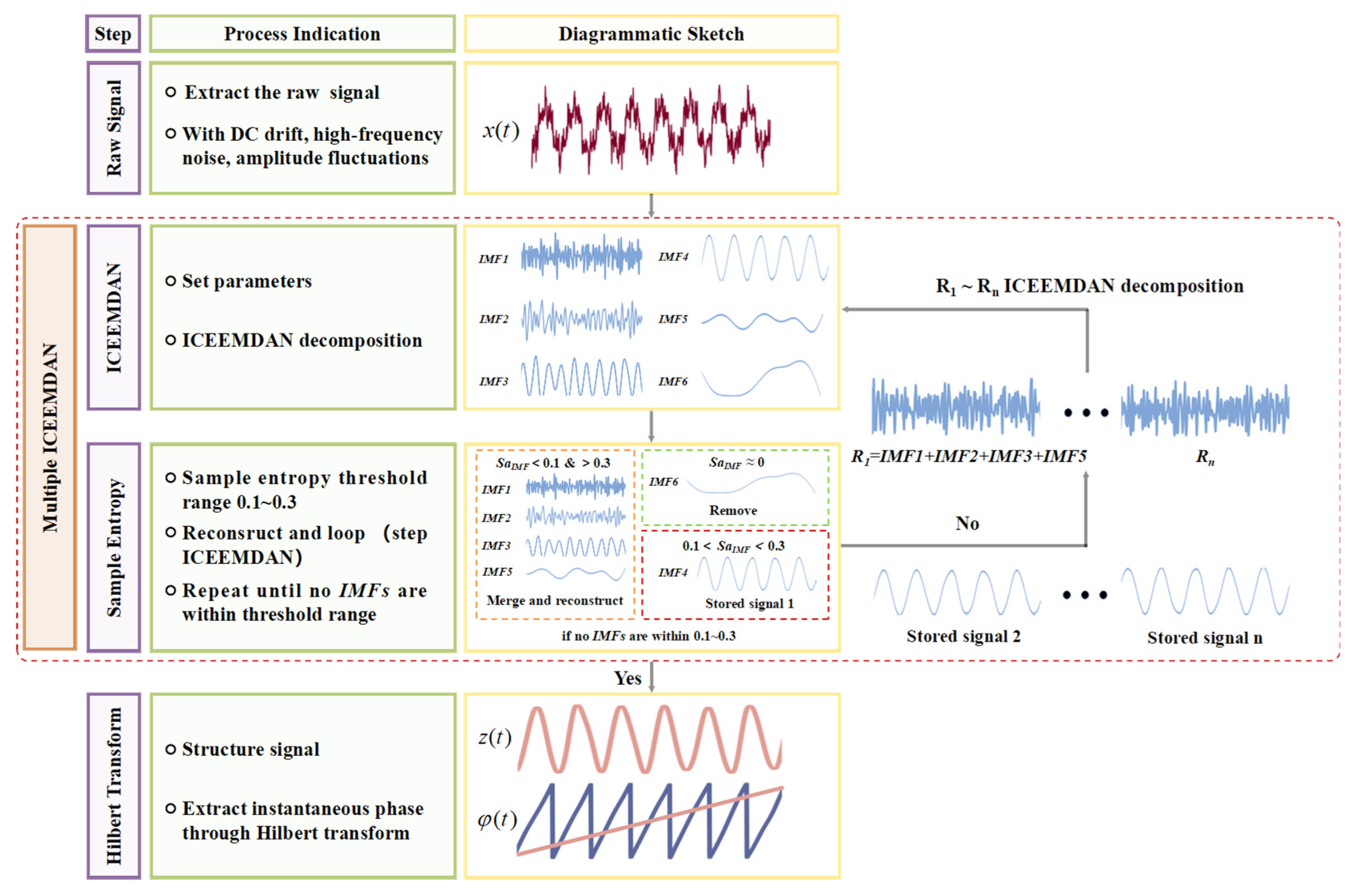
2.3. Multiple ICEEMDAN-HT Phase Unwrapping Based on Sample Entropy Criterion
- Firstly, the parameters for ICEEMDAN, including the standard deviation of white noise, the number of white noise trials, and the maximum number of iterations, are set. Then, the initial decomposition of the interferogram is performed to obtain the vector representation of IMFs:
- Secondly, the sample entropy threshold is set to 0.1~0.3. By judging whether is within the range of 0.1~0.3, the th IMFs that reach the threshold standard are saved. The remaining IMFs outside the threshold are summed and reconstructed, and the extremely low component with th sample entropy values close to zero is removed. The reconstructed signal of one decomposition is obtained and expressed as:
- Repeat step (2) until sample entropy values of all IMFs are outside the threshold range after one decomposition.
- Afterward, all the saved IMFs from each previous round of decomposition are combined to reconstruct the final signal, which is denoted as :
- The Hilbert Transform (HT) is applied to . HT can be considered as a 90-degree phase shifter, which can also filter out DC drift while realizing phase shift, and is defined as [19]:
- 6.
- Finally, the grating spacing is calculated according to Equation (5).
3. Experiment and Results Analysis
3.1. Simulation Experiment
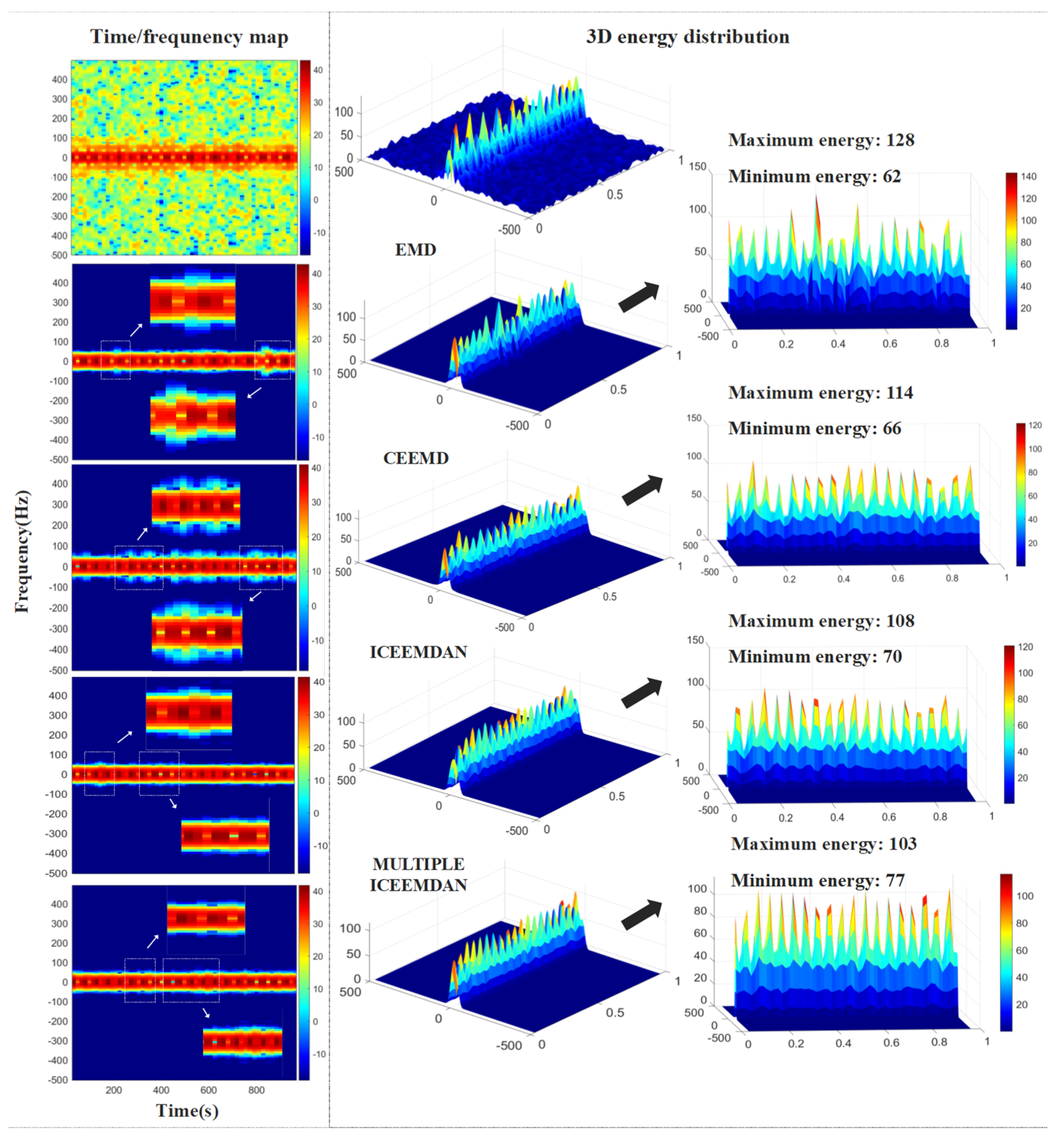
3.1.1. Performance Analysis of Multiple ICEEMDAN
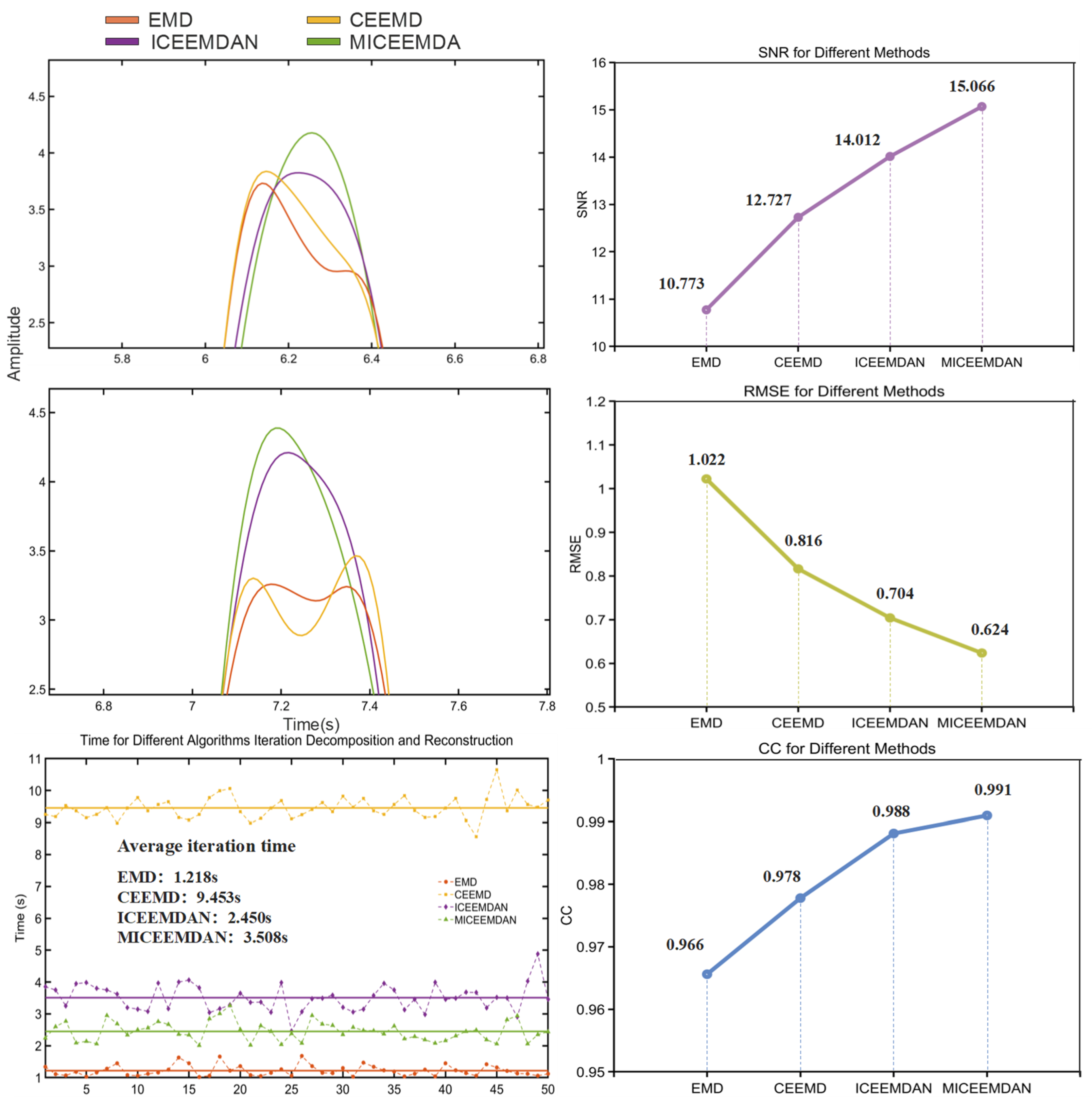
3.1.2. Algorithm Comparative Analysis
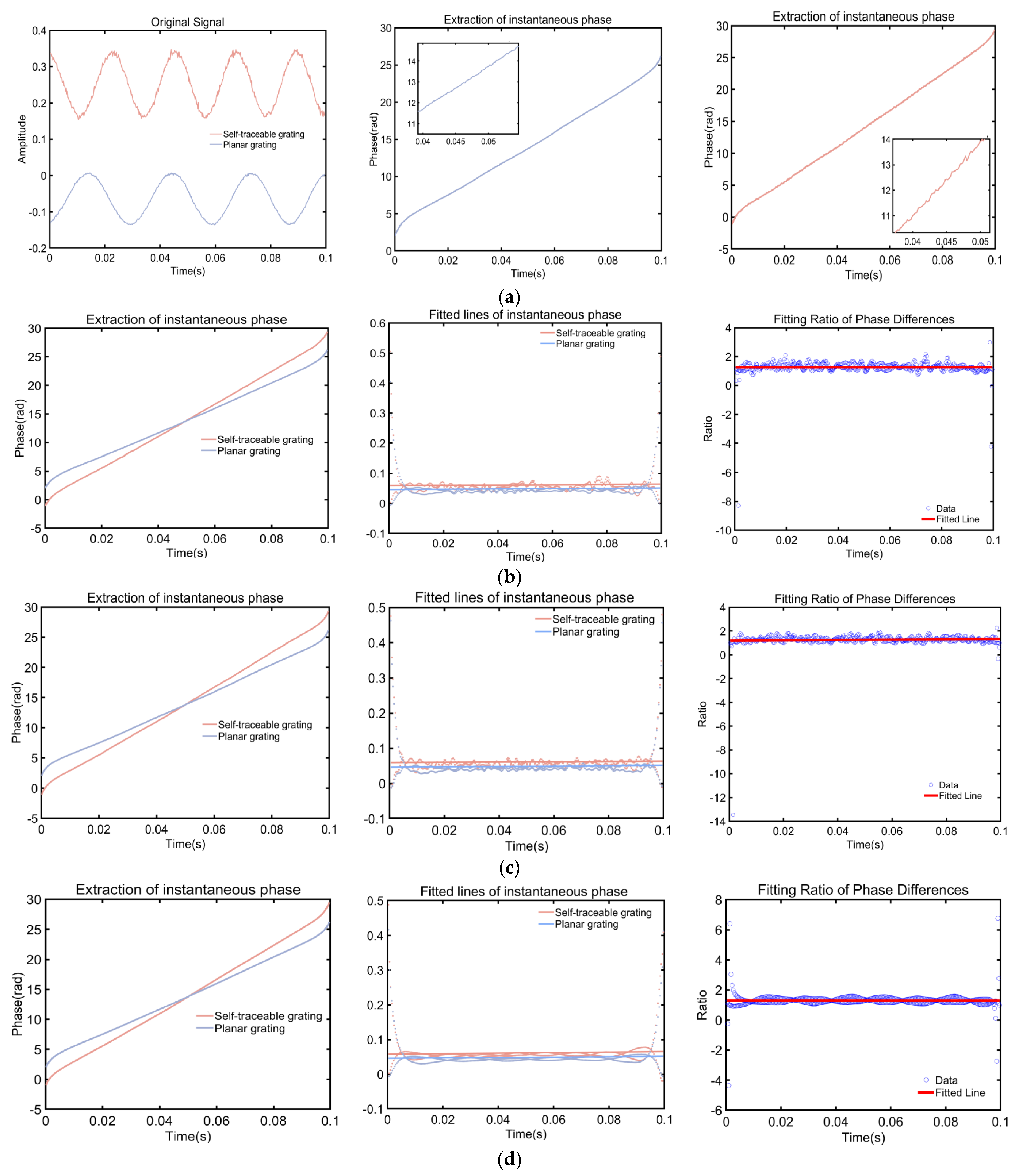
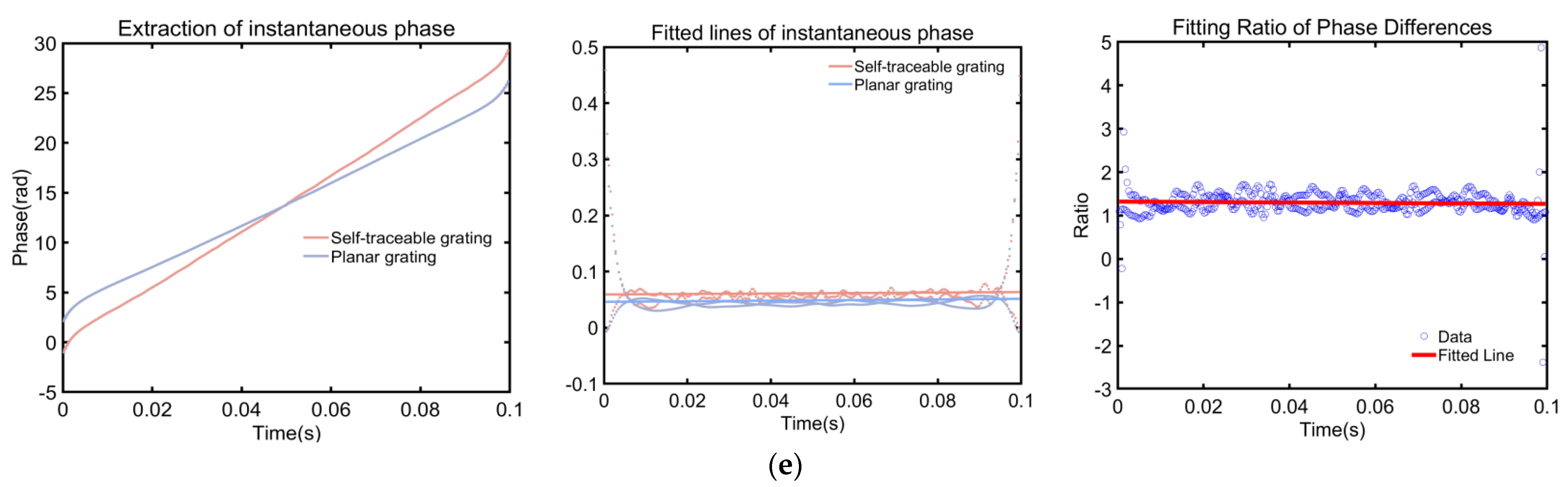
3.2. Spacing Calibration Experiment
4. Discussion
- In contrast to conventional signal decomposition methods where IMFs require secondary processing with other signal processing methods to obtain the final result, the extraction of IMFs in the Multiple ICEEMDAN method relies on the sample entropy criterion. This ensures an effective signal decomposition while also enhancing the efficiency of signal reconstruction.
- The Multiple ICEEMDAN method eliminates the phenomenon of mode mixing compared to EMD, resulting in a more complete decomposition. Compared to CEEMD, it reduces residual components and enhances decomposition efficiency. Compared to ICEEMDAN, the method increases the accuracy of reconstructed signals.
- The multiple ICEEMDAN-HT method is an exceptionally effective phase unwrapping technique, capable of improving the precision of grating phase extraction to the nanometer level.
- The multiple ICEEMDAN-HT method focuses on the decomposition, reconstruction, and phase extraction of interference signals. Therefore, whether it is a reflective or transmissive grating, this method can be applied to calibrate it.
- The iteration efficiency of Multiple ICEEMDAN is not ideal, thus necessitating the exploration of more advanced and rapid techniques to replace the sample entropy criterion, such as energy characteristics and singular spectrum analysis, to enhance the evaluation of algorithmic convergence behavior.
- The Multiple ICEEMDAN method can be combined with other signal processing techniques to conduct a more in-depth analysis of signal characteristics, thereby being applied to more complex nonlinear and non-stationary signal processing.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yin, Y.F.; Liu, Z.W.; Jiang, S.; Wang, W.; Yu, H.Z.; Jiri, G.; Hao, Q.; Li, W.H. High-precision 2D grating displacement measurement system based on double-spatial heterodyne optical path interleaving. Opt. Lasers Eng. 2022, 158, 107167. [Google Scholar] [CrossRef]
- Dominique, P.; Virginie, C.; Vincent, M. Integrated optics interferometer for high precision displacement measurement. In Proceedings of the SPIE, International Conference on Space Optics—ICSO 2000, Toulouse Labège, France, 5–7 December 2000. [Google Scholar]
- Cocco, D.; Sostero, G.; Zangrando, M. Technique for measuring the groove density of diffraction gratings using the long trace profiler. Rev. Sci. Instrum. 2003, 74, 3544–3548. [Google Scholar] [CrossRef]
- Liu, B.; Wang, Q.P.; Xu, X.D.; Fu, S.J. Measurements of groove density for concave gratings with the long trace profiler. Rev. Sci. Instrum. 2006, 77, 046106. [Google Scholar] [CrossRef]
- Xie, Y.F.; Jia, W.; Zhao, D.; Ye, Z.H.; Sun, P.; Xiang, C.C.; Wang, J.; Zhou, C.H. Traceable and long-range grating pitch measurement with picometer resolution. Opt. Commun. 2020, 476, 126316. [Google Scholar] [CrossRef]
- Xiang, X.S.; Jia, W.; Xiang, C.C.; Li, M.K.; Bu, F.T.; Zhou, C.H.; Wei, C.L. Long-range in situ picometer measurement of the period of an interference field. Appl. Opt. 2019, 58, 2929–2935. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.H.; Wang, G.C.; Wang, S.T.; Li, X.H. A Reflective-Type Heterodyne Grating Interferometer for Three-Degree-of-Freedom Subnanometer Measurement. IEEE Trans. Instrum. Meas. 2022, 71, 7007509. [Google Scholar] [CrossRef]
- Deng, X.; Dai, G.L.; Liu, J.; Hu, X.K.; Bergmann, D.; Zhao, J.; Tai, R.Z.; Cai, X.Y.; Li, Y.; Li, T.B.; et al. A new type of nanoscale reference grating manufactured by combined laser-focused atomic deposition and x-ray interference lithography and its use for calibrating a scanning electron microscope. Ultramicroscopy 2021, 226, 113293. [Google Scholar] [CrossRef] [PubMed]
- Zhou, W.Y.; Liu, Z.W.; Sun, Y.J.; Teng, H.R.; Wang, W.C.; Bayanheshig; Li, W.H. Bidirectional Littrow double grating interferometry for quadruple optical interpolation. Opt. Laser Technol. 2024, 175, 110751. [Google Scholar] [CrossRef]
- Josef, L.; Miroslava, H.; Jan, H.; Jindřich, O.; Ondřej, Č.; Miloslav, V.; Petra, S.; Milan, P. Advanced interferometry systems for dimensional measurement in nanometrology. In Optics and Measurement Conference; SPIE: Philadelphia, PA, USA, 2014. [Google Scholar]
- Hu, P.C.; Chang, D.; Tan, J.B.; Yang, T.R.; Yang, H.X.; Fu, H.J. Displacement measuring grating interferometer: A review. Front. Inf. Technol. Electron. Eng. 2019, 20, 631–654. [Google Scholar] [CrossRef]
- Du, H.; Zhang, W.T.; Xiong, X.M.; Zeng, Q.L.; Wang, Y.L.; Zhang, Y.T. Influence of installation error of grating interferometer on high-precision displacement measurement. Opt. Eng. 2021, 60, 045102. [Google Scholar] [CrossRef]
- Deng, X.; Li, T.B.; Cheng, X.B. Self-traceable grating reference material and application. Opt. Precis. Eng. 2022, 30, 2608–2625. [Google Scholar]
- Shang, P. Study on the Key Technology of High-Resolution Diffraction Grating Interferometric Transducer of Linear Displacements; Hefei University of Technology: Hefei, China, 2012. [Google Scholar]
- Yang, J.; Huang, J.H.; Lei, Y.H.; Zheng, J.B.; Shan, Y.Z.; Guo, D.Y.; Guo, J.C. Analysis of period and visibility of dual phase grating interferometer. Chin. Phys. B 2022, 31, 058701. [Google Scholar] [CrossRef]
- Wang, B.Z.; Li, W.J.; Peng, K.; Wang, Q.; Li, M.L. Time Domain Subdivision Method for Optical Grating Signal Based on Time Series Analysis. Nanotechnol. Precis. Eng. 2018, 1, 48–53. [Google Scholar]
- Wu, W.B.; Yuan, X.J. Analyzing spectral peak distribution of coupled signals using Fourier transform theory. Indian J. Phys. 2023, 97, 4509–4519. [Google Scholar]
- Yang, Z.H.; Yang, G.R.; Yang, L.H.; Zhang, Q. A reconstruction method for graph signals based on the power spectral density estimation. Digit. Signal Process. 2022, 122, 103347. [Google Scholar] [CrossRef]
- Saqib, A. Implementation of hilbert transform based high-resolution phase unwrapping method for displacement retrieval using laser self mixing interferometry sensor. Opt. Laser Technol. 2022, 149, 107887. [Google Scholar]
- Zhang, Y.J.; Xu, L.; Guan, Y.Q.; Zou, W.Z.; Guo, C.W.; Lei, L.H.; Fu, Y.X.; Guo, Z.Y.; Gu, Z.J.; Deng, X. Research on laser self-mixing nano-displacement measurement based on plane reflective holographic grating. Infrared Laser Eng. 2023, 52, 235–242. [Google Scholar]
- Eduardo, A.; Mario, E.; José, M.E.; Calixto, M.; Gerry, L.; Carlos, B. Comparison between traditional fast Fourier transform and marginal spectra using the Hilbert–Huang transform method for the broadband spectral analysis of the electroencephalogram in healthy humans. Eng. Rep. 2021, 3, e12367. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Deng, W.; Liu, Z.G.; Deng, Z.W.; Jia, X.Y.; Wang, Z.Y. Extraction of interference phase in frequency-scanning interferometry based on empirical mode decomposition and Hilbert transform. Appl. Opt. 2018, 57, 2299–2305. [Google Scholar] [CrossRef]
- Yang, K.Y.; Deng, Z.W.; Chen, W.J.; Yao, X.; Sun, H.F.; Shen, L.R. Phase-extracting method of optical frequency scanning interference signals based on the CEEMD-HT algorithm. Chin. Opt. 2023, 16, 682–700. [Google Scholar]
- Tan, J.S.; Ran, Z.; Wan, C. EEG signal recognition algorithm with sample entropy and pattern recognition. J. Comput. Methods Sci. Eng. 2023, 23, 2059–2068. [Google Scholar] [CrossRef]
- Zhou, W.Y.; Li, W.H.; Liu, L.; Sun, Y.J.; Wang, W.C.; Chen, G.X.; Liu, Z.W. Bidirectional two-degree-of-freedom grating interferometer with biased Littrow configuration. Opt. Commun. 2024, 557, 130333. [Google Scholar] [CrossRef]
- Lv, Q.; Liu, Z.W.; Wang, W.; Jiang, S.; Bayanheshig; Li, W. Fast method to detect and calculate displacement errors in a Littrow grating-based interferometer. Appl. Opt. 2019, 58, 3193–3199. [Google Scholar] [CrossRef]
- Wu, Z.H.; Huang, N.E. ENSEMBLE EMPIRICAL MODE DECOMPOSITION: A NOISE-ASSISTED DATA ANALYSIS METHOD. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Xiao, M.H.; Wang, Z.Y.; Zhao, Y.F.; Geng, G.S.; Dustdar, S.; Donta, P.K. A new fault feature extraction method of rolling bearings based on the improved self-selection ICEEMDAN-permutation entropy. ISA Trans. 2023, 143, 536–547. [Google Scholar] [CrossRef]
- Hua, Z.; Gao, B.K.; Yue, H.Y.; Cui, X.Y. Vibration measurement based on square arithmetic and multiple Hilbert transform for F—P interferometry. Laser Infrared 2021, 51, 1065–1069. [Google Scholar]


| The Type of Grating | Self-Traceable Grating | Planar Grating |
|---|---|---|
| Grating area material | Cr | / |
| Substrate material | Si | Float glass |
| Size/mm | 1.5 × 3 | 25 × 25 × 6 |
| Linear density (Lines/mm) | 4700 | 3600 |
| Spacing standard value/nm | 212.7705 ± 0.0049 | 277.8 |
| Littrow angle at maximum diffraction efficiency () | 72.5° | 46.8° |
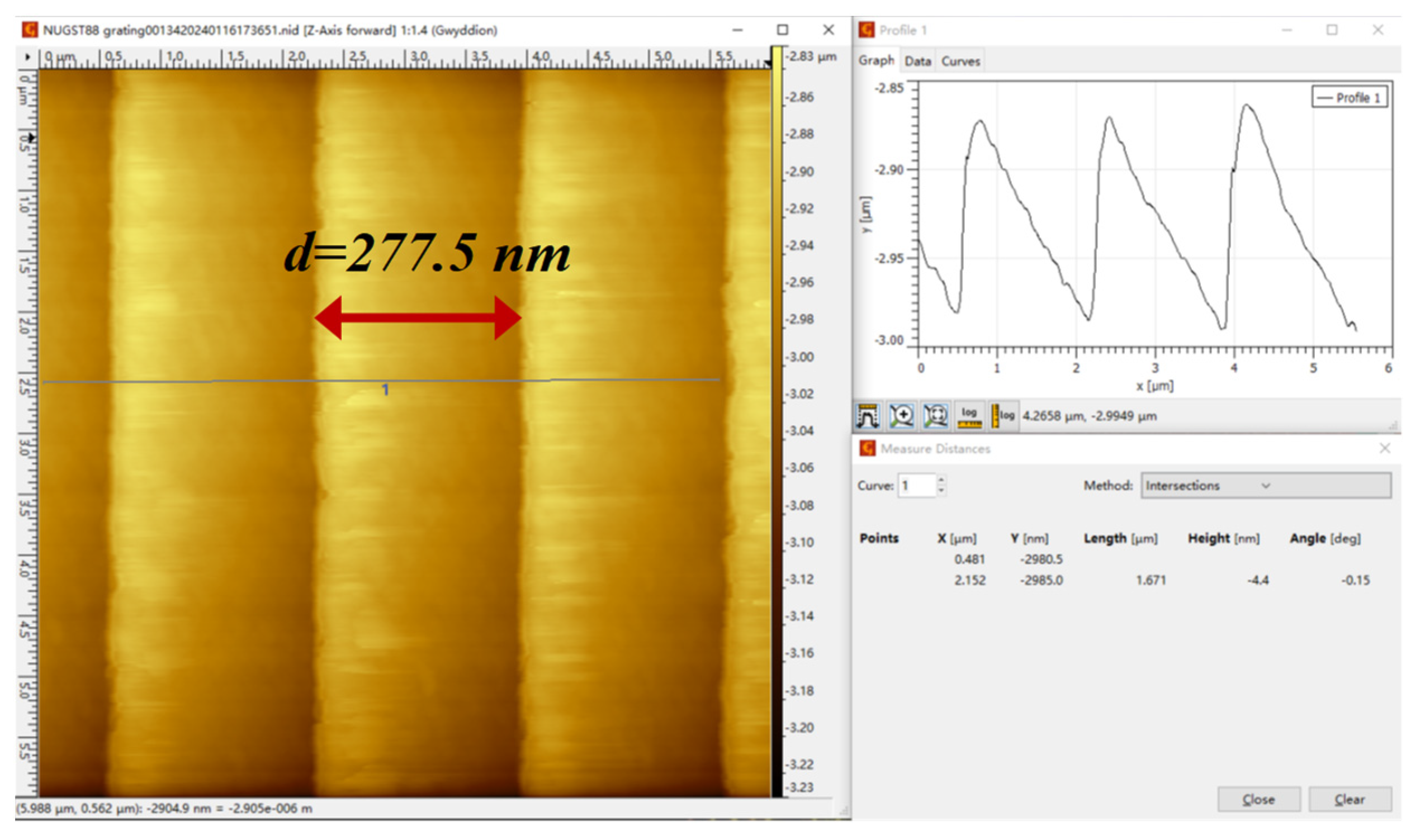
| Phase Unwrapping Method | Phase Difference Ratio within 0 to 0.1 s | Calibration Spacing for This Experiment/nm | Spacing Average of AFM Scans/nm | |
|---|---|---|---|---|
| 277.5 | ||||
| Std/nm | Re/% | |||
| EMD-HT | 1.2474 | 265.4 | 12.1 | 4.36 |
| CEEMD-HT | 1.2836 | 273.1 | 4.4 | 1.58 |
| ICEEMDAN-HT | 1.2954 | 275.6 | 1.9 | 0.68 |
| Multiple ICEEMDAN-HT | 1.3033 | 277.3 | 0.2 | 0.07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.; Sun, J.; Guan, Y.; Liu, L.; Guo, C.; Zhang, Y.; Wan, J.; Lei, L. Research on Dual-Grating Spacing Calibration Method Based on Multiple Improved Complete Ensemble Empirical Mode Decomposition with Adaptive Noise Combined with Hilbert Transform. Photonics 2024, 11, 443. https://doi.org/10.3390/photonics11050443
Zhu Y, Sun J, Guan Y, Liu L, Guo C, Zhang Y, Wan J, Lei L. Research on Dual-Grating Spacing Calibration Method Based on Multiple Improved Complete Ensemble Empirical Mode Decomposition with Adaptive Noise Combined with Hilbert Transform. Photonics. 2024; 11(5):443. https://doi.org/10.3390/photonics11050443
Chicago/Turabian StyleZhu, Yanzhen, Jiayuan Sun, Yuqing Guan, Liqin Liu, Chuangwei Guo, Yujie Zhang, Jun Wan, and Lihua Lei. 2024. "Research on Dual-Grating Spacing Calibration Method Based on Multiple Improved Complete Ensemble Empirical Mode Decomposition with Adaptive Noise Combined with Hilbert Transform" Photonics 11, no. 5: 443. https://doi.org/10.3390/photonics11050443
APA StyleZhu, Y., Sun, J., Guan, Y., Liu, L., Guo, C., Zhang, Y., Wan, J., & Lei, L. (2024). Research on Dual-Grating Spacing Calibration Method Based on Multiple Improved Complete Ensemble Empirical Mode Decomposition with Adaptive Noise Combined with Hilbert Transform. Photonics, 11(5), 443. https://doi.org/10.3390/photonics11050443




