Polarization Diffraction Gratings in PAZO Polymer Thin Films Recorded with Digital Polarization Holography: Polarization Properties and Surface Relief Formation
Abstract
1. Introduction
2. Materials and Methods
2.1. Samples Preparation
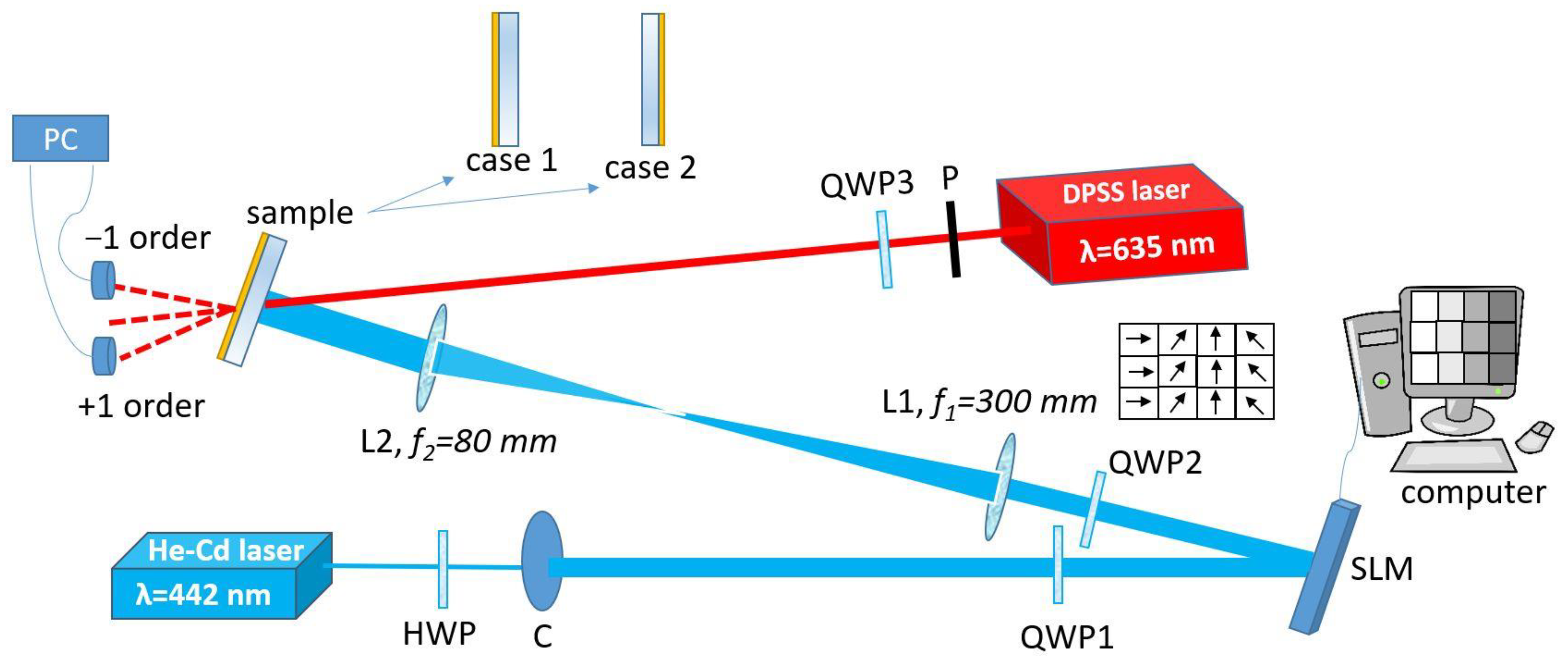
2.2. Optical Scheme for Digital Polarization Holographic Recording
2.3. Optical Setup for Polarization Properties Analysis
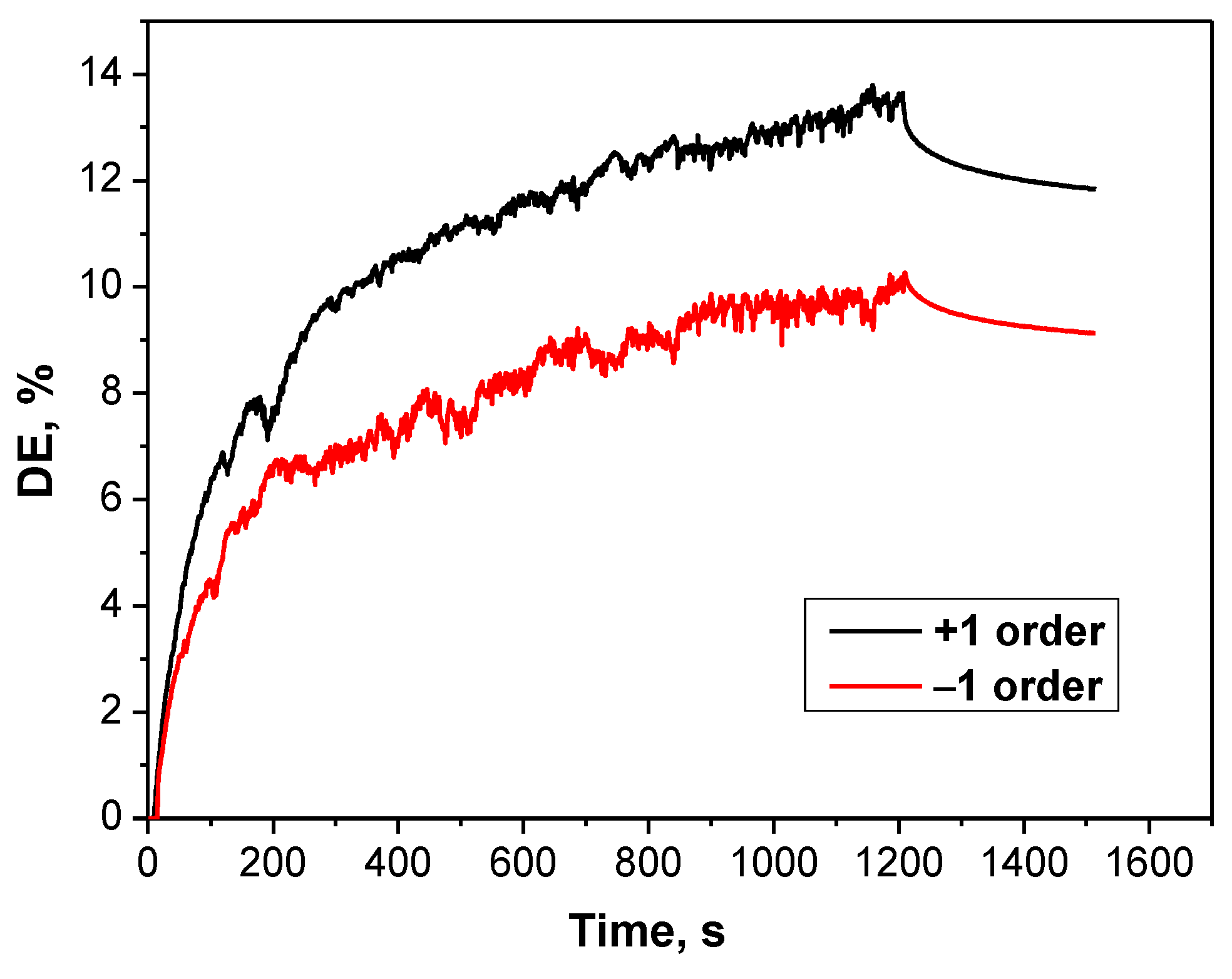
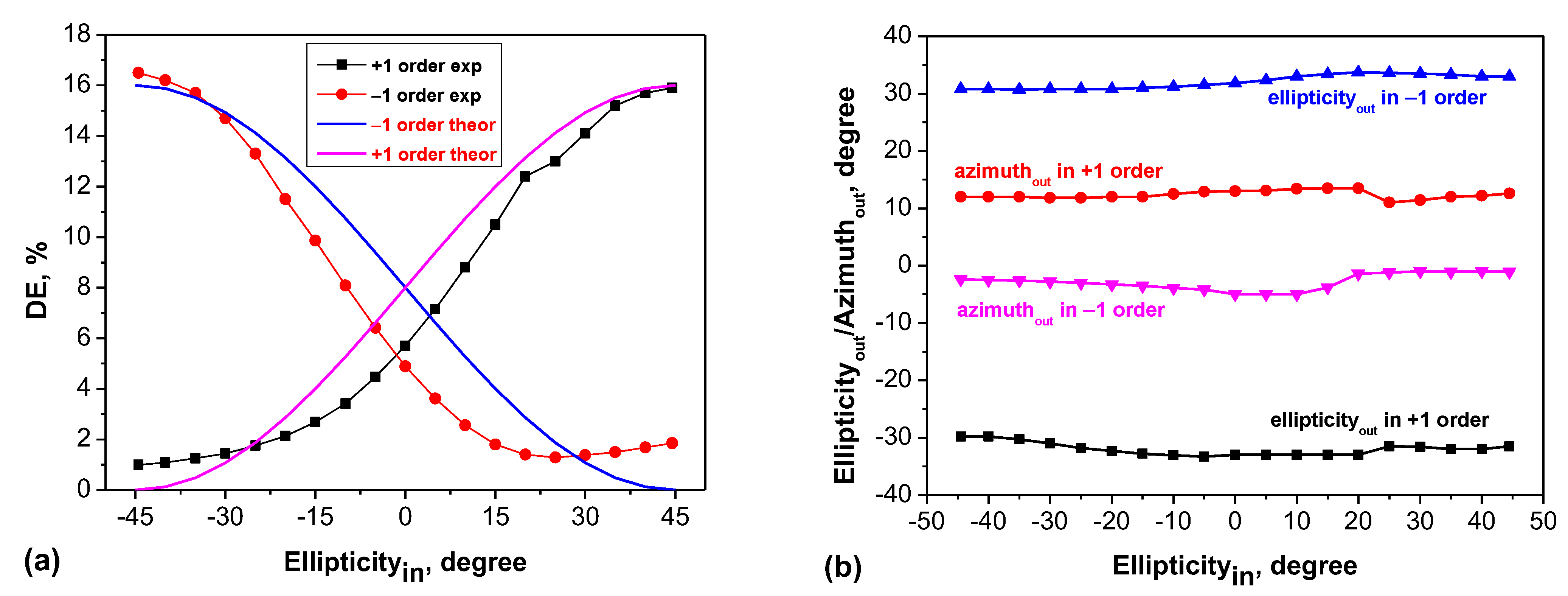
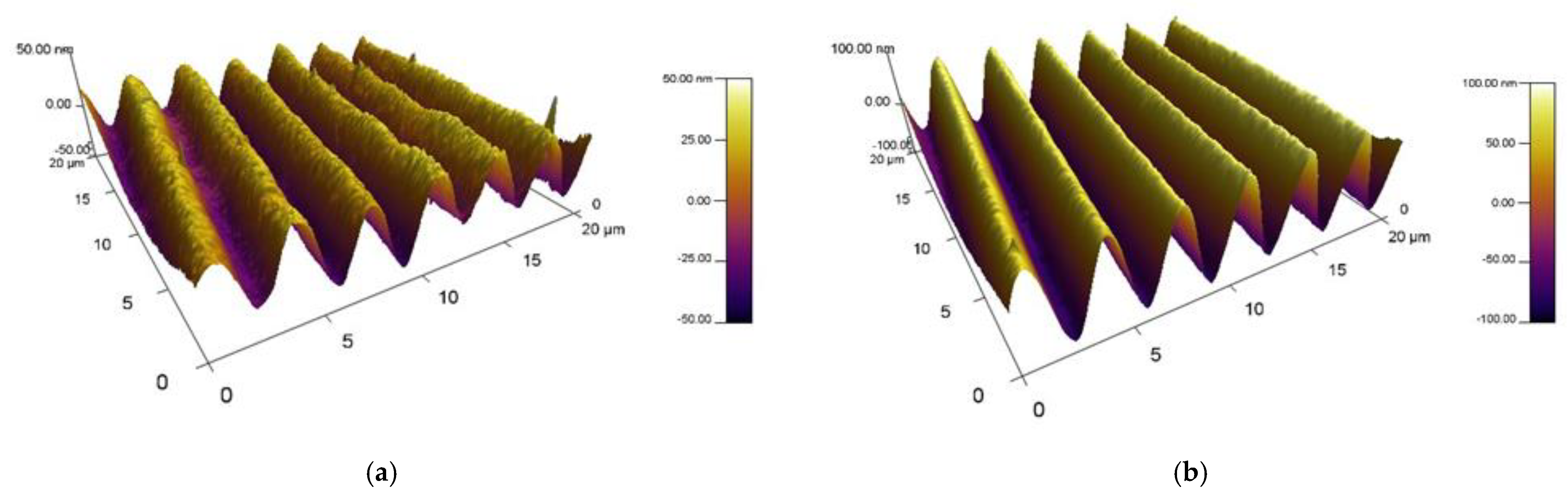
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gabor, D. A New Microscopic Principle. Nature 1948, 161, 777–778. [Google Scholar] [CrossRef] [PubMed]
- Leith, E.N.; Upatnieks, J. Reconstructed wavefronts and communication theory. J. Opt. Soc. Am. 1962, 52, 1123–1130. [Google Scholar] [CrossRef]
- Goodman, J.W.; Lawrence, R. Digital image formation from electronically detected holograms. Appl. Phys. Lett. 1967, 11, 77–79. [Google Scholar] [CrossRef]
- Hariharan, P. Basics of Holography; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar] [CrossRef]
- Azzam, R.M.A.; Bashara, N.M. Ellipsometry and Polarized Light; North-Holland Pub. Co.: Amsterdam, The Netherlands, 1977. [Google Scholar]
- Born, M.; Wolf, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference, and Diffraction of Light; Cambridge University Press: London, UK, 1999. [Google Scholar] [CrossRef]
- Pancharatnam, S. Generalized theory of interference, and its applications. Proc. Indian Acad. Sci. 1956, 44, 247–262. [Google Scholar] [CrossRef]
- Lohmann, A.W. Reconstruction of Vectorial Wavefronts. Appl. Opt. 1965, 4, 1667–1668. [Google Scholar] [CrossRef]
- Kakichashvili, S.D. Method for phase polarization recording of holograms. Sov. J. Quantum. Electron. 1974, 4, 795. [Google Scholar] [CrossRef]
- Todorov, T.; Nikolova, L.; Tomova, N. Polarization holography. 1: A new high-efficiency organic material with reversible photoinduced birefringence. Appl. Opt. 1984, 23, 4309–4312. [Google Scholar] [CrossRef] [PubMed]
- Colomb, T.; Dahlgren, P.; Beghuin, D.; Cuche, E.; Marquet, P.; Depeursinge, C. Polarization imaging by use of digital holography. Appl. Opt. 2002, 41, 27–37. [Google Scholar] [CrossRef] [PubMed]
- Hong, Y.F.; Zang, J.L.; Liu, Y.; Fan, F.L.; Wu, A.A.; Shao, L.; Kang, G.G.; Tan, X.D. Review and prospect of polarization holography. Chin. Opt. 2017, 10, 588–602. [Google Scholar] [CrossRef]
- Zhai, Y.; Cao, L.; Liu, Y.; Tan, X. A Review of Polarization-Sensitive Materials for Polarization Holography. Materials 2020, 13, 5562. [Google Scholar] [CrossRef]
- Natansohn, A.; Rochon, P.; Gosselin, J.; Xie, S. Azo polymers for reversible optical storage. 1. Poly [4′-[[2-(acryloyloxy)ethyl]ethylamino]-4-nitroazobenzene]. Macromolecules 1992, 25, 2268–2273. [Google Scholar] [CrossRef]
- Nikolova, L.; Ramanujam, P.S. Polarization Holography; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar] [CrossRef]
- Eich, M.; Wendorff, J.H.; Reck, B.D.; Ringsdorf, H.P. Reversible digital and holographic optical storage in polymeric liquid crystals. Makromol. Chem. Rapid Commun. 1987, 8, 59–63. [Google Scholar] [CrossRef]
- Priimagi, A.; Shevchenko, A. Azopolymer-Based Micro- and Nanopatterning for Photonic Applications. J. Polym. Sci. Part B Polym. Phys. 2014, 52, 163–182. [Google Scholar] [CrossRef]
- Nedelchev, L.; Mateev, G.; Nikolova, L.; Nazarova, D.; Ivanov, B.; Strijkova, V.; Stoykova, E.; Choi, K.; Park, J. In-line and off-axis polarization-selective holographic lenses recorded in azopolymer thin films via polarization holography and polarization multiplexing. Appl. Opt. 2022, 62, D1–D7. [Google Scholar] [CrossRef] [PubMed]
- Wang, X. Azo Polymers: Synthesis, Functions and Applications; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar] [CrossRef]
- Nedelchev, L.; Mateev, G.; Strijkova, V.; Salgueiriño, V.; Schmool, D.S.; Berberova-Buhova, N.; Stoykova, E.; Nazarova, D. Tunable Polarization and Surface Relief Holographic Gratings in Azopolymer Nanocomposites with Incorporated Goethite (α-FeOOH) Nanorods. Photonics 2021, 8, 306. [Google Scholar] [CrossRef]
- Martínez-Ponce, G.; Solano, C.E.; Rodríguez-González, R.J.; Larios-Lôpez, L.; Navarro-Rodríguez, D.; Nikolova, L. All-optical switching using supramolecular chiral structures in azopolymers. J. Opt. A Pure Appl. Opt. 2008, 10, 115006. [Google Scholar] [CrossRef]
- Blagoeva, B.; Nedelchev, L.; Nazarova, D.; Stoykova, E.; Park, J. Reversible supramolecular chiral structures induced in azopolymers by elliptically polarized light: Influence of the irradiation wavelength and intensity. Appl. Opt. 2021, 61, B147–B155. [Google Scholar] [CrossRef] [PubMed]
- Natansohn, A.; Rochon, P. Photoinduced motions in azo-containing polymers. Chem. Rev. 2002, 102, 4139–4176. [Google Scholar] [CrossRef]
- Rochon, P.; Batalla, E.; Natansohn, A. Optically induced surface gratings on anoaromatic polymer films. Appl. Phys. Lett. 1995, 66, 136–138. [Google Scholar] [CrossRef]
- Kim, D.; Li, L.; Kumar, J.; Tripathy, S.K. Laser-induced holographic surface relief gratings on nonlinear optical polymer films. Appl. Phys. Lett. 1995, 66, 1166–1168. [Google Scholar] [CrossRef]
- Holme, N.C.; Nikolova, L.; Ramanujam, P.S.; Hvilsted, S. An analysis of the anisotropic and topographic gratings in a side-chain liquid crystalline azobenzene polyester. Appl. Phys. Lett. 1997, 70, 1518–1520. [Google Scholar] [CrossRef]
- Cipparrone, G.; Pagliusi, P.; Provenzano, C.; Shibaev, V.P. Polarization holographic recording in amorphous polymer with photoinduced linear and circular birefringence. J. Phys. Chem. B 2010, 114, 8900–8904. [Google Scholar] [CrossRef] [PubMed]
- Martinez-Ponce, G. Mueller imaging polarimetry of holographic polarization gratings inscribed in azopolymer films. Opt. Express 2016, 24, 21364–21377. [Google Scholar] [CrossRef] [PubMed]
- Berberova-Buhova, N.; Nedelchev, L.; Mateev, G.; Stoykova, E.; Strijkova, V.; Nazarova, D. Influence of the size of Au nanoparticles on the photoinduced birefringence and diffraction efficiency of polarization holographic gratings in thin films of azopolymer nanocomposites. Opt. Mat. 2021, 121, 111560. [Google Scholar] [CrossRef]
- Nair, S.; Escobedo, C.; Sabat, R.G. Crossed Surface Relief Gratings as Nanoplasmonic Biosensors. ACS Sens. 2017, 2, 379–385. [Google Scholar] [CrossRef] [PubMed]
- Kryshenik, V.M.; Azhniuk, Y.M.; Kovtunenko, V.S. All-optical patterning in azobenzene polymers and amorphous chalcogenides. J. Non-Cryst. Solids 2019, 512, 112–131. [Google Scholar] [CrossRef]
- Lin, Y.; Xu, H.; Shi, R.; Lu, L.; Zhang, S.; Li, D. Enhanced diffraction efficiency with angular selectivity by inserting an optical interlayer into a diffractive waveguide for augmented reality displays. Opt. Express 2022, 30, 31244–31255. [Google Scholar] [CrossRef] [PubMed]
- Mateev, G.; Nedelchev, L.; Nikolova, L.; Ivanov, B.; Strijkova, V.; Stoykova, E.; Choi, K.; Park, J.; Nazarova, D. Two-Dimensional Polarization Holographic Gratings in Azopolymer Thin Films: Polarization Properties in the Presence or Absence of Surface Relief. Photonics 2023, 10, 728. [Google Scholar] [CrossRef]
- Nazarova, D.; Nedelchev, L.; Berberova-Buhova, N.; Mateev, G. Nanocomposite Photoanisotropic Materials for Applications in Polarization Holography and Photonics. Nanomaterials 2023, 13, 2946. [Google Scholar] [CrossRef]
- Ferreira, Q.; Gomes, P.; Raposo, M.; Giacometti, J.; Oliveira, O.; Ribeiro, P. Influence of ionic interactions on the photoinduced birefringence of poly [1-[4-(3-Carboxy-4-hydroxyphenylazo) benzene sulfonamido]-1,2-ethanediyl, sodium salt] films. J. Nanosci. Nanotechnol. 2007, 7, 2659–2666. [Google Scholar] [CrossRef]
- Madruga, C.; Filho, P.; Andrade, M.; Gonçalves, M.; Raposo, M.; Ribeiro, P. Birefringence dynamics of poly{1-[4-(3-carboxy-4-hydroxyphenylazo) benzenesulfonamido]-1,2-ethanediyl, sodium salt} cast films. Thin Solid Films 2011, 519, 8191–8196. [Google Scholar] [CrossRef]
- Nedelchev, L.; Ivanov, D.; Berberova, N.; Strijkova, V.; Nazarova, D. Polarization holographic gratings with high diffraction efficiency recorded in azopolymer PAZO. Opt. Quantum Electron. 2018, 50, 212. [Google Scholar] [CrossRef]
- Blagoeva, B.; Nedelchev, L.; Mateev, G.; Stoykova, E.; Nazarova, D. Diffraction efficiency of polarization holographic gratings recorded in azopolymer thin films coated using different solvents. In Photosensitive Materials and Their Applications; SPIE: Bellingham, WA, USA, 2020; Volume 11367, pp. 190–195. [Google Scholar] [CrossRef]
- Falcione, R.; Roldan, M.V.; Pellegri, N.; Goyanes, S.; Ledesma, S.A.; Capeluto, M.G. Increase of SRG modulation depth in azopolymers-nanoparticles hybrid materials. Opt. Mater. 2021, 115, 111015. [Google Scholar] [CrossRef]
- Stoilova, A.; Mateev, G.; Nazarova, D.; Nedelchev, L.; Stoykova, E.; Blagoeva, B.; Berberova, N.; Georgieva, S.; Todorov, P. Polarization holographic gratings in PAZO polymer films doped with particles of biometals. J. Photochem. Photobiol. A Chem. 2021, 411, 113196. [Google Scholar] [CrossRef]
- Takeda, M.; Ina, H.; Kobayashi, S. Fourier-Transform Method of Fringe- Pattern Analysis for Computer-Based Topography and Interferometry. J. Opt. Soc. Am. 1982, 72, 156–160. [Google Scholar] [CrossRef]
- Kim, M.K. Digital Holographic Microscopy: Principles, Techniques, and Applications; Springer: New York, NY, USA, 2011. [Google Scholar] [CrossRef]
- Schnars, U.; Falldorf, C.; Watson, J.; Jueptner, W. Digital Holography and Wavefront Sensing: Principles, Techniques and Applications; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Kostuk, R.K. Holography: Principles and Applications; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Shan, M.; Liu, L.; Zhong, Z.; Liu, B.; Zhang, Y. Direct phase retrieval for simultaneous dual-wavelength off-axis digital holography. Opt. Lasers Eng. 2019, 121, 246–251. [Google Scholar] [CrossRef]
- Tahara, T.; Ito, T.; Ichihashi, Y.; Oi, R. Single-shot incoherent color digital holographic microscopy system with static polarization-sensitive optical elements. J. Opt. 2020, 22, 105702. [Google Scholar] [CrossRef]
- Liu, L.; Shan, M.; Zhong, Z.; Liu, B.; Luan, G.; Diao, M.; Zhang, Y. Simultaneous dual-wavelength off-axis flipping digital holography. Opt. Lett. 2017, 42, 4331–4334. [Google Scholar] [CrossRef] [PubMed]
- Tahara, T.; Quan, X.; Otani, R.; Takaki, Y.; Matoba, O. Digital holography and its multidimensional imaging applications: A review. Microscopy 2018, 67, 55–67. [Google Scholar] [CrossRef]
- Kim, H.; Kim, D.H.; Lee, Y. Encryption of digital hologram of 3-D object by virtual optics. Opt. Express 2004, 12, 4912–4921. [Google Scholar] [CrossRef]
- Di, H.; Zheng, K.; Zhang, X.; Lam, E.Y.; Kim, T.; Kim, Y.S.; Poon, T.; Zhou, C. Multiple-image encryption by compressive holography. Appl. Оpt. 2012, 51, 1000–1009. [Google Scholar] [CrossRef] [PubMed]
- Javidi, B.; Kim, D. Three-dimensional-object recognition by use of single-exposure on-axis digital holography. Opt. Lett. 2005, 30, 236–238. [Google Scholar] [CrossRef] [PubMed]
- Stoykova, E.; Alatan, A.A.; Benzie, P.; Grammalidis, N.; Malassiotis, S.; Ostermann, J.; Zabulis, X. 3-D time-varying scene capture technologies—A survey. IEEE Transactions on Circuits and Systems for Video Technology 2007, 17, 1568–1586. [Google Scholar] [CrossRef]
- Liu, J.-P.; Tahara, T.; Hayasaki, Y.; Poon, T.-C. Incoherent Digital Holography: A Review. Appl. Sci. 2018, 8, 143. [Google Scholar] [CrossRef]
- Tiwari, V.S.; Bisht, N. Spatial Light Modulators and Their Applications in Polarization Holography; IntechOpen: London, UK, 2023. [Google Scholar] [CrossRef]
- Yang, Y.Q.; Forbes, A.; Cao, L.C. A review of liquid crystal spatial light modulators: Devices and applications. Opto-Electron. Sci. 2023, 2, 230026. [Google Scholar] [CrossRef]
- Chen, H.C.; Cheng, C. Holographic Optical Tweezers: Techniques and Biomedical Applications. Appl. Sci. 2022, 12, 10244. [Google Scholar] [CrossRef]
- Kuang, Z.; Li, J.; Edwardson, S.; Perrie, W.; Liu, D.; Dearden, G. Ultrafast laser beam shaping for material processing at imaging plane by geometric masks using a spatial light modulator. Opt. Lasers Eng. 2015, 70, 1–5. [Google Scholar] [CrossRef]
- Vijayakumar, A.; Kashter, Y.; Kelner, R.; Rosen, J. Coded aperture correlation holography–a new type of incoherent digital holograms. Opt. Express 2016, 24, 12430–12441. [Google Scholar] [CrossRef] [PubMed]
- Davis, J.A.; McNamara, D.E.; Cottrell, D.M.; Sonehara, T. Two-dimensional polarization encoding with a phase-only liquid-crystal spatial light modulator. Appl. Opt. 2000, 39, 1549–1554. [Google Scholar] [CrossRef]
- Singh, R.K. Digital Polarization Holography: Challenges and Opportunities. Eng. Proc. 2023, 34, 10. [Google Scholar] [CrossRef]
- De Sio, L.; Roberts, D.E.; Liao, Z.; Nersisyan, S.R.; Uskova, O.; Wickboldt, L.; Tabiryan, N.V.; Steeves, D.M.; Kimball, B.R. Digital polarization holography advancing geometrical phase optics. Opt. Express 2016, 24, 18297–18306. [Google Scholar]
- Shen, Y.; Wang, X.; Xie, Z.; Min, C.; Fu, X.; Liu, Q.; Gong, M.; Yuan, X. Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities. Light Sci. Appl. 2019, 8, 90. [Google Scholar] [CrossRef] [PubMed]
- Fernández, R.; Gallego, S.; Márquez, A.; Neipp, C.; Calzado, E.M.; Francés, J.; Morales-Vidal, M.; Beléndez, A. Complex Diffractive Optical Elements Stored in Photopolymers. Polymers 2019, 11, 1920. [Google Scholar] [CrossRef] [PubMed]
- Cazac, V.; Achimova, E.; Abashkin, V.; Prisacar, A.; Loshmanschii, C.; Meshalkin, A.; Egiazarian, K. Polarization holographic recording of vortex diffractive optical elements on azopolymer thin films and 3D analysis via phase-shifting digital holographic microscopy. Opt. Express 2021, 29, 9217–9230. [Google Scholar] [CrossRef] [PubMed]
- Tabiryan, N.V.; Nersisyan, S.R.; Xianyu, H.; Serabyn, E. Fabricating vector vortex waveplates for coronagraphy. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 3–10 March 2012; pp. 1–12. [Google Scholar] [CrossRef]
- Gong, L.; Ren, Y.; Liu, W.; Wang, M.; Zhong, M.; Wang, Z.; Li, Y. Generation of cylindrically polarized vector vortex beams with digital micromirror device. J. Appl. Phys. 2014, 116, 183105. [Google Scholar] [CrossRef]
- Tabiryan, N.V.; Serak, S.V.; Roberts, D.E.; Steeves, D.M.; Kimball, B.R. Thin waveplate lenses of switchable focal length—New generation in optics. Opt. Express 2015, 23, 25783–25794. [Google Scholar] [CrossRef] [PubMed]
- Strobelt, J.; Stolz, D.; Leven, M.; Soelen, M.V.; Kurlandski, L.; Abourahma, H.; McGee, D.J. Optical microstructure fabrication using structured polarized illumination. Opt. Express 2022, 30, 7308–7318. [Google Scholar] [CrossRef]
- Porfirev, A.; Khonina, S.; Ivliev, N.; Meshalkin, A.; Achimova, E.; Forbes, A. Writing and reading with the longitudinal component of light using carbazole-containing azopolymer thin films. Sci. Rep. 2022, 12, 3477. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Berberova-Buhova, N.; Nedelchev, L.; Mateev, G.; Nikolova, L.; Stoykova, E.; Ivanov, B.; Strijkova, V.; Hong, K.; Nazarova, D. Polarization Diffraction Gratings in PAZO Polymer Thin Films Recorded with Digital Polarization Holography: Polarization Properties and Surface Relief Formation. Photonics 2024, 11, 425. https://doi.org/10.3390/photonics11050425
Berberova-Buhova N, Nedelchev L, Mateev G, Nikolova L, Stoykova E, Ivanov B, Strijkova V, Hong K, Nazarova D. Polarization Diffraction Gratings in PAZO Polymer Thin Films Recorded with Digital Polarization Holography: Polarization Properties and Surface Relief Formation. Photonics. 2024; 11(5):425. https://doi.org/10.3390/photonics11050425
Chicago/Turabian StyleBerberova-Buhova, Nataliya, Lian Nedelchev, Georgi Mateev, Ludmila Nikolova, Elena Stoykova, Branimir Ivanov, Velichka Strijkova, Keehoon Hong, and Dimana Nazarova. 2024. "Polarization Diffraction Gratings in PAZO Polymer Thin Films Recorded with Digital Polarization Holography: Polarization Properties and Surface Relief Formation" Photonics 11, no. 5: 425. https://doi.org/10.3390/photonics11050425
APA StyleBerberova-Buhova, N., Nedelchev, L., Mateev, G., Nikolova, L., Stoykova, E., Ivanov, B., Strijkova, V., Hong, K., & Nazarova, D. (2024). Polarization Diffraction Gratings in PAZO Polymer Thin Films Recorded with Digital Polarization Holography: Polarization Properties and Surface Relief Formation. Photonics, 11(5), 425. https://doi.org/10.3390/photonics11050425




