Abstract
We propose a theoretical method for the deterministic shaping of quantum light via photon number state selective interactions. Nonclassical states of light are an essential resource for high-precision optical techniques that rely on photon correlations and noise reshaping. Notable techniques include quantum enhanced interferometry, ghost imaging, and generating fault-tolerant codes for continuous variable optical quantum computing. We show that a class of nonlinear-optical resonators can transform many-photon wavefunctions to produce structured states of light with nonclassical noise statistics. The devices, based on parametric down conversion, utilize the Kerr effect to tune photon-number-dependent frequency matching, inducing photon-number-selective interactions. With a high-amplitude coherent pump, the number-selective interaction shapes the noise of a two-mode squeezed cavity state with minimal dephasing, illustrated with simulations. We specify the requisite material properties to build the device and highlight the remaining material degrees of freedom which offer flexible material design.
1. Introduction
Systems that utilize quantum information resources generally take advantage of coherent macroscopic superposition and/or entanglement. The increased information density and sensitivity to measurements of such quantum states, compared to their classical counterparts, is central to their application in modern quantum information technologies like quantum key distribution [1,2], quantum computing [3,4,5], and metrology at the fundamental noise limit [6,7,8]. Efforts toward engineering the spatio-temporal profile of quantum states of light have already found great success [9,10,11]. This article focuses instead on shaping the noise statistics of quantum states of light for such applications. Both macroscopic superposition and entanglement are generically found in states supported by nonlinear systems [12,13]. However, optical nonlinearities are typically weak for closed systems. Much attention has therefore been paid to developing methods for generating quantum states of light which utilize wavefunction collapse as a source of nonlinear evolution, where a particular measurement outcome heralds the desired quantum state [14,15,16,17,18]. Though hugely successful, heralded state preparation is inherently non-deterministic, making sequential preparations low-probability events.
The approach presented here overcomes low-heralding success rates using the paradigm of deterministic generation of quantum states. Examples in the literature can be found where the probabilistic nature of measurement is circumvented [19,20,21,22,23,24,25,26,27,28,29,30,31].
One example utilizes the quantum Zeno effect [19,20,21]. By strongly coupling a specially engineered system to an environment, the state of the system is continuously projected to a subspace of states that are effectively uncoupled from the environment, called a decoherence free subspace (DFS). External driving fields may then evolve states deterministically and coherently within the DFS.
With the advent of epsilon-near-zero materials [22] and polariton-enhanced scattering, commonly facilitated by electronically induced transparency [23,24,25,26], large effective nonlinearities become increasingly realistic as well. When realized in a high-Q optical resonator, strong optical nonlinearities with relatively long evolution time and low loss facilitate deterministic quantum optical state engineering. Trapped atom and other quantum emitter systems show great promise for this application [20,21,27,28,29,30,31].
Such systems accomplish universal control of an oscillator state by relying on an array of emitters or by coupling to a single two-level emitter. With an array of quantum emitters, the quantum information content of a state of interest is first written onto the array, typically in a decoherence-free subspace, then mapped to super-radiant light-matter states which couple to an optical waveguide [20,21,27,28]. Alternatively, arbitrary state transformations may be realized in a cavity with a single quantum emitter by repeatedly addressing the emitter with a control beam to introduce a Berry phase to cavity field Fock states and applying coherent displacement operations to the cavity field in sequences prescribed within [29,30,31]. Notably, Krastanov et al. [30,31] utilize a dispersive coupling between the emitter and a microwave cavity field to realize a selective number-dependent arbitrary phase (SNAP) gate which selectively rotates the phase of each Fock state of the cavity field.
This work introduces an alternative technique for precision shaping of quantum noise statistics without the need for precise emitter engineering and addressing. We consider a material with first-, second-, and third-order electric susceptibilities at optical frequencies (it is straightforward to generalize our approach for nonperturbative constitutive relations) and show that when second- and third-order nonlinearities are comparable in strength, the optical Kerr effect alters the frequency matching condition for optical parametric oscillation such that the interaction between field states is strongly photon-number-dependent. Our analysis separates the phase-rotating interactions from the mode-mixing interactions, providing us a deeper intuition for the dynamics we observe. Specifically, we first solve the combined first- and third-order system exactly and study the second-order mode-mixing in the interaction picture. The general dynamical characteristics are illustrated and we utilize the effect to demonstrate a procedure for the deterministic generation of approximate Fock states, among other interesting states. General material constraints are highlighted and developed into figures of merit to guide the experimental realizations of this method.
2. Background
We begin with a brief discussion of electromagnetic field quantization. Dirac recognized that Hamiltonian mechanics have simple rules for canonical quantization, that Lagrangian mechanics are well suited for relativistic gauge invariant classical field theories, and that they both poorly handle what the other does well. So, to formulate relativistic quantum theory, he generalized Hamiltonian mechanics to handle systems with constraints [32]. His mechanics encode symmetries that are simple to write into a Lagrangian, into constraints on a Hamiltonian, recovering Hamilton’s equations of motion with a generalized Poisson bracket called the Dirac bracket. The canonical quantization of Dirac’s bracket reveals, in part, Dirac’s relativistic theory of quantum mechanics. Born and Infeld adopted Dirac’s procedure to show that Maxwell’s equations in the Coulomb gauge assume a Hamiltonian formulation [33,34] where the Hamiltonian is the classical field energy
and the fields obey a version of the canonical Dirac bracket relations,
with the second equation defining the transverse delta function (the transverse delta function captures the constraints on the field enforced by the Coulomb gauge. In a medium without free charges or free currents, Maxwell’s equations ensure that D and B are always transverse to the direction of radiation propagation, unlike E and H. Furthermore, since both D and B are divergenceless, so must be their commutator. The transverse delta function is consistent with these two properties. It has no divergence and acts as an ordinary delta function on transverse fields). According to Dirac’s canonical quantization, the field amplitudes are promoted to operators, and the Dirac brackets become commutators
Quesada et al. [35] later showed that, to correctly recover Maxwell’s equations in nonlinear dielectric media from the Born–Infeld Dirac brackets, it is imperative to consider the displacement field and magnetic flux density to be the fundamental dynamical variables. Here, ’fundamental’ indicates that D and B are Hermitian linear combinations of Bose operators, i.e., they are Boson fields, whereas the electric and magnetic fields E and H are generally higher polynomials of Bose operators. For modern derivations and perspectives of quantum field theory in linear dielectric media, see [36,37,38,39].
For a finite linear cavity, the eigenstates of the system are enforced by the dielectric structure and boundary conditions of the cavity. Let us restrict ourselves to one effective spatial dimension, scalar susceptibilities, and a single polarization of the field modes without loss of generality (our analysis depends only on the algebraic structure of the Hilbert space and the dynamics generated by the Hamiltonian, so is easily generalized to richer mode structures). This amounts to a single parameter family of eigenstates. Consider a uniform cavity of length L with periodic boundary conditions, as is the case for a micro-ring resonator [40]. The allowed wavenumbers, k, within the cavity are integer multiples of . The fields D and B are physical, therefore real-valued. Each may then be expanded with respect to the basis of eigenmodes in the following form:
where A represents the transverse cross-sectional area of the modes in the cavity (if the refractive index is not isotropic, A defines an effective cross-sectional area, discussed in [40]).
The field amplitudes of a single photon, —defined later—are determined such that the energy of a photon with well-defined momentum agrees with the Einstein energy of a photon, . Suppose a dispersive permitivity such that the Fourier components of the linear electric field and displacement field are related by . If the medium is dispersive, each frequency mode solves a different eigenvalue equation, so normalization requires special care [37]. We rescale the amplitude by the single photon amplitude, , and promote the amplitude variable to a Bose operator obeying the canonical commutation relations
The displacement field operator becomes
where we have adopted a common quantum optics phase convention of initial phase ; is the group velocity, and the refractive index of the mode with wave-vector k. The magnetic flux field operator obtains a similar form [37].
Having properly dealt with linear dispersion, the Hamiltonian for linear quantum optics takes the form of an infinite set of harmonic oscillators
Nonlinear Quantum Optics
We introduce nonlinear optics, assuming that the dispersion of nonlinear susceptibilities is negligible for frequency bands we are interested in. The electric field is related to the displacement field and polarization field, P, via [41]
We can recall from Equation (1) the electric field contribution to the field energy, . The energy term is handled in the linear part of the Hamiltonian upon quantization. The remaining interaction relays the effect of the nonlinear polarization .
We assume that the polarization at a point in space depends on the displacement field at that point, i.e., the response function is local. Expanding the nonlinear polarization in a power series of the displacement field amplitudes up to the third order, the part of the Hamiltonian associated with classical nonlinear dynamics is
where is the second-order displacement field susceptibility that is responsible for optical parametric oscillation (OPO)—often referred to as parametric down conversion. is the third-order displacement field susceptibility responsible for four effects: the two optical Kerr effects called self-phase modulation (SPM) and cross-phase modulation (XPM), a mode-mixing process called four-wave mixing (FWM), and a static-field-induced OPO. Both are defined by the power series expansion of the polarization field in terms of displacement field [40].
The ordinary nonlinear susceptibilities are defined analogously for the electric field [42], namely
Substituting the relation into Equation (10) and collecting terms with common powers of electric field, ignoring tensor structure and dispersion, yields the relations
3. Approach
We aim to show how strong Kerr nonlinearities affect OPO. The essential result is that photon-number-dependent frequency shifts from the Kerr effect generate a photon-number-dependent detuning in OPO. The number-dependent detuning is exploited for coherent deterministic number-selective shaping of noise statistics in select modes. To make this effect clear, we constrain our view to the subspace of three optical modes engaging in OPO, called signal, idler, and sum. We first solve the system exactly under the action of the sum of Hamiltonian terms that preserve photon number in each mode. Evolution under this Hamiltonian gives nontrivial structure to the time-dependent displacement field operator; it is scaled by a diagonal unitary operator with a frequency that is a function of the photon number operators. OPO is analyzed in the interaction picture, exhibiting photon-number-selective behavior. The nature of this behavior is discussed, and explored numerically in Section 4.1.
3.1. Eigenstates of Kerr Hamiltonian
The Hamiltonian from Equation (9) is responsible for two distinct photon number density-preserving processes, SPM and XPM, and a mode-mixing process, FWM. FWM is a rich effect, leading to optical frequency combs and soliton propagation in micro-resonators [43]. However, our aim is to study an entirely different phenomenon in the same environment, so we do not wish to handle these complications presently. We will suppose that the dispersion relation of our system is specified such that no FWM is phase-matched for the active modes.
Unlike FWM, SPM and XPM are always phase-matched. These effects, together with the linear Hamiltonian, dominate the phase dynamics of the system. The corresponding Hamiltonian is diagonal in the Fock basis and, equivalently, conserves photon number for each mode. Our present objective is to solve for the time evolution of the field operator under photon number density-preserving Hamiltonian such that , where , , and are defined in Equations (7) and (9). We later show how this time evolution affects , producing a photon-number-selective interaction under the right conditions. We will consider the dynamics of three modes interacting in the cavity: a sum, signal, and idler mode with frequencies and , respectively.
We assume permutation invariance of all susceptibilities and abbreviate the frequency dependence of Kerr susceptibilities (permutation invariance typically does not hold near resonance, where we expect our system to reside given the constraints derived later. However, accounting for variability in simply amounts to substituting the average in place of and does not qualitatively change the results). Furthermore, we uphold the rotating wave (secular) approximation and assume spatially constant third-order susceptibility. After ordering all permutations of the creation and annihilation operators to be simple powers of the mode number operators , the Hamiltonian pertaining to the sum, signal, and idler modes is
Heisenberg’s equation of motion, , tells us the time evolution for the field annihilation operators and . To condense our notation, let us define the Kerr frequencies
where are the frequencies of self-phase modulation and are the frequencies of cross-phase modulation. These frequencies are proportional to the classical Kerr frequency shifts in accordance with the relation where I is the classical intensity and is the mean photon number. The time evolution of each field annihilation operator under is
It should be noted that the exponentials above do not commute with the field annihilation operators. To further simplify our notation, we call , and use to represent the exponential operators on the right-hand side of Equation (14), such that
Substituting these operators into Equation (6) yields the time-dependent displacement field operator for the nonlinear field described by ,
The time-dependent displacement field operator is the essential result of this subsection and the starting point for our analysis in the following Section 3.2. Let us take a brief detour to understand how the operators affect optical pumping and derive our first constraint.
Pump Photon Blockade
The operators neatly quantify the photon blockade effect, reviewed in [26], which affects optical pumping of the resonator. To see this, consider a cavity pumped by a near-monochromatic beam that is near resonance to a cavity mode with wavenumber . As the photon number in the cavity increases from to , the frequency shifts by . If the frequency of the next excitation shifts out of the pump linewidth, the cavity will no longer be excited, i.e., additional photons are blockaded from entering by the photons already in the cavity. Consequently, obtaining a high cavity intensity requires a pump beam with a wide linewidth in the presence of very strong Kerr nonlinearities. However, a wide pump linewidth yields unwanted excitations, so it is best for the Kerr nonlinearities involving the pump frequency to be small.
If small Kerr frequencies at the pump frequency are challenging to achieve, we consider the following constraint: self-phase modulation by a positive susceptibility redshifts the frequency by . If , the largest photon number achievable in the cavity pumped by a beam with a spectral edge at some fraction f of is
When considering optical parametric oscillation in the next sections, we drive the sum frequency cavity mode with an external pump. It is most important that the external pump spectrum does not overlap with the signal and idler modes to avoid unwanted excitation. Therefore, it is necessary that and preferable that . We discuss later in Section 4.2, and simply note now, that a large coherent state for the sum mode minimizes dephasing and enhances OPO efficiency. Because unwanted excitations and high pump intensity are coincident, it is best for the Kerr nonlinearities involving the pump frequency to be negative, if not small.
3.2. Number-Selective Optical Parametric Oscillation
The previous section solved the Kerr Hamiltonian exactly and introduced the operators to simplify our analysis of optical parametric oscillation. With an exact time evolution for the Kerr photons in hand, we construct the Hamiltonian for number-selective optical parametric oscillation (NSOPO). In the interaction picture, the OPO Hamiltonian evolves via the photon number preserving propagator, . From Equation (9), we obtain the time-dependent OPO Hamiltonian in the interaction picture,
We assume the susceptibility is spatially local, spatially constant, and frequency permutation invariant (as is the case for , permutation invariance is not valid for the strong nonlinearities required of NSOPO. However, accounting for variability simply amounts to substituting the average in place of and does not qualitatively change the result). The time-dependent displacement field operators, Equation (16), are substituted into Equation (18). Terms of the form and are neglected by assuming the rotating wave approximation for the three modes, but the time dependence from the Kerr-induced frequency mismatch is preserved. All possible permutations of the three relevant mode contributions to the field operators are reordered to a common tractable form, accounting for the noncommutativity of a and . The simplified interaction Hamiltonian is thus
where h.c. denotes a Hermitian conjugate.
We suppose that the sum frequency mode is a high-amplitude coherent state such that . Then, we can reasonably replace the operator with the c-number without worrying much about dephasing effects. For example, if the shaping of signal and idler modes is done in a range of m photons, the purity of the manipulated quantum state is of the order of (See Section 4.2).
To simplify notation, we define the NSOPO complex squeezing parameter and OPO resonance detuning frequency such that
where
and
are the set of detuning weights for each photon number, as well as a static detuning .
The interaction Hamiltonian is now expressed compactly as
Without Kerr nonlinearities, non-degenerate parametric down-conversion generates two-mode squeezing between the signal and idler modes [44]. With Kerr nonlinearities, the squeezing parameter hosts a detuning oscillation with a photon-number-dependent frequency, making the two-mode squeezing amplitude dependent. Let us explore precisely how this feature affects the interaction.
The OPO detuning governs how number states experience two-mode squeezing. A simple, and very useful, case to study is when a large- coherent state is injected into the nonlinear cavity in the presence of a two-mode squeezed state of signal and idler frequencies. We choose to study NSOPO on a two-mode squeezed state rather than a single-mode state to highlight how noise shaping is identically present in the entangled signal and idler modes, though NSOPO may be realized with a single mode as well. Experimentally, NSOPO of a two-mode squeezed state would require a method for coherently injecting the state into the nonlinear cavity initially in the vacuum state. Acknowledging the technological challenge (this may be realized, for example, with an acousto-optic modulator), we will assume it is possible and investigate its consequences.
We assume an initial two-mode squeezed state—a state which is a superposition of all equal populations of signal and idler photons. Evident from the interaction operator , the difference in signal and idler photon numbers is a conserved quantity, so the state remains a superposition of equal photon numbers for all times, much less than the cavity decay time. When , the OPO detuning is independent of the sum frequency photon number and NSOPO is coherently driven by the sum frequency beam. Each OPO interaction event will decrement or increment the signal and idler photon numbers by one, transporting probability amplitude along the space of states. Adjacent states see a difference in detuning of
Let us suppose there is a photon number, , such that the detuning is minimal. We call the shape center. Then, the OPO Hamiltonian in Dirac notation takes the form
This Hamiltonian generates a particularly interesting evolution when and are of similar magnitude; however, it is challenging to describe analytically. We explore this behavior in the following section.
4. Results and Discussions
In the previous section, we developed a theoretical method for directly targeting photon number states to coherently shape the quantum statistics of an optical field in a cavity. In the following section, we numerically simulate the model and illustrate how the parameters can be controlled to generate quantum states with useful structure. The constraints established here and in Section 3 are elaborated on and brought together to determine what regions of parameter space are viable for experimental realization.
4.1. Simulations
The time-dependent Schrödinger equation corresponding to the interaction Hamiltonian, Equation (26), is numerically evolved with a Crank–Nicolson method, which preserves unitarity. Figure 1 reveals the characteristic behavior of NSOPO. It shows that probability amplitude tends to coalesce around number states separated by a spacing
where states see constructive interference from two-mode squeezing. These peaks rapidly fall off in amplitude when near the shape center, but fall off more slowly when away from the shape center maintaining a wide tail in their height distribution. The peak heights increase monotonically with until reaching a maximum, after which the peak begins to wind itself and develops a complicated structure.
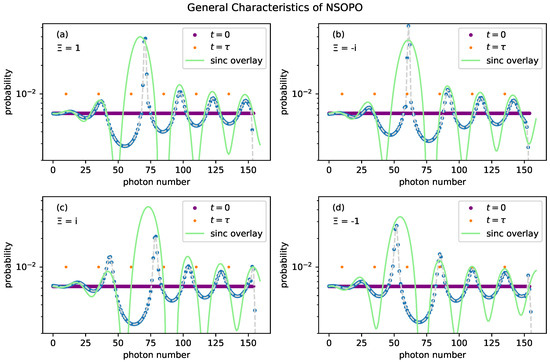
Figure 1.
General characteristics of NSOPO. In each plot, the state is initially a uniform real-valued distribution. The plots differ only in the phase of the NSOPO complex squeezing parameters . For all plots, the gouge center is , the Kerr detuning , and the evolution time . Orange dots are spaced by the predicted peak spacing, , and aligned with the shaping center. The green curve shows a first-order approximation of shaping that follows the peak positions and magnitude closely. The blue curve is the shaped photon probability distribution resulting from an initial uniform distribution.
The peak nearest the shape center deviates from periodic spacing, consequently shifting the pattern for states with a higher photon number. The location of the central peak depends on the phase of the NSOPO squeezing parameter . For , the peak is centered on the shape center. For , there is a deep trough at the shape center with the nearest peaks equidistant to the left and right. For , the nearest peak and trough are to the right and left (left and right) of the shape center. The plots in Figure 1 underlay the function
which approximately replicates the height and location of each peak, breaking accuracy at the central peak. This function is obtained by integrating the Hamiltonian over time and acts as a more tractable guideline for engineering states with shaping.
These shaping principles can be applied in several ways. Setting such that the shape center is aligned with the peak of a state and the peak spacing s to be greater than the width of the state, the photon number probability will coalesce into an approximate Fock state. Figure 2a illustrates this process, generating a state with signal photon number probabilities , . Alternatively, if the shape center is set far from the concentration of initial state probabilities, clean periodic oscillations in photon number probabilities, with a period s, are introduced into the state. Figure 2b–d illustrate this process: (b) shows precision shaping of a coherent state with ; (c) is the same as (b) but acting on a two-mode squeezed vacuum; (d) shows shaping with .
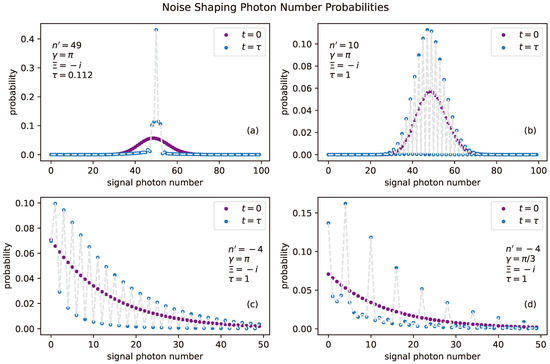
Figure 2.
Examples of photon probability shaping offered by NSOPO. (a) An approximate Fock state of accomplished by placing the shaping center on the peak of an initial coherent state with an amplitude of . (b) A precision shaping of the same coherent state. Parameter is chosen such that peak spacing s is two photons. (c) A two-mode squeezed vacuum state with . (d) A two-mode squeezed vacuum with .
In tandem with photon number probabilities, NSOPO offers control over states in optical phase space. The following demonstrates an interesting case of this control: generating a family of displaced Schrödinger’s cats with a single operation. It is important to remember that, in the Schrödinger picture, the modes experience self-phase modulation and cross-phase modulation via the Kerr effect. Introducing the condition into Equation (12), we see that the term of the Hamiltonian
generates nonlinear dynamics for the signal and idler modes. Noting that N is an integer, we see that states of a single mode are periodic in time t when each Kerr frequency satisfies , with m an integer. For simple rational values of m, the evolution maps coherent states to generalized coherent states [12].
We extend this argument to the two-mode squeezed state, recalling . We choose a preferred final state by selecting m to satisfy
Equation (27) provides a similar constraint regarding NSOPO peak spacing. If we suppose , then , making Equations (30) and (27) the same constraint with . Setting , we obtain a four-phase Schrödinger cat state. Figure 3 shows the action of NSOPO on a coherent state, (a), that is split into a generalized four-phase Schrödinger cat state, (b). Depending on the phase , NSOPO restricts the amplitude of the cat to two of four phases, shown in (c–f). The axes in each plot are independent phase space quadratures of the displacement field. Not shown in Figure 3, shifting the shape center by one rotates the action of NSOPO among the operations shown in (c–f). Namely, under , the plots map to each other according to . This behavior alludes to efficient quantum logic gates for macroscopic quantum states, though further investigation is needed to understand the range of this capability.
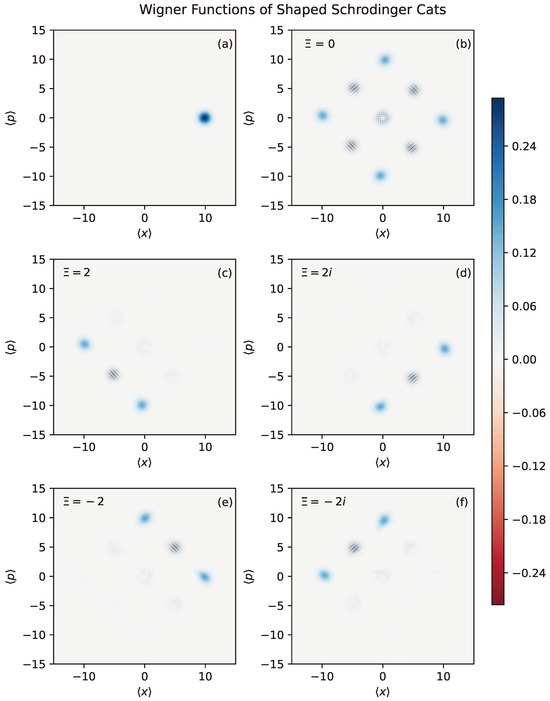
Figure 3.
(a) Wigner function of an initial coherent state of amplitude . (b) The coherent state subject to Kerr rotation without any NSOPO. (c–f) The state shaped with NSOPO complex squeezing parameter . In all plots, blue regions are positively valued and red regions are negative. Every state is shaped with parameters , and . As the phase of is varied by increments of , number-selective shaping changes predictably.
Figure 4 shows the effect of incoherent loss on the generation of an approximate Fock state, similar to that shown in Figure 2a. In this instance, an initial product state of a signal/idler two-mode coherent state with amplitude and a large coherent pump state is evolved according to the local Lindblad master equation
where and represents the incoherent decay rate of the cavity at the signal and idler frequencies.
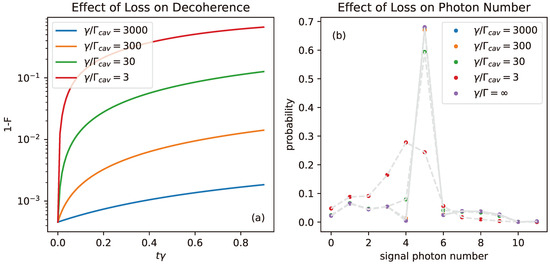
Figure 4.
Both plots present data from a simulation generating an approximate N = 5 Fock state in the presence of incoherent loss. The state is evolved from an initial two-mode squeezed coherent state of amplitude . The Hamiltonian parameters are , , and . Plot (a) shows the growth of quantum infidelity with respect to reciprocal NSOPO peak spacing . Each curve represents a different value of the strength-to-loss ratio where is the the adjacent state detuning and is the decay rate of the cavity at the signal and idler frequencies. Plot (b) shows the effect of loss on corresponding photon number probabilities.
To characterize the viability of the system for generating useful and pure quantum states, we introduce a parameter that is similar in spirit to cooperativity [45]. Cooperativity is defined for light-matter systems with specific quantum models of the material and quantifies the ratio of the light-matter interaction rate to the loss rate of the system. Our theory is derived from a constitutive relation, Equation (10), so it does not offer the detail required to provide the exact cooperativity. However the strength-to-loss ratio of the adjacent state detuning , i.e., the Kerr frequency of the signal-idler state, and the incoherent decay rate of the cavity at the signal and idler frequencies , serves a similar role.
Plot (a) shows the growth of quantum infidelity with respect to reciprocal NSOPO peak spacing . Each curve represents a different value of the strength-to-loss ratio . For , infidelity scales linearly with . For , , and , we find the numerical result
This inverse proportionality between the strength-to-loss ratio and infidelity is substantial. Interestingly, generating approximate Fock states of higher photon numbers require a smaller , such that the spacing is larger, thus high Fock state generation demands less of the strength-to-loss ratio for the same quantum fidelity.
4.2. Pump Dephasing
A key challenge to overcome for preserving the quantum coherence of noise-shaped states of light is to mitigate the dephasing effects of the pump beam. The two criteria to satisfy are a strong pump beam, quantified below, and a vanishing detuning weight for the pump frequency, . Specifically, we demand that the detuning weights satisfy
A vanishing pump detuning weight ensures that the desired OPO detuning is independent of pump photon number, rendering NSOPO not number-selective for the pump field. This condition is important because a pump photon-number-selective process implies that far fewer states in the entire Hilbert space contribute to OPO, dramatically decreasing the efficiency of the process. Furthermore, if the interactions were number-selective for the pump, the state of the pump field would vary dramatically for different possible interaction histories, resulting in strong dephasing.
When NSOPO is not number-selective for the pump, the OPO interaction is simply a displacement operation, which minimally disturbs the structure of the pump field. To illustrate, let us consider the state time-evolved under the OPO interaction with . The result is a superposition of products of shifted coherent states in the sum frequency and incremented number states in the signal and idler. The coherent states are, at most, shifted by a displacement corresponding to the maximum photon number change of the signal and idler. For large amplitude coherent states, shifts in the coherent states on the scale of shifts in the signal and idler yield minimal deviations in the overlap between the coherent pump states.
To obtain a generic measure of state purity, we note that the histories of Fock state amplitudes are carried along with NSOPO peaks. The pump beam coherent states that are entangled with either peak acquire dephasing contributions from pump beam coherent states with a mean shifted by the interval of photon numbers the NSOPO peak has traveled over its evolution. This entanglement between the pump, signal, and idler contributes a dephasing in the signal and idler density matrix. The purity of the signal/idler density matrix, , is well approximated by the squared overlap of the shifted and unshifted pump beam states. Thus, for a pump beam in a coherent state , signal/idler in initial two-mode squeezed coherent state , and spacing s, the purity measure is
4.3. Summary of Constraints and Figures of Merit
Five conditions must be met in order to realize coherent NSOPO. The following subsections summarize each condition, roughly ordered from simplest to most difficult to satisfy:
- 1.
- In the presence of strong Kerr nonlinearities, exciting a cavity pump field to high intensity requires a broad external pump linewidth. However, a broad external pump will excite superfluous modes in the system. Let us suppose the pump beam is a broad spectrum coherent state . To mitigate unintended interactions from modes above the signal and idler frequency, we restrict the magnitude of the sum mode self-phase modulation frequency by Equation (17) to obtainThus, it is essential for to be small or negative.
- 2.
- The purity measure Equation (34) indicates the constraintThe precision of noise-shaping is limited by the relative uncertainty of the signal/idler photon number noise with respect to the pump photon number noise and is generally easy to control.
- 3.
- Numerical simulations place useful values of in the range from to 10. For an order of magnitude estimate of this constraint, let us consider a case where and . Using the definitions of , , and g from Equations (6), (13), (21), and (25),The quantity is the single photon displacement field amplitude in Equation (6). Careful use of Equation (11) relates the displacement field susceptibilities to the more commonly measured electric field susceptibilities. Expanding the ratio with the definitions of each frequency yieldsThis criterion is straightforward to satisfy in real materials. For however large the magnitude of is, the strength of OPO can be increased with the intensity of the pump beam and the quantization volume.
- 4.
- As discussed in SubSection 4.2 above, shaping maintains quantum coherence if the pump field detuning weight vanishes, . Equation (33) provides a qualitative expression of the requisite smallness of . The upshot is that greater pump power requires higher precision in the proximity of to zero. This condition is easiest to satisfy if Kerr frequencies related to the pump are independently small, which is challenging if the other Kerr frequencies are to be incredibly large. Appendix A discusses a class of systems that can satisfy exactly this scenario by generating nonlinearities on resonance with the signal and idler, and off-resonance with the pump.
- 5.
- To apply the theory developed in this paper, all shaping should occur on a time scale shorter than that defined by the acceptable infidelity and desired spacing according towhere is the cavity decay time. This constrains the lower bound on the Kerr frequencies and . Let us assume and for simplicity. Restating the numerical result for the high-fidelity regime Equation (32), but substituting in the cavity lifetime , we obtainSubstituting from Equation (6) into the definition of the Kerr frequencies g from Equation (13), and relating to with Equation (11), we find that the strength-to-loss ratio isFinally, substituting in the classical form of the nonlinear refractive index , we obtain a figure of merit for NSOPO that is proportional to the strength-to-loss ratio,This figure of merit commands our attention; it is the most challenging constraint to practically satisfy among those in this list. Candidate systems will have large at the signal and idler frequencies and small at the sum frequency. In Appendix A, we show that compliance is likely attainable by addressing the state of the art for achieving strong nonlinearities with minimal loss and controllable group velocity and showing that these systems perform well within the boundary of the constraints.
4.4. Control Parameters
The shape center is controlled by modulating the linear refractive index of the material, and therefore the static detuning parameter , in time. To understand the extent of modulation we may ask, what are the possible rates of change for the shape center with respect to refractive index shifts? Let us recall the expression for , (23), which contains the frequency difference . In the simplest case, the frequencies are related to the fixed wavenumbers of each mode by
where is maximal, so is . Therefore, it is desirable for the refractive index of each mode to be near zero. This conclusion is agreeable with the figures of merit derived above. One can change the refractive index of the material by, for example, introducing a static field, or by utilizing acoustic oscillations in the cavity material.
The NSOPO squeezing parameter, (21), is primarily controlled by modulating the amplitude and phase of the pump beam. In practice, one should be aware that changing the shape center affects the strength of NSOPO in three ways:
- 1.
- Equation (26) shows that OPO strength is scaled by , where m is the signal photon number of the state being acted upon. Thus, the OPO strength is scaled by the shape center.
- 2.
- In some materials, e.g., organic materials, changing a static field to modulate the refractive index will reorient molecules affecting .
- 3.
- Static fields will also introduce a contribution to OPO strength .
Ultimately, determining the parameters for preparing a particular state will be a matter of empirical tuning guided by rough numerical estimates.
A final note on state control: if the static field can be modulated on a time scale faster than the state preparation time , more complicated shaping of the field noise statistics can be accomplished, beyond fixed shaping parameters.
5. Conclusions
We have proposed a novel method for the deterministic manipulation of quantum states of light. The underlying theoretical tools required for its implementation are developed and the physical constraints for its practical implementation described. The method utilizes strong Kerr nonlinearities to introduce photon number dependence into the frequency matching condition for optical parametric oscillation, rendering the OPO interaction photon-number-selective. Number-selective interactions expand the capabilities of current CV quantum optical state control and preparation techniques by introducing targeted deterministic manipulations to subspaces of a light field’s Fock space.
Simulations indicate the generation of highly nonclassical quantum states of light. We establish five necessary conditions to realize NSOPO in practice, which will aid the search for candidate materials and optical configurations. The constraints are consistent with a common figure of merit, , expressed in Equation (41). The best materials for NSOPO will have large at the signal and idler frequencies, and small at the sum frequency. The constraints can likely be realized in specialized systems that are driven into electronically induced transparency and spontaneously generated coherence.
Future research will aim to realize the requisite constraints in detailed models of highly resonant cavity light coupled with matter systems, with special attention paid to dark resonances. From specific models, the approach derived in this paper will be adapted to accommodate Hamiltonians beyond the simple cubic and quartic interactions treated above. These new models will be used to guide experimental design and to search for novel sculpted states. Future research will also investigate generation of entanglement between two uncorrelated signal and idler states, and study how noise shaping can be generalized to pulses of light, in particular to solitons in optical resonators with attention paid to mitigating the dephasing effects of quantum soliton propagation.
Author Contributions
Conceptualization, G.D.C. and M.G.K.; Data curation, G.D.C.; Formal analysis, G.D.C. and M.G.K.; Funding acquisition, M.G.K.; Investigation, G.D.C. and M.G.K.; Methodology, G.D.C. and M.G.K.; Project administration, M.G.K.; Resources, M.G.K.; Software, G.D.C.; Supervision, M.G.K.; Validation, G.D.C.; Visualization, G.D.C.; Writing—original draft, G.D.C.; Writing—review and editing, G.D.C. and M.G.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The code for simulations and original data presented in the study are openly available in the GitHub repository https://github.com/GarrettCompton/NSOPO.git.
Acknowledgments
We thank Ned and Nancy Wogman for the Wogman Physics Fellowship, the William J. Shelton Scholarship, and the donors to the Innovative Physics Fund and the Department of Physics for support.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
- The following abbreviations are used in this manuscript:
| OPO | Optical parametric oscillation |
| SPM | Self-phase modulation |
| XPM | Cross-phase modulation |
| FWM | Four-wave mixing |
| NSOPO | Number-selective optical parametric oscillation |
| TMSV | Two-mode squeezed vacuum |
| ENZ | Electronically induced transparency |
| CV | Continuous variable |
| DFS | Decoherence-free subspace |
| SGC | Spontaneously generated coherence |
Appendix A
The present theoretical paper describes how one might achieve the deterministic shaping of a Fock state. This appendix gives a plausibility argument that the required figure of merit is achievable. However, meeting the constraints discussed in Section 4.3 may require new materials and device architectures. Here, we individually consider the measured properties of known material systems to estimate a reasonable range of the figure of merit.
EIT is an example of a process that exhibits the requisite properties for NSOPO. Schmidt and Imamoglu [26] showed that a four-level system can be configured to obtain a giant cross-phase modulation strength. With the additional presence of spontaneously generated coherence (SGC), which can be accomplished in a five-level system [46], the EIT window can be shifted such that the Kerr nonlinearity is maximal when absorption is near zero. Furthermore, the five-level system proposed offers direct control over the group velocity, which ranges from highly sub- to super-luminal and with photon-number-dependent behavior [47].
Obtaining giant nonlinearities in near resonant systems with EIT gives us two other desirable features for NSOPO. The peaks of the linear and nonlinear susceptibilities are sufficiently sharp near resonance to make FWM minimal due to a rapidly increasing phase mismatch and rapidly decaying interaction strength. In addition, off-resonant nonlinearities will be comparatively weak. Such a system can be tuned so that the sum frequency is off resonance with the material while the signal and idler are on resonance. Then, Constraint (33) is satisfied by virtue of small Kerr nonlinearities at the pump frequency and FWM can be reliably neglected for all modes.
Bang and Doai, [46,47], report values of self and/or cross-phase modulating nonlinear index in a gas Rb with density atoms/ on the order of
In principle, the atom density can be made orders of magnitude greater in a solid-state device. With modest concentrations of the active molecule on the order of molecules/ [48], the third-order susceptibility for non-interacting molecules is enhanced in proportion to the molecular density, increasing the nonlinear index to
Supposing that the signal and idler wavelengths are on the order of 1 m, the resonator cross-sectional area is 1 m × 1 m, and the group velocity of the signal and idler are both c. Then, the figure of merit is to within an order of magnitude given by
For a length on the order of and cavity quality factor on the order [49,50], the infidelity is . This scenario is the upper boundary of feasible materials of this type, so we do not expect to reach it in practice, but it offers several orders of magnitude of leeway for trade-offs in designing materials and devices that shape photon statistics.
While this rough calculation shows the plausibility of deterministic shaping given known materials’ properties, an important question remains as to the plausibility of making a solid-state waveguide device. Realizing the benefits of EIT and SGC in a solid-state waveguide device would require a material that, in analogy, is made with atoms that do not strongly interact with each other. A possible material system is a dye-doped polymer, which can be fabricated into waveguides, and whose linear and nonlinear optical properties can be controlled with atom/molecule doping.
One way to incorporate the active atom/molecule into a solid is to use a polymer, sol-gel host, or other host—which would lead to higher dopant concentration, thus a larger nonlinearity [51]. Such materials can be made into thin films and fibers [52] and photolithographic techniques can be used to make waveguide resonators [53]. Interactions between the host material and the atom/molecule can be minimized by using molecular pincers—called chelates—to isolate them. Chelated rare-earth atoms are commonly used in amplifiers [54]. The ability to get higher densities of active molecules to increase nonlinearity, the flexibility of choosing molecules for their spectral properties, the shielding from the environment to mitigate dephasing through chelation, and the reduction of inhomogeneous broadening by cooling the material all provide the means for optimization.
Each of these approaches presents challenges, but designing a device is far beyond the scope of this paper. However, the numbers suggest that making a device for the deterministic shaping of quantum light statistics is possible and our work defines the material requirements that will guide future experimental efforts.
References
- Sangouard, N.; Simon, C.; Gisin, N.; Laurat, J.; Tualle-Brouri, R.; Grangier, P. Quantum repeaters with entangled coherent states. J. Opt. Soc. Am. B 2010, 27, A137. [Google Scholar] [CrossRef]
- Brask, J.B.; Rigas, I.; Polzik, E.S.; Andersen, U.L.; Sørensen, A.S. Hybrid Long-Distance Entanglement Distribution Protocol. Phys. Rev. Lett. 2010, 105, 160501. [Google Scholar] [CrossRef]
- Sakaguchi, A.; Konno, S.; Hanamura, F.; Asavanant, W.; Takase, K.; Ogawa, H.; Marek, P.; Filip, R.; Yoshikawa, J.I.; Huntington, E.; et al. Nonlinear feedforward enabling quantum computation. Nat. Commun. 2023, 14, 3817. [Google Scholar] [CrossRef]
- Gottesman, D.; Kitaev, A.; Preskill, J. Encoding a qubit in an oscillator. Phys. Rev. A 2001, 64, 012310. [Google Scholar] [CrossRef]
- Lidar, D.A.; Chuang, I.L.; Whaley, K.B. Decoherence-Free Subspaces for Quantum Computation. Phys. Rev. Lett. 1998, 81, 2594–2597. [Google Scholar] [CrossRef]
- Polino, E.; Valeri, M.; Spagnolo, N.; Sciarrino, F. Photonic quantum metrology. AVS Quantum Sci. 2020, 2, 024703. [Google Scholar] [CrossRef]
- Oszmaniec, M.; Augusiak, R.; Gogolin, C.; Kołodyński, J.; Acín, A.; Lewenstein, M. Random Bosonic States for Robust Quantum Metrology. Phys. Rev. X 2016, 6, 041044. [Google Scholar] [CrossRef]
- Unternährer, M.; Bessire, B.; Gasparini, L.; Perenzoni, M.; Stefanov, A. Super-resolution quantum imaging at the Heisenberg limit. Optica 2018, 5, 1150–1154. [Google Scholar] [CrossRef]
- Vasilev, G.S.; Ljunggren, D.; Kuhn, A. Single photons made-to-measure. New J. Phys. 2010, 12, 063024. [Google Scholar] [CrossRef]
- Morin, O.; Körber, M.; Langenfeld, S.; Rempe, G. Deterministic Shaping and Reshaping of Single-Photon Temporal Wave Functions. Phys. Rev. Lett. 2019, 123, 133602. [Google Scholar] [CrossRef]
- Huang, Y.; Qi, Z.; Yang, Y.; Li, Y.; Sun, Y.; Tang, Y.; Ni, F.; Li, L.; Zheng, Y.; Chen, X. Frequency-insensitive spatiotemporal shaping of single photon in multiuser quantum network. npj Quantum Inf. 2023, 9, 83. [Google Scholar] [CrossRef]
- Yurke, B.; Stoler, D. Generating quantum mechanical superpositions of macroscopically distinguishable states via amplitude dispersion. Phys. Rev. Lett. 1986, 57, 13–16. [Google Scholar] [CrossRef]
- Kolesnikow, X.C.; Bomantara, R.W.; Doherty, A.C.; Grimsmo, A.L. Gottesman-Kitaev-Preskill state preparation using periodic driving. arXiv 2023, arXiv:2303.03541. [Google Scholar]
- Asavanant, W.; Nakashima, K.; Shiozawa, Y.; Yoshikawa, J.I.; Furusawa, A. Generation of highly pure Schrödinger’s cat states and real-time quadrature measurements via optical filtering. Opt. Express 2017, 25, 32227. [Google Scholar] [CrossRef]
- Takase, K.; Yoshikawa, J.I.; Asavanant, W.; Endo, M.; Furusawa, A. Generation of optical Schrödinger cat states by generalized photon subtraction. Phys. Rev. A 2021, 103, 013710. [Google Scholar] [CrossRef]
- Chen, Y.R.; Hsieh, H.Y.; Ning, J.; Wu, H.C.; Chen, H.L.; Shi, Z.H.; Yang, P.; Steuernagel, O.; Wu, C.M.; Lee, R.K. Generation of heralded optical ‘Schroedinger cat’ states by photon-addition. arXiv 2023, arXiv:2306.13011. [Google Scholar]
- Fukui, K.; Endo, M.; Asavanant, W.; Sakaguchi, A.; Yoshikawa, J.I.; Furusawa, A. Generating the Gottesman-Kitaev-Preskill qubit using a cross-Kerr interaction between squeezed light and Fock states in optics. Phys. Rev. A 2022, 105, 022436. [Google Scholar] [CrossRef]
- Ben Hayun, A.; Reinhardt, O.; Nemirovsky, J.; Karnieli, A.; Rivera, N.; Kaminer, I. Shaping quantum photonic states using free electrons. Sci. Adv. 2021, 7, eabe4270. [Google Scholar] [CrossRef]
- Beige, A.; Braun, D.; Tregenna, B.; Knight, P.L. Quantum computing using dissipation to remain in a decoherence-free subspace. Phys. Rev. Lett. 2000, 85, 1762–1765. [Google Scholar] [CrossRef]
- González-Tudela, A.; Paulisch, V.; Chang, D.E.; Kimble, H.J.; Cirac, J.I. Deterministic Generation of Arbitrary Photonic States Assisted by Dissipation. Phys. Rev. Lett. 2015, 115, 163603. [Google Scholar] [CrossRef]
- Verstraete, F.; Wolf, M.M.; Ignacio Cirac, J. Quantum computation and quantum-state engineering driven by dissipation. Nat. Phys. 2009, 5, 633–636. [Google Scholar] [CrossRef]
- Vertchenko, L.; Nikitin, M.; Lavrinenko, A. Near-zero-index platform in photonics: Tutorial. J. Opt. Soc. Am. B 2023, 40, 1467. [Google Scholar] [CrossRef]
- Camacho-Guardian, A.; Bastarrachea-Magnani, M.; Pohl, T.; Bruun, G.M. Strong photon interactions from weakly interacting particles. Phys. Rev. B. 2022, 106, L081302. [Google Scholar] [CrossRef]
- Ribeiro, R.F.; Campos-Gonzalez-Angulo, J.A.; Giebink, N.C.; Xiong, W.; Yuen-Zhou, J. Enhanced optical nonlinearities under collective strong light-matter coupling. Phys. Rev. A 2021, 103, 063111. [Google Scholar] [CrossRef]
- Hu, X.X.; Zhao, C.L.; Wang, Z.B.; Zhang, Y.L.; Zou, X.B.; Dong, C.H.; Tang, H.X.; Guo, G.C.; Zou, C.L. Cavity-enhanced optical controlling based on three-wave mixing in cavity-atom ensemble system. Opt. Express 2019, 27, 6660–6671. [Google Scholar] [CrossRef]
- Imamoḡlu, A.; Schmidt, H.; Woods, G.; Deutsch, M. Strongly interacting photons in a nonlinear cavity. Phys. Rev. Lett. 1997, 79, 1467–1470. [Google Scholar] [CrossRef]
- Porras, D.; Cirac, J.I. Collective generation of quantum states of light by entangled atoms. Phys. Rev. A 2008, 78, 053816. [Google Scholar] [CrossRef]
- Perarnau-Llobet, M.; González-Tudela, A.; Cirac, J.I. Multimode Fock states with large photon number: Effective descriptions and applications in quantum metrology. Quantum Sci. Technol. 2020, 5, 025003. [Google Scholar] [CrossRef]
- Law, C.K.; Eberly, J.H. Arbitrary Control of a Quantum Electromagnetic Field. Phys. Rev. Lett. 1996, 76, 1055–1058. [Google Scholar] [CrossRef]
- Krastanov, S.; Albert, V.V.; Shen, C.; Zou, C.L.; Heeres, R.W.; Vlastakis, B.; Schoelkopf, R.J.; Jiang, L. Universal control of an oscillator with dispersive coupling to a qubit. Phys. Rev. A 2015, 92, 040303. [Google Scholar] [CrossRef]
- Heeres, R.W.; Vlastakis, B.; Holland, E.; Krastanov, S.; Albert, V.V.; Frunzio, L.; Jiang, L.; Schoelkopf, R.J. Cavity State Manipulation Using Photon-Number Selective Phase Gates. Phys. Rev. Lett. 2015, 115, 137002. [Google Scholar] [CrossRef]
- Dirac, P.A.M. Generalized Hamiltonian Dynamics. Can. J. Math. 1950, 2, 129–148. [Google Scholar] [CrossRef]
- Born, M.; Infeld, L. On the quantization of the new field equations I. Proc. R. Soc. Lond. 1934, 147, 522–546. [Google Scholar]
- Born, M.; Infeld, L. Foundations of the new field theory. Proc. R. Soc. Lond. A Math. Phys. Sci. 1934, 144, 425–451. [Google Scholar] [CrossRef]
- Quesada, N.; Sipe, J.E. Why you should not use the electric field to quantize in nonlinear optics. Opt. Lett. 2017, 42, 3443. [Google Scholar] [CrossRef]
- Bhat, N.A.R.; Sipe, J.E. Hamiltonian treatment of the electromagnetic field in dispersive and absorptive structured media. Phys. Rev. A 2006, 73, 063808. [Google Scholar] [CrossRef]
- Raymer, M.G. Quantum theory of light in a dispersive structured linear dielectric: A macroscopic Hamiltonian tutorial treatment. J. Mod. Opt. 2020, 67, 196–212. [Google Scholar] [CrossRef]
- Hillery, M.; Mlodinow, L.D. Quantization of electrodynamics in nonlinear dielectric media. Phys. Rev. A Gen. Phys. 1984, 30, 1860–1865. [Google Scholar] [CrossRef]
- Drummond, P.D.; Hillery, M. The Quantum Theory of Nonlinear Optics; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Quesada, N.; Helt, L.; Menotti, M.; Liscidini, M.; Sipe, J. Beyond photon pairs: Nonlinear quantum photonics in the high-gain regime. Adv. Opt. Photonics 2022, 14, 291–403. [Google Scholar] [CrossRef]
- Jackson, J.D. Electrodynamics, Classical. In Digital Encyclopedia of Applied Physics; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2003. [Google Scholar]
- Boyd, R.W. Nonlinear Optics, 4th ed.; Academic Press: San Diego, CA, USA, 2020. [Google Scholar]
- Pasquazi, A.; Peccianti, M.; Razzari, L.; Moss, D.J.; Coen, S.; Erkintalo, M.; Chembo, Y.K.; Hansson, T.; Wabnitz, S.; Del’Haye, P.; et al. Micro-combs: A novel generation of optical sources. Phys. Rep. 2018, 729, 1–81. [Google Scholar] [CrossRef]
- Alam, M.; Mandal, S.; Wahiddin, M.R. Squeezing, mixed mode squeezing, amplitude squared squeezing and principal squeezing in a non-degenerate parametric oscillator. Optik 2018, 157, 1035–1052. [Google Scholar] [CrossRef]
- Kroeze, R.M.; Marsh, B.P.; Lin, K.Y.; Keeling, J.; Lev, B.L. High Cooperativity Using a Confocal-Cavity–QED Microscope. PRX Quantum 2023, 4, 020326. [Google Scholar] [CrossRef]
- Bang, N.H.; Van Doai, L. Colossal Kerr nonlinearity without absorption in a five-level atomic medium. Sci. Rep. 2024, 14, 1554. [Google Scholar] [CrossRef]
- Van Doai, L. The effect of giant Kerr nonlinearity on group velocity in a six-level inverted-Y atomic system. Phys. Scr. 2020, 95, 035104. [Google Scholar] [CrossRef]
- Singer, K.D.; Kuzyk, M.G.; Holland, W.R.; Sohn, J.E.; Lalama, S.J.; Comizzoli, R.B.; Katz, H.E.; Schilling, M.L. Electro-optic phase modulation and optical second-harmonic generation in corona-poled polymer films. Appl. Phys. Lett. 1988, 53, 1800–1802. [Google Scholar] [CrossRef]
- Cheng, X.; Hong, J.; Spring, A.M.; Yokoyama, S. Fabrication of a high-Q factor ring resonator using LSCVD deposited Si3N4 film. Opt. Mater. Express 2017, 7, 2182–2187. [Google Scholar] [CrossRef]
- Ling, T.; Chen, S.L.; Guo, L.J. Fabrication and characterization of High Q polymer micro-ring resonator and its application as a sensitive ultrasonic detector. Opt. Express 2011, 19, 861–869. [Google Scholar] [CrossRef]
- Dirk, C.W.; Kuzyk, M.G. Squarylium dye-doped polymer systems as quadratic electrooptic materials. Chem. Mater. 1990, 2, 4–6. [Google Scholar] [CrossRef]
- Welker, D.J.; Tostenrude, J.; Garvey, D.W.; Canfield, B.K.; Kuzyk, M.G. Fabrication and characterization of single-mode electro-optic polymer optical fiber. Opt. Lett. 1998, 23, 1826–1828. [Google Scholar] [CrossRef]
- Zheng, J.; Lu, M.; Wagner, C.J.; Cunningham, B.T.; Eden, J.G. Spectral characteristics of single and coupled microresonator lasers comprising a replica-molded Bragg grating and dye-doped polymer. J. Opt. Soc. Am. B 2012, 29, 209. [Google Scholar] [CrossRef]
- Koeppen, C.; Yamada, S.; Jiang, G.; Garito, A.F.; Dalton, L.R. Rare-earth organic complexes for amplification in polymer optical fibers and waveguides. J. Opt. Soc. Am. B 1997, 14, 155. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).