Optimization of the Spot Spacings for Reducing Roughness in Laser-Induced Optical Breakdown Processes for Corneal Laser Vision Correction

Abstract

The aim of this work is to implement an algorithm that simulates a simplified cutting surface based on laser-induced optical breakdown (LIOB). The algorithm includes the definition of a possible positioning of the laser pulses and calculation of the roughness for different parameter settings (including LIOB threshold, pulse energies, and spot spacings) as the difference between simulated and ideal target cut (local differences within the cut, i.e., the waviness of the simulated cut vs. the homogeneity of the ideal target cut). Furthermore, optimizations of specific variables, such as spot distance (along the pathway), track distance (between lines/tracks), and pulse energy, are performed. The simulations suggest that lower pulse energies (well above the LIOB threshold) combined with asymmetric spacings (spot-to-track distance ratio >> 1) may be effective to lower the roughness of laser cuts generated by LIOB processes. The importance of lowering pulse energies (well above the threshold) emphasizes the need for the LIOB threshold to remain low (as low as possible). Reducing roughness by decreasing spacings (thus, increasing dose for same pulse energies) may have negative implications in visual recovery (risk for overdose). In all cases, the roughness is multiple times larger (rougher) than equivalent simulations for ablative procedures.

1. Introduction

In ophthalmology, laser-based operations are gaining importance and techniques in refractive surgery are improving. During the last couple of years, the femtosecond laser has played a key role in this field. This has led to several advantages like fewer complications during and after surgery and a more precise cut.

Femtosecond lasers are increasingly used in the medical sector, especially in ophthalmology. An important benefit of these lasers in comparison to a simple mechanic microkeratome is their high cut precision and fast recovery after surgery.

Common applications of femtosecond lasers are femtosecond-assisted LASIK or femtosecond laser cataract surgery, but their applicability is much wider.

Since the introduction of the femtosecond laser, there has been huge progress in refractive surgery. The newest surgical techniques allow correction of the refractive defects with a smaller surface cut than previously made. This method is minimally invasive and involves a very fast recovery.

The laser emits shorter pulses and hence smaller pulse energies than the excimer laser, another important instrument in refractive surgery. As presumed, it uses laser pulses in the femtosecond range. The laser interacts with tissue in such a way that a plasma and then a cavitation bubble is built. Thereby, vaporisation of the tissue only occurs if the laser energy in the focus exceeds a certain threshold. Using the femtosecond laser-induced optical breakdown (LIOB), surrounding tissue suffers from much less damage as compared to a mechanical blade.

In contrast to the advantages of the ultrashort laser, there are also negative optical side-effects such as rainbow glare [1]. This occurrence requires more investigation to achieve further improvement. One big issue is minimizing the roughness of a surface cut via femtosecond laser.

Accurate clinical outcomes and a reduction in the retreatment procedure are aims in ophthalmology. To achieve this, parameters of laser systems can be adjusted. Here, the femtosecond laser and the excimer laser play a crucial role. The optimization of different excimer laser systems for smoother laser ablations has already been described by Verma et al. [2]. In their study, Gaussian laser pulses with round and square spot geometries are used and placed on square reticules and triangular lattices. The roughness is then calculated using an ablation matrix that contains information about laser pulses in a single-layer ablation area. Also, the impact on ablation smoothness of some laser beam characteristics like super Gaussian order or spot overlap are evaluated. It must be considered that the assumption is made that all optimum values together are also an optimum. That means that there is no cross-influence between these parameters. The following results were found:

• Lower roughness for a smaller Gaussian order N (for an overlap distance smaller than 620 µm (corresponding to the size of a single spot));
• Smoother ablation for round spot geometries, compared to square spot geometries (for an overlap distance smaller than 620 µm (corresponding to the size of a single spot));
• Triangular lattices result in lower roughness;
• Lower spot energy and larger spot sizes produce less roughness.

For these settings, a spot overlap of 300 µm would cause minimum roughness and overlaps below this value do not improve the ablation smoothness. Furthermore, the simulated beam profile matched well with the theoretically modelled beam profile [2].

It needs to be considered that the femtosecond laser has other parameters and cannot be directly compared to excimer laser systems (to highlight the most important ones, excimer laser systems work in the ultraviolet regime vs. the infrared regime of femtosecond systems (directly affecting spot size), the pulse duration changes from ns (excimer) to fs (femtosecond systems), the pulse energy changes from mJ (excimer) to nJ (femtosecond systems), the spot size changes from mm (excimer) to µm (femtosecond systems), or the total number of pulses for a general procedure change from thousands of pulses (excimer) to millions of pulses (femtosecond systems)). For commercial femtosecond laser systems used for corneal laser vision correction, it has been found that laser energies lower than 115 nJ lead to faster recovery after surgery. However, it is also stated that further research must be done for detailed explanations of the interaction of parameters [3].

The aim of this work is to implement an algorithm that simulates a simplified cutting surface of such a system based on LIOB. To perform a cut with the laser, several laser pulses are placed next to each other by a positioning system. This work focuses on a simulation model of the depth profile of the spot build for different input parameters (spot distance ds, track distance dt and laser energy E) of the laser and the positioning system. Then, the roughness is calculated for specific critical points that are obtained as Voronoi vertices. The smoother the cut, the fewer complications arise. Afterwards, the spot distance ds, track distance dt and the laser energy E are optimized to achieve a smooth profile, i.e., to minimize the roughness (while respecting relevant boundary conditions).

2. Methods

In algorithmic geometry, Voronoi graphs play a significant role and are often used. To build a graph, a finite set of points must be transformed into polyhedral regions using a point that represents the centre of a region. This region is defined by the points, which are closer to the centre than to any other point in the region, referring to the Euclidean norm between two points. The edges of the polyhedral regions that are farthest away from its centres are called Voronoi vertices [4].

The algorithm includes the definition of possible positions for the laser pulses and a calculation of the roughness for different parameter settings (including LIOB threshold, pulse energies, and spot spacings). Certain critical points are considered (such as treatment dose or cutting time, which are determined in the simulation, and the simulation is “rejected” if those parameters do not meet the boundary conditions) and the difference between simulated and ideal target cut is determined (the ideal target cut is defined as the simplest surface (free of waviness) that meets the cutting requirements; in its simplest form, the ideal target cut is a 3-dimensional surface placed at known distances from the corneal surface). Furthermore, optimizations of specific variables, such as spot distance (along the pathway), track distance (between lines/tracks) and pulse energy, are performed to minimize the induced roughness (within clinically relevant boundary conditions).

To create a cut in the cornea using a femtosecond laser, laser pulses are placed along a trajectory consisting of arc-ring segments by a positioning system. The trajectory is defined by a radial step rs (distance between two arc segments), and a track distance dt (distance between two turns); the laser pulses are controlled via spot distance ds (distance between neighbouring laser spots), repetition rate of the laser f, and the energy of the laser pulses E. Furthermore, the virtual positioning system is characterized by an inbound scan sequence.

To find plausible pulse positions, a maximum repetition rate f_max and a limiting frequency f_limit, below which the energy output of the femtosecond laser may not be stable anymore, are considered.

To get a track distance between two turns, there must be several radial steps between arc segments in one round. After a given rotational angle (time interval), the radius is decreased by rs until the inner radius is reached (with a final radius smaller than rs) and the trajectory is finished.

For the cut in the cornea, laser pulses that produce LIOB in the cornea must be placed alongside each other, each pulse generating a cavitation bubble (because the laser energy E is set to exceed a certain threshold energy E_Th). Multiple cavitation bubbles that are close enough to each other are the reason for a confluent cut in the cornea. In this model, the shape of the bubble is assumed to be spheroidal and the diameter of the bubble d_bubble is given by

$$d_{bubble}=k\times \sqrt[3]{E-E_{Th}}$$

(1)

using the factor k that governs the growth of the bubble and which in this model is given by $k=1.5 \raisebox{1ex}{$\mu \mathrm{m}$}\!\left/ \!\raisebox{-1ex}{$\sqrt[3]{\mathrm{n}\mathrm{J}}$}\right.$ [5].

Important boundary conditions for achieving minimal roughness are a laser dose below 10 J/cm² and a time limit of 24 s for creating a single cut with a diameter of 8.5 mm.

The

Table 1. Relevant parameters of the simulation.

Parameter	Reference	Value
Cap diameter	dcap	8.5 mm
Maximum repetition rate of the laser	fmax	3000 KHz
Limiting frequency of the laser	flimit	60 KHz
Spot distance	ds	1–5 µm
Track distance	dt	1–5 µm
Radial step	rs	0.35 µm
Laser pulse energy	E	55–500 nJ
Threshold energy	ETh	47–65 nJ

shows relevant parameters of the simulation along with their values.

For determining the roughness, critical points are selected such that the difference/distance between the depth of ideal target profile and the depth of the simulated profile is locally a maximum of these points. Different methods have been considered.

Method 1: Here, overlaps of two and three bubbles are taken into consideration. For the overlap of two bubbles, intersections would be critical points. However, after visual inspection of the possible laser pulse positions, it can be observed by focusing on overlaps that there are more bubbles involved in overlapping than just two. Consequently, a better result than only using two bubble intersections was achieved by using the three-bubble model. For this model, a bubble, its adjacent bubble, and the nearest bubble in an inner or outer segment is considered. Points of two two-bubble intersections are connected with a line and the intersection point of these lines is taken as the new critical point. An even better result would be possible if more than three bubbles are considered, but this would be overly complex and time-consuming.

Method 2: Another way to determine critical points is by using Voronoi vertices as critical points. For this method, a complete algorithm to obtain Voronoi vertices has been implemented [6].

Both methods have been compared and the Voronoi method was selected due to its better performance. Ultimately, Voronoi vertices best fulfil the condition that the difference/distance between the depth of the ideal target profile and the depth of the simulated profile is the maximum. In this work, roughness is defined by the RMS of the difference in simulated vs. target-cutting depth for all Voronoi vertices (the local differences within the cutting surface (i.e., the waviness of the simulated cut vs. the homogeneity of the ideal target cut)).

To obtain the depth in the achieved surface in the overlapping regions, the maximum value of all corresponding overlapped bubbles (single depths) is taken. This is a simplification of the model. In reality, the depth created by the overlapping laser pulses onto previous cavitations bubbles may show cumulative effects.

To minimize the roughness for a cut, several parameters need to be evaluated/optimized and all other parameters are fixed. In this work, three different evaluation/optimization strategies are considered:

-

Evaluation of the roughness in relation to the treatment dose for a constant pulse energy, via modification of ds, dt; such that ds/dt = constant.

-

Optimization of laser energy by evaluating the roughness in relation to the pulse energy (above the threshold) for a constant treatment dose, via modification of pulse energy, ds, and dt; such that E/(ds × dt) = constant and ds/dt = constant.

-

Optimization of the asymmetry ratio (ds/dt) by evaluating the roughness in relation to the asymmetry ratio for constant pulse energy and treatment dose, via modification of ds and dt; such that ds × dt = constant = E/dose.

3. Results

Evaluation of the roughness in relation to the treatment dose for a constant pulse energy, via modification of ds, dt; such that ds/dt = constant.

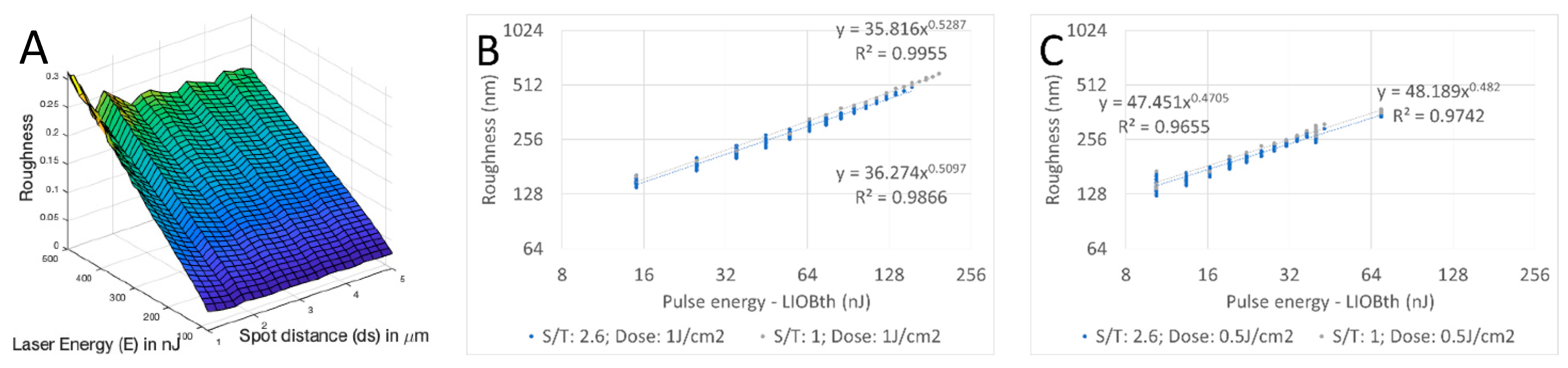
In this strategy, the spot distance ds and the track distance dt take the values from 1 µm to 5 µm in steps of 0.2 µm. The roughness is calculated for each combination of ds and dt for different laser energies (and different LIOB threshold values) E₁ = 100 nJ with E_Th1 = 65 nJ, and E₂ = 57 nJ with E_Th2 = 47 nJ (more combinations have been simulated but are not presented).

In Figure 1A, a three-dimensional plot for the laser energy E₁ = 100 nJ (with E_Th1 = 65 nJ) with ds in µm as the x axis, dt in µm as the y axis, and the roughness as the z axis is shown. A univariate plot of the roughness in relation to the treatment dose for a constant pulse energy, via modification of ds, dt; such that ds/dt = constant is presented in Figure 1B for the laser energy E₁ = 100 nJ (with E_Th1 = 65 nJ) and Figure 1C for the laser energy E₂ = 57 nJ (with E_Th2 = 47 nJ).

Optimization of laser energy by evaluating the roughness in relation to the pulse energy (above the threshold) for a constant treatment dose, via modification of pulse energy, ds, and dt; such that E/(ds × dt) = constant and ds/dt = constant.

To optimize the laser energy E and spot distance ds, the laser dose has been fixed to the following values 1 J/cm² (for E_Th1 = 65 nJ), and 500 mJ/cm² (for E_Th2 = 47 nJ) (more combinations have been simulated but are not presented).

In the process, the laser energy E takes values from 55 nJ to 500 nJ in steps of 5 nJ and the spot distance ds takes the same values as in the first evaluation (1 µm to 5 µm in steps of 0.2 µm).

In Figure 2A, a three-dimensional plot for a dose of 1 J/cm² (with E_Th1 = 65 nJ) with ds in µm as the x axis, E in nJ as the y axis, and the roughness as the z axis is shown. A univariate plot of the roughness in relation to the pulse energy (above the threshold) for a constant treatment dose, via modification of pulse energy, ds, and dt; such that E/(ds × dt) = constant and ds/dt = constant is presented in Figure 2B for a dose of 1 J/cm² (with E_Th1 = 65 nJ) and Figure 2C for a dose of 500 mJ/cm² (with E_Th2 = 47 nJ).

In Figure 2A, the roughness increases for larger laser energy E, especially for small spot distances ds. The optimum value for the spot distance ds_Opt decreases whereas the optimum laser energy E_Opt increases for an increasing laser dose.

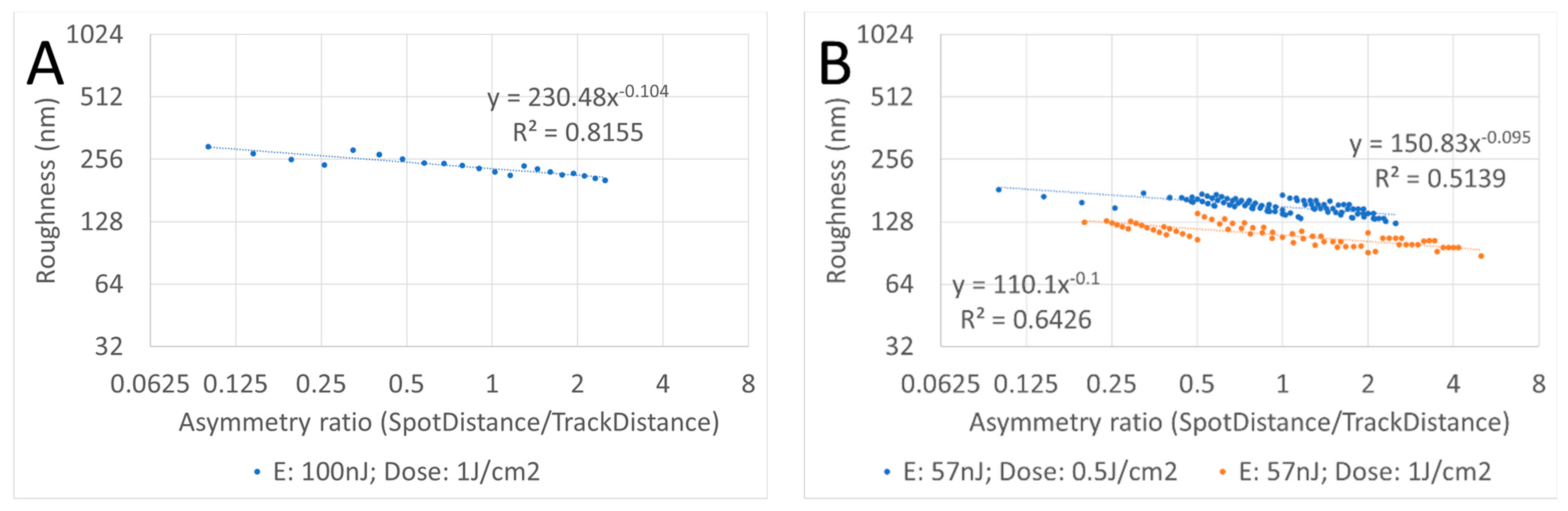
Optimization of the asymmetry ratio (ds/dt) by evaluating the roughness in relation to the asymmetry ratio for constant pulse energy and treatment dose, via modification of ds and dt; such that ds × dt = constant = E/Dose.

To optimize the asymmetry ratio, pulse energy and laser dose have been fixed to the following values: 100 nJ and 1 J/cm² (for E_Th1 = 65 nJ), and 57 nJ and 500 mJ/cm² (for E_Th2 = 47 nJ) (more combinations have been simulated but are not presented).

A univariate plot of the roughness in relation to the asymmetry ratio for constant pulse energy and treatment dose, via modification of ds and dt; such that ds × dt = constant = E/dose is presented in Figure 3A for a pulse energy of 100 nJ and dose of 1 J/cm² (with E_Th1 = 65 nJ) and in Figure 3B for a pulse energy of 57 nJ and dose of 500 mJ/cm² (with E_Th2 = 47 nJ).

Roughness is dependent on the asymmetry ratio (spot distance/track distance). Higher asymmetry ratios (for the same pulse energies and treatment dose via larger spot distances with tighter track distances) reduce roughness.

The analyses support the following findings with respect to reducing the roughness of the cut:

(1)

Tighter pulses (spacings) using constant pulse energies lead to lower roughness;

(2)

Lower pulse energies for the same dose lead to lower roughness;

(3)

Asymmetric settings with a spot distance larger than track distance, for the same pulse energies and treatment dose, lead to lower roughness;

(4)

For a given dose, lower pulse energies are more important than asymmetric settings.

4. Discussion

We simulated a single-layer cutting surface based on a virtual version of how a femtosecond laser works. Our definition of roughness already prevents the trivial case in which no bubble is simulated, or bubbles are so far apart that most of the surface is not cut. Where the bubbles do not cut, the maximum difference occurs (the ideal target cut considers a homogenous band of bubble effects). This is the reason why we did not merely use the standard deviation of the simulated cut, but the RMS of the simulated vs. ideal target cut.

Lowering pulse energies combined with asymmetric spacings may be effective in reducing the roughness of femtosecond corneal surgery while keeping a safe dose low. The optimized roughness remains, however, many fold larger (rougher) than equivalent simulations for ablative procedures [2]. The simulations by Verma et al. [2] showed induced roughness of 50 nm or less (down to 10 nm); whereas, in this work, the best simulations only reach slightly less than 100 nm induced roughness. In a real scenario, one must bear in mind that ablative procedures work by removing the volume, and thus (as described in the work by Verma et al. [2]) roughness will likely increase with ablation depth and volume. On the contrary, lenticule extraction procedures are based on delineating the contour of an enclosed volume and so induced roughness will be largely independent of the enclosed volume (but only the contribution of the anterior and posterior surfaces of the cut).

For the optimization of the spot distance ds and track distance dt (Figure 1), the roughness is minimal for small distances, obviously. The boundary conditions must be considered and then the smallest distances can be selected. For larger pulse energies combined with the smallest spot distance and track distance, the dose may increase beyond the boundary condition (safety limit).

For a constant energy, roughness increases continuously for larger track distances dt and stepwise for larger spot distances ds.

The outcome that roughness decreases for smaller laser energies (Figure 2) confirms the results of recent research [7]. For larger energies, the size of bubbles (and so the depth etched in the cornea) is bigger and consequently, the difference between the ideal target profile and the simulated profile, and so the roughness, is larger.

On the other hand, the fact that the radius of the bubble and consequently the overlap of the bubble increases for higher energies if the spot distance and track distance remain the same confirms or explains that a higher dose (either for a constant pulse energy with tighter spacings, or constant spacings with higher pulse energies) results in lower roughness, but also that for a constant dose (E/(ds × dt) = constant), roughness increases for higher pulse energies.

In this optimization (Figure 2), the optimum laser energy E and spot distance ds can be found for a given dose. With these parameters, the track distance dt is calculated. For small energies and increasing spot distance ds, the track distances dt (calculated as dt = E/(ds × dose)) may take values smaller than 1 µm for relatively large spot distances ds (thus out of the range considered in this work).

Because a higher laser dose means that laser pulses are closer to each other, it is obvious that the roughness decreases for higher laser doses. For the same laser dose, smaller spot distances ds lead to higher track distances dt (eventually leaving a gap between consecutive turns) and the optimum is achieved for lower pulse energies combined with larger spot distances (asymmetric spacings with ds > dt) because consecutive turns statistically/pseudo-stochastically tend to “fill the gaps” and place pulses nearby (small dt) in between pulse positions (separated by large ds) of the neighbouring turns [8].

The simulations included in this work are extremely time-consuming because Voronoi vertices are used for the critical points. An alternative method is investigating the sparsity of the profile image and applying compressive sensing techniques to reduce the number of samples needed for the evaluation [9].

It would be useful to have a third boundary condition so that there will only be a real confluent cut if the depth is larger than zero everywhere (thus an effective 2-dimensional overlap of the bubbles is required). This may be incorporated as a dynamic additional boundary condition to constrain energy and spot and track distances.

To obtain the depth in the achieved surface in the overlapping regions, the maximum value of all corresponding overlapped bubbles (single depths) was taken. This is a simplification of the model. In reality, the depth, created by the overlapping laser pulses onto previous cavitations bubbles, may show cumulative effects. Most likely, these cumulative effects are neither linearly additive (unlike for the excimer laser ablation), nor governed by the max function. Yet, they are likely closer to the max function concept, so the max function represents a reasonable simplification.

As it can be inferred from Figure 2B,C and derived from the equation for bubble size, roughness depends on the geometry of a single bubble and the respective spot and track distances (i.e., the overlap along and across the pathway). Mathematically, this means that it is dependent on the factor k, and the amount of energy exceeding the LIOB threshold (E − E_Th), and independent of the actual LIOB threshold.

It can be figured out that two different model parameters lead to the same bubble size (thus, roughness behaviours):

$$d_{bubble}=k_1\times \sqrt[3]{E_1-E_{Th1}}=k_2\times \sqrt[3]{E_2-E_{Th2}}$$

(2)

This means that all obtained curves can be theoretically converted to equivalent pulse energies for models based on a different factor k or LIOB threshold (E_Th):

$$E_2=E_{Th2}+{\left(\frac{k_1}{k_2}\right)}^3\times \left(E_1-E_{Th1}\right)$$

(3)

In our simulations, we have considered two different LIOB thresholds (E_Th as 65 nJ and 47 nJ), but due to the lengthy simulations, we considered only a single bubble size factor (k = 1.5). This value is similar to what has been used in previous publications [5], but it is also compatible (and to some extent explains and supports) the minimum doses used for different commercial devices [10] (as well as Ivan Gabric, personal communication) [11]. According to this, VisuMax (Carl Zeiss Meditec, Jena, Germany) would have a E_Th value close to 73 nJ (using $k=1.5 \raisebox{1ex}{$\mu \mathrm{m}$}\!\left/ \!\raisebox{-1ex}{$\sqrt[3]{\mathrm{n}\mathrm{J}}$}\right.$, leading to a bubble diameter of 4.5 µm for 100 nJ as in the cited work, leading to 494 mJ/cm² as minimum dose), whereas ATOS (SCHWIND eye-tech-solutions, Kleinostheim, Germany) would have a E_Th value close to 49 nJ (using $k=1.5 \raisebox{1ex}{$\mu \mathrm{m}$}\!\left/ \!\raisebox{-1ex}{$\sqrt[3]{\mathrm{n}\mathrm{J}}$}\right.$, leading to a bubble diameter of 4.7 µm for 80 nJ, leading to 360 mJ/cm² as minimum dose as in the personal communication (80 nJ in 7.4 µm (ds) × 3.0 µm (dt))) [11].

A higher dose is “bad” for the biology of the cornea (overdose, more severe insult to the tissue) even if, formally, this may lead to lower roughness [12]. Further, a lower pulse E is more important than asymmetry (yet with pulse E > 1.5 × E_Th, as per previous works) [13].

Finally, for already optimized low pulse E (~1.5 × E_Th), asymmetric spacings with ds >> dt induce less roughness than symmetric spacings (ds~dt, e.g., VisuMax), and both induce less roughness than asymmetric with ds < dt (Z8 by Ziemer (Port, Switzerland) or ELITA by Johnson & Johnson Vision (Milpitas, CA, USA)). This is also consistent with recent publications in lenticule extraction [14].

Equivalent findings were determined for other rotational trajectories such as Archimedes spiral (merely with rs < 38 pm) or concentric circles (merely rs = dt), as the two extremes of rotational trajectories. Further, the simulations were performed for an inbound scan sequence, yet equivalent results have been obtained for simulations using outbound scan sequences.

The asymmetry ds >> dt may seem surprising and counterintuitive yet it is “inadvertently” known, and it also holds for meander scan pathways. When comparing square reticules vs. triangular/hexagonal lattices with regards to a filling-factor for circular spots, it becomes obvious that triangular/hexagonal lattices offer a much better filling-factor (with the gaps representing areas of tissue bridges) [15]. Triangular/hexagonal lattices represent an asymmetry ratio (ds/dt) of either $\frac{2}{\sqrt[3]{3}}\cong 1.155$ or actually $2\times \sqrt[3]{3}\cong 3.464$. This confirms that the advantage of asymmetric spacings (with ds > dt) holds “universally”.

Further, the primary role of lowering pulse E in reducing roughness makes it even more important that the LIOB threshold (E_Th) remains low (as low as possible). This is because roughness is dependent on the amount of E exceeding the LIOB threshold (E − E_Th), and independent of E_Th ($d_{bubble}=k\times \sqrt[3]{E-E_{Th}}$); yet optimum E ~ 1.5 × E_Th. Then, only a low LIOB threshold makes 1.5 × E_Th − E_Th = E_Th/2 (i.e., the optimum amount of E exceeding the LIOB threshold) low, and that grows with the LIOB threshold. Thus, the more important it is that the LIOB threshold stays low (as low as possible).

According to this, we would actually recommend the following settings: E ~ 1.6 × E_Th; asymmetry ratio = ds/dt > 2; with optimum dose as published before [5]. Leading to exemplary valid settings of 80 nJ in 5.9 µm (ds) × 2.8 µm (dt) in ATOS (484 mJ/cm²) or 100 nJ in 4.5 µm (ds) × 3.5 µm (dt) for VisuMax (635 mJ/cm²) (115 nJ in 6.0 µm (ds) × 3.5 µm (dt) for VisuMax (548 mJ/cm²) would have been better, but this not possible to parametrize in the commercial VisuMax system).

For Z8, according to this model (estimated E_Th = 27 nJ), settings of 43 nJ in 4.7 µm (ds) × 2.2 µm (dt) (416 mJ/cm²) would be optimum, whereas 57 nJ in 5.1 µm (ds) × 2.5 µm (dt) (447 mJ/cm²) would be optimum for ELITA (estimated E_Th = 36 nJ) (yet, apparently, both settings are not possible to parametrize in these commercial systems, which further seem to use the opposite asymmetry, with ds << dt).

We initially thought that a more extensive body of literature according to the state-of-the-art technology would include more works from previous publications. We have searched for similar works (directly related to the roughness induced by cumulative LIOB processes in the cornea) and could simply not find them. But the impact of induced roughness in vision and corneal laser vision correction has been addressed before. For excimer laser systems (ablative procedures), it has been shown that reducing pulse energy is a key driver in reducing roughness [16]. This has been also empirically demonstrated for femtosecond systems [17,18]. Both correspond to our simulation findings and also shared in laboratory experiences with excimer ablation procedures [19]. But it is not only the energy that is responsible for roughness; spot placement (spacings) also plays an important role, as demonstrated for excimer based corneal ablations [20,21]. Interface roughness after laser vision correction has been associated with lower postoperative visual acuity for both femtosecond-based treatments (lenticule extraction) [22], and excimer-based corneal ablations [23] whereas simulations show that random and patterned roughness induce distinct effects in visual perception [24]. Apparently, refraction (myopia vs. hyperopia) does not seem to play a major role in the induced roughness [25], but the depth of the cut in the tissue does [26].

5. Conclusions

The presented algorithm simulates a single-layer cut in the cornea and can calculate the roughness. It has been shown that certain parameters of the laser can improve the smoothness and so the outcome of the treatment. A simple statement that small spot distance, small track distance and a high laser energy result in minimal roughness cannot be made because several factors interact. Nevertheless, it must also be considered that this optimization contains a simplified model and that the real depth profile may be different from the simulated one. To assess this, empirical tests on PMMA (synthetic plastic) or porcine eyes can be performed, and the roughness can be compared.

In the future, a translation from MATLAB R2019a functions into C++ would improve the speed of the simulation because the current computation time takes too long (several weeks of uninterrupted computing to generate the final simulations presented here). In addition, the impact of other parameters like the minimum laser frequency for which the energy output is stable can be examined. Moreover, the roughness can be evaluated for other critical points.

To conclude, the femtosecond laser is an important instrument in ophthalmology, especially in refractive surgery, and it is used increasingly. To have a fast recovery and no complications, it is essential to optimize the laser.

The simulations suggest that lower pulse energies (well above the LIOB threshold) combined with asymmetric spacings (spot-to-track distance ratio >> 1) may be effective to lower the roughness of laser cuts generated by LIOB processes. The importance of lowering pulse energies (well above the threshold) emphasizes the need for the LIOB threshold to remain low (as low as possible). Reducing roughness by decreasing spacings (thus, increasing the dose for same pulse energies) may have negative implications in visual recovery (risk of overdose). The optimized roughness is multiple times larger (rougher) than equivalent simulations for ablative procedures.