Classical Scattering of High-Energy Electrons off Ultra-Intense Laser Beams Taking into Account Radiation Reaction

Abstract

The head-on scattering of electrons with energies from a few MeV to 5 GeV off ultrashort and ultra-intense laser pulses at petawatt intensities is investigated. Radiation reaction (RR) effects are included through the correction terms given by the Landau–Lifshitz equation. Full paraxial fields for the laser are used, including their longitudinal electric and magnetic components, and both the fundamental Gaussian TEM₀₀ mode as well as the orbital angular momentum (OAM) mode with $(l,p)=(1,0)$ are studied. We compare the expected behavior, as regards the influence of RR, at near-infrared (NIR) and at vacuum ultraviolet (VUV) or X-ray wavelengths.

1. Introduction

As ultrafast and ultra-intense laser technology expands the extreme-intensity frontier, new challenges appear. Today the laser peak intensity record has been achieved at CoReLS (Republic of Korea), focusing a multi-petawatt laser very tightly (f/1.1); see [1]. It is clear that at intensities much higher than this, close to ${10}^{29}$ W/cm², what is called the Sauter–Schwinger limit, with a tight focused laser beam, pair production, electron/positron showers, and other exotic phenomena are expected [2,3]. A proper theory for such photon–photon collisions (this is why we insist on a tight focus and not in a quasi-plane wave) was developed by Breit and Wheeler [4], and extended later on by Reiss [5]. There are a lot of papers and excellent reviews that consider this scenario and the best path to arrive at it; see for example [6,7,8]. However, this limit is not likely to be achieved in the laboratory frame over the coming years or decades. One very clever alternative was the SLAC E-144 experiment [9]. This experiment sought a photon–photon collision to generate an electron–positron pair, using a relatively intense laser (a terawatt laser at that time was a really large laser) and a gamma source. Fortunately, the existing sources of gamma rays are now brilliant enough for this purpose and the gamma source was created by Compton scattering from the 46 GeV SLAC high-brilliance electron beam. The main indication of the pair creation was the presence of positrons (the laser-generated electron was more difficult to detect due to the presence of a large number of accelerated electrons).

The progression of the laser peak power has been astonishing during the two decades after the invention of the chirped pulse amplification (CPA) technique by Strickland and Mourou [10], but now this increase seems to be close to saturation, around a few tens of petawatts, at least with a single beam. Coherent combination of multiple beams seems a very promising possibility, although this is going to take years to be applied to such extreme lasers.

Meanwhile, one basic question is what is it going to happen in the region between the present-day achievable power level of ${10}^{23}$ W/cm², and the critical intensity of ${10}^{29}$ W/cm². Two basic effects are foreseen: one is the radiation reaction and the other is the pair cascade. In both cases, we need an electron driven by such fields. In the first case, the driven electron is going to radiate (as any accelerated charged particle does) and the radiation is relevant enough to affect its trajectory. In the second case, the combination of the electron’s static field plus the laser field is enough to trigger the pair production.

In the quest for the Schwinger limit, a number of effects are expected to appear and maybe to be dominant in the dynamics. Among them, the radiation reaction from electrons driven by such extreme fields. The radiation reaction from a driven electron is an old recurrent problem [11,12,13,14,15,16] that is the subject of extensive studies at present. Most of these are on the possibility of synchronizing an electron bunch accelerated by the laser wakefield acceleration (LWFA) mechanism against a second, counter-propagating, laser pulse [17,18]. LWFA was introduced by Tajima and Dawson [19] and it is now considered as the way to achieve ultraviolent electron acceleration. Electrons can be ionized to several GeV in a few millimeters when driven by a ultra-intense femtosecond laser with a convenient focusing (long focal length) on a convenient gas target (with the appropriate density). However, all those simulations imply an all-optical laser scenario with two ultra-intense laser pulses being synchronized, which complicates the experimental set-up. The problem has also received recent attention regarding quantum effects; see, for example [20,21], and a number of experiments have been performed [22,23] searching specifically for characteristic QED features in laser-accelerated electrons synchronized with the driving laser. In addition to radiation reaction (that we understand as the effect of the relativistically emitted radiation of the emitting electron’s trajectory), the radiation itself gives very valuable information on the driven electron. This has been deeply studied in the literature [24,25,26,27,28,29]. The emission spectra and other features from those relativistically driven electrons can also give valuable information on the dynamics.

Due to the availability of extreme lasers, LWFA can be used to create an accelerated electron bunch colliding with a second laser pulse synchronized to the first one on the femtosecond scale. Typically, a long focal length beam shining on a gas target is used to accelerate the electrons, while a second pulse, counter-propagating to the first one and tightly focused (short focal length), is used to drive the electrons. However, LWFA generates a wide spectrum of electron energies and makes such an experiment more difficult to analyze due to the broad spectrum. In the present paper, we consider electrons pre-accelerated against a laser field (moving head-on). We consider just a mono-energetic beam of electrons, coming probably from a multi-GeV linear accelerator. Such devices generate higher energies and moreover narrower spectra (and much less instabilities that the filamentation instabilities typical of the LWFA mechanism). Therefore, we consider that they can be an ideal scenario for clean observations of radiation reaction free of collective plasma effects and from laser-plasma propagation instabilities. In Europe, for example the EU-XFEL in Hamburg is able to generate 17 GeV electron beams [30]. A number of XFEL are in construction or in operation in America and Asia, and some of them may consider the possibility of having a petawatt or multi-petawatt laser because of the quick evolution of such lasers. Today, 10 PW lasers able to be focused to ${10}^{23}$ W/cm² are a robust and available technology. Therefore, sooner or later collisions between multi-GeV electron beams and multi-PW lasers, tightly focused, will be a realistic scenario. We present in this paper a way to analyze this.

In this context, radiation reaction can be of paramount relevance. One of the main problems when considering extreme intensities is the huge ponderomotive force that prevents electrons initially at rest or non-relativistically moving from entering the extreme-intensity region. Because of that, electrons accelerated against the laser pulse could be a good alternative. However, in this case radiation reaction can be the dominant effect in the dynamics of the strongly driven electrons, slowing down their initial speed and precluding them from entering the extreme-intensity region.

In the present paper, we consider electrons pre-accelerated against a laser field (moving head-on) and we study the influence of the radiation reaction on their dynamics based on the Landau–Lifshitz equation, which is known to solve some of the problems that plague, for example, the Lorentz–Abraham–Dirac (LAD) equation. A systematic study is carried out characterizing the asymptotic values of the electrons’ energy and momentum when interacting with an ultra-intense laser in the TEM₀₀ (Gaussian) or the $(l,p)=(1,0)$ OAM (orbital angular momentum) modes, and the scaling of energy loss due to RR as a function of the relativistic ${\gamma }_0$ factor. The meaning of “scattering” as it is used in this paper can be summarized as follows: at $t=0$, we have two systems that are non-interacting (the high-energy electron and the laser pulse) because they are spatially well separated. In the considered counter-propagating geometry, both systems interact for a while, and, at large t, both systems become separated and non-interacting again, although the electron eventually experiences a more or less substantial change in its mechanical properties. The paper aims at a characterization of the final state of the electrons as a function of their energy and location across the laser pattern. Please note that while the laser substantially affects the electron, the effect of the latter on the laser is deemed negligible.

The paper is organized as follows:

Section 2 includes the model vector and scalar potentials used in the numerical computations of the paper. The Landau–Lifshitz equation of motion in MKS units is introduced, justifying the inclusion of just the term that depends on ${\gamma }^2$ for the computations that follow.

Section 3 presents the numerical results for the head-on scattering of high-energy electrons, uniformly and randomly distributed across the transverse beam pattern, off an ultra-intense near-infrared laser of small beam waist ($w_0$ = 10 $\mathsf{\mu }$m) and intensity of 10²¹ W/cm². Two modes are considered for the laser beam, the fundamental TEM₀₀ mode and the OAM $(l,p)=(1,0)$, and the initial kinetic energy of the electrons is varied in the range from 5 MeV to 5 GeV. The asymptotic distributions of energy and momentum are characterized for both laser modes. As an extension to the results in this section, a laser pulse of intensity 10²² W/cm² and $w_0$ = 4 $\mathsf{\mu }$m or $w_0=10$ $\mathsf{\mu }$m against an electron beam of 2.5 GeV is studied.

Section 4 considers the electron scattering off an ultra-intense ultraviolet or X-ray laser at the same peak intensities as in Section 3, also including the radiation reaction effects. The similarities and differences among these different ranges in laser wavelength are highlighted, and their experimental implications are discussed.

Finally, a section discussing the main results and the prospects for future developments is included.

2. Mathematical Model for Ultra-Intense Laser Fields and Equation of Motion Including Radiation Reaction

In order to describe the electromagnetic fields of the ultrashort and ultra-intense laser, we have chosen vector $\mathbf{A}=A_x\mathbf{i}+A_y\mathbf{j}+A_z\mathbf{k}$ and scalar $\Phi$ potentials satisfying the paraxial wave equation and the Lorentz gauge condition. They are known to be a reasonable model for the transverse structure of pulsed lasers fields. More details about the derivation of the paraxial wave equation for laser physics can be found in [31,32], among others. The paraxial wave equation admits as exact solutions several families of modes, the Hermite–Gauss or the Laguerre–Gauss ones being among the best known and widely studied in the literature.

Following our derivations in [32], we have chosen in this paper the Laguerre–Gauss modes, with $A_y=A_z=0$, i.e., the vector potential is fully perpendicular to the laser propagation axis, z, and the resulting $\mathbf{E}$ field is (basically) linearly polarized along the x-axis.

The electric and magnetic fields of the laser pulse are obtained according to the general rules:

$$\begin{array}{ccc}& & \mathbf{E}=-\frac{\partial \mathbf{A}}{\partial t}-{\nabla }_{\mathbf{x}}\Phi ,\mathbf{B}={\nabla }_{\mathbf{x}}\times \mathbf{A}\hfill \end{array}$$

(1)

taking real parts whenever necessary.

2.1. Generalities on the Paraxial Approximation and Model Vector Potential

We shall disregard $A_{z,ex}$ and $A_{y,ex}$ completely and exactly from the outset, by imposing:

$$\begin{array}{ccc}& & A_{z,ex}=0,A_{y,ex}=0\hfill \end{array}$$

(2)

prior to imposing the paraxial approximation. As a general rule, the paraxial (subscript $par$) approximation for the exact (subscript $ex$) potentials $X_{ex}={\Phi }_{ex}, {\overline{A}}_{ex}$ is expressed as $X_{ex}\simeq X_{par}$. The approximation is based upon assuming that $\frac{{\partial }^2}{\partial z^2}{X}_{ex}$ can be neglected compared to $\left(2k_0\frac{\partial }{\partial z}\right)X_{ex}$. $k_0={\omega }_0/c=2\pi /{\lambda }_0$ is the wavevector of the laser. So, in the framework of the paraxial approximation, one has

$$\begin{array}{ccc}& & \left({\nabla }_{\overline{x}}^2+2i{k}_0\frac{\partial }{\partial z}\right)X_{par}=0\hfill \end{array}$$

(3)

Under the approximations mentioned above, the scalar potential is fixed by the constraint to fulfill the Lorentz gauge condition, and hence it is given by

$$\begin{array}{ccc}& & \frac{\partial }{\partial x}{A}_{x,par}=\frac{i{\omega }_0}{c^2}{\Phi }_{par}\hfill \end{array}$$

(4)

For the electric and magnetic fields, one obtains:

$$\begin{array}{ccc}& & E_{x,par}=i{\omega }_0{A}_{x,par}\hfill \end{array}$$

(5)

$$\begin{array}{ccc}& & E_{y,par}=0\hfill \end{array}$$

(6)

$$\begin{array}{ccc}& & E_{z,par}=-i{k}_0{\Phi }_{par}\hfill \end{array}$$

(7)

$$\begin{array}{ccc}& & B_{x,par}=0\hfill \end{array}$$

(8)

$$\begin{array}{ccc}& & B_{y,par}=i{k}_0{A}_{x,par}\hfill \end{array}$$

(9)

$$\begin{array}{ccc}& & B_{z,par}=-\frac{\partial }{\partial y}{A}_{x,par}\hfill \end{array}$$

(10)

Equations (5)–(10) give rise to solutions of the Maxwell equations to leading paraxial approximation. Note that $E_z$ and $B_z$ given by those equations are not zero in general, and are systematically included in the computations reported in Section 3 and Section 4 unless otherwise noted.

In this paper, specific use will be made of electromagnetic waves with orbital angular momentum (OAM or Laguerre–Gauss modes) with prescribed values of the integer parameters l, p. Two cases have been studied, namely, the standard Gaussian TEM₀₀ mode, corresponding to $(l,p)=(0,0)$, and a mode with net orbital angular momentum characterized by $(l,p)=(1,0)$. These modes are generated by the functions $g_{l,p}$ given below.

Let $\rho ={(x^2+y^2)}^{1/2}$ and for given $k_0(>0)$ let

$$\begin{array}{ccc}& & g_{0,0}={(2/\pi )}^{1/2}exp[-\frac{{\rho }^2}{w{\left(z\right)}^2}]exp[i\frac{z}{z_0}\frac{{\rho }^2}{w{\left(z\right)}^2}]f(\frac{z}{z_0})\hfill \end{array}$$

(11)

$$\begin{array}{ccc}& & f(\frac{z}{z_0})=\frac{w_0}{w\left(z\right)}exp[-iarctan\frac{z}{z_0}]\hfill \end{array}$$

(12)

$$\begin{array}{ccc}& & w\left(z\right)=w_0{(1+{(z/z_0)}^2)}^{1/2},z_0=\frac{k_0{w}_0^2}{2}\hfill \end{array}$$

(13)

$$\begin{array}{ccc}& & {ϵ}_0=\frac{w_0}{z_0}=\frac{2}{k_0{w}_0}\hfill \end{array}$$

(14)

$w_0$ gives the beam waist size, $z_0$ is the Rayleigh range, ${ϵ}_0$ is a dimensionless coefficient, not to be confused with the dielectric permittivity of vacuum, that accounts for the relative importance of the longitudinal field components $E_z,B_z$ with respect to the transverse ones.

$g_{0,0}$ corresponds to $l=p=0$. For general integer values of l, p, one can consider the following functions (directly related to the Laguerre–Gauss (LG) functions $L{G}_{l,p}(\rho ,z)$):

$$\begin{array}{ccc}& & g_{l,p}={[\frac{p!}{(\mid l\mid +p)!}]}^{1/2}{L}_p^{\mid l\mid }(\frac{2{\rho }^2}{w{\left(z\right)}^2}){(\frac{2^{1/2}\rho }{w\left(z\right)})}^{\mid l\mid }\times expi[l\varphi -(2p+\mid l\mid )arctan\frac{z}{z_0}]g_{00}\hfill \end{array}$$

with $\varphi =arctan(y/x)$. $L_p^{\mid l\mid }\left(u\right)$ are the generalized Laguerre polynomials:

$$\begin{array}{ccc}& & L_p^{\mid l\mid }\left(u\right)=\sum _{m=0}^p{(-1)}^m\frac{(\mid l\mid +p)!}{(p-m)!(\mid l\mid +m)!m!}{u}^m\hfill \end{array}$$

(15)

A very important property of any $g_{l,p}$, for general integer $l,p$, is that

$$\begin{array}{ccc}& & ({\nabla }_{\overline{x}}^2+2i{k}_0\frac{\partial }{\partial z})g_{l,p}=0\hfill \end{array}$$

(16)

The comparison of Equation (16) with Equation (3) shows that $g_{l,p}$ provides one important case of paraxial approximation. In fact, we use here either $A_x=A_0{g}_{0,0}exp[i(k_{0}z-{\omega }_{0}t)]$ or $A_x=A_0{g}_{1,0}exp[i(k_{0}z-{\omega }_{0}t)]$ (times a Gaussian envelope to model the laser pulse shape) as the vector potential to generate the laser fields.

2.2. Radiation Reaction for Relativistic Electrons: Landau–Lifshitz Approximation

The interaction of the incoming radiation with a classical relativistic electron gives rise to an additional electromagnetic field generated by the electron itself. The net effect of the last electromagnetic field can be accounted for by adding to the standard Lorentz force an effective force named radiation reaction (${\mathbf{F}}_{RR}$). Then, the exact equation of motion for the three-dimensional position $\mathbf{x}=\mathbf{x}\left(t\right)$ of the relativistic electron at time t, including both the Lorentz and radiation reaction forces, reads

$$\frac{d[m\gamma (t\left)\mathbf{v}\right(t)]}{dt}=e[{\mathbf{E}}_{in}+\mathbf{v}\left(t\right)\times {\mathbf{B}}_{in}]+{\mathbf{F}}_{RR}$$

(17)

$$\gamma \left(t\right)=\frac{1}{\sqrt{1-{(d\mathbf{x}/dt)}^2/c^2}}$$

(18)

The analysis of the features involved in the radiation reaction force has a convoluted story during the 20th century, and is well documented, see, for example, ref. [21] for a recent review of this topic, also addressing some historical issues. Such features involve pre-acceleration and other unwanted items. Landau and Lifshitz proposed [33] an approximate formula for the radiation reaction force, to be denoted ${\mathbf{F}}_{RR,LL}$, which avoids, pragmatically from the outset, the various unwanted features. The Landau and Lifshitz approximation ${\mathbf{F}}_{RR}\simeq {\mathbf{F}}_{RR,LL}$ has been incorporated in the computations of a good number of authors. It reads (MKS units), in terms of the electric ($\mathbf{E}$) and magnetic ($\mathbf{B}$) fields and the electron velocity $\mathbf{v}=d\mathbf{x}/dt$:

$$\begin{array}{ccc}& & {\mathbf{T}}_0=\frac{e^4}{6\pi {ϵ}_0{m}^2{c}^4}\{c\mathbf{E}\times \mathbf{B}+c\mathbf{B}\times (\mathbf{B}\times \mathbf{v})+\frac{1}{c}\mathbf{E}(\mathbf{v}·\mathbf{E})\}\hfill \end{array}$$

(19)

$$\begin{array}{ccc}& & {\mathbf{T}}_1=\frac{e^3}{6\pi {ϵ}_{0}m{c}^3}\{(\frac{\partial }{\partial t}+\mathbf{v}\left(t\right)·\nabla )\mathbf{E}+\mathbf{v}\left(t\right)\times (\frac{\partial }{\partial t}+\mathbf{v}\left(t\right)·\nabla )\mathbf{B}\}\gamma \left(t\right)\hfill \end{array}$$

(20)

$$\begin{array}{ccc}& & {\mathbf{T}}_2=\frac{-e^4}{6\pi {ϵ}_0{m}^2{c}^5}\{{(\mathbf{E}+\mathbf{v}\left(t\right)\times \mathbf{B})}^2-\frac{1}{c^2}{(\mathbf{E}·\mathbf{v}\left(t\right))}^2\}{\gamma }^2\left(t\right)\mathbf{v}\left(t\right)\hfill \end{array}$$

(21)

$${\mathbf{F}}_{RR,LL}(\mathbf{E},\mathbf{B})={\mathbf{T}}_0+{\mathbf{T}}_1+{\mathbf{T}}_2$$

(22)

The standard approximation consists in using Equation (17), ${\mathbf{F}}_{RR}\simeq {\mathbf{F}}_{RR,LL}$ and Equation (22), with the total fields $\mathbf{E}$, $\mathbf{B}$ replaced, respectively, by the incoming fields ${\mathbf{E}}_{in}$, ${\mathbf{B}}_{in}$. Then,

$$\begin{array}{ccc}& & \frac{d[m\gamma (t\left)\mathbf{v}\right(t)]}{dt}=e[{\mathbf{E}}_{in}+\mathbf{v}\left(t\right)\times {\mathbf{B}}_{in}]+{\mathbf{F}}_{RR,LL}({\mathbf{E}}_{in},{\mathbf{B}}_{in})\hfill \end{array}$$

(23)

Equation (22) displays three terms with quite definite dependences on the relativistic $\gamma$ factor, namely, one term is independent of it, another one is linear in $\gamma$, and a third goes as ${\gamma }^2$. It is numerically found that, in the counter-propagating geometry considered in this paper, the term in ${\gamma }^2$ dominates by far the other two, so only the latter one has been included in the numerical simulations to be reported below. The advantage of this choice and simplification is a significant speed up in the computations while, at the same time, losing no relevant information. Note that we make no claim here that this procedure is of general validity. If another interaction scheme different from head-on collision is used, the relative importance of the different terms in the Landau–Lifshitz equation has to be checked in detail.

3. Head-On Scattering off an Ultra-Intense Near-Infrared (NIR) Laser

We report in this section the results on the asymptotic values of kinetic energy and momentum for scattered electrons, of initial kinetic energy in the range from 5 MeV to 5 GeV, in a head-on collision off an ultra-intense NIR laser.

The rationale of the computations is as follows: a laser pulse that is initially well apart from the electron population is propagated in the +z direction and interacts in a head-on collision geometry with mono-energetic electrons. These electrons are (initially) uniformly and randomly generated with circular symmetry in the perpendicular $xy$ plane up to a radius equal to $1.5\times w_0$. $z_{00}$ (the initial z-coordinate of the electrons, not to be confused with the Rayleigh range denoted $z_0$ in this paper) is always set equal to zero. For notational consistency, the initial positions of the electrons in the transverse plane are denoted with $x_{00},y_{00}$.

Two laser modes are considered, the fundamental TEM₀₀ mode and the OAM mode with $(l,p)=(1,0)$. Laser characteristics common to both laser modes are as follows: ${\lambda }_0$ = 800 nm, beam waist $w_0$ = 10 $\mathsf{\mu }$m, x-polarization, $A_{0x}=46.2560\times {10}^{-3}$ V.s/m, equivalent to an intensity of 10²¹ W/cm², T_pulse = 8 × ${\lambda }_0/c$. The Gaussian envelope of the laser pulse is initially centered at −24 × ${\lambda }_0$, which means that it has (initially) a negligible influence on the electrons, since they are well apart from the pulse bulk. Full paraxial $\mathbf{E}$ and $\mathbf{B}$ fields have been used, this means that in addition to the transverse components we have also included convenient longitudinal components $E_z$ and $B_z$, different from zero in general, so as to insure that $\nabla ·\mathbf{E}=0$ and $\nabla ·\mathbf{B}=0$.

The beam waist size and laser intensity considered are feasible in modern extreme light multi-PW facilities operative around the globe [34], in particular APOLLON in France or ELI-NP in Romania, among others. Notice that although the peak intensity considered here is relatively modest (two orders of magnitude below the peak intensity record), the waist is relatively large and, therefore, a lot of power is needed. We remark that this beam waist of $w_0$ = 10 $\mathsf{\mu }$m corresponds to a large focal number. It is well known that the focal number N (that is, the relation between the focal length and the beam diameter) is related to the beam waist by the expression $w_0=0.87{\lambda }_{0}N$. Therefore, the beam waist we have considered corresponds approximately to $N=15$, that is a quite large focal number. We do this because with such a large waist the Rayleigh length is quite long too and the dynamics of the RR is clean and apparent. Moreover, such large-focus experiments are of interest for many applications, including electron acceleration. The study of RR with a very tight focus is certainly going to be of interest too. However, incoming electrons are going to be expelled from that region due to the huge ponderomotive effect. We consider that the study of RR at lower intensities and higher volumes can be of a more general interest because it is feasible with today’s lasers. We are interested in the dynamics of the driven electrons considering the slowing down related to RR. The emitted radiation pattern is not going to be considered now.

3.1. Scattering off a Laser Pulse in the TEM₀₀ Mode

This subsection addresses the effect of radiation reaction (RR) in the scattering of electrons off an ultrashort and ultra-intense NIR laser pulse in the fundamental or TEM₀₀ mode. The characteristics of the laser pulse have been kept constant in the computations that follow, and the initial kinetic energy of the incoming electrons has been varied in the range from 5 MeV to 5 GeV. For each initial energy, typically 8192 electrons, sampling the transverse pattern of the laser up to $1.5\times w_0$, are used in the computations.

After a sufficiently long integration time, here typically 64 optical cycles, the kinetic energy and momentum are recorded and eventually plotted against the initial position of the electrons. The criterion for the integration time is the absence of any noticeable perturbation in the final mechanical magnitudes of the electron, such as velocity, acceleration, or gamma factor. The 64 optical cycles alluded to is a reasonable compromise between numerical efficiency and the obtention of final states for the electron that closely fit a uniform motion. The influence of RR is included, as predicted by the Landau–Lifshitz equation.

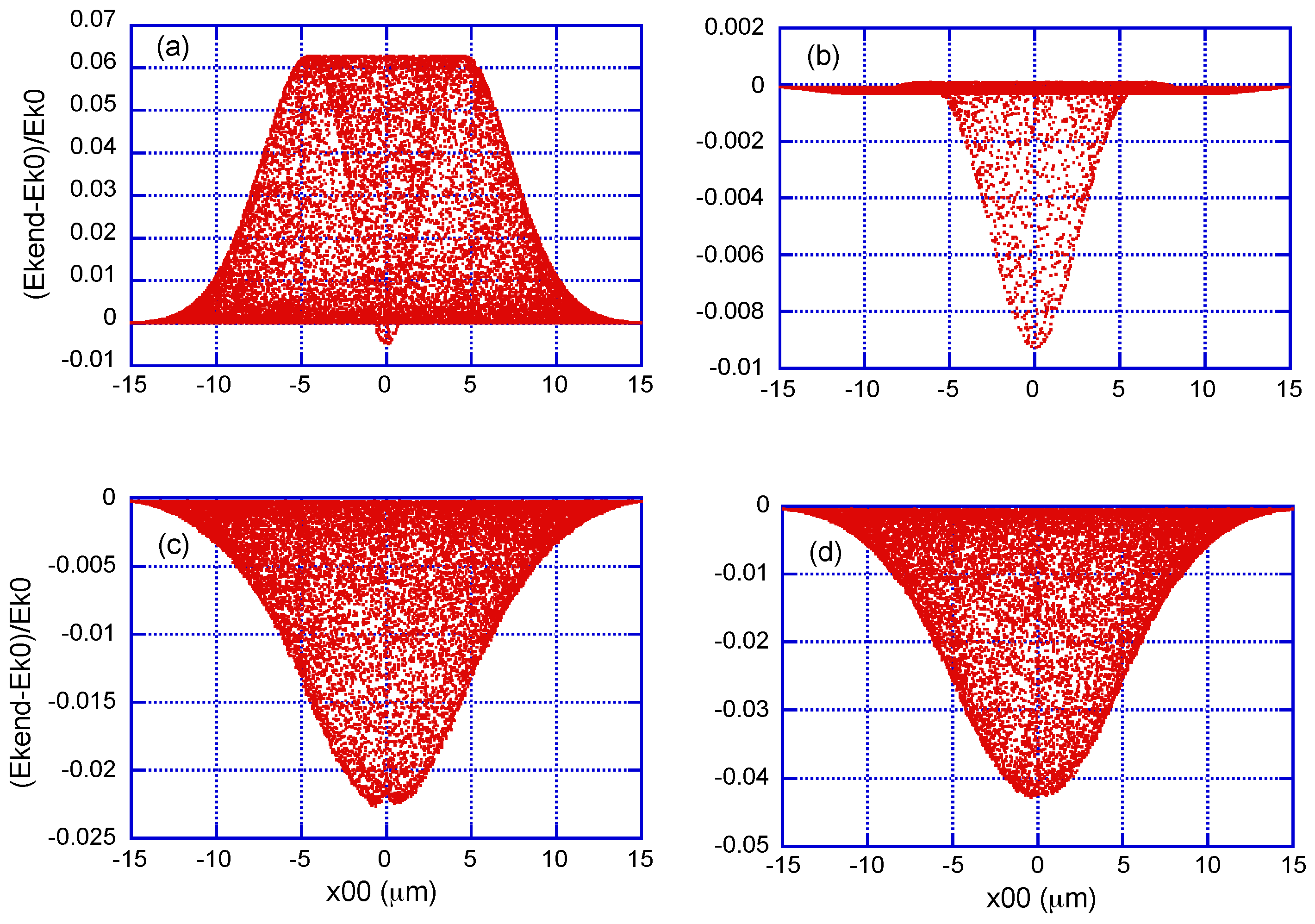
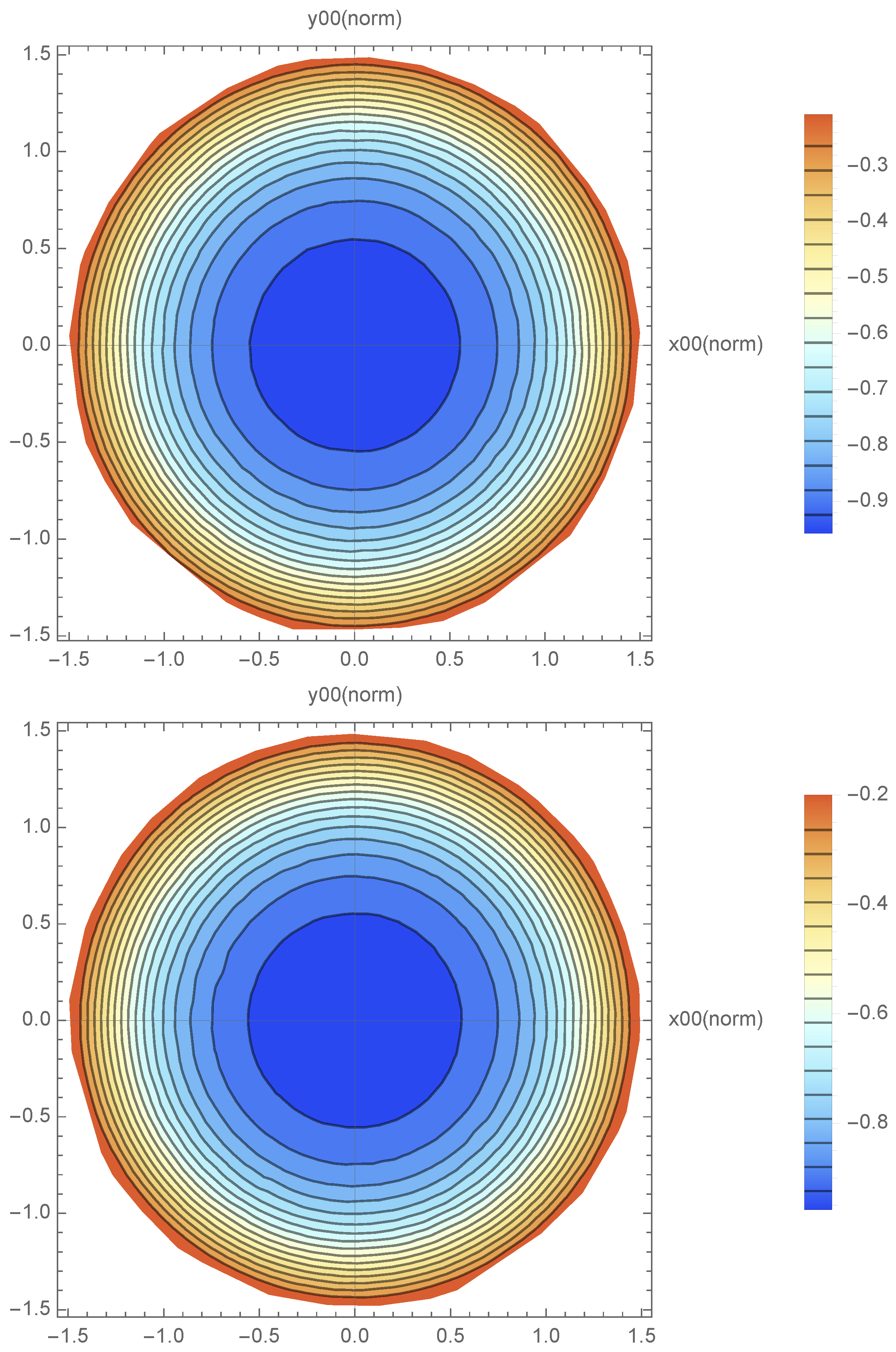
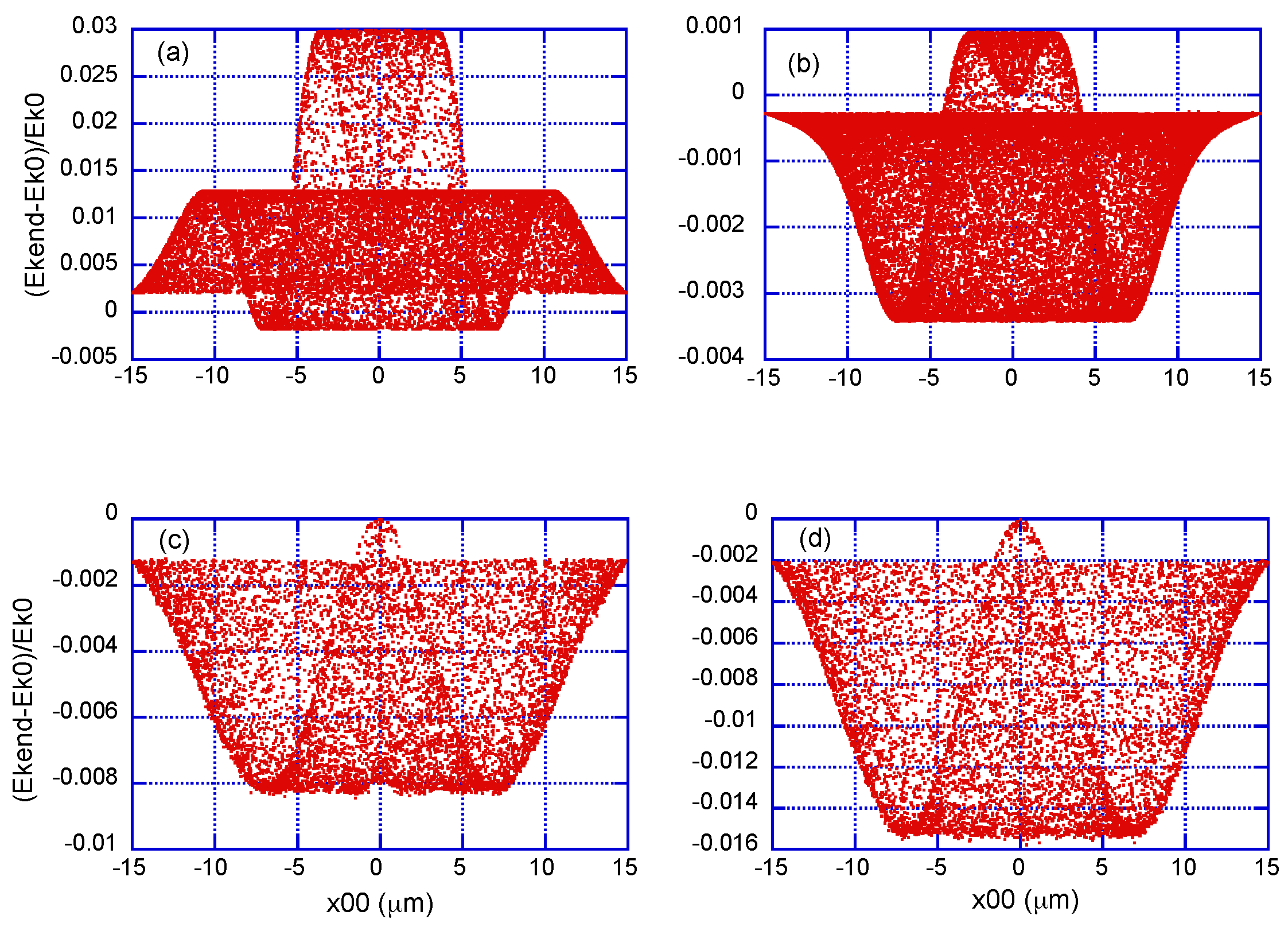
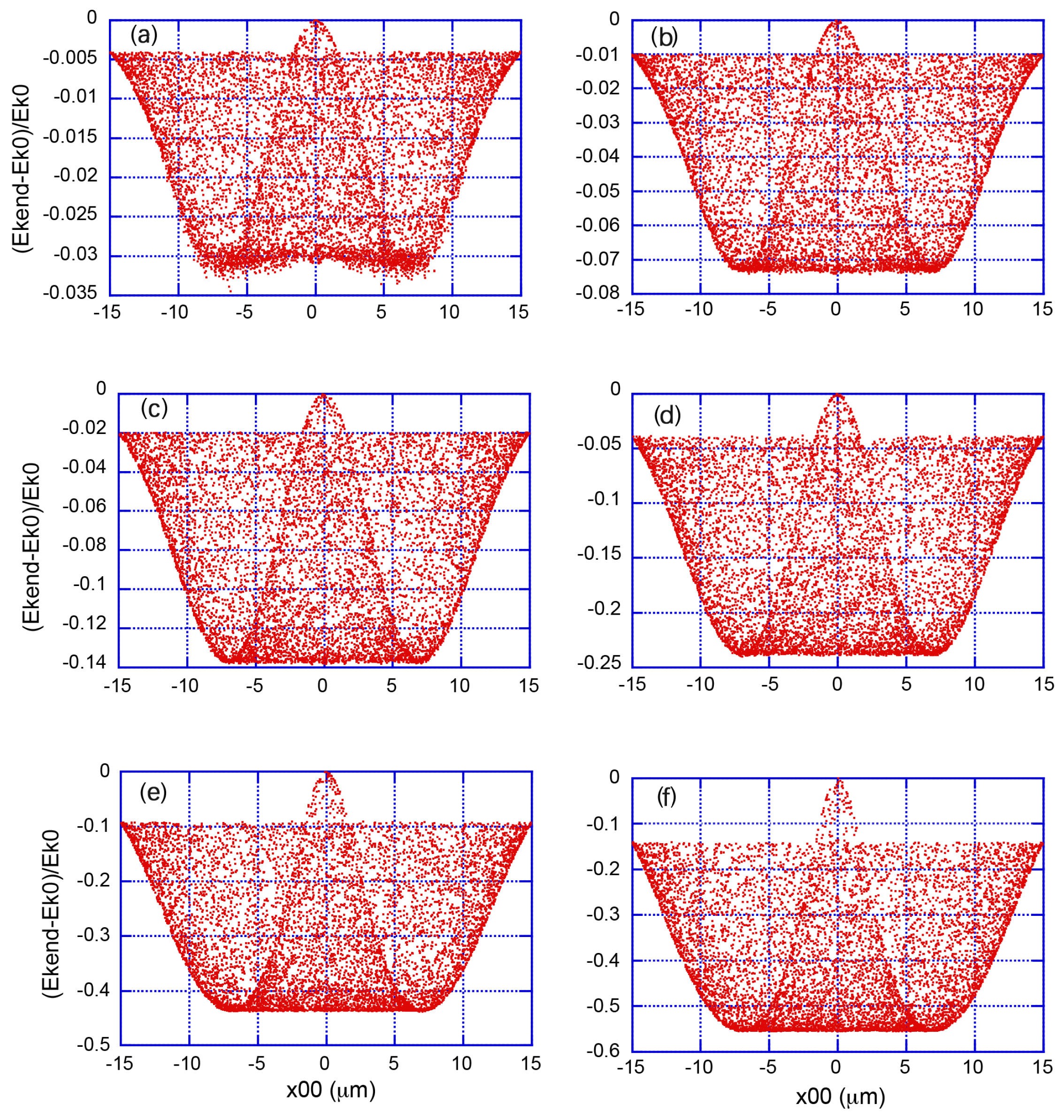
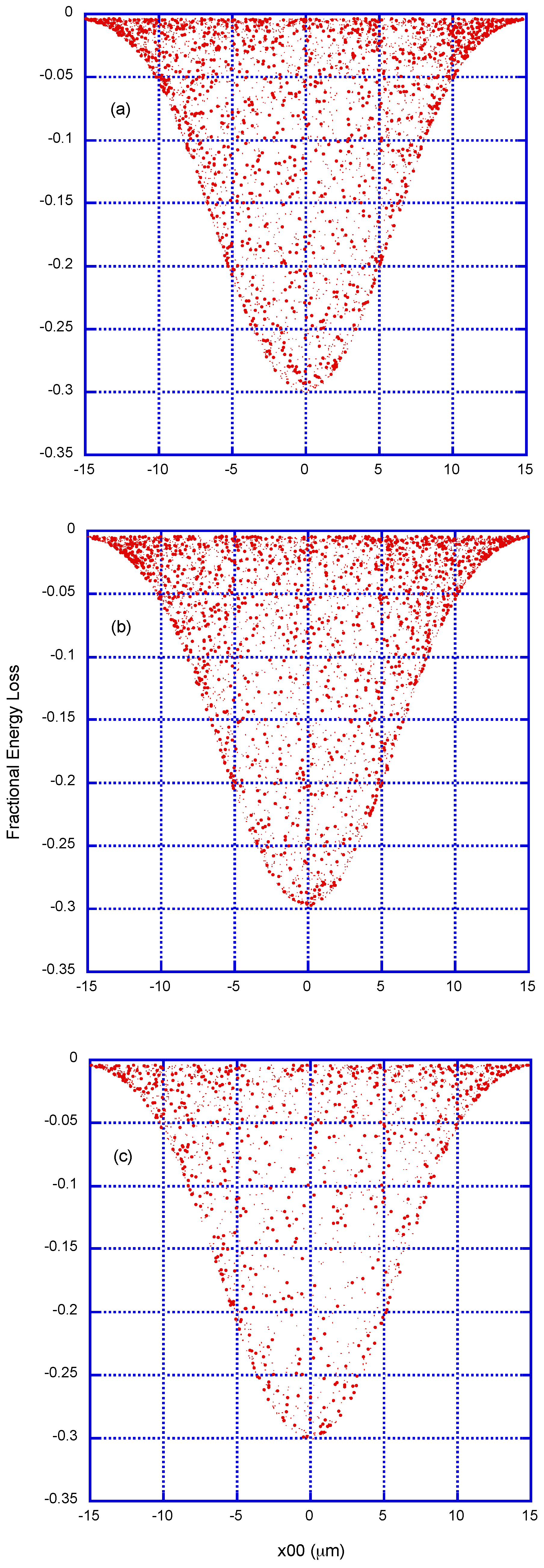
Figure 1 and Figure 2 show the asymptotic distributions of kinetic energy ($\Delta =(E_{kend}-E_{kin0})/E_{kin0}$, i.e., the fractional change in kinetic energy with respect to the initial one, is actually plotted) after the electrons have interacted with the laser, labeled with the initial value of the $x_{00}$ coordinate, for initial kinetic energies in the range from 5 MeV to 50 MeV (Figure 1) and from 100 MeV to 5 GeV (Figure 2). Actual 2D distributions should be visualized by rotating these plots around the vertical axis passing through $x_{00}=0$. In all the cases studied, the computed distributions are (to within numerical accuracy) rotationally symmetric with respect to the propagation direction of the laser.

For the smallest value of the initial kinetic energy (5 MeV), the prediction is a moderate gain of energy from the laser pulse, except perhaps at the very center of the transverse profile, even with the inclusion of radiation reaction. For progressively larger values of $E_{kin0}$, the effect of including radiation reaction is a net overall loss in energy, with a pattern reminiscent of the TEM₀₀ profile. At 5 GeV, there seems to be a flattening of the energy loss at a level of 80% of the initial energy. Please note that the reported energy losses are due specifically to radiation reaction: if this term is not included in the equations of motion, one obtains changes in the final energy (for $E_{kin0}=$ 500 MeV, say) that are typically less than a few parts in 10,000, even if the laser pulse is of very high intensity and has a nontrivial transverse structure. 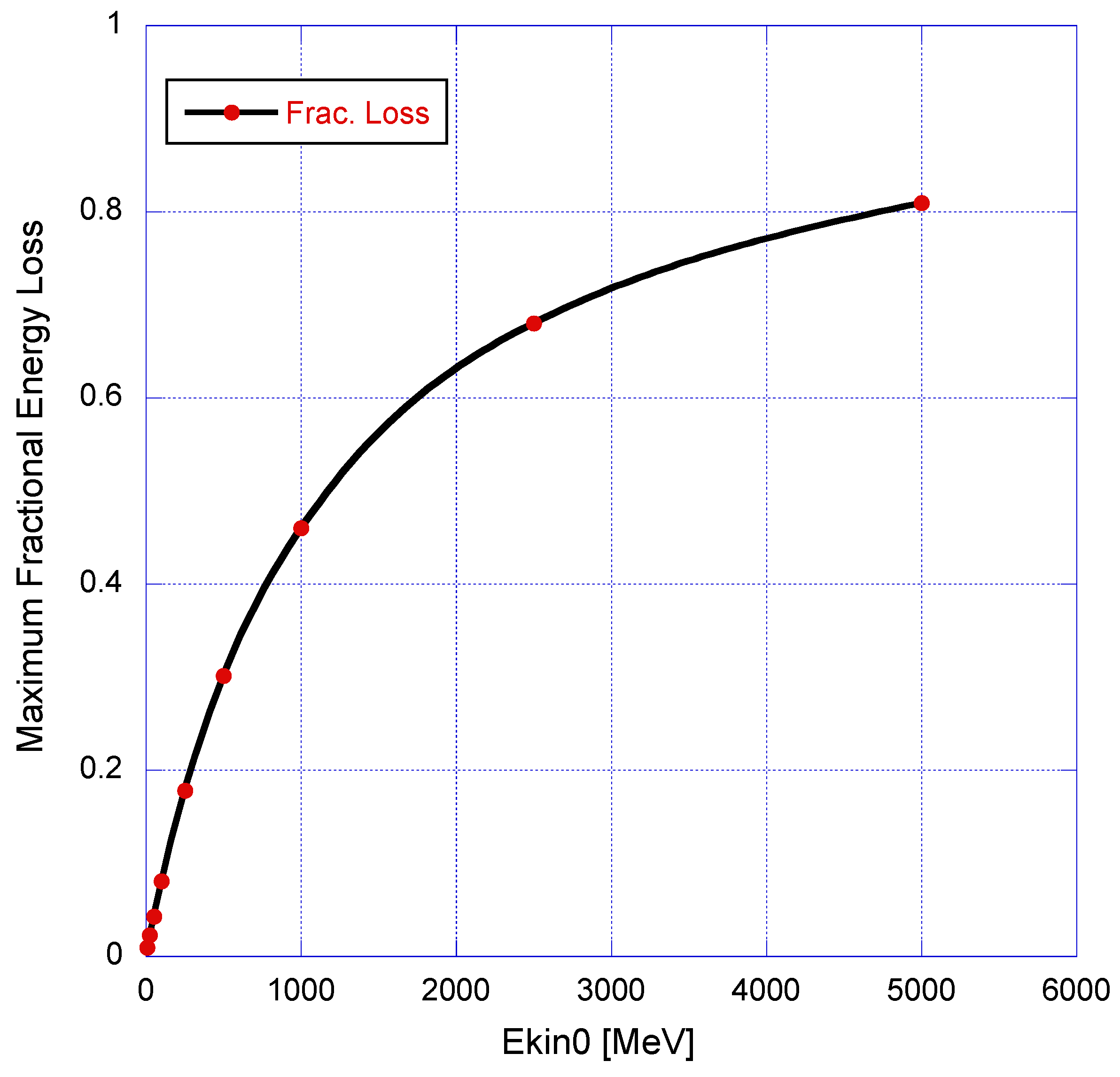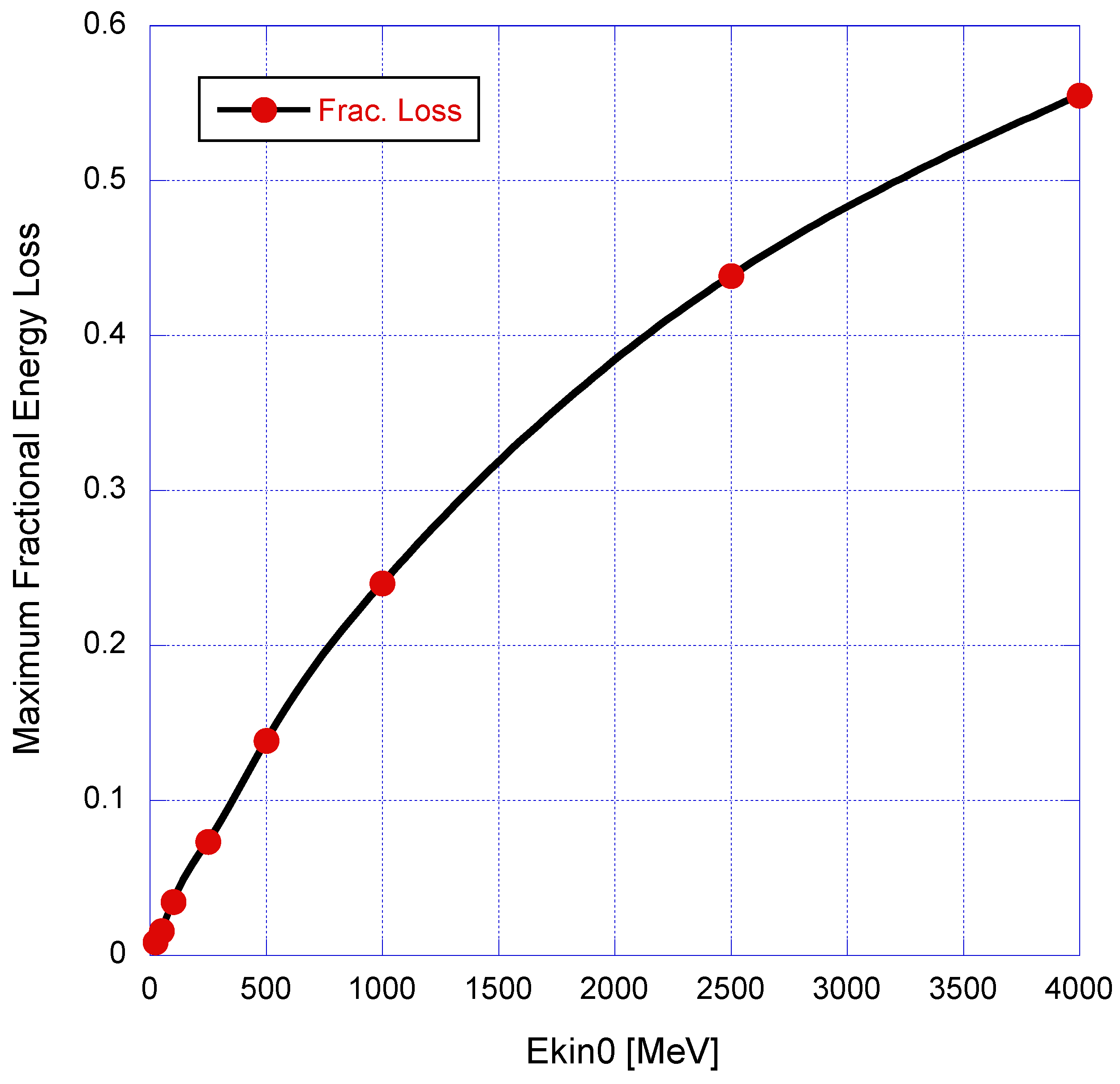Figure 3 gives the maximum fractional energy loss ($\Delta$) as a function of the initial kinetic energy $E_{kin0}$. As stated before, for the TEM₀₀ mode the largest energy loss occurs at or very near to the transverse pattern center, where the intensity of the laser is maximum.

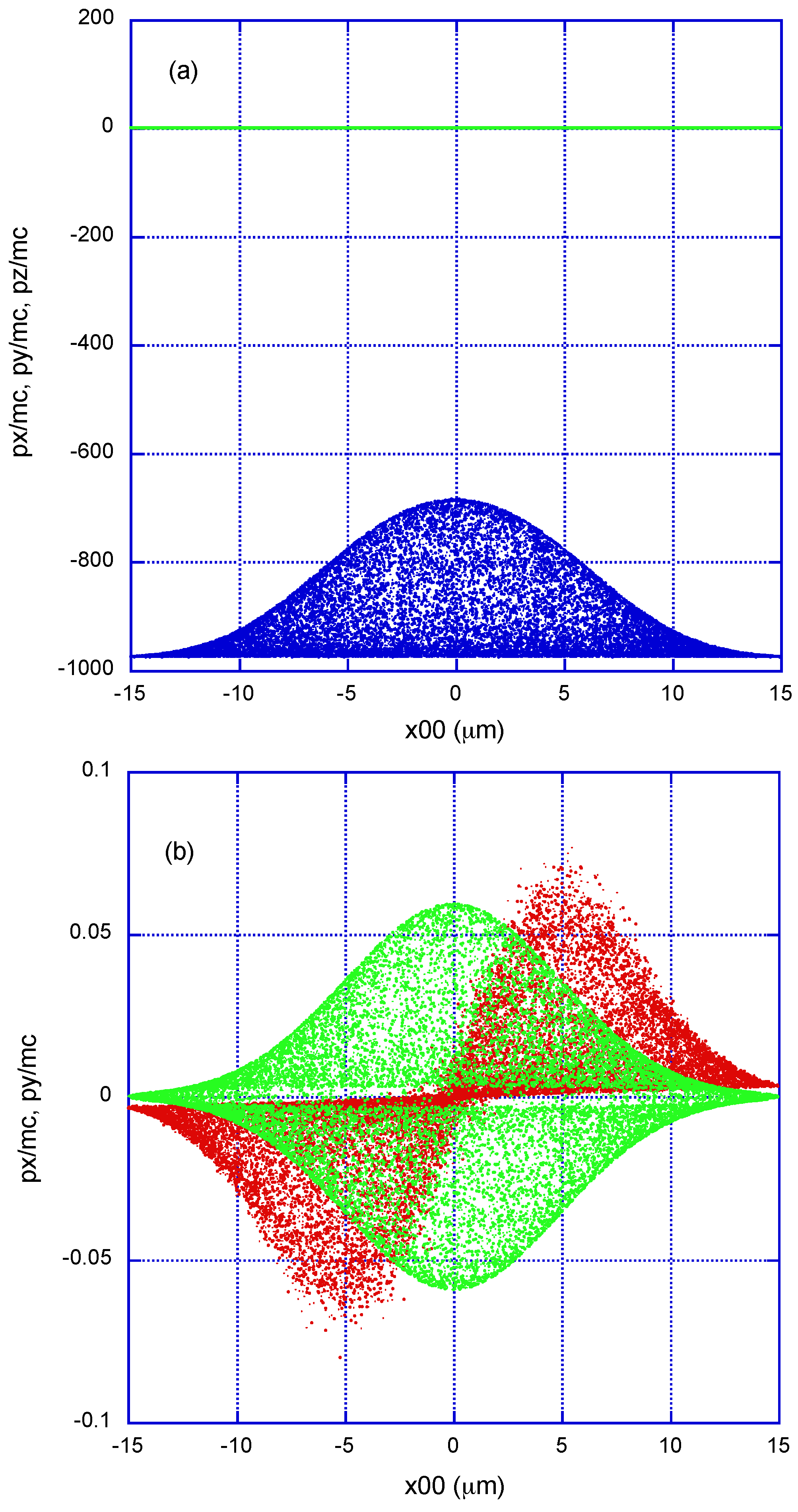
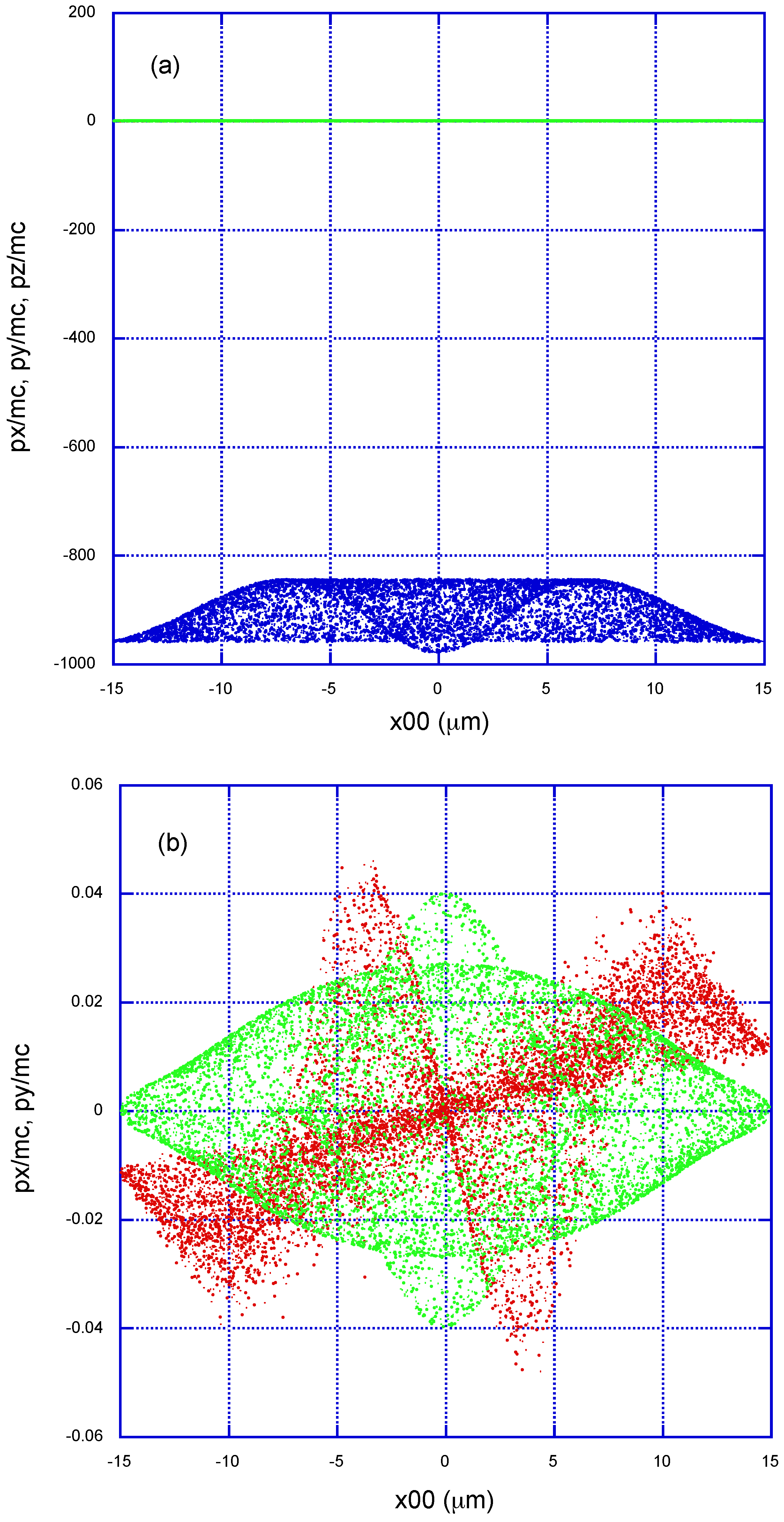
It is interesting to point out that the energy loss due to RR is (basically) linked to a braking of the relativistic linear momentum component along the laser propagation axis. This is shown in Figure 4, where the asymptotic distribution of the normalized momentum components ($\mathbf{p}/mc=\gamma \mathit{\beta }$) is given for the case of electrons of initial $E_{kin0}$ = 500 MeV. The color code in this figure is red, green, and blue correspond to $p_x/\left(mc\right),p_y/\left(mc\right)$, and $p_z/\left(mc\right)$, respectively. Panel (a) shows an asymptotic $p_z/\left(mc\right)$ distribution with the shape of the TEM₀₀ mode, with maximum braking (as an absolute value) in the order of 30%, coincident with the energy loss in Figure 2. The other two momentum components hardly contribute to the RR energy loss; i.e., it seems that at large energies the movement (including RR) is approximately one-dimensional, but not quite, as shown in the distributions of $p_x/\left(mc\right)$ and $p_y/\left(mc\right)$ in panel (b) of Figure 4. The asymptotic modulus of the momentum transverse to the propagation axis, $\sqrt{(}{p}_x^2+p_y^2)$, also shows a rotationally symmetric pattern, in this case with a symmetry similar to the intensity of the OAM $(l,p)=(1,0)$ mode.

As an extension to the results in this subsection, we report on scattering for a laser pulse of intensity 10²² W/cm² against an electron beam of 2.5 GeV, and for both $w_0=4$ $\mathsf{\mu }$m and $w_0=10$ $\mathsf{\mu }$m. Figure 5 shows that in terms of normalized transverse position, i.e., $x_{00}/w_0,y_{00}/w_0$ the asymptotic energy distributions are nearly the same for both beam waist sizes. A maximum of 95.7% energy loss from radiation reaction is found at positions near to the center of the TEM₀₀ profile, where the laser intensity is larger.

3.2. Scattering off a Laser Pulse in the OAM $(l,p)=(1,0)$ Mode

This subsection addresses the effect of radiation reaction (RR) in the scattering of electrons off an ultrashort and ultra-intense NIR laser pulse with net orbital angular momentum, namely, the OAM $(l,p)=(1,0)$ mode. Apart from the laser mode, the pulse characteristics and the initial kinetic energy of the incoming electrons are the same as in the previous subsection, except that the maximum energy studied here is 4 GeV instead of 5 GeV.

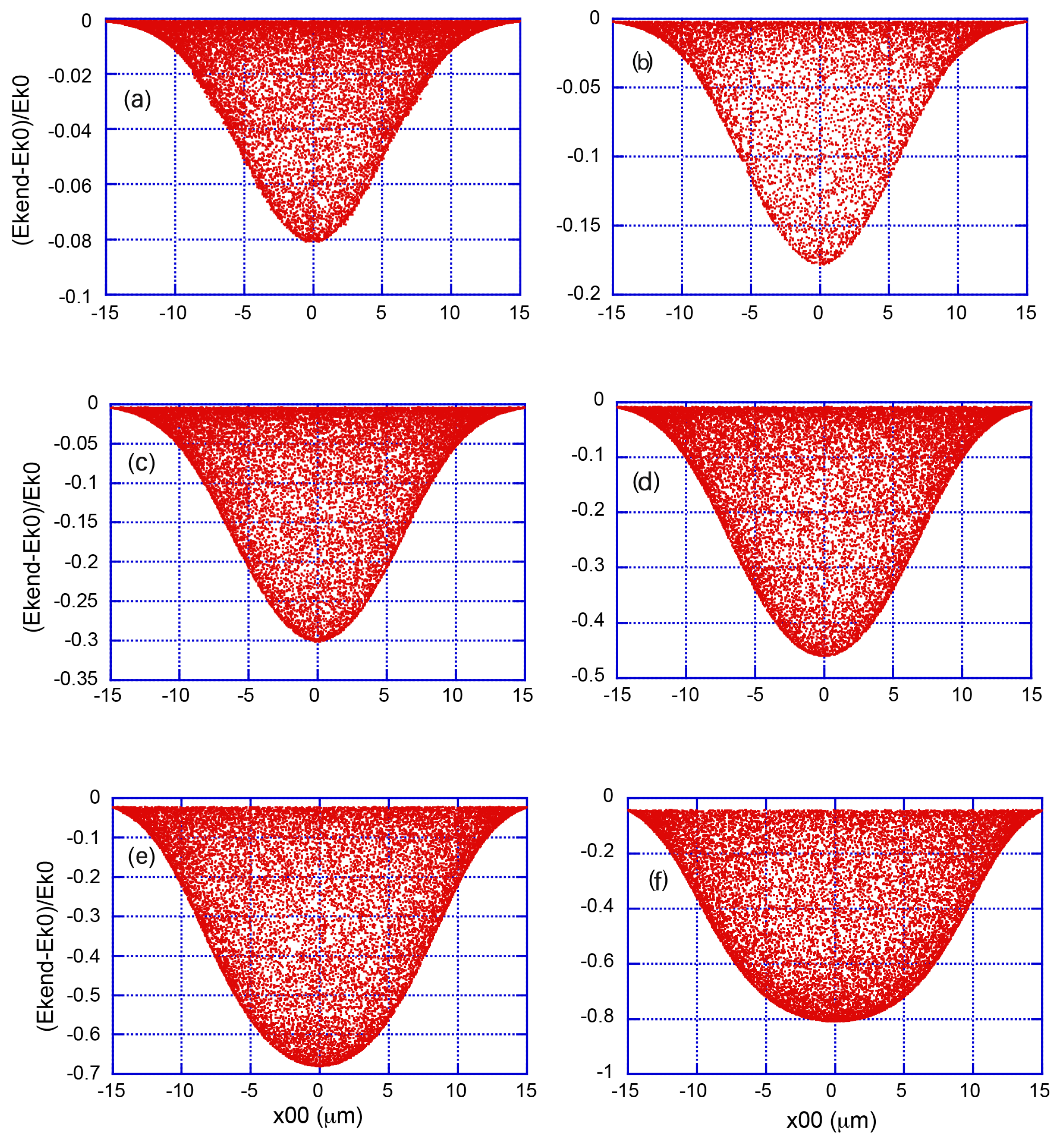
Figure 6 and Figure 7 give the asymptotic values of the kinetic energy as projected onto the x-axis. The computed distributions are (to within numerical accuracy) rotationally symmetric with respect to the propagation axis. At $E_{kin0}$ 5 MeV and 10 MeV there are more or less wide zones in $x_{00}$, for which there is a (moderate) energy gain. For $E_{kin0}\ge$ 25 MeV, there is an overall energy loss across the transverse beam pattern that should be attributed to the effect of radiation reaction, reaching a maximum of 55% energy loss at 4 GeV. The asymptotic energy pattern is now more complex, but closely resembles the intensity pattern of the OAM mode.

Figure 8 gives the maximum fractional energy loss as a function of initial kinetic energy $E_{kin0}$. For the OAM mode, this maximum energy loss occurs at or very near to the transverse pattern position(s), where the intensity of the laser fields is a maximum. When comparing the energy losses in both modes, one has to take into account the difference on maximum electric field, due to the definitions of laser fields given in Section 2.

In this case too, the energy loss due to RR is linked to a braking of the relativistic linear momentum component along the laser propagation axis. This is shown in Figure 9, where the asymptotic distribution of normalized momentum components ($\mathbf{p}/mc=\gamma \mathit{\beta }$) is given for the case of electrons of initial $E_{kin0}$ = 500 MeV. The color code in this figure is red, green, and blue correspond to $p_x/\left(mc\right),p_y/\left(mc\right)$, and $p_z/\left(mc\right)$, respectively. Figure 9a shows an asymptotic $p_z/\left(mc\right)$ distribution with a shape similar to the intensity of the OAM mode, and (maximum) braking values that compare very well with the maximum energy loss in the corresponding panel in Figure 7. The other two momentum components hardly contribute to the RR energy loss, i.e., it seems again, for the OAM mode, that at large energies the movement (including RR) is approximately one-dimensional.

4. Head-On Scattering off an Ultra-Intense Vacuum Ultra Violet (VUV) or X-ray Laser

There are by now some extremely high intensity free-electron laser facilities worldwide, the emission wavelengths of which can reach the VUV or even the X-ray domain. Of particular interest for us here are the European XFEL facility and LCLS-II (see, for example, [35,36] and references therein), which have plans to reach very substantial amounts of radiation at wavelengths as short as $0.4$ Å in the near future. According to the available information for these facilities, intensity levels in the order of ${10}^{21}$ W/cm² for pulses of a few tens of femtoseconds seem reasonable at those short wavelengths.

To compare the effects of RR in two quite-far-apart frequency (or wavelength) ranges, we have performed scattering computations for the following laser parameters: ${\lambda }_0$ = 80 nm or ${\lambda }_0$ = 8 nm, beam waist $w_0$ = 10 $\mathsf{\mu }$m, x-polarization, $A_{0x}=46.2560\times {10}^{-4}$ V.s/m (for ${\lambda }_0$ = 80 nm) or $A_{0x}=46.2560\times {10}^{-5}$ V.s/m (for ${\lambda }_0$ = 8 nm), equivalent in both cases to an intensity of ${10}^{21}$ W/cm², $T_{pulse}$ = 80 × ${\lambda }_0/c$ or $T_{pulse}$ = 800 × ${\lambda }_0/c$ according to the chosen wavelength, meaning a pulse length equal to the case of the NIR laser reported in Section 3. Notice that the waist for the VUV or X-ray laser is probably too large. However, we prefer to keep this value in order to facilitate a quick and direct comparison to the IR case. In all the cases, the Gaussian envelope of the laser pulse is initially well apart from the electron population, which means that it has (initially) a negligible influence on them.

Full paraxial $\mathbf{E}$ and $\mathbf{B}$ fields have been included, i.e., $B_z$ and $E_z$ are different from zero in general. Only the fundamental TEM₀₀ mode is considered in this section. The laser intensity is relevant to XFEL, and the chosen wavelength is within range of this facility. One should take into account that the shorter the fundamental ${\lambda }_0$ (and pulse lengths of a few tens of femtoseconds), the more optical cycles must be integrated in order to capture the electron dynamics.

Figure 10 shows the asymptotic energy distributions (in terms of $\Delta =(E_{kend}-E_{kin0})/E_{kin0}$) for three different wavelengths (800, 80, and 8 nm) and for $E_{kin0}=$ 500 MeV. The number of samples computed in the cases of 800 nm and 80 nm is 4096, while 2048 are used for 8 nm. It is found that, within numerical accuracy (to better than 0.3%), these distributions are the same, irrespective of the laser wavelength, provided pulse length, beam waist, and peak intensity are equal.

Although no change in the asymptotic energy distribution is found, the interaction of XFEL radiation with electrons in the hundreds of MeV energy range should give rise, in nearly forward scattering to the electron velocity, to extremely blue-shifted photons (taking into account that now the fundamental wavelength of the XFEL is extremely short) of $\lambda$ as short as ${10}^{-3}$ Å. An adequate control of these extremely short $\lambda$ photons may perhaps foster attosecond and/or nuclear photo-reactions research.

5. Conclusions and Discussion

Mono-energetic electrons with initial kinetic energies from 5.0 MeV up to 5.0 GeV, scattered by ultra-intense pulsed laser beams in head-on collision, are studied here. Two types of pulsed laser beams are considered in the paraxial approximation: the fundamental TEM₀₀ Gaussian mode and the OAM mode with $(l,p)=(1,0)$. Radiation reaction effects are accounted for by including the Landau–Lifshitz force [33] in the standard Lorentz equation for the electron: this furnishes a rather practical approximation. The electron samples that are scattered by the laser pulse are shaped initially as a disk extending randomly and uniformly up to a radius of 1.5 $\times w_0$, with $z_{00}$ = 0. The laser/electron interaction time is sufficiently long so that the final state of the latter is a free, constant velocity motion. Under these conditions, the asymptotic distributions for energy and/or momentum are computed against the initial electron positions, taken as a label for the electrons in the sample.

From initial energies of 25 MeV and higher, the inclusion of radiation reaction implies an overall energy loss to the electrons, with a transverse pattern which is rotationally symmetric and very close in shape to the transverse intensity of the laser. At a fixed intensity of ${10}^{21}$ W/cm², the maximum fractional energy loss increases with energy, reaching 80% at $E_{kin0}=$ 5 GeV for the TEM₀₀ mode. Sample results for $E_{kin0}=$ 2.5 GeV and a laser intensity of ${10}^{22}$ W/cm² show that the maximum energy loss reaches 95.7% at positions near to the center of the TEM₀₀ profile, where the laser intensity is larger.

Computations have been performed mainly assuming that the laser wavelength is in the near-infrared range, ${\lambda }_0=$ 800 nm. However, the influence of the wavelength on radiation reaction is also investigated, with the aim of extending the results in the NIR domain towards the new facilities operating at VUV or even X-ray wavelengths. The results obtained at ${\lambda }_0=$ 80 nm and ${\lambda }_0=$ 8 nm (VUV and X-ray ranges) suggest that (keeping the pulse length and power level constant) wavelength has a negligible influence on the asymptotic energy distribution.

It is numerically found that the asymptotic energy ($m_0{c}^2(\gamma -1)$) and normalized momentum $(p_z/mc)$ distributions are closely linked, with the projection of the momentum transverse to the main propagation direction playing a minor role. Especially at large $E_{kin0}$, the motion seems to become simplified, being nearly one-dimensional. These aspects should perhaps be further investigated in the case of very tight laser focus (very small beam waist, $w_0$), since then it would be known whether the longitudinal (paraxial) field components would become larger, with a potential influence on dynamics.

The computations reported in this paper can be extended to include the emitted radiation, and the authors are currently working on this issue. Once this has been achieved, we could contribute to simulate experiments like those reported in [23], as well as other scenarios that have been receiving recent interest, like the interaction of high-energy electrons from conventional accelerators with ultra-intense lasers. The experimental results reported in [23] are rather challenging to simulate, since they include a broadband spectrum of electrons as well as the betatron radiation, in addition to plasma instabilities due to the filamentation processes along the gas target. Hence, they combine the RR effect we are interested in with other phenomenology that can mask the results on RR. In turn, we propose to study a much cleaner scenario, a MeV–GeV electron beam with a (relatively) narrow energy spectrum (accelerated with a conventional accelerator). This scenario is possible in systems as the European XFEL HIBEF experiment, among others. The idea of including ultrafast ultra-intense lasers against GeV electron beams has been receiving growing attention in recent years and our studied scenario is quite relevant for that purpose.

This paper investigates a basic phenomenon which may be the first to become manifest as the power of the laser beam becomes increasingly intense: the radiation reaction effects on relativistic electrons. This is accomplished for electron energies covering three orders of magnitude and for intensities up to ${10}^{22}$ W/cm², which are now available in the most advanced extreme light facilities worldwide. That makes the various predictions obtained here a target for experimental tests.