A Comprehensive Study on Elasticity and Viscosity in Biomechanics and Optical Properties of the Living Human Cornea
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants
2.2. In Vivo Corneal Assessment: Geometrical, Optical and Biomechanical Corneal Parameters
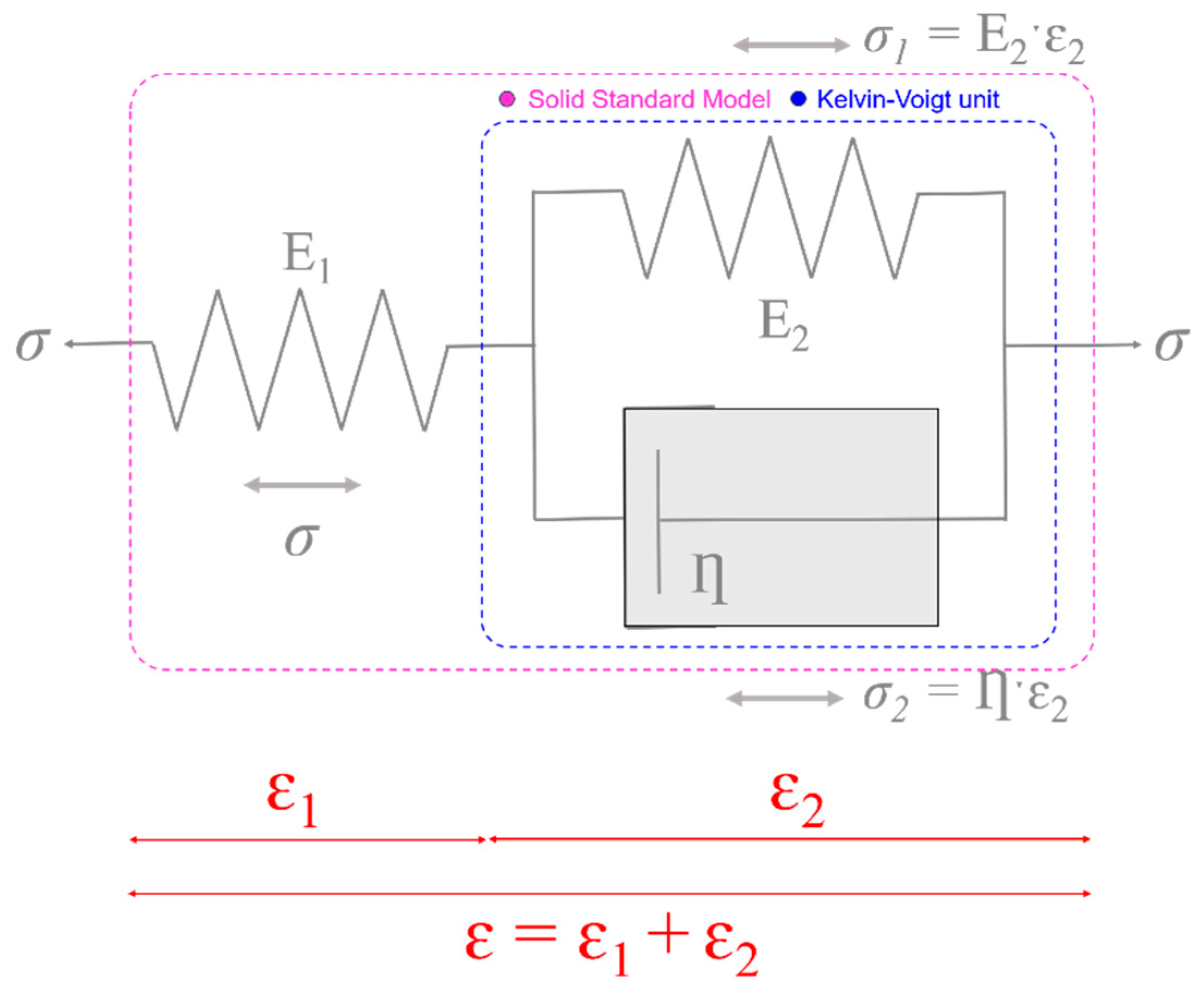
2.3. The Three-Element Standard Linear Solid Model
2.4. Experimental Calculation of Elastic and Time-Dependent Biomechanical Properties
2.5. Statistical Analysis
3. Results
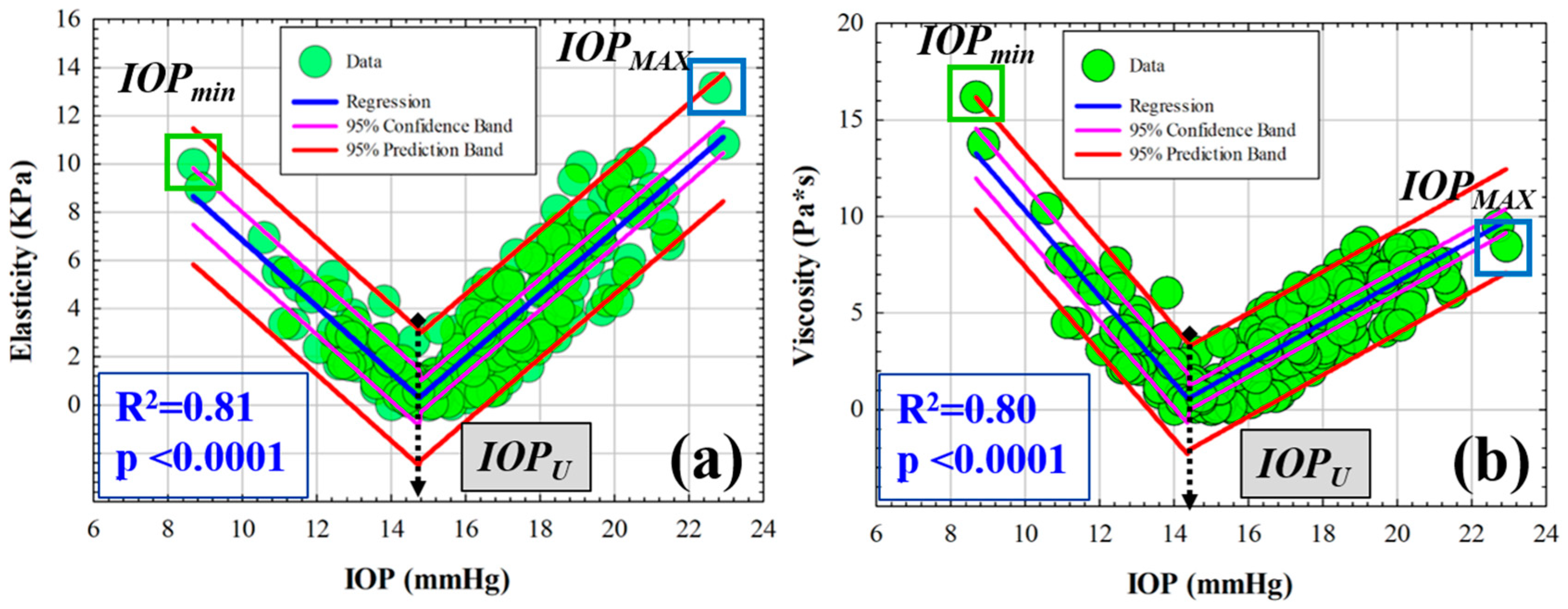
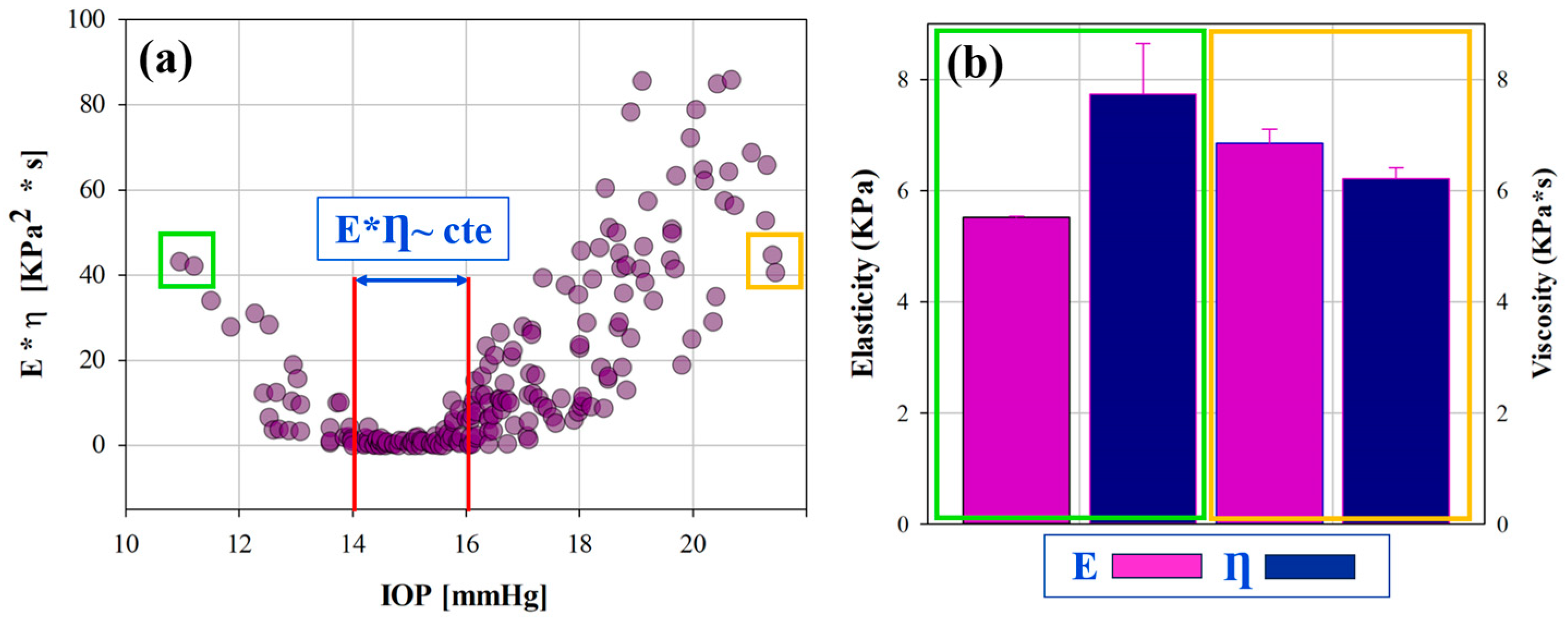
3.1. Efect of IOP on Elastic, Viscoelastic and Viscous Properties of the Cornea
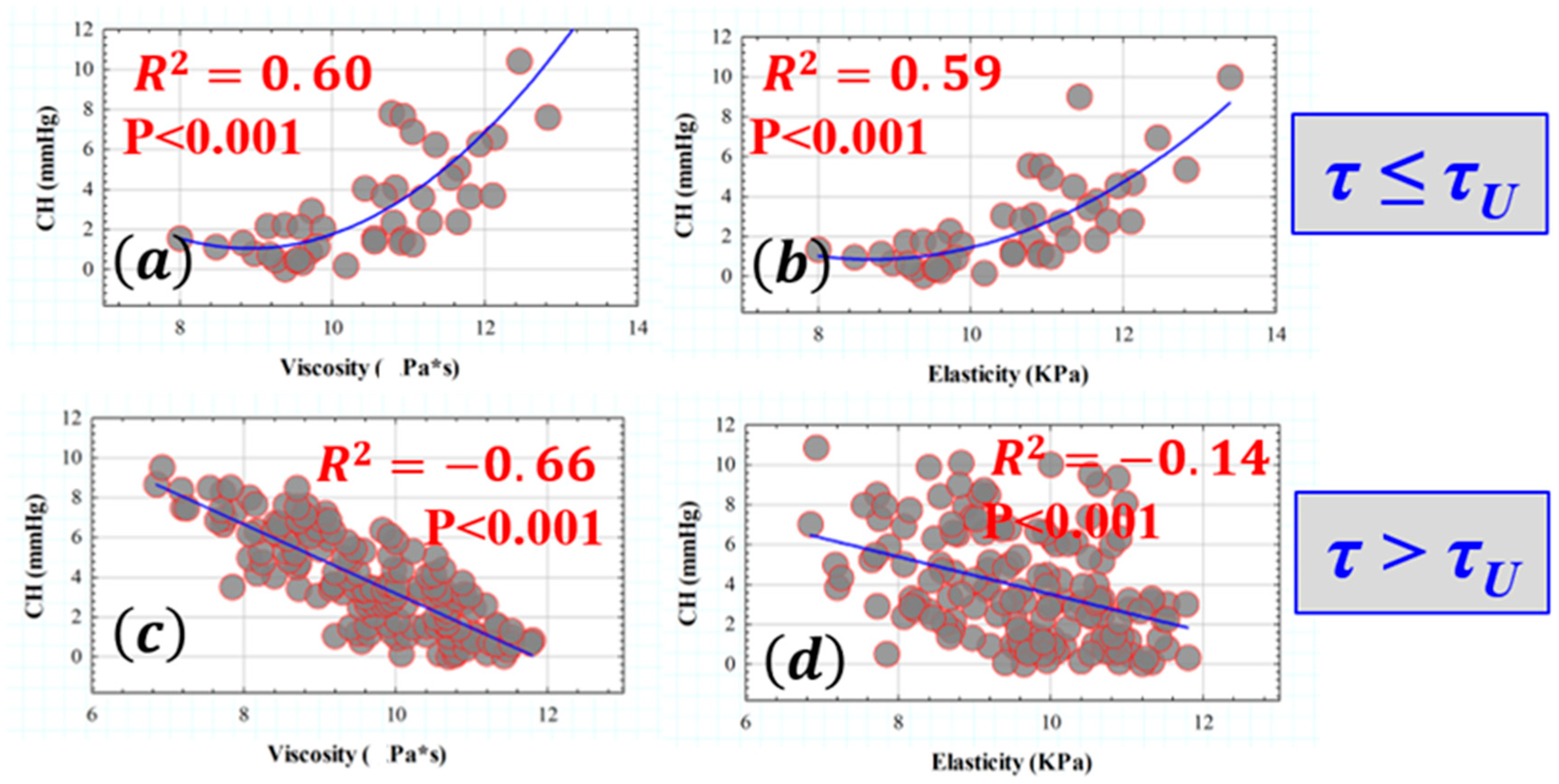
3.2. Retardation Time as a Biomechanical Behavior Threshold: Role of Elasticity and Viscosity on Corneal Viscoelasticity
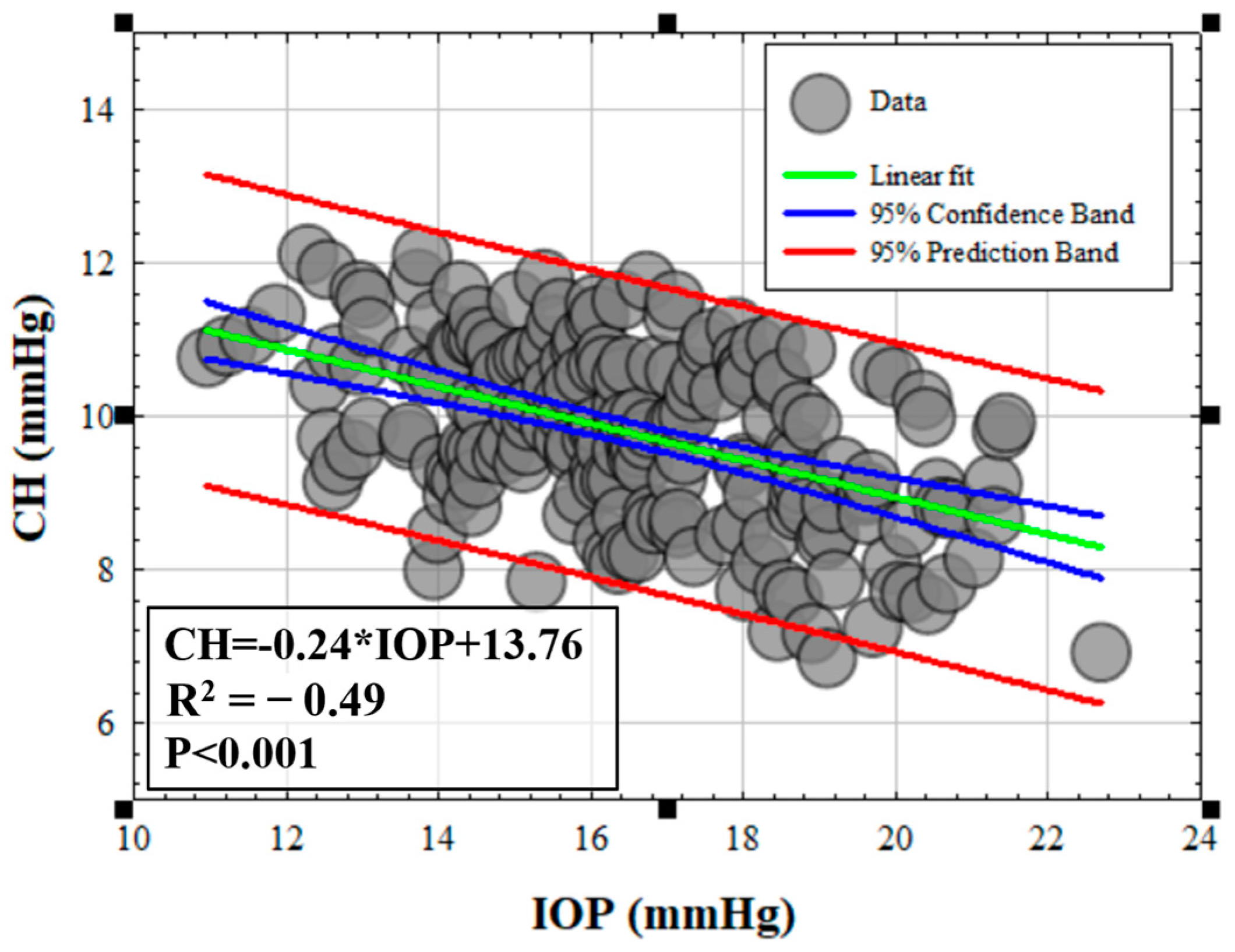
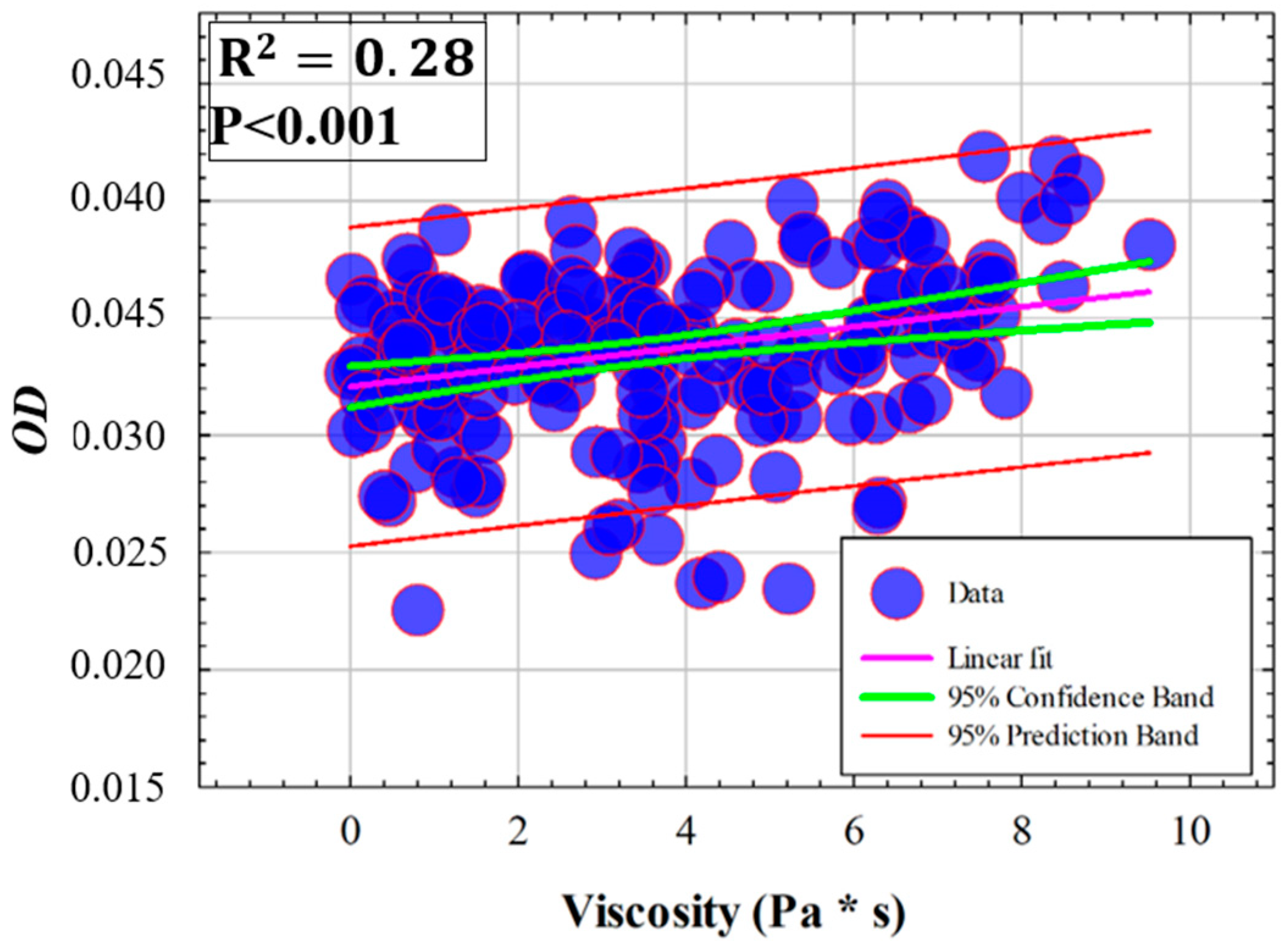
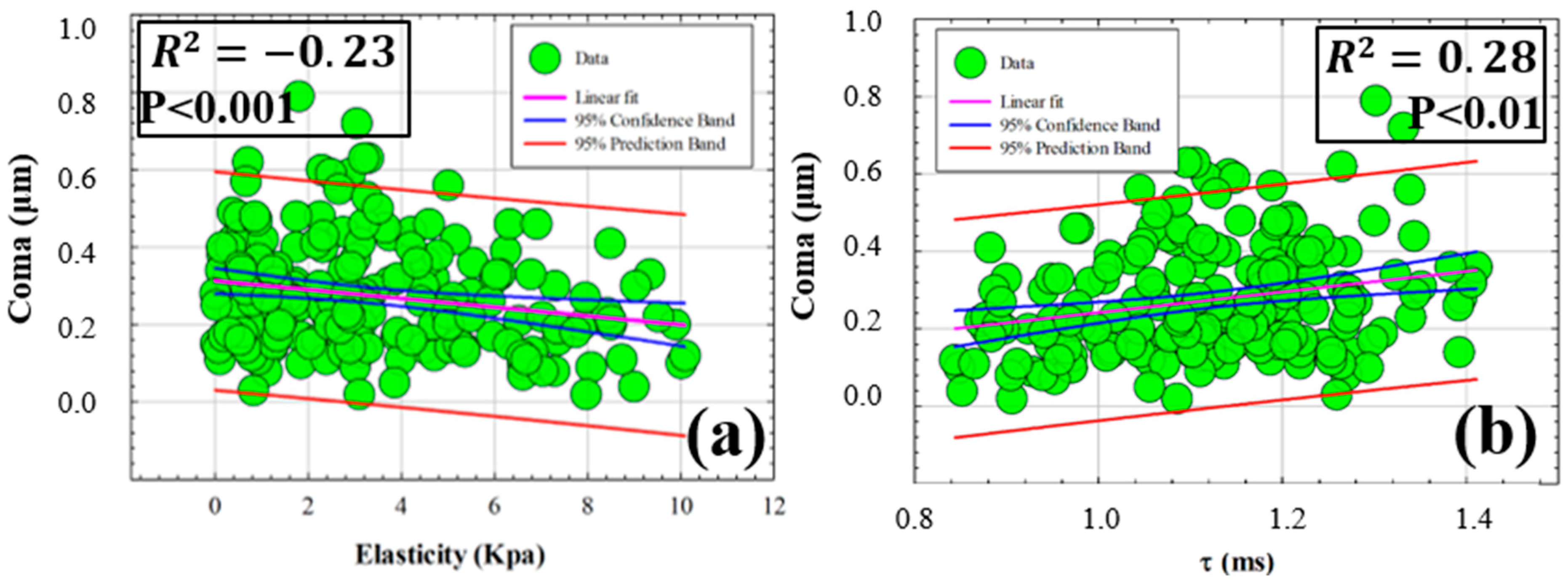
3.3. Influence of Elasticity and Time-Dependent Parameters on Corneal Optical Properties
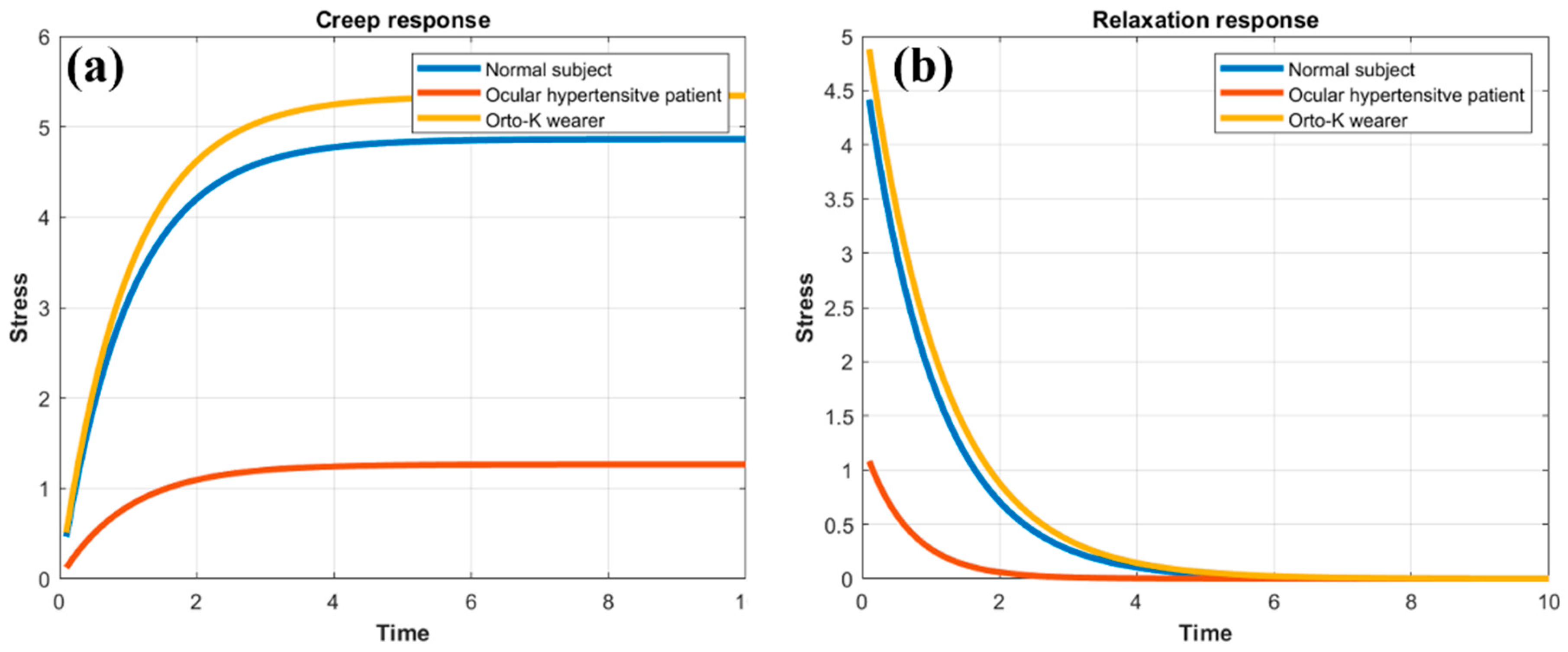
3.4. Creep Relaxation Response of the Human Cornea as a Function of Elasticity and Viscosity
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Meek, K.M. Corneal collagen–its role in maintaining corneal shape and transparency. Biophys. Rev. 2009, 1, 83–93. [Google Scholar] [CrossRef] [PubMed]
- Espana, E.M.; Birk, D.E. Composition, structure and function of the corneal stroma. Exp. Eye Res. 2020, 198, 108137. [Google Scholar] [CrossRef] [PubMed]
- Meek, K.M.; Knupp, C. Corneal structure and transparency. Prog. Retin. Eye Res. 2015, 49, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Bell, J.S.; Hayes, S.; Whitford, C.; Sanchez-Weatherby, J.; Shebanova, O.; Terrill, N.J.; Sørensen, T.L.M.; Elsheikh, A.; Meek, K.M. Tropocollagen springs allow collagen fibrils to stretch elastically. Acta Biomater. 2022, 142, 185–193. [Google Scholar] [CrossRef] [PubMed]
- Chong, J.; Dupps, W.J., Jr. Corneal biomechanics: Measurement and structural correlations. Exp. Eye Res. 2021, 205, 108508. [Google Scholar] [CrossRef] [PubMed]
- Wilson, A.; Marshall, J. A review of corneal biomechanics: Mechanisms for measurement and the implications for refractive surgery. Indian J. Ophthalmol. 2020, 68, 2679–2690. [Google Scholar] [PubMed]
- Marinescu, M.; Dascalescu, D.; Constantin, M.; Coviltir, V.; Burcel, M.; Darabus, D.; Ciuluvica, R.; Stanila, D.; Potop, V.; Alexandrescu, C. Corneal Biomechanics—An Emerging Ocular Property with a Significant Impact. Maedica 2022, 17, 925–930. [Google Scholar] [PubMed]
- Kaushik, S.; Pandav, S.S. Ocular Response Analyzer. J. Curr. Glaucoma Pract. 2012, 6, 17–19. [Google Scholar] [CrossRef] [PubMed]
- Lan, G.; Twa, M.D.; Song, C.; Feng, J.; Huang, Y.; Xu, J.; Qin, J.; An, L.; Wei, X. In vivo corneal elastography: A topical review of challenges and opportunities. Comput. Struct. Biotechnol. J. 2023, 21, 2664–2687. [Google Scholar] [CrossRef]
- Eltony, A.M.; Shao, P.; Yun, S.H. Measuring mechanical anisotropy of the cornea with Brillouin microscopy. Nat. Commun. 2022, 13, 1354. [Google Scholar] [CrossRef]
- Terai, N.; Raiskup, F.; Haustein, M.; Pillunat, L.E.; Spoerl, E. Identification of biomechanical properties of the cornea: The ocular response analyzer. Curr. Eye Res. 2012, 37, 553–562. [Google Scholar] [CrossRef] [PubMed]
- Salouti, R.; Bagheri, M.; Shamsi, A.; Zamani, M. Corneal Parameters in Healthy Subjects Assessed by Corvis ST. J. Ophthalmic Vis. Res. 2020, 15, 24–31. [Google Scholar] [CrossRef] [PubMed]
- Yun, S.H.; Chernyak, D. Brillouin microscopy: Assessing ocular tissue biomechanics. Curr. Opin. Ophthalmol. 2018, 29, 299–305. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Asroui, L.; Tarib, I.; Dupps, W.J., Jr.; Scarcelli, G.; Randleman, J.B. Motion-Tracking Brillouin Microscopy Evaluation of Normal, Keratoconic, and Post-Laser Vision Correction Corneas. Am. J. Ophthalmol. 2023, 254, 128–140. [Google Scholar] [CrossRef] [PubMed]
- Ávila, F.J.; Marcellán, M.C.; Remón, L. In Vivo Biomechanical Response of the Human Cornea to Acoustic Waves. Optics 2023, 4, 584–594. [Google Scholar] [CrossRef]
- Kobayashi, A.S.; Staberg, L.G.; Schlegel, W.A. Viscoelastic properties of human cornea. Exp. Mech. 1973, 13, 497–503. [Google Scholar] [CrossRef]
- Lakes, R.S. Viscoelastic Solids; CRC Press: Boca Raton, FL, USA, 1999; pp. 15–61. [Google Scholar]
- Zimprich, L.; Diedrich, J.; Bleeker, A.; Schweitzer, J.A. Corneal Hysteresis as a Biomarker of Glaucoma: Current Insights. Clin. Ophthalmol. 2020, 14, 2255–2264. [Google Scholar] [CrossRef] [PubMed]
- Glass, D.H.; Roberts, C.J.; Litsky, A.S.; Weber, P.A. A Viscoelastic Biomechanical Model of the Cornea Describing the Effect of Viscosity and Elasticity on Hysteresis. Investig. Ophthalmol. Vis. Sci. 2008, 49, 3919–3926. [Google Scholar] [CrossRef] [PubMed]
- Su, P.; Yang, Y.; Xiao, J.; Song, Y. Corneal hyper-viscoelastic model: Derivations, experiments, and simulations. Acta Bioeng. Biomech. 2015, 17, 73–84. [Google Scholar]
- Whitford, C.; Movchan, N.V.; Studer, H.; Elsheikh, A. A viscoelastic anisotropic hyperelastic constitutive model of the human cornea. Biomech. Model. Mechanobiol. 2018, 17, 19–29. [Google Scholar] [CrossRef]
- Ahmed, H.M.; Salem, N.M.; Al-Atabany, W. Human cornea thermo-viscoelastic behavior modelling using standard linear solid model. BMC Ophthalmol. 2023, 23, 250. [Google Scholar] [CrossRef] [PubMed]
- Kelly, P. Solid Mechanics Part I: An Introduction to Solid Mechanics Solid Mechanics Lecture Notes University of Auckland. 2013. Available online: https://pkel015.connect.amazon.auckland.ac.nz/SolidMechanicsBooks/Part_I/index.html (accessed on 29 April 2024).
- Liu, J.; Roberts, C.J. Influence of corneal biomechanical properties on intraocular pressure measurement: Quantitative analysis. J. Cataract. Refract. Surg. 2005, 31, 146–155. [Google Scholar] [CrossRef] [PubMed]
- Brinson, H.F.; Brinson, L.C. Polymer Engineering Science and Viscoelasticity; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Jannesari, M.; Mosaddegh, P.; Kadkhodaei.; Kasprzak, H.; Jabbarvand Behrouz, M. Numerical and clinical investigation on the material model of the cornea in Corvis tonometry tests: Differentiation between hyperelasticity and viscoelasticity. Mech. Time Depend. Mater. 2018, 23, 373–384. [Google Scholar] [CrossRef]
- Barco, O.; Ávila, F.J.; Marcellán, C.; Remón, L. Corneal retardation time as an ocular hypertension disease indicator. Biomed. Phys. Eng. Express 2024, 10, 015014. [Google Scholar] [CrossRef] [PubMed]
- Deol, M.; Taylor, D.A.; Radcliffe, N.M. Corneal hysteresis and its relevance to glaucoma. Curr. Opin. Ophthalmol. 2015, 26, 96–102. [Google Scholar] [CrossRef] [PubMed]
- Mikula, E.R.; Jester, J.V.; Juhasz, T. Measurement of an Elasticity Map in the Human Cornea. Investig. Ophthalmol. Vis. Sci. 2016, 57, 3282–3286. [Google Scholar] [CrossRef] [PubMed]
- Rahmati, S.M.; Razaghi, R.; Karimi, A. Biomechanics of the keratoconic cornea: Theory, segmentation, pressure distribution, and coupled FE-optimization algorithm. J. Mech. Behav. Biomed. Mater. 2021, 113, 104155. [Google Scholar] [CrossRef] [PubMed]
- Francis, M.; Matalia, H.; Nuijts, R.M.M.A.; Haex, B.; Shetty., R.; Sinha Roy, A. Corneal Viscous Properties Cannot Be Determined From Air-Puff Applanation. J. Refract. Surg. 2019, 35, 730–736. [Google Scholar] [CrossRef] [PubMed]
- Dana, D.; Mihaela, C.; Raluca, I.; Miruna, C.; Catalina, I.; Miruna, C.; Schmitzer, S.; Catalina, C. Corneal hysteresis and primary open angle glaucoma. Rom. J. Ophthalmol. 2015, 59, 252–254. [Google Scholar]
- Nossair, A.A.; Kassem, M.K.; Eltanamly, R.M.; Alahmadawy, Y.A. Corneal Hysteresis, Central Corneal Thickness, and Intraocular Pressure in Rheumatoid Arthritis, and Their Relation to Disease Activity. Middle East Afr. J. Ophthalmol. 2021, 28, 174–179. [Google Scholar]
- Murtagh, P.; O’Brien, C. Corneal Hysteresis, Intraocular Pressure, and Progression of Glaucoma: Time for a “Hyst-Oric” Change in Clinical Practice? J. Clin. Med. 2022, 11, 2895. [Google Scholar] [CrossRef] [PubMed]
- Blanco-Dominguez, I.; Duch, F.; Reyes, J.; Polo, V.; Abad, J.M.; Gomez-Barrera, M.; Olate-Perez, Á. Permanent corneal opacification after refractive surgery with a combined technique: Photorefractive keratectomy (PRK) and accelerated cross-linking (PRK Xtra) in healthy patients. J. Français D’ophtalmologie 2021, 44, e141–e143. [Google Scholar] [CrossRef] [PubMed]
- Abyaneh, M.H.; Wildman, R.D.; Ashcroft, I.A.; Ruiz, P.D. A hybrid approach to determining cornea mechanical properties in vivo using a combination of nano-indentation and inverse finite element analysis. J. Mech. Behav. Biomed. Mater. 2013, 27, 239–248. [Google Scholar] [CrossRef] [PubMed]
- Lombardo, G.; Serrao, S.; Rosati, M.; Lombardo, M. Analysis of the viscoelastic properties of the human cornea using Scheimpflug imaging in inflation experiment of eye globes. PLoS ONE 2014, 9, e112169. [Google Scholar] [CrossRef]
- Touboul, D.; Roberts, C.; Kérautret, J.; Garra, C.; Maurice-Tison, S.; Saubusse, E.; Colin, J. Correlations between corneal hysteresis, intraocular pressure, and corneal central pachymetry. J. Cataract. Refract. Surg. 2008, 34, 616–622. [Google Scholar] [CrossRef]


| Parameter [Units] | Technology | Description |
|---|---|---|
| Rcor (mm) | Dual Scheimpflug analyzer | Mean corneal radii |
| 2·Xcor (mm) | Dual Scheimpflug analyzer | Corneal applanation diameter |
| CCT (μm) | Dual Scheimpflug analyzer | Central corneal thickness |
| OD (n.u) | Dual Scheimpflug analyzer | Optical density |
| SA (μm) | Dual Scheimpflug analyzer | Spherical aberration |
| Trefoil (μm) | Dual Scheimpflug analyzer | Trefoil term |
| Coma (μm) | Dual Scheimpflug analyzer | Coma term |
| IOPcc (mmHg) | ORA | Corneal-compensated intraocular pressure |
| CH (mmHg) | ORA | Corneal hysteresis |
| (a) | ||||||
|---|---|---|---|---|---|---|
| IOPcc (mmHg) | CCT (μm) | Rcor (mm) | CH (mmHg) | E (KPa) | Ƞ (Pa· s) | Τ (ms) |
| 16.51 ± 2.32 | 555.75 ± 29.49 | 7.89 ± 0.30 | 9.78 ± 1.16 | 3.44 ± 2.67 | 3.57 ± 2.39 | 1.12 ± 0.13 |
| (b) | ||||||
| OD (pd/μm) | SA (μm) | Trefoil (μm) | Coma (μm) | |||
| 0.034 ± 0.004 | −0.15 ± 0.08 | 0.19 ± 0.13 | 0.27 ± 0.14 | |||
| Normal Cornea | Ocular Hypertensive | Ortho-K User | |
|---|---|---|---|
| E (Kpa) | 3.44 | 13.23 | 3.13 |
| Ƞ (Pa · s) | 3.57 | 8.62 | 3.47 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ávila, F.J.; del Barco, Ó.; Marcellán, M.C.; Remón, L. A Comprehensive Study on Elasticity and Viscosity in Biomechanics and Optical Properties of the Living Human Cornea. Photonics 2024, 11, 524. https://doi.org/10.3390/photonics11060524
Ávila FJ, del Barco Ó, Marcellán MC, Remón L. A Comprehensive Study on Elasticity and Viscosity in Biomechanics and Optical Properties of the Living Human Cornea. Photonics. 2024; 11(6):524. https://doi.org/10.3390/photonics11060524
Chicago/Turabian StyleÁvila, Francisco J., Óscar del Barco, María Concepción Marcellán, and Laura Remón. 2024. "A Comprehensive Study on Elasticity and Viscosity in Biomechanics and Optical Properties of the Living Human Cornea" Photonics 11, no. 6: 524. https://doi.org/10.3390/photonics11060524
APA StyleÁvila, F. J., del Barco, Ó., Marcellán, M. C., & Remón, L. (2024). A Comprehensive Study on Elasticity and Viscosity in Biomechanics and Optical Properties of the Living Human Cornea. Photonics, 11(6), 524. https://doi.org/10.3390/photonics11060524






