Experimental State Observer of the Population Inversion of a Multistable Erbium-Doped Fiber Laser
Abstract
1. Introduction
2. Laser Model
2.1. Complete EDFL Model
2.2. Normalized Equations of EDFL
3. State Observer Design
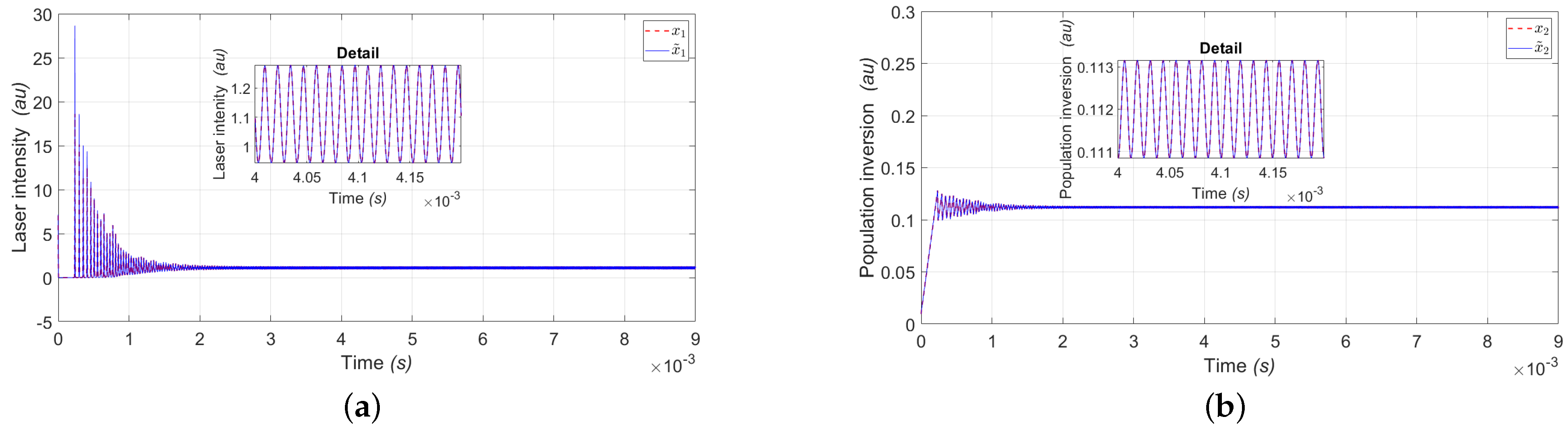
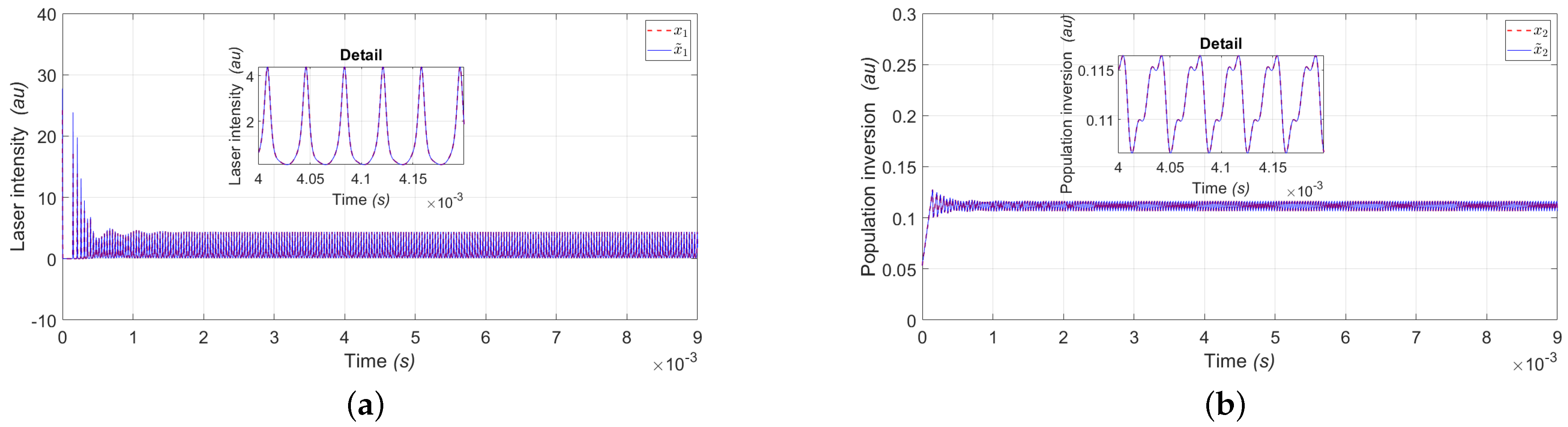
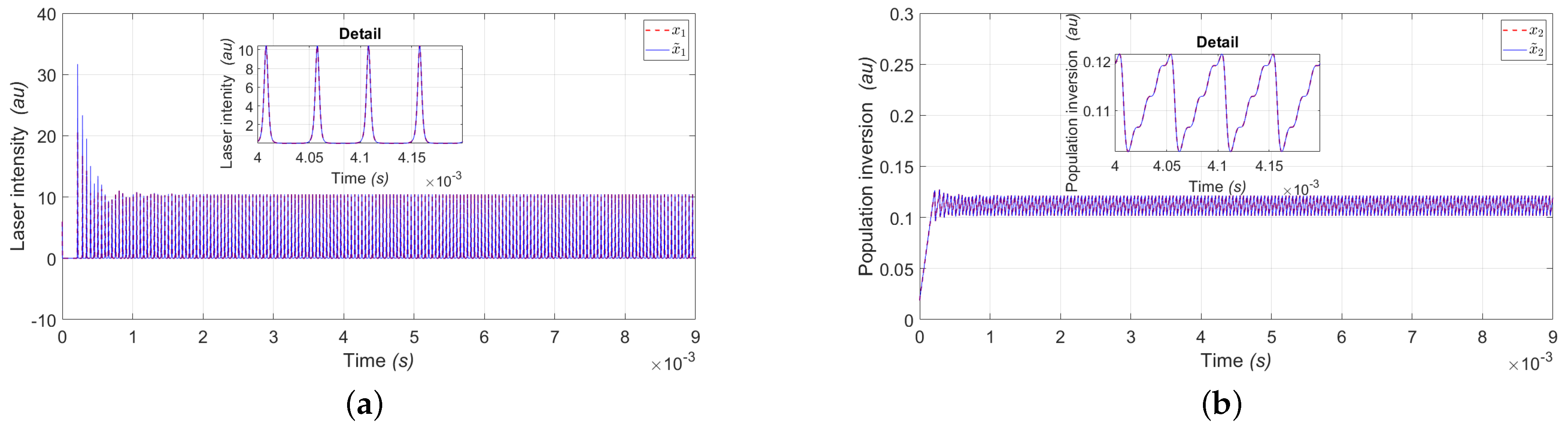
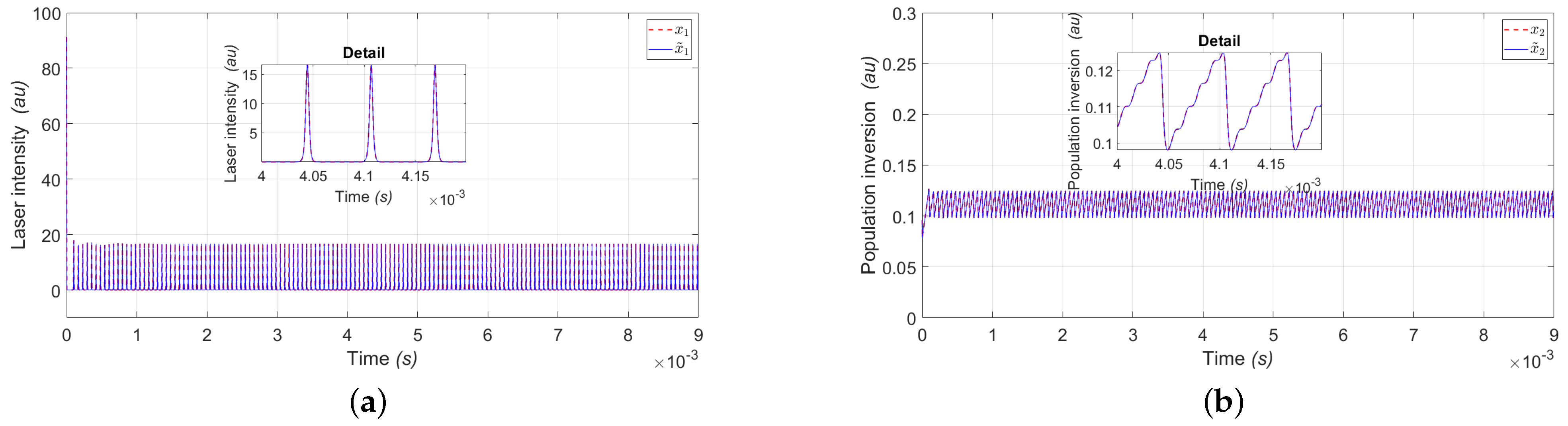
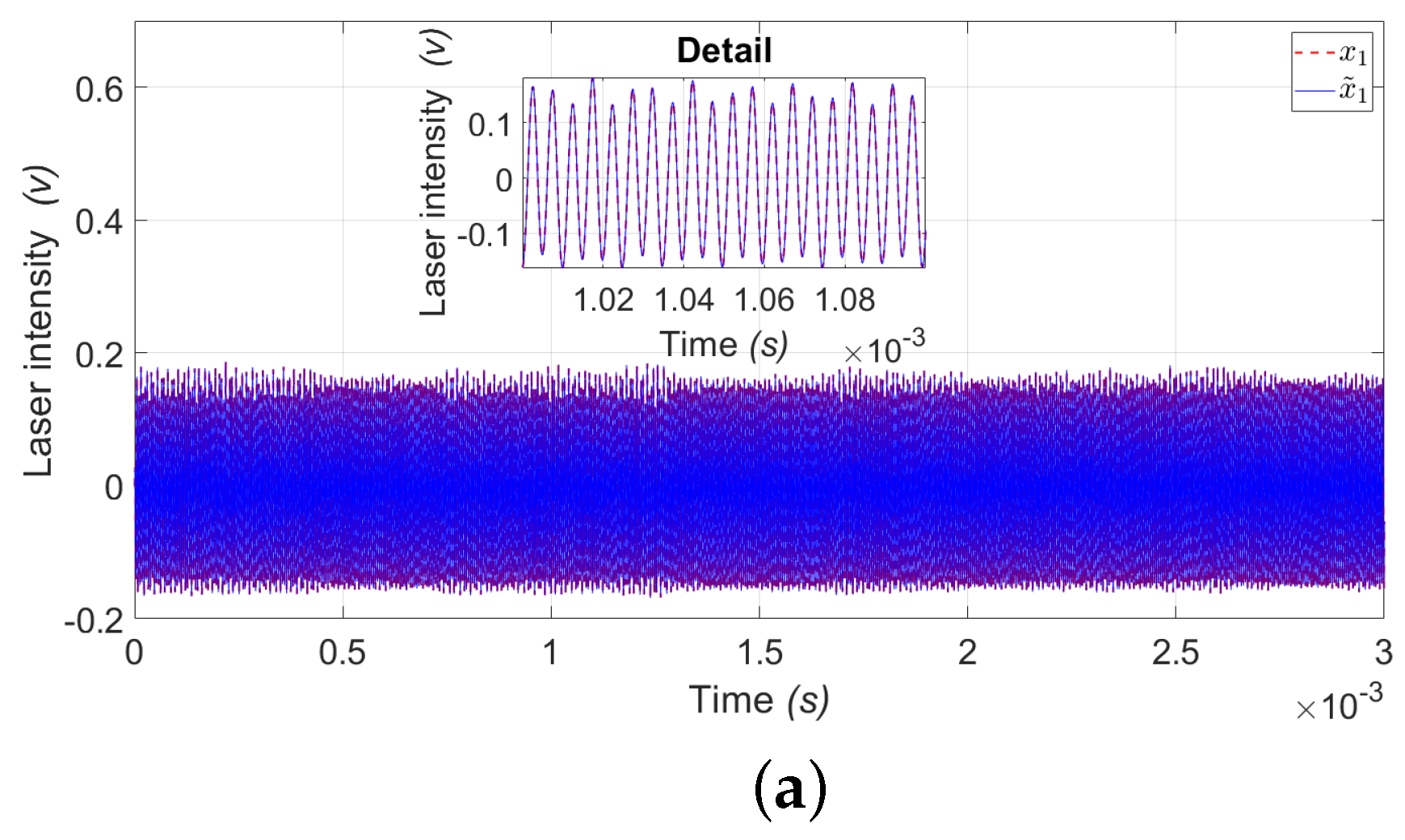
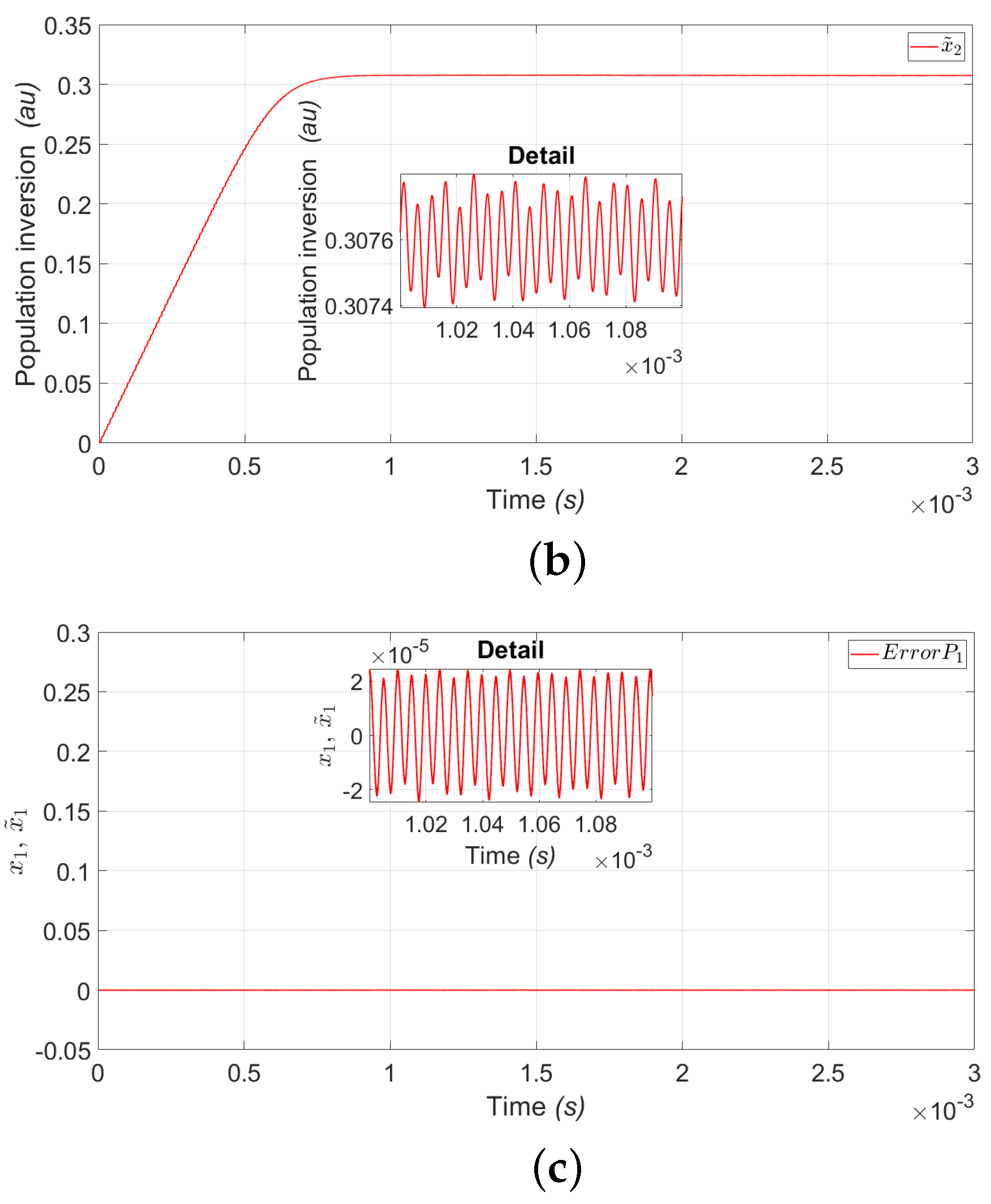
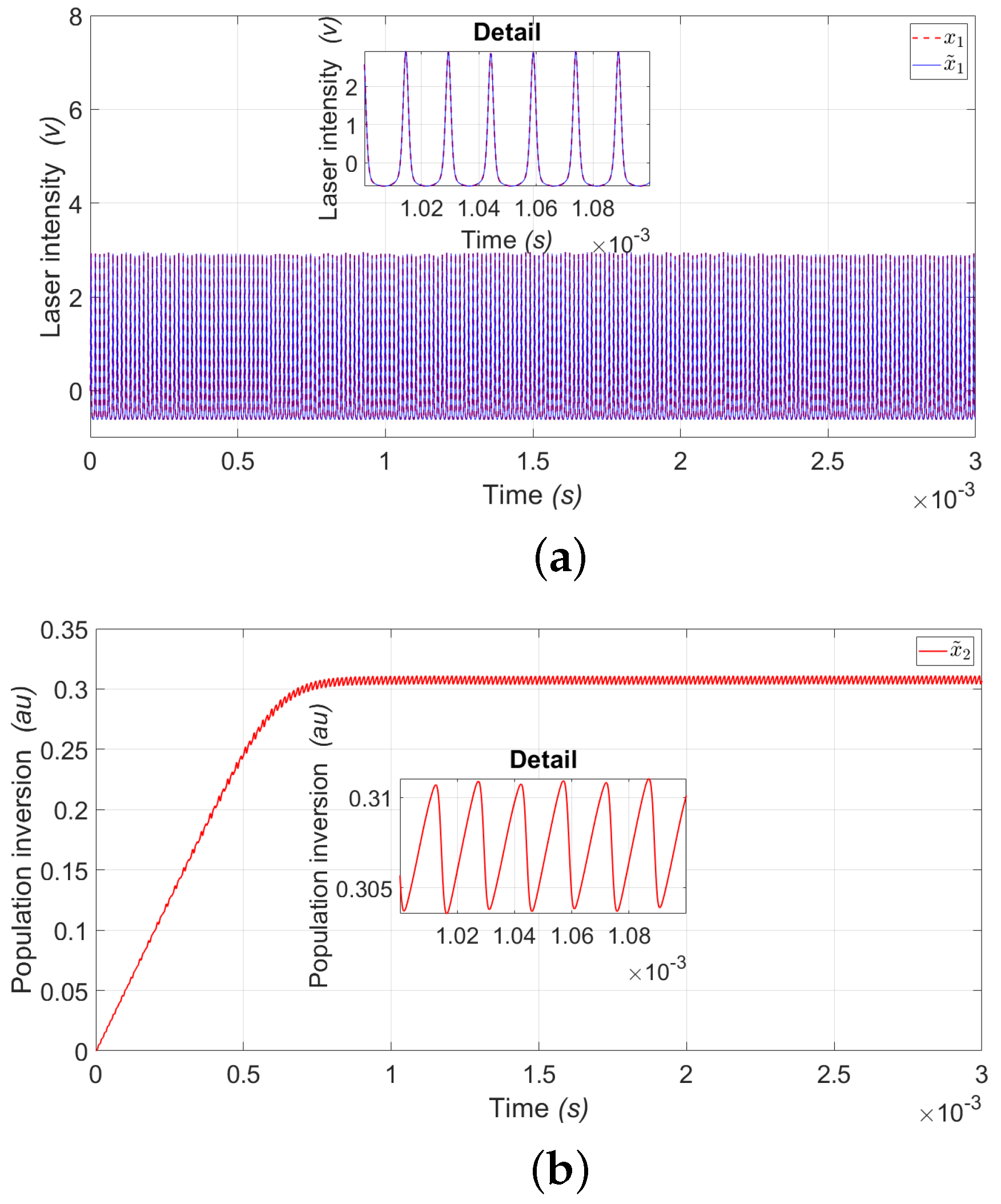
4. Simulation Results
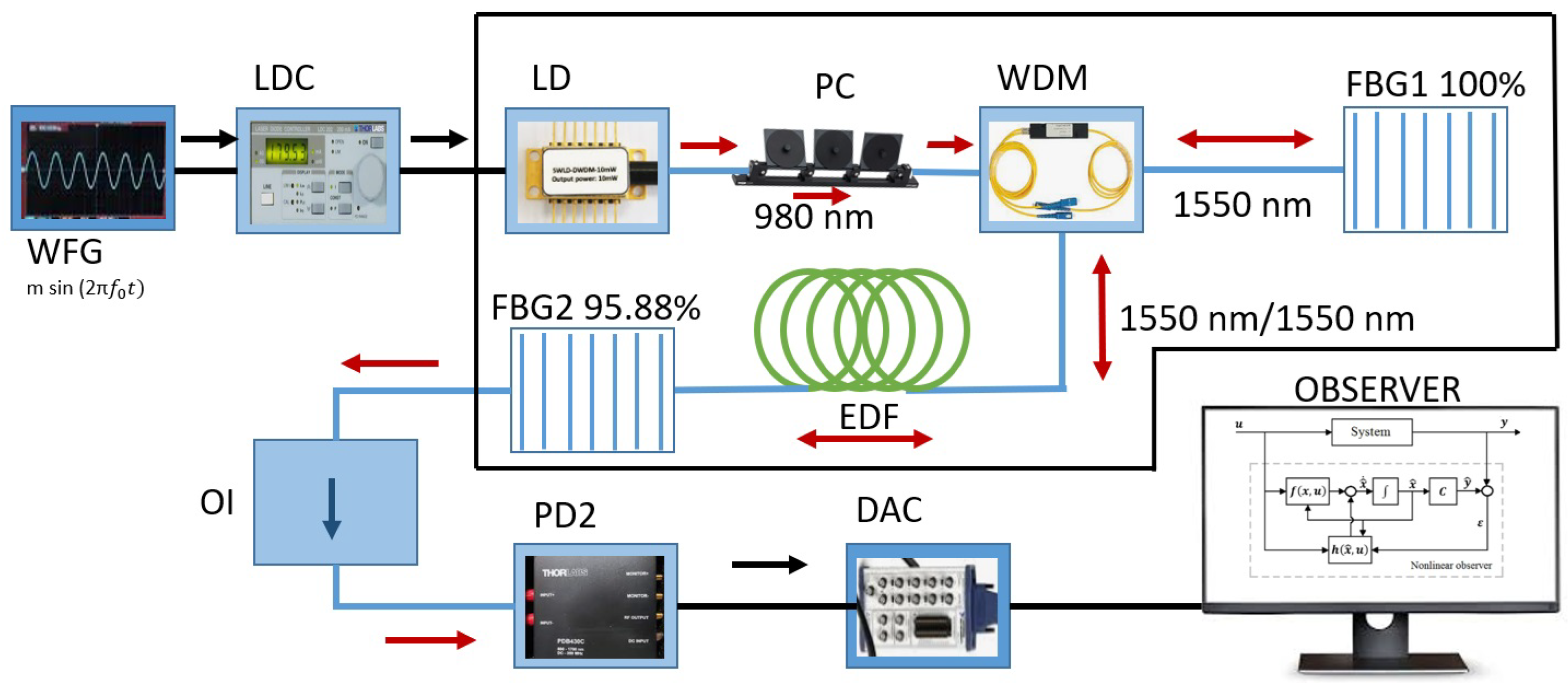
5. Experimental Setup
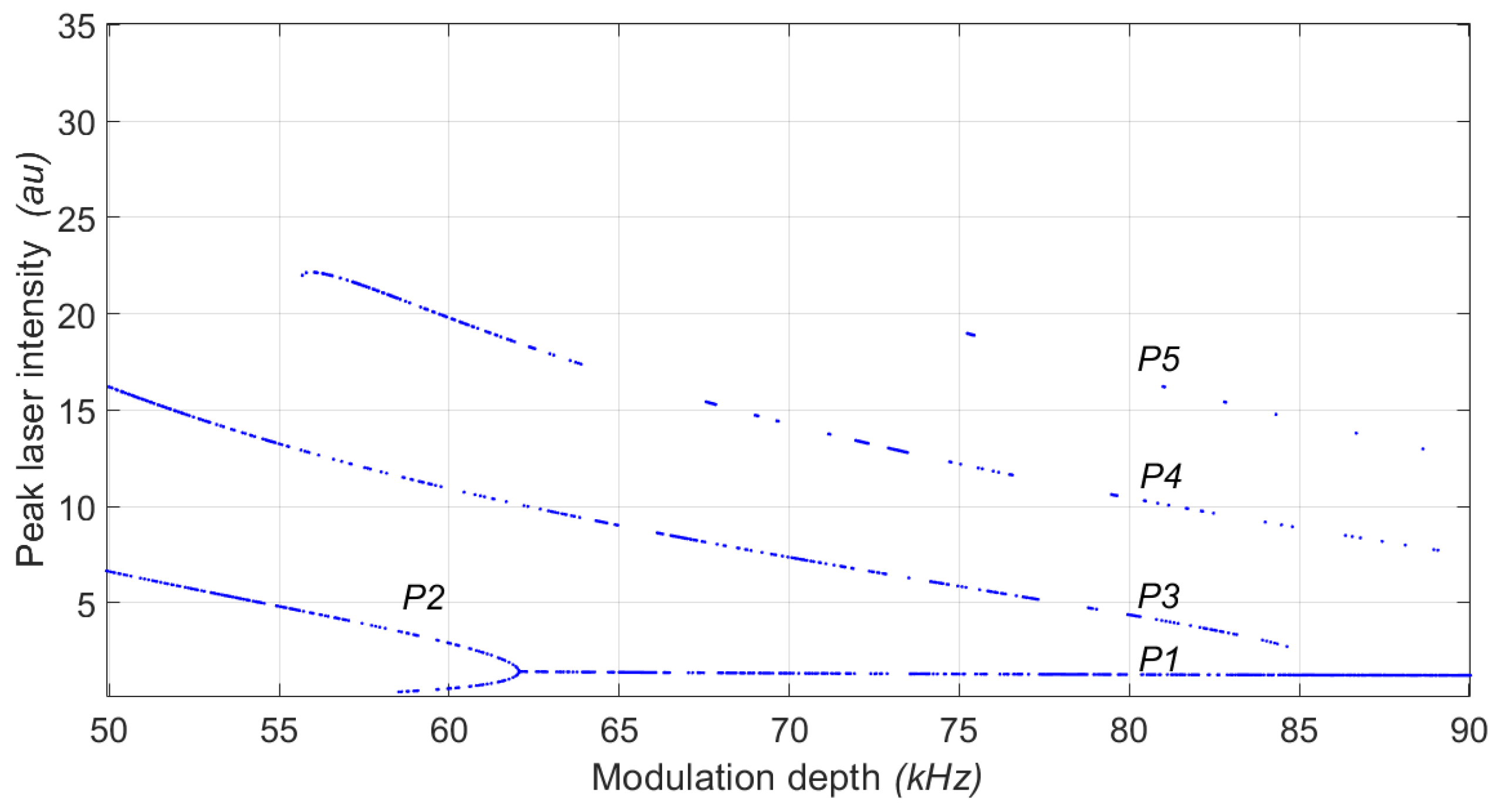
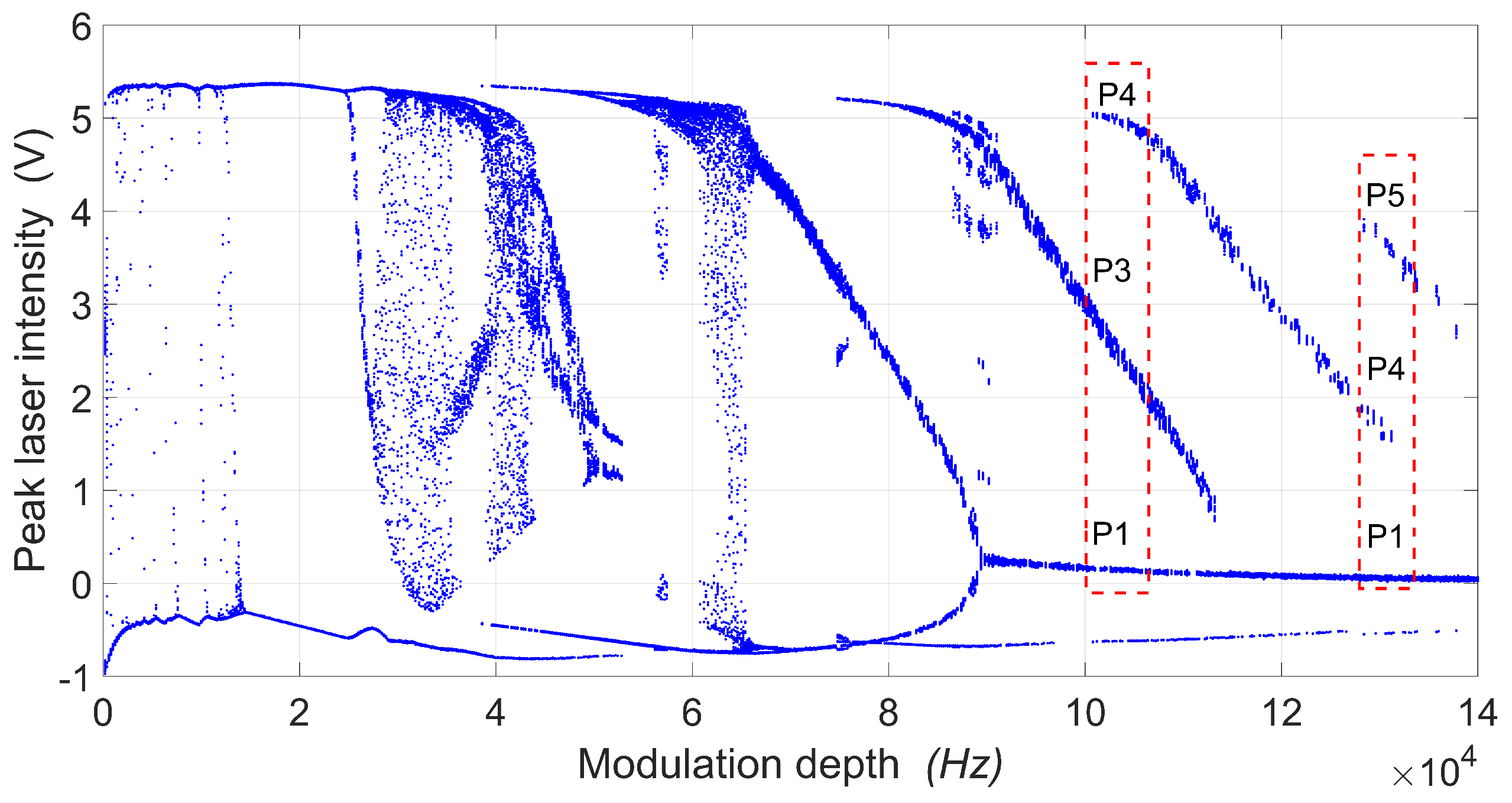
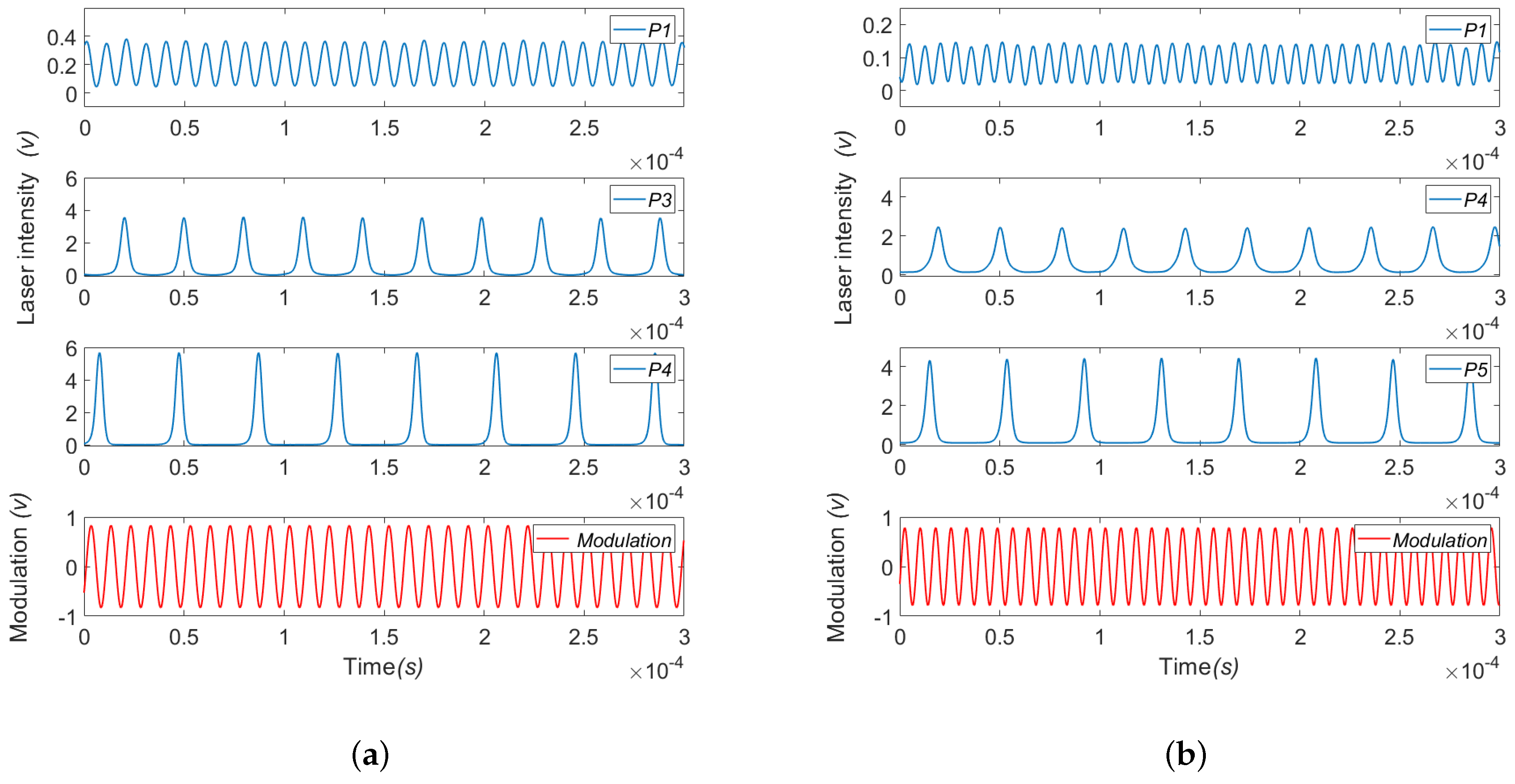
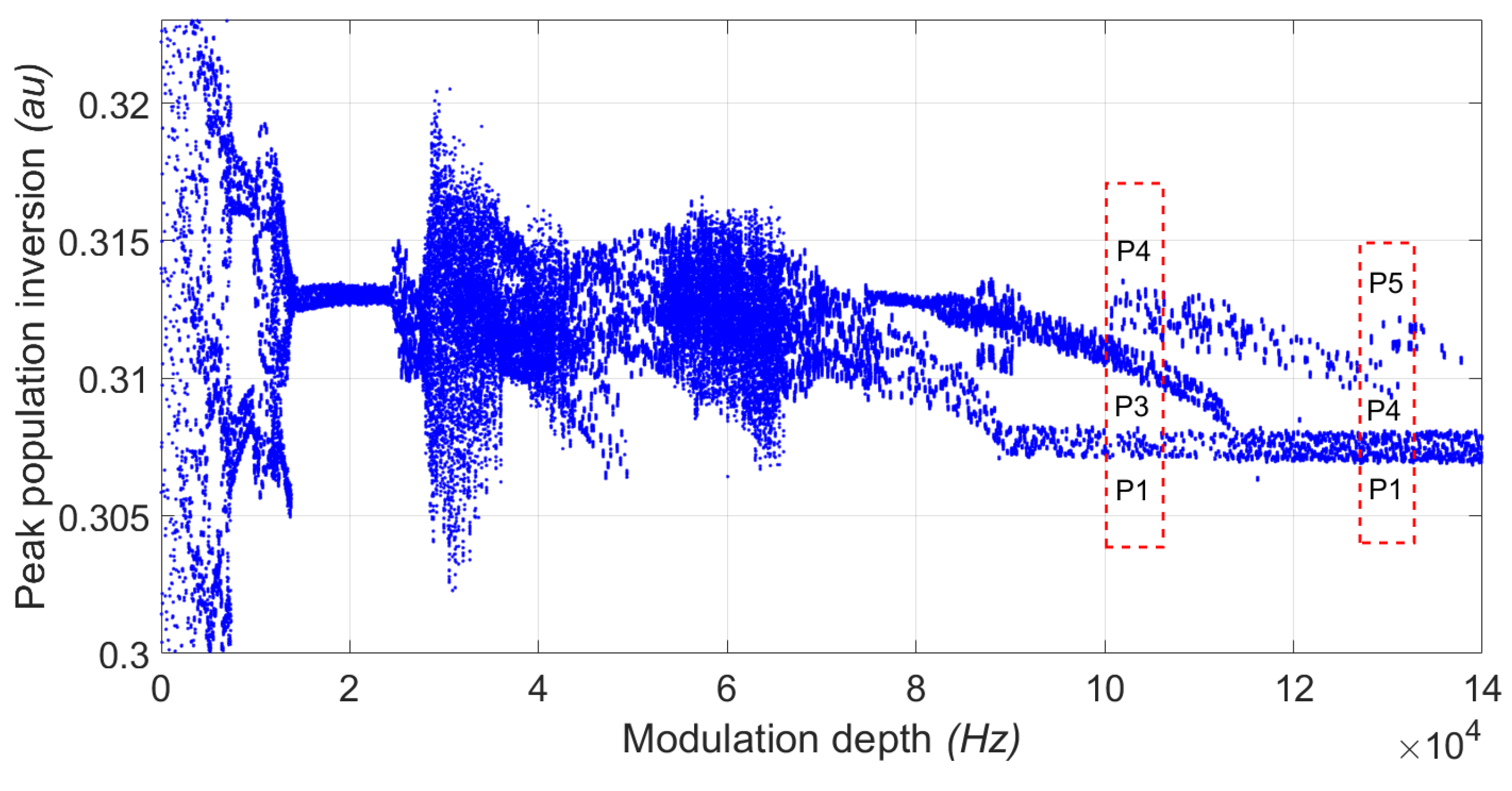
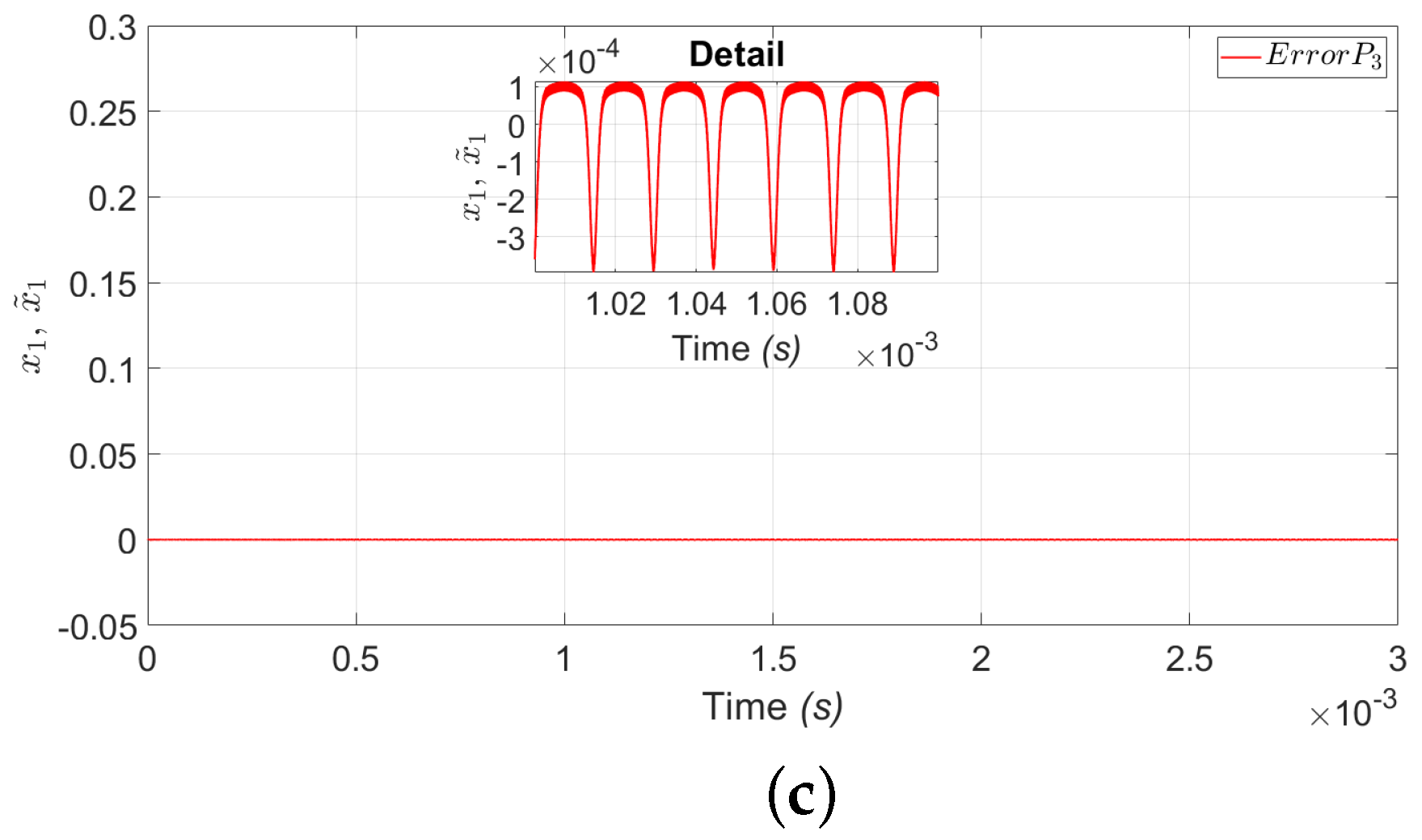
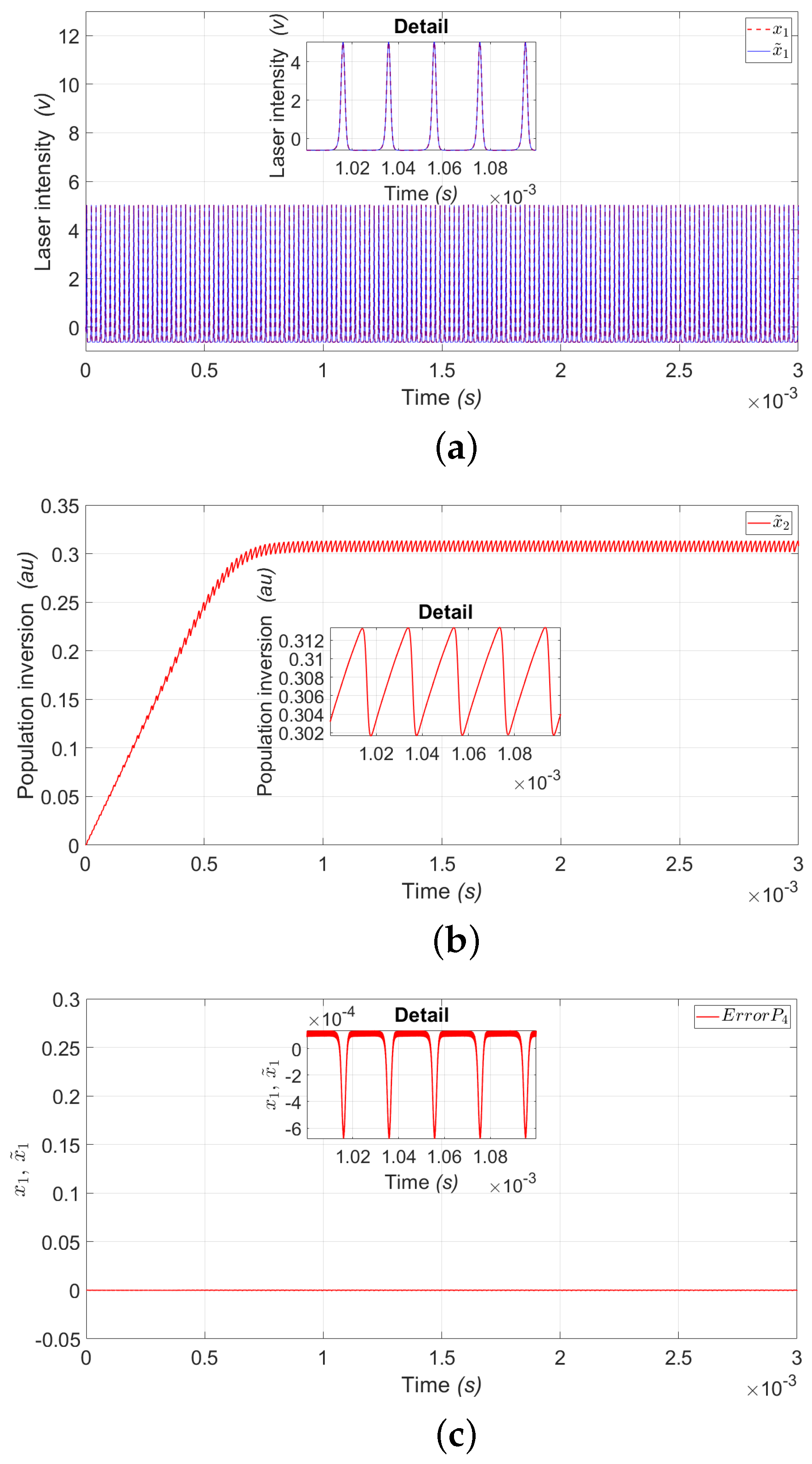
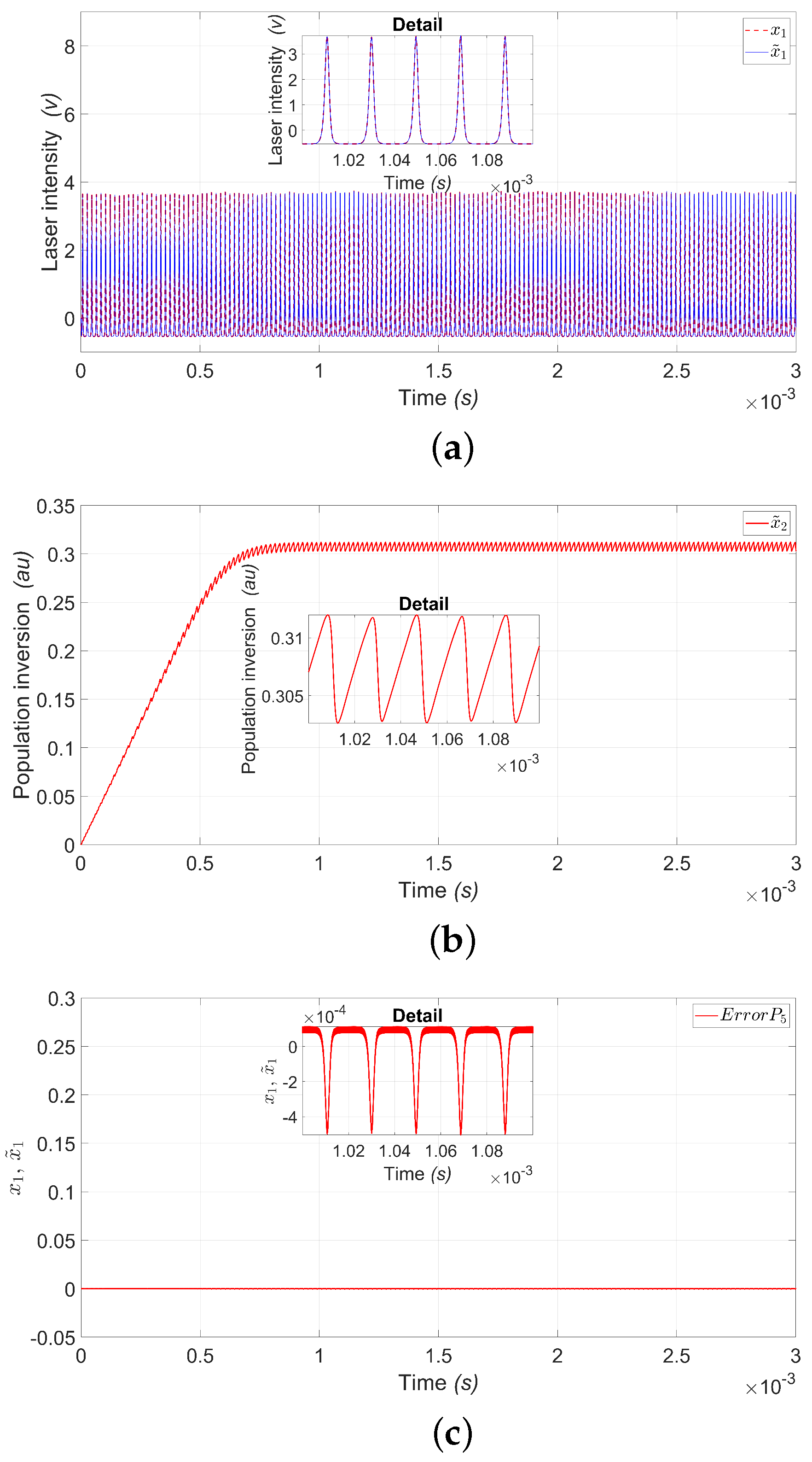
5.1. Experimental Bifurcation Diagrams and Time Series
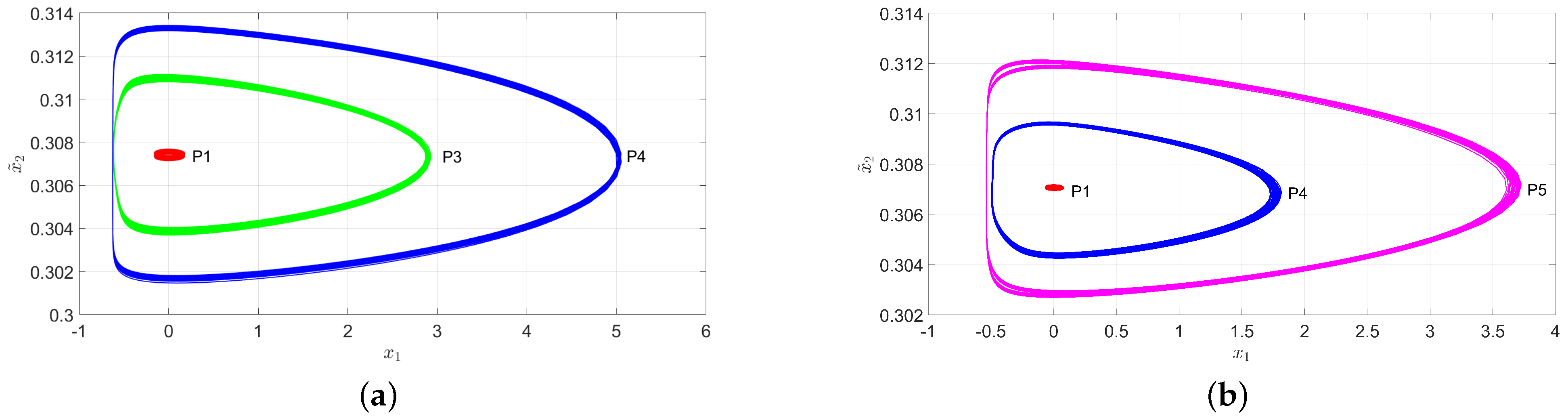
5.2. Experimental Phase Space
5.3. Mean Square Error
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Stability Analysis
References
- Weiss, C.; Vilaseca, R. Dynamics of Lasers; Wiley-VCH: New York, NY, USA, 1991; Volume 1. [Google Scholar]
- Ricci, L.; Perinelli, A.; Castelluzzo, M.; Euzzor, S.; Meucci, R. Experimental Evidence of Chaos Generated by a Minimal Universal Oscillator Model. Int. J. Bifurc. Chaos 2021, 31, 2150205. [Google Scholar] [CrossRef]
- Arecchi, F.; Gadomski, W.; Meucci, R. Generation of chaotic dynamics by feedback on a laser. Phys. Rev. A 1986, 34, 1617. [Google Scholar] [CrossRef] [PubMed]
- Arecchi, F.; Meucci, R.; Gadomski, W. Laser dynamics with competing instabilities. Phys. Rev. Lett. 1987, 58, 2205. [Google Scholar] [CrossRef] [PubMed]
- Guevara, M.R.; Glass, L.; Mackey, M.C.; Shrier, A. Chaos in neurobiology. IEEE Trans. Syst. Man, Cybern. 1983, SMC-13, 790–798. [Google Scholar] [CrossRef]
- Shastri, B.J.; Nahmias, M.A.; Tait, A.N.; Wu, B.; Prucnal, P.R. SIMPEL: Circuit model for photonic spike processing laser neurons. Opt. Express 2015, 23, 8029–8044. [Google Scholar] [CrossRef]
- Tiana-Alsina, J.; Quintero-Quiroz, C.; Masoller, C. Comparing the dynamics of periodically forced lasers and neurons. New J. Phys. 2019, 21, 103039. [Google Scholar] [CrossRef]
- Volterra, V. Variazioni e Fluttuazioni del Numero D’individui in Specie Animali Conviventi; Società anonima tipografica: Pistoia, Italy, 1926. [Google Scholar]
- Lotka, A.J. Contribution to the theory of periodic reactions. J. Phys. Chem. 2002, 14, 271–274. [Google Scholar] [CrossRef]
- Lotka, A.J. Analytical note on certain rhythmic relations in organic systems. Proc. Natl. Acad. Sci. USA 1920, 6, 410–415. [Google Scholar] [CrossRef]
- Schwartz, I.B.; Smith, H. Infinite subharmonic bifurcation in an SEIR epidemic model. J. Math. Biol. 1983, 18, 233–253. [Google Scholar] [CrossRef]
- Sprott, J.C.; Sprott, J.C. Chaos and Time-Series Analysis; Oxford University Press: Oxford, UK, 2003; Volume 69. [Google Scholar]
- Rössler, O.E. An equation for continuous chaos. Phys. Lett. A 1976, 57, 397–398. [Google Scholar] [CrossRef]
- Hou, Z.; Kang, N.; Kong, X.; Chen, G.; Yan, G. On the non-equivalence of Lorenz system and Chen system. arXiv 2009, arXiv:0904.3594. [Google Scholar]
- Čelikovskỳ, S.; Chen, G. On a generalized Lorenz canonical form of chaotic systems. Int. J. Bifurc. Chaos 2002, 12, 1789–1812. [Google Scholar] [CrossRef]
- Lü, J.; Chen, G. A new chaotic attractor coined. Int. J. Bifurc. Chaos 2002, 12, 659–661. [Google Scholar] [CrossRef]
- Matsumoto, T. A chaotic attractor from Chua’s circuit. IEEE Trans. Circuits Syst. 1984, 31, 1055–1058. [Google Scholar] [CrossRef]
- Chua, L.; Komuro, M. Matsumoto: The double scroll family. IEEE Trans. Circuits Syst 1986, 33, 1072–1118. [Google Scholar] [CrossRef]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Haken, H. Analogy between higher instabilities in fluids and lasers. Phys. Lett. A 1975, 53, 77–78. [Google Scholar] [CrossRef]
- Ling, K.; Lim, K. State observer design using deterministic least squares technique. In Proceedings of the 35th IEEE Conference on Decision and Control, Kobe, Japan, 13 December 1996. [Google Scholar]
- Farhangfar, A.; Shor, R. State Observer Design for a Class of Lipschitz Nonlinear System with Uncertainties. IFAC-PapersOnLine 2020, 53, 283–288. [Google Scholar] [CrossRef]
- Savin, S.; Jatsun, S.; Vorochaeva, L. State observer design for a walking in-pipe robot. EDP Sci. 2018, 161, 03012. [Google Scholar] [CrossRef]
- Chen, X.; Kano, H. State observer for a class of nonlinear systems and its application to machine vision. IEEE Trans. Autom. Control 2004, 49, 2085–2091. [Google Scholar] [CrossRef]
- Chen, X.; Zhai, G. State observer for a class of nonlinear systems and its application. In Proceedings of the International Conference on Control Applications, Glasgow, UK, 18–20 September 2002. [Google Scholar]
- Rosolowski, E.; Michalík, M. Fast identification of symmetrical components by use of a state observer. IEE Proc. Gener. Transm. Distrib. 1994, 141, 617–622. [Google Scholar] [CrossRef]
- Jones, L.; Lang, J. A state observer for the permanent-magnet. IEEE Trans. Ind. Electron. 1989, 36, 374–382. [Google Scholar] [CrossRef]
- Magallón, D.A.; Castañeda, C.E.; Jurado, F.; Morfin, O.A. Design of a Morlet wavelet control algorithm using super–twisting sliding modes applied to an induction machine. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar]
- Ciccarella, G.; Dalla Mora, M.; Germani, A. A Luenberger-like observer for nonlinear systems. Int. J. Control 1993, 57, 537–556. [Google Scholar] [CrossRef]
- Kim, T.; Shim, H.; Cho, D.D. Distributed Luenberger observer design. In Proceedings of the 2016 IEEE 55th Conference on Decision and Control (CDC), Las Vegas, NV, USA, 12–14 December 2016; pp. 6928–6933. [Google Scholar]
- Celani, F. A Luenberger-style observer for robot manipulators with position measurements. In Proceedings of the 2006 14th Mediterranean Conference on Control and Automation, Ancona, Italy, 28–30 June 2006; pp. 1–6. [Google Scholar]
- Afri, C.; Andrieu, V.; Bako, L.; Dufour, P. State and parameter estimation: A nonlinear Luenberger observer approach. IEEE Trans. Autom. Control 2016, 62, 973–980. [Google Scholar] [CrossRef]
- Andrieu, V.; Praly, L. On the existence of a Kazantzis–Kravaris/Luenberger observer. SIAM J. Control Optim. 2006, 45, 432–456. [Google Scholar] [CrossRef]
- Andrieu, V.; Praly, L. Remarks on the existence of a Kazantzis-Kravaris/Luenberger observer. In Proceedings of the 2004 43rd IEEE Conference on Decision and Control (CDC)(IEEE Cat. No. 04CH37601), Nassau, Bahamas, 14–17 December 2004; Volume 4, pp. 3874–3879. [Google Scholar]
- Birk, J.; Zeitz, M. Extended Luenberger observer for non-linear multivariable systems. Int. J. Control 1988, 47, 1823–1836. [Google Scholar] [CrossRef]
- Li, X.D.; Xu, C.Z.; Peng, Y.; Tucsnak, M. On the numerical investigation of a Luenberger type observer for infinite-dimensional vibrating systems. IFAC Proc. Vol. 2008, 41, 7624–7629. [Google Scholar] [CrossRef]
- Lang, R.; Kobayashi, K. External optical feedback effects on semiconductor injection laser properties. IEEE J. Quantum Electron. 1980, 16, 347–355. [Google Scholar] [CrossRef]
- Fischer, I.; Liu, Y.; Davis, P. Synchronization of chaotic semiconductor laser dynamics on subnanosecond time scales and its potential for chaos communication. Phys. Rev. A 2000, 62, 011801. [Google Scholar] [CrossRef]
- Vanwiggeren, G.D.; Roy, R. Communication with chaotic lasers. Science 1998, 279, 1198–1200. [Google Scholar] [CrossRef]
- Donati, S.; Mirasso, C.R. Introduction to the feature section on optical chaos and applications to cryptography. IEEE J. Quantum Electron. 2002, 38, 1138–1140. [Google Scholar] [CrossRef]
- Ohtsubo, J.; Davis, P. Chaotic optical communication. Unlocking Dynamical Diversity: Optical Feedback Effects on Semiconductor Lasers; John Wiley & Sons: New York, NY, USA, 2005; pp. 307–334. [Google Scholar]
- Soriano, M.C.; Ruiz-Oliveras, F.; Colet, P.; Mirasso, C.R. Synchronization properties of coupled semiconductor lasers subject to filtered optical feedback. Phys. Rev. E 2008, 78, 046218. [Google Scholar] [CrossRef] [PubMed]
- Arecchi, F.T.; Harrison, R.G. Instabilities and Chaos in Quantum Optics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 34. [Google Scholar]
- Lacot, E.; Stoeckel, F.; Chenevier, M. Dynamics of an erbium-doped fiber laser. Phys. Rev. A 1994, 49, 3997. [Google Scholar] [CrossRef] [PubMed]
- Tehranchi, A.; Kashyap, R. Extremely efficient DFB lasers with flat-top intra-cavity power distribution in highly erbium-doped fibers. Sensors 2023, 23, 1398. [Google Scholar] [CrossRef] [PubMed]
- Reategui, R.; Kir’yanov, A.; Pisarchik, A.; Barmenkov, Y.O.; Il’ichev, N. Experimental study and modeling of coexisting attractors and bifurcations in an erbium-doped fiber laser with diode-pump modulation. Laser Phys. 2004, 14, 1277–1281. [Google Scholar]
- Pisarchik, A.N.; Jaimes-Reátegui, R.; Sevilla-Escoboza, R.; Huerta-Cuellar, G.; Taki, M. Rogue waves in a multistable system. Phys. Rev. Lett. 2011, 107, 274101. [Google Scholar] [CrossRef]
- Huerta-Cuellar, G.; Pisarchik, A.; Kir’yanov, A.; Barmenkov, Y.O.; del Valle Hernández, J. Prebifurcation noise amplification in a fiber laser. Phys. Rev. E 2009, 79, 036204. [Google Scholar] [CrossRef]
- Esqueda de la Torre, J.O.; García-López, J.H.; Jaimes-Reátegui, R.; Huerta-Cuellar, G.; Aboites, V.; Pisarchik, A.N. Route to chaos in a unidirectional ring of three diffusively coupled erbium-doped fiber lasers. Photonics 2023, 10, 813. [Google Scholar] [CrossRef]
- Sevilla-Escoboza, R.; Pisarchik, A.N.; Jaimes-Reátegui, R.; Huerta-Cuellar, G. Selective monostability in multi-stable systems. Proc. R. Soc. A Math. Phys. Eng. Sci. 2015, 471, 20150005. [Google Scholar] [CrossRef]
- Pisarchik, A.; Jaimes-Reátegui, R.; Sevilla-Escoboza, R.; Huerta-Cuellar, G. Multistate intermittency and extreme pulses in a fiber laser. Phys. Rev. E Statistical, Nonlinear, Soft Matter Phys. 2012, 86, 056219. [Google Scholar] [CrossRef]
- Huerta-Cuellar, G.; Pisarchik, A.N.; Barmenkov, Y.O. Experimental characterization of hopping dynamics in a multistable fiber laser. Phys. Rev. E Statistical, Nonlinear, Soft Matter Phys. 2008, 78, 035202. [Google Scholar] [CrossRef] [PubMed]
- Pisarchik, A.N.; Kir’yanov, A.V.; Barmenkov, Y.O.; Jaimes-Reátegui, R. Dynamics of an erbium-doped fiber laser with pump modulation: Theory and experiment. J. Opt. Soc. Am. B 2005, 22, 2107–2114. [Google Scholar] [CrossRef]
- Magallón, D.A.; Jaimes-Reátegui, R.; García-López, J.H.; Huerta-Cuellar, G.; López-Mancilla, D.; Pisarchik, A.N. Control of multistability in an erbium-doped fiber laser by an artificial neural network: A numerical approach. Mathematics 2022, 10, 3140. [Google Scholar] [CrossRef]
| Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|
| L | 70 cm | 1.45 | cm | ||
| 8.7 nm | 20 cm | cm |
| Coefficient | Value | Coefficient | Value | Coefficient | Value |
|---|---|---|---|---|---|
| 0.4 | 0.5 | ||||
| 2.0 | 0.4 | ||||
| 0.038 | |||||
| R | 0.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Magallón-García, D.A.; López-Mancilla, D.; Jaimes-Reátegui, R.; García-López, J.H.; Huerta Cuellar, G.; Ontañon-García, L.J.; Soto-Casillas, F. Experimental State Observer of the Population Inversion of a Multistable Erbium-Doped Fiber Laser. Photonics 2024, 11, 951. https://doi.org/10.3390/photonics11100951
Magallón-García DA, López-Mancilla D, Jaimes-Reátegui R, García-López JH, Huerta Cuellar G, Ontañon-García LJ, Soto-Casillas F. Experimental State Observer of the Population Inversion of a Multistable Erbium-Doped Fiber Laser. Photonics. 2024; 11(10):951. https://doi.org/10.3390/photonics11100951
Chicago/Turabian StyleMagallón-García, Daniel Alejandro, Didier López-Mancilla, Rider Jaimes-Reátegui, Juan Hugo García-López, Guillermo Huerta Cuellar, Luis Javier Ontañon-García, and Fabian Soto-Casillas. 2024. "Experimental State Observer of the Population Inversion of a Multistable Erbium-Doped Fiber Laser" Photonics 11, no. 10: 951. https://doi.org/10.3390/photonics11100951
APA StyleMagallón-García, D. A., López-Mancilla, D., Jaimes-Reátegui, R., García-López, J. H., Huerta Cuellar, G., Ontañon-García, L. J., & Soto-Casillas, F. (2024). Experimental State Observer of the Population Inversion of a Multistable Erbium-Doped Fiber Laser. Photonics, 11(10), 951. https://doi.org/10.3390/photonics11100951








