Characterization of Holmium-Doped Fiber Using AOM and Considering Pair-Induced Quenching and Fiber Length
Abstract
1. Introduction
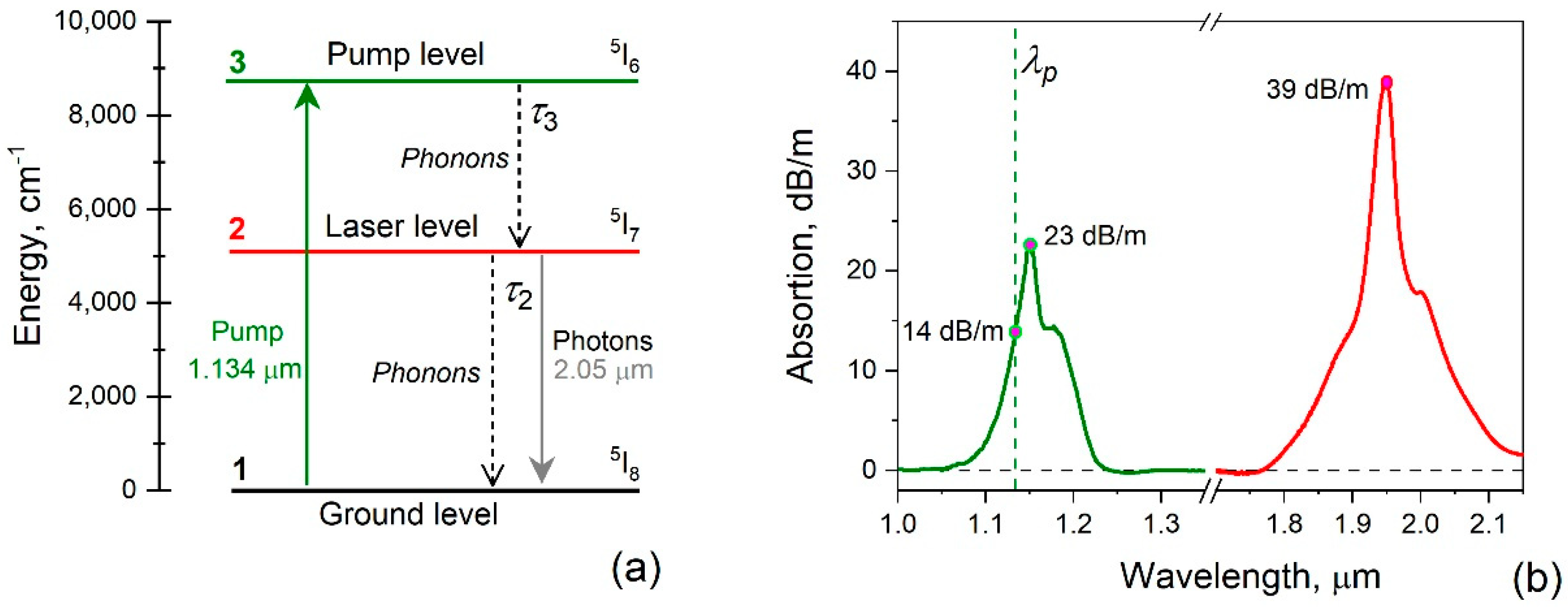
2. HDF Absorption Spectrum
3. Measurement of the Laser Level Lifetime
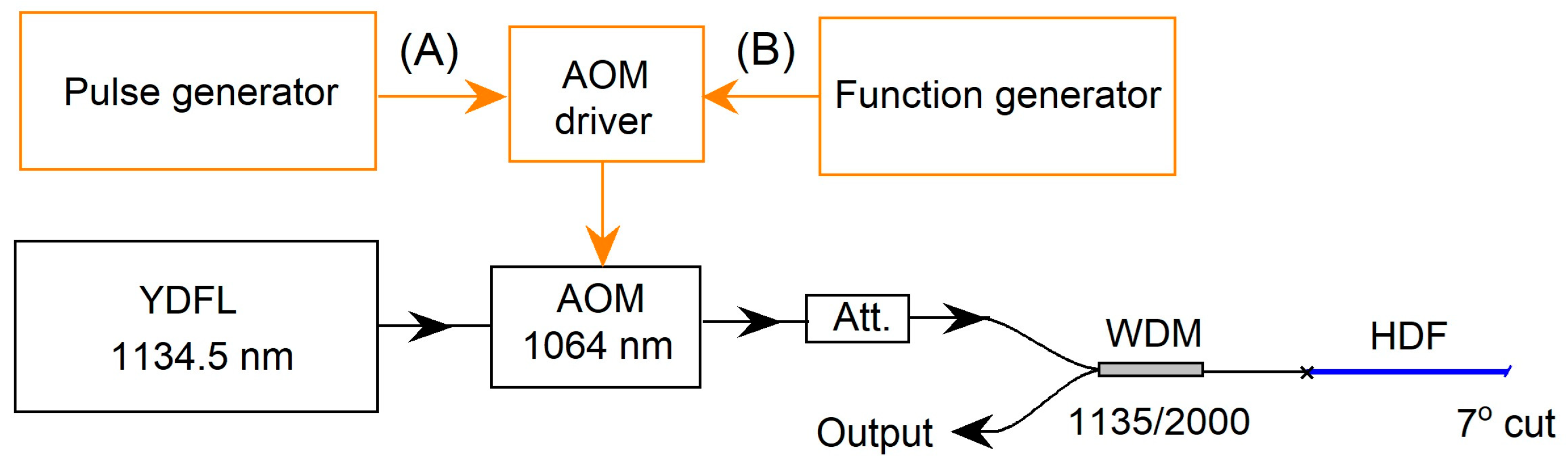
3.1. Experimental Setup
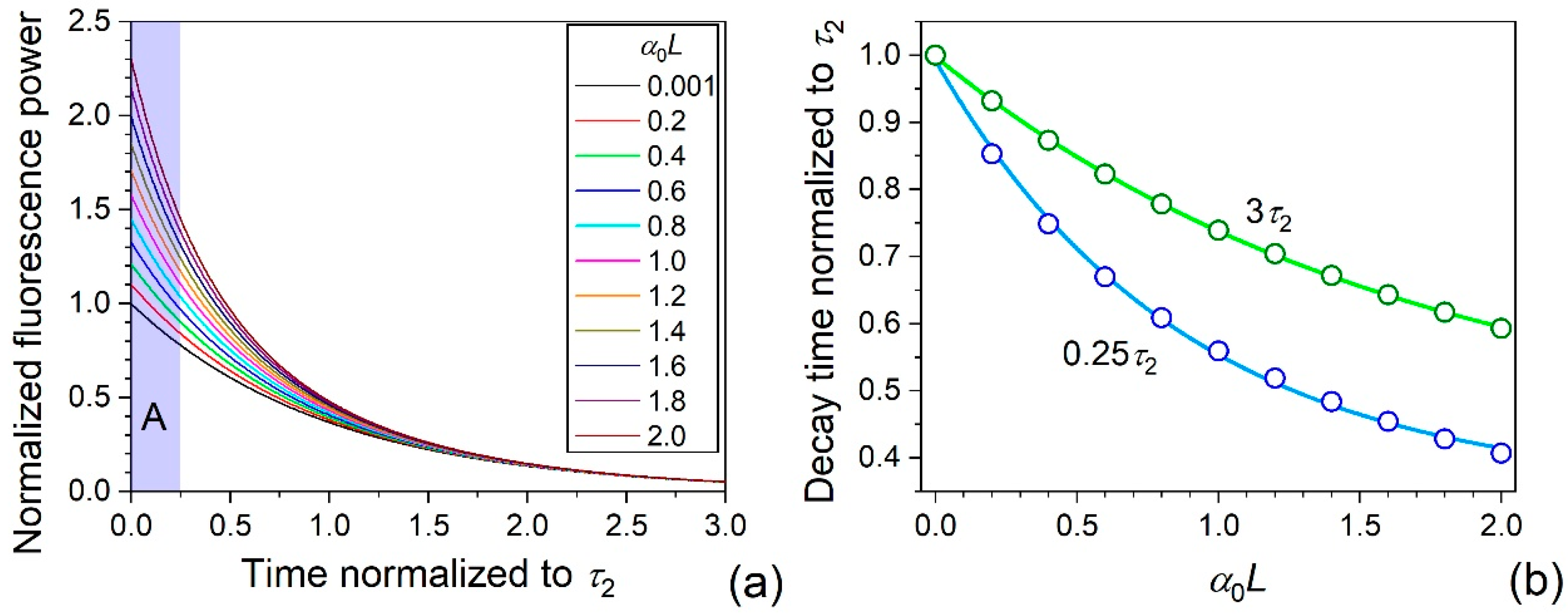
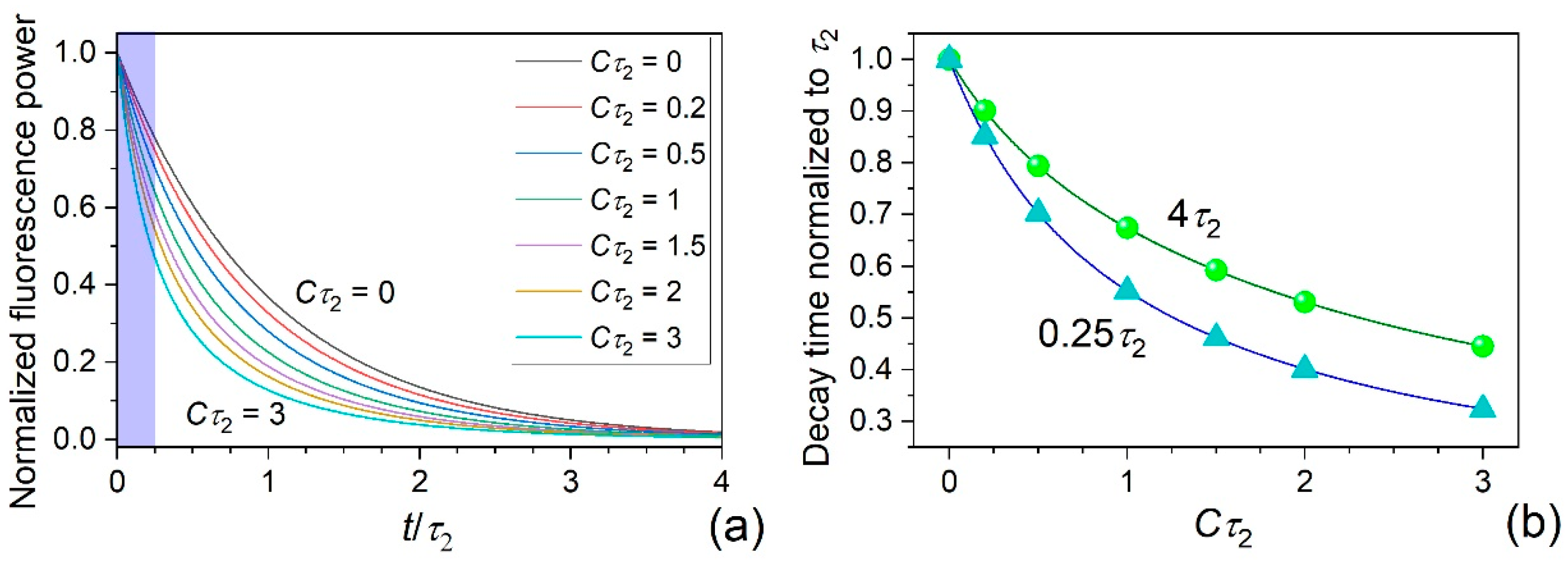
3.2. Theoretical Background
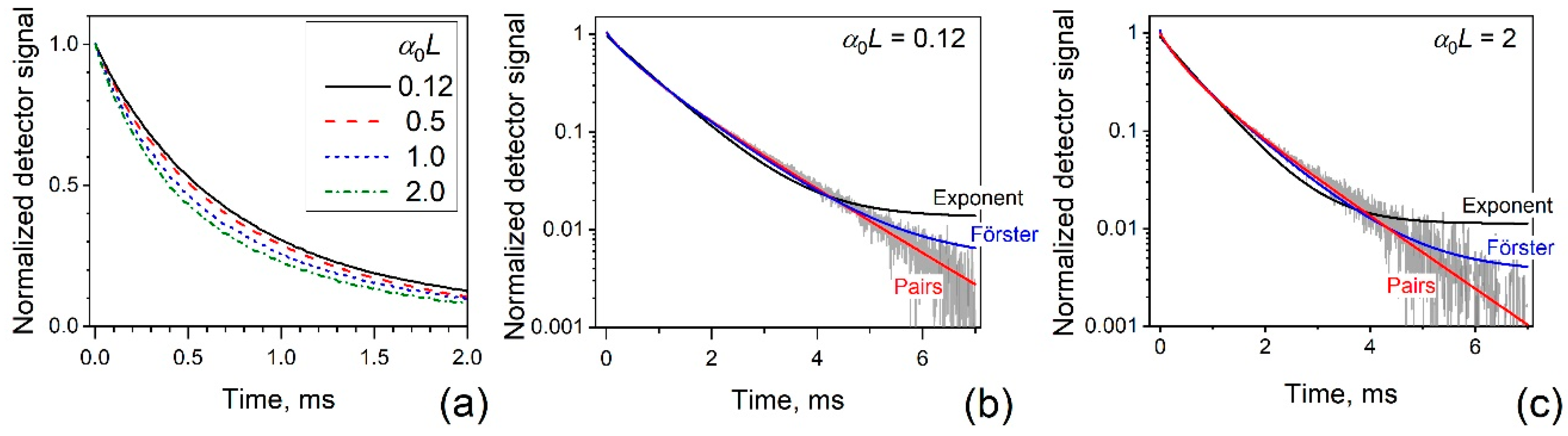
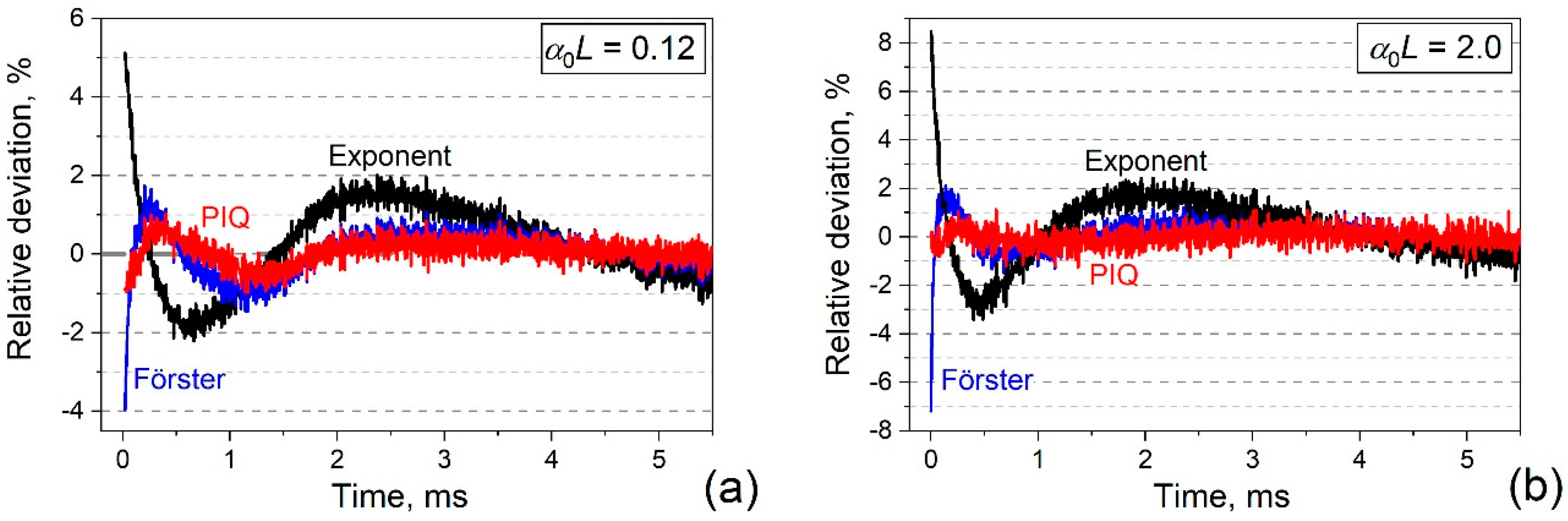
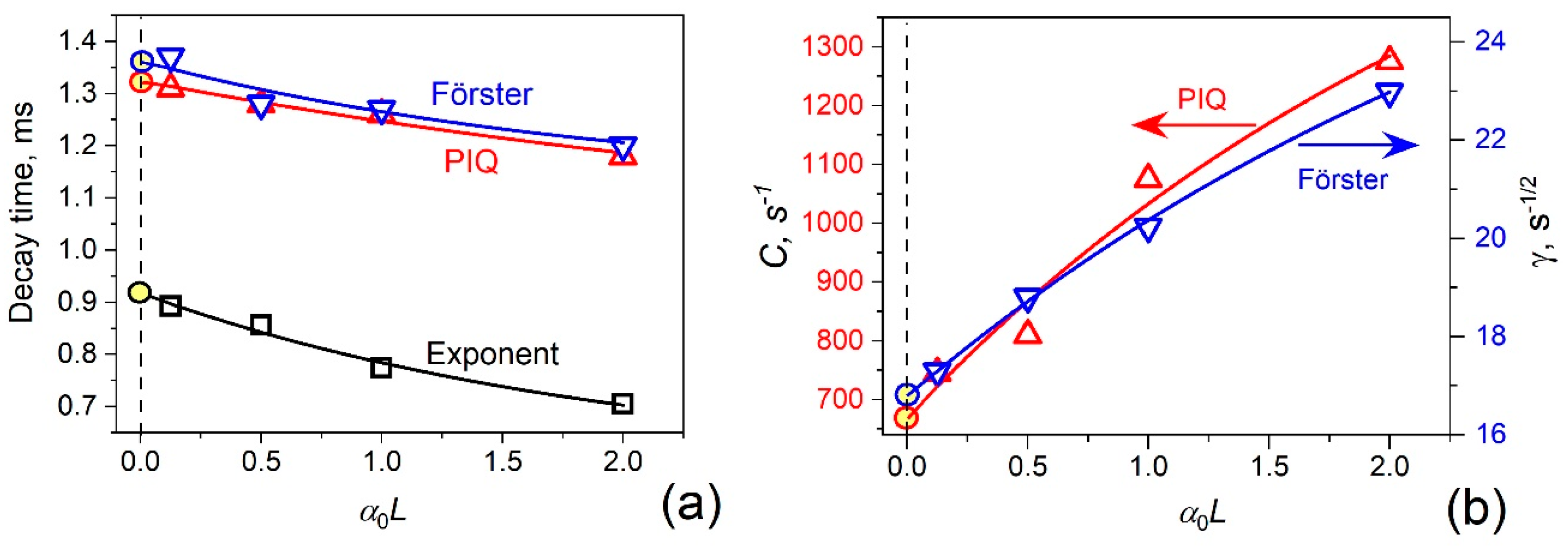
3.3. Experimental Results
4. The Pump Level Lifetime
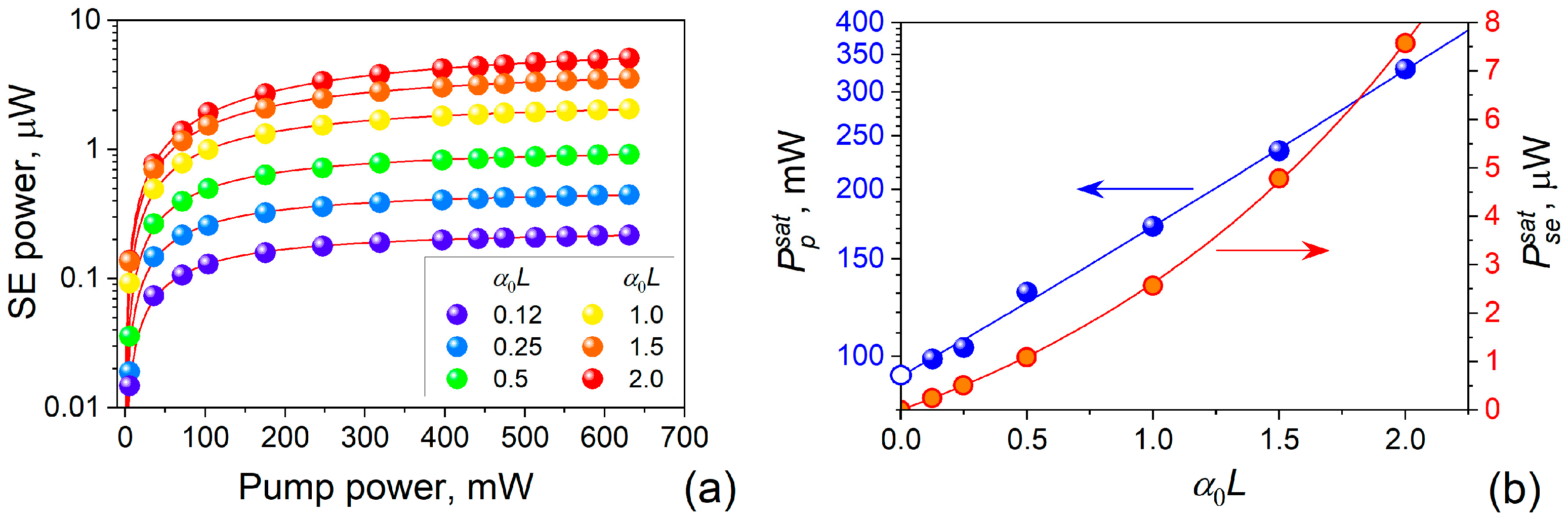
5. Saturation Powers
6. Absorption Cross-Sections, Holmium Concentration, and Fluorescence Quantum Efficiency
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Louot, C.; Sanson, F.; Motard, A.; Ibach, T.; Manek-Hönninger, I.; Berrou, A.; Dalloz, N.; Robin, T.; Cadier, B.; Hildenbrand-Dhollande, A. Emission Wavelength Limits of a Continuous-Wave Thulium-Doped Fiber Laser Source Operating at 1.94 µm, 2.09 µm or 2.12 µm. Photonics 2024, 11, 246. [Google Scholar] [CrossRef]
- Holmen, L.G.; Shardlow, P.C.; Barua, P.; Sahu, J.K.; Simakov, N.; Hemming, A.; Clarkson, W.A. Tunable holmium-doped fiber laser with multiwatt operation from 2025 nm to 2200 nm. Opt. Lett. 2019, 44, 4131–4134. [Google Scholar] [CrossRef] [PubMed]
- Antipov, S.O.; Kamynin, V.A.; Medvedkov, O.I.; Marakulin, A.V.; Minashina, L.A.; Kurkov, A.S.; Baranikov, A.V. Holmium fibre laser emitting at 2.21 µm. Quant. Electron. 2013, 43, 603–604. [Google Scholar] [CrossRef]
- Layne, C.B.; Lowdermilk, W.H.; Weber, M.J. Multiphonon relaxation of rare-earth ions in oxide glasses. Phys. Rev. B 1977, 16, 10–20. [Google Scholar] [CrossRef]
- Digonnet, M.J.F. Rare-Earth-Doped Fiber Lasers and Amplifiers, 2nd ed.; Marcel Dekker, Inc.: New York, NY, USA, 2001; Chapter 2. [Google Scholar] [CrossRef]
- Vladimirskaya, A.D.; Kamynin, V.A.; Lobach, I.A. Single-Frequency Holmium-Doped Fiber Laser with Saturable Absorber. In Proceedings of the IEEE of 23rd International Conference of Young Professionals in Electron Devices and Materials (EDM), Altai, Russia, 30 June–4 July 2022; IEEE: New York, NY, USA, 2022; pp. 360–363. [Google Scholar] [CrossRef]
- Chamorovskiy, A.Y.; Marakulin, A.V.; Kurkov, A.S.; Leinonen, T.; Okhotnikov, O.G. High-Repetition-Rate Q-Switched Holmium Fiber Laser. IEEE Photonics J. 2012, 4, 679–683. [Google Scholar] [CrossRef]
- Lee, J.; Lee, J.H. A Passively Q-Switched Holmium-Doped Fiber Laser with Graphene Oxide at 2058 nm. Appl. Sci. 2021, 11, 407. [Google Scholar] [CrossRef]
- Ahmad, H.; Ismail, N.N.; Aidit, S.N.; Reduan, S.A.; Samion, M.Z.; Yusoff, N. 2.08 µm Q-switched holmium fiber laser using niobium carbide-polyvinyl alcohol (Nb2C-PVA) as a saturable absorber. Opt. Commun. 2021, 490, 126888. [Google Scholar] [CrossRef]
- Wu, K.S.; Ottaway, D.; Munch, J.; Lancaster, D.G.; Bennetts, S.; Jackson, S.D. Gain-switched holmium-doped fibre laser. Opt. Express 2009, 17, 20872–20877. [Google Scholar] [CrossRef]
- Pal, D.; Sen, R.; Pal, A. Gain Switched All-Fiber Holmium Laser at 2.1 micron. In Proceedings of the IEEE Workshop on Recent Advances in Photonics (WRAP), Hyderabad, India, 18–19 December 2017; IEEE: New York, NY, USA, 2017; pp. 1–2. [Google Scholar] [CrossRef]
- Wang, J.; Han, J.; He, J.; Liao, C.; Wang, Y. High-energy mode-locked holmium-doped fiber laser operating in noise-like pulse regime. Opt. Lett. 2019, 44, 4491–4494. [Google Scholar] [CrossRef]
- Hu, P.; Mao, J.; Zhou, X.; Feng, T.; Nie, H.; Wang, R.; Zhang, B.; Li, T.; He, J.; Yang, K. Multiple soliton mode-locking operations of a Holmium-doped fiber laser based on nonlinear polarization rotation. Opt. Laser Technol. 2023, 161, 109218. [Google Scholar] [CrossRef]
- Tu, L.; Tang, Z.; Li, K.; Wang, J.; Lin, H.; Zhang, W.; Lue, Q.; Guo, C.; Ruan, S. All-polarization-maintaining mode-locked Holmium-doped fiber laser based upon nonlinear polarization evolution. Infrared Phys. Technol. 2024, 136, 105054. [Google Scholar] [CrossRef]
- Ahmad, H.; Kamaruzzaman, K.; Samion, M.Z.; Ithnahaini, M.U.M.; Zulkifli, M.Z. Mode-locking in holmium doped fiber laser operating at 2.06 µm using manganese violet. Opt. Quant. Electron. 2024, 56, 1091. [Google Scholar] [CrossRef]
- Taylor, J.H.; Yates, H.W. Atmospheric Transmission in the Infrared. J. Opt. Soc. Am. 1957, 47, 223–226. [Google Scholar] [CrossRef]
- Lin, P.; Wang, T.; Ma, W.; Chen, J.; Jiang, Z.; Yu, C. 2-μm Free-Space Data Transmission Based on an Actively Mode-Locked Holmium-Doped Fiber Laser. IEEE Photonics Technol. Lett. 2020, 32, 223–226. [Google Scholar] [CrossRef]
- Kopyeva, M.S.; Filatova, S.A.; Kamynin, V.A.; Trikshev, A.I.; Kozlikina, E.I.; Astashov, V.V.; Loschenov, V.B.; Tsvetkov, V.B. Ex-Vivo Exposure on Biological Tissues in the 2-μm Spectral Range with an All-Fiber Continuous-Wave Holmium Laser. Photonics 2022, 9, 20. [Google Scholar] [CrossRef]
- Shi, W.; Fang, Q.; Zhu, X.; Norwood, R.A.; Peyghambarian, N. Fiber lasers and their applications [Invited]. Appl. Opt. 2014, 53, 6554–6568. [Google Scholar] [CrossRef] [PubMed]
- Refaat, T.F.; Singh, U.N.; Yu, J.; Petros, M.; Ismail, S.; Kavaya, M.J.; Davis, K.J. Evaluation of an airborne triple-pulsed 2 μm IPDA lidar for simultaneous and independent atmospheric water vapor and carbon dioxide measurements. Appl. Opt. 2015, 54, 1387–1398. [Google Scholar] [CrossRef]
- Caron, J.; Durand, Y. Operating wavelengths optimization for a spaceborne lidar measuring atmospheric CO2. Appl. Opt. 2009, 48, 5413–5422. [Google Scholar] [CrossRef]
- Olowinsky, A.; Rösner, A. Laser Welding of Polymers: Established process but still not at its best. Laser Tech. J. 2012, 9, 52–56. [Google Scholar] [CrossRef]
- Beaumont, B.; Bourdon, P.; Barnini, A.; Kervella, L.; Robin, T.; Le Gouët, L. High Efficiency Holmium-Doped Triple-Clad Fiber Laser at 2120 nm. J. Lightw. Technol. 2022, 40, 6480–6485. [Google Scholar] [CrossRef]
- Le Gouët, J.; Gustave, F.; Bourdon, P.; Robin, T.; Laurent, A.; Cadier, B. Realization and simulation of high-power holmium doped fiber lasers for long-range transmission. Opt. Express 2020, 28, 22307–22320. [Google Scholar] [CrossRef] [PubMed]
- Kir’yanov, A.V.; Barmenkov, Y.O.; Villegas-Garcia, I.L.; Cruz, J.L.; Andres, M.V. Highly Efficient Holmium-Doped All-Fiber ∼2.07-μm Laser Pumped by Ytterbium-Doped Fiber Laser at ~1.13 μm. IEEE J. Select. Top. Quant. Electron. 2018, 24, 0903108. [Google Scholar] [CrossRef]
- Jin, X.; Lou, Z.; Chen, Y.; Zhou, P.; Zhang, H.; Xiao, H.; Liu, Z. High-power dual-wavelength Ho-doped fiber laser at >2 μm tandem pumped by a 1.15 μm fiber laser. Sci. Rep. 2017, 7, 42402. [Google Scholar] [CrossRef]
- Alharbi, A.G.; Kanwal, F.; Ghafoor, S.; Habib, N.; Kanwal, B.; Atieh, A.; Kousar, T.; Mirza, J. Performance Optimization of Holmium Doped Fiber Amplifiers for Optical Communication Applications in 2–2.15 μm Wavelength Range. Photonics 2022, 9, 245. [Google Scholar] [CrossRef]
- Hemming, A.; Simakov, N.; Davidson, A.; Bennetts, S.; Hughes, M.; Carmody, N.; Davies, P.; Corena, L.; Stepanov, D.; Haub, J.; et al. A monolithic cladding pumped holmium-doped fibre laser. In Proceedings of the 2013 Conference on Lasers and Electro-Opics, San Jose, CA, USA, 9–14 June 2013. [Google Scholar] [CrossRef]
- Hemming, A.; Simakov, N.; Oermann, M.; Carter, A.; Haub, J. Record efficiency of a holmium-doped silica fibre laser. In Proceedings of the Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 5–10 June 2016; pp. 1–2. Available online: https://ieeexplore.ieee.org/document/7788732 (accessed on 19 December 2016).
- Wang, X.; Hu, L.; Xu, W.; Wang, S.; Zhang, L.; Yu, C.; Chen, D. Spectroscopic properties of Ho3+ and Al3+ co-doped silica glass for 2-μm laser materials. J. Lumin. 2015, 166, 276–281. [Google Scholar] [CrossRef]
- Edvardsen, A.W.; Holmen, L.G. Kinetics of pair-induced quenching in holmium-doped optical fibers. Opt. Express 2024, 32, 13166–13180. [Google Scholar] [CrossRef]
- Jackson, S.D. The spectroscopic and energy transfer characteristics of the rare earth ions used for silicate glass fibre lasers operating in the shortwave infrared. Laser Photonics Rev. 2009, 3, 466–482. [Google Scholar] [CrossRef]
- Kamrádek, M.; Kašík, I.; Aubrecht, J.; Mrázek, J.; Podrazký, O.; Cajzl, J.; Vařák, P.; Kubeček, V.; Peterka, P.; Honzátko, P. Nanoparticle and Solution Doping for Efficient Holmium Fiber Lasers. IEEE Photonics J. 2019, 11, 7103610. [Google Scholar] [CrossRef]
- Ryabochkina, P.A.; Chabushkin, A.N.; Kosolapov, A.F.; Kurkov, A.S. Absorption and luminescence characteristics of 5I7 → 5I8 transitions of the holmium ion in Ho3+-doped aluminosilicate preforms and fibres. Quant. Electron. 2015, 45, 102–104. [Google Scholar] [CrossRef]
- Walsh, B.M. Judd-Ofelt theory: Principles and practices. In Advances in Spectroscopy for Lasers and Sensing; Di Bartolo, B., Forte, O., Eds.; Springer: Dordrecht, The Netherlands, 2006. [Google Scholar] [CrossRef]
- Jarabo, S.; Álvarez, J.M. Experimental cross sections of erbium-doped silica fibers pumped at 1480 nm. Appl. Opt. 1998, 37, 2288–2295. [Google Scholar] [CrossRef]
- Barmenkov, Y.O.; Kir’yanov, A.V.; Miguel, V.; Andrés, M.V. Spectroscopic properties of holmium-aluminum-germanium co-doped silica fiber. Fiber Integr. Opt. 2020, 39, 185–202. [Google Scholar] [CrossRef]
- Kamrádek, M.; Kašík, I.; Aubrecht, J.; Mrázek, J.; Podrazký, O.; Cajzla, J.; Vařák, P.; Kubeček, V.; Peterka, P.; Honzátko, P. Holmium-doped optical fibers for efficient fiber lasers. In Proceedings of the SPIE of Photonics Europe, Strasbourg, France, 6–10 April 2020; Volume 11355, p. 113550. [Google Scholar] [CrossRef]
- Berkdemir, C.; Özsoy, S. The Effects of Complex Energy Transfer Dynamics and Gaussian Profiles on the Performance of High-Concentration EDFAs. J. Lightw. Technol. 2009, 27, 4642–4649. [Google Scholar] [CrossRef]
- Kir’yanov, A.V.; Barmenkov, Y.O.; Sandoval-Romero, G.E.; Escalante-Zarate, L. Er3+ Concentration Effects in Commercial Erbium-Doped Silica Fibers Fabricated Through the MCVD and DND Technologies. IEEE J. Quant. Electron. 2013, 49, 511–521. [Google Scholar] [CrossRef]
- Kir’yanov, A.V.; Dvoyrin, V.V.; Mashinsky, V.M.; Barmenkov, Y.O.; Dianov, E.M. Nonsaturable absorption in alumino-silicate bismuth-doped fibers. J. Appl. Phys. 2011, 109, 023113. [Google Scholar] [CrossRef]
- Huang, C.; Tang, Y.; Wang, S.; Zhang, R.; Zheng, J.; Xu, J. Theoretical Modeling of Ho-Doped Fiber Lasers Pumped by Laser-Diodes Around 1.125 µm. J. Lightw. Technol. 2012, 30, 3235–3240. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barmenkov, Y.; Muniz-Cánovas, P.; Cruz, J.-L.; Andrés, M.V. Characterization of Holmium-Doped Fiber Using AOM and Considering Pair-Induced Quenching and Fiber Length. Photonics 2024, 11, 1043. https://doi.org/10.3390/photonics11111043
Barmenkov Y, Muniz-Cánovas P, Cruz J-L, Andrés MV. Characterization of Holmium-Doped Fiber Using AOM and Considering Pair-Induced Quenching and Fiber Length. Photonics. 2024; 11(11):1043. https://doi.org/10.3390/photonics11111043
Chicago/Turabian StyleBarmenkov, Yuri, Pablo Muniz-Cánovas, José-Luis Cruz, and Miguel V. Andrés. 2024. "Characterization of Holmium-Doped Fiber Using AOM and Considering Pair-Induced Quenching and Fiber Length" Photonics 11, no. 11: 1043. https://doi.org/10.3390/photonics11111043
APA StyleBarmenkov, Y., Muniz-Cánovas, P., Cruz, J.-L., & Andrés, M. V. (2024). Characterization of Holmium-Doped Fiber Using AOM and Considering Pair-Induced Quenching and Fiber Length. Photonics, 11(11), 1043. https://doi.org/10.3390/photonics11111043





