Abstract
This work addresses the optimized planning of survivable optical 5G Xhaul access networks employing passive Wavelength Division Multiplexing (WDM) technologies. Specifically, it focuses on the reliability of optical transmission paths connecting remote radio sites to a central hub ensured by using a novel, cost-effective, flexible, and dedicated path protection (DPP-F) scheme, protecting against single-link failures. The proposed DPP-F network protection approach allows for switching of individual wavelengths or the complete multiplexed WDM signal, flexibly applying the best switching option according to given traffic demands. Concurrently, it enables traffic aggregation on the transmission paths from the end and intermediate nodes to minimize the overall network deployment cost. The problem of selecting primary (working) and backup (protection) paths, together with the selection of the best switching and traffic aggregation options, is modeled and solved as a mixed-integer linear programming (MILP) optimization problem. To evaluate the cost savings achieved with DPP-F, we compare it with two reference DPP schemes based on switching the entire multiplexed WDM signal (DPP-M) and individual wavelengths (DPP-W). Numerical experiments conducted across a wide range of network scenarios reveal, among other things, that DPP-F’s performance is at least as good as that of the reference methods, bringing significant cost savings (from several to tens of percent) in most of the analyzed network scenarios.
1. Introduction
Xhaul networks constitute the transport infrastructure connecting the distributed elements of radio access networks (RAN), such as radio access points (radio units, RU) spread over an area with computing “radio cloud” resources (distributed and central units, DU/CU), usually located at a central site (hub), and with the core network (CN). Xhaul includes the fronthaul, midhaul, and backhaul network segments, and is present in 5th generation mobile networks (5G) [1,2] as well as being foreseen in future 6th generation (6G) networks [3].
Optical fiber networks based on WDM technologies, alongside Ethernet transmission which relies on packet switching, are considered the most suitable and cost-effective solutions for implementing Xhaul networks [4,5,6]. In particular, passive WDM systems stand out for their cost efficiency due to their simplified operation without the need for signal amplification and dispersion compensation, making them well-suited for Xhaul networks spanning limited distances [4,7]. WDM facilitates the aggregation of multiple high-capacity links, each operating on distinct wavelengths, within a single fiber optic connection. This is achieved by deploying optical multiplexers (MUX) at the termination points of the transmission paths and at intermediate nodes using optical add-drop multiplexers (OADMs), enabling efficient utilization of the fiber infrastructure [8,9,10]. Simultaneously, the Ethernet technology, enhanced with time-sensitive networking (TSN) mechanisms supporting latency-sensitive data flows [11], increases the efficiency of optical links through statistical multiplexing, which optimizes the transmission of packets containing radio data aggregated at remote locations [12,13]. An exemplary commercial solution offering the previously mentioned capabilities is the flexiHaul system, comprising passive WDM components and a TSN switch [14,15,16].
Ensuring the resilience of 5G Xhaul transport networks against failure is crucial to maintaining the expected availability of mobile services [2]. This requirement is particularly significant for ultra-reliable and low-latency communications (URLLC) services and in networks aggregating traffic from many sources, wherein the failure of a link could result in the loss of connectivity for numerous remote sites. Implementing protection mechanisms is one approach to enhancing network reliability [2]. This article focuses on this issue.
The literature review situating the problem addressed and the main contributions of this work are presented below.
1.1. Related Works
In related works, the authors of [17] presented a heuristic approach to designing survivable dense WDM (DWDM) ring transport networks in 5G metro/access networks protected against single-fiber failures. Shehata et al. [18] focused on placing radio baseband units (BBUs) in survivable centralized RANs (C-RANs) based on WDM transport networks. The research conducted by Khorsandi et al. [19] tackled the task of planning dedicated primary and backup lightpaths within a 5G C-RAN connected using a WDM network to ensure resilience against both BBU and fiber failures. Solutions based on the dedicated path protection (DPP) [20,21] and shared path protection (SPP) [21] approaches have been proposed for the packet layer of a 5G Xhaul network, protecting against both DU/CU and link failures. Lashgari et al. [22] addressed the SPP problem in the midhaul network segment; however, the focus was primarily on the packet layer design, similar to the studies in [20,21]. Most of the related works mentioned above concern optical networks offering flexible transmission and switching capabilities, typical for active optical devices, which are an expensive solution for access networks. Also, these works assume pre-deployed networks and neglect to account for the intricacies of designing the optical layer.
Regarding 5G Xhaul networks based on passive WDM technologies, it is essential to strategically place transmission resources and address transmission constraints at the physical layer. These constraints include factors such as the impact of the optical power budget on transmission distance, which is crucial for achieving reliable network solutions. Recently, the designing of an optical layer in packet-optical 5G Xhaul networks using passive WDM solutions was researched in unprotected [8,9] and protected [10] networks. In particular, a DPP mechanism based on the 1:1 optical protection architecture using pairs of 1 × 2 optical switches introduced at the remote and hub sites for protecting individual wavelengths—refereed to as DPP-W—was proposed and studied in [10]. This architecture enables aggregate traffic from several remote sites on a transmission path, which reduces the demand for optical fiber resources and, consequently, the network deployment costs at lighter traffic conditions. However, as traffic volume increases, so does the cost related to the installed switches, and this may surpass that of the DPP solution without such traffic aggregation, in which the entire WDM signal is switched (referred to as DPP-M) [10].
1.2. Research Objective and Contributions
The primary objective of this study is to develop and evaluate an optimized DPP scenario allowing for wavelength aggregation from remote and intermediate nodes. In particular, to overcome the above-discussed drawback of DPP-W, we propose a novel DPP approach for passive optical 5G Xhaul access networks, hereafter called DPP-F, which relies on the flexible and optimal selection of the switching option, either DPP-M or DPP-W, independently for each remote site. The switching selection problem is not trivial, as the decision to protect the entire WDM signal decreases the switching cost; however, it also precludes signal aggregation on a traversing path increasing the demand for optical fiber resources. Therefore, to find the cost trade-off between the use of optical switches and fiber resources, we formulate the DPP-F network planning problem as a MILP optimization problem. Solving the MILP model provides an optimal DPP-based protection solution for a passive WDM optical network, minimizing the overall network deployment cost.
This work’s main novelty is proposing a cost-effective DPP-F network protection approach that outperforms previous DPP solutions for passive WDM optical 5G Xhaul networks. The key contributions of the research are outlined as follows:
- Formulation of a MILP model for planning survivable passive optical 5G Xhaul access networks with flexible and optimal selection of the DPP switching option.
- Assessment of cost savings resulting from the use of the DPP-F scheme versus the reference DPP-M and DPP-W schemes in different network scenarios.
The main difference between DPP-F and the DPP-W and DPP-M methods studied in [10] is that DPP-F flexibly and intelligently enables the optimal selection of the protection scheme according to the network/traffic scenario, whereas the alternative methods do not.
To our knowledge, the DPP-F optimization issue, the benefits of the DPP-F scheme, and the MILP model introduced have not yet been explored in the existing literature.
The article is organized as follows: Section 2 introduces the network model, outlines the network scenario’s main assumptions, and describes the studied network protection scenarios. Section 3 presents the MILP optimization model for planning a passive optical Xhaul network deploying the DPP-F protection scenario. Section 4 reports and discusses the results of the numerical experiments. Eventually, Section 5 presents the conclusions.
2. Network Model
This section presents the model of the protected optical Xhaul network considered, which includes this study’s main assumptions and the DPP schemes studied.
2.1. Main Assumptions
The optical xHaul network is modeled as graph , where and denote the set of nodes (remote and the hub) and the set of links, respectively. Each network link comprises multiple optical fibers, ensuring adequate fiber resources to realize connections between remote sites and the hub. The set of wavelengths available within a single optical fiber is denoted as , and represents the WDM system capacity.
We define the set of traffic demands as , with each demand corresponding to a remote node that requires a specific number of protected wavelength connections , where , to connect the node to the hub. All connections associated with a given demand are multiplexed using an optical MUX device and are carried on the same optical transmission path (OTP, also called a path), on which the required number of wavelengths is allocated. The deployment of two separate transmission paths—a primary (working) path and a secondary (backup) path—ensures protection against single-link failures. Switching between the paths in case of failure is ensured using 1 × 2 optical switches installed at the connection end nodes. The switches can switch individual wavelengths or the multiplexed WDM signals depending on their placement, i.e., either before or after the MUX (see Figure 1). We assume that the working connections are realized only on the primary paths, whereas the backup wavelengths are allocated strictly on the backup paths.
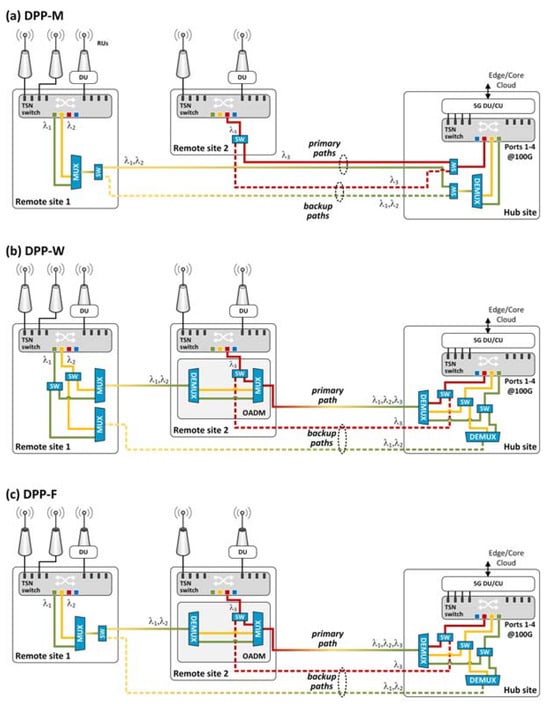
Figure 1.
Exemplary deployment of analyzed dedicated path protection schemes in a passive optical 5G Xhaul access network: (a) DPP with multiplexed signal switching, (b) DPP with wavelength switching, and (c) DPP with flexible switching; “SW” denotes an optical switch.
An OTP can be either direct, where the end nodes are linked using a direct fiber connection (like the paths in Figure 1a) or traversing, where at least one OADM aggregating wavelengths from an intermediate node is installed on the path (see the primary path in Figure 1b). Set represents candidate paths that can be set up for demand . Namely, each path , where , represents a fiber optic route from the remote node associated with demand d to the hub node. Set comprises the candidate paths of demand d including link . Set comprises the candidate paths of demand traversing the remote node of demand d, enabling aggregation of its wavelength connections. Let be the set of all candidate paths. To meet the stringent latency requirements of latency-sensitive 5G services, we assume a propagation latency limit of 50 µs, which restricts the maximum allowable OTP length to 10 km. Hence, set includes only the paths not exceeding this length. The length of path p and the maximum allowable number of OADMs on path p are denoted as and , respectively. Let be the maximum transmission distance (TD) for an OTP with N installed OADMs. Then, is the largest N such that does not exceed , i.e., .
Table 1 summarizes the notation used in network modeling.

Table 1.
Sets and parameters used in network modeling.
2.2. Transmission Distance Estimation Model
The same transmission model as in [10] is applied to calculate the TD values . The TD of a passive optical transmission system is limited by the optical power budget (P) and depends on the attenuation of optical components on the OTP [23]. Given the assumption of short distances, factors that could impact transmission other than the power budget (e.g., signal dispersion) are not accounted for. Define P as , where represents the minimal transmitter outer optical modulation amplitude, and denotes the receiver sensitivity [24]. For a protected OTP, with optical switches and traffic aggregation using N ONDMs, the TD for different N can be estimated as follows:
where , , denote, respectively, the MUX loss, the switch loss, and the connector loss; represents the maintenance margin; and is the fiber loss coefficient. Equation (1) expresses the use of two MUXes at the end path nodes and two MUXes per each OADM unit installed on the path, where each MUX and its connectors introduce attenuation . In addition, two optical switches with associated connectors, two connectors at the path end, and the maintenance margin are considered. Eventually, the denominator reflects the decrease in TD with the fiber attenuation.
2.3. Dedicated Path Protection Schemes
The two baseline DPP schemes, investigated in [10] in the context of passive WDM optical Xhaul networks, are the following:
- DPP-M assumes the protection of the entire WDM signal using an optical switch placed after multiplexing the wavelengths (with a MUX) at a remote node, as shown in Figure 1a. In case of a link failure on the primary path, the WDM signal is switched and transmitted over the backup path. This mechanism requires the remote sites to be connected to the hub using direct OTPs.
- DPP-W realizes the protection of individual wavelengths with dedicated optical switches placed before the signal multiplexing stage; see Figure 1b. If a link fails, only the wavelengths on the affected primary paths are switched to their backup paths. Since individual wavelengths are protected, DPP-W allows them to be aggregated from intermediate nodes on traversing paths.
DPP-M minimizes the utilization of optical switches, as it needs only a pair per each remote site (one of the switches installed at the hub). Still, dedicated primary and backup fiber connections are required to carry the protected WDM signals, which may be costly if the fiber resources are expensive. DPP-W addresses this issue by aggregating traffic from several nodes on a single OTP, reducing the fiber demand. However, the cost related to optical switches may increase considerably if many wavelengths need to be protected.
The DPP-F scheme introduced in this work aims to optimize the deployment cost of DPP in passive WDM optical Xhaul networks and mitigate the drawbacks of DPP-W and DPP-M mentioned above. The main idea behind DPP-F is the flexibility in selecting the most suitable switching option for each remote node, as shown in Figure 1c, enabling cost optimization. In particular, nodes with low traffic demands may opt to aggregate their traffic on single OTPs, similar to DPP-W, thus reducing the utilization of costly fiber resources. On the other hand, for nodes with high traffic demands exploiting the WDM resources extensively, it may be cheaper to aggregate and switch the WDM signals (as in DPP-M). Unlike DPP-W and DPP-M, DPP-F can provide a cost-efficient protection solution regardless of traffic conditions.
Figure 1 illustrates an exemplary deployment of the discussed DPP schemes in a passive optical 5G Xhaul network. In the example, DPP-M requires four optical fiber strands, four optical switches, and two MUX devices (one operating as a demultiplexer) to establish four direct OTPs and to switch the WDM signals at remote sites 1 and 2, and at the hub. The DPP-W scenario involves only three OTPs, with a reduced demand for fiber resources, but at the cost of four additional MUXes and two more switches to protect individual wavelengths at both remote sites and the hub. Finally, DPP-F combines the DPP-M switching scheme applied in remote site 1, where the whole WDM signal is switched, with DPP-W used in remote site 2, where single wavelength is switched. By these means, DPP-F preserves the low demand for fiber as in DPP-W, simultaneously requiring a smaller number of optical components, i.e., five MUXes and five switches. This exemplary DPP-F deployment will be the most cost-effective in a network with a high fiber lease cost compared to the cost of optical components.
The critical issue in deploying the DPP-F scenario is planning and configuring protected OTPs, including selecting switching options (WDM vs. single wavelengths) for individual remote nodes and aggregating traffic from intermediate nodes. The DPP-F network planning problem is not straightforward, as it involves many decision variables. Therefore, in the next section, we model it as a MILP optimization problem, which can be solved in a computer environment using dedicated MILP solvers [25,26].
3. Optimization Model
In this section, we formulate the DPP-F network planning problem as an MILP optimization problem. The network planning concerns jointly conducting the following steps:
- selecting a switching option, either DPP-W or DPP-M, at a remote site and the hub for each demand ;
- establishing and assigning protected (disjoint) paths, either direct or traversing, for carrying primary and backup connections between the remote sites and the hub;
- placing OADMs on traversing paths at selected intermediate nodes for traffic aggregation in the optical layer assuming the TD constraint (see Section 2);
- assigning the same and unique wavelength to each connection of a demand on the primary and backup path assuming the WDM system capacity constraint.
The MILP model formulation uses a set of binary, integer, and continuous problem variables, presented and defined in Table 2.

Table 2.
Problem variables used in the MILP model.
The optimization goal of the network planning problem is minimizing the optical network deployment cost, which embraces the following three components:
- The cost of the fiber required for establishing OTPs. Similar to [10], the cost analysis in this work assumes a 1-year leasing cost of the dark fiber.
- The cost of the MUXs aggregating wavelengths and filtering optical signals at the intermediate and end nodes of OTPs.
- The cost of the optical switches for switching the optical signals between primary and backup connections in the case of a link failure.
Accordingly, the MILP optimization objective function (denoted as z) representing the overall path protection deployment cost in the network is defined as follows:
where denotes the cost of the dark fiber lease (per km/year), is the cost of a MUX, and is the cost of an optical switch. In optimization objective (2), the coefficient of value two represents the transmission directions. This coefficient does not appear in the last term since the optical switch considered is bi-directional [27].
The MILP problem constraints are defined below.
- Selection of primary and backup paths
The first set of constraints is responsible for selecting protected disjoint paths to carry the traffic demands between the hub and remote nodes.
The assignment of the primary and backup path is assured for each traffic demand by the following constraints, respectively:
In the above constraints, each assigned path can be either a path selected from the set of candidate paths of given demand d or an existing path traversing the remote node of the demand and terminating at some other remote node. The latter means the demand aggregates on the traversing path using an OADM. It is indicated by binary variables and , which take the value one for the demand d using a traversing primary and backup path, respectively. In such case, the choice of other demand to which demand d aggregates is indicated by variables and for the primary and backup path, respectively, and determined by constraints:
Whenever variables / take the value one, a primary/backup path must be selected for demand from the set of candidate paths traversing the remote node of demand d, which is assured by constraints:
Whether both primary and backup paths are selected and set up for demand d is expressed by variable , which is determined by constraints:
If the primary/backup path set up for demand d aggregates some other demand, then variables / are equal to one, which is imposed by the constraints:
Concurrently, whenever a dedicated primary/backup path is not set up for demand d, i.e., the demand is aggregated on a traversing path, it cannot aggregate other demands, which is imposed by constraints:
If either primary or backup paths are not set up for demand d (i.e., ) or any of these paths aggregate some other demand (i.e., or ), then variable is equal to zero, which is imposed by constraints:
To protect the connections against single-link failures, the primary and backup paths assigned to each demand should be disjointed, i.e., they must not share links. To this end, the following constraints are formulated.
Whether the primary/backup path selected for demand d includes link e is expressed by variables /, which are determined by constraints:
Whether the primary/backup path selected for demand and aggregating demand d includes link e is expressed by variables /, which are determined by constraints:
The disjointness of the primary and backup path assigned to each demand, where the paths can be either direct or traversing, is assured using the above-specified variables in the following constraints:
- Wavelength assignment and traffic aggregation
The second set of constraints assures the assignment of wavelengths on transmission paths to realize given traffic demands while satisfying specific traffic aggregation limits.
The assignment of wavelengths is assured for each traffic demand by the following constraints:
where wavelengths requested by demand d are selected by activating (i.e., set to the one) the variables related to these wavelengths.
Any two demands can use the same wavelength unless they are aggregated on the same primary or backup path, which is assured by constraints:
Whether wavelength w is selected for demand d aggregated on the primary/backup path selected for demand is expressed by variables /, which are determined by constraints:
Each wavelength w can be assigned to at most one demand d aggregated on the primary/backup path selected for demand , which is assured by constraints:
The capacity of the WDM system and the number of OADMs that can be inserted on a transmission path are two factors limiting the aggregation of wavelengths on the paths. The following constraints impose these limits.
First, the overall number of wavelengths assigned for demand d on its primary/backup path and for all other demands aggregated on this path cannot exceed the WDM capacity (W), which is assured by constraints:
Second, the overall number of demands aggregated on the primary/backup path p selected for demand cannot exceed the maximum number of OADMs allowable on this path (), which is assured by constraints:
- Utilization of optical components
The following constraints allow us to estimate the utilization of optical components required in the network to deploy the DPP-F protection scenario. This estimation is necessary to calculate the network cost in the objective function.
The length of optical fiber used on all selected primary and backup paths in one transmission direction, represented by variable , is calculated as follows:
The number of required MUXes in one transmission direction, represented by variable , is calculated as follows:
The above constraint accounts for the following possible cases. Any demand aggregated on a traversing primary/backup path (i.e., when , ) will need a pair of MUXes to realize the OADM functionality. If the demand consists of only one wavelength (i.e., ) and uses a dedicated primary/backup path aggregating other demands, then a MUX at the hub node will be needed to disaggregate the wavelengths on such a path. Larger demands (i.e., ) that use a dedicated primary/backup path (i.e., when , ) need two MUXes at the path ends. However, if both the primary and backup path are set up for a remote site (i.e., ), then the number of MUXes is reduced to just one MUX required at this site (see remote site 1 in Figure 1c). Moreover, only one MUX is needed at the hub if these paths do not aggregate other demands (i.e., when ), as shown in Figure 1a.
The number of optical switches, represented by variable , is calculated as follows:
In Constraint (37), if both the primary and the backup path are set up for demand d (i.e., ), then one optical switch is sufficient to switch the aggregated WDM signal at the remote node (as for remote site 1 in Figure 1c). Otherwise, the wavelengths are switched separately, resulting in the total number of switches needed (see remote site 2 in Figure 1c). Similarly, if both the primary and the backup path set up for demand d do not aggregate other demands (i.e., ), then one optical switch can switch the aggregated WDM signal at the hub node (similar as in Figure 1a). Otherwise, switches are needed to switch particular wavelengths (see the hub site in Figure 1b).
Solving the above-presented MILP model using a dedicated MILP solver, such as CPLEX [25] or GUROBI [26], allows for the optimal selection of switching options, either of the WDM signal or individual wavelengths for particular remote sites, providing the most cost-effective protection solution under given traffic demands.
Remark 1.
The DPP-F network planning problem addressed in the paper is modeled as an MILP problem as it involves binary (decision) and integer variables, which have to take values of 0 or 1 for the former and integer values for the latter in a feasible problem solution. Note that relaxing the MILP problem to an LP problem by allowing the binary/integer variables to take real (continuous) values and solving it using the Simplex method would spoil the solutions’ feasibility due to flow bifurcation (splitting), as discussed in [28]. Therefore, to provide a feasible solution, the network planning problem addressed must be solved as a MILP problem (not LP). In general, the wavelength assignment problems and single-path routing problems are modeled using MILP [28], and such an approach is assumed in this work.
Remark 2.
The above MILP formulation reminds the model in [10], as solving it will result in the DPP-W and DPP-M solutions in specific traffic scenarios. Still, it is more general since it can provide flexible/optimized protection solutions (enabled by DPP-F) lying between DPP-W and DPP-M. Note that the formulation in [10] models only the DPP-W and DPP-M scenarios, the latter by fixing selected variables to zero, as described in the remarks in [10]. However, it does not allow for modeling the DPP-F scenario, in which the flexible protection selection decisions are taken “intelligently” according to traffic demands and are not imposed by fixing variables in advance. This flexibility is achieved by implementing dedicated variables (, ) and constraints (Constraints (9)–(11), Constraints (14)–(18), and modified Constraints (36)–(37)), which are absent in [10].
4. Results and Discussion
The DPP schemes are evaluated in three mesh network topologies presented in Figure 2: MESH-9, MESH20, and MESH-38, with link lengths distributed uniformly between 1 and 3 kilometers. For more detailed characteristics of the topologies, refer to [10].
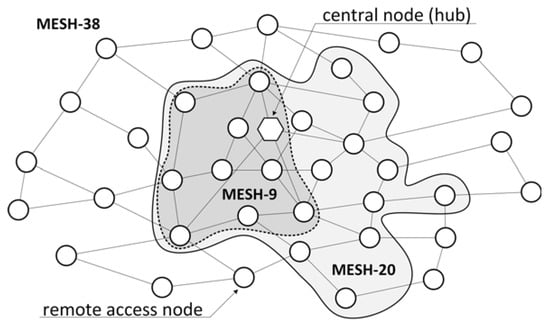
Figure 2.
Network topologies: MESH-9, MESH-20, and MESH-38.
We consider a WDM optical transmission system carrying wavelengths [15]. The transmission system parameters and the cost of optical components, reported in Table 3, are as in [10] and represent realistic values (see [10] for detailed references for these data).

Table 3.
Transmission system parameters and cost values.
A k-shortest path algorithm is used to obtain candidate routing paths. Up to paths in MESH-9, and paths in MESH-20 and MESH-38 are generated for each pair of nodes, which is a good trade-off between the MILP computation times and optimization results [10]. The analysis is performed for different traffic loads (denoted as ), representing the average number of wavelengths to be carried between the hub and a remote node.
The MILP network optimization models—developed for the proposed protection scenario DPP-F in Section 3 and presented for the reference scenarios DPP-W and DPP-M in [10]—are solved using the CPLEX solver v. [25]. The solver is run on a GHz Ryzen Threadripper-class workstation with 32 CPU cores and 128 GB RAM. The overall protection deployment cost (z) is the primary performance metric used in the analysis. The results are obtained with a 10-minute computation time limit.
Figure 3, Figure 4 and Figure 5 show the overall cost of deploying protection schemes DPP-M, DPP-W, and DPP-F (z, represented by bars) in networks MESH-9, MESH-20, and MESH-38, respectively. Also, we report the relative difference in network cost (cost savings, denoted as ) of scheme DPP-F when compared to DPP-M and DPP-W. The analysis is performed in a function of traffic load () for MUX loss dB (left charts) and dB (right charts), assuming the lowest fiber lease cost considered ().
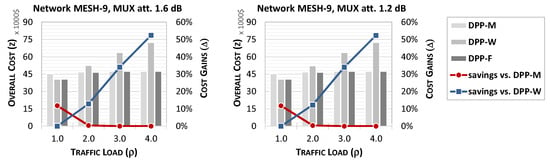
Figure 3.
Overall deployment cost of protection scenarios DPP-M, DPP-W, and DPP-F (z, bars) and relative cost savings of DPP-F vs. DPP-M and DPP-W (, lines) as a function of traffic load, assuming 1.6 dB (left) and 1.2 dB (right) MUX loss, and in network MESH-9.
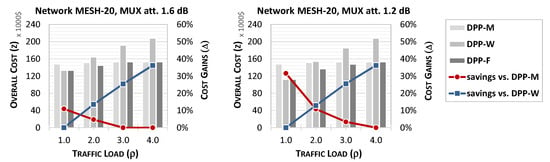
Figure 4.
Overall deployment cost of protection scenarios DPP-M, DPP-W, and DPP-F (z, bars) and relative cost savings of DPP-F vs. DPP-M and DPP-W (, lines) as a function of traffic load, assuming 1.6 dB (left) and 1.2 dB (right) MUX loss, and in network MESH-20.
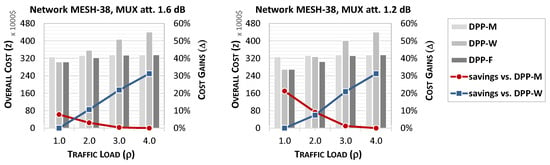
Figure 5.
Overall deployment cost of protection scenarios DPP-M, DPP-W, and DPP-F (z, bars) and relative cost savings of DPP-F vs. DPP-M and DPP-W (, lines) as a function of traffic load, assuming 1.6 dB (left) and 1.2 dB (right) MUX loss, and in network MESH-38.
In Figure 3, Figure 4 and Figure 5, we can see that the overall cost of deploying the protection scenario DPP-F is the lowest without regard to the network load. This is because DPP-F can apply the best DPP option, adjusting it to the traffic conditions at a given remote node. In particular, it assures the performance of DPP-W at lower traffic loads when aggregating wavelengths from intermediate remote nodes is profitable. Concurrently, it performs like DPP-M at high traffic loads, where it is beneficial to aggregate wavelengths at the end remote node only, which reduces the use of expensive optical switches. The relative cost savings of DPP-F vs. DPP-M are about for and dB in all three networks, and achieve up to 20–30% for dB in larger networks. The higher cost savings at dB are due to the corresponding lower attenuation on the transmission paths, which translates into the capability of traffic aggregation from a higher number of intermediate nodes on a single path. Concurrently, the relative cost savings of DPP-F vs. DPP-W reach up to in MESH-9 and about 30–35% in the larger networks when and without regard for the MUX loss.
Figure 6 shows the cost of individual optical components in detail, such as fibers, MUXes, and switches, utilized in different protection scenarios for different traffic loads () in the analyzed networks, assuming MUX loss dB and fiber cost .
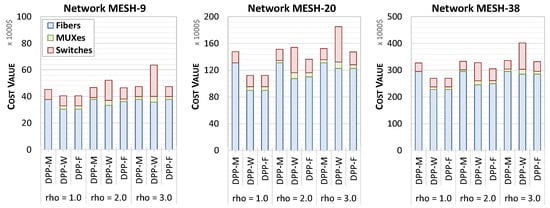
Figure 6.
Overall cost of particular optical components in different protection scenarios for different traffic loads () in analyzed networks, assuming dB and .
In all the analyzed cases in Figure 6, the fiber cost (depicted as a blue segment of the bars) is the most significant contributor to the overall network cost. The fiber cost is the highest in the DPP-M protection scenario, where direct protection and backup transmission paths must be established between the hub and each remote node. Aggregating wavelengths from intermediate remote nodes involves a higher usage of MUXes in DPP-W and DPP-F, resulting in a higher overall cost of this element (depicted as a green segment) in these protection scenarios than in DPP-M. In DPP-W, where dedicated optical switches protect individual wavelength connections, the cost of involved optical switches (depicted as a red segment) increases considerably with the traffic load. As a result, the overall cost of DPP-W can exceed even that of DPP-M (as earlier noted in [10]). The DPP-F protection scheme eliminates this drawback as it flexibly applies the most appropriate DPP scheme according to traffic demands, decreasing the use of optical switches and leading to the lowest network protection cost.
The fiber cost may differ considerably depending on the environmental scenario (e.g., rural, dense urban) [29,30]. It impacts the DPP-M protection deployment cost, as DPP-M does not aggregate traffic from intermediate nodes but requires direct primary and backup transmission paths to/from all remote nodes, which results in high demand for fiber resources. Therefore, in Figure 7, we analyze the relative cost savings achieved with DPP-F compared to DPP-M as a function of the dark fiber lease cost (), assuming different traffic loads () and dB.
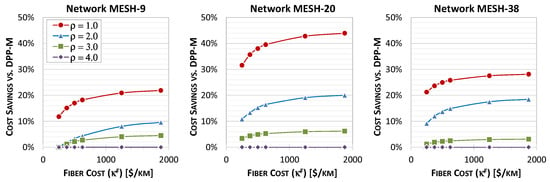
Figure 7.
Relative cost savings of protection scenario DPP-F vs. DPP-M as a function of fiber lease cost for different traffic loads () in analyzed networks, assuming dB.
Figure 7 shows that the cost savings () from using DPP-F instead of the DPP-M protection scenario increase with the fiber lease cost. It happens in each traffic scenario except for , where all transmission paths are saturated with the traffic carried to/from the end remote nodes, and aggregating wavelengths from intermediate nodes is impossible in DPP-F. In this case, DPP-F provides the same protected transmission paths as DPP-M, and there is no difference in performance between both of the protection scenarios (i.e., ). The highest cost savings, most prominent in larger mesh networks, are achieved for and , where reaches up to 22%, 44% and 28%, respectively, in MESH-9, MESH-20, and MESH-38. The high fiber lease costs correspond to large urban environments, as indicated in [29]. Therefore, DPP-F is a more suitable protection scenario than DPP-M for urban networks, especially dense 5G networks with many remote nodes and low/moderate traffic demands, which can be aggregated on the transmission paths.
Figure 8 shows the relative cost savings achieved with DPP-F compared to DPP-W as a function of the dark fiber lease cost (), assuming different traffic loads () and dB. Contrary to the above-discussed results comparing DPP-F with DPP-M, the cost savings () from using DPP-F instead of DPP-W decrease with the fiber cost. It is reasonable as both protection schemes enable traffic aggregation in the optical layer, which optimizes the use of fiber resources. As the fiber cost increases and becomes a dominant cost factor, the overall cost of DPP-W will approach the cost of DPP-F. Except for , for which both DPP scenarios have the same exact cost as they use the same number of optical components (as shown in Figure 6); DPP-F always provides some cost savings, which are the most prominent for lower fiber cost values.
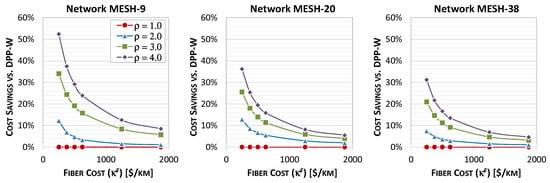
Figure 8.
Relative cost savings of protection scenario DPP-F vs. DPP-W as a function of fiber lease cost for different traffic loads () in analyzed networks, assuming dB.
Summarizing the results shown in Figure 7 and Figure 8, DPP-F appears to be the most cost-effective DPP scenario in the range of average traffic loads. For extremely low and high traffic loads, DPP-W and DPP-M are good alternatives, respectively. Eventually, in dense urban network scenarios with very high fiber lease costs, both DPP-F and DPP-W are suitable solutions. The latter involves a slightly higher cost (of some percent in the analyzed networks) related to the higher demand for optical switching devices.
5. Conclusions
This paper presented a novel dedicated path protection scheme with flexible switching for passive optical 5G Xhaul access networks to enhance network survivability while optimizing cost-efficiency. DPP-F flexibly selects between whole WDM signal switching and individual wavelength switching based on traffic conditions and network topology. Using the formulated MILP model, the cost of the DPP-F scenario was compared to conventional schemes, specifically DPP-W and DPP-M, which represent individual wavelength and entire WDM signal switching, respectively.
The numerical analysis showed the DPP-F’s efficiency in leveraging optical switching and fiber resources, leading to notable reductions in network deployment costs across diverse traffic and topological scenarios. Specifically, DPP-F exhibited cost savings ranging from several to tens of percent over the reference methods, showcasing its potential in dense and ultra-reliable network configurations. The main advantage of DPP-F is that it assures the lowest-cost DPP solution in a planned network independent of traffic demands. In contrast, DPP-W and DPP-M are efficient only under specific traffic conditions, respectively, low or high traffic demands. As a result, DPP-F outperforms both reference DPP schemes in a range of intermediate traffic loads while preserving the best performance of DPP-W and DPP-M at very low and high loads.
In future studies, we will focus on the cost-effective selection and placement of OADMs of diverse capacity and cost in survivable optical xHaul networks and on shared path protection schemes. We will also explore heuristic strategies ensuring the practical design of protected transport paths in passive optical Xhaul networks with larger topologies.
Funding
This research was supported by National Science Centre, Poland under grant number 2018/31/B/ST7/03456.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Chih-Lin, I.; Korhonen, J.; Huang, J.; Han, L. RAN Revolution with NGFI (xhaul) for 5G. IEEE J. Lightw. Technol. 2018, 36, 541–550. [Google Scholar]
- O-RAN Alliance. Xhaul Transport Requirements Tech. Spec. v1.0. 2021. Available online: https://www.o-ran.org/ (accessed on 25 April 2024).
- Sizer, T.; Samardzija, D.; Viswanathan, H.; Le, S.T.; Bidkar, S.; Dom, P.; Harstead, E.; Pfeiffer, T. Integrated Solutions for Deployment of 6G Mobile Networks. IEEE J. Lightw. Technol. 2022, 40, 346–357. [Google Scholar] [CrossRef]
- O-RAN Alliance. WDM-based Fronthaul Transport Tech. Spec. v4.0. 2024. Available online: https://www.o-ran.org/ (accessed on 25 April 2024).
- O-RAN Alliance. Xhaul Packet Switched Architectures and Solutions Tech. Spec. v7.0. 2024. Available online: https://www.o-ran.org/ (accessed on 25 April 2024).
- IEEE 1914.1-2019; IEEE Standard for Packet-based Fronthaul Transport Networks. IEEE: Piscataway, NJ, USA, 2019.
- Ericsson. Optimized Optical Solutions for Mobile Transport Networks (White Paper). 2022. Available online: https://www.ericsson.com/en/reports-and-papers/white-papers/optimized-optical-solutions-for-mobile-transport-networks/ (accessed on 14 June 2022).
- Klinkowski, M.; Jaworski, M. Planning of Optical Connections in 5G Packet-Optical xHaul Access Network. Appl. Sci. 2022, 12, 1146. [Google Scholar] [CrossRef]
- Klinkowski, M.; Jaworski, M. Cost-Aware Optimization of Optical Add-Drop Multiplexers Placement in Packet-Optical xHaul Access Networks. Appl. Sci. 2023, 13, 4862. [Google Scholar] [CrossRef]
- Klinkowski, M.; Jaworski, M. Dedicated Path Protection with Wavelength Aggregation in 5G Packet-Optical xHaul Access Networks. IEEE J. Lightw. Technol. 2023, 41, 1591–1602. [Google Scholar] [CrossRef]
- IEEE 802.1CM-2018; IEEE Standard for Local and Metropolitan Area Networks—Time-Sensitive Networking for Fronthaul. IEEE: Piscataway, NJ, USA, 2018.
- Common Public Radio Interface: eCPRI V2.0 Interface Specification. Ericsson AB, Huawei Technologies Co. Ltd., NEC Corporation and Nokia. 2019. Available online: http://www.cpri.info/downloads/eCPRI_v_2.0_2019_05_10c.pdf (accessed on 16 August 2024).
- IEEE 1914.3-2018; IEEE Standard for Radio over Ethernet Encapsulations and Mappings. IEEE: Piscataway, NJ, USA, 2018.
- HFR Networks. flexiHaul Packet xHaul Solution. Available online: https://hfrnet.com/ (accessed on 25 April 2024).
- HFR. flexiHaul xWave 400G Data Sheet. Available online: https://hfrnetworks.com/ (accessed on 25 April 2024).
- HFR Networks. flexiHaul Packet M-Series TSN Switch Data Sheet. Available online: https://hfrnetworks.com/ (accessed on 25 April 2024).
- Wong, E.; Grigoreva, E.; Wosinska, L.; Machuca, C.M. Enhancing the Survivability and Power Savings of 5G Transport Networks based on DWDM Rings. OSA/IEEE J. Opt. Commun. Netw. 2017, 9, D74–D85. [Google Scholar] [CrossRef]
- Shehata, M.; Ayoub, O.; Musumeci, F.; Tornatore, M. Survivable BBU Placement for C-RAN over Optical Aggregation Networks. In Proceedings of the ICTON, Bucharest, Romania, 1–5 July 2018. [Google Scholar]
- Khorsandi, B.M.; Raffaelli, C. BBU location algorithms for survivable 5G C-RAN over WDM. Comput. Netw. 2018, 144, 53–63. [Google Scholar] [CrossRef]
- Khorsandi, B.M.; Tonini, F.; Amato, E.; Raffaelli, C. Dedicated Path Protection for Reliable Network Slice Embedding Based on Functional Splitting. In Proceedings of the ICTON, Angers, France, 9–13 July 2019. [Google Scholar]
- Khorsandi, B.M.; Colle, D.; Tavernier, W.; Raffaelli, C. Dedicated and shared solutions for reliable function splitting in 5G X-haul. Phot. Netw. Commun. 2020, 40, 245–255. [Google Scholar] [CrossRef]
- Lashgari, M.; Wosinska, L.; Monti, P. A Shared-Path Shared-Compute Planning Strategy for a Resilient Hybrid C-RAN. In Proceedings of the ICTON, Angers, France, 9–13 July 2019. [Google Scholar]
- DeCusatis, C. Handbook of Fiber Optic Data Communication—A Practical Guide to Optical Networking, 4th ed.; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
- 100G Lambda MSA. 100G-LR1-20, 100G-ER1-30 and 100G-ER1-40 Tech. Spec. Rev 1.1. Available online: http://100glambda.com/ (accessed on 14 June 2022).
- IBM. CPLEX Optimizer. Available online: http://www.ibm.com/ (accessed on 1 September 2024).
- Gurobi Optimization, LLC. Gurobi Optimizer Reference Manual. 2024. Available online: https://www.gurobi.com/ (accessed on 1 September 2024).
- HYGJ Communication Technology. Optical Line Protection System. Available online: https://www.gjsun.com/upload/products/2021102211504217.pdf (accessed on 14 October 2022).
- Pióro, M.; Medhi, D. Routing, Flow, and Capacity Design in Communication and Computer Networks; Morgan Kaufmann: Burlington, MA, USA, 2004. [Google Scholar]
- CTC Technology & Energy. Dark Fiber Lease Considerations. Available online: https://www.ctcnet.us/DarkFiberLease.pdf (accessed on 25 April 2024).
- DSS Operator. Cennik Uslug. Available online: http://www.dssoperator.pl/wp-content/uploads/3.-Umowa-Ramowa-Zalacznik-2-Cennik-Uslug.pdf (accessed on 14 March 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).