Abstract
We propose a single-pixel non-imaging target recognition scheme which that exploits the singular values of target objects. By choosing the first few singular values and the corresponding unitary matrices in the singular value decomposition of all the targets, we form the measurement matrices to be projected onto the target in a single-pixel non-imaging scheme. One can quickly and accurately recognize the target images after directly recording the single-pixel signals. From the simulation and experimental results, we found that the accuracy of target recognition was high when the first three singular values were used. The efficiency of target recognition was improved by randomly rearranging the orders of the row vectors in the measurement matrix. Therefore, our research results offer a novel perspective for recognizing non-imaging targets.
1. Introduction
In recent years, single-pixel imaging (SPI) has garnered increasing attention for its unique behaviors and potential applications [1,2,3]. SPI projects a set of patterns onto the target and records a series of single-pixel signals. The image is reconstructed by correlating the single-pixel signals and the projected patterns. SPI enables the acquisition of 2D or 3D images using only a single-pixel detector [1,2,3,4,5,6,7]. It not only substantially reduces costs but also offers significant advantages in challenging conditions such as atmospheric turbulence, non-visible wavelengths, and low-light environments, where conventional imaging methods may fall short. SPI finds diverse applications in remote sensing [4,5], 3D measurements [6,7], image encryption [8], edge detection [9,10], image recognition [11,12,13], image classification and tracking [14], X-ray imaging [15], and fluorescence imaging [16]. However, SPI is limited by the prolonged acquisition times and diminished imaging quality. It has been a primary focus of research in this domain to reduce both image sampling and reconstruction time while improving image quality [17,18,19,20].
Singular value decomposition (SVD) [21,22,23,24] is a versatile technique employed for tasks such as denoising, image restoration, and feature extraction. By applying SVD, an image can be represented in a lower-dimensional form, facilitating efficient data compression and processing. In computer vision, SVD aids in selecting the most representative and significant features from the data, which can be utilized in image registration, object recognition, classification, clustering, and other machine learning tasks, thereby providing a powerful tool for image processing and analysis [23,24]. In 2021, Qu et al. proposed a blind color watermarking scheme utilizing single-pixel imaging (SPI), redistributed invariant lifting wavelet transform (RILWT) and singular value decomposition (SVD) [25]. In 2024, Deng et al. developed a single-pixel imaging method based on a deep learning network-enhanced singular value decomposition (DLSVD) [26]. These approaches demonstrated improved image reconstruction quality, particularly at low sampling ratios.
In certain practical applications, target recognition becomes an important task. Most available target classification systems are based on image acquisition and analysis, with the classification algorithms relying on features extracted from the target images [27]. Consequently, image-based target classification systems typically employ an acquisition-extraction strategy, where the system first captures the image of the target and then applies specific image analysis algorithms to extract features for classification [28,29]. However, this approach necessitates high-speed imaging techniques that can incur significant time costs and result in the generation of large volumes of data, which require adequate data storage, bandwidth, and processing capabilities. Furthermore, the complex image analysis algorithms typically involve high computational costs. The imaging process not only complicates the computational tasks but also prolongs the time needed for validating and recognizing the target objects. Therefore, eliminating the imaging step while simplifying the recognition computation could significantly enhance target recognition efficiency and reduce computational costs.
There have been notable advancements in non-imaging single-pixel target recognition in recent years. Chen et al. [30] proposed a single-pixel non-imaging perceptual hashing object recognition scheme. This approach utilizes Fourier spectral acquisition technology and a perceptual hashing algorithm to achieve non-imaging object recognition with fewer measurements. He et al. [31] introduced a handwritten digit recognition method based on single-pixel imaging and deep neural networks (DNNs). This approach achieves high recognition accuracy with reduced sampling requirements. However, the deep learning training process may encounter unavoidable interferences in practical applications, which can affect the stability of the network model. Additionally, He et al. [32] proposed a novel single-pixel non-imaging target classification scheme. This method employs principal component analysis (PCA) along with traditional classification models for classification purposes. This method offers higher recognition accuracy and demonstrates more stable feature extraction capabilities in noisy environments. The target recognition techniques mentioned above involve complex calculations or training processes, which can be challenged in a non-imaging scheme by combining SVD and SPI.
In this paper, we propose a novel non-imaging single-pixel target recognition scheme based on SVD. This method leverages the uniqueness and descending order properties of singular values in matrices of natural objects. It involves performing SVD on the two-dimensional information of the target object, and using the orthogonal matrices corresponding to the singular values to generate illumination patterns. These projection images are then labeled in a predefined sequence. The illumination patterns are projected onto the target object, and reflected light signals are collected using a single-pixel detector with no spatial resolution. If the peak position of the reflected light signal matches the target object’s label, recognition is successful. This method directly identifies the target by observing the peak positions of reflected light signals without requiring subsequent imaging computations, thereby significantly reducing computational complexity. Simultaneously, we evaluate recognition performance using contrast ratio and optimize the scheme to achieve non-imaging target recognition with fewer measurements.
Our paper is organized as follows. In Section 2, we detail the principles and method of target recognition with SVD in a single-pixel non-imaging scheme. Section 3 details the simulation and experimental validation of the method, showing that non-imaging target recognition can be achieved with fewer measurements. The conclusion of our work is in Section 4.
2. Methods
In the preprocessing stage, the target image from the simulation experiment was converted to a grayscale image and resized to the required dimensions. This preprocessing step provided the two-dimensional data of the target object for the experiment. The objects to be recognized were sequentially labeled, and SVD was performed on the target image. The left and right singular matrices corresponding to each singular value were used to construct the projection patterns. Subsequently, a pseudoinverse single-pixel imaging experiment was conducted. Recognition was deemed successful if the label corresponding to the peak value of the reflected light signals obtained from a set of experiments matched the target object.
We employed a classical pseudoinverse single-pixel imaging system, where reflected light signals are obtained by calculating the inner product between the measurement matrix and the target object. The experimental setup is illustrated in Figure 1. The light intensity information for the i-th object image can be represented as:
where denotes the measurement matrix, where each of its row vectors is considered an illumination pattern . represents the one-dimensional signal values of the i-th target object, and signifies potential noise during the measurement process. Each illumination pattern is projected onto the target object, and a reflected light signal is obtained by the single-pixel detector. This process can be formulated as Equation (3):
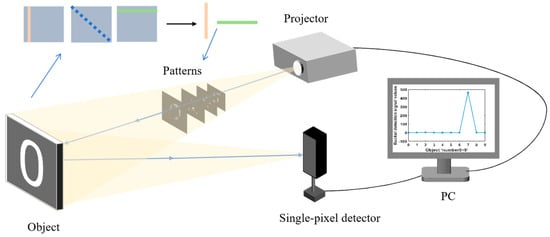
Figure 1.
The experimental setup of the proposed scheme.
The primary method for constructing our measurement matrix is as follows.
- (1)
- According to Cauchy–Schwarz inequality, for any two vectors and , if and only if there is for some , the Formula (5) is equal. This corresponds to the single-pixel imaging system described in Equation (3), where greater similarity between the projected speckle patterns and the target object’s characteristics leads to higher reflected light signal intensity .
- (2)
- Singular value decomposition (SVD) was employed to process the preprocessed two-dimensional information of the target object, as illustrated in Figure 2.
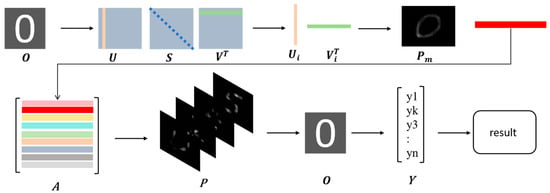 Figure 2. The projection speckle pattern for recognition was designed using singular value decomposition.
Figure 2. The projection speckle pattern for recognition was designed using singular value decomposition.
The one-dimensional data of the i-th target object was reshaped into two-dimensional data and then processed using singular value decomposition (SVD):
where T represents matrix transposition. Corresponding to the j-th singular value , the Kronecker product of the j-th row of the left singular matrix and the j-th column of the right singular matrix generate a projected speckle pattern , described by:
After obtaining the projected speckle patterns, the next step involves reshaping these patterns into row vectors:
and embedding them into the measurement matrix. For instance, we chose j = 2 in Equations (9) and (10) in our simulation and experiment. All the patterns form a feature library for target recognition. Subsequently, experiments were conducted using a single-pixel imaging system to obtain reflected light signal values. Recognition of the target was based on whether the peak positions in the reflected light signals matched the target. Ideally, a single illumination pattern suffices for non-imaging target identification. Thus, it not only reduced sampling frequency required but also eliminated the imaging process. We introduced the contrast of a set of experimental reflected light signals to evaluate recognition performance. The contrast ratio is defined by:
A higher contrast ratio indicates better recognition performance. Experimental schemes were optimized based on contrast ratios using a method that integrated two singular values to design projected speckle patterns, as outlined in Section 3.
3. Simulation and Experimental Results
3.1. Simulation and Result
The simulation experiments were conducted using the MATLAB R2022a (MathWorks, Natick, MA, USA)platform. We selected the digits 0 to 9 as identification objects, and all images were standardized to a 32 × 32 pixel format. Initially, singular value decomposition (SVD) was performed on the two-dimensional data of the target images. Each target object had 32 singular values, but only those with optimal recognition performance were selected for designing the projected speckle patterns. The resulting patterns, which encode the target image features, were arranged in the measurement matrix by label and used in a single-pixel imaging system to obtain reflected light signals. According to Cauchy–Schwarz inequality, the reflected light intensity rises with the similarity between the speckle pattern and the object’s inherent features. Thus, recognition success was determined by directly observing whether the peak value of the reflected light signals corresponded to the correct label position. Simulation results are depicted in Figure 3, where (a), (b), (c), and (d) show the reflected light signal values obtained by extracting features using the first four singular values, respectively. In each bar graph, the x-axis represents the number of simulation experiments, the y-axis denotes the predefined label order, and the z-axis shows the reflected light signal. The maximum reflected light intensity for each simulation is marked with a red star at the top of the bars. Labels were assigned in the order of 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Recognition was considered successful if the red star was positioned along the diagonal. The results indicated that (a), (b), and (c) achieved successful recognition, whereas (d) misidentified 8 as 5. This is because of the singular value decomposition property: the further back a singular value is, the less characteristic information it contains. Recognition failures began to occur with the fourth singular value, suggesting that only the first three singular values be considered for further analysis. It is noteworthy that the reflected light intensities in (a) were significantly higher compared to those in (b), (c), and (d). This was due to the singular value decomposition, where the first singular value contained the object that was most informative and far larger than the latter singular values. However, the extensive feature information also included more similarities with other objects. It can be seen that the difference between the columns marked in red in (a) and other columns is much smaller than that in (b) and (c), which is obviously not conducive to the realization of target recognition. Therefore, the first singular value was not the optimal choice for our method. Next, we optimized the experimental scheme based on the above simulation results and introduced contrast ratio to analyze the recognition effect.
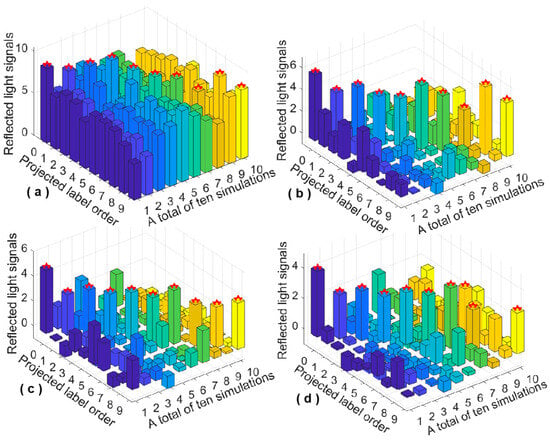
Figure 3.
Simulation and comparison diagram of the bucket detection signal measured by a single singular value, (a), (b), (c), and (d) show the reflected light signal values obtained by extracting features using the first four singular values, respectively.
Figure 4 presents the contrast bar graph for the simulation. Figure 4a illustrates the contrast ratio obtained by selecting a single singular value for the simulation experiments, while (b) depicts the contrast bar graph derived by optimizing our experimental scheme using two singular values. It is evident that the performance of our optimized scheme, which utilizes the combination of two singular values, was significantly enhanced. The scheme with the combination of the second and third singular values had the highest simulation contrast, indicating a robust single-pixel imaging-free identification performance. Therefore, we opted for this scheme in the design of the projection speckle to enhance the stability and generalization of the method for target recognition.
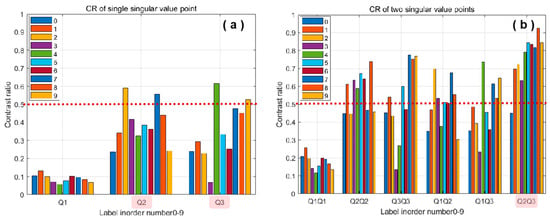
Figure 4.
Contrast ratio comparison between a single singular value and two singular values combined. (a) The contrast ratio obtained by selecting a single singular value for the simulation experiments; (b) The contrast bar graph derived by optimizing our experimental scheme using two singular values.
The method of combining the second and third singular values was as follows: firstly, the second singular value of the target object is used as the speckle coefficient, as shown by:
Secondly, the third singular value is utilized to generate the projection speckle pattern, as seen in:
In the next subsection, we analyze the comparison between the simulation results of the method and the actual experimental results.
3.2. Experimental Results
In the actual experiment, the target object was positioned parallel to the projector. The computer controlled both the projector and the single-pixel detector. The projector sequentially displayed predesigned lighting modes based on a predefined label sequence and projected these onto the target object. At this stage, the only light source was the projector. The projector switched lighting modes every 0.2 s, while the single-pixel detector synchronously sampled the detection signal. Figure 5 illustrates the comparison between experimental and simulation results. Figure 5a shows the target object and the corresponding projection image and (b) presents a bar chart comparing the simulation and experimental results of the barrel detection signal. In Figure 5b, the x-axis represents the number of groups of experiments. A total of 10 groups of simulations and experiments were conducted, with red bars denoting simulation results and blue bars indicating experimental results. The y-axis displays the predesigned label sequence, marked in the order 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. The z-axis represents the reflected light intensities. The results demonstrated successful identification of the target objects, with a high degree of agreement between experimental and simulation data, further validating the feasibility of the experimental scheme.
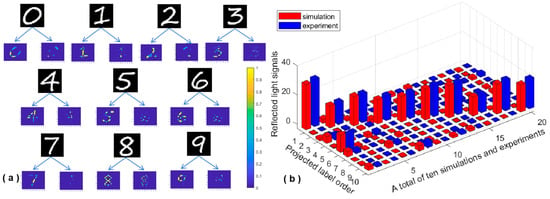
Figure 5.
Experiments with numbers as objects. (a) Ten digital objects and the corresponding projection mode of each object, in the order of “0,” “1,” “2,” “3,” “4,” “5,” “6,” “7,” “8,” “9” from left to right and from top to bottom; (b) comparison diagram of barrel detection signals measured by simulation and experiment.
To further investigate the practicality of the experimental scheme, we incorporated a permutation matrix and conducted the experiment after randomizing the order of the labels. Taking the identification of the digit 9 as an example, we performed 20 trials, with results depicted in Figure 6. The x-axis represents the number of projection patterns, the y-axis denotes the number of experiments, and the z-axis shows the reflected light intensities. The results reveal a distribution that aligns with a normal distribution, with a 60% probability of successful identification achieved using the first five projection patterns. This indicates that the scheme can achieve target identification within the first half of a group of experiments, thereby further demonstrating the practicality of the proposed experimental scheme.
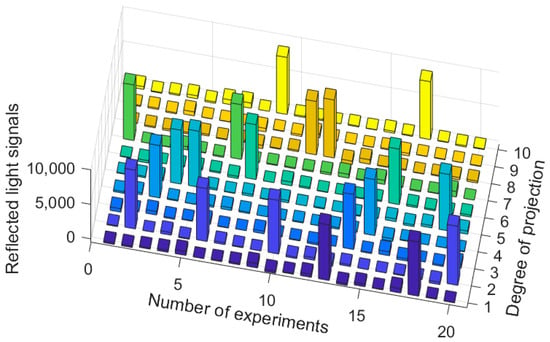
Figure 6.
The result of the experiment by shuffling the label order of ten digital objects.
Finally, to elaborate on the scheme’s advantages during the computational identification phase, particularly in terms of time saving, we conducted a comparative analysis on the MATLAB simulation platform. Specifically, we compared our calculation method with the time cost of the perceptive hash algorithm based on the discrete Fourier transform (DFT) [30]. The target objects remained the same as in the aforementioned experiment, namely, digital images representing the numbers 0–9. To ensure reliable data, we recorded the calculation time by averaging the results from 100 recognition iterations per object. As illustrated in Figure 7, our proposed scheme demonstrates a significantly reduced computation time, achieving a 54% time saving compared to the perceptual hashing algorithm based on the discrete Fourier transform (DFT).
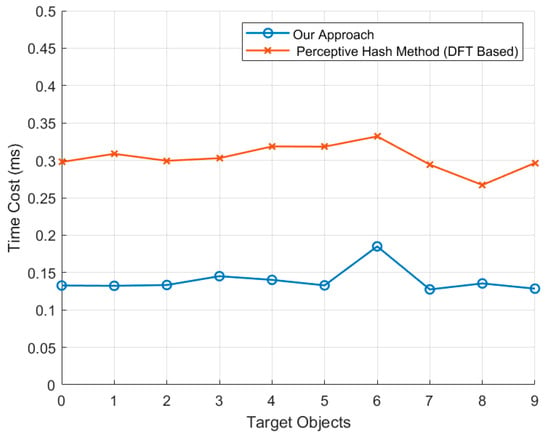
Figure 7.
Comparison of time costs (ms). The horizontal axis represents the target objects labeled from number 0 to number 9, totaling ten objects, while the vertical axis indicates the computation time required for the recognition stage. The blue circle line denotes our proposed method, while the red star line corresponds to the perceptual hashing method based on the discrete Fourier transform (DFT).
4. Conclusions
We have proposed a single-pixel non-imaging target recognition scheme based on SVD to achieve efficient target recognition without relying on imaging computation processes. Simulations and experiments were performed with ten different numbers by extracting the singular value features to form the measurement matrix. Experimental validation demonstrated that the scheme not only saves sampling time but also achieves effective recognition by using only the first two singular values, thereby enhancing feature extraction efficiency. Importantly, this recognition method is straightforward and intuitive, requiring no complex computation or comparison processes: target identification is achieved simply by observing the maximum light intensity signal, greatly simplifying the recognition process. Furthermore, to assess the universality and practicality of this scheme, we performed additional experiments by randomizing the projection sequence. Our research provides new insights into non-imaging target recognition and holds potential for broader practical applications.
Author Contributions
Conceptualization, L.-S.C. and Y.-N.Z.; software, C.R.; validation, L.-S.C. and Y.-N.Z.; resources, C.W.; writing—original draft preparation, L.-S.C.; writing—review and editing, D.-Z.C.; visualization, L.-S.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundations of China under grants 62105278 and 11674273.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Gatti, A.; Brambilla, E.; Bache, M.; Lugiato, L.A. Ghost imaging with thermal light: Comparing entanglement and classical correlation. Phys. Rev. Lett. 2004, 93, 093602. [Google Scholar] [CrossRef] [PubMed]
- Duarte, M.F.; Davenport, M.A.; Takhar, D.; Laska, J.N.; Sun, T.; Kelly, K.F.; Baraniuk, R.G. Single-pixel imaging via compressive sampling. IEEE Signal Process. Mag. 2008, 25, 83–91. [Google Scholar] [CrossRef]
- Edgar, M.P.; Gibson, G.M.; Padgett, M.J. Principles and prospects for single-pixel imaging. Nat. Photonics 2019, 13, 13–20. [Google Scholar] [CrossRef]
- Kang, Z.; Ma, L.; Kang, Y.; Yao, Y.; Zhang, T. Experiments of ghost imaging with pseudo-thermal light for remote sensing applications. In Proceedings of the AOPC 2015: Optical and Optoelectronic Sensing and Imaging Technology, Beijing, China, 5–7 May 2015; Volume 9674, pp. 658–666. [Google Scholar]
- Lu, X.; Zheng, X.; Yuan, Y. Remote sensing scene classification by unsupervised representation learning. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5148–5157. [Google Scholar] [CrossRef]
- Sun, M.J.; Zhang, J.M. Single-pixel imaging and its application in three-dimensional reconstruction: A brief review. Sensors 2019, 19, 732. [Google Scholar] [CrossRef]
- Osorio Quero, C.A.; Durini, D.; Rangel-Magdaleno, J.; Martinez-Carranza, J. Single-pixel imaging: An overview of different methods to be used for 3D space reconstruction in harsh environments. Rev. Sci. Instrum. 2021, 92, 111501. [Google Scholar] [CrossRef] [PubMed]
- Jiao, S.; Zhou, C.; Shi, Y.; Zou, W.; Li, X. Review on optical image hiding and watermarking techniques. Opt. Laser Technol. 2019, 109, 370–380. [Google Scholar] [CrossRef]
- Sui, L.; Wang, J.; Tian, A.; Asundi, A. Optical image hiding under framework of computational ghost imaging based on an expansion strategy. Opt. Express 2019, 27, 7213–7225. [Google Scholar]
- Ren, H.; Zhao, S.; Gruska, J. Edge detection based on single-pixel imaging. Opt. Express 2018, 26, 5501–5511. [Google Scholar] [CrossRef]
- Feng, J.; Jiao, S.; Gao, Y.; Lei, T.; Du, L. Design of optimal illumination patterns in single-pixel imaging using image dictionaries. IEEE Photonics J. 2020, 12, 1–9. [Google Scholar] [CrossRef]
- Latorre-Carmona, P.; Traver, V.J.; Sánchez, J.S.; Tajahuerce, E. Online reconstruction-free single-pixel image classification. Image Vis. Comput. 2019, 86, 28–37. [Google Scholar] [CrossRef]
- Zou, X.; Huang, X.; Liu, C.; Tan, W.; Bai, Y.; Fu, X. Target recognition based on pre-processing in computational ghost imaging with deep learning. Opt. Laser Technol. 2023, 167, 109807. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, X.; Zheng, S.; Yao, M.; Zheng, G.; Zhong, J. Image-free classification of fast-moving objects using “learned” structured illumination and single-pixel detection. Opt. Express 2020, 28, 13269–13278. [Google Scholar] [CrossRef] [PubMed]
- Gilbert, A.J.; Miller, B.W.; Robinson, S.M.; White, T.A.; Pitts, W.K.; Jarman, K.D.; Seifert, A. A single-pixel X-ray imager concept and its application to secure radiographic inspections. Nucl. Instrum. Methods A 2017, 861, 90–97. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, X.; Zheng, G.; Zhong, J. Hadamard single-pixel imaging versus Fourier single-pixel imaging. Opt. Express 2017, 25, 19619–19639. [Google Scholar] [CrossRef]
- Liu, Y.; Suo, J.; Zhang, Y.; Dai, Q. Single-pixel phase and fluorescence microscope. Opt. Express 2018, 26, 32451–32462. [Google Scholar] [CrossRef]
- Ma, M.; Sun, Q.; Gao, X.; Wang, G.; Deng, H.; Zhang, Y.; Zhong, X. High-efficiency single-pixel imaging using discrete Hartley transform. AIP Adv. 2021, 11, 075211. [Google Scholar] [CrossRef]
- Nie, X.; Zhao, X.; Peng, T.; Scully, M.O. Sub-Nyquist computational ghost imaging with orthonormal spectrum-encoded speckle patterns. Phys. Rev. A 2022, 105, 043525. [Google Scholar] [CrossRef]
- Yao, J.; Jiang, Z.; Lv, X.; Peng, Q.; Zhao, X.; Song, L. Adaptive Fourier single-pixel imaging based on directional energy continuity in high frequencies. Opt. Lasers Eng. 2023, 162, 107406. [Google Scholar] [CrossRef]
- Golub, G.H.; Reinsch, C. Singular value decomposition and least squares solutions. In Handbook for Automatic Computation: Volume II: Linear Algebra; Springer: Berlin/Heidelberg, Germany, 1971; pp. 134–151. [Google Scholar]
- Tufts, D.W.; Kumaresan, R.; Kirsteins, I. Data adaptive signal estimation by singular value decomposition of a data matrix. Proc. IEEE 1982, 70, 684–685. [Google Scholar] [CrossRef]
- Hou, Z. Adaptive singular value decomposition in wavelet domain for image denoising. Pattern Recognit. 2003, 36, 1747–1763. [Google Scholar] [CrossRef]
- Zhang, H.Y.; Tao, M.; Ai, K. 2-D TSVD algorithm applied in image debluring problem. Comput. Eng. Appl. 2008, 44, 60–62. [Google Scholar]
- Qu, G.; Meng, X.; Yang, X.; Wu, H.; Wang, P.; He, W.; Chen, H. Optical color watermarking based on single-pixel imaging and singular value decomposition in invariant wavelet domain. Opt. Lasers Eng. 2021, 137, 106376. [Google Scholar] [CrossRef]
- Deng, Y.; She, R.; Liu, W.; Lu, Y.; Li, G. Single-pixel imaging based on deep learning enhanced singular value decomposition. Sensors 2024, 24, 2963. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Zhan, R.; Zhai, Q.; Wang, W.; Zhang, J. Multi-view radar target recognition based on multitask compressive sensing. J. Electromagn. Waves 2015, 29, 1917–1934. [Google Scholar] [CrossRef]
- Chen, W. Ghost identification based on single-pixel imaging in big data environment. Opt. Express 2017, 25, 16509–16516. [Google Scholar] [CrossRef]
- Torkkola, K. Feature extraction by non-parametric mutual information maximization. J. Mach. Learn. Res. 2003, 3, 1415–1438. [Google Scholar]
- Chen, H.; Shi, J.; Liu, X.; Niu, Z.; Zeng, G. Single-pixel non-imaging object recognition by means of Fourier spectrum acquisition. Opt. Commun. 2018, 413, 269–275. [Google Scholar] [CrossRef]
- He, X.; Zhao, S.M.; Wang, L. Handwritten digit recognition based on ghost imaging with deep learning. Chin. Phys. B 2021, 30, 054201. [Google Scholar] [CrossRef]
- He, Z.; Dai, S. Image-free single-pixel classifier using feature information measurement matrices. AIP Adv. 2024, 14, 045316. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).