Abstract
A key issue of X-ray free-electron lasers is the quality of the photoelectron beams generated from a photocathode by laser pulses in the high-gradient RF gun. Controlling the shape of these laser pulses can strongly reduce the transverse emittance of the generated electron bunch. For this purpose, a laser pulseshaper at 515 nm is presented that can be used directly with alkali antimonide photocathodes for photoemission. The first results regarding generation and measurement of flattop and parabolic pulses as well as introduction of modulations for THz generation are presented and show the potential for emittance optimization with 3D ellipsoidal pulses with the proposed pulseshaper. The experiments are carried out for CsTe photocathodes, which require second harmonic generation of the shaped pulses and thus allow investigation of pulseshape preservation in nonlinear frequency conversion processes.
1. Introduction
X-ray free electron lasers require short, high-brightness electron bunches with charge up to the nanocoulomb level. To maximize the single bunch brightness B means to concentrate the highest possible charge Q in the smallest 6D phase-space volume
where are the normalized RMS emittances in all three axes. However, high charge and low transverse emittance are conflicting goals due to space charge effects. Furthermore, the overall transverse emittance has contributions from the intrinsic cathode emittance , the RF-induced emittance , and contributions from the surrounding magnets as the solenoid magnet as well as magnetic field components at the surface of the cathode introduced by the solenoid magnet (cf. [1,2,3]):
The space charge contribution is the term that motivates the importance of laser pulseshaping to control the charge distribution of the electron bunch in photoinjectors, which could help to avoid nonlinear space charge forces and minimize the emittance growth for high bunch charges. For achieving high-brightness electron bunches, photoinjectors are usually driven by complex laser systems with tens of picosecond pulse duration with several MHz repetition rates, which are actively synchronized to the linear accelerator. The driver laser wavelength depends on the bandgap of the photocathode material and is in the UV range for widely used CsTe or metal cathodes.
An advantageous distribution to drive photoinjectors is a transverse and longitudinal flattop in order to homogenize the charge distribution in the electron bunch. With such flattop pulses, low emittances of up to 2 nC bunch charge were demonstrated at the Photo Injector Test Facility at DESY in Zeuthen (PITZ) [4] using the a pulse-stacking technique with birefringent filters [5,6] and a beamshaping aperture (BSA) to generate a laser pulse distribution close to a homogeneously filled cylinder.
The ideal distribution for an electron bunch with minimized emittance is a uniformly filled 3D ellipsoid that has space charge fields that have a linear dependence on the position within the distribution [7,8,9]. The resulting density distributions are therefore immune to space-charge-induced phase space dilution. For X-ray free-electron lasers, this shape has the advantage of mitigating emittance growth and being notably less prone to halo formation.
The first scheme to generate such distributions using photoemission electron sources was proposed by Serafini [10] and subsequently refined by Luiten et al. [11] using an ultrashort laser impinging on a fast photoemitter in a strong accelerating electric field. The operating parameters of the electron source are chosen such that the distribution evolution is dominated by linear space charge force and is often referred to as “blow-out regime”, which uses pulses in the order of sub-100 femtoseconds and high gradients at the cathode. The generation of 3D ellipsoids in this regime is usually achieved by frequency-tripled titanium–sapphire lasers, being limited to a tens of kHz repetition rate. Improvements in this scheme are ongoing [12,13,14,15,16] for their potential to increase the peak brilliance of X-ray FELs and in ultrafast electron diffraction (UED). However, this scheme has drawbacks for high charges due to the formation of image charges close to the photocathode [17].
To achieve higher repetition rates on a multi-MHz level, fourth harmonic generation Nd-doped, and later Yb-doped, solid state lasers [18,19], or recently developed fiber lasers [20,21] are driving photoinjectors of X-ray free-electron lasers to achieve high peak and average brightness for experiments. Due to their narrow spectral bandwidth, their pulse duration is limited between 0.25 ps and 8 ps, and thus they are less suitable to exploit the blow-out regime despite proof of principle experiments [22]. Realizing pulseshaping schemes with these lasers is a challenging task since their low bandwidth and gain narrowing in amplifier stages hamper straightforward implementation of spatial-light-modulator-based 4f geometries. Since the 3D ellipsoidal distribution is coupled transversely and longitudinally, not only is the generation challenging but the characterization is also difficult using commonly used pulse characterization methods that integrate one component of the distribution; this also holds true for many diagnostic methods used in the accelerator facility.
One way to realize such distributions from these lasers was proposed by Mironov et al. [23] using chirped pulses and an LCOS SLM (liquid crystal on silicon spatial light modulator) in a zero-dispersion grating stretcher setup. The stretching of the bandwidth-limited laser pulse is realized such that the relation of frequency and temporal domain is almost linear and allows spectral shaping that directly translates into the temporal pulse structure. For characterization of the pulseshape, a scanning cross-correlator [24] was used. Furthermore, these kinds of pulses allow for implementation of the slit scan technique using a 2D spectrograph to characterize the pulseshape [23]. A version of the proposed scheme to generate ellipsoidal pulses has been installed at PITZ and was upgraded over the past few years [25]. Other promising approaches are the application of profiled Chirped Volume Bragg gratings [26], the implementation of an absorption mask for amplitude shaping [27], or the usage of oppositely chirped pulses for frequency conversion [28]. However, when pulseshaping is realized in the IR, a two-step frequency conversion to green and then UV is required, which is susceptible to instabilities when trying to achieve high conversion efficiencies. This degrades the quality of the shaped pulse that produces photoelectrons at the cathode [25].
Here, we propose a scheme that uses the same pulseshaping method as used for IR lasers [23,25] and adapt it for 515 nm wavelength, which has the advantage of being directly applicable to alkali antimonide photocathodes [29]. Working with green light is a good compromise regarding having powerful lasers and the availability of efficient pulseshaping devices for operation with 1 MHz repetition rate at several watts of average power. However, since alkali antimonide photocathodes are still under testing and not regularly used at accelerator facilities, the pulseshaping scheme is studied for CsTe photocathodes. Here, the proposed shaping at 515 nm wavelength has the advantage that only one conversion step to UV is needed, which reduces the susceptibility to instabilities compared to a two-stage frequency conversion for IR lasers. Ultimately, although flattop pulses are often used to drive photoinjectors at X-ray FELs today, the benefits of 3D ellipsoidal pulses can be used for further upgrades of the facilities, e.g., for CW operation with lower gun gradients [30,31,32]. Section 2 provides an overview of the PITZ accelerator and its diagnostics, the requirements on photocathode laser systems at accelerator facilities, the design of the pulseshaper, and the used characterization methods for shaped pulses. Pulseshaping results, both with optical diagnostics and characterization of the resulting electron bunch in Section 3, are followed by the discussion of the extension of the pulseshaping scheme for 3D ellipsoidal pulses in Section 4.
2. Materials and Methods
2.1. PITZ Overview
The Photo Injector Test Facility at DESY in Zeuthen (PITZ) is dedicated to the research, development, and characterization of RF photoinjectors and related technologies. It was built more than 2 decades ago to demonstrate the electron source requirements for the Free-electron LASer in Hamburg (FLASH) [33,34], and the European XFEL [35,36]. The PITZ accelerator (Figure 1) consists of a radio frequency (RF) photo gun and an RF booster cavity, both standing wave resonators operating at 1.3 GHz and powered by two separate 10 MW klystrons. The RF gun with a nominal accelerating gradient of 60 MV/m and a high quantum efficiency (QE 5–10%) CsTe photocathode is capable of generating high-charge electron bunches with a nominal maximum beam mean momentum of 6.3 MeV/c. Further electron beam acceleration is realized via a booster cavity for reaching a final beam momentum of up to 23 MeV/c. The RF systems and photocathode lasers run at a 10 Hz duty cycle (macropulse structure) of up to 650 µs duration which is filled with 1 MHz or 4.5 MHz pulses, depending on the photocathode laser system in use (micropulse structure). The PITZ accelerator is equipped with comprehensive electron beam manipulation and diagnostics, including several sets of quadrupole magnets, scintillator screens, beam emittance measurement systems (EMSY), beam position monitors, and charge measurement instruments. A transverse deflecting structure (TDS) [37,38,39,40] can be used for longitudinal bunch profiling. The electromagnetic field in the TDS is perpendicular to the propagation direction of the electron bunch and the bunch is then encoded to a transverse profile on a view screen, similar to the working principle of a streak camera. A screen in the phase space tomography section (PST) is utilized as detector for the deflected beam.
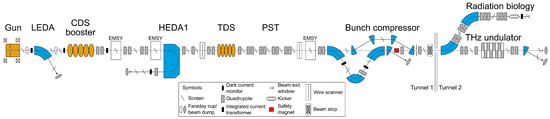
Figure 1.
Layout of PITZ. Photoelectrons from the CsTe cathode are accelerated in the RF gun and further accelerated up to 23 MeV/c in the booster. The momentum of the electron beam can be characterized in dispersive arms (LEDA, HEDA1). The longitudinal electron beam distribution is measured by a TDS on a screen in the phase space tomography section (PST). The emittance of the electron beam can be measured at different positions in the beamline (EMSY).
The beamline of PITZ is continuously evolving to fulfill the research tasks serving the needs of European XFEL. The main task is the development, conditioning, and characterization of RF guns for both free-electron lasers FLASH and European XFEL. Here, the development of a new gun type will help to increase the number of electron bunches served per second from 27,000 up to 45,000 [41]. Another project is cathode development and characterization. Tests with new green photocathodes are ongoing [29], which would simplify the photocathode laser systems because no conversion to UV is necessary for them, relaxing the requirements for the laser system. In addition, pulseshaping schemes become directly available at green wavelengths, which are not working in UV due to high absorption or narrow spectral bandwidth. The second part of the beamline is dedicated to applications. Making use of the high-brightness electron source and its diagnostics, PITZ is also able to drive a THz SASE FEL [42] and to study radiation biology with ultra-high dose rates in a separate beamline, which is currently under development [43]. Both applications require up to 5 nC electron bunch charges with low emittance.
2.2. Laser Overview
The laser system for emittance optimization of the electron bunch in the PITZ accelerator is a commercial Yb:KGW CPA system (Light Conversion PHAROS, Vilnius, Lithuania) with an oscillator output for synchronization with a master oscillator and high power outputs with 1 MHz repetition rate for 1030 nm, 515 nm and 257.5 nm wavelengths. The green output of the laser (260 fs pulse duration and up to 10 µJ pulse energy) enters a grating stretcher to achieve linearly chirped pulses of 10 ps duration, which are then used for amplitude shaping in a 4-f zero-dispersion stretcher, where the reftroreflecting mirror at 2-f is a spatial light modulator (Hamamatsu Photonics LCOS-SLM X10468, Hamamatsu, Japan).
2.2.1. Synchronization to the Master Oscillator
One issue to take care of for photocathode lasers at accelerator facilities is the synchronization of the RF phases in the photoinjector and the laser pulse, and here the commonly used implementation for photocathode lasers at DESY is applied [44]. The 1.3 GHz timing signal for the RF klystrons and the laser are derived from the master oscillator clock. The oscillator of the laser system is equipped with a coarse piezo translator (12 µm range) and a fine piezo translator (3 µm range) to maintain the cavity length for synchronization. By detection of the oscillator output signal with a fast photo diode, comparison to the reference signal of the master oscillator and controlling the piezo voltages, a feedback loop is formed based on a MicroTCA 4.0 timing system. By minimizing the beating to the 1.3 GHz reference signal by adjusting the oscillator’s cavity length (close to 72.22 MHz), synchronization to the RF klystrons is established. A timing jitter of 200 fs rms for synchronization to 1.3 GHz is routinely achieved. The 10 Hz macropulse trigger is generated from a central timing unit.
2.2.2. Amplitude Shaping and Pulseshaper Design
With the advance of LCOS SLMs, shaping of femtosecond pulses became a standard technique for generation of user-defined waveforms [45] and LCOS SLM-based pulseshaping schemes were established for photocathode lasers. For Titanium:Sapphire lasers with their large spectral bandwidth, operating close to the bandwidth limit, phase-shaping is applied to control the shape of the pulse. For Yb doped lasers, phaseshaping has only little effect due to the small bandwidth of the amplifying medium dominated by gain narrowing. An alternative approach is amplitude shaping, where the desired spectral shape is cut out of the spectral distribution of the initial laser pulse in case these are temporally and spectrally coupled (Figure 2). This coupling is achieved by stretching the initial bandwidth limited pulses in a grating stretcher to approximately 10 ps. However, amplitude shaping introduces losses, which reduce achievable electron bunch charges in the accelerator for different pulseshapes.
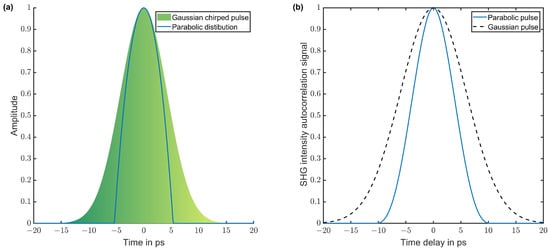
Figure 2.
Amplitude shaping of chirped pulses. (a) The bandwidth-limited laser pulses undergo stretching to achieve 10 ps pulse duration and linear coupling between pulse duration and wavelength (green area). A parabolic shape can be cut out from this distribution (blue line). (b) Corresponding SHG intensity autocorrelation of the stretched Gaussian input pulse (black dashed) and the parabolic pulse (blue line).
In Figure 2a, a parabolic distribution is cropped from a chirped Gaussian pulse indicated by the blue line. Parabolic distributions are good approximations to the later envisioned ellipsoidal pulses but neglect transversal and longitudinal coupling. Advantageous for the parabolic shape is its large overlap with the Gaussian distribution, which ensures low losses in the pulseshaper.
However, characterization of a specific pulseshape can be challenging, as demonstrated in Figure 2b, where SHG intensity autocorrelation traces of the unshaped Gaussian and the parabolic distribution are shown. Despite the difference in pulse duration, judgment of the pulseshape becomes inconclusive and demands for more advanced pulse characterization methods (cf. Section 2.2.3).
Several design considerations have to be taken into account for implementation of amplitude shaping in a high-transmission 4-f zero-dispersion stretcher at 515 nm for photoinjector application. Instead of common setups with two gratings, the laser beam should pass only one grating in a folded double pass configuration. To further reduce alignment complexity, separation of input and output beam is realized by a polarizing beamsplitter. Furthermore, input and output beam should have the same polarization to allow for implementation of identical additional pulseshapers for the later envisioned 3D amplitude shaping. Amplitude shaping is realized by installation of a quarter-wave plate in the 2f beam path to achieve circular polarization on the LCOS SLM, similar to adjusting the polarization axis of the light to the axis of a 2D LCOS SLM [46,47]. The realization of the pulseshaper is shown in Figure 3. The LCOS SLM (Hamamatsu X10458 with HR coating for 1030 nm and 515 nm) allows for shaping on one spatial component (neither influenced by the grating nor the cylindrical lens) and the spectrum. The cylindrical lens collimates the spectrum on the surface of the LCOS SLM and its focal length determines the 4-f geometry. The transmission grating (Ibsen Photonics PCG-3039.5/450-810) has a much higher diffraction efficiency for s-polarization compared to p-polarization. Thus, for the return pass over the transmission grating at the exit of the shaper, it serves as a polarization filter and primarily an s-polarized beam is sent to the half-wave plate and Faraday rotator (Electro-Optics Technology, Inc., Traverse City, MI, USA, 515 nm, +45°). In the backward direction, the polarization is in sum not turned and the s-polarized beam is reflected by the polarizing beamsplitter.
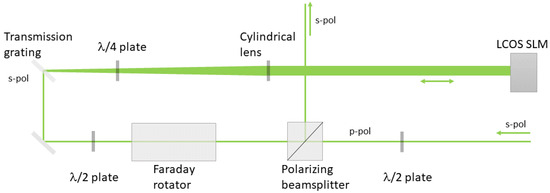
Figure 3.
Setup of the pulseshaper. An s-polarized chirped beam enters the pulseshaper; it is then converted to p-polarization to be transmitted by the polarizing beamsplitter. A Faraday rotator (forward direction) and a half-wave plate rotate it back to s-polarization to have maximum diffraction efficiency from the transmission grating. A cylindrical lens compensates the angular dispersion of the grating. The LCOS SLM can introduce controlled phase variations to spatial components. Amplitude shaping for the SLM is realized by insertion of a quarter-wave plate in the shaper arm. Only light that is s-polarized after double passing the quarter-wave plate and additional phase shift by the LCOS SLM is transmitted by the grating. After passing through the half-wave plate and the Faraday rotator (backward direction), the s-polarized beam component is coupled out by the polarizing beamsplitter.
The pulseshaper is capable of shaping the pulse in the spectral domain (which corresponds to temporal domain or longitudinal domain for the electron bunch) and one transverse domain. Moreover, 3D control of the pulseshape becomes possible with insertion of a second pulseshaper of the same type but with 90° image rotation between the shapers. However, since the 3D ellipsoid is rotational symmetric, applying amplitude shaping in two planes can produce only quadratic approximations with edges. While the usage of additional pulseshapers would give better approximations to the 3D ellipsoid, total beam transmission and alignment complexity hinder application in experimental implementations for photocathode lasers.
2.2.3. Pulseshaping Diagnostics
The optical diagnostics for chirped green laser pulses and the shaped pulses can be grouped into spectrographic techniques and temporal pulse characterization. Following the proof-of-principle experiment for 3D ellipsoidal pulseshaping of chirped pulses [23], pulseshaping diagnostics of the same type were realized on the laser table at PITZ: High-resolution Czerny–Turner 2D imaging spectrographs for green und UV wavelengths allowing slit-scan technique measurements. The detectors in the 2D imaging spectrographs are a Prosilica GC 1350 (Allied Vision, Stadtroda, Germany, 1060 × 1024 pixel, 7.2 pm spectral resolution) for 515 nm and a CM-140-GE-UV (JAI, Copenhagen, Denmark, 1392 × 1040 pixel, 6.5 pm spectral resolution) for 257 nm.
An imaging cross-correlator design is available for characterization of UV pulses and in particular 3D pulseshapes [24]. If the pulses are not 3D-shaped and at 515 nm, much simpler pulse diagnostics can be used, e.g., commercial spectrometers (OceanOptics HR2000+, Orlando, FL, USA; 478.8–555.3 nm, 38 pm spectral resolution). Also, temporal pulseshape characterization for 515 nm simplifies to intensity autocorrelation measurements with SHG FROG option, where the UV spectrograph serves as detector.
SHG FROG [48] is one of the standard measurement techniques for ultrashort laser pulses in the femtosecond and picosecond regime. FROG measurements allow for iterative reconstruction of the electric field of the laser pulse. However, SHG FROG can only be applied to IR and green laser pulses but not to UV laser pulses due to strong absorption of the resulting wavelength. For UV pulses, characterization using nonfrequency converting techniques such as polarization-gate (PG), self-diffraction (SD), or transient-grating (TG) FROG is in principle possible [49] and a TG FROG was realized in the laser lab. However, due to pulse energies in the 100 nJ range and pulse duration of tens of picoseconds, the achievement of necessary intensities for nonlinear interaction is very challenging, especially for more sophisticated pulseshapes created by amplitude shaping.
2.2.4. Beam Transport to the Photocathode
The distance between the pulseshaper with optional UV conversion for CsTe photocathodes and the photocathode in the RF gun is approximately 40 m. This distance is divided into multiple relays to achieve high beam stability via imaging on the photocathode. The whole beamline is equipped with dualband optics, which are coated for 515 nm and 257 nm wavelength, to support investigation of alkali antimonide and CsTe photo cathodes.
After exiting the pulseshaper, the beam is focused with a lens (f = 10 cm) into a 1 mm thick BBO crystal to achieve SHG conversion efficiencies above 20% for Gaussian temporal pulseshapes. The focus in the BBO crystal is imaged by a 4-f relay (1:1, l = 3000 mm) to a pinhole of 100 µm diameter to improve the spatial quality of the UV beam without spatial pulseshaping. Another 4-f imaging system (l = 13,000 mm) with variable magnification follows allowing for adjustment of the beam diameter to the experimental demands of the accelerator to image the pinhole to the beamshaping aperture (BSA). The final 4-f imaging system (1:1, l = 22,000 mm) images the BSA onto the photocathode. After the pinhole, a variable beam attenuator based on a half-wave plate and two Brewster plates is installed to adjust the charge of the electron bunch.
Typical laser pulse energies for green 10 ps Gaussian pulses are 1.6 µJ after the pulseshaper, which are then converted to 370 nJ UV pulses. The pinhole cuts away approximately 60% of the beam and after the variable attenuator 150 nJ leave the laser table and are imaged to the BSA. Depending on the desired beam diameter on the photocathode, the focusing conditions on the laser table can be adjusted to achieve 120 nJ in regular operation, which corresponds with a quantum efficiency of 5% () to 1.2 nC bunch charge. Further extension of the setup with a second pulseshaper of the same type will reduce the achievable charge by another factor of two (cf. Section 4.2).
However, despite applications for the THz SASE FEL and radiation biology requiring several nC bunch charge, the major aim of the laser system and the pulseshaper is the investigation of emittance reduction with 3D ellipsoidal pulses at lower gun gradients and charges between 100 pC and 250 pC for routine operation, which then can be transferred to European XFEL. Application of this pulseshaping scheme with multi-nC bunch charges and low emittance using 3D ellipsoidal pulses becomes possible if alkali antimonide photocathodes are used, which avoid the necessity of UV conversion. Since these pulses are spectrally and spatially shaped, spatial cutting by a pinhole or the BSA should be avoided and above 700 nJ pulse energy should reach the cathode.
3. Results
As first experiments, simple pulseshapes that can be achieved using a setup with a single LCOS SLM (Figure 3) were investigated. Different detectors are possible as a feedback system for the pulseshaper. These signals can be either on the laser table (green or UV imaging spectrograph) or the TDS in the PITZ accelerator. There are several advantages and disadvantages of each feedback system. Using the green spectrograph provides the most direct access to the pulseshaping capabilities of the setup. However, if CsTe cathodes are used, UV conversion of the pulse becomes necessary and detrimental effects such as group velocity mismatch or spatial walk-off can occur. The UV spectrograph can be used to account for frequency-conversion-related pulse quality deterioration. For investigating the influence of the UV conversion further, SHG FROG measurements of the shaped green pulses are possible. When designing the focusing geometry and crystal thickness in the FROG similar to the one used in UV conversion for the cathode, similar deterioration effects should occur. The pulse reconstruction of the FROG measurement can then be used as quality assessment for the influence of the UV conversion. The characterization of the electron bunch produced from the photocathode can be realized using the TDS, which is located 10.642 m downstream of the cathode surface, and a scintillating screen (12.278 m downstream of the cathode surface) serves as a detector. The machine parameters of the PITZ facility remain unchanged for the following measurements. The BSA was 1.0 mm diameter and the beam mean momenta were 5.38 MeV/c and 17.3 MeV/c after gun and booster, respectively, for which both phases were chosen close to the maximum mean momentum gain.
Having many different diagnostics available, a compromise between fast data acquisition for automated optimization of the pulseshaper masks (spectrometer and 2D imaging spectrographs) and precise optical characterization (FROG or cross-correlation) or measurement of the achieved electron bunch duration in the accelerator (TDS) for selected pulseshaper masks has to be made. In the case of an almost linear relationship between the spectral and temporal domain (longitudinal domain of the electron bunch), a simple calibration between all the detectors becomes possible.
3.1. Gaussian Pulses
Without applying any mask to the shaper, Gaussian pulses of 10 ps pulse duration are transmitted by the pulseshaper setup and then converted to UV to generate photoelectrons from the CsTe cathode. The green spectrum after the shaper is shown in Figure 4a. The generated electron bunches are characterized by TDS measurements for bunch charges of 5 pC (Figure 4b) and 175 pC (Figure 4c). These measurements are taken for unchanged parameters of the PITZ accelerator. For the low-charge case, space charge can be neglected and the measured pulse duration of 10 ps FWHM is in good agreement with SHG FROG measurements of the stretched green laser pulse (Figure 5). For the high-charge case, space charge has to be considered and elongates the electron bunch to 15 ps FWHM.
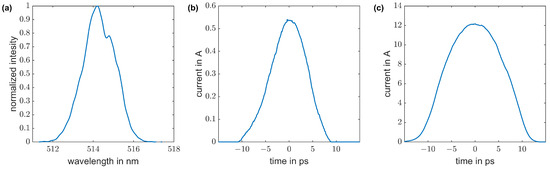
Figure 4.
Characterization of Gaussian laser pulses. Spectrum of the green laser pulses (a) after stretching to 10 ps FWHM. After UV conversion, photoelectrons are generated from the cathode. The longitudinal electron distribution is characterized by TDS for low charge (b) and for high charge (c).
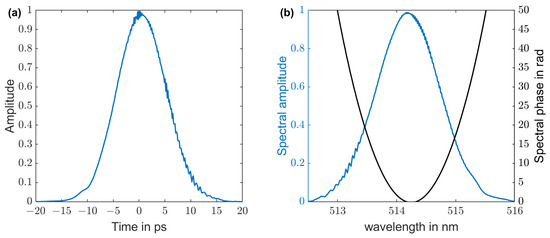
Figure 5.
FROG reconstruction of the electric fields of the stretched Gaussian pulses. The pulse duration after the stretcher is measured to 11.0 ps FWHM (a). The spectral width is 1.27 nm (b) and the spectral phase is parabolic and dominated by group delay dispersion of 10 fs by the grating stretcher.
Comparing the measured TDS trace for low charge (Figure 4b) with the spectrum of the laser pulse (Figure 5b) allows for calibration of the spectral bandwidth with the achieved duration of the electron bunch: . This calibration factor can be used in further pulseshaping experiments for estimation of the resulting electron bunch duration after amplitude shaping. However, this value is only valid for low-charge cases and as long as the pulse stretcher remains unchanged.
3.2. Optical Characterization of Parabolic Pulses
Analyzing the resulting pulseshapes after optimization with SHG FROG provides a reconstruction of the green shaped laser pulse. This is influenced by similar effects as group velocity mismatch and spatial walk-off when the focusing geometry and crystal thickness are chosen, similar to the frequency conversion for the CsTe photocathode. Hence, the FROG reconstruction can be used as a figure of merit for pulseshape preservation during frequency conversion in a nonlinear crystal. Here, the generation of a temporally parabolic shaped pulse is studied, which is a good approximation to the later-envisioned ellipsoidal pulses. The SLM is optimized with the Czerny–Turner spectrograph for green wavelength in a feedback loop for generation of parabolic pulses. The corresponding shaper mask is shown in Figure 6a in grayscale (black corresponds to zero transmission and white to maximum transmission of the amplitude). Then, the shaped pulses are characterized by measuring an SHG FROG trace (Figure 6c).
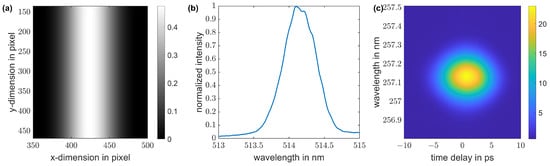
Figure 6.
Pulseshaping experiment for a parabolic pulse. (a) Applied mask on the spatial light modulator. (b) Measured green spectrum after the pulseshaper. (c) Measured SHG FROG trace.
Compared to the stretched Gaussian input pulses coming into the shaper with a 10 ps FWHM duration, the pulse duration is reduced to 5.3 ps due to the applied amplitude masking (Figure 7). Deviations from the parabolic shape can be explained by discretization artifacts of the SLM mask and the frequency conversion in a 0.5 mm thick BBO crystal, similar to the one used for UV conversion of the pulse for photoelectron generation. This could be improved by adjusting the feedback algorithm for pulseshaping.
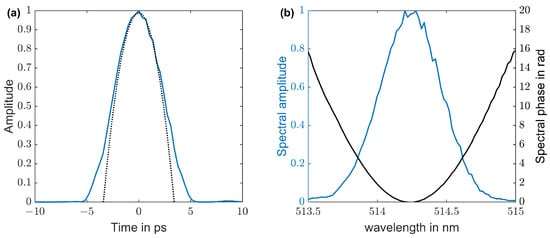
Figure 7.
Reconstruction of the electric field of a parabolic pulse by FROG algorithm. (a) Reconstructed temporal pulseshape of 5.3 ps FWHM (blue) and parabolic fit (black dotted). (b) Reconstructed spectral amplitude of 0.50 nm FWHM (blue) and phase (black).
The spectral width is reduced compared to the input Gaussian pulses due to the amplitude masking. The parabolic shape of the spectral phase is introduced by stretching the 260 fs pulses from the laser to 10 ps. Comparing the calibration factor to the value of the result from the Gaussian pulse shows approximately 30% deviation in this purely optical pulse characterization. The reasons for this deviation could be the noncollinear focusing geometry in SHG FROG compared to collinear UV conversion for photoelectron generation. Considering the total width of the green spectrum (Figure 6b) and the total width of the temporal profile (Figure 7a), the calibration factor becomes larger and provides close agreement with the Gaussian pulse and indicates that total width would be a better suited value to estimate the bandwidth to electron bunch duration ratio for shaped pulses.
3.3. Generation of Flattop Pulses
Flattop pulses are often used as pulseshapes for photoinjectors. Here, the generation of temporal flattop pulses was investigated with the electron bunch in the TDS as a feedback diagnostic for the pulseshaping. By applying a simple binary mask (Figure 8a), a flattop distribution can be approximated out of the initial Gaussian distribution on the scintillating screen. The spectral distribution after the SLM measured with the commercial spectrometer is shown in Figure 8b. After UV conversion, the beam was analyzed with an imaging 2D spectrograph. In Figure 8c,d, modulations from the sharp edges of the SLM mask are visible. The generated electron bunches are characterized by TDS measurements for bunch charges of 5 pC (Figure 8e) and 108 pC (Figure 8f). For the low-charge case, a pulseshape close to a flattop shape with 2.5 ps rise/fall time and 3 ps plateau is measured. The rise/fall time is similar to flattop pulses achieved with the pulse stacking technique [5], but the plateau region is quite short due to the amplitude shaping of 10 ps Gaussian pulses. Further stretching of the input pulses would increase the plateau region. For high charge, space charge forces stretch the pulse to 9 ps FWHM with significant smoothing.
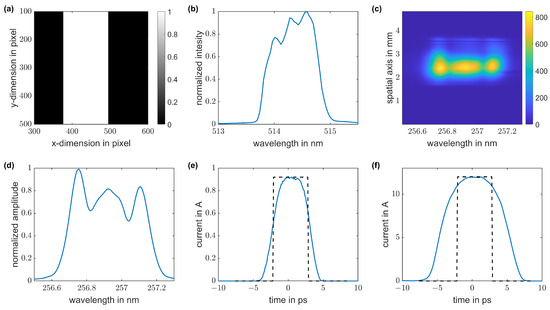
Figure 8.
Generation of flattop pulses. A simple binary mask is applied to the pulseshaper (a) to cut a flattop out of the initial Gaussian distribution. Green spectrum after the SLM (b) and signal of the 2D UV spectrograph (c) show modulations from the sharp edges of the SLM mask. The integrated UV spectrum is shown in (d). The longitudinal electron distribution is characterized by TDS for low charge (e) and for high charge (f). The black dashed line indicates a flattop pulse of 5 ps duration for comparison.
Comparing the calibration factor for the total widths of the green spectrum (Figure 8b) and the TDS trace for low charge, (Figure 8e) agrees with the result from the Gaussian pulse, taking into account the spectral resolution of the commercial spectrometer and also the hard edges in the spectrum by the applied mask of the SLM. However, the resulting flattop electron bunch shape in the TDS showed better quality compared to smoothened masks.
3.4. Modulated Pulses for THz Generation
The SLM modulations can also be introduced in a controlled manner, which can be used for self-seeding of a THz FEL [50]. The lower limit for the duration of the modulations is the cathode response time in the order of hundreds of femtoseconds for CsTe [40,51]. The shaped pulse with the modulations together with strong space charge forces lead to nonlinear oscillations in the longitudinal phase space of the modulated electron bunch, which results in an enhanced spectral density also at higher frequencies than the modulation frequency, which includes the THz FEL resonance frequency and can be used for seeding. To achieve THz modulations in the pulse, a bar mask has been applied (Figure 9a), where the transmission level of the mask has been modified to achieve similar amplitude levels for the modulations at the spectrometer for green wavelength (Figure 9b). After UV conversion, these modulations are also visible in the UV spectrograph, and it should be noted that only three of four modulations are converted from green wavelengths to UV due to the large chirp of the pulse (Figure 9c). The reason for the observed loss of the first modulation in the spectrum and also in time domain is the lower intensity for that modulation, which is not sufficient for efficient UV conversion. It can be observed in the integrated UV spectrum (Figure 9d) that a there is weak signal from the first modulation, which is allusively visible as a shoulder. Compared to the green spectrum, which was measured with the commercial spectrometer, the UV spectrum shows stronger modulations. These are in better agreement with the applied mask due to the higher resolution of the 2D UV spectrograph. The generated electron bunches are characterized by TDS measurements for bunch charges of 5 pC (Figure 9e) and 55 pC (Figure 9f). For the low-charge case, a modulation with a peak distance of 2 ps is visible, which corresponds to a 600 µm wavelength. For the high-charge case, the modulations are hardly visible anymore due to the onset of space charge effects.
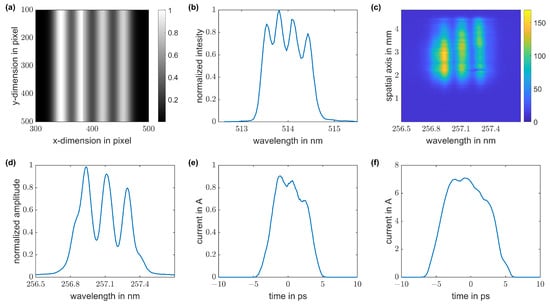
Figure 9.
Generation of THz-modulated pulses. A bar mask is applied to the pulseshaper (a) to introduce THz modulations of the initial Gaussian distribution. These modulations can be observed in the green spectrum after the SLM (b) and after UV conversion in the 2D UV spectrograph (c). The integrated UV spectrum is shown in (d). The longitudinal electron distribution is characterized by TDS for low charge (e) and for high charge (f) with visible modulations with 2 ps separation.
The separation of the peaks in Figure 9b of 0.3 nm corresponds to 2.3 ps taking into account the calibration factor from the Gaussian pulses, which agrees with the TDS measurement for low charge (Figure 9d) taking into account the resolution limit of the commercial spectrometer. Thus, with this calibration, fine adjustments and automation of the modulations for THz FEL seeding become possible.
4. Discussion
4.1. Amplitude Shaping with a Single Pulseshaper
The designed amplitude shaper for 515 nm wavelength has been tested with frequently used pulseshapes, and those were characterized with optical diagnostics on the laser table and the resulting electron bunches were characterized with TDS measurements. First of all, the usage of CsTe photocathodes requires UV conversion of the shaped pulse. If the focusing conditions and the resulting beam transport to the photocathode are not adjusted for each pulseshape, as in the experiment, the UV conversion efficiency is heavily affected by the applied amplitude mask and its accompanied losses. This can be observed by the decreased achievable charge for the same accelerator conditions when changing from Gaussian pulses (no mask applied) to flattop pulses (only central part of the pulse is transmitted) and modulated pulses for THz generation (high losses are introduced by amplitude shaping), where the shaped pulses could only be partially transferred to UV. However, the desired pulseshapes were successfully observed for the electron bunches in the accelerator. When alkali antimonide photocathodes are available, the necessity for UV conversion is omitted. Then, the effect of the losses introduced by the amplitude shaping would be lessened and allow for increased modulations in the masks since no intensity requirements for UV conversion have to be met.
4.2. Towards 3D Ellipsoidal Pulses at Green Wavelengths
For achieving 3D ellipsoidal pulses at green wavelength, the laser pulse has to undergo a second pulseshaper of the same type but rotated by 90° by a dove prism. Also, proper imaging of both Fourier planes of each shaper becomes necessary to achieve a proper coupling of both spatial dimensions. With the so-achieved x- and y- shaping, the ellipsoidal shape can be approximated but is limited by the 90° rotation and cannot achieve full radial symmetry. Previous results with the same type of pulseshaping in the IR have shown 3D ellipsoidal distributions at PITZ [25]. However, the two-stage frequency conversion with nonlinear crystals strongly reduced the quality of the resulting UV pulse, which hampers finding a trade-off between conversion efficiency and pulseshape preservation. The adaptation of the pulseshaping scheme to 515 nm allows for direct application of the shaped pulses without frequency conversion when alkali antimonide photocathodes for pulse energies at the µJ level are available, being suitable for all applications at PITZ, e.g., low-emittance electron bunches for beam dynamics studies, for driving the THz SASE FEL and for studies on radiation biology. Furthermore, reduction in the space charge forces by generation of 3D ellipsoidal laser pulses will pave the way for future upgrades of X-ray free-electron lasers [31]. Currently, photocathode laser development tends towards compact fiber-laser-based approaches with integrated pulseshapers for generation of desired temporal pulseshapes, e.g., flattop pulses, in the pre-amplification stages [20,21]. However, these lasers are limited to shaping in the spectral domain only and pulse quality reduction is expected due to subsequent amplification stages and the two-stage frequency conversion to UV. Thus, the presented approach offers more flexibility in controlling the pulseshape for developing an optimized photocathode laser system for further optimizing the electron beam quality.
5. Conclusions and Outlook
An SLM pulseshaper for 515 nm wavelength has been installed at one of the photocathode lasers at PITZ. The first pulseshaping experiments have been carried out and show the potential of the proposed scheme. As the first experiments regarding flattop pulses and pulses with THz modulations were generated, converted to UV, and correspondingly shaped, electron bunches were characterized by TDS measurements. Further extension of the pulseshaper will allow for generation of 3D ellipsoidal distributions, which can be directly applied to CsKSb photocathodes or require only one conversion step if CsTe photocathodes are used.
Author Contributions
Conceptualization, M.K. and F.S.; methodology, A.H., J.G. and M.G.; investigation, A.H.; formal analysis, A.H.; writing—original draft preparation, A.H.; writing—review and editing, A.H., J.G., M.G., M.K. and F.S.; project administration, M.G., M.K. and F.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the European XFEL research and development program.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data could be provided by the authors upon reasonable request.
Acknowledgments
We thank the PITZ shift crew for preparation and operation of the accelerator. Further support of the Technical Infrastructure group and the Computing Center at DESY in Zeuthen is acknowledged.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| BBO | Beta Barium Borate |
| BSA | Beamshaping aperture |
| DESY | Deutsches Elektronen-Synchrotron |
| EMSY | Emittance measurement system |
| FLASH | Free-electron laser in Hamburg |
| FROG | Frequency-resolved optical gating |
| HEDA | High-energy dispersive arm |
| LCOS | Liquid crystal on silicon |
| LEDA | Low-energy dispersive arm |
| PITZ | Photo Injector Test Facility at DESY in Zeuthen |
| RF | Radio frequency |
| SHG | Second harmonic generation |
| SLM | Spatial light modulator |
| TDS | Transverse deflecting system |
| XFEL | X-ray free-electron laser |
References
- Serafini, L.; Rosenzweig, J.B. Envelope analysis of intense relativistic quasilaminar beams in rf photoinjectors: A theory of emittance compensation. Phys. Rev. E 1997, 55, 7565–7590. [Google Scholar] [CrossRef]
- Limborg-Deprey, C.; Tomizawa, H. Maximizing brightness in photoinjectors. Int. J. Mod. Phys. 2007, 22, 3864–3881. [Google Scholar] [CrossRef]
- Sannibale, F. High-brightness electron injectors for high-duty cycle X-ray free electron lasers. Front. Phys. 2023, 11, 1187346. [Google Scholar] [CrossRef]
- Krasilnikov, M.; Stephan, F.; Asova, G.; Grabosch, H.J.; Groß, M.; Hakobyan, L.; Isaev, I.; Ivanisenko, Y.; Jachmann, L.; Khojoyan, M.; et al. Experimentally minimized beam emittance from an L-band photoinjector. Phys. Rev. ST Accel. Beams 2012, 15, 100701. [Google Scholar] [CrossRef]
- Will, I. Generation of flat-top picosecond pulses by means of a two-stage birefringent filter. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2008, 594, 119–125. [Google Scholar] [CrossRef]
- Liu, F.; Huang, S.; Si, S.; Zhao, G.; Liu, K.; Zhang, S. Generation of picosecond pulses with variable temporal profiles and linear polarization by coherent pulse stacking in a birefringent crystal shaper. Opt. Express 2019, 27, 1467–1478. [Google Scholar] [CrossRef] [PubMed]
- Kapchinskij, I.M.; Vladimirskij, V.V. Limitations Of Proton Beam Current In A Strong Focusing Linear Accelerator Associated with The Beam Space Charge. In Proceedings of the 2nd International Conference on High-Energy Accelerators, Geneva, Switzerland, 14–19 September 1959; pp. 274–287. [Google Scholar]
- Reiser, M. Theory and Design of Charged Particle Beams; Wiley-VCH: Weinheim, Germany, 2008. [Google Scholar]
- Ha, G.; Kim, K.J.; Power, J.G.; Sun, Y.; Piot, P. Bunch shaping in electron linear accelerators. Rev. Mod. Phys. 2022, 94, 25006. [Google Scholar] [CrossRef]
- Serafini, L. Improving the beam quality of RF guns by correction of RF and space-charge effects. AIP Conf. Proc. 1992, 279, 645–674. [Google Scholar] [CrossRef]
- Luiten, O.J.; van der Geer, S.B.; de Loos, M.J.; Kiewiet, F.B.; van der Wiel, M.J. How to Realize Uniform Three-Dimensional Ellipsoidal Electron Bunches. Phys. Rev. Lett. 2004, 93, 094802. [Google Scholar] [CrossRef]
- Li, Y.; Lewellen, J.W. Generating a Quasiellipsoidal Electron Beam by 3D Laser-Pulse Shaping. Phys. Rev. Lett. 2008, 100, 74801. [Google Scholar] [CrossRef]
- Musumeci, P.; Moody, J.T.; England, R.J.; Rosenzweig, J.B.; Tran, T. Experimental Generation and Characterization of Uniformly Filled Ellipsoidal Electron-Beam Distributions. Phys. Rev. Lett. 2008, 100, 244801. [Google Scholar] [CrossRef] [PubMed]
- Piot, P.; Sun, Y.E.; Maxwell, T.J.; Ruan, J.; Secchi, E.; Thangaraj, J.C.T. Formation and acceleration of uniformly filled ellipsoidal electron bunches obtained via space-charge-driven expansion from a cesium-telluride photocathode. Phys. Rev. ST Accel. Beams 2013, 16, 010102. [Google Scholar] [CrossRef]
- Xu, T.; Doran, D.S.; Liu, W.; Piot, P.; Power, J.G.; Whiteford, C.; Wisniewski, E. Demonstration of eigen-to-projected emittance mapping for an ellipsoidal electron bunch. Phys. Rev. Accel. Beams 2022, 25, 44001. [Google Scholar] [CrossRef]
- Faillace, L.; Agustsson, R.; Behtouei, M.; Bosco, F.; Bruhwiler, D.; Camacho, O.; Carillo, M.; Fukasawa, A.; Gadjev, I.; Giribono, A.; et al. High field hybrid photoinjector electron source for advanced light source applications. Phys. Rev. Accel. Beams 2022, 25, 63401. [Google Scholar] [CrossRef]
- Rosenzweig, J.; Cook, A.; England, R.; Dunning, M.; Anderson, S.; Ferrario, M. Emittance compensation with dynamically optimized photoelectron beam profiles. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2006, 557, 87–93. [Google Scholar] [CrossRef]
- Will, I.; Templin, H.I.; Schreiber, S.; Sandner, W. Photoinjector drive laser of the FLASH FEL. Opt. Express 2011, 19, 23770–23781. [Google Scholar] [CrossRef] [PubMed]
- Winkelmann, L.; Choudhuri, A.; Grosse-Wortmann, U.; Hartl, I.; Li, C.; Mohr, C.; Müller, J.; Peters, F.; Pfeiffer, S.; Salman, S. The European XFEL Photocathode Laser. In Proceedings of the 39th in Free Electron Laser Conference, Proc. FEL’19, Hamburg, Germany, 26–30 August 2019; JACoW Publishing: Geneva, Switzerland, 2019; pp. 423–426. [Google Scholar] [CrossRef]
- Gilevich, S.; Alverson, S.; Carbajo, S.; Droste, S.; Edstrom, S.; Fry, A.; Greenberg, M.; Lemons, R.; Miahnahri, A.; Polzin, W.; et al. The LCLS-II Photo-Injector Drive Laser System. In Proceedings of the Conference on Lasers and Electro-Optics, Optica Publishing Group, Virtual Conference, 11–14 May 2020; p. SW3E.3. [Google Scholar] [CrossRef]
- Li, C.; Akcaalan, O.; Frede, M.; Grosse-Wortmann, U.; Hartl, I.; Mohr, C.; Puncken, O.; Seidel, M.; Tuennermann, H.; Vidoli, C.; et al. Photocathode Laser Development for Superconducting X-ray Free Electron Lasers at DESY. In Proceedings of the 12th in International Particle Accelerator Conference, Proc. IPAC’21, Virtual Conference, 24–28 May 2021; JACoW Publishing: Geneva, Switzerland, 2021; pp. 3599–3601. [Google Scholar] [CrossRef]
- O’Shea, B.; Rosenzweig, J.B.; Asova, G.; Bähr, J.; Hänel, M.; Ivanisenko, Y.; Khojoyan, M.; Krasilnikov, M.; Staykov, L.; Stephan, F.; et al. Measurement of self-shaped ellipsoidal bunches from a photoinjector with postacceleration. Phys. Rev. ST Accel. Beams 2011, 14, 012801. [Google Scholar] [CrossRef]
- Mironov, S.Y.; Potemkin, A.K.; Gacheva, E.I.; Andrianov, A.V.; Zelenogorskii, V.V.; Krasilnikov, M.; Stephan, F.; Khazanov, E.A. Shaping of cylindrical and 3D ellipsoidal beams for electron photoinjector laser drivers. Appl. Opt. 2016, 55, 1630–1635. [Google Scholar] [CrossRef]
- Zelenogorskii, V.; Andrianov, A.; Gacheva, E.; Gelikonov, G.; Krasilnikov, M.; Mart’yanov, M.; Mironov, S.; Potemkin, A.; Syresin, E.; Stephan, F.; et al. Scanning cross-correlator for monitoring uniform 3D ellipsoidal laser beams. Quantum Electron. 2014, 44, 76. [Google Scholar] [CrossRef]
- Koschitzki, C.; Qian, H.; Aboulbanine, Z.; Adhikari, G.; Aftab, N.; Boonpornprasert, P.; Georgiev, G.; Good, J.; Gross, M.; Hoffmann, A.; et al. Chirped Pulse Laser Shaping for High Brightness Photoinjectors. In Proceedings of the 40th International Free Electron Laser Conference, Proc. FEL2022, Trieste, Italy, 22–26 August 2022; JACoW Publishing: Geneva, Switzerland, 2022; pp. 345–348. [Google Scholar] [CrossRef]
- Mironov, S.Y.; Poteomkin, A.K.; Gacheva, E.I.; Andrianov, A.V.; Zelenogorskii, V.V.; Vasiliev, R.; Smirnov, V.; Krasilnikov, M.; Stephan, F.; Khazanov, E.A. Generation of 3D ellipsoidal laser beams by means of a profiled volume chirped Bragg grating. Laser Phys. Lett. 2016, 13, 055003. [Google Scholar] [CrossRef]
- Gacheva, E.I.; Martyanov, M.A.; Poteomkin, A.K.; Kuzmin, I.V.; Mironov, S.Y. Shaping ellipsoidal laser pulses in the scheme with black analog masks for photoinjector applications. Laser Phys. Lett. 2023, 20, 125002. [Google Scholar] [CrossRef]
- Kuzmin, I.V.; Mironov, S.Y.; Martyanov, M.A.; Potemkin, A.K.; Khazanov, E.A. Highly efficient fourth harmonic generation of broadband laser pulses retaining 3D pulse shape. Appl. Opt. 2021, 60, 3128–3135. [Google Scholar] [CrossRef] [PubMed]
- Mohanty, S.K.; Krasilnikov, M.; Oppelt, A.; Stephan, F.; Sertore, D.; Monaco, L.; Pagani, C.; Hillert, W. Development and Characterization of Multi-Alkali Antimonide Photocathodes for High-Brightness RF Photoinjectors. Micromachines 2023, 14, 1182. [Google Scholar] [CrossRef]
- Brinkmann, R.; Schneidmiller, E.; Sekutowicz, J.; Yurkov, M. Prospects for CW and LP operation of the European XFEL in hard X-ray regime. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2014, 768, 20–25. [Google Scholar] [CrossRef]
- Sekutowicz, J.; Ayvazyan, V.; Barlak, M.; Branlard, J.; Cichalewski, W.; Grabowski, W.; Kostin, D.; Lorkiewicz, J.; Merz, W.; Nietubyc, R.; et al. Research and development towards duty factor upgrade of the European X-ray Free Electron Laser linac. Phys. Rev. ST Accel. Beams 2015, 18, 50701. [Google Scholar] [CrossRef]
- Zhang, H.; Gilevich, S.; Miahnahri, A.; Alverson, S.; Brachmann, A.; Duris, J.; Franz, P.; Fry, A.; Hirschman, J.; Larsen, K.; et al. The LCLS-II Photoinjector Laser Infrastructure. arXiv 2023, arXiv:2307.12030. [Google Scholar]
- Andruszkow, J.; Aune, B.; Ayvazyan, V.; Baboi, N.; Bakker, R.; Balakin, V.; Barni, D.; Bazhan, A.; Bernard, M.; Bosotti, A.; et al. First Observation of Self-Amplified Spontaneous Emission in a Free-Electron Laser at 109 nm Wavelength. Phys. Rev. Lett. 2000, 85, 3825–3829. [Google Scholar] [CrossRef]
- Ackermann, W.; Asova, G.; Ayvazyan, V.; Azima, A.; Baboi, N.; Baehr, J.; Balandin, V.; Beutner, B.; Brandt, A.; Bolzmann, A.; et al. Operation of a free-electron laser from the extreme ultraviolet to the water window. Nat. Photonics 2007, 1, 336–342. [Google Scholar] [CrossRef]
- Altarelli, M.; Brinkmann, R.; Chergui, M.; Decking, W.; Dobson, B.; Düsterer, S.; Grübel, G.; Graeff, W.; Graafsma, H.; Hajdu, J.; et al. XFEL: The European X-ray Free-Electron Laser; Technical Design Report; DESY: Hamburg, Germany, 2006. [Google Scholar] [CrossRef]
- Decking, W.; Abeghyan, S.; Abramian, P.; Abramsky, A.; Aguirre, A.; Albrecht, C.; Alou, P.; Altarelli, M.; Altmann, P.; Amyan, K.; et al. A MHz-repetition-rate hard X-ray free-electron laser driven by a superconducting linear accelerator. Nat. Photonics 2020, 14, 391–397. [Google Scholar] [CrossRef]
- Stein, W.E.; Sheffield, R.L. Electron micropulse diagnostics and results for the Los Alamos free electron laser. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 1986, 250, 12–18. [Google Scholar] [CrossRef]
- Altenmueller, O.H.; Larsen, R.R.; Loew, G.A. Investigations of Traveling-Wave Separators for the Stanford Two-Mile Linear Accelerator. Rev. Sci. Instrum. 2004, 35, 438–442. [Google Scholar] [CrossRef]
- Röhrs, M.; Gerth, C.; Schlarb, H.; Schmidt, B.; Schmüser, P. Time-resolved electron beam phase space tomography at a soft x-ray free-electron laser. Phys. Rev. ST Accel. Beams 2009, 12, 050704. [Google Scholar] [CrossRef]
- Loisch, G.; Chen, Y.; Koschitzki, C.; Qian, H.; Gross, M.; Hannah, A.; Hoffmann, A.; Kalantaryan, D.; Krasilnikov, M.; Lederer, S.; et al. Direct measurement of photocathode time response in a high-brightness photoinjector. Appl. Phys. Lett. 2022, 120, 104102. [Google Scholar] [CrossRef]
- Krasilnikov, M.; Aboulbanine, Z.; Adhikari, G.; Aftab, N.; Boonpornprasert, P.; Bousonville, M.; Brinker, F.; Castro Carballo, M.E.; Georgiev, G.; Good, J.; et al. RF Performance of a Next-Generation L-Band RF Gun at PITZ. In Proceedings of the 31st International Linear Accelerator Conference, LINAC2022, Liverpool, UK, 28 August–2 September 2022; JACoW Publishing: Geneva, Switzerland, 2022; pp. 699–702. [Google Scholar] [CrossRef]
- Krasilnikov, M.; Aboulbanine, Z.; Adhikari, G.; Aftab, N.; Boonpornprasert, P.; General, R.; Georgiev, G.; Good, J.; Gross, M.; Heuchling, L.; et al. First Lasing of the THz SASE FEL at PITZ. In Proceedings of the 40th International Free Electron Laser Conference, Proc. FEL2022, Trieste, Italy, 22–26 August 2022; JACoW Publishing: Geneva, Switzerland, 2022; pp. 4–6. [Google Scholar] [CrossRef]
- Stephan, F.; Gross, M.; Grebinyk, A.; Aboulbanine, Z.; Amirkhanyan, Z.; Budach, V.; Ehrhardt, V.H.; Faus-Golfe, A.; Frohme, M.; Germond, J.F.; et al. FLASHlab@PITZ: New R&D platform with unique capabilities for electron FLASH and VHEE radiation therapy and radiation biology under preparation at PITZ. Phys. Medica 2022, 104, 174–187. [Google Scholar] [CrossRef]
- Przygoda, K.; Rybaniec, R.; Butkowski, L.; Gerth, C.; Peier, P.; Schmidt, C.; Steffen, B.; Schlarb, H. MicroTCA.4-Based RF and Laser Cavities Regulation Including Piezocontrols. IEEE Trans. Nucl. Sci. 2017, 64, 1389–1394. [Google Scholar] [CrossRef]
- Wefers, M.M.; Nelson, K.A. Generation of high-fidelity programmable ultrafast optical waveforms. Opt. Lett. 1995, 20, 1047–1049. [Google Scholar] [CrossRef]
- Frumker, E.; Silberberg, Y. Phase and amplitude pulse shaping with two-dimensional phase-only spatial light modulators. J. Opt. Soc. Am. B 2007, 24, 2940–2947. [Google Scholar] [CrossRef]
- Weiner, A.M. Femtosecond pulse shaping using spatial light modulators. Rev. Sci. Instrum. 2000, 71, 1929–1960. [Google Scholar] [CrossRef]
- Trebino, R.; De Long, K.W.; Fittinghoff, D.N.; Sweetser, J.N.; Krumbügel, M.A.; Richman, B.A.; Kane, D.J. Measuring ultrashort laser pulses in the time-frequency domain using frequency-resolved optical gating. Rev. Sci. Instrum. 1997, 68, 3277–3295. [Google Scholar] [CrossRef]
- Sweetser, J.N.; Fittinghoff, D.N.; Trebino, R. Transient-grating frequency-resolved optical gating. Opt. Lett. 1997, 22, 519–521. [Google Scholar] [CrossRef]
- Neumann, J.G.; Fiorito, R.B.; O’Shea, P.G.; Loos, H.; Sheehy, B.; Shen, Y.; Wu, Z. Terahertz laser modulation of electron beams. J. Appl. Phys. 2009, 105, 53304. [Google Scholar] [CrossRef]
- Aryshev, A.; Shevelev, M.; Honda, Y.; Terunuma, N.; Urakawa, J. Femtosecond response time measurements of a Cs2Te photocathode. Appl. Phys. Lett. 2017, 111, 33508. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).