Abstract
In this work, we introduce a novel variance reduction approach utilising the integral formulation of the radiative transfer equation to calculate the radiance in a planar symmetric slab geometry. Due to its integral nature, our method offers a fundamental advantage over well-established variance reduction methods such as the local estimate technique. As opposed to the local estimate procedure, photons add to the overall radiance not only at specific points of interaction but also throughout each consecutive path element; hence, our variance reduction approach can be thought of as an integral local estimate method. This facilitates a substantial enhancement in statistical efficiency, especially in scenarios where only a small number of scattering events or a high attenuation along the detection paths is to be anticipated. To evaluate the overall performance of the integral approach, we incorporated it into a self-developed GPU-accelerated Monte Carlo software, together with a conventional local estimate implementation adapted to slab geometry for a comprehensive comparison.
1. Introduction
The fraction of radiant power reflected or transmitted by a sample in a specific direction is given by the angular reflectance (AR) or transmittance (AT). Consequently, these quantities are relevant in a wide range of research areas where the interaction of light with scattering media is of interest, including atmospheric science [1,2,3,4], radiation therapy [5,6,7], photodynamic therapy [8], forest surface or soil studies [9,10,11], and computer graphics [12,13], in the form of the bidirectional reflectance distribution function (BRDF). In this context, the Monte Carlo (MC) method, which provides a numerical solution to the radiative transfer equation (RTE), is often the tool of choice for theoretical investigations, as it is considered the gold standard for numerical modelling of light propagation in turbid media.
In many cases, when the MC approach is used to simulate the AR or AT, the signal is not detected in discrete directions, as ideally desired, but rather in extended angular bins [3,4,11,14,15,16]. This implies that the signal is always obtained as a sum over an angular range and deviations from discrete detection angles are to be anticipated. This can be partially compensated for by a higher angular resolution, but the variance will increase as hardly any energy packets, called photons in MC terminology, contributes to the individual detection directions. To this end, a number of variance reduction methods (VRMs) [17,18,19] have been introduced by the Monte Carlo community to address these types of problems. A well-established VRM technique is the local estimate (LE) method, also called last flight estimation, the method of expected values and the method of statistical evaluation, which, by virtue of its simplicity and intuitiveness, is typically used to improve the statistics when the probability of a photon contributing to the signal is close to zero due to the detector’s limited spatial extent, or when the signal is detected within a limited field of view. The LE method involves computing the probability of a photon being scattered in the direction of the detector at each point of interaction. Thus, each scattering event adds a contribution to the overall signal. However, in cases of thin layers or low scattering media, only a limited number of LE contributions are obtained due to the small set of interaction points. Additionally, it is critical to consider the attenuation along the detection path when calculating LE weights. For large angles with respect to the surface normal, this results in inadequate statistics for individual scattering events due to the high level of attenuation along the extended detection paths.
In this work, we present a novel type of VRM, derived from the integral form of the RTE, which, similar to the LE method, allows the calculation of the contributions for arbitrary detection directions, i.e., the contributions to all angles of the AT or AR, during the propagation of a photon. In this case, however, the calculation of the radiance contributions extends beyond discrete interaction points to integrally account for each individual path section, which is why our VRM can also be regarded as an integral LE (iLE) method. The incorporation of entire path segments thus allows a significant variance improvement compared to the LE method, especially in the cases specified above. The sole drawback of this type of approach is that it is limited to geometries for which analytical expressions can be derived, namely, in the case presented here, the planar symmetric radiance calculation for a slab of infinite lateral extent, as, while there are several analytical solutions available for the RTE to calculate the planar radiance, for cases of extreme optical properties, a high computational cost must often be incurred to ensure the accuracy and stability of results. To assess the efficacy of our novel approach, we integrated the iLE method into a self-developed GPU (graphics processing unit)-accelerated MC software. Additionally, we adapted the LE technique to slab geometry and incorporated it into the same MC framework for a thorough comparison.
The rest of the paper is structured as follows. In Section 2, the theoretical framework of the LE and iLE methods is introduced together with the algorithmic implementation by means of pseudo-code. In Section 3, the results are presented and discussed; in particular, the benchmark testing and comparison of the two methods based on selected examples are considered. To conclude, the primary results of this study are summarised in Section 4.
2. Methodology
2.1. Local Estimate Method
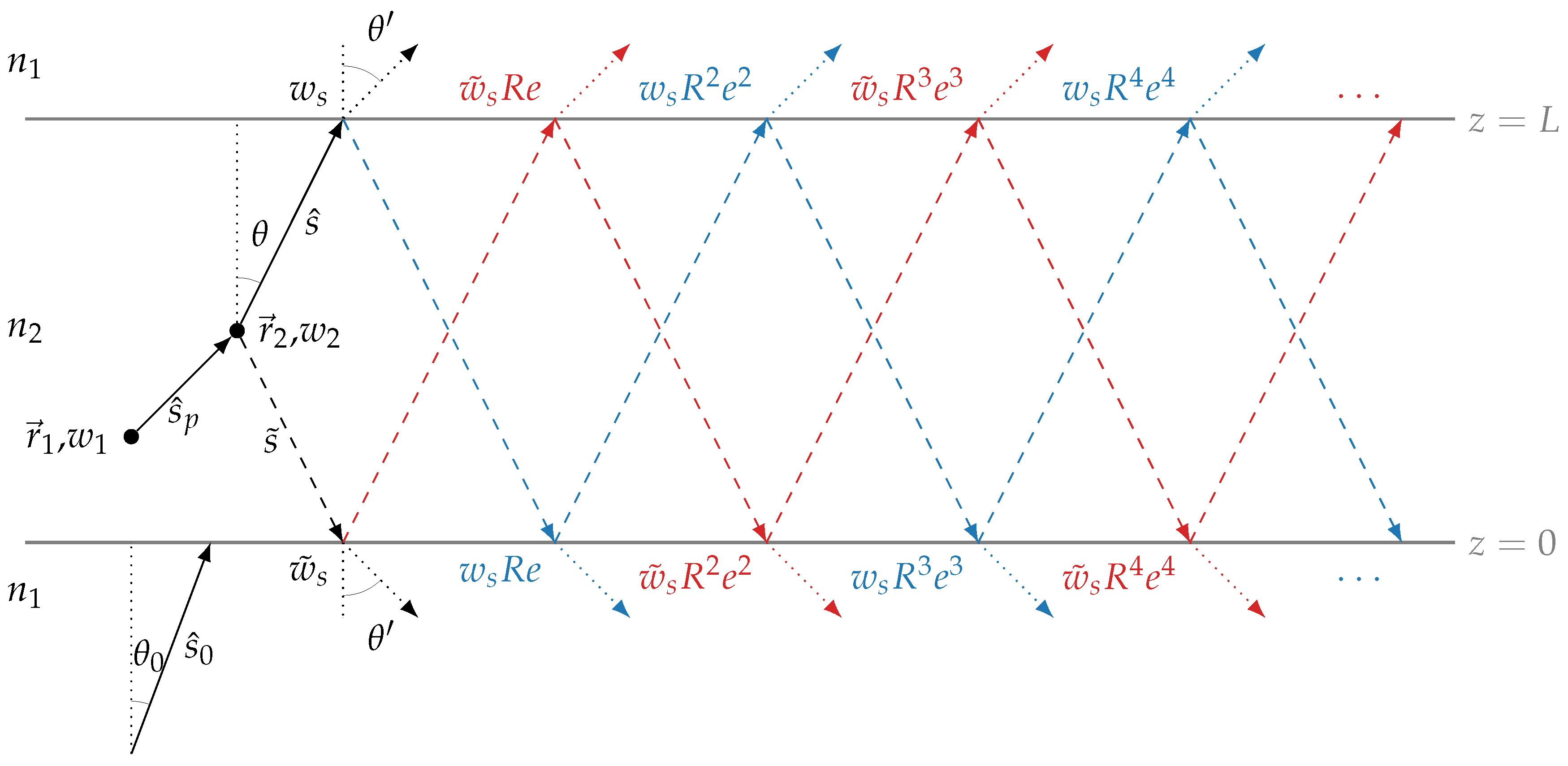
To reduce the variance of an MC simulation applying the LE method, at each point of interaction, i.e., each scattering event, the probability that a photon is scattered to a given target position and reaches the detector ballistically without any further interactions is calculated. Accordingly, each photon at each scattering event contributes to the detector signal with an adjusted weight that takes into account the scattering function of the medium and the attenuation along the detection path. For spatially resolved signals, the calculation of the local estimation weights is straightforward and can be found in the literature [19,20]. However, when using the MC method to simulate the radiance at the surface, which in turn can be transferred to the AR or AT, considering a laterally infinite layered geometry as shown in Figure 1, any multiple reflections that could contribute to the signal of a particular detection direction must be included in the calculation of the LE weights in the case of a refractive index mismatch (). The composition of the LE weights for this particular case is illustrated in Figure 1.
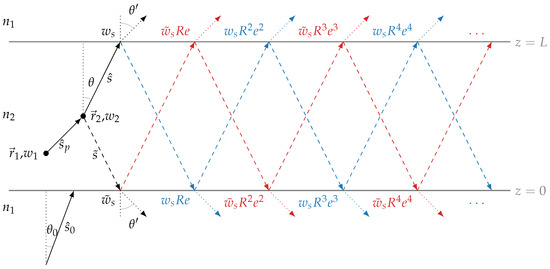
Figure 1.
Schematic representation showing the composition of local estimate weights for a single scattering event and detection direction indicating the radiance contributions at the respective interface. To calculate the transmittance or reflectance in the detection direction after refraction, the last interaction at the interface must be taken into account according to Equation (10) or Equation (11), respectively. The photons are launched from a collimated source at an angle onto the lower boundary surface ().
Consider a photon at location , with weight and normalised direction of propagation , which, following the well-known MC methodology [21,22], travels along a free path
to location , where is a random number drawn from a uniform distribution and is the scattering coefficient of the medium under consideration. Therefore, the initial weight is reduced to
where is the absorption coefficient. At this point, the first “direct” LE contribution , the upper black solid line, to the radiance in the detection direction on the transmission side () is
where and is the scattering phase function, which gives the probability that a photon propagating in direction will be scattered in direction , and is the extinction coefficient. If we continue to follow the direct path with the weight , the blue dashed line, a photon can contribute to the same detection direction again at after having been reflected at the upper boundary layer and subsequently reflected at the lower one, and, therefore, this needs to be included. The corresponding updated weight is , where is the Fresnel reflectance as a function of the polar angle and
accounts for the attenuation along the reflected path. Similarly, we can calculate the contributions of all subsequent reflections (Figure 1). The sum of all the contributions of the direct path can thus be summarised and calculated via a geometric series
In addition to the direct path, a photon at the interaction point could also hit the lower boundary layer () at the angle , the black dashed line, and after (multiple) reflection(s) it may again contribute to the same detection direction at . Similarly, the sum of the individual contributions can be determined via a geometric series
where
The total contribution of LE at the interaction point to the radiance in the transmission direction is, therefore,
Due to the symmetry present here, the LE contribution
in the reflection direction can also be calculated simultaneously. This is done by swapping the weights and in Equations (5) and (6), as is immediately apparent from the contributions shown in Figure 1 at the lower boundary surface. Finally, to obtain the AT or AR from the radiance, one must consider the reflection loss and refraction at the interface, alongside the consequent modification of the solid angle element [22]
where is the respective outer angle after refraction relative to the surface normal (see Figure 1).
2.2. Integral Local Estimate Method
For the integral local estimate method, we first require the integral form of the planar symmetric RTE, which is usually written in integro-differential form as
where is the source term. To that end, we first extend the scattering operator to an integral over all the arguments of the radiance as
To obtain an integral equation for , we seek a kernel function that satisfies
under the appropriate boundary conditions for an infinite slab with Fresnel specular reflections at the bottom and top surfaces
Additionally, we also need the response of the propagation operator on the left hand side to the source term , which is the ballistic or unscattered contribution to the total radiance, fulfilling
Of course, must satisfy the same boundary conditions that were imposed on K. Then, the complete radiance can be written as
which is the integral equation we sought. It is easy to see that if both K and satisfy the required boundary conditions, then I will satisfy them as well. The differential Equation (14) for the kernel function under the Fresnel boundary conditions (15) and (16) can be solved in closed form. The solution is given by
and the derivation of the integral kernel can be found in Appendix A. Here, is the “reflected” direction to (see Figure 1), with
The solution for depends on the exact source term which is used, i.e., for the commonly assumed collimated source given by with incident direction , the result is
which can also be deduced from Equation (19). Again, is the reflected direction to . The integral Equation (18) can be treated in two ways. First, one could attempt to solve it directly, circumventing the complicated approximation methods that stem from the original integro-differential form of the RTE [23]. Second, one could insert a given approximation (that does not solve the equation) on the right hand side, which usually leads to a superior expression for the radiance [24]. Here, we use the radiance predicted by the Monte Carlo simulation, which is a collection of path segments p, each with direction between and
where the indices of the z limits were suppressed. One of these path elements can then be inserted into (18) on the right hand side, dropping the ballistic term , which may be re-added later. Evaluating this at for and at for then leads to the contribution of the path element to the radiance at the top and bottom interfaces, which will be called and , respectively. Note that the other halves of and with respect to can be computed via the boundary conditions (15) and (16). Immediately performing the angular integration, we get
and
We then introduce two abbreviations and , defined as
and
where is the path length. After evaluating the remaining integrals in (23) and (24), the final results for with and with can then be written using these abbreviations as
and
Note that if the observation angles are always taken relative to the outward surface normal, the values of X and Y in (27) and (28) only differ by a sign. However, if the denominators in or given by
are close to zero, large cancellation errors can occur in the numerical evaluation of (25) or (26). In these cases, the expressions for X or Y can be replaced by the expansions
and
2.3. Monte Carlo Implementation
For the following benchmark test of the LE and iLE variance reduction methods described in Section 2.1 and Section 2.2, both were integrated into a self-developed GPU-accelerated MC program. The basic simulation routine will now be illustrated in more detail using the pseudo-code provided in Algorithms 1–3. It should be noted that the main purpose of this section is to show the basic algorithmic integration of the variance reduction methods. For the exact technical implementation, the authors refer readers to the Git Repository (https://github.com/dreitzle/radMC/tree/master, accessed on 20 December 2023), where the complete source code can be found. The GPU code was implemented in OpenCL and the host code in both Python and C++.
Starting with the Monte Carlo framework, Algorithm 1 outlines the propagation of a single photon in the geometry depicted in Figure 1. In lines 1–5, the starting position and direction of the photon are set. In the following, it is always assumed that the started photons hit the lower boundary () at an angle of incidence , where is the angle after the initial refraction at the surface (see Figure 1). Note that only the z-component of the photon position is stored, as this is the only spatial component needed for further calculations. Furthermore, the direction of propagation is described by the cosine and sine terms of the spherical coordinates, as these are needed to calculate the LE and iLE contributions, respectively, thus avoiding a previous coordinate transformation. Prior to the actual propagation loop, the initial photon weight is adjusted in line 6 according to the Fresnel reflectivity. A photon eventually propagates through the medium until its weight falls below a critical value . Russian roulette then decides with a given survival probability q whether the photon with the adjusted weight will continue to propagate or will be terminated with a probability of . For the propagation itself, an MC variant was chosen, in which photons are always scattered at interaction points, and the weight is then reduced according to the absorption properties of the medium (compare Section 2.1). Similarly, when interacting with interfaces, photons are always reflected and the weight is adjusted according to the Fresnel equations. It is worth noting that when a reflection event takes place in lines 12–16 or 17–21, there is no immediate change in direction or weight and is initially only monitored using the Boolean variable . The reason for this is that the calculation of the radiance contributions in line 22 can then be called at exactly one point in the code, which allows for better synchronisation of the workgroups, achieving better performance. The algorithmic procedure to calculate the radiance contributions using LE and iLE can be seen in Algorithms 2 and 3, respectively.
The LE implementation first examines whether a photon has already gone through one of the boundary layers. Since the method does not include direct detector contributions, there is no calculation of the radiance contributions in this situation. If the interaction point is located in the medium, the reflectivity is computed for a given detection angle and the weight taking into account the attenuation along the reflection path, as seen in Equation (4). Then the calculation of the contributions is carried out as described in Section 2.1 for each angle and the related angles . Continuing with the iLE procedure (Algorithm 3), a similar scheme is adopted; however, it is redundant to test whether the interaction point is outside the medium at the beginning, as the weights are calculated integrally up to the interfaces. Note that inside the second for loop in lines 10–19 both denominators, and , are checked for proximity to zero to prevent cancellation errors while calculating X and Y, as explained in Section 2.2. If one of the denominators falls below its respective threshold or , the corresponding X or Y is replaced by its expansion, where has been found to give numerically stable results. Finally, for improved readability, the variables , , and are introduced in lines 20–22, from which the respective contributions to the radiance are calculated.
| Algorithm 1 Single photon propagation |
|
| Algorithm 2 Calculate radiance contributions using LE |
|
| Algorithm 3 Calculate radiance contributions using integral LE |
|
3. Results and Discussion
The effectiveness of the iLE method was tested for different optical properties and compared with the LE method as a reference. To create representative comparison conditions, both methods have been integrated into the same self-developed MC framework, as described in Section 2. For prior validation of the MC code, the simulated results were first compared to an analytical solution of the RTE obtained using the method [24], and excellent agreement was found. In the context of the VRM benchmark test, the mean and variance of the simulated radiance were determined from 100 runs at a fixed computation time of 1.2 s per run, calculating 512 detection angles simultaneously. The Russian roulette parameters were set to and for all test cases. All calculations were performed on an NVIDIA A10 graphics card using a thread count of 8192.
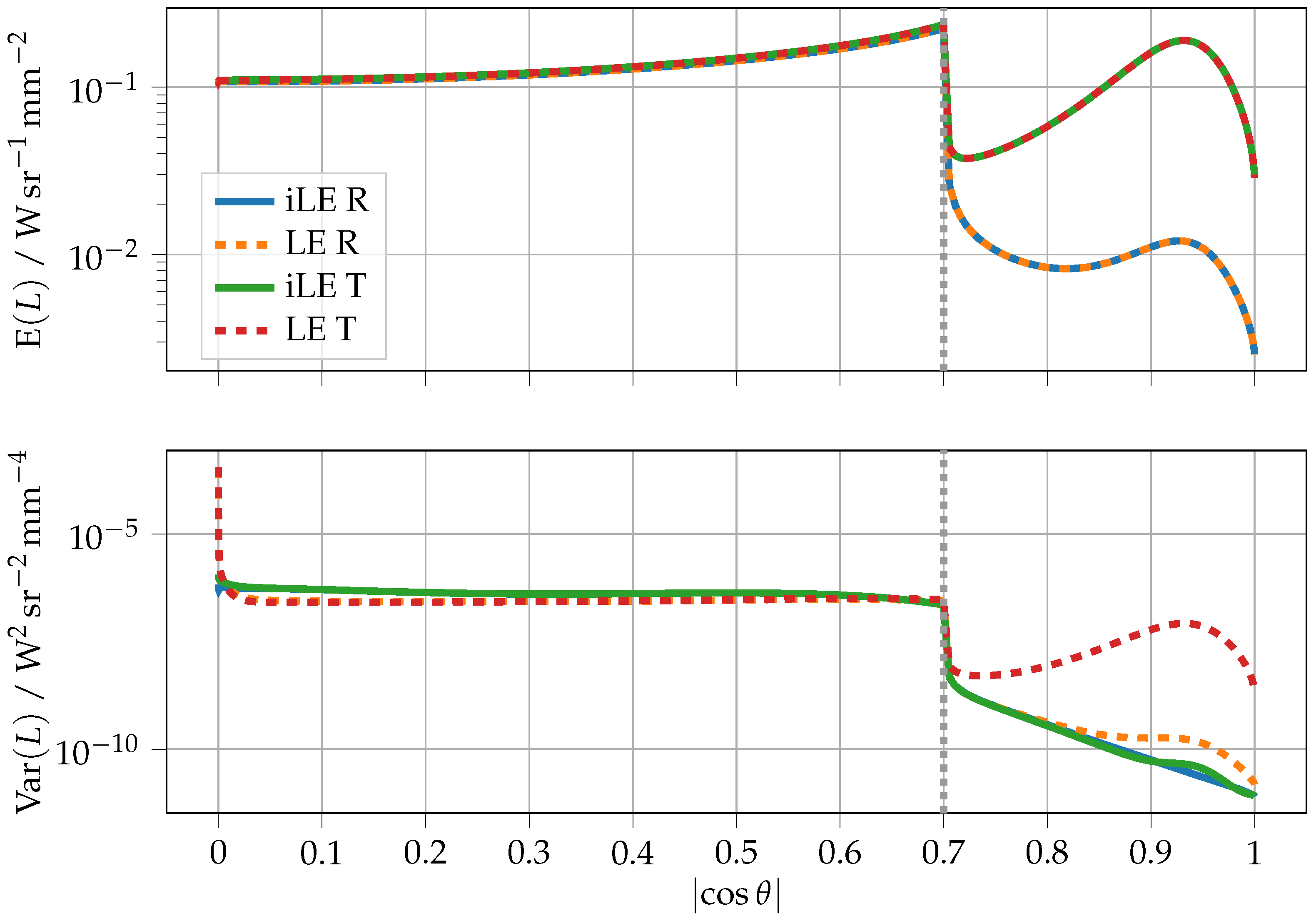
First, we consider the case of a thin layer with a thickness of , a reduced scattering coefficient of , and an absorption coefficient of (see Figure 2). The Henyey–Greenstein phase function [25] with an anisotropy factor of was chosen as the scattering function. In such a scenario, only a limited number of scattering events can be expected until the exit from the medium, so the iLE method, which, in contrast to the LE method, not only contributes to the radiance for individual scattering events but also allows the calculation of radiance contributions along the entire path segments, should be advantageous. This is confirmed by considering the variance in Figure 2. Above the total reflectance range , the iLE method provides a variance improvement in reflectance of up to one order of magnitude and in transmittance of up to three orders of magnitude. It should be noted that the time dependence for both variance reduction methods was examined for all examples considered here and it was found, as expected, that the variance of both methods averaged over all angles decreases approximately with , where N is the number of simulated photons. Consequently, the variance improvement corresponds to a reduction in simulation time of the same order of magnitude. As there tend to be very few interaction points up to the point of exit, especially in the transmission direction, this is also where the greatest improvement over the LE method is observed. Of particular interest is the range around , which corresponds to the cosine of the angle of incidence after initial refraction at the interface. In this angular range, a peak in the mean radiance can be observed in both the refraction and transmission directions. The incident light angle of 30° combined with the phase function that favours forward scattering leads to photons of lower scattering order inducing an extended maximum, which can be mapped more effectively by the iLE method. It is important to note that the radiance is measured directly below the surface. Thus, for example, when comparing the simulated data with measured reflectance curves, only the region above the cosine of the critical angle of total reflection would be relevant since the radiance within the total reflection region would not be visible from the outside. Nevertheless, in the area of total reflection, the two methods show an equalisation, with the LE method being even slightly better for most of the angular range. However, for shallow viewing angles, which are almost parallel to the surface, the trend is reversed, as the long detection paths and the associated enormous attenuation mean that the individual LE weights make hardly any contribution, so the iLE method again proves to be superior by several orders of magnitude. In general, a further variance improvement via the iLE method compared to LE can be achieved by fine-tuning the parameters of the Russian roulette. In particular, the threshold can significantly reduce the variance for computationally intensive iLE weights, as it prevents the propagation of photons that do not contribute significantly to the radiance.
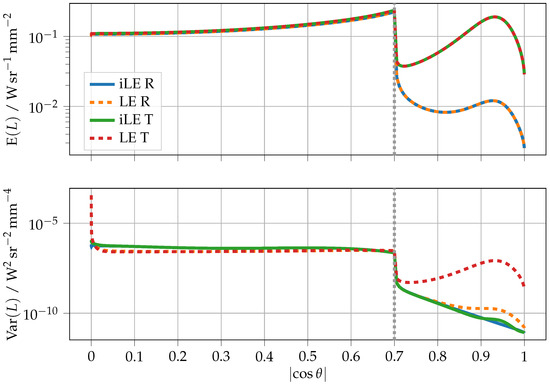
Figure 2.
Mean and variance of the simulated radiance in reflection (R) and transmission (T) for the parameters , , , , , , and . For the externally measurable reflectance or transmittance, only the angular range to the right of the grey dotted line, which marks the critical angle of total reflection, is of relevance. The radiance shown here can be converted to the AT or AR using Equation (10) or Equation (11), respectively.
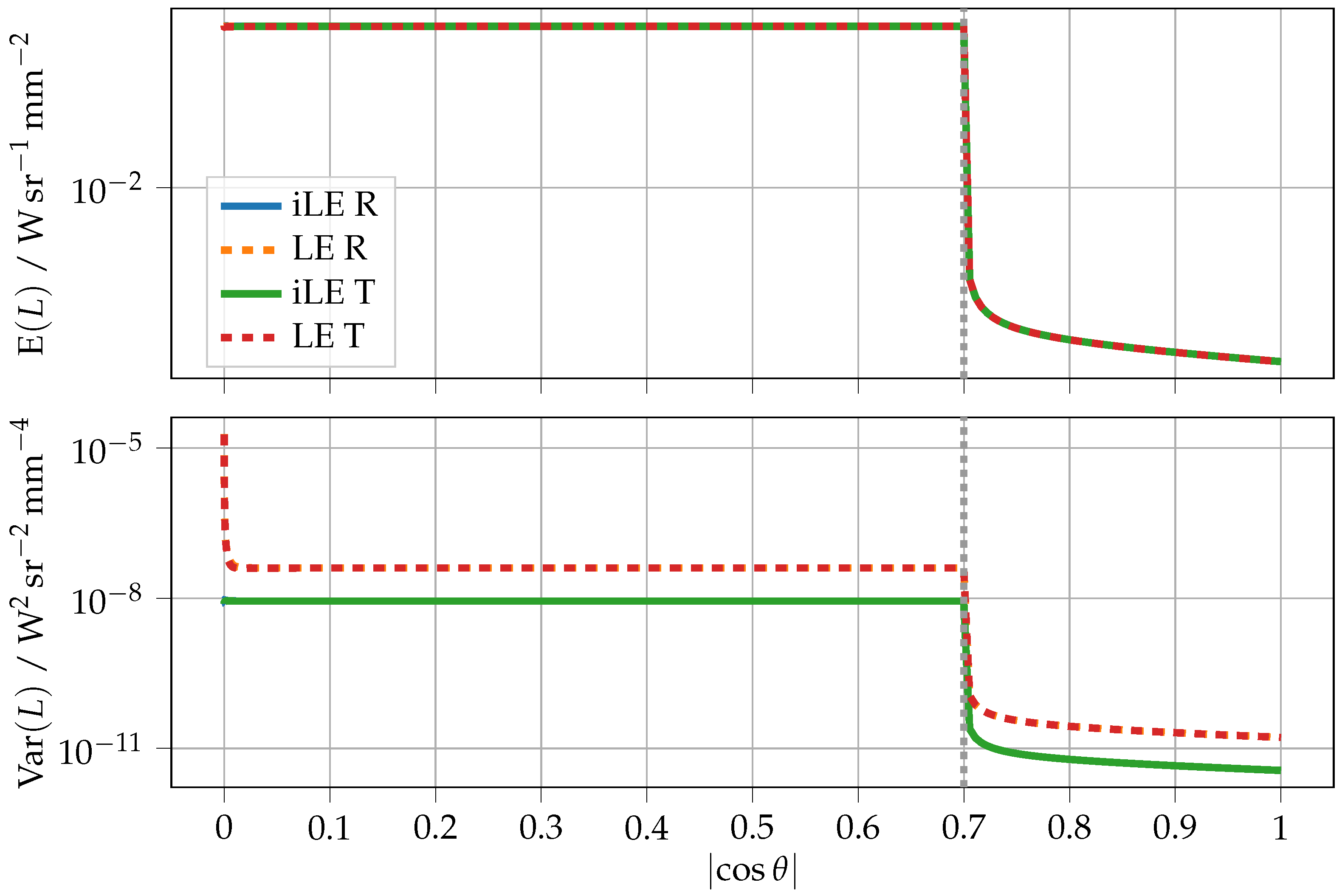
For the next comparison, we examined the same parameters as those depicted in Figure 2, but this time with isotropic scattering, where . This causes two pivotal changes within the mean radiance, as shown in Figure 3. First, the radiance curves in the transmission and reflection directions are now almost identical, since isotropic “sources” are almost evenly distributed across the thin layer. Secondly, the once visible peak around disappears. Moreover, reducing the g-factor also leads to a reduction in , which further reduces the likelihood of scattering events, now giving the iLE method a lower variance across the full angular range. Note that since in this instance, the mean transmitted and reflected radiances are nearly identical, the variance of each method’s transmission and reflectance curve are also superimposed.
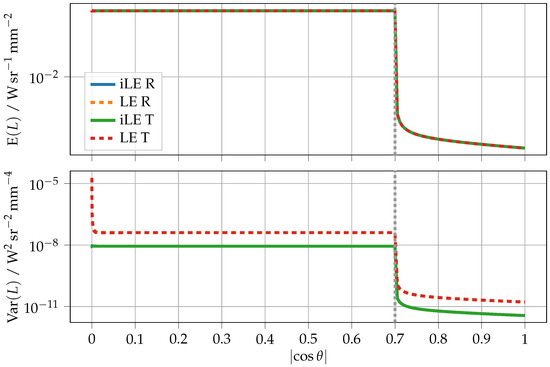
Figure 3.
Mean and variance of the simulated radiance in reflection (R) and transmission (T) for the parameters , , , , , , and . For the externally measurable reflectance or transmittance, only the angular range to the right of the grey dotted line, which marks the critical angle of total reflection, is of relevance. The radiance shown here can be converted to the AT or AR using Equation (10) or Equation (11), respectively.
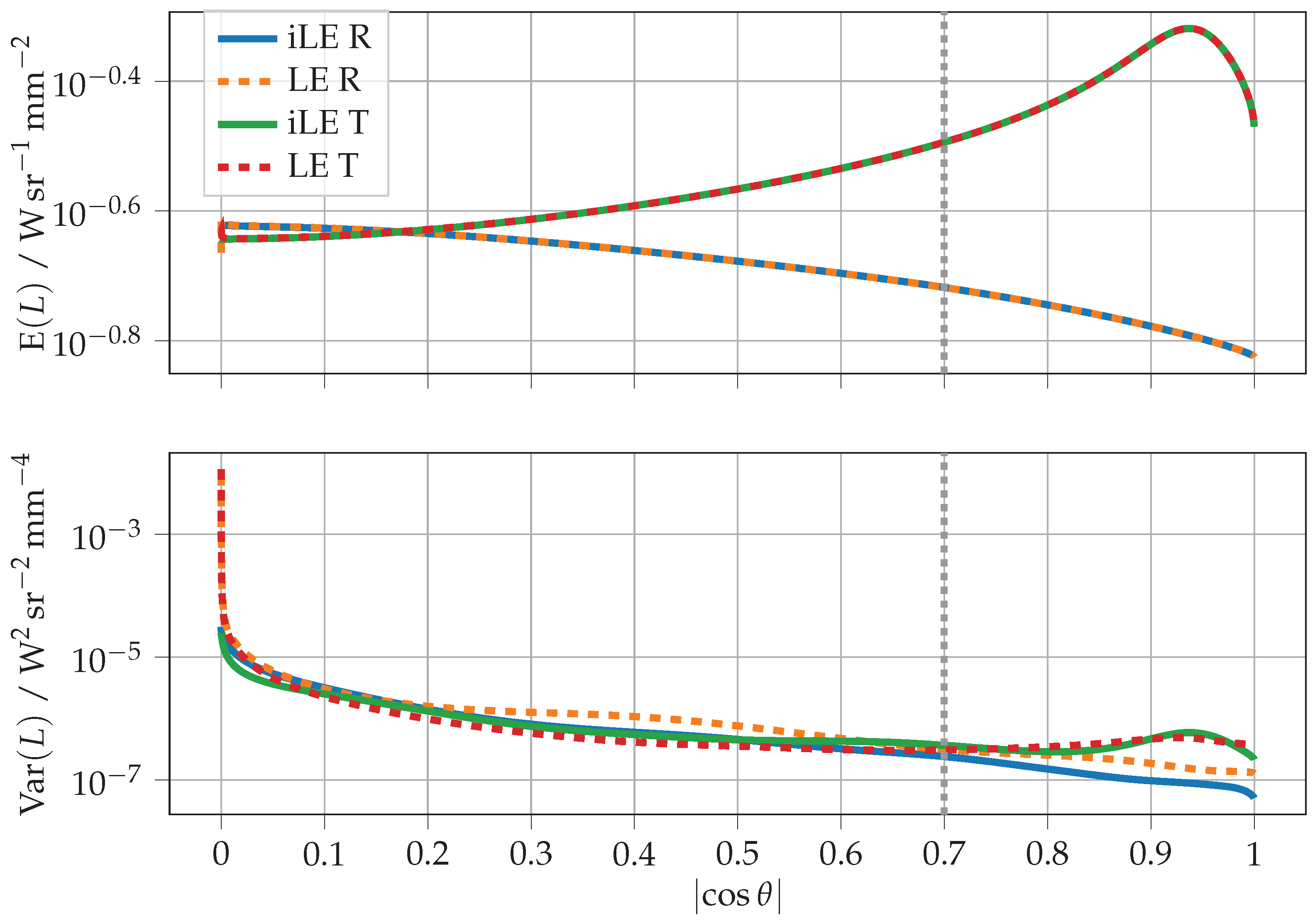
For a final test, see Figure 4, we again examine the same parameter set as in the first comparison, but for a substantially higher layer thickness of and a lower absorption of . Consequently, we anticipate a significant rise in potential interaction points in the medium and a marked decrease in attenuation along the propagation paths. This results in a noteworthy enhancement in the statistics for the LE technique, leading to almost similar variance for both VRMs across the majority of the angular range. Nonetheless, despite this specific situation, the iLE method still attains a substantial improvement of several orders of magnitude in variance for the relatively flat viewing angles.
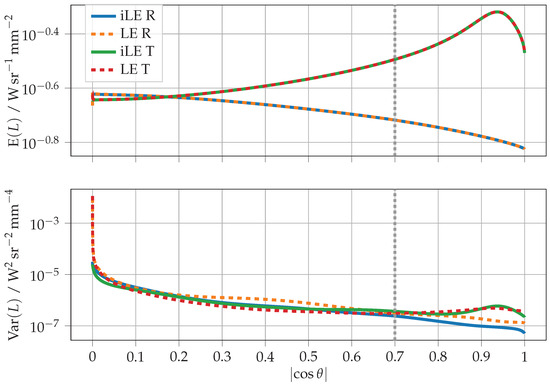
Figure 4.
Mean and variance of the simulated radiance in reflection (R) and transmission (T) for the parameters , , , , , , and . For the externally measurable reflectance or transmittance, only the angular range to the right of the grey dotted line, which marks the critical angle of total reflection, is of relevance. The radiance shown here can be converted to the AT or AR using Equation (10) or Equation (11), respectively.
4. Conclusions
A novel VRM, based on the integral form of the RTE, was introduced and benchmarked against the well-established LE method as a reference. To this end, the iLE and LE techniques were integrated into a self-developed Monte Carlo framework to conduct a thorough assessment of both methods’ statistical efficacy. The fundamental advantage of the iLE method lies in its integral nature, in which, unlike the LE technique, not only do individual scattering events contribute to the total radiance, but each individual path element adds integrally to the overall signal. This is also reflected in the test cases that have been examined. For a thin layer of 0.1 mm, where only a limited number of scattering events occur within the medium, a variance enhancement of up to three orders of magnitude could be observed below the critical angle of total reflection. This translates to a reduction in the simulation time by the same order of magnitude. Furthermore, for nearly horizontal viewing angles, where the attenuation along the detection path is exceptionally high, the variance could be improved even further for all scenarios under study. However, an increased layer thickness of 10 mm results in a substantial improvement in the statistics of the LE methods, so that in this case, both approaches yield comparable results, except for at shallow viewing angles, where the iLE method continues to provide significantly lower variance. In conclusion, the iLE method can be seen as an enhanced LE that allows a major improvement in statistics for media with low optical density and when near horizontal viewing angles are of interest, while still providing similarly good results for all other scenarios. Beyond the apparent application of simulating AR and AT data for arbitrary sets of optical parameters, the method is also predestined for solving inverse problems, since the simulated results yield perfectly smooth curves, owing to the fact that each path segment contributes to the full angular range. In forthcoming studies, the authors will strive to expand the methodology to structured illumination to enable its application in spatial frequency domain imaging (SFDI). In this domain, a considerable advantage of the introduced method is expected especially for large spatial frequencies, for which conventional Monte Carlo codes are very inefficient. Furthermore, there is a clear interest in extending the iLE method for spatially resolved radiance calculations to increase its general applicability.
Author Contributions
Conceptualization, D.H. and D.R.; methodology, D.H., D.R. and A.L.; software, D.H. and D.R.; validation, D.H. and D.R.; formal analysis, D.H. and D.R.; investigation, D.H. and D.R.; resources, A.K.; data curation, D.H. and D.R.; writing—original draft preparation, D.H.; writing—review and editing, D.R. and A.K.; visualization, D.H.; supervision, A.K.; project administration, D.H. and D.R.; funding acquisition, A.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under project number KI 538/19-3 and by the Ministerium für Wirtschaft, Arbeit und Tourismus Baden-Württemberg under project number BW1_0096/02.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data sets are synthetic and produced by the published MC program. Archived source code at the time of publication is available as a Zenodo snapshot (https://doi.org/10.5281/zenodo.10300609, accessed on 20 December 2023).
Acknowledgments
The authors would like to thank Lars Heiler for reviewing the theory section and the corresponding GPU code.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Derivation of the Integral Kernel
To derive the kernel function (19), we have to solve the radiative transfer Equation (14) under the reflecting boundary conditions (15) and (16) for a slab of thickness L. We introduce the parametrisation
In particular, we have , yielding with the desired radiance. Inserting into (14) results in
In the following, we consider two cases. First, for , we obtain from the value . Integrating (A2) over gives
where
Second, for , setting gives . Again, integrating (A2) over leads to
We note that the values in (A3) and in (A5) are not yet known. To incorporate the boundary conditions (15) and (16), we additionally need the values for the reflected radiance and . From (A5), we find
which is the same as
with . Similarly, we obtain from (A3) the boundary value
We now can use the BC to obtain the following system of linear equations
where in both equations, for the unknowns and . The corresponding solution is given by
With these values at hand, we can compute () as well as (), yielding in view of (A3) and (A5),
Then, inserting (A4) and combining the expressions for the two cases results in the final form, see Equation (19), for the kernel function.
References
- Vincendon, M.; Langevin, Y.; Poulet, F.; Bibring, J.P.; Gondet, B. Recovery of surface reflectance spectra and evaluation of the optical depth of aerosols in the near-IR using a Monte Carlo approach: Application to the OMEGA observations of high-latitude regions of Mars. J. Geophys. Res. Planets 2007, 112, E08S13. [Google Scholar] [CrossRef]
- Barker, H.; Goldstein, R.; Stevens, D. Monte Carlo Simulation of Solar Reflectances for Cloudy Atmospheres. J. Atmos. Sci. 2003, 60, 1881–1894. [Google Scholar] [CrossRef]
- Bréon, F.M. Reflectance of Broken Cloud Fields: Simulation and Parameterization. J. Atmos. Sci. 1992, 49, 1221–1232. [Google Scholar] [CrossRef]
- McKee, T.; Cox, S. Simulated Radiance Patterns for Finite Cubic Clouds. J. Atmos. Sci. 1976, 33, 2014–2020. [Google Scholar] [CrossRef]
- Janecek, M.; Moses, W. Simulating Scintillator Light Collection Using Measured Optical Reflectance. IEEE Trans. Nucl. Sci. 2010, 57, 964–970. [Google Scholar] [CrossRef]
- Janecek, M.; Moses, W. Optical Reflectance Measurements for Commonly Used Reflectors. IEEE Trans. Nucl. Sci. 2008, 55, 2432–2437. [Google Scholar] [CrossRef]
- Trigila, C.; Moghe, E.; Roncali, E. Technical Note: Standalone application to generate custom reflectance Look-Up Table for advanced optical Monte Carlo simulation in GATE/Geant4. Med. Phys. 2021, 48, 2800–2808. [Google Scholar] [CrossRef] [PubMed]
- Barajas, O.; Ballangrud, A.; Miller, G.; Moore, R.; Tulip, J. Monte Carlo modelling of angular radiance in tissue phantoms and human prostate: PDT light dosimetry. Phys. Med. Biol. 1997, 42, 1675. [Google Scholar] [CrossRef]
- Disney, M.; Lewis, P.; North, P. Monte Carlo ray tracing in optical canopy reflectance modelling. Remote Sens. Rev. 2000, 18, 163–196. [Google Scholar] [CrossRef]
- North, P. Three-dimensional forest light interaction model using a Monte Carlo method. IEEE Trans. Geosci. Remote Sens. 1996, 34, 946–956. [Google Scholar] [CrossRef]
- Cooper, K.; Smith, J. A Monte Carlo Reflectance Model for Soil Surfaces with Three-Dimensional Structure. IEEE Trans. Geosci. Remote Sens. 1985, GE-23, 668–673. [Google Scholar] [CrossRef]
- Kurt, M.; Edwards, D. A Survey of BRDF Models for Computer Graphics. SIGGRAPH Comput. Graph. 2009, 43, 1–7. [Google Scholar] [CrossRef]
- Guarnera, D.; Guarnera, G.; Ghosh, A.; Denk, C.; Glencross, M. BRDF Representation and Acquisition. Comput. Graph. Forum 2016, 35, 625–650. [Google Scholar] [CrossRef]
- Flock, S.; Patterson, M.; Wilson, B.; Wyman, D. Monte Carlo modeling of light propagation in highly scattering tissues. I. Model predictions and comparison with diffusion theory. IEEE Trans. Biomed. Eng. 1989, 36, 1162–1168. [Google Scholar] [CrossRef]
- Wong, B.; Mengüç, M. Comparison of Monte Carlo techniques to predict the propagation of a collimated beam in participating media. Numer. Heat Transf. Part B Fundam. 2002, 42, 119–140. [Google Scholar] [CrossRef]
- Wang, L.; Jacques, S.; Zheng, L. MCML—Monte Carlo modeling of light transport in multi-layered tissues. Comput. Methods Progr. Biomed. 1995, 47, 131–146. [Google Scholar] [CrossRef]
- Pincus, R.; Evans, K. Computational Cost and Accuracy in Calculating Three-Dimensional Radiative Transfer: Results for New Implementations of Monte Carlo and SHDOM. J. Atmos. Sci. 2009, 66, 3131–3146. [Google Scholar] [CrossRef]
- Iwabuchi, H. Efficient Monte Carlo Methods for Radiative Transfer Modeling. J. Atmos. Sci. 2006, 63, 2324–2339. [Google Scholar] [CrossRef]
- Buras, R.; Mayer, B. Efficient unbiased variance reduction techniques for Monte Carlo simulations of radiative transfer in cloudy atmospheres: The solution. J. Quant. Spectrosc. Radiat. Transf. 2011, 112, 434–447. [Google Scholar] [CrossRef]
- Marchuk, G.; Mikhailov, G.; Nazareliev, M.; Darbinjan, R.; Kargin, B.; Elepov, B. The Monte Carlo Methods in Atmospheric Optics; Springer: Berlin/Heidelberg, Germany, 1980; p. 208. [Google Scholar]
- Wilson, B.; Adam, G. A Monte Carlo model for the absorption and flux distributions of light in tissue. Med. Phys. 1983, 10, 824–830. [Google Scholar] [CrossRef]
- Martelli, F.; Binzoni, T.; Bianco, S.D.; Liemert, A.; Kienle, A. Light Propagation through Biological Tissue and Other Diffusive Media: Theory, Solutions, and Validations, 2nd ed.; SPIE: Bellingham, WA, USA, 2022; p. 51. [Google Scholar]
- Machida, M. Rotated Reference Frames in Radiative Transport Theory; Progress in Optics; Elsevier: Amsterdam, The Netherlands, 2023. [Google Scholar] [CrossRef]
- Liemert, A.; Reitzle, D.; Kienle, A. Hybrid method for solving the radiative transport equation. In Proceedings of the Diffuse Optical Spectroscopy and Imaging IX, Munich, Germany, 25–29 June 2023; Contini, D., Hoshi, Y., O’Sullivan, T.D., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2023; Volume 12628, p. 126281G. [Google Scholar] [CrossRef]
- Henyey, L.; Greenstein, J. Diffuse radiation in the galaxy. Astrophys. J. 1941, 93, 70–83. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).