A Comprehensive Study on Phase Sensitive Amplification and Stimulated Brillouin Scattering in Nonlinear Fibers with Longitudinally Varying Dispersion
Abstract
:1. Introduction
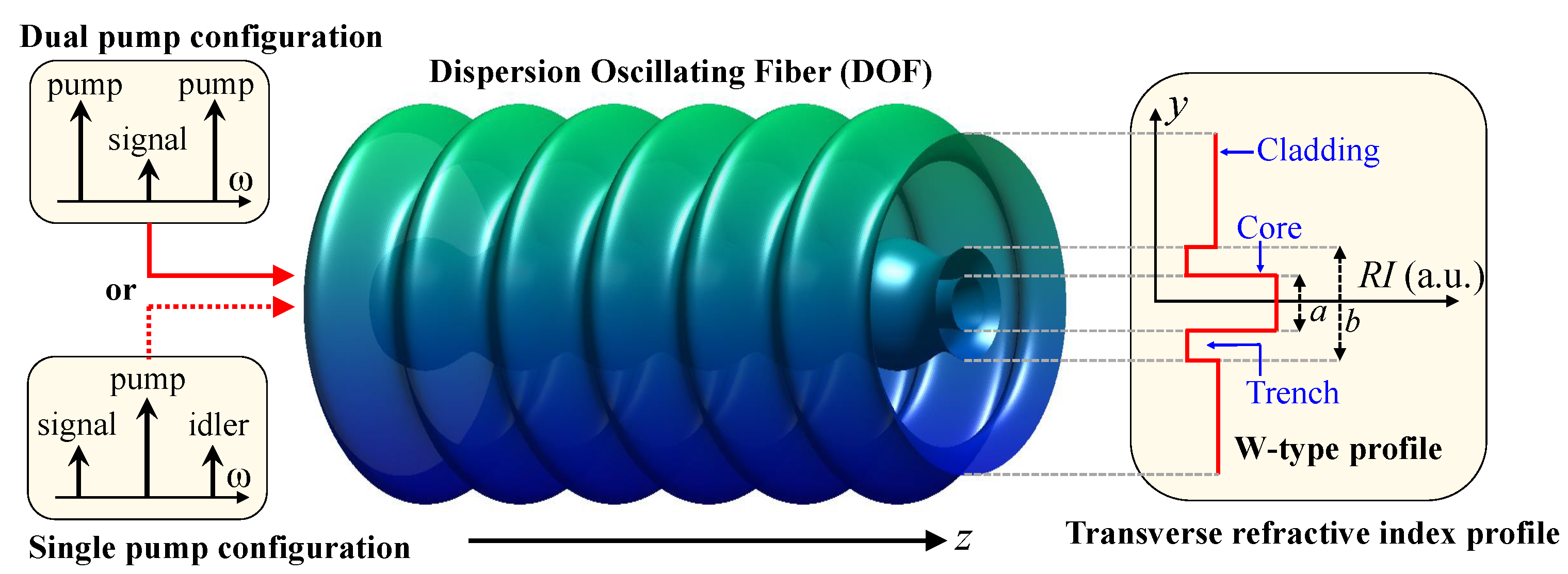
2. Fiber Parameters
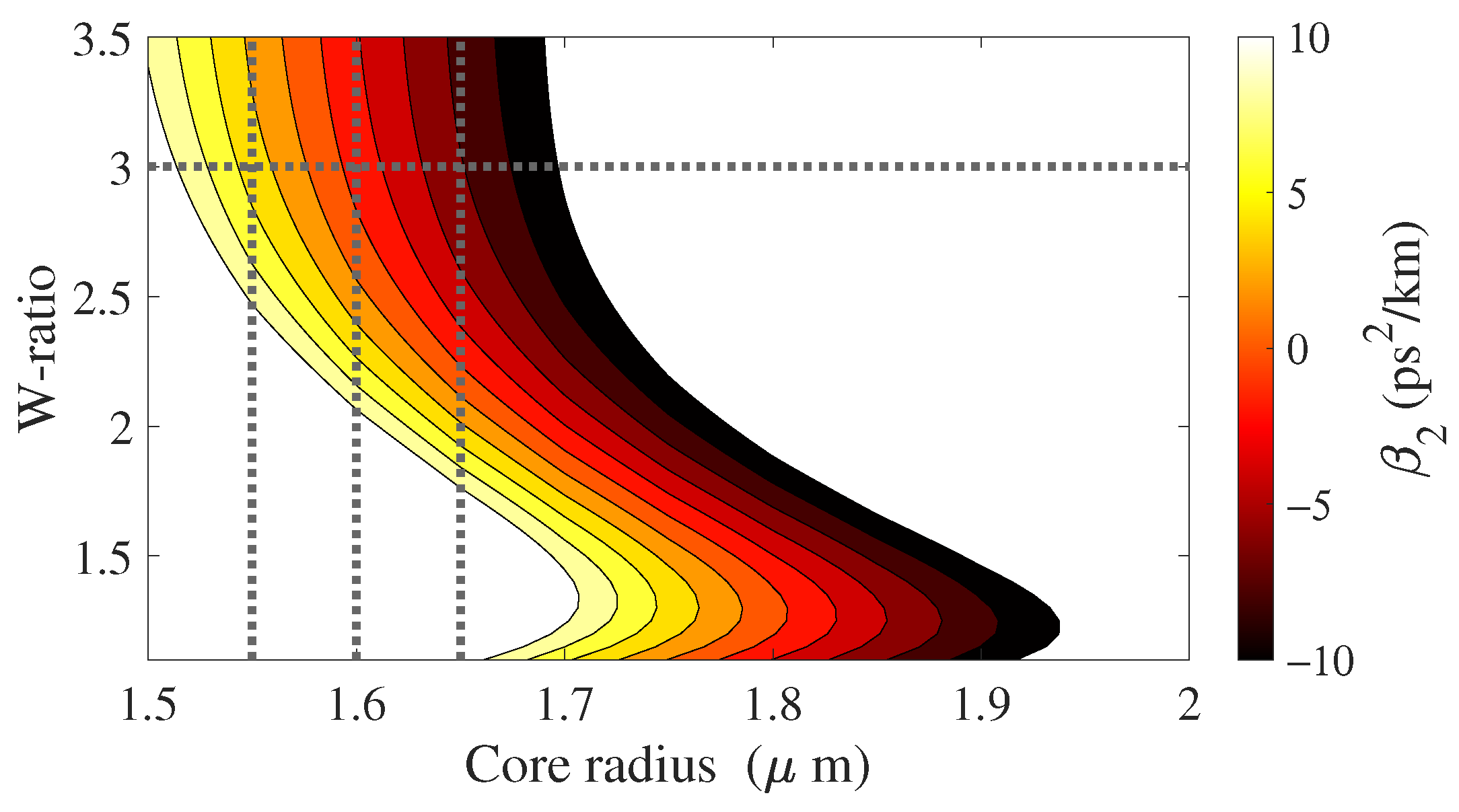
2.1. Dispersion Parameters
2.2. Nonlinear Coefficient
3. PSA in a DOF
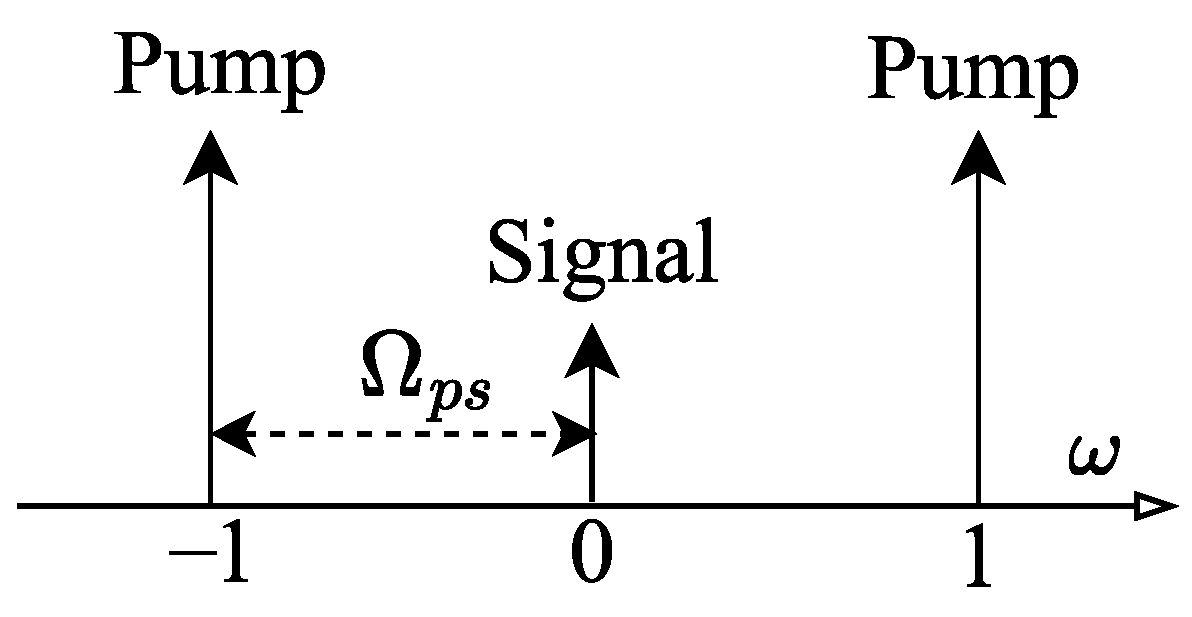
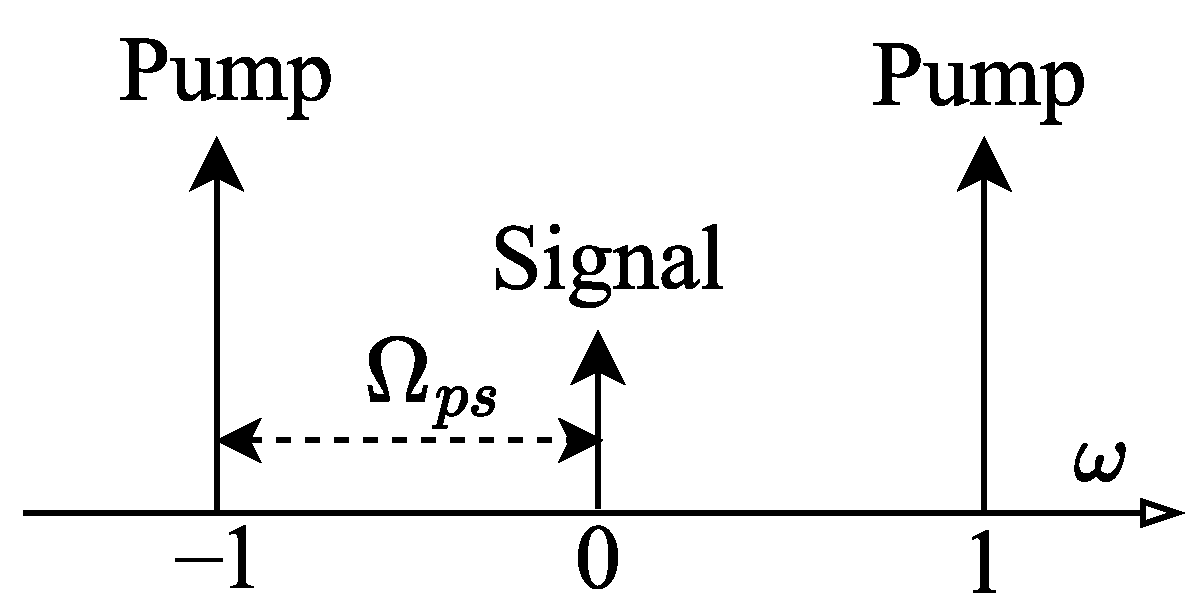
3.1. Analytical Model of the PSA: Single Pump Configuration
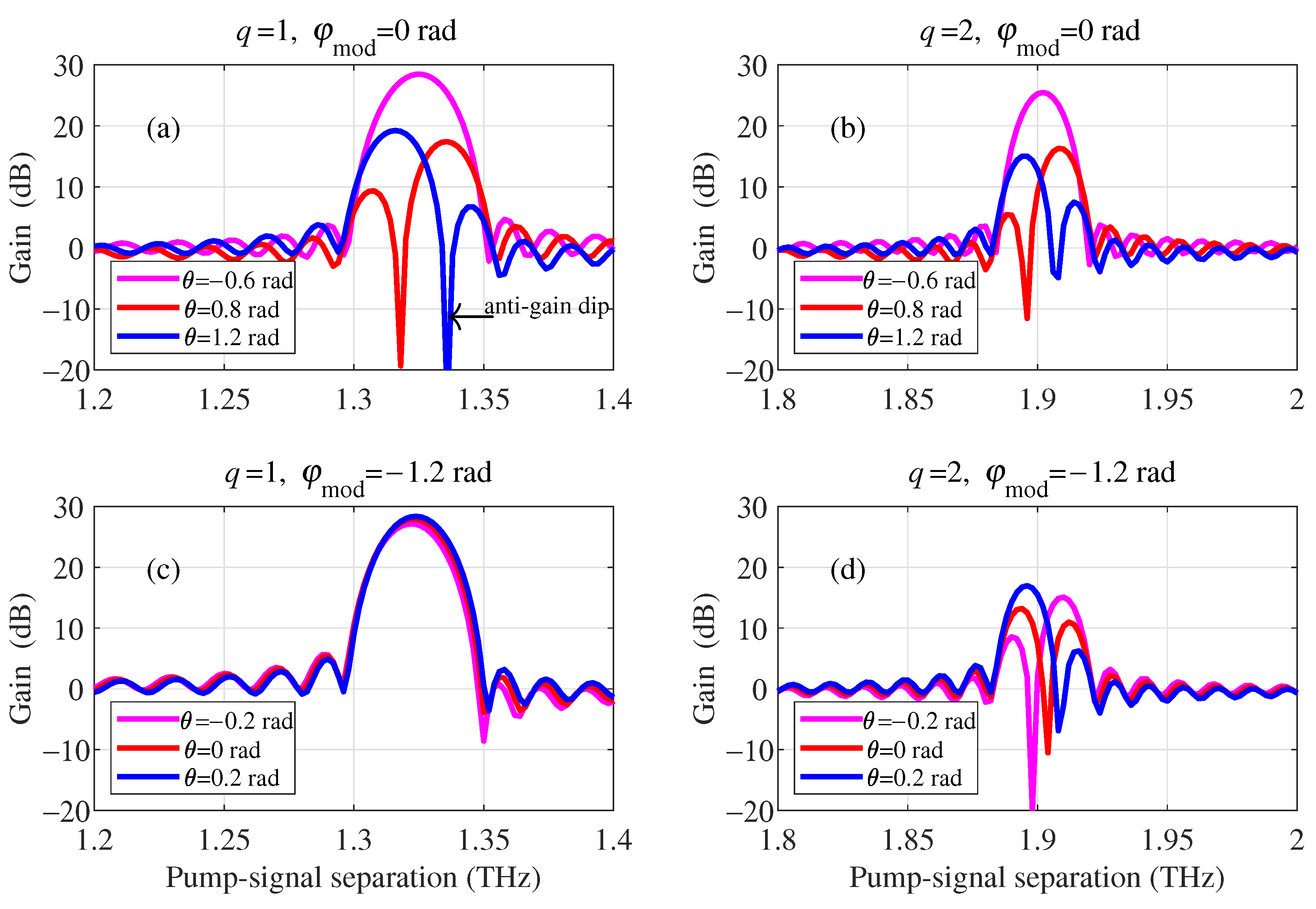
3.2. Role of Pump Phase and Modulation Phase on Signal Gain
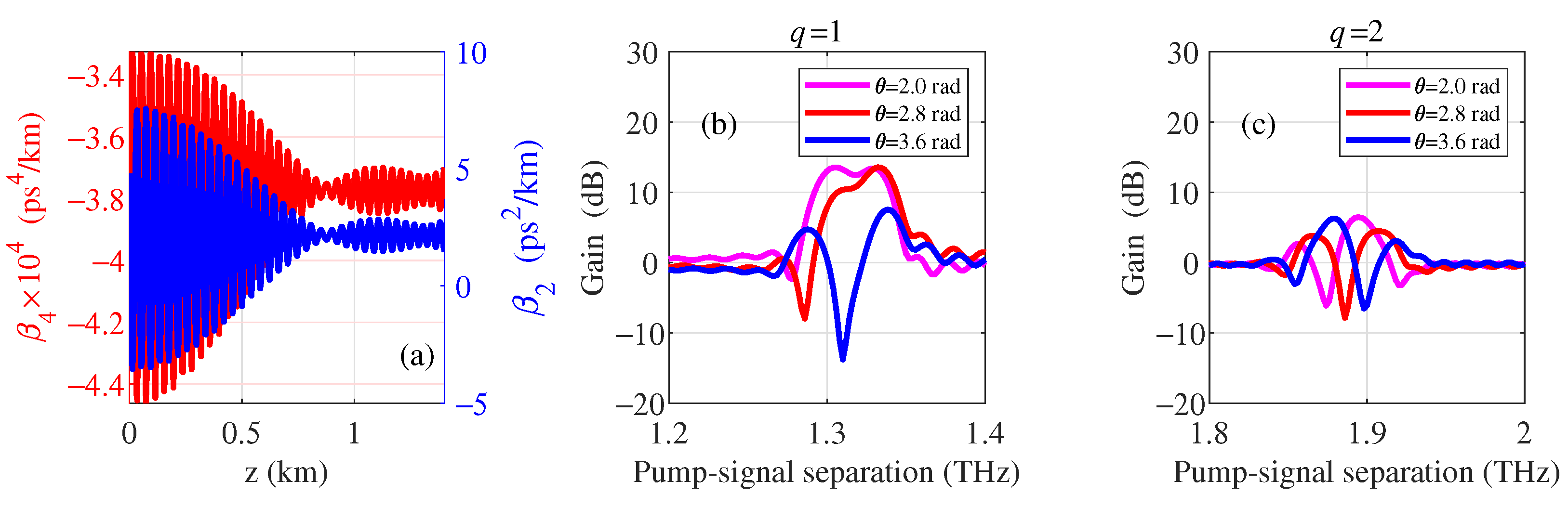
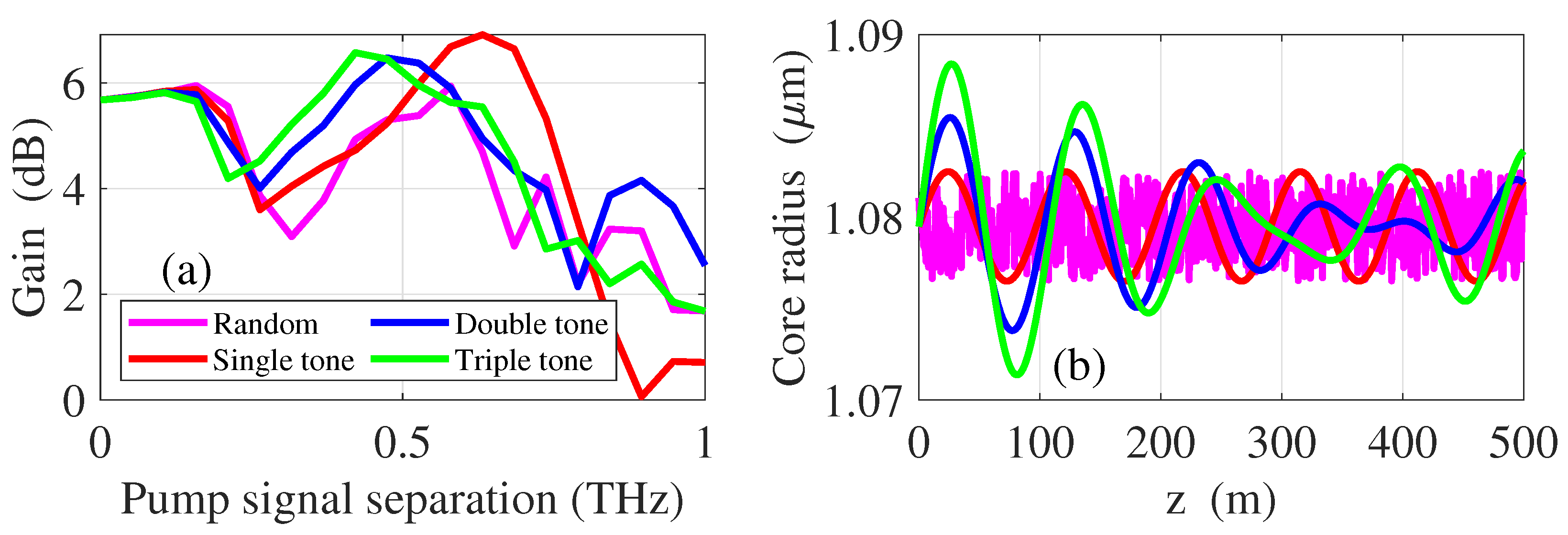
3.3. DOF with Multiple Frequency of Dispersion Modulation
4. PSA in a DOF: Dual Pump Configuration
4.1. Analytical Model: Three Wave Approach
4.2. Numerical Model: Nonlinear Schrödinger Equation (NLSE)
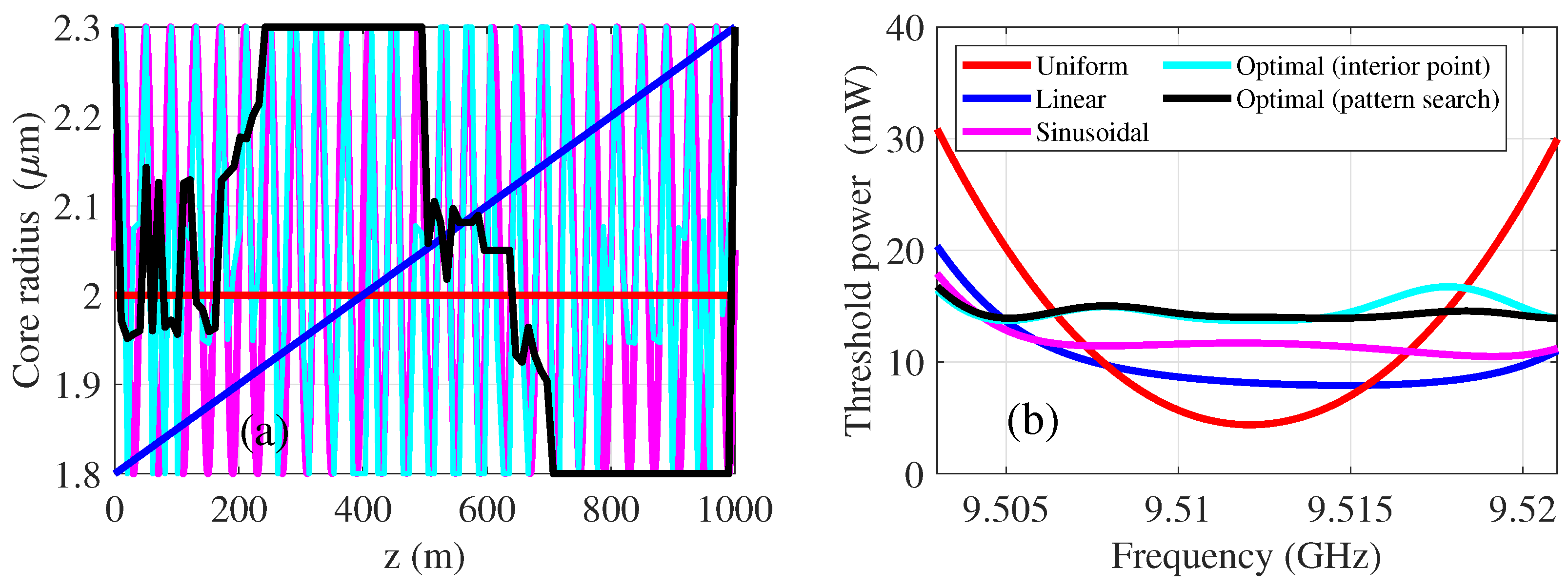
4.3. Profile Optimization for Larger PSA Gain
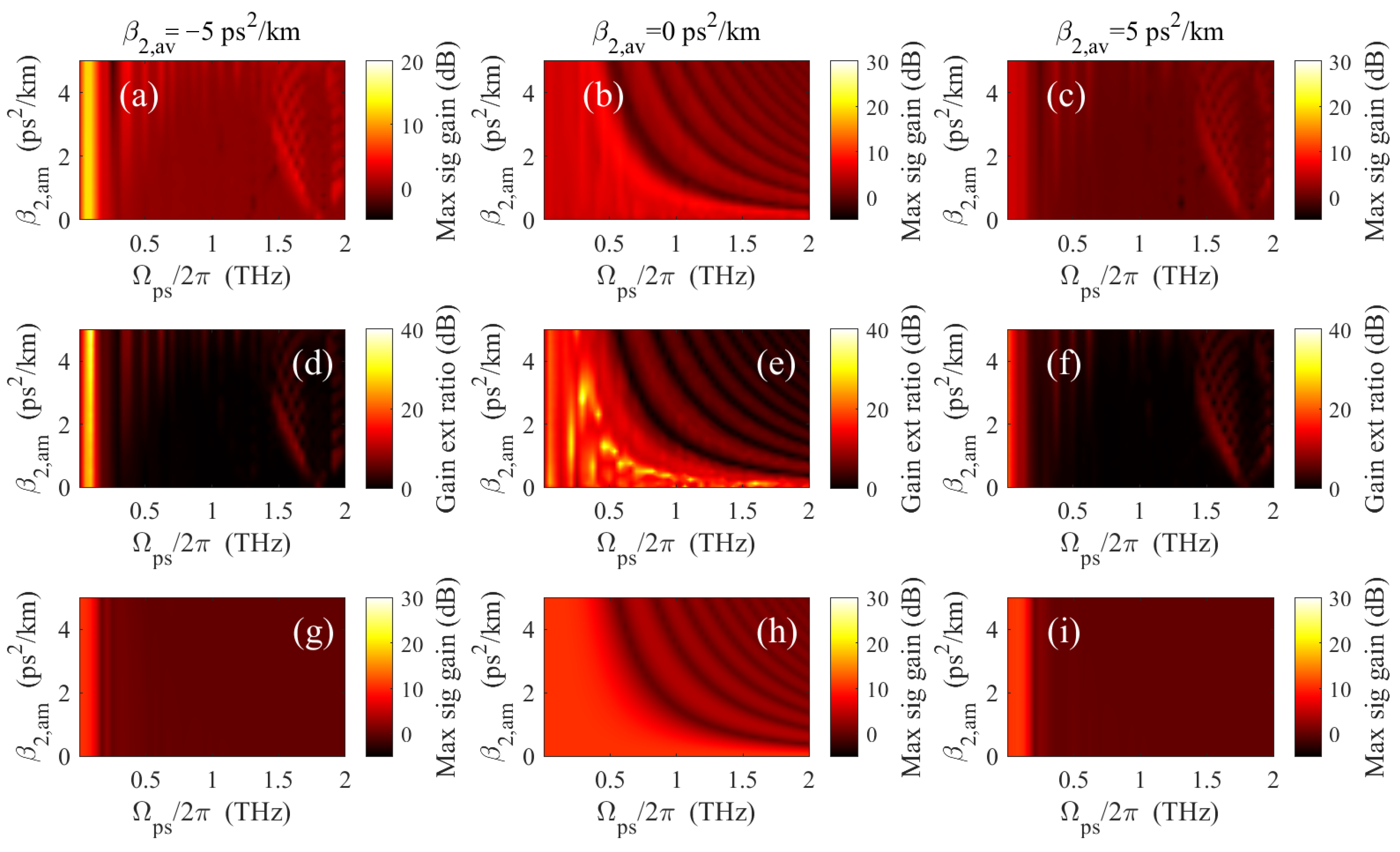
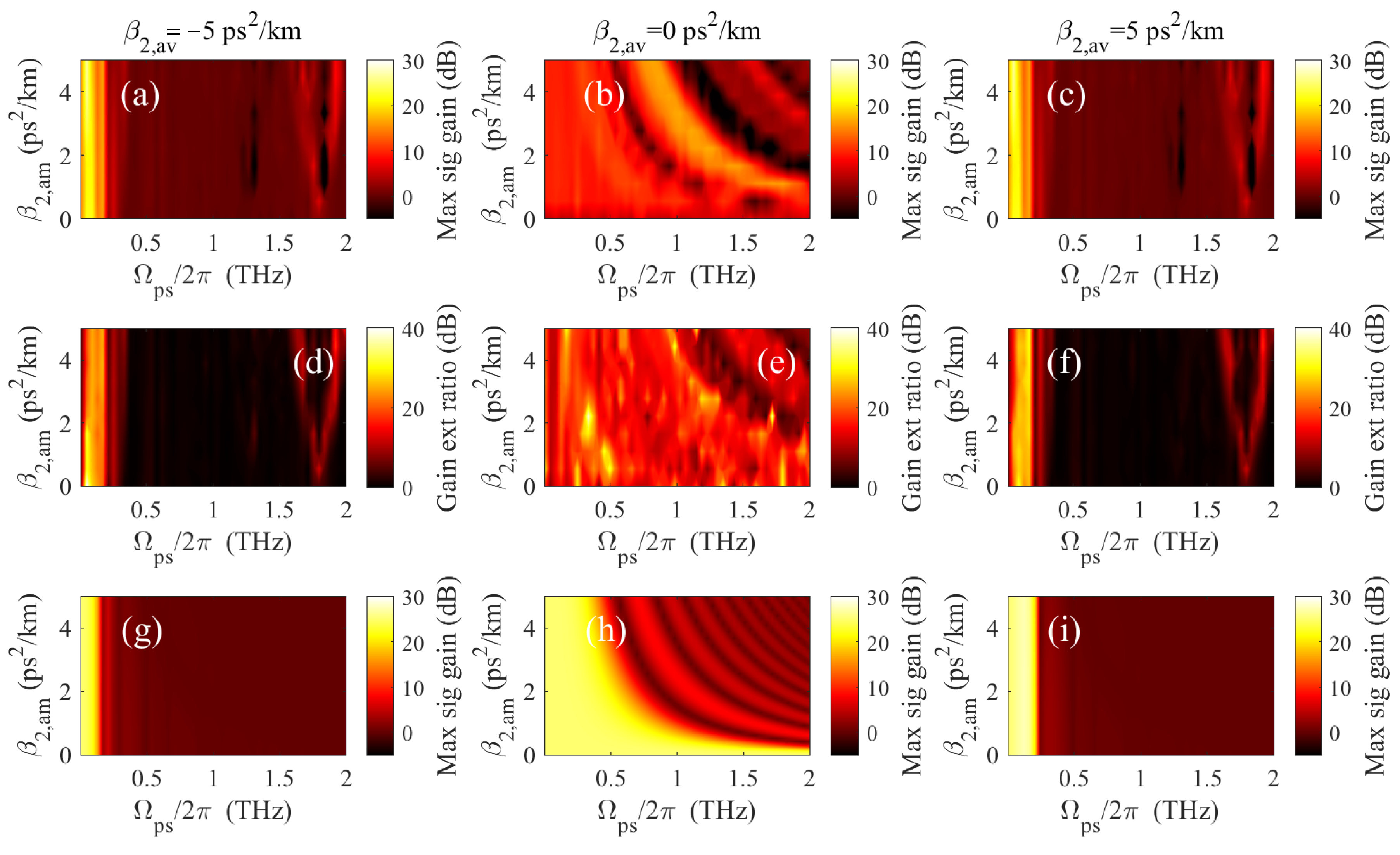
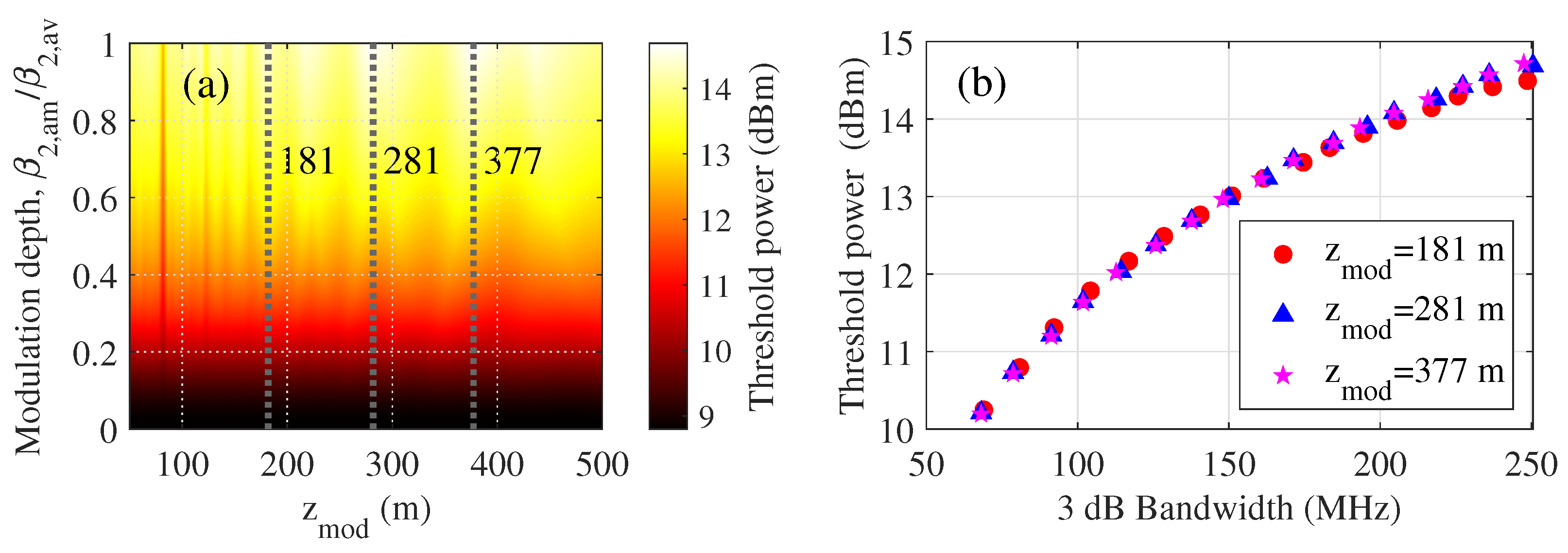
4.4. Numerical Results with Scanning of Dispersion Oscillation Parameters
5. SBS in a DOF
5.1. Theory of SBS
5.2. Steady State Analysis
5.3. Numerical Optimization of Longitudinal Fiber Profile for SBS Mitigation
6. Experiments on SBS Mitigation and Parametric Amplification with a DOF
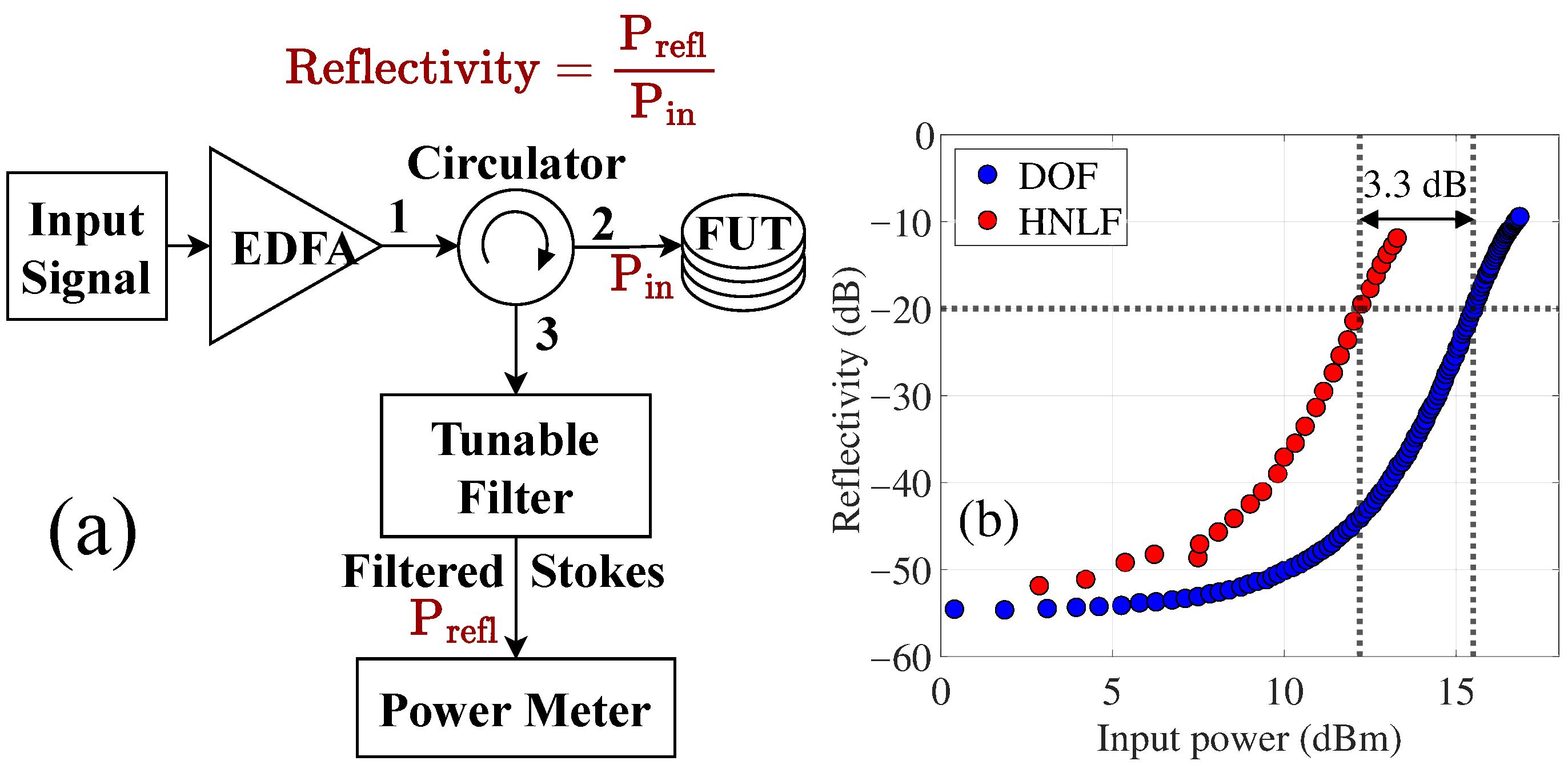
6.1. Comparison of SBS Threshold
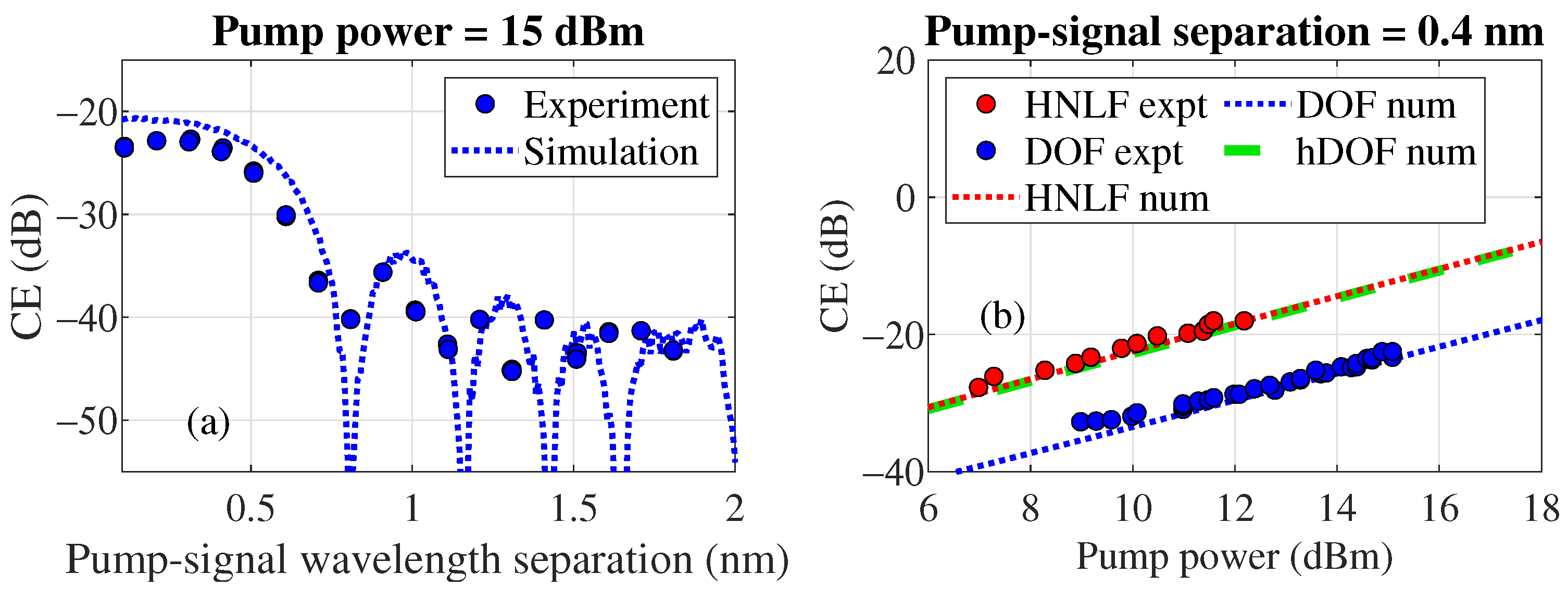
6.2. Comparison of Conversion Efficiency (CE)
7. Discussion
7.1. Single Pump PSA with DOF
7.2. Dual Pump PSA with DOF
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Caves, C.M. Quantum limits on noise in linear amplifiers. Phys. Rev. D 1982, 26, 1817. [Google Scholar] [CrossRef]
- Lim, O.K.; Grigoryan, V.; Shin, M.; Kumar, P. Ultra-low-noise inline fiber-optic phase-sensitive amplifier for analog optical signals. In Proceedings of the Optical Fiber Communication Conference, San Diego, CA, USA, 24–28 February 2008; p. OML3. [Google Scholar]
- Tong, Z.; Lundström, C.; Andrekson, P.A.; Karlsson, M.; Bogris, A. Ultralow noise, broadband phase-sensitive optical amplifiers, and their applications. IEEE J. Sel. Top. Quantum Electron. 2011, 18, 1016–1032. [Google Scholar] [CrossRef]
- Malik, R.; Kumpera, A.; Lorences-Riesgo, A.; Andrekson, P.; Karlsson, M. Frequency-resolved noise figure measurements of phase (in) sensitive fiber optical parametric amplifiers. Opt. Express 2014, 22, 27821–27832. [Google Scholar] [CrossRef]
- Andrekson, P.A.; Karlsson, M. Fiber-based phase-sensitive optical amplifiers and their applications. Adv. Opt. Photonics 2020, 12, 367–428. [Google Scholar] [CrossRef]
- Tang, R.; Devgan, P.S.; Grigoryan, V.S.; Kumar, P.; Vasilyev, M. In-line phase-sensitive amplification of multi-channel CW signals based on frequency nondegenerate four-wave-mixing in fiber. Opt. Express 2008, 16, 9046–9053. [Google Scholar] [CrossRef]
- Sodré, A.C.; Cañas-Estrada, N.; Noque, D.F.; Borges, R.M.; Melo, S.A.; González, N.G.; Oliveira, J.C. Photonic-assisted microwave amplification using four-wave mixing. IET Optoelectron. 2016, 10, 163–168. [Google Scholar] [CrossRef]
- Zhao, P.; Kakarla, R.; Karlsson, M.; Andrekson, P.A. Enhanced analog-optical link performance with noiseless phase-sensitive fiber optical parametric amplifiers. Opt. Express 2020, 28, 23534–23544. [Google Scholar] [CrossRef]
- Kakarla, R.; Schröder, J.; Andrekson, P.A. One photon-per-bit receiver using near-noiseless phase-sensitive amplification. Light. Sci. Appl. 2020, 9, 153. [Google Scholar] [CrossRef]
- Fedorov, M. Entanglement of multiphoton states in polarization and quadrature variables. Laser Phys. 2019, 29, 124006. [Google Scholar] [CrossRef]
- Droques, M.; Kudlinski, A.; Bouwmans, G.; Martinelli, G.; Mussot, A. Experimental demonstration of modulation instability in an optical fiber with a periodic dispersion landscape. Opt. Lett. 2012, 37, 4832–4834. [Google Scholar] [CrossRef]
- Finot, C.; Fatome, J.; Sysoliatin, A.; Kosolapov, A.; Wabnitz, S. Competing four-wave mixing processes in dispersion oscillating telecom fiber. Opt. Lett. 2013, 38, 5361–5364. [Google Scholar] [CrossRef]
- Feng, F.; Fatome, J.; Sysoliatin, A.; Chembo, Y.; Wabnitz, S.; Finot, C. Wavelength conversion and temporal compression of pulse train using dispersion oscillating fibre. Electron. Lett. 2014, 50, 768–770. [Google Scholar] [CrossRef]
- Mussot, A.; Conforti, M.; Trillo, S.; Copie, F.; Kudlinski, A. Modulation instability in dispersion oscillating fibers. Adv. Opt. Photonics 2018, 10, 1–42. [Google Scholar] [CrossRef]
- Mazhirina, Y.A.; Mel’nikov, L.A.; Sysoliatin, A.; Konyukhov, A.I.; Gochelashvili, K.S.; Venkitesh, D.; Sarkar, S. Parametric amplification in optical fibre with longitudinally varying dispersion. Quantum Electron. 2021, 51, 692. [Google Scholar] [CrossRef]
- Chatterjee, D.; Bouasria, Y.; Xie, W.; Labidi, T.; Goldfarb, F.; Fsaifes, I.; Bretenaker, F. Investigation of analog signal distortion introduced by a fiber phase sensitive amplifier. J. Opt. Soc. Am. B 2020, 37, 2405–2415. [Google Scholar] [CrossRef]
- Smith, N.; Doran, N. Modulational instabilities in fibers with periodic dispersion management. Opt. Lett. 1996, 21, 570–572. [Google Scholar] [CrossRef]
- Fourcade-Dutin, C.; Bassery, Q.; Bigourd, D.; Bendahmane, A.; Kudlinski, A.; Douay, M.; Mussot, A. 12 THz flat gain fiber optical parametric amplifiers with dispersion varying fibers. Opt. Express 2015, 23, 10103–10110. [Google Scholar] [CrossRef]
- Da Ros, F.; Dalgaard, K.; Lei, L.; Xu, J.; Peucheret, C. QPSK-to-2× BPSK wavelength and modulation format conversion through phase-sensitive four-wave mixing in a highly nonlinear optical fiber. Opt. Express 2013, 21, 28743–28750. [Google Scholar] [CrossRef]
- Xie, W.; Fsaifes, I.; Bretenaker, F. Optimization of a degenerate dual-pump phase-sensitive optical parametric amplifier for all-optical regenerative functionality. Opt. Express 2017, 25, 12552–12565. [Google Scholar] [CrossRef]
- Baillot, M.; Gay, M.; Peucheret, C.; Michel, J.; Chartier, T. Phase quadrature discrimination based on three-pump four-wave mixing in nonlinear optical fibers. Opt. Express 2016, 24, 26930–26941. [Google Scholar] [CrossRef]
- Chatterjee, D.; Bouasria, Y.; Goldfarb, F.; Hassouni, Y.; Bretenaker, F. Optimization of the conversion efficiency and evaluation of the noise figure of an optical frequency converter based on a dual-pump fiber phase sensitive amplifier. Opt. Express 2022, 30, 45676–45693. [Google Scholar] [CrossRef]
- Marhic, M.E. Fiber Optical Parametric Amplifiers, Oscillators and Related Devices; Cambridge University Press: Cambridge, MA, USA, 2008. [Google Scholar]
- Konyukhov, A.; Mavrin, P.; Suchita; Sobhanan, A.; Venkitesh, D.; Gochelashvili, K.; Sysoliatin, A. Phase-sensitive amplification in dispersion oscillating fibers. Laser Phys. 2021, 31, 085402. [Google Scholar] [CrossRef]
- Yoshizawa, N.; Imai, T. Stimulated Brillouin scattering suppression by means of applying strain distribution to fiber with cabling. J. Light. Technol. 1993, 11, 1518–1522. [Google Scholar] [CrossRef]
- Rothenberg, J.E.; Thielen, P.A.; Wickham, M.; Asman, C.P. Suppression of stimulated Brillouin scattering in single-frequency multi-kilowatt fiber amplifiers. In Proceedings of the Fiber Lasers V: Technology, Systems, and Applications, San Jose, CA, USA, 21–24 January 2008; Volume 6873, pp. 104–110. [Google Scholar]
- Imai, Y.; Shimada, N. Dependence of stimulated Brillouin scattering on temperature distribution in polarization-maintaining fibers. IEEE Photonics Technol. Lett. 1993, 5, 1335–1337. [Google Scholar] [CrossRef]
- Hansryd, J.; Dross, F.; Westlund, M.; Andrekson, P.; Knudsen, S. Increase of the SBS threshold in a short highly nonlinear fiber by applying a temperature distribution. J. Light. Technol. 2001, 19, 1691. [Google Scholar] [CrossRef]
- Dianov, E.M.; Zel’dovich, B.Y.; Karasik, A.Y.; Pilipetskiĭ, A.N. Feasibility of suppression of steady-state and transient stimulated Brillouin scattering. Sov. J. Quantum Electron. 1989, 19, 1051. [Google Scholar] [CrossRef]
- Kikuchi, K.; Lorattanasane, C. Design of highly efficient four-wave mixing devices using optical fibers. IEEE Photonics Technol. Lett. 1994, 6, 992–994. [Google Scholar] [CrossRef]
- Zeringue, C.; Dajani, I.; Naderi, S.; Moore, G.T.; Robin, C. A theoretical study of transient stimulated Brillouin scattering in optical fibers seeded with phase-modulated light. Opt. Express 2012, 20, 21196–21213. [Google Scholar] [CrossRef]
- Supradeepa, V. Stimulated Brillouin scattering thresholds in optical fibers for lasers linewidth broadened with noise. Opt. Express 2013, 21, 4677–4687. [Google Scholar] [CrossRef]
- Anderson, B.; Flores, A.; Holten, R.; Dajani, I. Comparison of phase modulation schemes for coherently combined fiber amplifiers. Opt. Express 2015, 23, 27046–27060. [Google Scholar] [CrossRef]
- Gordienko, V.; Szabó, Á.; Stephens, M.; Vassiliev, V.; Gaur, C.; Doran, N. Limits of broadband fiber optic parametric devices due to stimulated Brillouin scattering. Opt. Fiber Technol. 2021, 66, 102646. [Google Scholar] [CrossRef]
- Agrawal, G. Nonlinear Fiber Optics, 5th ed.; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Mussot, A.; Durecu-Legrand, A.; Lantz, E.; Simonneau, C.; Bayart, D.; Maillotte, H.; Sylvestre, T. Impact of pump phase modulation on the gain of fiber optical parametric amplifier. IEEE Photonics Technol. Lett. 2004, 16, 1289–1291. [Google Scholar] [CrossRef]
- Wong, K.K.; Marhic, M.E.; Kazovsky, L.G. Phase-conjugate pump dithering for high-quality idler generation in a fiber optical parametric amplifier. IEEE Photonics Technol. Lett. 2003, 15, 33–35. [Google Scholar] [CrossRef]
- Shiraki, K.; Ohashi, M.; Tateda, M. Suppression of stimulated Brillouin scattering in a fibre by changing the core radius. Electron. Lett. 1995, 31, 668–669. [Google Scholar] [CrossRef]
- Lundin, R. Dispersion flattening in a W fiber. Appl. Opt. 1994, 33, 1011–1014. [Google Scholar] [CrossRef]
- Snyder, A.; Love, J. Optical Waveguide Theory; Chapman and Hall: London, UK, 1983; Chapter 19. [Google Scholar]
- Boyd, R.W. Nonlinear Optics; Academic Press: Cambridge, MA, USA, 2020. [Google Scholar]
- Inoue, K. Influence of multiple four-wave-mixing processes on quantum noise of dual-pump phase-sensitive amplification in a fiber. JOSA B 2019, 36, 1436–1446. [Google Scholar] [CrossRef]
- Chatterjee, D.; Bouasria, Y.; Goldfarb, F.; Bretenaker, F. Analytical seven-wave model for wave propagation in a degenerate dual-pump fiber phase sensitive amplifier. JOSA B 2021, 38, 1112–1124. [Google Scholar] [CrossRef]
- Hansryd, J.; Andrekson, P.A.; Westlund, M.; Li, J.; Hedekvist, P.O. Fiber-based optical parametric amplifiers and their applications. IEEE J. Sel. Top. Quantum Electron. 2002, 8, 506–520. [Google Scholar] [CrossRef]
- Ferrini, G.; Fsaifes, I.; Labidi, T.; Goldfarb, F.; Treps, N.; Bretenaker, F. Symplectic approach to the amplification process in a nonlinear fiber: Role of signal-idler correlations and application to loss management. J. Opt. Soc. Am. B 2014, 31, 1627–1641. [Google Scholar] [CrossRef]
- Xie, W.; Fsaifes, I.; Labidi, T.; Bretenaker, F. Investigation of degenerate dual-pump phase sensitive amplifier using multi-wave model. Opt. Express 2015, 23, 31896–31907. [Google Scholar] [CrossRef]
- Wong, K.K.; Marhic, M.E.; Uesaka, K.; Kazovsky, L.G. Polarization-independent two-pump fiber optical parametric amplifier. IEEE Photonics Technol. Lett. 2002, 14, 911–913. [Google Scholar] [CrossRef]
- Hu, H.; Jopson, R.; Gnauck, A.; Dinu, M.; Chandrasekhar, S.; Xie, C.; Randel, S. Parametric amplification, wavelength conversion, and phase conjugation of a 2.048-Tbit/s WDM PDM 16-QAM signal. J. Light. Technol. 2015, 33, 1286–1291. [Google Scholar] [CrossRef]
- Chatterjee, D.; Konyukhov, A.; Sysoliatin, A.; Venkitesh, D. Phase-Sensitive Amplification in a Dispersion Oscillating Fiber with Two Pumps. In Proceedings of the Asia Communications and Photonics Conference, Shanghai, China, 24–27 October 2021; p. W2A.3. [Google Scholar]
- Stolen, R.; Bjorkholm, J. Parametric amplification and frequency conversion in optical fibers. IEEE J. Quantum Electron. 1982, 18, 1062–1072. [Google Scholar] [CrossRef]
- Smith, R.G. Optical power handling capacity of low loss optical fibers as determined by stimulated Raman and Brillouin scattering. Appl. Opt. 1972, 11, 2489–2494. [Google Scholar] [CrossRef]
- Haneef, S.M.; Prashanth, P.; Venkitesh, D.; Srinivasan, B. Modeling Stimulated Brillouin Scattering in LEAF Using Finite Difference Method. In Proceedings of the International Conference on Fibre Optics and Photonics, Virtual, 13–16 December 2014; p. S5A.39. [Google Scholar]
- MATLAB, Version R2021b; The MathWorks Inc.: Natick, MA, USA, 2021.
- Brackett, C.A.; Acampora, A.S.; Sweitzer, J.; Tangonan, G.; Smith, M.T.; Lennon, W.; Wang, K.C.; Hobbs, R.H. A scalable multiwavelength multihop optical network: A proposal for research on all-optical networks. J. Light. Technol. 1993, 11, 736–753. [Google Scholar] [CrossRef]
- Dong, L. Limits of stimulated Brillouin scattering suppression in optical fibers with transverse acoustic waveguide designs. J. Light. Technol. 2010, 28, 3156–3161. [Google Scholar]





| Nonlinear Medium | Advantage | Disadvantage |
|---|---|---|
| Highly nonlinear fiber (HNLF) | High gain and low noise figure; Typical nonlinear coefficient is high, ∼10 (W km)−1 | High power required to invoke nonlinearities, low stimulated Brillouin scattering (SBS) threshold |
| Periodically poled Lithium Niobate (PPLN) | Moderate gain and compact | High power required to invoke nonlinearities |
| Semiconductor optical amplifier (SOA) | Compact | High noise figure |
| Dispersion oscillating fiber (DOF) | High SBS threshold, low noise figure, moderate (potentially large) gain | High power required to invoke nonlinearities since experimental nonlinear coefficient in this work is 3.5 (W km)−1. However this value can be increased by using a preform of a HNLF |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chatterjee, D.; Sunder, S.; Krishna, M.; Yadav, S.; Sysoliatin, A.; Gochelashvili, K.; Semjonov, S.; Venkitesh, D.; Konyukhov, A. A Comprehensive Study on Phase Sensitive Amplification and Stimulated Brillouin Scattering in Nonlinear Fibers with Longitudinally Varying Dispersion. Photonics 2024, 11, 3. https://doi.org/10.3390/photonics11010003
Chatterjee D, Sunder S, Krishna M, Yadav S, Sysoliatin A, Gochelashvili K, Semjonov S, Venkitesh D, Konyukhov A. A Comprehensive Study on Phase Sensitive Amplification and Stimulated Brillouin Scattering in Nonlinear Fibers with Longitudinally Varying Dispersion. Photonics. 2024; 11(1):3. https://doi.org/10.3390/photonics11010003
Chicago/Turabian StyleChatterjee, Debanuj, Sugeet Sunder, Mrudula Krishna, Suchita Yadav, Alexej Sysoliatin, Konstantin Gochelashvili, Sergey Semjonov, Deepa Venkitesh, and Andrey Konyukhov. 2024. "A Comprehensive Study on Phase Sensitive Amplification and Stimulated Brillouin Scattering in Nonlinear Fibers with Longitudinally Varying Dispersion" Photonics 11, no. 1: 3. https://doi.org/10.3390/photonics11010003
APA StyleChatterjee, D., Sunder, S., Krishna, M., Yadav, S., Sysoliatin, A., Gochelashvili, K., Semjonov, S., Venkitesh, D., & Konyukhov, A. (2024). A Comprehensive Study on Phase Sensitive Amplification and Stimulated Brillouin Scattering in Nonlinear Fibers with Longitudinally Varying Dispersion. Photonics, 11(1), 3. https://doi.org/10.3390/photonics11010003






