Abstract
We present a new design of a random Raman fiber laser based on a graded-index multimode fiber as the media composing the cavity that allows the generation of narrow spectral lines. We carried out spectral measurements using an optical heterodyning technique by projecting multimode radiation onto the fundamental mode of a standard single-mode fiber. The measurements confirmed the presence of localized ultra-narrow short-lived modes. We measured the powers of the modes and found it to be significantly higher (up to 25 mW) compared with those in a random Raman laser based on a single-mode fiber (<2 mW), while preserving the same typical lifetimes of a few milliseconds.
1. Introduction
Random lasers are optical generators with feedback distributed randomly across their cavity [1]. Generation of this kind has been shown in different laser types, including dye [2], semiconductor [3], solid-state [4], and fiber [5,6] lasers. The absence of a well-defined cavity does not lead to a modeless radiation spectrum; instead, the open cavity’s character is propitious to the multimode behavior [7].
In fiber lasers, the random feedback organized within a fiber piece may remarkably alter the generation properties. Multiple wave interferences that are reflected from either natural or artificial reflectors along the fiber result in ultra-narrow “random” modes [8], stochastically distributed across the spectrum, which promote the multimode operation of several narrow lines [9] or single-mode generation [10,11]. For instance, random arrays of fiber Bragg gratings (FBGs) successfully stabilize the generation of Er-doped fiber lasers [12].
Weak Rayleigh backscattering from intrinsic inhomogeneities within the silica glass may also be employed as the source of optical feedback [1]. This simplest random feedback may govern the generation process as well, despite its extremely small value. Modes, appearing due to Rayleigh backscattering, are defined by the interplay between a plethora of weak random cavities, have linewidths down to several kHz and positions at random places within the spectrum [13]. The utilization of long fiber cavities or auxiliary ring fiber cavities ensures sufficient integral optical feedback for laser generation [14,15] as well as for the self-injection locking of Er-doped fiber lasers [16] or semiconductor lasers [17], narrowing the short-term linewidth down to the sub-kHz level [18], as well as producing effective parametric generation [19]. Note that nonlinear interactions that are well above the threshold strongly influence this generation, removing any signs of narrow modes [20,21], though filtering may give narrower linewidths even in these regimes [22].
Apart from single-mode regimes, Rayleigh backscattering feedback may provide multimode operation or fast switching between sequentially generated modes. Such regimes have been obtained in fiber random lasers with different types of gain, including stimulated Brillouin scattering [23], semiconductor amplifiers [24], rare-earth doped fibers [25] or Raman gain [26]. Thus, in [27], these modes were studied in the context of optical extreme event occurrence with emphasis on the probability distribution function type; near the threshold, this takes the form of Frechet distribution.
The regime of mode switching a narrow mode, defined by Rayleigh backscattering in a long fiber spool, exists only for a finite time of about units or tens of ms, which is significantly smaller that in random lasers employing very short fiber pieces for Rayleigh feedback (lifetimes of fractions of seconds [25]) or random arrays of FBGs (lifetimes of tens of seconds [9]). There are several reasons for such behavior. First, the lifetime is limited by technical noises (such as temperature variations because of heating by radiation or weak mechanical vibrations affecting the experimental setup), which leads to the decomposition of stochastic grating, resulting in the switching dynamics [28]. Second, the lasing process itself might comprise some mechanisms of narrow mode cessation. The candidates for mode disturbing and switching are nonlinear interactions [29]. Cross-phase modulation with a pump and four-wave mixing with other modes in the spectrum are both inevitable phenomena, for instance, for random Raman fiber lasers because of their high pump and generation powers.
The random fiber lasers operating in the regime of generating narrow intermitting modes seem to be an attractive light source for super-resolution spectroscopy [30,31]. In this approach to high-resolution spectral measurements, the moderate resolution of a spectrum analyzer is significantly enhanced with repetitive measurements of the narrow-band irradiation source. Essentially, the wavelength of the source must be changed randomly across the whole spectral range of interest. Thus, the ultra-narrow linewidth, along with the random spectral position of the modes generated in random fiber lasers (RFLs), allows for achieving a high spectral resolution even with a low-resolution conventional spectrum analyzer. n recent realizations of super-resolved spectroscopy, either a volume laser based on a colloidal suspension of active microparticles or a fiber laser based on Bragg gratings were considered, that are the RFLs with slow mode dynamics. Since the performance of the method is largely determined by the quality of the random laser source, the proposed implementations are not of practical interest, since the low speed of mode switching requires a long data acquisition process. Thus, spectroscopy with a random fiber laser based on a random array of fiber Fabry–Perot cavities, with a small mode-switching rate, imposes minutes-long data collection [31]. From a practical point of view, to achieve the effective implementation of a high-resolution spectroscopy system, it is necessary to be able to match the frequencies of mode occurrence with the speed and range of operation of the spectrum analyzer used.
For fast and sensitive super-resolved measurements, both the wavelength-switching rate of the radiation source and its power should be large enough. Random fiber lasers with Rayleigh backscattering and Raman gain appear to be the best choices among random fiber lasers, as they provide the shortest life-times and leave room for output power increase due to the high pump rate. Therefore, enhancing the efficiency of random Raman fiber lasers operating in a narrow mode regime, for instance, by acquiring a larger number of narrow modes or enhancing their output powers, appears to be a relevant problem. The output powers of generated modes may be limited by different nonlinear processes that redistribute the energy of the modes. Among these are stimulated Brillouin scattering or different Kerr-nonlinear mode interactions [32,33], so special attention should be paid to reduce their impact.
Different techniques might be promising to tailor the properties of random Raman fiber lasers. Previously, it was demonstrated that random feedback may be utilized for Raman generation in multimode fibers [34,35]. The multimode fibers, among other things, allow the observation of non-trivial linear and nonlinear dynamics in amplifiers [36], as well as in tailoring the generation of fiber lasers [37]. A lower level of Kerr-effect-based nonlinearities, as well as higher non-linear thresholds in comparison with single-mode fibers [38,39], potentially originated from the larger mode effective areas and may pave the way towards better performance in terms of narrow mode properties.
In the present manuscript, we demonstrate the generation of narrow spectral modes, emerging in the radiation of random Raman fiber lasers, utilizing a graded-index multimode fiber (MM) as the active medium instead of the conventionally used single-mode fibers. We study the properties of the modes, measure their actual peak power for the first time and compare their characteristics with those of modes generated in a random laser based on a conventional single-transverse-mode fiber. The laser based on the MM fiber turned out to generate considerably more powerful narrow spectral components.
2. Materials and Methods
The laser under study has a forward-pumping scheme; a pump wave radiation from a Raman fiber laser operating at 1455 nm, with maximum powers up to 5 W, is launched at the multimode fiber through the wavelength-division multiplexer (WDM), which acts as the gain and delivers generation around 1550 nm, owing to stimulated Raman scattering (see Figure 1a). The random cavity was formed using 17 km of the graded-index multimode (MM) fiber Corning 50/125 with a core diameter of 50 μm. The larger areas of the transverse modes of the MM fiber results in roughly an order of magnitude lower, in all types of nonlinear interactions, than in a standard single-mode (SM) SMF-28 fiber.
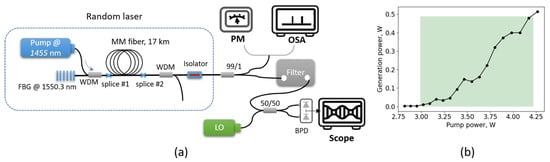
Figure 1.
(a) The experimental setup. FBG—fiber Bragg grating, WDM—wavelength-division multiplexer, ISO—isolator, LO—local oscillator, BPD—balanced photodetector, PM—power meter, OSA—grating-based single-pixel spectrometer. (b) Total output power versus the pump power. A green square indicates the output power range supporting narrow-mode generation.
At the third port of the WDM, a fiber Bragg grating (FBG) with a central wavelength of 1550.35 nm was placed to reduce the generation threshold of the laser by closing up the cavity from one side with considerably high reflection. The FBG was inscribed into a piece of standard SMF-28 fiber. The output of the multimode fiber was spliced with another single-mode WDM to remove residual pump light from the system, followed by an optical isolator and the measurement system. Thus, the measurements were performed on the projection of the field at the output of the multimode fiber on a fundamental mode of the standard single-mode fiber. Using a commercial optical time domain reflectometer (OTDR) operating at 1550 nm, we made sure that there was no detectable back-reflection at the splices within the cavity or in the measurement system after the optical isolator. Thus, we ensured the truly random nature of the feedback that closes up the cavity formed by the MM fiber spool and the FBG at the pump side.
Using both the OTDR technique and the direct cut-off method, we estimated the losses at the output of the MM–SMF splice (splice #2 at the Figure 1a) would be no larger than 1 dB if a weak single-mode radiation from the SMF-28 fiber was launched at the MM fiber spool through splice 1 (see Figure 1a). In addition, we verified this loss value by direct measurements using the cut-off method. To achieve this, we repeated the splicing of MM and SMF fibers several times, each time measuring the power coming from the cleaved end of the MM fiber before the splicing, and measuring the output power after the splice followed by the additional 20 m of spooled SMF fiber after splice #2 to eliminate the contribution of cladding modes to the measured power. Splicing losses varied from splice to splice in the range from 1 to 3 dB. Depending on exactly how the amplitudes of different transverse modes are distributed, different losses at the MM–SMF splice can be expected [40]. We estimated the losses by calculating the overlap integrals of different modes with the fundamental mode of the SMF-28 fiber; they appeared to be about 20 dB if the input power was evenly distributed across 50 first transverse modes of the MM fiber, and only 0.7 dB if the whole power was contained in the fundamental mode. Thus, we concluded that the reason for the significantly lower observed losses may be incomplete energy mixing between different transverse modes of the fiber. The indirect confirmation of the weakness of mode mixing can be an estimate of the length required to obtain a stationary distribution, which, for step-index MM fibers, can reach several kilometers or more [41]. Within the spooled fiber, enhanced mode coupling may be expected, though for a coil with a diameter of 8 cm (such as that used in the current work), this effect of additional mode mixing can probably be neglected [42]. For example, in [43], to describe the experimental observations, it was assumed that, when the fundamental mode of the GRIN fiber is excited due to the weak coupling between neighboring modes, an exponential distribution with a maximum power in the fundamental mode is possible. This process was described in more detail in a recent paper [44]. In general, the dynamics of the modes in the fiber under consideration require additional research, though the mode coupling is estimated to be weak. At the same time, it should be noted that even the fundamental mode of the MM fiber under consideration has a larger area than the fundamental mode of a single-mode fiber SMF-28.
Splice losses #1 have not been measured, but can be estimated and will be different for pump radiation and lasing radiation. For the pump radiation propagating from the SMF fiber forming the WDM in the multimode fiber, the losses will be negligible. For lasing radiation propagating from the MM fiber to the SMF fiber of the WDM in the reverse direction, we expect the losses to be of the same order of magnitude as the losses in splice #1. The presence of these losses will lead to some noticeable decrease in the effective reflection coefficient of the Bragg grating inscribed in the SMF fiber. However, due to the peculiarities of the power characteristics of a random laser, varying the strength of point reflectors over a wide range does not practically change the threshold power [45]. Thus, losses at the splice #1 do not need to be taken into account.
We studied the output generation powers with an optical power meter and studied the spectra with the grating-based single-pixel optical spectrometer Yokogawa AD6370. As the spectrometer has a low acquisition rate and is unable to fully describe the properties of the output light, optical heterodyning was implemented to reveal the fast dynamics of the spectrum. For this, the output radiation is filtered using a 4 GHz tunable optical filter, adjusted to a wavelength of 1550.35 nm. The filtered radiation is then coupled with the radiation of a local oscillator (a semiconductor single-mode tunable laser PurePhotonics PPCL550 with a wavelength of 1550.35 nm and long-term linewidth of 2 MHz) at the balanced photoreceiver with a bandwidth of 20 GHz. The beating signal is measured with an oscilloscope with a 1 GHz bandwidth.
The optical heterodyning method can be utilized for quantitative power measurements of every localized mode, appearing in the spectrum after the proper determination of the system’s sensitivity. For this purpose, an auxiliary single-frequency tunable semiconductor laser was used as a light source with known power, whose radiation was injected into the measurement system instead of a studied random laser (through a 99:1 coupler). By tuning the wavelength of the auxiliary laser, we change its detuning against the local oscillator. For different values of wavelength detuning, the spectral power density was obtained using optical heterodyning and was compared to the known power of the auxiliary laser; in this way, the calibration process was implemented and the response function of the measurement system was obtained in the whole frequency band.
3. Results and Discussion
The laser generation in the proposed configuration starts with a pump power of 3 W. The larger threshold value, compared to a similar scheme based on 32 km of SMF-28 fiber (0.9 W [1]), is due to the smaller Raman gain coefficient and higher losses at the splices of single- and multimode fibers. The net optical conversion efficiency reaches 12% at a pump power of 4.1 W. Please note that the power characteristics in Figure 1b were obtained as a result of short-term measurements (with the typical measurement time of about 0.1 ms). At such times, the average laser power experiences noticeable fluctuations due to the stochastic nature of the generation of random modes, of which the probability of observing is also affected by the presence of external noise. These result in the non-smooth dependence of the output power, as shown in Figure 1b.
The stochastics generation of narrow modes was observed in a wide range of output powers—up to 500 mW (Figure 1b). The presence of narrow modes was revealed in the optical spectrum, measured both with the conventional grating-based spectrometer (Figure 2a) and using the heterodyning technique (Figure 2b). Note that the range of powers supporting the narrow generation is significantly larger compared to the SMF fiber-based laser with 32 km of SMF-28 where, at 100 mW of output power, the generation of narrow modes stops. This expansion of the power range might be attributed, as we will discuss later, to the lower nonlinear coefficient in multimode fibers.
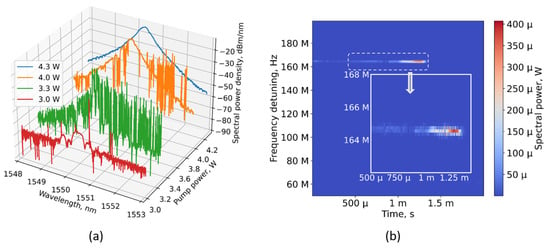
Figure 2.
(a) Generation spectra measured with the grating-based single-pixel spectrometer. (b) An example of the time dynamics of the small part of the output generation spectrum measured with optical heterodyning, presenting a rise in the spectral mode. The pump power is 3.1 W.
The spectrogram, which is the fast dynamics of the spectrum obtained with optical heterodyning, indicates that a single localized mode, once present, evolves in the spectrum for a certain temporal interval until dissipation (see Figure 2b). The characteristic evolution time (hereafter named “mode lifetime”) amounts to 1–10 ms or tens of double cavity passes. The measured spectral width of a single mode is of the order of 1 MHz due to the finite local oscillator’s linewidth. The actual linewidth is expected to be in the kHz range [24].
Notably, there is a huge number of modes appearing at the red-wavelength wing of the spectrum taken with grating-based spectral measurements (see Figure 2a). Earlier, we demonstrated that cascade SBS processes are clearly observed in the generation regime under study [46] and result in power transfer to the longer wavelengths. The effect indicates that some of the narrow modes acquire large enough powers to pass over the threshold of the stimulated Brillouin scattering (SBS) process. Given the core diameter of 50 μm, the fiber losses of 0.23 dB/km and the estimated fundamental mode radius of 7.8 μm, the SBS threshold in a long multimode fiber can be estimated as 14 mW for the fundamental mode propagation [47]. Note that mode coupling should further increase this threshold, hinting at the characteristic powers of the narrow modes. For comparison, the same estimation for the SMF-28 fiber gives 4 mW for the 32 km of the SMF fiber length.
Optical heterodyning allows for the measurement of the optical power, delivered by a single localized mode. With the help of the calibration described in Section 2, we determined the power dynamics of each detected narrow mode. A single mode’s power achieves up to tens of mW, which is in good agreement with the estimations for the SBS threshold. The probability distribution function (PDF) of the maximum powers for different modes has an extremum at approximately 2 mW and a long tail for high-intense modes (see Figure 3a). Notably, the distribution function does not change significantly with the pump power increase; a similar PDF is observed for the highest pump power, supporting the generation of narrow modes. To stress the importance of mode power enhancement in multimode fibers, we studied the same distribution for the narrow modes generated in the standard SMF-28 fiber. In this case, modes comprise substantially less energy. The shape of the distribution is different; there is no long tail in high-power events, and their average corresponds to roughly 500 μW (Figure 3b). One of the possible reasons for higher-power modes in a multimode fiber laser is the higher threshold for the SBS process; thus, the modes are amplified to higher powers before the Brillouin scattering occurs.
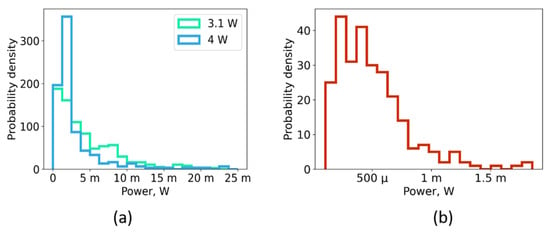
Figure 3.
(a) Probability density for the maximum power of the narrow spectral modes, appearing in the MM-fiber-based random laser for two different pump powers. (b) Probability density of the output powers measured for narrow spectral modes in the laser based on 32 km of standard single-mode SMF-28 fiber.
With optical heterodyning, we measured the distribution of mode lifetimes (Figure 4a). The distribution is quite narrow with a maximum at about 2 ms. Its shape shows a marginal dependence on the pump power. Interestingly, localized mode lifetimes in the multimode fiber are nearly the same as in the single-mode fiber (compare Figure 4a,b). Thus, one may suggest that the lifetimes in a particular experiment are determined mainly by external noises that lead to a change in the spatial distribution of random reflectors, which, in turn, leads to a decrease in the quality factor of a mode and the stopping generation at a given wavelength [24,28].
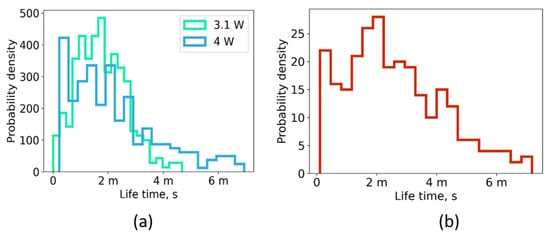
Figure 4.
Lifetimes of narrow modes measured in (a) the MM-fiber-based random laser for two pump powers and (b) the laser based on the standard single-mode SMF-28 fiber.
The joint distributions of lifetimes and powers of the modes evidently differ for different pump powers. At the threshold (with the pump power of 3.1 W), there is only a slight correlation between the mode power and its lifetime. At the higher pump power of 4 W, the distribution indicates that intense modes tend to experience faster demolition, while weaker ones (with powers of 1–2 mW) evolve for longer durations (see Figure 5b; the events with smaller power are more likely to have larger lifetimes). This implicitly corresponds to the suggestion that the higher powers of the modes result in mode destruction because of certain nonlinear processes.
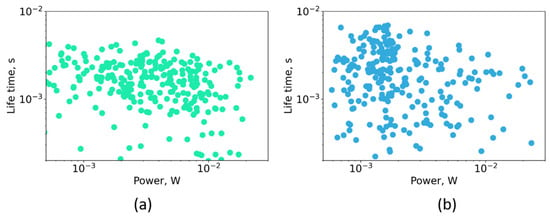
Figure 5.
Distribution of mode lifetime depending on the maximum generation power in the mode for different pump powers: (a) 3.1 W; (b) 4 W.
We performed an analysis of the transverse distribution of the generated narrow modes. The setup under study implies the projection of multimode radiation, propagating towards the output, on the fundamental mode of the SM fiber at splice #2 (see Figure 1a). For this, we measured the power statistics of the spectral modes sequentially for different eccentricities introduced between the cores of the MM fiber and the SM fiber at the output splice (#2 in the Figure 1). Increasing the eccentricity, one can probe the electrical field at the different offsets from the multimode fiber core with the smaller-core SMF-28 fiber. The eccentricity was controlled with the corresponding setting of the fusion splice Fujikura FSM-80S.
We found that, for the larger eccentricities, the power statistics of narrow spectral modes changes drastically, with the maximum achievable powers decreasing. Thus, with a shift between the cores of the order of 10 μm, the measured powers dropped by two orders of magnitude (see Figure 6). To eliminate the possible influence of the output splice losses and effects of the different distributions of different transverse modes of the graded-index multimode fiber [48], we measured losses directly using OTDR and found it to be not higher than 10 dB for the largest eccentricity of 10 μm. Thus, the spectral mode’s profound power decrease for large shifts makes us assume that the generated modes are present, to a greater extent, in transverse modes with smaller mode indexes. In other words, effectively, a clean-up of the transverse distribution of the modes occurs, which has already been proven for Raman fiber lasers with graded-index multimode fibers operating in a highly nonlinear regime [49,50]. Such lasers have been shown to exhibit a tendency toward thermalization (an exponential decrease in the occupancy of transverse modes), which is likely due to the interplay between the linear and nonlinear coupling interactions between the different modes [43].
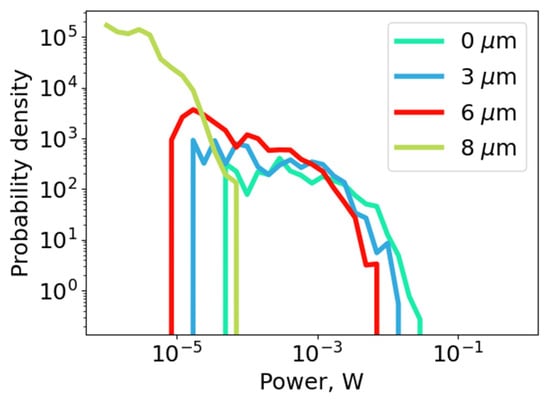
Figure 6.
Probability distribution function of the narrow spectral mode’s power for different eccentricities between MM and SMF-28 fibers in the output splice.
4. Conclusions
We observed narrow spectral modes, generated in the Raman fiber laser, based on a graded-index multimode fiber with random feedback due to Rayleigh backscattering. The modes are easily found in a broad range of the output powers up to 500 mW. Importantly, the output radiation experiences an at least partial Raman clean-up effect, tending to appear in transverse modes with lower mode indexes. The power of a single random mode may exceed 10 mW with the average value of several mW, which is considerably higher compared to the power of random modes in random Raman fiber lasers based on a single-mode fiber.
Author Contributions
Conceptualization, I.D.V.; methodology, I.D.V. and O.A.G.; writing—original draft preparation, I.D.V.; writing—review and editing, I.D.V., O.A.G. and D.V.C.; visualization, I.D.V.; supervision, I.D.V. and D.V.C.; project administration, D.V.C.; funding acquisition, D.V.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Ministry of Science and Higher Education of the Russian Federation (FSUS-2021-0015).
Data Availability Statement
The data underlying the results presented in this paper are not publicly available but may be obtained from the authors upon reasonable request.
Acknowledgments
The authors would like to acknowledge M. D. Gervaziev and A. Y. Kolesnikova for their fruitful discussions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gomes, A.S.L.; Moura, A.L.; de Araújo, C.B.; Raposo, E.P. Recent Advances and Applications of Random Lasers and Random Fiber Lasers. Prog. Quantum Electron. 2021, 78, 100343. [Google Scholar] [CrossRef]
- Lawandy, N.M.; Balachandran, R.M.; Gomes, A.S.L.; Sauvain, E. Laser Action in Strongly Scattering Media. Nature 1994, 368, 436–438. [Google Scholar] [CrossRef]
- Leong, E.S.P.; Chong, M.K.; Yu, S.F.; Pita, K. Sol–Gel ZnO–SiO2 Composite Waveguide Ultraviolet Lasers. IEEE Photonics Technol. Lett. 2004, 16, 2418–2420. [Google Scholar] [CrossRef]
- Noginov, M.A. Solid-State Random Lasers; Springer Series in Optical Sciences; Springer: New York, NY, USA, 2005; Volume 105, ISBN 0-387-23913-8. [Google Scholar]
- de Matos, C.; Menezes, L.D.S.; Brito-Silva, A.; Martinez Gámez, M.; Gomes, A.S.L.; de Araújo, C. Random Fiber Laser. Phys. Rev. Lett. 2007, 99, 153903. [Google Scholar] [CrossRef] [PubMed]
- Gagné, M.; Kashyap, R. Demonstration of a 3 MW Threshold Er-Doped Random Fiber Laser Based on a Unique Fiber Bragg Grating. Opt. Express 2009, 17, 19067. [Google Scholar] [CrossRef] [PubMed]
- Wiersma, D.S. The Physics and Applications of Random Lasers. Nat. Phys. 2008, 4, 359–367. [Google Scholar] [CrossRef]
- Bliokh, Y.; Chaikina, E.I.; Lizárraga, N.N.; Méndez, E.R.; Freilikher, V.; Nori, F. Disorder-Induced Cavities, Resonances, and Lasing in Randomly Layered Media. Phys. Rev. B 2012, 86, 054204. [Google Scholar] [CrossRef]
- Lizárraga, N.; Puente, N.P.; Chaikina, E.I.; Leskova, T.A.; Méndez, E.R. Single-Mode Er-Doped Fiber Random Laser with Distributed Bragg Grating Feedback. Opt. Express 2009, 17, 395. [Google Scholar] [CrossRef]
- Popov, S.M.; Butov, O.V.; Bazakutsa, A.P.; Vyatkin, M.Y.; Chamorovskii, Y.K.; Fotiadi, A.A. Random Lasing in a Short Er-Doped Artificial Rayleigh Fiber. Results Phys. 2020, 16, 102868. [Google Scholar] [CrossRef]
- Niu, Y.; Jia, P.; Su, J.; Wang, J.; An, G.; Ren, Q.; Xiong, J. Tunable Random Fiber Laser Based on Dual-Grating Structure. Photonics 2023, 10, 644. [Google Scholar] [CrossRef]
- Deng, J.; Li, Y.; Shen, M.; Shu, X. Single-Frequency Random Distributed Bragg Reflector Fiber Laser. J. Light. Technol. 2022, 40, 4385–4390. [Google Scholar] [CrossRef]
- Yoshino, T. Simple Theoretical Approach for Spectral Properties of Rayleigh Backscattering Feedback Fibre Lasers. Electron. Lett. 2011, 47, 1040. [Google Scholar] [CrossRef]
- Yin, G.; Saxena, B.; Bao, X. Tunable Er-Doped Fiber Ring Laser with Single Longitudinal Mode Operation Based on Rayleigh Backscattering in Single Mode Fiber. Opt. Express 2011, 19, 25981. [Google Scholar] [CrossRef] [PubMed]
- Pang, Y.; Xu, Y.; Zhao, X.; Qin, Z.; Liu, Z. Stabilized Narrow-Linewidth Brillouin Random Fiber Laser with a Double-Coupler Fiber Ring Resonator. J. Light. Technol. 2022, 40, 2988–2995. [Google Scholar] [CrossRef]
- de Matos, C.J.S.; Popov, S.V.; Taylor, J.R. Short-Pulse, All-Fiber, Raman Laser with Dispersion Compensation in a Holey Fiber. Opt. Lett. 2003, 28, 1891–1893. [Google Scholar] [CrossRef] [PubMed]
- Spirin, V.V.; Bueno Escobedo, J.L.; Korobko, D.A.; Mégret, P.; Fotiadi, A.A. Stabilizing DFB Laser Injection-Locked to an External Fiber-Optic Ring Resonator. Opt. Express 2020, 28, 478. [Google Scholar] [CrossRef]
- Skvortsov, M.I.; Abdullina, S.R.; Podivilov, E.V.; Vlasov, A.A.; Kharasov, D.R.; Fomiryakov, E.A.; Nikitin, S.P.; Treshchikov, V.N.; Babin, S.A. Extreme Narrowing of the Distributed Feedback Fiber Laser Linewidth due to the Rayleigh Backscattering in a Single-Mode Fiber: Model and Experimental Test. Photonics 2022, 9, 590. [Google Scholar] [CrossRef]
- Tovar, P.; von der Weid, J.P.; Wang, Y.; Chen, L.; Bao, X. A Random Optical Parametric Oscillator. Nat. Commun. 2023, 14, 6664. [Google Scholar] [CrossRef]
- Fan, M.; Wang, Z.; Wu, H.; Sun, W.; Zhang, L. Low-Threshold, High-Efficiency Random Fiber Laser with Linear Output. IEEE Photonics Technol. Lett. 2015, 27, 319–322. [Google Scholar] [CrossRef]
- Liu, W.; Ma, P.; Zhou, P. Unified Model for Spectral and Temporal Properties of Quasi-CW Fiber Lasers. J. Opt. Soc. Am. B 2021, 38, 3663. [Google Scholar] [CrossRef]
- Wang, P.; Lin, S.; Zhang, J.; Bao, X.; Ni, L.; Qi, Y.; Wang, Z. Efficient 1054 nm Raman Random Fiber Laser. Photonics 2023, 10, 851. [Google Scholar] [CrossRef]
- Tovar, P.; von der Weid, J.P. Dynamic Evolution of Narrow Spectral Modes in Stochastic Brillouin Random Fiber Lasers. IEEE Photonics Technol. Lett. 2021, 33, 1471–1474. [Google Scholar] [CrossRef]
- Tovar, P.; Temporão, G.; von der Weid, J.P. Longitudinal Mode Dynamics in SOA-Based Random Feedback Fiber Lasers. Opt. Express 2019, 27, 31001. [Google Scholar] [CrossRef] [PubMed]
- Lima, B.C.; Tovar, P.; Moura, A.L.; von der Weid, J.P. Replica Symmetry Breaking in a Rayleigh Backscattering-Based Random Fiber Laser. J. Opt. Soc. Am. B 2023, 40, 1680. [Google Scholar] [CrossRef]
- Kirik, A.E.; Vatnik, I.D.; Churkin, D.V. Direct Measurements of Localized Spectral Modes in Random Distributed Feedback Fiber Laser. Results Phys. 2021, 28, 104651. [Google Scholar] [CrossRef]
- Lima, B.C.; Tovar, P.; von der Weid, J.P. Generalized Extreme-Value Distribution of Maximum Intensities and Lévy-like Behavior in an SOA-Based Random Feedback Laser Emission. J. Opt. Soc. Am. B 2020, 37, 987. [Google Scholar] [CrossRef]
- Bliokh, Y.; Chaikina, E.I.I.; Vatnik, I.D.D.; Churkin, D.V. Temporal Variation of the Spectrum of a Continuously Pumped Random Fiber Laser: Phenomenological Model. J. Opt. Soc. Am. B 2019, 36, 408. [Google Scholar] [CrossRef]
- Fotiadi, A.A. Random Lasers: An Incoherent Fibre Laser. Nat. Photonics 2010, 4, 204–205. [Google Scholar] [CrossRef]
- Boschetti, A.; Taschin, A.; Bartolini, P.; Tiwari, A.K.; Pattelli, L.; Torre, R.; Wiersma, D.S. Spectral Super-Resolution Spectroscopy Using a Random Laser. Nat. Photonics 2020, 14, 177–182. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, S.; Zheng, C.; Zhang, W. Coherent Random Fiber Laser-Enabled Super-Resolution Spectroscopy. ACS Photonics 2023, 10, 2670–2678. [Google Scholar] [CrossRef]
- Babin, S.A.; Churkin, D.V.; Ismagulov, A.E.; Kablukov, S.I.; Podivilov, E.V. Spectral Broadening in Raman Fiber Lasers. Opt. Lett. 2006, 31, 3007–3009. [Google Scholar] [CrossRef] [PubMed]
- Kablukov, S.I.; Zlobina, E.A.; Podivilov, E.V.; Babin, S.A. Output Spectrum of Yb-Doped Fiber Lasers. Opt. Lett. 2012, 37, 2508. [Google Scholar] [CrossRef] [PubMed]
- Babin, S.A.; Dontsova, E.I.; Kablukov, S.I. Random Fiber Laser Directly Pumped by a High-Power Laser Diode. Opt. Lett. 2013, 38, 3301–3303. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Fan, C.; Yao, T.; Xiao, H.; Leng, J.; Zhou, P.; Nemov, I.N.; Kuznetsov, A.G.; Babin, S.A. Brightness Enhancement in Random Raman Fiber Laser Based on a Graded-Index Fiber with High-Power Multimode Pumping. Opt. Lett. 2021, 46, 1185. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.-H.; Haig, H.; Wu, Y.; Ziegler, Z.; Wise, F. Accurate Modeling of Ultrafast Nonlinear Pulse Propagation in Multimode Gain Fiber. J. Opt. Soc. Am. B 2023, 40, 2633. [Google Scholar] [CrossRef]
- Dostovalov, A.; Wolf, A.; Munkueva, Z.; Skvortsov, M.; Abdullina, S.; Kuznetsov, A.; Babin, S. Continuous and Discrete-Point Rayleigh Reflectors Inscribed by Femtosecond Pulses in Singlemode and Multimode Fibers. Opt. Laser Technol. 2023, 167, 109692. [Google Scholar] [CrossRef]
- Murray, M.J.; Davis, A.; Redding, B. Multimode Fiber Φ-OTDR with Holographic Demodulation. Opt. Express 2018, 26, 23019. [Google Scholar] [CrossRef]
- Wright, L.G.; Wu, F.O.; Christodoulides, D.N.; Wise, F.W. Physics of Highly Multimode Nonlinear Optical Systems. Nat. Phys. 2022, 18, 1018–1030. [Google Scholar] [CrossRef]
- Yablon, A.D. Optical Fiber Fusion Splicing; Springer Series in Optical Sciences; Springer: Berlin/Heidelberg, Germany, 2005; Volume 103, ISBN 978-3-540-23104-2. [Google Scholar]
- Hurand, S.; Chauny, L.-A.; El-Rabii, H.; Joshi, S.; Yalin, A.P. Mode Coupling and Output Beam Quality of 100–400 Μm Core Silica Fibers. Appl. Opt. 2011, 50, 492. [Google Scholar] [CrossRef]
- Röhrer, C.; Kleem, G.; Ahmed, M.A.; Graf, T. Analysis of Fundamental-Mode Beam Transport in Highly Multimode Fibers. J. Light. Technol. 2017, 35, 3637–3642. [Google Scholar] [CrossRef]
- Kharenko, D.S.; Gervaziev, M.D.; Kuznetsov, A.G.; Podivilov, E.V.; Wabnitz, S.; Babin, S.A. Mode-Resolved Analysis of Pump and Stokes Beams in LD-Pumped GRIN Fiber Raman Lasers. Opt. Lett. 2022, 47, 1222. [Google Scholar] [CrossRef] [PubMed]
- Sidelnikov, O.S.; Kuznetsov, A.G.; Kharenko, D.S.; Gervaziev, M.D.; Podivilov, E.V.; Fedoruk, M.P.; Wabnitz, S.; Babin, S.A. Transverse Mode Distribution in Multimode Diode-Pumped Raman Fiber Laser. J. Opt. Soc. Am. B 2023, 40, 3269. [Google Scholar] [CrossRef]
- Turitsyn, S.K.; Babin, S.A.; Churkin, D.V.; Vatnik, I.D.; Nikulin, M.; Podivilov, E.V. Random Distributed Feedback Fibre Lasers. Phys. Rep. 2014, 542, 133–193. [Google Scholar] [CrossRef]
- Kirik, A.E.; Aprelov, N.A.; Vatnik, I.D.; Churkin, D.V. Observation of Cascade Brillouin Processes in Random Distributed Feedback Raman Fiber Lasers. In Proceedings of the Quantum and Nonlinear Optics IX; He, Q., Li, C.-F., Kim, D.-S., Eds.; SPIE: Bellingham, WA, USA, 2023; p. 23. [Google Scholar]
- Mocofanescu, A.; Wang, L.; Jain, R.; Shaw, K.D.; Gavrielides, A.; Peterson, P.; Sharma, M.P. SBS Threshold for Single Mode and Multimode GRIN Fibers in an All Fiber Configuration. Opt. Express 2005, 13, 2019. [Google Scholar] [CrossRef]
- Popoff, S.M.; Gostev, P. Simple Module to Find Numerically Propagation Mode Profiles and Propagation Constants of Multimode Fibers of Arbitrary Radial Index Profiles. 2023. Available online: https://zenodo.org/records/5524192 (accessed on 1 December 2023).
- Terry, N.B.; Alley, T.G.; Russell, T.H.; Engel, K.T. An Explanation of SRS Beam Cleanup in Graded-Index Fibers and the Absence of SRS Beam Cleanup in Step-Index Fibers. Opt. Express 2007, 15, 17509. [Google Scholar] [CrossRef]
- Zlobina, E.A.; Kablukov, S.I.; Wolf, A.A.; Nemov, I.N.; Dostovalov, A.V.; Tyrtyshnyy, V.A.; Myasnikov, D.V.; Babin, S.A. Generating High-Quality Beam in a Multimode LD-Pumped All-Fiber Raman Laser. Opt. Express 2017, 25, 12581. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).