1. Introduction
Linear chirp generation in an optical field has widespread applications, such as optical pulse compression [
1] and temporal Fourier processing based on time lenses [
2,
3,
4]. Since the chirp is the time derivative of the phase, a linear chirp can be achieved via electro-optic phase modulation with parabolic drive signals or cross-phase modulation with a parabolic pump pulse in nonlinear elements [
5,
6]. Therefore, parabolic waveform generation consequently has attracted considerable attention.
Many schemes for parabolic pulse generation have been reported in recent decades. One method is implemented by the envelope revolution through propagation in optical fibers. This scheme takes advantage of the self-similar propagation of short pulses, in which a pulse with a parabolic intensity profile propagates in fibers with normal group-velocity dispersion (GVD) and strong nonlinearity. However, this process is greatly limited by third-order dispersion and the fiber parameters needs to be precisely controlled [
7,
8]. Another scheme involves generating bright and dark parabolic pulses through an array waveguide. In this method, the intensity and phase of each harmonic component of an optical short pulse are manipulated line-by-line in the spectral domain, finally synthesizing a parabolic pulse in the time domain because of the mapping relationship from the frequency domain to the time domain. However, the stability and complexity limit its application [
9]. Some schemes for parabolic pulse generation based on the Mach–Zehnder modulator (MZM) are also reported. One proposal is that a Gaussian pulse is stretched to realize the wavelength-to-time mapping, and the mapped signal is modulated by an MZM with an appropriately designed drive signal to obtain a parabolic pulse [
10]. In addition, the modulation characteristics of MZMs can also be utilized for parabolic pulse generation. In this case, the transmission curve of an MZM can be mapped into the time domain by applying a drive signal with a linear edge, e.g., a triangular pulse, which eventually outputs a parabolic pulse because the peak or valley of the transmission curve of an MZM approaches a parabolic function [
11]. In order to generate accurate parabolic pulses, a simple scheme for parabolic pulse generation is demonstrated, in which a parabola can be expressed as a quadratic function and consequently implemented by the product of two linear functions. Although this method is mathematically intuitionistic, the system is relatively complicated because of the cascade of multiple modulators [
12]. In [
13], an approach for parabolic pulse generation based on an optical fiber loop mirror is proposed and experimentally demonstrated. This approach is able to flexibly achieve a higher operation bandwidth, such as parabolic pulse generation with repetition frequencies of 8, 9 and 10 GHz. However, due to the use of a non-reciprocal Sagnac interferometer and a highly nonlinear fiber (HNLF), the polarization stability of the system and power requirements are relatively high.
In this paper, a simpler parabolic waveform generator based on the chirp characteristics of a DML is proposed. The desired chirp signal can be obtained by the carrier dynamics of a DML under a triangular drive signal. By setting the modulation depth appropriately, the chirped signal can be linearly mapped into the time domain via an optical filter with a linear edge. Finally, the mapped signal is spontaneously multiplied by the envelope function of the modulated signal to successfully generate a dark, bright parabolic pulse and a frequency-doubled bright pulse, which agrees with the theoretical expectation well.
2. Operation Principle
Theoretically, when a DML is driven by an electrical pulse
, an optical signal with an intensity of
with a chirp of
will be output. The chirp of the output light field is given in [
14]
where
is the line-width enhancement factor of the laser,
is the envelope of drive signal and
is the adiabatic chirp coefficient. In the expression of
,
is the optical confinement factor,
is the gain saturation factor of the laser,
is the volume of the active region,
is the differential quantum efficiency,
h is the Planck constant and
is the optical angular frequency. Since all of the parameters are fixed for a certain DML,
is a constant. In Equation (
1), the first term denotes the transient chirp and the second term represents the adiabatic chirp. When the laser bias current is much larger than the threshold, the transient chirp term can be neglected and the total chirp can be simplified to [
15]
Equation (
2) shows that the chirp
is a linear function of the drive signal, but it has the opposite sign to
. As we know, an optical filter with a linear filtering window can be regarded as a frequency discriminator, which can linearly map the chirp to intensity [
16]. Its transmission curve is shown in
Figure 1.
The corresponding spectral transfer function is written as
where K and −K are the slope of the rising and falling edges of the filtering window, respectively. Here, the conditions of the central wavelength
of the chirped signal located at the linear edge of the filtering window and its bandwidth completely covered by the linear part are assumed. After passing through such a filter, the output of the chirped signal can be deduced as [
16]
where
or
,
or
are constants. Therefore, the signal after the frequency discriminator is the multiplication of two functions, which are the envelope function and the chirp function. The output expression
or
can be understood as a mapping of chirp to intensity. An interesting thing is that when the optical carrier is placed on the rising edge of the filter window, the chirp-to-intensity mapping gives the opposite phase, while it gives the same phase when placing the optical carrier on the falling edge of the filtering window. At the same time, placing the carrier at different heights of the filtering window edge results in different direct currents (DCs) on the mapped intensity signal. Obviously, Equation (
4) implies that a parabolic pulse can be achieved once the input signal
is a triangular pulse.
As described by Equation (
2), a modulated triangular pulse has an intensity profile of
and a chirp of
if the laser bias current is much larger than the threshold. Meanwhile, assuming that there is a filter with a sufficient filtering window width, placing the carrier at different positions will result in countless chirp-to-intensity mappings. As can be seen from Equation (
4), there are two typical chirp-to-intensity mappings,
and
, which are represented as
and
, respectively. Specifically, placing the optical carrier at two different positions on the rising edge of the filtering window yields two special chirp-to-intensity mappings. Thus, three types of parabolic pulses can be generated.
In general, a normalized triangular pulse stream
in the first period can be written as [
17]:
where
T is the period of the triangular pulse.
Case 1 is shown in
Figure 2. The optical carrier is placed on the rising edge of the filtering window, where
and
are out of phase. At this point, by adjusting the position of the central wavelength in the filtering window, there are two special values, whose corresponding chirp-to-intensity mappings are represented as
and
.
When the optical carrier is located at the upper part of the rising edge of the filtering window, one adjusts the window to change the value in Equation (
4) so that the DC difference between the mapped intensity
and
is
, as shown in
Figure 2a.
Mathematically,
features the triangular profile, so it can be expressed as:
Since the signal originally has an envelope of
, after the filter, the composite signal is the spontaneous multiplication of
and
, which can be expressed as:
From Equation (
7), the parabolic expressions for the first and second half periods are the same, and the coefficient of the quadratic term is negative. The curve changes from minimum to maximum in the interval
and from maximum to minimum in the interval
, resulting in a bright parabola with a vertex at
. This indicates the generation of a bright parabolic pulse stream with the same period as the triangular drive signal. Another point is that the amplitude of the mapped intensity does not affect the shape of the multiplied parabolic pulse.
Then, by slightly shifting the filtering window, the optical carrier is located in the lower part of the rising edge of the filtering window. In this case, the mapped intensity
has the same DC as
and gives an intensity function of
with an inverse phase, as shown in
Figure 2b. At this time,
and its multiplication by
can be expressed as:
It can be seen from Equation (
9) that the coefficient of the quadratic term is negative. One interesting thing is that there are two parabolic pulses within the time interval of
T, which indicates that the generated parabolic pulse stream has a repetition frequency twice that of the triangular drive signal.
Similarly, when the optical carrier is placed on the falling edge of the filtering window, case 2 is achieved, as shown in
Figure 3. The mapped intensity
and
are out of phase; furthermore, the DC between them is the same.
In this case,
and its multiplication by
can be expressed as:
From Equation (
11), it can be seen that the coefficient of the quadratic term parabolas is positive, which gives a dark parabolic pulse. The function value in the interval
increases from a minimum to a maximum, and decreases from the same maximum to the same minimum in the interval
. Thus, Equation (
11) presents a periodic dark parabolic stream with the same period of the triangular drive signal.
As one can see from Equations (7), (9) and (11), all three situations are parabolas with different characteristics. The first case generates bright parabolic pulses of fundamental and double frequencies, while the second case generates a dark parabolic pulse. In particular, by comparing
Figure 2a,b, the multiplication results present obvious differences with different DCs because a small fluctuation in the parameters for the multiplication operation can have a significant impact on the results.
Mathematically, the Fourier expansion of a periodic triangular signal is [
18]
where
and
are two constants and
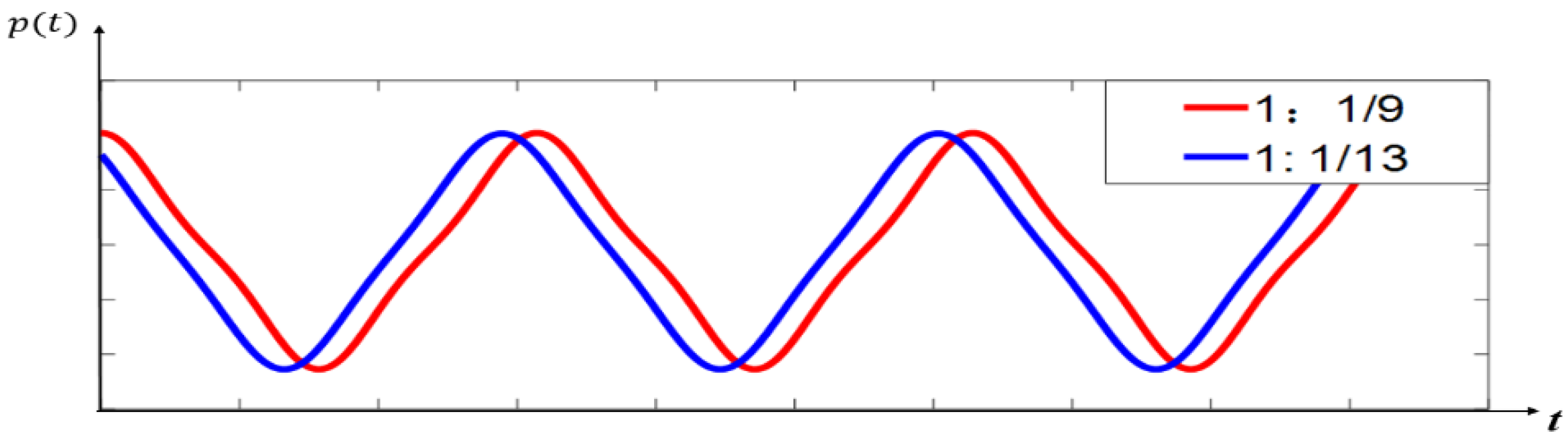
is the fundamental angular frequency. Usually, a triangular waveform with second-order approximation is good enough. However, in order to obtain a triangular pulse with a better linear edge, one can adjust the coefficient ratio of harmonic components appropriately within a certain tolerance range, and the optimized triangular waveform can be expressed as
By comparing the coefficient ratio of harmonic components (1:1/9 and 1:1/13), as seen in
Figure 4, the linear edge of the optimized triangular waveform is greatly improved.
To further evaluate the quality of the optimized and standard waveform, we introduce the goodness of fit in mathematical statistics to evaluate the results, which is defined as the fitting degree between the regression line and the observed value and expressed as
where
is the calculated value,
is the average value of the calculated value and
is the standard value. If
is closer to 1, the fitting effect will be better [
19,
20]. The optimized triangular waveform is 0.9696. Starting from the triangular pulse, the
values of the generated three parabolic waveforms are 0.9967, 0.9967 and 0.9754, respectively, which shows that the obtained parabolic pulses are acceptable.
3. Experiments and Results
To verify the feasibility of the proposed parabolic waveform generator, an experimental demonstration with the configuration shown in
Figure 5 was implemented. The system mainly includes a triangular pulse generator, a DML and an optical filter. In this system, the distributed feedback DML (DFB-DML) is the key device, and it has a modulation bandwidth of 18 GHz, a threshold current of 30 mA, an output power of 11 dBm and a cavity length of about 200 um. To satisfy the operation requirements mentioned before, the bias current was set at 80 mA. The frequency bandwidth of the used photodetector (PD, Finisar XPDV210R) is 50 GHz.
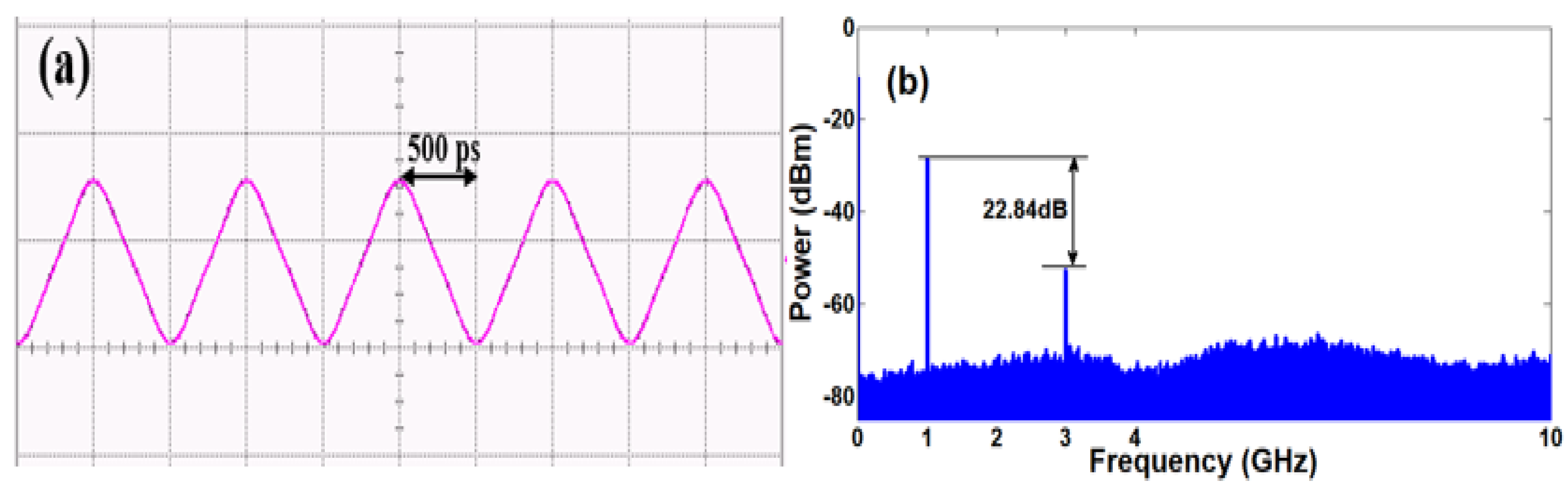
Firstly, a triangular waveform generator outputs a 1 GHz drive signal with second-order approximation. The corresponding waveform and electrical spectrum are monitored by an oscilloscope (86100D Infiniium DCA−X, Agilent, Santa Clara, CA, USA) and an electrical spectrum analyzer (ESA, Agilent N9010A EXA), respectively, as shown in
Figure 6a,b. From the electrical spectrum, the power ratio between the first-order component and third-order component is 22.84 dB, which agrees with the expected coefficient ratio of 1:1/13.
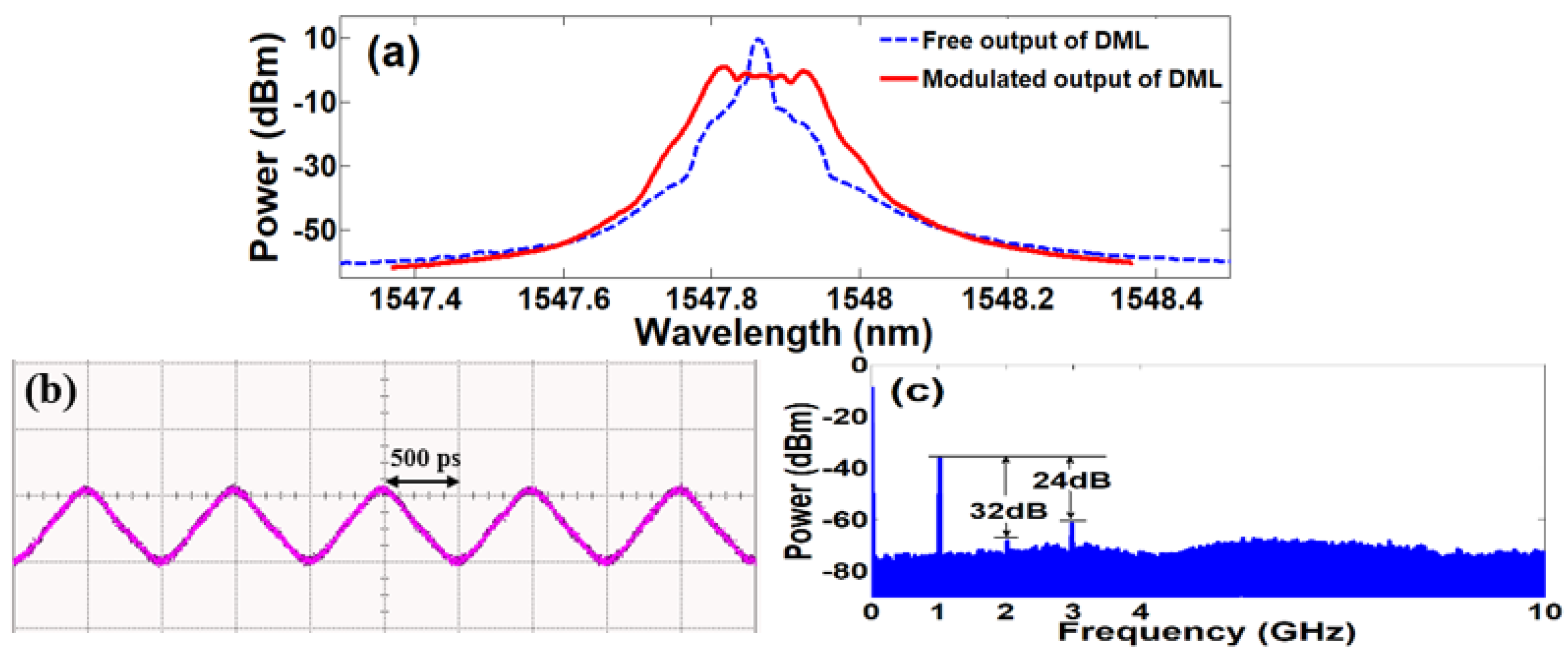
When the signal is applied on a DML with a wavelength of 1547.86 nm, optical triangular pulses with a certain chirp are generated, the optical spectrum of which was measured via an optical spectrum analyzer (OSA, YOKOGAWA AQ6370C), as shown in
Figure 7a. Waveform and electrical spectra are given in
Figure 7b,c. Clearly, the modulated signal is a triangular pulse, which is the same as the input signal. A Gaussian optical filter (Optical Tunable Filter, OTF−320) can linearly map the chirp signal to the intensity signal in the time domain because it has a quasi-linear edge. For the three different cases described in
Section 2, experiments were carried out one by one. In case 1, by setting the carrier on the upper part of the rising edge of the filter, a bright parabolic waveform can be output, as given by
Figure 8b.
At the same time, the carrier was placed at the lower part of the rising edge of the filter, which leads to a bright parabolic pulse with a doubled frequency, as shown in
Figure 9. Finally, for case 2, by fine tuning the filter window, the optical carrier is located at the falling edge of the filter, as shown in
Figure 10a. It should be noted that we mainly adjust the window of the filter to obtain the desired filtering position during the operation, because the wavelength of the DML is fixed. This process transforms the triangular pulse to a dark parabolic pulse.
Figure 10b,c gives the corresponding waveform and electrical spectra. The experimental result is consistent with the standard parabolic waveform.
Figure 11 shows the tunability of the system. Dark, bright and the doubled bright parabolic waveforms with repetition frequencies of 2 and 3 GHz are generated under 2 GHz and 3 GHz triangular drive signals, respectively. From the experimental results shown above, this scheme presents good flexibility and results in all cases.